A Sustainable Supply Chain Model with a Setup Cost Reduction Policy for Imperfect Items under Learning in a Cloudy Fuzzy Environment
Abstract
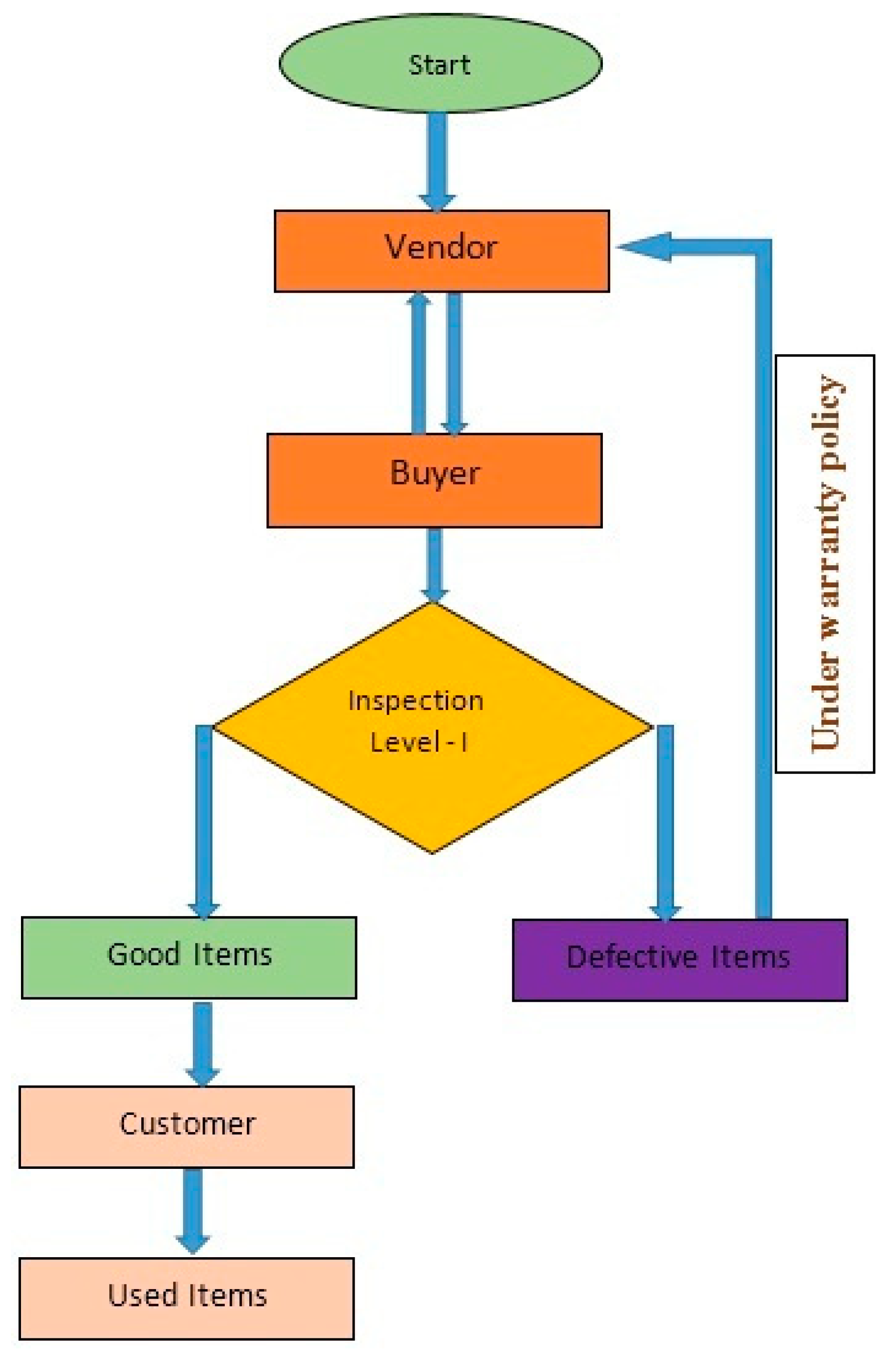
:1. Short Outlook of the Abstract through a Flowchart
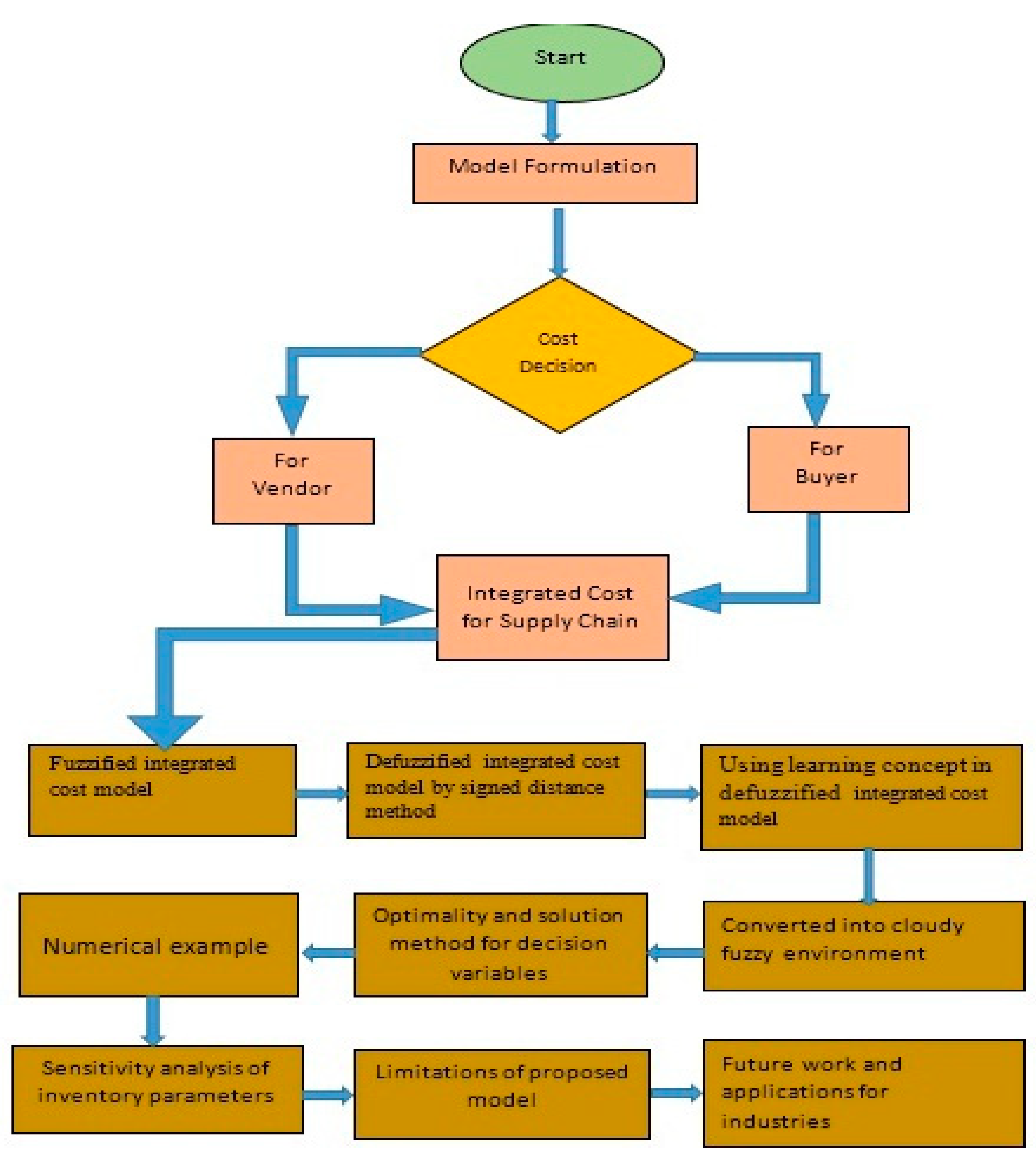
2. Explanation of the Proposed Model through a Flowchart
3. Basic Introduction
3.1. EOQ and Imperfection Literature Review
3.2. Carbon Emission Literature Review
3.3. Supply Chain Literature Review
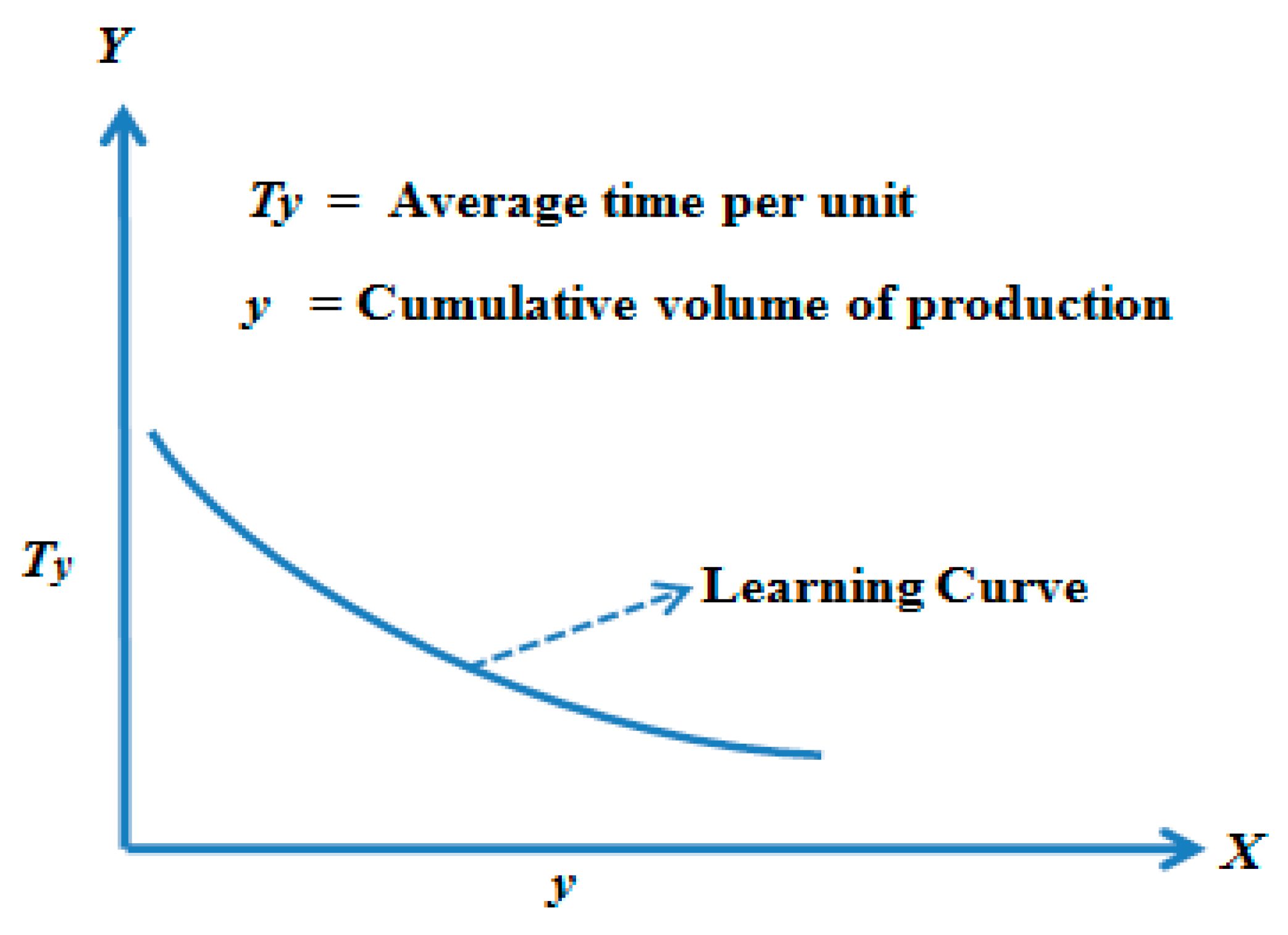
3.4. Learning Literature Review
3.5. Fuzzy and Cloudy Fuzzy Literature Review
3.6. Our Proposed Work with Research Gap
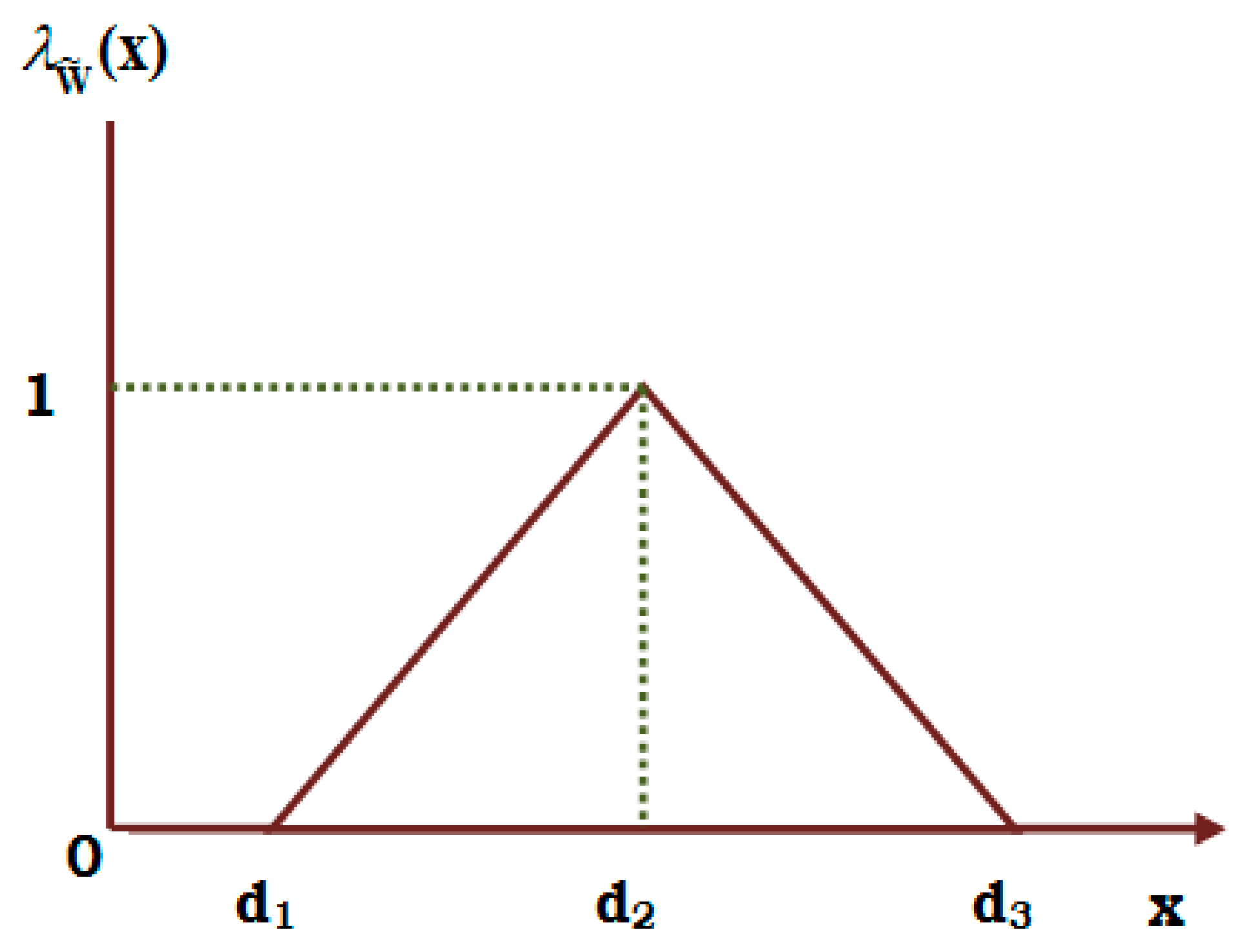
3.7. Basic Definitions
4. Model’s Assumptions and Notations
4.1. Notations for the Model Parameters
| D | Demand rate of the items (unit per year); |
| Demand rate in fuzzy environment (unit per year); | |
| Upper deviation of demand rate in fuzzy environment (unit per year); | |
| Lower deviation of demand rate in fuzzy environment (unit per year); | |
| Triangular fuzzy number for the demand rate; | |
| M (Decesion Variable) | Order quantity in fuzzy environment (units); |
| B (Decesion Variable) | Backorder lot size in fuzzy environment (units); |
| W | Production rate of items (unit per year); |
| N | Number of freights; |
| α | Defective percentage in the ordered lot with uniform probability density function f(α) |
| Ab | Ordering cost from buyer side (USD per order); |
| hb | Holding cost from buyer side (USD per unit per year); |
| Sb | Inspection cost from buyer side (USD per year); |
| Cb | Backordering cost from buyer side (USD per year); |
| hv | Holding cost from vendor side (USD per unit per year); |
| Fc | Fixed carbon emission cost from vendor side (USD per transport); |
| Vc | Variable carbon emission cost from vendor side (USD per unit); |
| FT | Fixed transportation cost from vendor side (USD per transport); |
| VT | Variable transportation cost from vendor side (USD per unit); |
| AV | Initial setup cost from vendor side (USD per setup); |
| µ | Investment in the setup cost from vendor side; |
| AV1 (µ) where π is known input parameter | Setup cost from vendor side (USD per setup) after investment; |
| Ip = | A particular investment; |
| ωv = | Unit warranty cost from vendor side for imperfect-quality items; |
| ωm = | Waste management cost for waste-quality items; |
| l = | Learning rate; |
| n = | Number of shipments |
| Ψb (N, M, B) | Total inventory cost for the buyer (USD) side; |
| ΨbF (N, M, B) | Total fuzzy inventory cost for the buyer (USD) side; |
| ΨbdF (N, M, B) | Total defuzzified inventory fuzzy cost for the buyer (USD) side; |
| ΨV (N, M, µ) | Total inventory cost for the vendor (USD) side; |
| ΨVF (N, M, µ) | Total fuzzy inventory cost for the vendor (USD) side; |
| ΨVdF (N, M, µ) | Total defuzzified inventory fuzzy cost for the vendor (USD) side; |
| ΨI (N, M, B, µ) | Total integrated inventory cost for the supply chain (USD); |
| ΨIF (N, M, B, µ) | Total integrated fuzzy inventory cost for the supply chain (USD); |
| ΨIdF (N, M, B, µ) | Total defuzzified integrated fuzzy inventory cost for the supply chain (USD); |
| ΨIdFL(N, M, B, µ) | Total defuzzified integrated fuzzy inventory cost for the supply chain (USD) under learning effect and cloudy fuzzy environment. |
4.2. Assumptions for the Model Parameters
- ➢
- In this proposed model, a single vendor, a single buyer and one type of item are assumed in the supply chain.
- ➢
- During transportation, lead time is known and constant for the supply chain.
- ➢
- Shortages are completely backlogged.
- ➢
- In the proposed supply chain model, it is considered that the demand rate of the item is imprecise in nature and also treated as a triangular fuzzy number.
- ➢
- The learning effect is involved in the lower and upper deviation of the fuzzy demand rate under a cloudy fuzzy environment.
- ➢
- Waste management costs are included for waste products from the buyer side.
- ➢
- Fixed and variable costs of carbon emission are included from the vendor side.
- ➢
- The vendor includes the warranty cost () for each imperfect-quality item.
- ➢
- The vendor sells the imperfect-quality item in another market at a low price.
- ➢
- The inspection process is considered as lead time for the supply chain.
- ➢
- The buyer inspects the whole received lot from the vendor for each cycle length and also includes the inspection cost for this task.
- ➢
- The cost of keeping for the buyer decreases as shipping increases, , because the holding cost is inversely related to the shipment, where is the fixed part of the holding cost, is the variable holding cost (this part decreases when shipment () increases) and is a constant parameter.
- ➢
- The cost of ordering for the buyer decreases as shipment increases, , because the ordering cost is inversely related to the shipment, where is the fixed part of the ordering cost, is the variable ordering cost (this part decreases when shipment () increases) and is a constant parameter where and are the fixed ordering cost, is the shipment and is a supporting parameter.
- ➢
- A particular investment is included for reducing the setup cost, and it can be defined, , is a known input parameter and is investment in the setup cost from the vendor side. This consideration shows that an increase in investment amount for the supporting of the supply chain lowers the setup cost because the relation between setup cost and investment is inverse.
- ➢
- The lot size of the item includes defectives. The rate of defectives follows the probability density function (pdf), and it is also presumed that , so as to ensure the manufacturing capacity is enough to fulfill the annual demand of the buyer.
- ➢
- The production process is managed by the vendor, and the produced goods are sent to the buyer in numerous replacements without undergoing an initial screening test. This results in the delivery of a certain quantity of faulty items, which are distributed uniformly.
- ➢
- The carbon emissions resulting from numerous shipments and transportation are considered. We have included a tax for carbon emissions.
- ➢
- The buyer includes the waste management cost due to waste products and reduces the loss from this cost.
5. Mathematical Formulation of Proposed Model
5.1. Theoretical Strategy of the Proposed Model
5.2. Problem Definition of Proposed Model
5.3. Vendor’s Decision Strategy Outlook
- i.
- Transportation cost: The vendor is responsible for the shipment of the items as per the deal, and the total transportation cost is the sum of the fixed and variable transportation costs, which are given as follows:
- ii.
- Carbon emission cost: The vendor includes the carbon emission cost due to the shipping of the products from the vendor’s place to the buyer’s place, and the total carbon emission cost is the sum of fixed and variable carbon emission costs.
5.4. Buyer’s Decision Strategy Outlook
5.5. Integrated Perspective of Vendor and Buyer for the Supply Chain
5.6. Proposed Supply Chain Model under Fuzzy Environment
5.7. Proposed Supply Chain Model under Learning in Fuzzy Environment
5.8. Proposed Supply Chain Model under Learning in Cloudy Fuzzy Environment
5.9. Optimality, Solution Method and Convexity of the Total Integrated Fuzzy Cost
5.10. Algorithm and Solution Method for
5.11. The Buyer’s Decision Strategy (Individually)
5.12. The Vendor’s Decision Strategy (Individually)
5.13. Numerical Analysis
5.14. Observation and Discussion of the Proposed Model
6. Sensitivity Analysis
Observations and Managerial Insights
- Impact of buyer’s holding cost
- Impact of vendor’s holding cost
- Impact of fixed transportation cost
- Impact of fixed carbon emission cost
- Impact of variable transportation cost
- Impact of variable carbon emission cost
- Impact of setup cost reduction parameter
- Impact of learning rate
- Impact of cloudy demand parameters
- Impact of upper and lower deviations of cloudy demand rate
- Impact of percentage of defectives
- Impact of unusable percentage of defectives
7. Concluding Remarks
7.1. Conclusions
7.2. Limitation and Future Scope of Our Present Study
7.3. Application of Our Present Study
7.4. Research Limitations of Our Proposed Study
7.5. Practical Implications and Future Scope
7.6. Social Implications of Our Proposed Study
7.7. Originality of Our Present Study
Funding
Data Availability Statement
Conflicts of Interest
References
- Salameh, M.K.; Jaber, M.Y. Economic production quantity model for items with imperfect quality. Int. J. Prod. Econ. 2000, 64, 59–64. [Google Scholar] [CrossRef]
- Biel, K.; Glock, C.H. Systematic literature review of decision support models for energy-efficient production planning. Comput. Ind. Eng. 2016, 101, 243–259. [Google Scholar] [CrossRef]
- Jaggi, C.K.; Mittal, M. Economic order quantity model for deteriorating items with imperfect quality. Int. J. Ind. Eng. Comput. 2011, 32, 107–113. [Google Scholar]
- Wee, H.M.; Yu, J.; Chen, M.C. Optimal inventory model for items with imperfect quality and shortage backordering. Omega 2007, 35, 7–11. [Google Scholar] [CrossRef]
- Eroglu, A.; Ozdemir, G. An economic order quantity model with defective items and shortages. Int. J. Prod. Econ. 2007, 106, 544–549. [Google Scholar] [CrossRef]
- Roy, M.D.; Sana, S.S.; Chaudhuri, K. An optimal shipment strategy for imperfect items in a stock-out situation. Math. Comput. Model. 2011, 54, 2528–2543. [Google Scholar] [CrossRef]
- Sarkar, B. Supply chain coordination with variable backorder, inspection and discount policy for fixed lifetime products. Math. Probl. Eng. 2016, 20, 1–14. [Google Scholar] [CrossRef]
- Jaggi, C.K.; Yadavalli, V.S.S.; Sharma, A.; Tiwari, S. A fuzzy EOQ model with allowable shortage under different trade credit terms. Appl. Math. Inf. Sci. 2016, 10, 785–805. [Google Scholar] [CrossRef]
- Sebatjane, M.; Adetunji, O. Economic order quantity model for growing items with imperfect quality. Oper. Res. Perspect. 2019, 6, 100088. [Google Scholar] [CrossRef]
- Öztürk, H. A deterministic production inventory model with defective items, imperfect rework process and shortages backordered. Int. J. Oper. Res. 2020, 39, 237–261. [Google Scholar] [CrossRef]
- Gautam, P.; Khanna, A.; Jaggi, C.K. An integrated green supply chain model with product recovery management towards a cleaner system. J. Clean. Prod. 2021, 320, 128850. [Google Scholar] [CrossRef]
- Jayaswal, M.K.; Mittal, M. Learning-based inventory model for deteriorating imperfect quality items under inflation. Int. J. Manag. Pract. 2022, 15, 429–444. [Google Scholar] [CrossRef]
- Narang, P.; De, P.K. An imperfect production-inventory model for reworked items with advertisement, time and price dependent demand for non-instantaneous deteriorating item using genetic algorithm. Int. J. Math. Oper. Res. 2023, 24, 53–77. [Google Scholar] [CrossRef]
- Taleizadeh, A.A.; Naghavi-Alhoseiny, M.S.; Cárdenas-Barrón, L.E.; Amjadian, A. Optimization of price, lot size and backordered level in an EPQ inventory model with rework process. RAIRO-Oper. Res. 2024, 58, 803–819. [Google Scholar] [CrossRef]
- Tang, S.; Wang, W.; Yan, H.; Hao, G. Low carbon logistics: Reducing shipment frequency to cut carbon emissions. Int. J. Prod. Econ. 2015, 164, 339–350. [Google Scholar] [CrossRef]
- Wang, Q.; Wu, J.; Zhao, N.; Zhu, Q. Inventory control and supply chain management: A green growth perspective. Resour. Conserv. Recycl. 2019, 145, 78–85. [Google Scholar] [CrossRef]
- Zhu, L.; Zhou, J.; Yu, Y.; Zhu, J. Emission-dependent production for environment aware demand in cap-and-trade system. J. Adv. Manuf. Syst. 2017, 16, 67–80. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, P.; Li, Z.; Yu, H. Modeling the effects of low-carbon emission constraints on mode and route choices in transportation networks. Procedia-Soc. Behav. Sci. 2013, 96, 329–338. [Google Scholar] [CrossRef]
- Sarkar, B.; Ganguly, B.; Sarkar, M.; Pareek, S. Effect of variable transportation and carbon emission in a three-echelon supply chain model. Transp. Res. Part E Logist. Transp. Rev. 2016, 91, 112–128. [Google Scholar] [CrossRef]
- Tiwari, S.; Daryanto, Y.; Wee, H.M. Sustainable inventory management with deteriorating and imperfect quality items considering carbon emission. J. Clean. Prod. 2018, 192, 281–292. [Google Scholar] [CrossRef]
- Gautam, P.; Khanna, A. An imperfect production inventory model with setup cost reduction and carbon emission for an integrated supply chain. Uncertain Supply Chain. Manag. 2018, 6, 271–286. [Google Scholar] [CrossRef]
- Thomas, A.; Mishra, U. A sustainable circular economic supply chain system with waste minimization using 3D printing and emissions reduction in plastic reforming industry. J. Clean. Prod. 2022, 345, 131128. [Google Scholar] [CrossRef]
- Sharma, N.; Jain, M.; Sharma, D. ANFIS and metaheuristic optimization for green supply chain with inspection and rework. arXiv 2024, arXiv:2401.09154. [Google Scholar]
- Nobil, E.; Cárdenas-Barrón, L.E.; Garza-Núñez, D.; Treviño-Garza, G.; Céspedes-Mota, A.; de Jesús Loera-Hernández, I.; Nobil, A.H. Sustainability inventory management model with warm-up process and shortage. Oper. Res. Perspect. 2024, 12, 100297. [Google Scholar] [CrossRef]
- Ruidas, S.; Seikh, M.R.; Nayak, P. K A production inventory model with interval-valued carbon emission parameters under price-sensitive demand. Compu. Ind. Eng. 2021, 154, 107154. [Google Scholar] [CrossRef]
- Jaber, M.Y.; Goyal, S.K.; Imran, M. Economic production quantity model for items with imperfect quality subject to learning effects. Int. J. Prod. Econ. 2008, 115, 143–150. [Google Scholar] [CrossRef]
- Khan, M.; Jaber, M.Y.; Wahab, M.I.M. Economic order quantity model for items with imperfect quality with learning in inspection. Int. J. Prod. Econ. 2010, 124, 87–96. [Google Scholar] [CrossRef]
- Bazan, E.; Jaber, M.Y.; Zanoni, S. Supply chain models with greenhouse gases emissions, energy usage and different coordination decisions. Appl. Math. Model. 2015, 39, 5131–5151. [Google Scholar] [CrossRef]
- Sahoo, S.; Acharya, M.; Patnaik, S. Sustainable intuitionistic fuzzy inventory models with preservation technology investment and shortages. Int. J. Reason.-Based Intell. Syst. 2022, 14, 8–18. [Google Scholar] [CrossRef]
- Rajput, N.; Pandey, R.K.; Chauhan, A. Fuzzy optimization of a Production Model with CNTFN Demand Rate under Trade-Credit Policy. IJMOR 2022, 21, 200–220. [Google Scholar] [CrossRef]
- Gautam, P.; Kishore, A.; Khanna, A.; Jaggi, C.K. Strategic defect management for a sustainable green supply chain. J. Clean. Prod. 2019, 233, 226–241. [Google Scholar] [CrossRef]
- Jamal, A.M.M.; Sarker, B.R.; Wang, S. An ordering policy for deteriorating items with allowable shortage and permissible delay in payment. J. Oper. Res. Soc. 1997, 48, 826–833. [Google Scholar] [CrossRef]
- Rout, C.; Paul, A.; Kumar, R.S.; Chakraborty, D.; Goswami, A. Integrated optimization of inventory, replenishment and vehicle routing for a sustainable supply chain under carbon emission regulations. J. Clean. Prod. 2021, 316, 128256. [Google Scholar] [CrossRef]
- Singh, A.; Goel, A. Design of the supply chain network for the management of textile waste using a reverse logistics model under inflation. Energy 2024, 292, 130615. [Google Scholar] [CrossRef]
- Maity, S.; Chakraborty, A.; De, S.K.; Pal, M. A study of an EOQ model of green items with the effect of carbon emission under pentagonal intuitionistic dense fuzzy environment. Soft. Comput. 2023, 27, 15033–15055. [Google Scholar] [CrossRef]
- Jaber, M.Y.; Bonney, M. Optimal lot sizing under learning considerations: The bounded learning case. Appl. Math. Model. 1996, 20, 750–755. [Google Scholar] [CrossRef]
- Marchi, B.; Zanoni, S.; Zavanella, L.E.; Jaber, M.Y. Supply chain models with greenhouse gases emissions, energy usage, imperfect process under different coordination decisions. Int. J. Prod. Econ. 2019, 211, 145–153. [Google Scholar] [CrossRef]
- Chu, P.; Chung, K.J.; Lan, S.P. Economic order quantity of deteriorating items under permissible delay in payments. Comput. Oper. Res. 1998, 25, 817–824. [Google Scholar] [CrossRef]
- Pal, B.; Sana, S.S.; Chaudhuri, K. Three-layer supply chain–a production-inventory model for reworkable items. Appl. Math. Comput. 2012, 219, 530–543. [Google Scholar] [CrossRef]
- Giri, B.C.; Masanta, M. Developing a closed-loop supply chain model with price and quality dependent demand and learning in production in a stochastic environment. Int. J. Syst. Sci. Oper. Logist. 2020, 7, 147–163. [Google Scholar] [CrossRef]
- Alamri, O.A.; Jayaswal, M.K.; Khan, F.A.; Mittal, M. An EOQ Model with Carbon Emissions and Inflation for Deteriorating Imperfect Quality Items under Learning Effect. Sustainability 2022, 14, 1365. [Google Scholar] [CrossRef]
- Sangal, I.; Agarwal, A.; Rani, S. A fuzzy environment inventory model with partial backlogging under learning effect. Int. J. Comput. Appl. 2016, 137, 25–32. [Google Scholar] [CrossRef]
- Jaggi, C.K.; Pareek, S.; Goel, S.K.; Nidhi. An inventory model for deteriorating items with ramp type demand under fuzzy environment. Int. J. Logist. Syst. Manag. 2015, 22, 436–463. [Google Scholar] [CrossRef]
- Jaggi, C.K.; Sharma, A.; Jain, R. EOQ model with permissible delay in payments under fuzzy environment. In Analytical Approaches to Strategic Decision-Making: Interdisciplinary Considerations; IGI Global: Hershey, PA, USA, 2014; pp. 281–296. [Google Scholar]
- Sharma, L.K.; Vishal, V.; Singh, T.N. Developing novel models using neural networks and fuzzy systems for the prediction of strength of rocks from key geomechanical properties. Measurement 2017, 102, 158–169. [Google Scholar] [CrossRef]
- Patro, R.; Acharya, M.; Nayak, M.M.; Patnaik, S. A fuzzy EOQ model for deteriorating items with imperfect quality using proportionate discount under learning effects. Int. J. Manag. Decis. Mak. 2018, 17, 171–198. [Google Scholar] [CrossRef]
- Bhavani, G.D.; Meidute-Kavaliauskiene, I.; Mahapatra, G.S.; Činčikaitė, R. A Sustainable Green Inventory System with Novel Eco-Friendly Demand Incorporating Partial Backlogging under Fuzziness. Sustainability 2022, 14, 9155. [Google Scholar] [CrossRef]
- Jayaswal, M.K.; Mittal, M.; Alamri, O.A.; Khan, F.A. Learning EOQ model with trade-credit financing policy for imperfect quality items under cloudy fuzzy environment. Mathematics 2022, 10, 246. [Google Scholar] [CrossRef]
- Alamri, O.A. Sustainable Supply Chain Model for Defective Growing Items (Fishery) with Trade Credit Policy and Fuzzy Learning Effect. Axioms 2023, 12, 436. [Google Scholar] [CrossRef]
- Alsaedi, B.S.; Alamri, O.A.; Jayaswal, M.K.; Mittal, M. A sustainable green supply chain model with carbon emissions for defective items under learning in a fuzzy environment. Mathematics 2023, 11, 301. [Google Scholar] [CrossRef]
- Padiyar, S.S.; Bhagat, N.; Singh, S.R.; Punetha, N.; Dem, H. Production policy for an integrated inventory system under cloudy fuzzy environment. Int. J. Appl. Decis. Sci. 2023, 16, 255–299. [Google Scholar]
- Mahata, G.C.; De, S.K.; Bhattacharya, K.; Maity, S. Three-echelon supply chain model in an imperfect production system with inspection error, learning effect, and return policy under fuzzy environment. Int. J. Syst. Sci. Oper. Logist. 2023, 10, 1962427. [Google Scholar] [CrossRef]
- Sugapriya, C.; Saranyaa, P.; Nagarajan, D.; Pamucar, D. Triangular intuitionistic fuzzy number based backorder and lost sale in production, remanufacturing and inspection process. Expert Syst. Appl. 2024, 240, 122261. [Google Scholar] [CrossRef]
- Garg, H.; Sugapriya, C.; Rajeswari, S.; Nagarajan, D.; Alburaikan, A. A model for returnable container inventory with restoring strategy using the triangular fuzzy numbers. Soft Comput. 2024, 28, 2811–2822. [Google Scholar] [CrossRef]
- Shah, H.; Patel, M. An EOQ model for deteriorating items when demand is cloud fuzzy. Int. J. Logist. Syst. Manag. 2021, 42, 140–152. [Google Scholar] [CrossRef]
- De, S.K.; Mahata, G.C. A cloudy fuzzy economic order quantity model for imperfect-quality items with allowable proportionate discounts. J. Ind. Eng. Int. 2019, 15, 571–583. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Fuzzy Sets and Systems: Theory and Applications; Academic Press: New York, NY, USA, 1980. [Google Scholar]
- Turk, S.; Ozcan, E.; John, R. Multi-objective optimization in inventory planning with supplier selection. Expert Syst. Appl. 2017, 78, 51–63. [Google Scholar] [CrossRef]
- Wu, K.S.; Ouyang, L.Y. 2003. An integrated single-vendor single-buyer inventory system with shortage derived algebraically. Prod. Plann. Contr. 2003, 14, 555–561. [Google Scholar] [CrossRef]
- Masanta, M.; Giri, B.C. A closed-loop supply chain model with learning effect, random return and imperfect inspection underprice-and quality-dependent demand. Opsearch 2022, 59, 1094–1115. [Google Scholar] [CrossRef]
- Xu, J.; Chen, Y.; Bai, Q. A two-echelon sustainable supply chain coordination under cap-and-trade regulation. J. Clean. Prod. 2016, 135, 42–56. [Google Scholar] [CrossRef]
- Das, S.; Shaikh, A.A.; Bhunia, A.K.; Konstantaras, I. Warranty, free service and rework policy for an imperfect manufacturing system with SAR sensitive demand under emission taxation. Comput. Ind. Eng. 2024, 187, 109765. [Google Scholar] [CrossRef]
- Kazemi, N.; Shekarian, E.; Cárdenas-Barrón, L.E.; Olugu, E.U. Incorporating human learning into a fuzzy EOQ inventory model with backorders. Comput. Ind. Eng. 2015, 87, 540–542. [Google Scholar] [CrossRef]
- Björk, K.M. An analytical solution to a fuzzy economic order quantity problem. Int. J. Approx. Reason. 2009, 50, 485–493. [Google Scholar] [CrossRef]
- Wright, T.P. Factors affecting the cost of airplanes. J. Aeronaut. Sci. 1936, 3, 122–128. [Google Scholar] [CrossRef]
- Hsu, J.T.; Hsu, L.F. An integrated vendor-buyer cooperative inventory model for items with imperfect quality and shortage backordering. Adv. Decis. Sci. 2013, 65, 493–505. [Google Scholar] [CrossRef]
- Chang, H.C. An application of fuzzy sets theory to the EOQ model with imperfect quality items. Comp. Comput. Oper. Res. 2004, 31, 2079–2092. [Google Scholar] [CrossRef]
- Yu, J.C.; Wee, H.M.; Chen, J.M. Optimal ordering policy for a deteriorating item with imperfect quality and partial backordering. J. Chin. Inst. Ind. Eng. 2005, 22, 509–520. [Google Scholar] [CrossRef]
- Chung, K.J.; Huang, Y.F. Retailer’s optimal cycle times in the EOQ model with imperfect quality and a permissible credit period. Qual. Quant. 2006, 40, 59–77. [Google Scholar] [CrossRef]
- Konstantaras, I.; Skouri, K.; Jaber, M.Y. Inventory models for imperfect quality items with shortages and learning in inspection. Appl. Math. Model. 2012, 36, 5334–5343. [Google Scholar] [CrossRef]
- Sulak, H. An EOQ model with defective items and shortages in fuzzy sets environment. Int. J. Soc. Sci. Educ. Res. 2015, 2, 915–929. [Google Scholar] [CrossRef]
- Shekarian, E.; Olugu, E.U.; Abdul-Rashid, S.H.; Kazemi, N. An economic order quantity model considering different holding costs for imperfect quality items subject to fuzziness and learning. J. Intell. Fuzzy Syst. 2016, 30, 2985–2997. [Google Scholar] [CrossRef]
- Khanna, A.; Gautam, P.; Jaggi, C.K. Inventory modeling for deteriorating imperfect quality items with selling price dependent demand and shortage backordering under credit financing. Int. J. Math. Eng. Manag. Sci. 2017, 2, 110. [Google Scholar] [CrossRef]
- Rajeswari, S.; Sugapriya, C. Fuzzy economic order quantity model with imperfect quality items under repair option. J. Res. Lepidoptera 2020, 51, 627–643. [Google Scholar]
- Tahami, H.; Fakhravar, H. A fuzzy inventory model considering imperfect quality items with receiving reparative batch and order. Eur. J. Engin. Tech. Res. 2020, 5, 1179–1185. [Google Scholar]
- Jayaswal, M.K.; Mittal, M.; Sangal, I. Ordering policies for deteriorating imperfect quality items with trade-credit financing under learning effect. Int. J. Syst. Assur. Eng. Manag. 2021, 12, 112–125. [Google Scholar] [CrossRef]
- Aderohunmu, R.; Mobolurin, A.; Bryson, N. Joint vendor-buyer policy in JIT manufacturing. J. Oper. Res. Soc. 1995, 46, 375–385. [Google Scholar] [CrossRef]

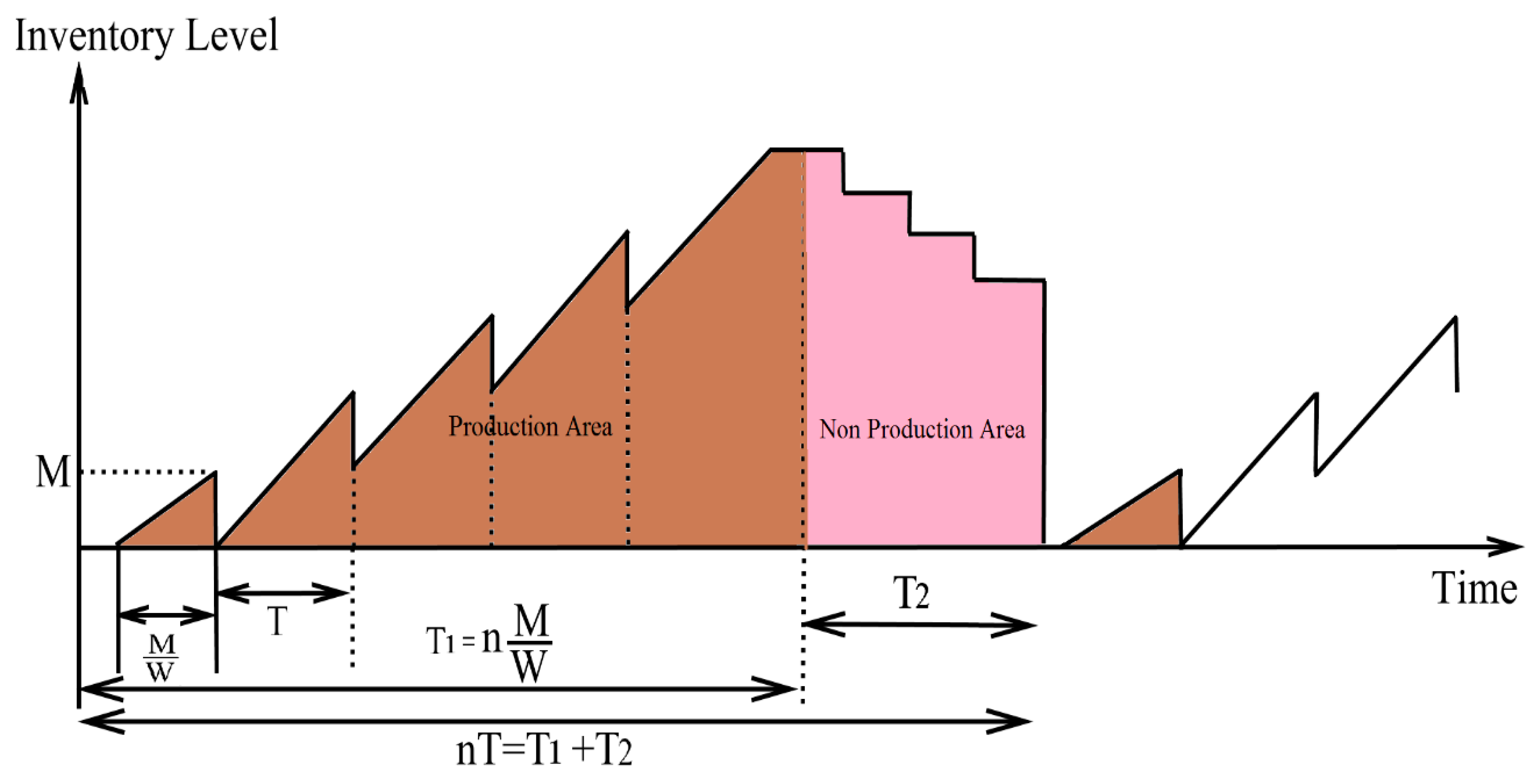
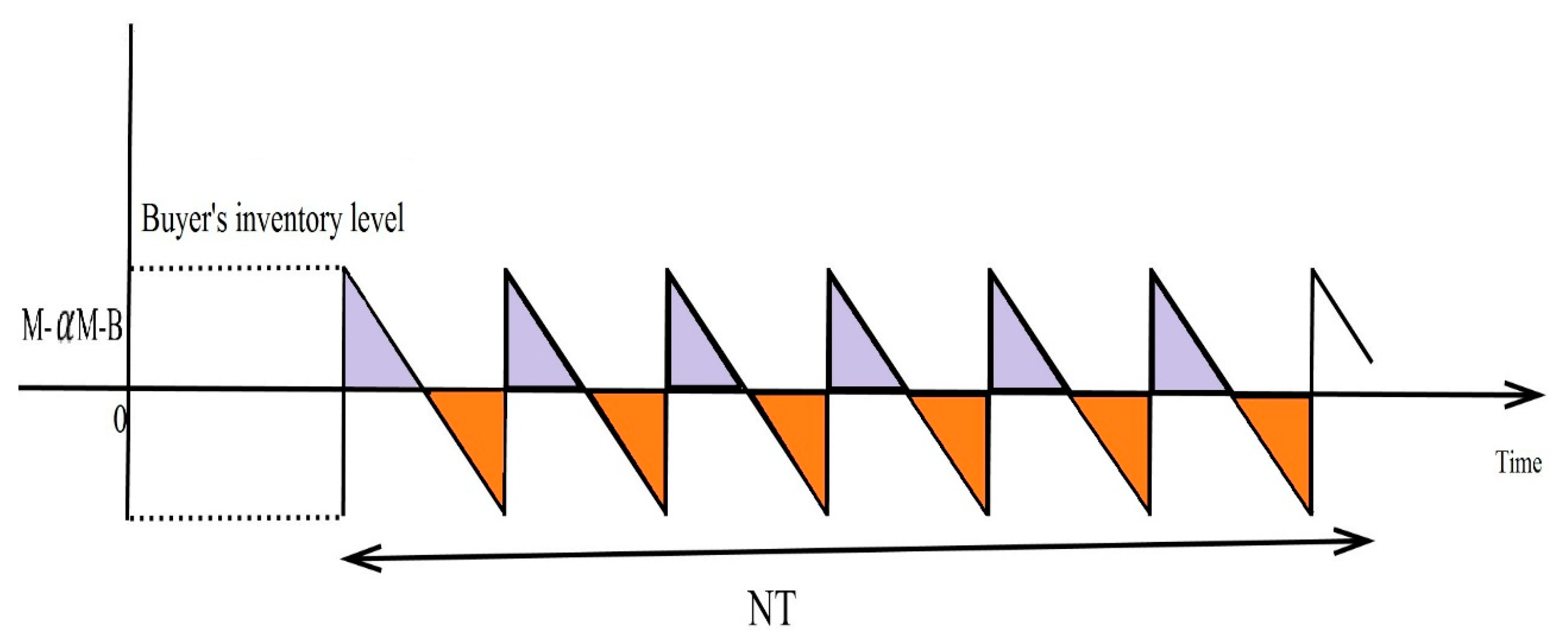



| Authors’ Contribution | Imperfect Items | Supply Chain | Waste Management Cost | Setup Cost Reduction Policy | Warranty Policy | Carbon Emissions | Cloudy Fuzzy Environment | Learning in Cloudy Fuzzy |
|---|---|---|---|---|---|---|---|---|
| Shah and Patel [55] | ✓ | ✓ | ||||||
| De and Mahata [56] | ✓ | ✓ | ||||||
| Dubois and Prade [57] | ✓ | ✓ | ✓ | |||||
| Salameh and Jaber [1] | ✓ | |||||||
| Turk et al. [58] | ✓ | |||||||
| Wu et al. [59] | ✓ | |||||||
| Jayaswal et al. [48] | ✓ | ✓ | ✓ | |||||
| Masanta and Giri [60] | ✓ | |||||||
| Xu et al. [61] | ✓ | ✓ | ||||||
| Padiyar et al. [51] | ✓ | ✓ | ||||||
| Mahata et al. [52] | ✓ | ✓ | ✓ | ✓ | ||||
| Das et al. [62] | ✓ | ✓ | ✓ | ✓ | ✓ | |||
| Singh and Goel [34] | ✓ | ✓ | ✓ | |||||
| Current study | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Input Parameters | Numerical Values | Input Parameters | Numerical Values |
|---|---|---|---|
| 160,000 units per year | 50,000 units per year | ||
| USD 300 per order | USD 25 per order | ||
| USD 0.1 per unit | USD 5 per delivery | ||
| USD 5 per unit | USD 10 per unit per unit | ||
| USD 0.5 per unit | USD 2 per unit per year | ||
| USD 3 per unit per year | USD 200 per order | ||
| USD 100 per order | 0.79 | ||
| USD 2 per unit | USD 30 per unit | ||
| USD 1000 per setup | USD 0.00140 | ||
| 0.04% | 0.01% | ||
| 10,000 units per year | 5000 units per year | ||
| 0.15 | 0.13 | ||
| USD 0.5 per unusable item | 2 |
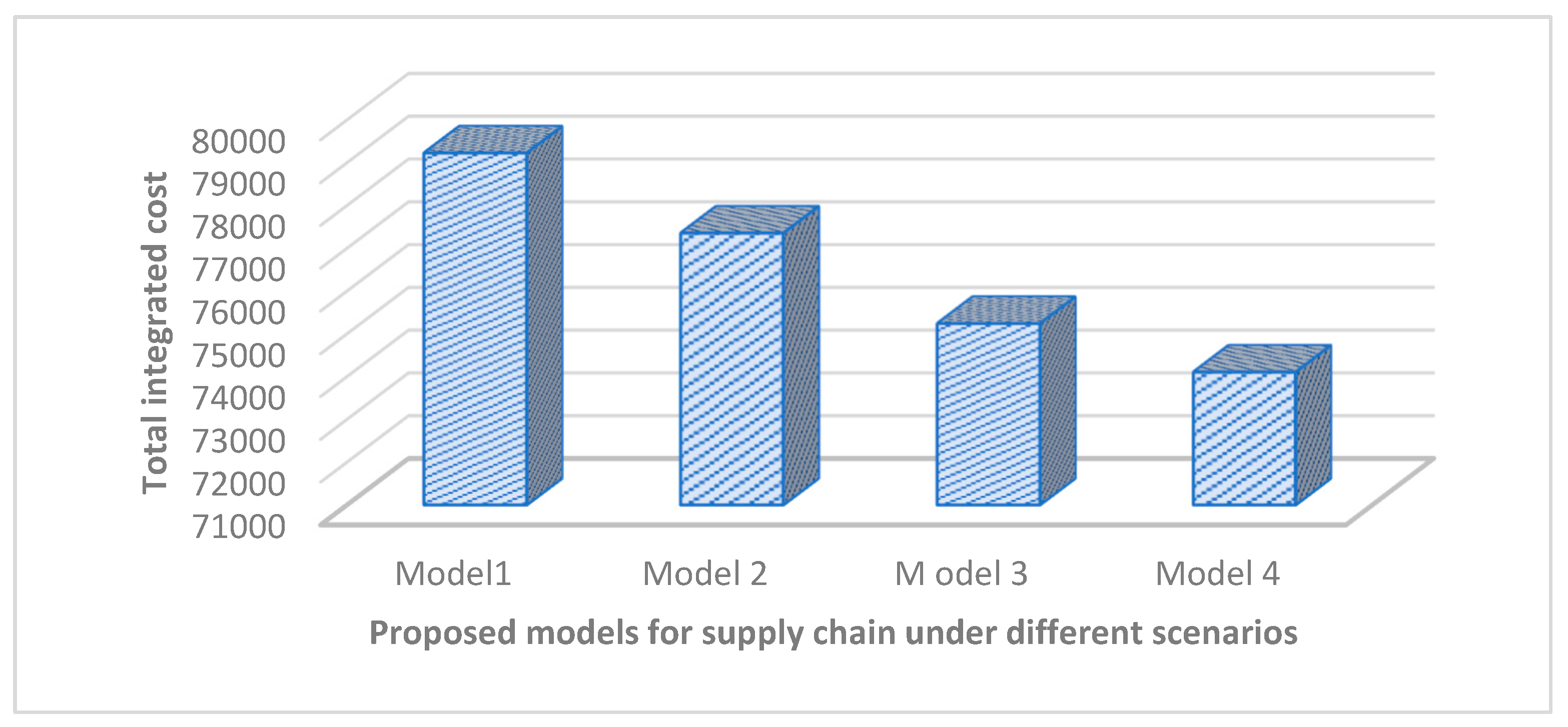
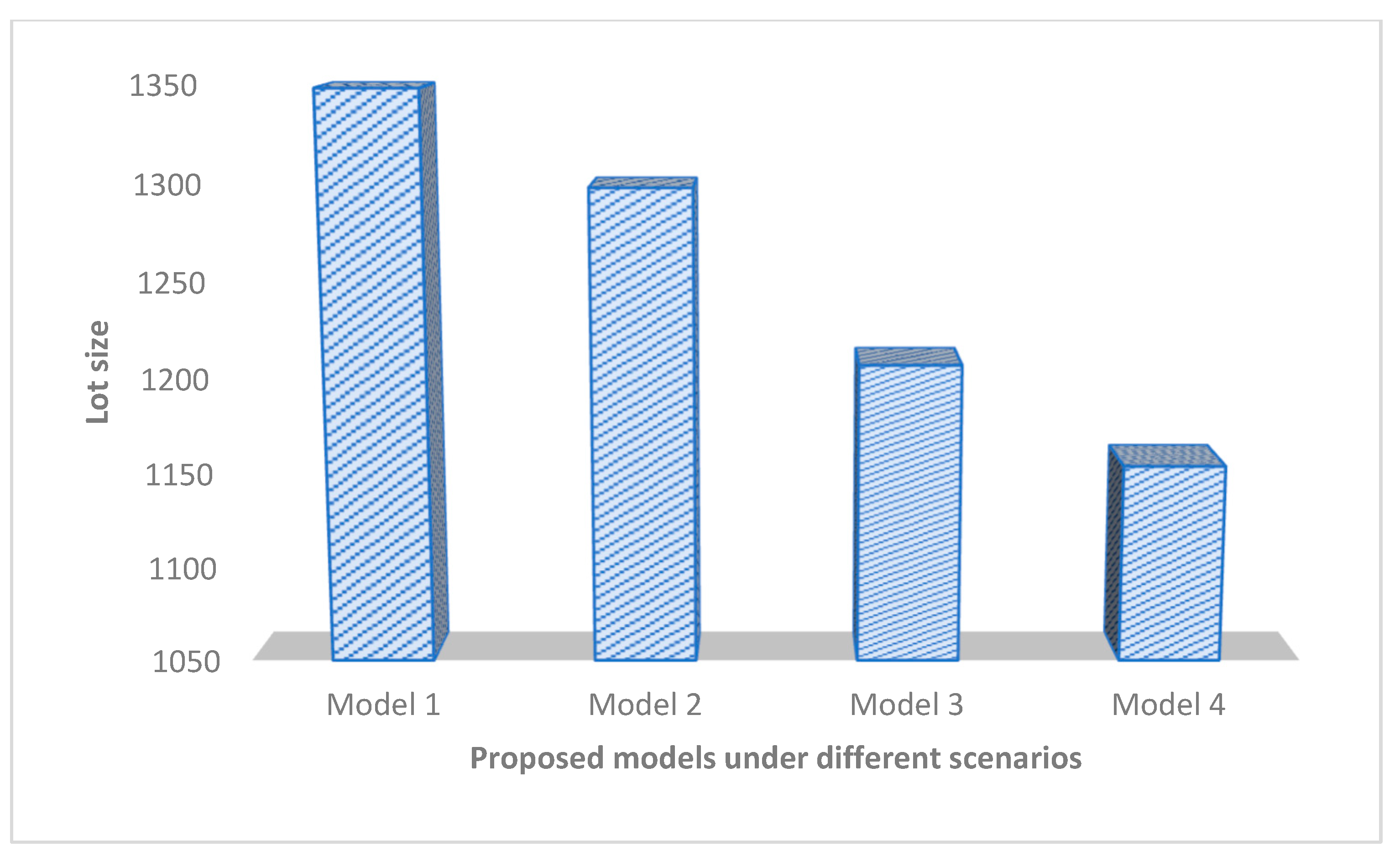
| Shipment | Order Quantity | Shortage Units | Total Integrated Inventory Cost (USD) | ||
|---|---|---|---|---|---|
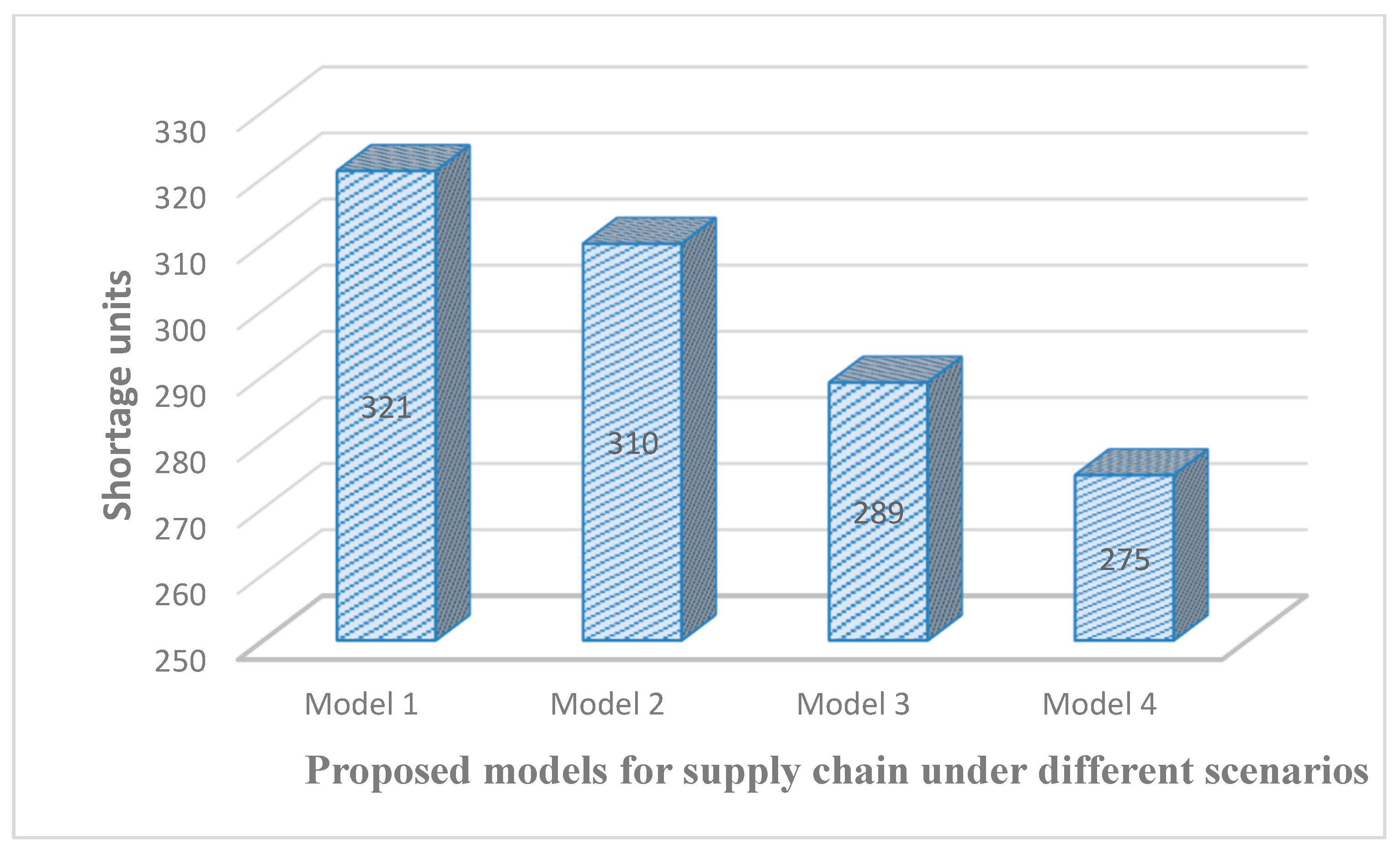
| Crisp model with waste management cost | 11 | 1348.75 | 321.67 | 250 | 79,228.87 |
| Model with fuzzy environment | 9 | 1298.74 | 310.98 | 246 | 77,354.97 |
| Model with learning in fuzzy environment with learning rate 0.152 | 6 | 1207.11 | 289.65 | 235 | 75,241.98 |
| Model with learning in cloudy fuzzy environment with learning rate 0.152 | 5 | 1154.56 | 275.98 | 193 | 74,105.85 |
| Authors | Investment in Setup as a Decision Variable | Lot Size as a Decision Variable | Shortage Units as a Decision Variable | Shipment as a Decision Variable | Total Profit/ Total Cost EOQ/EPQ/Supply Chain |
|---|---|---|---|---|---|
| Salsmeh and Jaber [1] | Not calculated | 1439 units | - | Not calculated | USD 1,212,235 |
| Chang [67] | Not calculated | 1429 units | - | Not calculated | USD 121,366.72 |
| Yu et al. [68] | Not calculated | 1288 units | 28 units | Not calculated | USD 1,212,148 |
| Chung and Huang [69] | Not calculated | 196 units | Not calculated | USD 346,583.3 | |
| Eroglu and Ozdemir [5] | Not calculated | 2129 units | 595 units | Not calculated | USD 341,116.89 |
| Jaber et al. [27] | Not calculated | 1440 units | - | Not calculated | USD 1,217,452 |
| Khan et al. [35] | Not calculated | 2201 units | 2112 units | Not calculated | USD 1,222,394 |
| Jaggi and Mittal [18] | Not calculated | 1283 units | - | Not calculated | USD 1,224,183 |
| Konstantaras et al. [70] | Not calculated | 666 units | - | Not calculated | USD 68,985 |
| Jaggi et al. [43] | Not calculated | 1642 units | 674 units | Not calculated | USD 347,086 |
| Sulak [71] | Not calculated | 2149 units | 594.53 | Not calculated | USD 341,121.2 |
| Shekarian et al. [72] | Not calculated | 5000 units | Not calculated | USD 11,000,000 | |
| Khanna et al. [73] | Not calculated | 899 units | 283 units | Not calculated | USD 707,837 |
| Patro et al. [46] | Not calculated | 1117 units | Not calculated | USD 1,273,420 | |
| Jayaswal et al. [48] | Not calculated | 1336 units | - | Not calculated | USD 1,206,930 |
| Rajeswari and Sugapriya [74] | Not calculated | 3423 units | - | Not calculated | USD 1,197,300 |
| Tahami and Fakhravar [75] | Not calculated | 1295 units | - | Not calculated | USD 1,212,072 |
| Jayaswal et al. [76] | Not calculated | 3756 units | - | Not calculated | USD 1,142,850 |
| Alamri et al. [49] | Not calculated | 48,225 units | - | Not calculated | USD 1,662,440 |
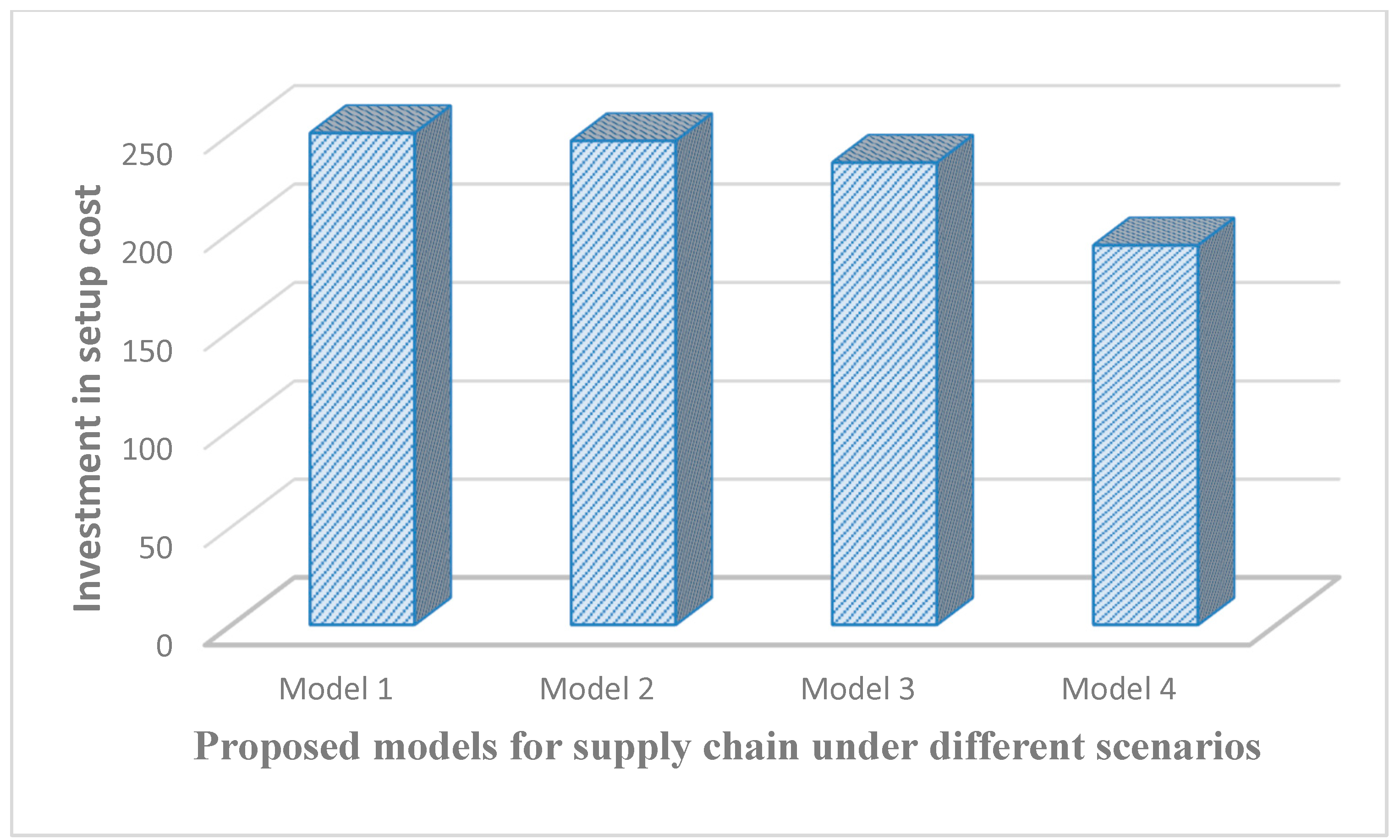
| Our paper under supply chain | Calculated, USD 193 | 1154 units | 275.98 units | Calculated, 5 | Total inventory fuzzy cost for the supply chain USD 74,105.85 |
|
Buyer’s Holding Cost hb |
Shipment N* |
Lot Size M(N*) |
Stortage Units B(N*) | Total Integrated Fuzzy Cost Ψ EC(USD) |
|---|---|---|---|---|
| 2.50 | 2 | 1406.87 | 228.18 | 73,805.15 |
| 3.75 | 3 | 1218.76 | 245.23 | 73,905.45 |
| 5.00 | 5 | 1154.56 | 275.98 | 74,105.85 |
|
Vendor’s Holding Cost hv |
Shipment N* |
Lot Size M(N*) |
Stortage Units B(N*) | Total Integrated Fuzzy Cost Ψ EC(USD) |
|---|---|---|---|---|
| 1.00 | 9 | 992.32 | 254.18 | 73,874.65 |
| 3.00 | 7 | 1098.76 | 265.23 | 73,986.89 |
| 5.00 | 5 | 1154.56 | 275.98 | 74,105.85 |
| Fixed Transportation Cost FT |
Shipment N* |
Lot Size M(N*) |
Stortage Units B(N*) | Total Integrated Fuzzy Cost Ψ EC(USD) |
|---|---|---|---|---|
| 12.00 | 10 | 997.54 | 203.52 | 73,898.31 |
| 18.00 | 8 | 1088.32 | 255.81 | 73,903.43 |
| 25.00 | 5 | 1154.56 | 275.98 | 74,105.85 |
| Fixed Carbon Emission Cost Fc |
Shipment N* |
Lot Size M(N*) |
Stortage Units B(N*) | Total Integrated Fuzzy Cost Ψ EC(USD) |
|---|---|---|---|---|
| 2.50 | 9 | 1087.54 | 252.52 | 73,798.17 |
| 3.75 | 8 | 1098.65 | 261.81 | 73,898.51 |
| 5.00 | 5 | 1154.56 | 275.98 | 74,105.85 |
| Variable Transportation Cost VT |
Shipment N* |
Lot Size M(N*) |
Stortage Units B(N*) | Total Integrated Fuzzy Cost Ψ EC(USD) |
|---|---|---|---|---|
| 0.050 | 5 | 1154.56 | 275.98 | 74,070.97 |
| 0.075 | 5 | 1154.56 | 275.98 | 74,065.87 |
| 0.100 | 5 | 1154.56 | 275.98 | 74,105.85 |
| Variable Carbon Emission Cost Vc |
Shipment N* |
Lot Size M(N*) |
Stortage Units B(N*) | Total Integrated Fuzzy Cost Ψ EC(USD) |
|---|---|---|---|---|
| 2.50 | 5 | 1154.56 | 275.98 | 73,170.1 |
| 3.75 | 5 | 1154.56 | 275.98 | 73,265.87 |
| 5.00 | 5 | 1154.56 | 275.98 | 74,105.85 |
| Setup Cost Reduction Input Parameter Cost π |
Shipment N* |
Lot Size M(N*) |
Stortage Units B(N*) |
Investment in Setup Cost (μ*) | Total Integrated Fuzzy Cost Ψ EC(USD) |
|---|---|---|---|---|---|
| 0.0007 | 5 | 1159.65 | 278.09 | 0 | 74,145.10 |
| 0.0010 | 5 | 1159.45 | 279.78 | 0.000001 | 74,135.87 |
| 0.0014 | 5 | 1154.56 | 275.98 | 193.65 | 74,105.85 |
| Learning Rate l |
Shipment N* |
Lot Size M(N*) |
Stortage Units B(N*) | Total Integrated Fuzzy Cost Ψ EC(USD) |
|---|---|---|---|---|
| 0.149 | 10 | 985.65 | 289.09 | 75,798.09 |
| 0.150 | 8 | 1062.17 | 281.78 | 74,835.92 |
| 0.152 | 5 | 1154.56 | 275.98 | 74,105.85 |
| 0.154 | 5 | 1154.56 | 275.98 | 74,105.85 |
| 0.156 | 5 | 1154.56 | 275.98 | 74,105.85 |
|
Cloud Parameter ρ (0 < ρ < 0) |
Cloud Parameter σ (0 < σ < 0) |
Shipment N* |
Lot Size M(N*) |
Stortage Units B(N*) | Total Integrated Fuzzy Cost Ψ EC(USD) |
|---|---|---|---|---|---|
| 0.02 | 0.01 | 8 | 1174.56 | 278.98 | 74,110.12 |
| 0.03 | 0.02 | 8 | 1174.56 | 278.98 | 74,110.12 |
| 0.04 | 0.03 | 8 | 1174.56 | 278.98 | 74,110.12 |
| 0.05 | 0.04 | 8 | 1174.56 | 278.98 | 74,110.12 |
| 0.06 | 0.05 | 8 | 1174.56 | 278.98 | 74,110.12 |
| 0.09 | 0.08 | 8 | 1174.56 | 278.98 | 74,110.12 |
| 0.15 | 0.13 | 5 | 1154.56 | 275.98 | 74,105.85 |
|
Upper Deviation of Demand Rate |
Lower Deviation of Demand Rate |
Shipment N* |
Lot Size M(N*) |
Stortage Units B(N*) | Total Integrated Fuzzy Cost Ψ EC(USD) |
|---|---|---|---|---|---|
| 10,000 | 5000 | 5 | 1174.56 | 278.98 | 74,105.85 |
| 11,000 | 6000 | 7 | 1103.56 | 288.98 | 74,144.97 |
| 12,000 | 7000 | 6 | 1087.56 | 292.98 | 74,198.65 |
| Percentage of Defectives α |
Shipment N* |
Lot Size M(N*) |
Stortage Units B(N*) | Total Integrated Fuzzy Cost Ψ EC(USD) |
|---|---|---|---|---|
| 0.04 | 5 | 1154.56 | 275.98 | 74,105.85 |
| 0.05 | 5 | 1159.71 | 265.78 | 74,980.13 |
| 0.06 | 5 | 1164.41 | 256.98 | 75,210.08 |
| Waste Percentage of Unusable Products δ |
Shipment N* |
Lot Size M(N*) |
Stortage Units B(N*) | Total Integrated Fuzzy Cost Ψ EC(USD) |
|---|---|---|---|---|
| 0.01 | 5 | 1154.56 | 275.98 | 74,105.85 |
| 0.02 | 5 | 1156.01 | 271.07 | 74,117.13 |
| 0.03 | 5 | 1157.05 | 273.08 | 75,119.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsaedi, B.S.O. A Sustainable Supply Chain Model with a Setup Cost Reduction Policy for Imperfect Items under Learning in a Cloudy Fuzzy Environment. Mathematics 2024, 12, 1603. https://doi.org/10.3390/math12101603
Alsaedi BSO. A Sustainable Supply Chain Model with a Setup Cost Reduction Policy for Imperfect Items under Learning in a Cloudy Fuzzy Environment. Mathematics. 2024; 12(10):1603. https://doi.org/10.3390/math12101603
Chicago/Turabian StyleAlsaedi, Basim S. O. 2024. "A Sustainable Supply Chain Model with a Setup Cost Reduction Policy for Imperfect Items under Learning in a Cloudy Fuzzy Environment" Mathematics 12, no. 10: 1603. https://doi.org/10.3390/math12101603
APA StyleAlsaedi, B. S. O. (2024). A Sustainable Supply Chain Model with a Setup Cost Reduction Policy for Imperfect Items under Learning in a Cloudy Fuzzy Environment. Mathematics, 12(10), 1603. https://doi.org/10.3390/math12101603






