An Adaptive Cubature Kalman Filter Based on Resampling-Free Sigma-Point Update Framework and Improved Empirical Mode Decomposition for INS/CNS Navigation

Abstract

For the degradation of the filtering performance of the INS/CNS navigation system under measurement noise uncertainty, an adaptive cubature Kalman filter (CKF) is proposed based on improved empirical mode decomposition (EMD) and a resampling-free sigma-point update framework (RSUF). The proposed algorithm innovatively integrates improved EMD and RSUF into CKF to estimate measurement noise covariance in real-time. Specifically, the improved EMD is used to reconstruct measurement noise, and the exponential decay weighting method is introduced to emphasize the use of new measurement noise while gradually discarding older data to estimate the measurement noise covariance. The estimated measurement noise covariance is then imported into RSUF to directly construct the posterior cubature points without a resampling step. Since the measurement noise covariance is updated in real-time and the prediction cubature points error is directly transformed to the posterior cubature points error, the proposed algorithm is less sensitive to the measurement noise uncertainty. The proposed algorithm is verified by simulations conducted on the INS/CNS-integrated navigation system. The experimental results indicate that the proposed algorithm achieves better performance for attitude angle.

1. Introduction

Inertial navigation systems (INS) and celestial navigation systems (CNS) are critical components in the field of robotics navigation. The INS relies on inertial sensors, typically gyroscopes and accelerometers, to measure the vehicle’s linear and angular accelerations, from which position, velocity, and attitude information are deduced through integration and estimation algorithms [1,2,3]. This self-contained system is invaluable in environments where external signals, such as GPS, are unreliable or unavailable. On the other hand, CNS utilizes celestial bodies such as stars, planets, or the sun as reference points to determine the vehicle’s orientation and position relative to the earth [4]. However, INS is susceptible to errors over time, particularly due to sensor drift and accumulated inaccuracies from the double integration of acceleration data [5,6,7,8]. CNS, while highly accurate over longer durations and distances, struggles with real-time computational demands and requires a clear line of sight to celestial bodies, making it less effective under certain operational conditions such as daytime or in heavily clouded skies [9]. The INS/CNS navigation model, therefore, integrates these two systems to compensate for each other’s shortcomings. It corrects INS drift using precise CNS observations, while the continuous INS operation fills gaps in CNS availability, enhancing the overall system autonomy and navigation reliability. Key to this integration is an accurate state estimation model encompassing attitude, velocity, position errors, and sensor inaccuracies, with consideration for low-frequency star sensor errors in celestial observations [10].

The importance of INS/CNS-integrated navigation in robot navigation systems cannot be overstated. In scenarios where GPS signals are unavailable or unreliable, such as indoor environments, urban canyons, or underwater operations, INS/CNS systems offer a viable alternative for maintaining accurate navigation. Moreover, in applications requiring high-precision navigation, such as autonomous aerial refueling, spacecraft rendezvous and docking, or unmanned aerial vehicle (UAV) surveillance missions, INS/CNS systems play a pivotal role in ensuring mission success [10].

Despite the promise of INS/CNS-integrated navigation, several formidable research challenges persist. Foremost among these challenges is the development of robust sensor fusion algorithms capable of seamlessly integrating data from disparate sensors while compensating for errors, biases, and uncertainties inherent in each sensor modality. Furthermore, ensuring the resilience of these systems to environmental factors such as electromagnetic interference, dynamic motion, and changing lighting conditions presents a significant hurdle [11,12]. Therefore, the state estimation problem holds great significance in the INS/CNS navigation [13]. It remains one of the most prominent research challenges and has garnered significant attention from the research community [14]. Typically, Kalman-based filtering is used in integrated navigation to achieve state estimation. For integrated navigation, the Kalman filter (KF) exhibits excellent performance for estimating the state of a linear system [15]. The navigation system models, however, typically exhibit nonlinearity, and as a result, the extended Kalman filter (EKF), unscented Kalman filter (UKF), and cubature Kalman filtering (CKF) have emerged as the prevailing nonlinear filtering methods in current practice [16,17,18]. The EKF is a fundamental extension of the KF. It incorporates the linear approximation and utilizes the Kalman filter to estimate the state [19]. UKF uses the unscented transform to approximate the probability distribution of the system state [20]. The CKF is an innovative nonlinear filtering approach that effectively estimates states in high-dimensional systems. It utilizes the spherical-radial cubature rule to enhance numerical stability and accuracy [1,21]. Additionally, CKF imposes a lower computational load compared to UKF, as it utilizes $2n$ cubature points instead of $2n+1$ sigma points [5]. In particular, to further improve the ability of CKF, the CKF based on the RSUF is proposed, which can directly construct the posterior sigma point without a resampling step [22]. Nevertheless, the aforementioned nonlinear filters rely heavily on precise prior statistical information regarding process and measurement noise [23]. Inaccurate noise statistics will lead to a deterioration in performance. In the INS/CNS navigation, the precision of the system state equation can be significantly enhanced by employing ultra-high accuracy inertial measurement units (IMUs) [13]. However, the CNS is inevitably influenced by the external environment. This influence can lead to variations in measurement noise, which may change slowly or be uncertain. Consequently, the INS/CNS system can fail to deliver superior navigation results [14].

Aiming to address the issue of uncertain measurement noise in the navigation system, some adaptive filters have been suggested to improve the robustness of the navigation device against measurement noise uncertainty, including particle-based filters [24], maximum likelihood-based filters [25], Huber-based Kalman filters [26], and maximum correntropy criterion-based Kalman filters (MCKF) [13]. Particle-based filters are an effective method employed to tackle the uncertainty of measurement noise in state estimation. They operate by employing a multitude of particles to approximate the likelihood distribution of the state. However, the use of many particles to estimate the likelihood distribution results in a high degree of computational complexity. The maximum likelihood-based filter is unbiased in terms of minimum covariance when measurements are independent and identically distributed. However, all currently available maximum likelihood-based filters are developed within the context of linear systems, making them inappropriate for nonlinear state estimation. The Huber-based Kalman filter has emerged as a widely used technique. It leverages the maximum likelihood regression criterion to tackle problems associated with measurement noise uncertainty. However, this method tends to choose measurements with substantial errors, which can subsequently introduce considerable errors into the filter. The MCKF algorithm utilizes the correntropy basis to mitigate the influence of measurement noise uncertainty on the filtering performance. However, they do not fully exploit the heavy-tailed characteristics inherent in uncertain measurement noises, which consequently restrict the accuracy of the estimation. The filters based on EMD and variational mode decomposition (VMD) have garnered significant attention in current research [23,27]. The methods of EMD and VMD, however, suffer from the issues of mode mixing and endpoint effects, which result in inaccurate reconstruction of measurement noise [23].

Research in this area focuses on improving the INS/CNS system’s robustness against uncertainties—primarily measurement noise—a significant contributor to reduced navigation accuracy. The paper highlights an innovative method: an adaptive CKF based on an RSUF and improved EMD. The novelty lies in directly and dynamically addressing measurement noise and importing it into RSUF to construct the posterior cubature points without a resampling step, thus reducing filter sensitivity to noise uncertainties. Through simulations of an aircraft’s INS/CNS attitude determination system, the proposed method demonstrates marked improvements, emphasizing its effectiveness in attitude angle accuracy. This method underscores the research’s commitment to advancing INS/CNS navigation robustness, ensuring dependable and accurate navigation even under challenging measurement noise conditions. In summary, the research objectives of the work are threefold: (1) Develop an adaptive filtering technique. To design an adaptive CKF specifically tailored for an INS/CNS navigation system that confronts the challenge of measurement noise uncertainty. This filter integrates a unique combination of an RSUF with an improved EMD. (2) Real-time noise covariance estimation. To achieve the real-time, high-precision estimation of the measurement noise covariance. The methodology involves reconstructing the measurement noise sequence using the improved EMD and implementing an exponential decay weighting strategy to dynamically allocate the reconstructed noise between successive time steps. (3) Enhance navigation accuracy and reliability. To significantly improve the accuracy and reliability of attitude determination in INS/CNS systems by effectively tracking variations in measurement noise characteristics. The proposed algorithm aims to outperform state-of-the-art algorithms in scenarios where measurement noise is either initially unknown or varies over time.

The rest of the paper is arranged as follows. The reconstruction of measurement noise based on improved EMD is devised in Section 2. In Section 3, an adaptive cubature Kalman filter is presented. In Section 4, the result of the simulation is presented. Finally, the conclusion of the paper is drawn in Section 5.

2. Improved EMD for Reconstruction of Measurement Noise

In this section, we initially review EMD. Subsequently, we present an improved EMD to tackle the issues related to mode mixing and endpoint effects. Additionally, the RSUF-based CKF is employed to predict multi-step measurements and expand the measurement sequence. Finally, the improved EMD is employed to reconstruct the measurement noise by utilizing the extended measurement sequence.

2.1. Empirical Mode Decomposition

The EMD is a signal processing technique that employs smoothing to decompose signals into intrinsic mode function (IMF) exhibiting distinct characteristics and fluctuations at different scales [28]. The instantaneous amplitude and frequency of the signal can be obtained by Hilbert transformation for each IMF. In contrast to the Fast Fourier Transform (FFT), the Hilbert transform can handle non-stationary and transient problems. The amplitude and frequency of the IMF obtained through the Hilbert transform vary over time, thereby eliminating superfluous simple harmonics introduced to account for signal non-stationarity and enhancing the flexibility and convenience of signal analysis.

The process of the EMD algorithm is as follows [28]:

(1)

Initialize $i$, the extreme value points on a given signal $s(t)$ are determined and then linked together using cubic spline curves to construct both upper and lower envelopes.

(2)

The difference $\widehat{s}(t)$ between the signal $s(t)$ and the mean $m(t)$ of these envelopes is calculated: $\widehat{s}(t)=s(t)-m(t)$.

(3)

Treat $\widehat{s}(t)$ as the new signal $s(t)$ and repeat the above steps until $\widehat{s}(t)$ meets the IMF’s two conditions: (1) The equality or a maximum difference of one must be maintained between the quantities of extreme points and zeros; (2) the time axis exhibits local symmetry in the signal. At this time, $\widehat{s}(t)$ becomes the first-order IMF selected by the original signal and is denoted as $IM{F}_i(t)$.

(4)

Calculate $s(t)=s(t)-IM{F}_i(t)$, $i=i+1$, and return to step (1) until the residual signal $r(t)$ of the $n$-th order becomes a monotonic function and cannot be further divided into IMF, i.e., we can represent the original signal $s(t)$ as $s(t)={\displaystyle \sum _{i=1}^{n}IM{F}_i(t)+}r(t)$.

The above process involves decomposing the data into multiple IMFs and a residual component. The EMD decomposition is entirely driven by the data itself, starting from characteristic time scales to generate diverse basis functions for direct adaptive sifting of signals, resulting in a finite number of IMF components.

2.2. Improved Empirical Mode Decomposition

During the process of EMD, there are issues of mode mixing and endpoint effects, leading to the loss of specific physical meaning in the decomposed IMFs. To address this problem, this section presents an improved EMD method. This method reconstructs the signal sequence by repeatedly changing the position of noise distribution, averaging multiple reconstructed signal sequences, and compressing signal noise into lower-order IMFs with a smaller computational cost. The purpose is to reduce decomposition errors in lower-order IMFs and significantly improve the accuracy of EMD. The method is described as follows:

(1)

The signal $s(t)$ is decomposed by EMD, and the $\overline{n}$-order IMF and residual signal $r(t)$ are obtained;

(2)

Because noise has high-frequency characteristics, the first two orders of IMF are considered noise signals, and we obtain the noise signal: $sn(t)={\displaystyle \sum _{i=1}^{2}IM{F}_i}$;

(3)

Arbitrarily change the position distribution of noise signal $sn(t)$ for $ii$ times to obtain $ii$ new noise distribution sequences $s{n}_{ii}(t)$: $s{n}_{ii}(t)=Alter[sn(t)]$, $ii=1,2,\cdots$, where $Alter[\cdot ]$ denotes the operation of arbitrarily changing the position distribution.

(4)

Construct $ii$ signals with different noise distributions while maintaining the signal-to-noise ratio identical to the original signal: $s_{ii}(t)=s{n}_{ii}(t)+{\displaystyle \sum _{i=3}^{\overline{n}}IM{F}_i}+r(t)$;

(5)

Average $ii$ signals with different noise distributions to obtain a noise compressed signal ${\widehat{s}}_{ii}(t)$: ${\widehat{s}}_{ii}(t)=\frac{1}{ii+1}\left[{\displaystyle \sum _{i=1}^{ii}{s}_i(t)}+s(t)\right]$;

(6)

The noise compression signal ${\widehat{s}}_{ii}(t)$ is decomposed by the EMD method, where the first-order IMF is the noise sequence to be obtained.

2.3. Measurement Noise Reconstruction

To reconstruct the measurement noise sequence, we first utilize predicted measurements to extend the measurement sequence. The sequence of measurement accumulated at time $k-1$ is represented as ${\left\{{\mathit{z}}_{k-1}(t)\right\}}_{t=k-N}^{k-1}$, where ${\mathit{z}}_{k-1}(t)$ denotes the measurement at time $t$ and $N$ represents a positive integer.

The estimated measurement ${\widehat{\mathit{z}}}_{k\left|k\right.}$ at instant $k$ is obtained using the RSUF-based CKF, where it is set to ${\widehat{\mathit{z}}}_{k\left|k\right.}=h({\widehat{x}}_{k\left|k\right.})$, $h(\cdot )$ represents the measurement equation, and ${\widehat{x}}_{k\left|k\right.}$ represents the state estimation at instant $k$. In general, the state is only predicted when there is no measurement update, denoted as ${\widehat{x}}_{k\left|k\right.}={\widehat{x}}_{k\left|k-1\right.}$. Here, ${\widehat{x}}_{k\left|k-1\right.}$ represents the one-step prediction of the state at instant $k$. The predicted sequence of measurements is consequently denoted as

$$\left\{\begin{array}{l}{\mathit{z}}_{k-1}(k)={\widehat{\mathit{z}}}_{k\left|k\right.}=h({\widehat{x}}_{k\left|k-1\right.})\hfill \\ {\mathit{z}}_{k-1}(k+1)={\widehat{\mathit{z}}}_{k+1\left|k+1\right.}=h({\widehat{x}}_{k+1\left|k\right.})\hfill \\ ⋮\hfill \\ {\mathit{z}}_{k-1}(k+L-1)={\widehat{\mathit{z}}}_{k+L-1\left|k+L-1\right.}=h({\widehat{x}}_{k+L-1\left|k+L-2\right.})\hfill \end{array}\right.$$

(1)

Finally, the extension of the measurement sequence can be expressed as ${\left\{{\mathit{z}}_{k-1}(t)\right\}}_{t=k-N}^{k+L-1}$. The improved EMD method is used to decompose the extended measurement sequence, and the first IMF ($IM{F}_1$) obtained from the decomposition represents the reconstructed measurement noise sequence ${\widehat{\mathit{v}}}_{k-1}$, that is, ${\widehat{\mathit{v}}}_{k-1}=IM{F}_1$.

According to ${\widehat{\mathit{v}}}_{k-1}$, the covariance of measurement noise can be estimated:

$${\widehat{\mathit{R}}}_{k-1}=\frac{1}{N-1}\cdot {\displaystyle \sum _{t=k-N+1}^{k-1}}{\left\{{\widehat{\mathit{v}}}_{k-1}(t)\right\}}^2$$

(2)

where ${\widehat{\mathit{v}}}_{k-1}(i)$ denotes the $i$-th component of the measurement noise sequence.

As the filtering progresses, the state error covariance tends to stabilize. In the absence of measurement updates, only predictions are made for the state, resulting in a relatively small predicted measurement error over a short period. The estimated covariance of the measurement noise error in Equation (2) does not consider the reconstructed measurement noise from the extended part, thus preventing potential errors arising from expansion.

The estimation method for the covariance of measurement noise in Equation (2) employs the equal weighting average approach over a fixed time window of width $N-1$. The weighting given to both the old and latest measurement noises is identical. When there is a change in the actual value of the covariance of the measurement noise, the estimation by Equation (2) significantly diverges from its true value, thereby indirectly constraining the corrective impact of Kalman gain. Therefore, by using the reconstructed sequence ${\widehat{\mathit{v}}}_{k-1}$ of measurement noise and applying the exponential decay weighting method, we can rewrite the estimation of the measurement noise covariance at instant $k-1$ as

$${\widehat{\mathit{R}}}_{k-1}=\frac{1-b_{k-1}}{N-1}\cdot {\displaystyle \sum _{t=k-N+1}^{k-2}}{\left\{{\widehat{\mathit{v}}}_{k-1}(t)\right\}}^2+b_{k-1}\cdot {\left\{{\widehat{\mathit{v}}}_{k-1}(k-1)\right\}}^2$$

(3)

where $b_{k-1}=\frac{b-b^{k-1}}{1-b^{k-1}}$, the range of $b$ is [0.99, 0.999] [29].

In general, the section holds pivotal significance in the overall context of the paper as it outlines a critical advancement in dealing with uncertainties prevalent in measurement noise, a common impediment to the accuracy and reliability of navigation systems like INS/CNS. By proposing an improved version of the EMD, we innovatively address two key limitations—mode mixing and endpoint effects—that have historically plagued conventional EMD applications. Mode mixing, where distinct signal components intertwine, and endpoint effects, which distort signal decomposition at signal boundaries, can lead to inaccuracies in noise reconstruction. The improved EMD methodology rectifies these issues, ensuring a cleaner separation and more precise extraction of the measurement noise component from the overall signal. This refined noise signal is then dynamically managed across successive time steps using an exponential decay weighting scheme, which prioritizes recent noise samples over older ones. Such a strategy allows for a more adaptable and realistic representation of the noise characteristics that evolve. The significance lies in the direct application of this noise reconstruction in the adaptive CKF, where real-time estimation of measurement noise covariance is integrated. By incorporating the estimated measurement noise covariance into the RSUF, the filter becomes less susceptible to noise uncertainty-induced inaccuracies, translating to improved navigation performance, particularly in terms of attitude angle estimation.

Inference-wise, this section underscores the potential for significant enhancements in navigation system performance through advanced signal processing techniques. By mitigating measurement noise uncertainties in real-time, the proposed algorithm provides the method for more robust and reliable navigation implementation, especially crucial in challenging environments where noise profiles may fluctuate or be initially unknown. This innovation demonstrates the viability of integrating sophisticated noise-handling mechanisms within complex navigation systems like INS/CNS to achieve superior navigation accuracy and dependability.

3. An Adaptive Cubature Kalman Filter

3.1. Resampling-Free Sigma-Point Update Framework

To clearly describe the proposed adaptive cubature Kalman filter, we first briefly review the RSUF [22].

The prior cubature point error matrix ${\tilde{\mathit{X}}}_k^{-}$, posterior cubature point error matrix ${\tilde{\mathit{X}}}_k^{+}$, and corresponding weight $\mathit{W}$ are defined as

$${\tilde{\mathit{X}}}_k^{-}=\left[{\mathit{X}}_{1,k\left|k-1\right.}-{\widehat{\mathit{x}}}_{k\left|k-1\right.},{\mathit{X}}_{2,k\left|k-1\right.}-{\widehat{\mathit{x}}}_{k\left|k-1\right.},\cdots ,{\mathit{X}}_{2n,k\left|k-1\right.}-{\widehat{\mathit{x}}}_{k\left|k-1\right.}\right]$$

(4)

$${\tilde{\mathit{X}}}_k^{+}=\left[{\mathit{X}}_{1,k\left|k-1\right.}-{\widehat{\mathit{x}}}_{k\left|k\right.},{\mathit{X}}_{2,k\left|k-1\right.}-{\widehat{\mathit{x}}}_{k\left|k\right.},\cdots ,{\mathit{X}}_{2n,k\left|k-1\right.}-{\widehat{\mathit{x}}}_{k\left|k\right.}\right]$$

(5)

$$\mathit{W}=diag\left(\left[{\mathsf{\omega }}_1,{\mathsf{\omega }}_2,\cdots ,{\mathsf{\omega }}_{2n}\right]\right)$$

(6)

where ${\widehat{\mathit{x}}}_{k\left|k-1\right.}$ and ${\widehat{\mathit{x}}}_{k\left|k\right.}$ represent the predicted state and estimated state at instant $k$, respectively; ${\mathit{X}}_{i,k\left|k-1\right.}=f({\mathsf{\xi }}_{i,k-1})$, $f(\cdot )$ represents the state function, ${\mathsf{\xi }}_{i,k-1}$ represents the cubature point, ${\mathsf{\omega }}_i$ denotes the weight of the cubature point, $i=1,2,\cdots ,2n$; $n$ represents the state dimension, $diag(\cdot )$ represents the diagonal operation of the matrix. The error matrix for posterior cubature point, denoted as ${\tilde{\mathit{X}}}_k^{+}$, can be obtained through the equation ${\tilde{\mathit{X}}}_k^{+}={\mathsf{\gamma }}_k{\tilde{\mathit{X}}}_k^{-}$ to satisfy the following constraint equations.

$${\tilde{\mathit{X}}}_k^{-}\mathsf{\omega }=0,{\tilde{\mathit{X}}}_k^{+}\mathsf{\omega }=0$$

(7)

$${\tilde{\mathit{X}}}_k^{-}\mathit{W}{\left({\tilde{\mathit{X}}}_k^{-}\right)}^T={\widehat{\mathit{P}}}_{k\left|k-1\right.}-{\mathit{Q}}_{k-1}$$

(8)

$${\tilde{\mathit{X}}}_k^{+}\mathit{W}{\left({\tilde{\mathit{X}}}_k^{+}\right)}^T={\widehat{\mathit{P}}}_{k\left|k\right.}-\Delta {\mathit{R}}_k$$

(9)

where ${\widehat{\mathit{P}}}_{k\left|k-1\right.}$ and ${\widehat{\mathit{P}}}_{k\left|k\right.}$ represent the predicted and estimated state error covariance at instant $k$, respectively; $\mathsf{\omega }=\left[{\mathsf{\omega }}_1,{\mathsf{\omega }}_2,\cdots ,{\mathsf{\omega }}_{2n}\right]$, $\Delta {\mathit{R}}_k$ represents the uncertainty matrix caused by noise, $\Delta {\mathit{R}}_k={\mathsf{\Lambda }}_k{\mathit{K}}_k{\mathit{R}}_k{\mathit{K}}_k^T$, ${\mathsf{\Lambda }}_k$ denotes the scale matrix, ${\mathit{K}}_k$ denotes the filtering gain, $R_k$ denotes the covariance of measurement noise.

Under the constraint of Equations (8) and (9), it can be obtained:

$${\mathsf{\gamma }}_k={\mathit{M}}_k^{+}{\left({\mathit{M}}_k^{-}\right)}^{-1}$$

(10)

where ${\mathit{M}}_k^{+}=chol\left({\widehat{\mathit{P}}}_{k\left|k\right.}-\Delta {\mathit{R}}_k\right)$, ${\mathit{M}}_k^{-}=chol\left({\widehat{\mathit{P}}}_{k\left|k-1\right.}-{\mathit{Q}}_{k-1}\right)$, $chol\left(\cdot \right)$ represents the Cholesky decomposition.

As ${\tilde{\mathit{X}}}_k^{-}$ represents the residue of instantiated points for Gaussian expectation, according to Equations (5) and (10), the resulting new cubature points are obtained by

$$\begin{array}{l}{\xi }_{i,k}={\widehat{\mathit{x}}}_{k\left|k\right.}+{\widehat{\mathit{X}}}_{i,k}^{+}\\ ={\widehat{x}}_{k\left|k\right.}+{\mathit{M}}_k^{+}{\left({\mathit{M}}_k^{-}\right)}^{-1}\left({\mathit{X}}_{i,k\left|k-1\right.}-{\widehat{\mathit{x}}}_{k\left|k-1\right.}\right)\end{array}$$

(11)

3.2. Adaptive Cubature Kalman Filter

The effectiveness of the CKF linear data assimilation framework diminishes when the significance of measurement noise uncertainty cannot be disregarded. In this section, the RSUF and improved EMD techniques are employed to enhance the CKF, thereby enhancing both the robustness of the gain matrix update in RSUF and preserving more information during the update of CKF. The specific description of the adaptive filtering algorithm is as follows.

For a discrete-time system model of the navigation system, which is described as

$${\mathit{x}}_k=f({\mathit{x}}_{k-1})+{\mathit{w}}_{k-1}$$

(12)

$${\mathit{z}}_k=h({\mathit{x}}_k)+{\mathit{v}}_k$$

(13)

where ${\mathit{x}}_k\in R^n$ represents the $n$-dimensional state, ${\mathit{z}}_k\in R^m$ represents the $m$-dimensional measurement at instant $k$; ${\mathit{w}}_{k-1}$ denotes the process noise, ${\mathit{v}}_k$ denotes the measurement noise, and their respective covariances are denoted by ${\mathit{Q}}_{k-1}$ and ${\mathit{R}}_k$; $h(\cdot )$ denotes the measurement function.

Given the ${\mathit{Q}}_{k-1}$, ${\mathit{R}}_k$, state estimation ${\widehat{\mathit{x}}}_{k-1\left|k-1\right.}$ and its error covariance ${\widehat{\mathit{P}}}_{k-1\left|k-1\right.}$ at instant $k-1$, and then compute the cubature points ${\mathsf{\xi }}_{i,k-1}$ according to Equations (14)–(16).

$${\mathit{S}}_{k-1|k-1}=chol({\widehat{\mathit{P}}}_{k-1|k-1})$$

(14)

$${\mathsf{\xi }}_{i,k-1}={\mathit{S}}_{k-1\left|k-1\right.}{\widehat{\mathsf{\omega }}}_i+{\widehat{\mathit{x}}}_{k-1\left|k-1\right.},i=1,\dots ,2n$$

(15)

$${\widehat{\mathsf{\omega }}}_i=\left\{\begin{array}{l}\sqrt{n}{\mathit{e}}_i,i=1,\dots ,n\\ -\sqrt{n}{\mathit{e}}_{i-n},i=n+1,\dots ,2n\end{array}\right.$$

(16)

where ${\mathit{e}}_i$ represents the $i-\mathrm{th}$ column of an identity matrix with dimensions $n\times n$.

Calculate the predicted state of the integrated navigation system and its associated error covariance.

$${\widehat{\mathit{x}}}_{k\left|k-1\right.}={\displaystyle \sum _{i=1}^{2n}{\mathsf{\omega }}_i}f\left({\mathsf{\xi }}_{i,k-1}\right)$$

(17)

$${\widehat{\mathit{P}}}_{k\left|k-1\right.}={\displaystyle \sum _{i=1}^{2n}{\mathsf{\omega }}_i}\left[f\left({\mathsf{\xi }}_{i,k-1}\right)-{\widehat{\mathit{x}}}_{k\left|k-1\right.}\right]{\left[f\left({\mathsf{\xi }}_{i,k-1}\right)-{\widehat{\mathit{x}}}_{k\left|k-1\right.}\right]}^T+{\mathit{Q}}_{k-1}$$

(18)

where ${\mathsf{\omega }}_i=\frac{1}{2n}$.

Then, the prior cubature point error matrix ${\tilde{\mathit{X}}}_k^{-}$ is calculated.

$${\mathit{X}}_{i,k\left|k-1\right.}=f\left({\mathsf{\xi }}_{i,k-1}\right),i=1,2,\cdots ,2n$$

(19)

$${\tilde{\mathit{X}}}_k^{-}=\left[{\mathit{X}}_{1,k\left|k-1\right.}-{\widehat{\mathit{x}}}_{k\left|k-1\right.},{\mathit{X}}_{2,k\left|k-1\right.}-{\widehat{\mathit{x}}}_{k\left|k-1\right.},\cdots ,{\mathit{X}}_{2n,k\left|k-1\right.}-{\widehat{\mathit{x}}}_{k\left|k-1\right.}\right]$$

(20)

${\tilde{\mathit{X}}}_k^{-}$ is updated by

$${\tilde{\mathit{X}}}_k^{-}=chol\left({\widehat{\mathit{P}}}_{k\left|k-1\right.}\right){\left[chol\left({\widehat{\mathit{P}}}_{k\left|k-1\right.}-{\mathit{Q}}_{k-1}\right)\right]}^{-1}{\tilde{\mathit{X}}}_k^{-}$$

(21)

Generate the propagation cubature point for approximating the likelihood function using Equation (22).

$${\stackrel{︹}{\mathit{X}}}_{i,k\left|k-1\right.}={\widehat{\mathit{x}}}_{k\left|k-1\right.}+{\tilde{\mathit{X}}}_{i,k}^{-},i=1,2,\cdots ,2n$$

(22)

where ${\tilde{\mathit{X}}}_{i,k}^{-}$ represents the i-th column of ${\tilde{\mathit{X}}}_k^{-}$.

Furthermore, the predicted measurement ${\widehat{\mathit{z}}}_{k\left|k-1\right.}$, the predicted measurement error covariance ${\widehat{\mathit{P}}}_{{\widehat{z}}_{k\left|k-1\right.}}$, and the cross-covariance ${\widehat{\mathit{P}}}_{{\widehat{x}}_{k\left|k-1\right.}{\widehat{z}}_{k\left|k-1\right.}}$ between the predicted state and the predicted measurement are computed by

$${\widehat{\mathit{z}}}_{k\left|k-1\right.}={\displaystyle \sum _{i=1}^{2n}{\mathsf{\omega }}_i}h\left({\stackrel{︹}{\mathit{X}}}_{i,k\left|k-1\right.}\right)$$

(23)

$${\widehat{\mathit{P}}}_{{\widehat{z}}_{k\left|k-1\right.}}={\displaystyle \sum _{i=1}^{2n}{\mathsf{\omega }}_i}\left(h\left({\stackrel{︹}{\mathit{X}}}_{i,k\left|k-1\right.}\right)-{\widehat{\mathit{z}}}_{k\left|k-1\right.}\right){\left(h\left({\stackrel{︹}{\mathit{X}}}_{i,k\left|k-1\right.}\right)-{\widehat{\mathit{z}}}_{k\left|k-1\right.}\right)}^T+{\widehat{\mathit{R}}}_k$$

(24)

$${\widehat{\mathit{P}}}_{{\widehat{x}}_{k\left|k-1\right.}{\widehat{z}}_{k\left|k-1\right.}}={\displaystyle \sum _{i=1}^{2n}{\mathsf{\omega }}_i}\left(f\left({\mathsf{\xi }}_{i,k-1}\right)-{\widehat{\mathit{x}}}_{k\left|k-1\right.}\right){\left(h\left({\stackrel{︹}{\mathit{X}}}_{i,k\left|k-1\right.}\right)-{\widehat{\mathit{z}}}_{k\left|k-1\right.}\right)}^T$$

(25)

where the measurement noise reconstruction method proposed in this paper is used to obtain the measurement noise sequence ${\left\{{\mathit{z}}_k(t)\right\}}_{t=k-N+1}^{k+L}$, and then the measurement noise covariance ${\widehat{\mathit{R}}}_k$ can be estimated by Equation (3).

Update the state estimation ${\widehat{\mathit{x}}}_{k\left|k\right.}$ and its error covariance ${\widehat{\mathit{P}}}_{k\left|k\right.}$ by

$${\widehat{\mathit{x}}}_{k\left|k\right.}={\widehat{\mathit{x}}}_{k\left|k-1\right.}+{\mathit{K}}_k\left({\mathit{z}}_k-{\widehat{\mathit{z}}}_{k\left|k-1\right.}\right)$$

(26)

$${\widehat{\mathit{P}}}_{k\left|k\right.}={\widehat{\mathit{P}}}_{k\left|k-1\right.}-{\mathit{K}}_k{\widehat{\mathit{P}}}_{{\widehat{z}}_{k\left|k-1\right.}}{\mathit{K}}_k^T$$

(27)

where Kalman gain ${\mathit{K}}_k={\widehat{\mathit{P}}}_{{\widehat{x}}_{k\left|k-1\right.}{\widehat{z}}_{k\left|k-1\right.}}{\left({\widehat{\mathit{P}}}_{{\widehat{z}}_{k\left|k-1\right.}}\right)}^{-1}$.

Finally, update the posterior cubature point error matrix ${\tilde{\mathit{X}}}_k^{+}$, and the cubature points ${\mathsf{\xi }}_{i,k}$ for the next filtering.

$${\tilde{\mathit{X}}}_k^{+}={\mathsf{\gamma }}_k{\tilde{\mathit{X}}}_k^{-}$$

(28)

$${\mathsf{\xi }}_{i,k}={\widehat{\mathit{x}}}_{k\left|k\right.}+{\tilde{\mathit{X}}}_{i,k}^{+},i=1,2,\cdots ,2n$$

(29)

where ${\tilde{\mathit{X}}}_{i,k}^{+}$ denotes the i-th column of ${\tilde{\mathit{X}}}_k^{+}$.

To achieve a more accurate and adaptive estimation of the measurement noise covariance, the above process constructs the measurement noise sequence and eliminates mode mixing and endpoint effects by the improved EMD and RSUF. In addition, updating the weights of the reconstructed measurement noise by the exponential decay weighting method achieved better tracking performance for variations in the covariance of actual measurement noise.

3.3. Computational Complexity Analysis

In this section, we employ Floating-Point Operations (FLOPs) as a measure to assess the computational complexity of the proposed algorithm. Drawing upon our previous research [13], we have determined that the overall computational complexity of the RSUF-based CKF is $\frac{47n^3}{3}+10n^2+10n^{2}m+8n{m}^2+8nm+m^3+m^2+m$. Notice that the primary distinction between the CKF based on RSUF and the algorithm proposed is in the process of the extension of the measurement sequence; improved EMD decomposes the measurement sequence, reconstructs measurement noise, and estimates covariance of measurement noise. The improved EMD decomposition process’s computational complexity is impacted by the length of the measurement sequence $(L+N)$, as well as the number of iterations $M$ and $\overline{M}$. As $(L+N)$, $M$, and $\overline{M}$ increase, there is a noticeable rise in the computational complexity associated with implementing the improved EMD. Therefore, the computational complexity of the proposed algorithm can be represented as

$$\begin{array}{l}{C}_{proposed}=\frac{47n^3}{3}+10n^2+10n^{2}m+8n{m}^2+8nm+5m^3+(2N-5)m^2+(L+N+1)m+\\ (M+\overline{M}+ii+2)(L+N)m\overline{n}+(2m-1){(L+N)}^2\end{array}$$

(30)

The derivation of Equation (30) is given in Appendix A.

4. Performance Evaluation and Discussions

In this section, the proposed algorithm is subjected to the aircraft’s INS/CNS attitude determination simulation system. First, the INS/CNS navigation model is introduced. Then, the filtering performance of the proposed algorithm is analyzed.

4.1. INS/CNS Navigation System Model

Based on the attitude errors, velocity errors, position errors, and star sensor low-frequency errors, the INS/CNS navigation system model is constructed as [9]

$${\mathbf{X}}_k=\mathbf{F}({\mathbf{X}}_{k-1})+{\mathbf{W}}_{k-1}$$

(31)

where $\mathbf{X}$ represents the 18-dimensional state vector, $\mathbf{X}={\left[\begin{array}{cccccc}\mathsf{\varphi }& \mathsf{\delta }\mathbf{V}& \mathsf{\delta }\mathbf{S}& \mathsf{\Xi }& \mathsf{\Theta }& \mathsf{\delta }\mathsf{\theta }\end{array}\right]}^{\mathrm{T}}$, $\mathsf{\varphi }=\left[\begin{array}{ccc}{\mathsf{\varphi }}_x& {\mathsf{\varphi }}_y& {\mathsf{\varphi }}_z\end{array}\right]$ represents the misalignment angle, $\mathsf{\delta }\mathbf{V}=\left[\begin{array}{ccc}\mathsf{\delta }{\mathrm{V}}_x& \mathsf{\delta }{\mathrm{V}}_y& \mathsf{\delta }{\mathrm{V}}_z\end{array}\right]$ denotes the velocity error, $\mathsf{\delta }\mathbf{S}=\left[\begin{array}{ccc}\mathsf{\delta }{\mathrm{S}}_x& \mathsf{\delta }{\mathrm{S}}_y& \mathsf{\delta }{\mathrm{S}}_z\end{array}\right]$ represents the position error, $\mathsf{\Xi }=\left[\begin{array}{ccc}{\mathsf{\Xi }}_x& {\mathsf{\Xi }}_y& {\mathsf{\Xi }}_z\end{array}\right]$ denotes the gyro constant drift, $\mathsf{\Theta }=\left[\begin{array}{ccc}{\mathsf{\Theta }}_x& {\mathsf{\Theta }}_y& {\mathsf{\Theta }}_z\end{array}\right]$ denotes the accelerometer constant bias, and $\mathsf{\delta }\mathsf{\theta }=\left[\begin{array}{ccc}\mathsf{\delta }{\mathsf{\theta }}_x& \mathsf{\delta }{\mathsf{\theta }}_y& \mathsf{\delta }{\mathsf{\theta }}_z\end{array}\right]$ denotes the low-frequency error of the star sensor.

Next, we consider constructing measurement equations for INS/CNS navigation system based on the measurement of attitude error [9].

$${\mathbf{Z}}_k=\mathbf{H}{\mathbf{X}}_k+{\mathbf{V}}_k$$

(32)

where $\mathbf{H}$ denotes the measurement matrix, ${\mathbf{V}}_k$ denotes the measurement noise.

The INS/CNS navigation model serves as the foundation for assessing the performance of the proposed algorithm. In addition to the system model provided by Equation (31), which describes the state evolution over time, we delve deeper into the intricacies of the measurement equations (Equation (32)) and how they interact with the system states. Specifically, we outline the structure of the measurement matrix $\mathbf{H}$ that relates the system states ${\mathbf{X}}_k$ to the measurements ${\mathbf{Z}}_k$, accounting for the various error sources such as star sensor noise, gyro drift, and accelerometer bias. For a comprehensive understanding, we also discuss the impact of the measurement noise characteristics on the navigation solution, considering the low-frequency errors $\mathsf{\delta }\mathsf{\theta }$ and their contribution to overall system accuracy. Please refer to our work in reference [9] for these specific details.

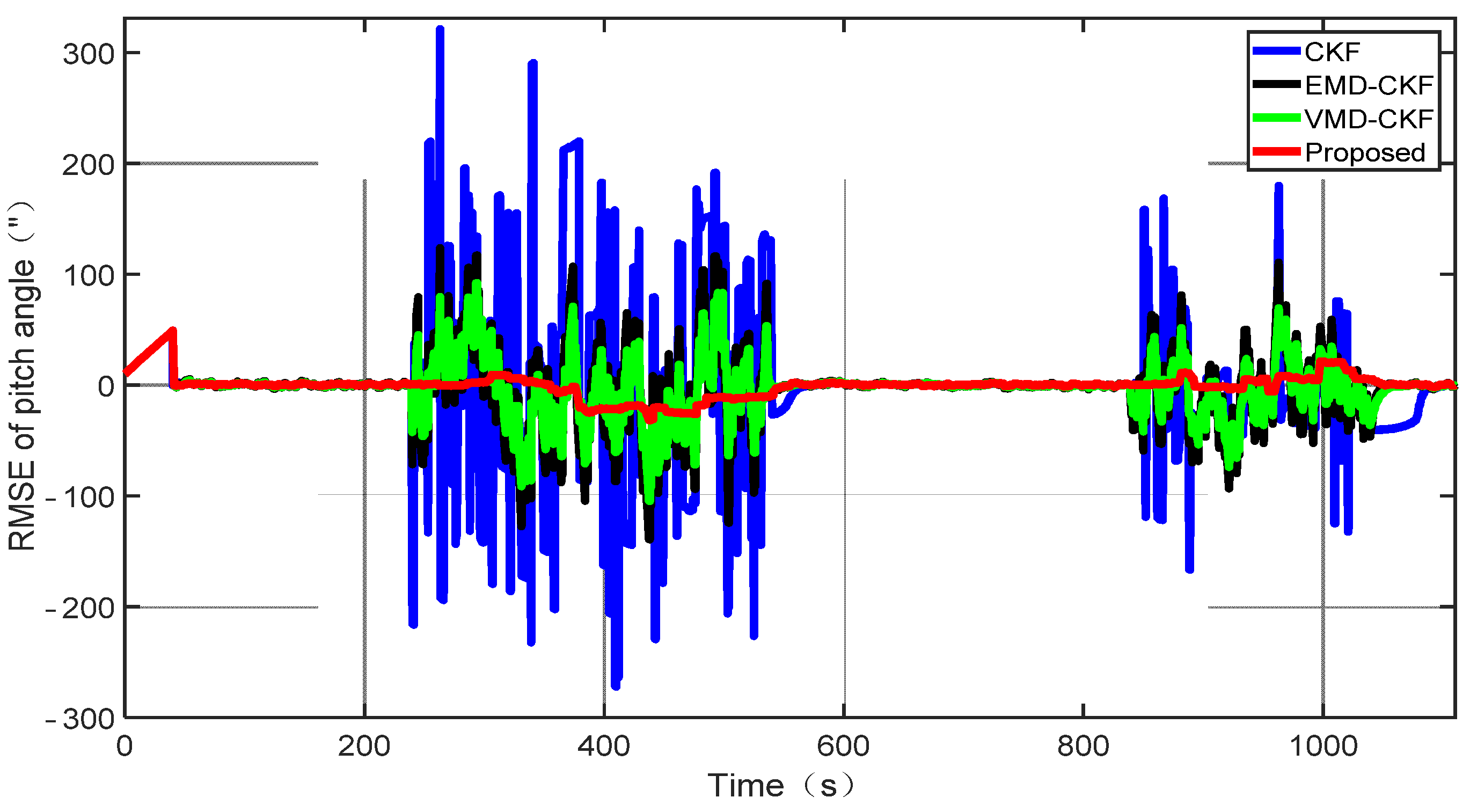
4.2. Simulation and Analysis

Monte Carlo simulation experiments were carried out to thoroughly assess the effectiveness of the proposed algorithm for the flight of an aircraft using an INS/CNS navigation attitude determination system. The trajectory depicted in Figure 1 represents a dynamic flight path specifically designed to mimic the actual movements of a highly dynamic aircraft, as described in reference [13]. The starting point of the aircraft is $({116.34}^{\circ } \mathrm{E},{39.98}^{\circ } \mathrm{N})$. The simulated flight time of the aircraft is set to 1110 s, and the INS/CNS system starts operating after the aircraft enters outer space at the 40th second.

Table 1. The parameters for the simulation.

Parameter	Value
Initial pitch angle	90°
Initial velocity	(355.49 m/s, 0 m/s, 0 m/s)
Random noises of gyro	0.5°/h
Constant drift of gyro	1°/h
Random noises of accelerometer	50 μg
Constant bias of accelerometer	100 μg
Random noises of star sensor	$3^{″}$
Fixed time window $N$	15
Predicted measurement sequence length $L$	10

displays the simulation parameters.

In the simulation experiment, we compared the proposed algorithm with CKF, EMD-CKF, and VMD-CKF [23] algorithms, in which the EMD-CKF algorithm utilizes the EMD to effectively separate noise from measurement information while estimating the noise covariance for updating the parameters of CKF. In addition, 100 Monte Carlo experiments were conducted, and the experimental results were analyzed using root mean square error (RMSE) and average root mean square error (ARMSE) [23].

$$RMS{E}_k=\sqrt{\frac{1}{G}{\displaystyle \sum _{i=1}^G{(x_k^i-{\widehat{x}}_{k\left|k\right.}^i)}^2}}$$

(33)

$$ARMSE=\frac{1}{T}{\displaystyle \sum _{k=1}^{T}RMS{E}_k}$$

(34)

where $G$ represents the quantity of Monte Carlo experiments and $T$ denotes the number of filtering.

In addition, we set the measurement noise at the initial moment of filtering to ${\mathit{R}}_0={(3^{″})}^2\cdot {\mathit{I}}_{3\times 3}$. To simulate the measurement noise as time-varying noise, we set its covariance to vary based on ${\mathit{R}}_0$, namely

$${\mathit{R}}_k=\left\{\begin{array}{l}50{\mathit{R}}_0, 240 s\le k\le 540 s\\ 30{\mathit{R}}_0, 840 s\le k\le 1040 s\\ {\mathit{R}}_0, \mathrm{others}\end{array}\right.$$

(35)

Figure 2, Figure 3 and Figure 4 illustrate the RMSEs for yaw, roll, and pitch angles, respectively. The ARMSEs of attitude angle are presented in

Table 2. ARMSE for the attitude angle.

Method	ARMSE for the Yaw Angle (″)	ARMSE for the Roll Angle (″)	ARMSE for the Pitch Angle (″)
CKF	92.55	83.92	88.84
EMD-CKF	35.26	31.93	31.78
VMD-CKF	25.84	22.77	23.93
Proposed method	11.23	14.51	21.41

. Figure 2, Figure 3 and Figure 4 show that in the measurement noise uncertainty scenario, the CKF yields higher RMSEs for the attitude angle compared to EMD-CKF, VMD-CKF, and our proposed algorithm. In addition, it is worth noting that the RMSEs obtained by our proposed algorithm are the smallest. The primary factor lies in the inability of CKF to dynamically track variations in the covariance of measurement noise, while EMD-CKF, VMD-CKF, and the proposed algorithm have the capability to dynamically modify the measurement noise covariance. The EMD-CKF algorithm, in contrast to CKF, emphasizes the measurement signal itself. By employing EMD, EMD-CKF effectively separates the noise present in the measurement and provides real-time estimation of the covariance of this noise. However, EMD suffers from mode mixing and endpoint effects, leading to inaccurate estimation of measurement noise by EMD-CKF. VMD-CKF reduces the influence of mode mixing and endpoint effects via adaptively reconstructing the measurement noise, thus performing better than EMD-CKF. The proposed algorithm employs the RSUF, noise compression, and reasonable allocation of the reconstructed measurement noise ratio between the previous and current time to enhance the capability of estimating measurement noise covariance for effectively tracking the changes in its actual value. In addition, the estimated measurement noise covariance is imported into RSUF to directly construct the posterior cubature points without a resampling step. Therefore, compared to other algorithms, the proposed algorithm has stronger robustness to the measurement noise uncertainty. The results in Table 2 confirm the above conclusion. As we can see, compared with the ARMSEs of attitude angle obtained by CKF, the values obtained by EMD-CKF are reduced by more than 61%, VMD-CKF is reduced by more than 72%, and the proposed algorithm is reduced by more than 75%.

To assess the computational efficiency of the proposed algorithm, we carried out a series of tests. These tests included Monte Carlo simulation trials, which we executed by using the software (Matlab R2023a).

Table 3. Running time.

	CKF	EMD-CKF	VMD-CKF	Proposed Method
Time (s)	0.097	0.416	0.251	0.502

and Figure 5 describe the time and time comparison histograms required to complete the simulation of CKF, EMD-CKF, VMD-CKF, and the proposed algorithm, respectively. They reveal that the computation times for the proposed algorithm, EMD-CKF and VMD-CKF exceed those of CKF. This increase is attributable to their need to adaptively modify measurement noise covariance at each step of the process. Notably, the proposed algorithm’s process requires additional inverse and decomposition operations compared to EMD-CKF and VMD-CKF, resulting in a slightly longer computation time for the EMD-CKF.

5. Conclusions

This paper proposes an adaptive CKF, based on the RSUF and improved EMD, for the INS/CNS attitude determination navigation system under measurement noise uncertainty. The proposed algorithm achieves real-time, high-precision estimation of measurement noise covariance by reconstructing measurement noise. Theoretical analysis and simulation results demonstrate that the proposed algorithm exhibits superior accuracy than CKF, EMD-CKF, and VMD-CKF when confronted with measurement noise that is either unknown or subject to variations over time. However, the algorithm also encounters challenges predominantly linked to its computational complexity. The reliance on EMD for noise reconstruction and covariance estimation introduces a computational overhead proportional to the length of the measurement sequence and the number of iterations required. This complexity escalates significantly with longer sequences and a higher number of iterations, potentially straining computational resources and limiting real-time application feasibility, especially in resource-constrained environments.

In future research, we will concentrate on alleviating these drawbacks and capitalizing on the algorithm’s strengths by investigating the following: (1) Exploring deep learning methodologies to enhance computational efficiency. Neural networks, specifically designed for signal processing tasks, can learn efficient representations and noise patterns, potentially reducing the need for iterative EMD processes. (2) Developing adaptive control mechanisms that dynamically adjust the number of EMD iterations based on the instantaneous signal-to-noise ratio or other metrics could balance precision and computational demands, ensuring optimal performance across varying noise environments.