Abstract
This paper delves into the realm of cryptographic analysis by employing mixed-integer linear programming (MILP), a powerful tool for automated cryptanalysis. Building on this foundation, we apply the division property method alongside MILP to conduct a comprehensive cryptanalysis of the IIoTBC (industrial Internet of Things block cipher) algorithm, a critical cipher in the security landscape of industrial IoT systems. Our investigation into IIoTBC System A has led to identifying a 14-round integral distinguisher, further extended to a 22-round key recovery. This significant finding underscores the cipher’s susceptibility to sophisticated cryptanalytic attacks and demonstrates the profound impact of combining the division property method with MILP in revealing hidden cipher weaknesses. In the case of IIoTBC System B, our innovative approach has uncovered a full-round distinguisher. We provide theoretical validation for this distinguisher and uncover a pivotal structural issue in the System B algorithm, specifically the non-diffusion of its third branch. This discovery sheds light on inherent security challenges within System B and points to areas for potential enhancement in its design. Our research, through its methodical examination and analysis of the IIoTBC algorithm, contributes substantially to the field of cryptographic security, especially concerning industrial IoT applications. By uncovering and analyzing the vulnerabilities within IIoTBC, we enhance the understanding of cipher robustness and pave the way for advancements in securing industrial IoT communications.
MSC:
52B12
1. Introduction
1.1. Background
The rapid evolution of the industrial Internet of Things (IIoT) [,,] heralds a new era in industrial automation and data exchange. This advancement, however, brings with it a heightened need for robust security solutions, particularly in cryptographic algorithms that can operate efficiently in resource-constrained environments. The industrial Internet of Things block cipher (IIoTBC) algorithm, specifically designed for IIoT applications [,,,,], emerges as a pivotal innovation in this context. It strikes a crucial balance between computational efficiency and the stringent security requirements of industrial systems, ensuring data integrity and confidentiality in environments where traditional cryptographic solutions may prove infeasible.
IIoTBC [] is primarily intended for securing industrial IoT environments, where it can be deployed at the sensor node level. It provides a first line of defense by allowing sensor data to circulate as ciphertext, thus enhancing privacy and security in industrial settings. Recognizing the rapid increase in industrial IoT users, IIoTBC is developed as a lightweight cipher to protect user privacy. It aims to fully realize its functions while minimizing the use of hardware devices. The round function of IIoTBC involves AddRoundkey, S-box permutation, and 1-bit left rotation. These operations are designed to be simple and consume fewer resources, making IIoTBC suitable for hardware implementation, particularly in resource-constrained environments. The IIoTBC algorithm is a strategically designed cipher that addresses the specific security requirements of the industrial IoT sector. Its lightweight design, flexible structure, and efficient hardware implementation make it an ideal solution for protecting data in resource-constrained IoT devices, especially in industrial settings where data security is paramount.
Despite its innovative design and promising applications, the security analysis of the IIoTBC algorithm remains incomplete. While IIoTBC is engineered to be lightweight and efficient, the robustness of its cryptographic mechanisms under various attack vectors has not been thoroughly evaluated. Conducting such an analysis is crucial for identifying potential vulnerabilities and validating the algorithm’s efficacy in providing secure data transmission within industrial IoT environments. By systematically investigating IIoTBC’s security properties, researchers can ensure that it meets the stringent security standards required for protecting sensitive industrial data.
1.2. Related Works
Integral cryptanalysis is a method of cryptanalysis that is used to attack symmetric key block ciphers [,,,]. This form of analysis is crucial for evaluating the strength of cryptographic algorithms against structured attacks. Integral cryptanalysis typically involves examining the behavior of algorithmic transformations over sets of plaintexts and observing specific patterns in the resulting ciphertexts. The discovery of these patterns, or distinguishers, can be instrumental in uncovering vulnerabilities within the cipher, thus providing valuable insights into its security profile [,,].
The division property, introduced by Todo at EUROCRYPT 2015 [] as a generalized integral property, is currently recognized as the most efficient and accurate method for detecting integral distinguishers. This property can effectively exploit algebraic degree information to identify balanced output bits, as evidenced by its successful application in breaking the full MISTY1 cipher. However, the initial version of the division property was word-oriented, focusing solely on the algebraic degree of nonlinear exponents and lacking the ability to utilize the internal structure of ciphers in a detailed manner.
Todo and Morii introduced the bit-based division property at FSE 2016 to address this limitation. This included both the conventional bit-based division property and the three-subset bit-based division property. Wang et al. later demonstrated that the three-subset bit-based division property could be used to recover the exact superpoly in cube attacks. This concept was further refined by Hao et al., leading to the three-subset bit-based division property without unknown subsets (3SDPwoU). Recently, Hebborn et al. pointed out that the 3SDPwoU, viewed from the perspective of the parity set actually determines the presence or absence of certain monomials in the polynomial representation of the cipher output [,,].
At ASIACRYPT 2020, Hu et al. introduced the concept of monomial prediction, which reinterprets division properties directly from the polynomial viewpoint. By counting monomial trails, they could ascertain whether a monomial from the plaintext or initialization vector (IV) appears in the cipher output polynomial. It was subsequently demonstrated that monomial prediction and the 3SDPwoU are equivalent in their application [,,,,,,].
Mixed-integer linear programming (MILP) has emerged as a groundbreaking tool in the realm of automated cryptanalysis. MILP’s ability to model complex cryptographic operations through linear inequalities offers a systematic and efficient approach to uncovering potential weaknesses in cipher algorithms [,,,,]. By translating cryptographic structures into MILP models, researchers can leverage powerful computational techniques to analyze and break ciphers in ways that were previously unfeasible, making it an indispensable tool in modern cryptanalysis [,,,,].
Despite the robustness of MILP in integral cryptanalysis, the design of the IIoTBC algorithm did not specifically account for resistance to such analysis. Therefore, assessing IIoTBC’s resilience against integral cryptanalysis using MILP is essential for ensuring its security in industrial IoT environments.
1.3. Our Contributions
Application of Division Property and MILP. We have innovatively applied the division property method and mixed-integer linear programming (MILP) to conduct a comprehensive automated cryptanalysis of the IIoTBC algorithm.
Discovery of Integral Distinguishers. Our analysis has unveiled a 14-round integral distinguisher for IIoTBC System A and a full-round distinguisher for System B, revealing crucial insights into the structural strengths and vulnerabilities of these systems.
Extended Cryptanalysis and Structural Insights. For System A, we extended our findings to a 22-round key recovery, demonstrating the practical impact of the discovered vulnerabilities. In System B, we identified a significant structural issue—the lack of diffusion in its third branch—which highlights a critical area for potential improvement.
Our work represents a significant stride in the automated cryptanalysis of IIoTBC, offering a deeper understanding of its security aspects and potential areas for improvement. By systematically exposing and scrutinizing the algorithm’s vulnerabilities, this research contributes significantly to the advancement of cryptographic security in industrial IoT applications, a domain that is becoming increasingly crucial in our digitally connected world.
1.4. Organization
In Section 2, we review the basics of the cipher, division property, and MILP-based cryptanalysis. In Section 3, we present the details of constructing the MILP automatic search model and the distinguisher for IIoTBC. The process of key recovery for IIoTBC-A is detailed in Section 4, which is followed by a theoretical elucidation of the distinguisher for IIoTBC-B in Section 5. Finally, Section 6 provides a concise conclusion of our findings.
2. Preliminaries
2.1. Notations
In this subsection, we present the notations used throughout this paper. Let and denote as the n-bit string over . Let denote the integer ring and denote the set of all n-dimensional vectors with coordinates over . For easier expression, we give the description of notations used in this paper in Table 1.

Table 1.
Definition of notation.
For any , we define as the i-th bit of a, and the Hamming weight is calculated by . Furthermore, for any , the vectorial Hamming weight of is defined as .
For any and , we define if for all i. Otherwise, . For an integral distinguisher, denotes s successive active bits, denotes s successive constant bits, denotes s successive balanced bits, and denotes s successive unknown bits.
Definition 1
(Bit Product Function). Let be a function from to . For any and , the bit product function is defined as
Let be a function from to . For any , , the bit product function is defined as
2.2. IIoTBC Block Cipher
The algorithm [] is a lightweight block cipher designed for the security of industrial IoT (IIoT). It features a variable system structure that adapts to different security requirements and is particularly suited for environments with limited hardware resources, such as sensor nodes in IIoT. works with 128-bit keys and has a block size of 64 bits. It offers two system structures, System A and System B, catering to different microcontroller unit (MCU) capabilities.
2.2.1. System A Structure (IIoTBC-A)
IIoTBC-A is optimized for 8-bit MCUs, which are commonly used in industrial IoT settings. It is based on an eight-branch generalized Feistel structure, as shown in Figure 1.
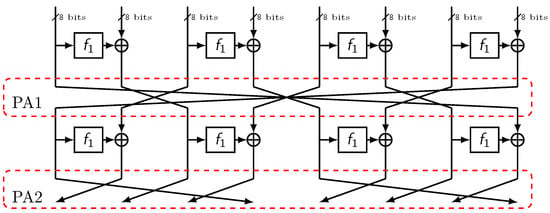
Figure 1.
The encryption process of IIoTBC-A.
Each branch undergoes a transformation that involves the use of a function , which incorporates steps like AddRoundkey, S-box permutation, and a 1-bit left rotation, as shown in Figure 2. The S-box is as follows.
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| S(x) | 5 | D | 9 | 4 | 6 | 3 | F | 1 | B | 8 | E | 0 | 7 | 2 | C | A |

Figure 2.
The round function of IIoTBC-A.
Functions PA1 and PA2 are utilized for the exchange of branch data positions. This is crucial in ensuring data diffusion across the branches.
The algorithm executes these steps for 32 rounds, enhancing the security with each iteration.
2.2.2. System B Structure (IIoTBC-B)
IIoTBC-B is designed for 16-bit MCUs, which offer better data processing capabilities and more memory compared to 8-bit MCUs. Unlike IIoTBC-A, IIoTBC-B uses a four-branch generalized Feistel structure, as shown in Figure 3. This reflects a more complex and secure approach, suitable for the enhanced capabilities of 16-bit MCUs.
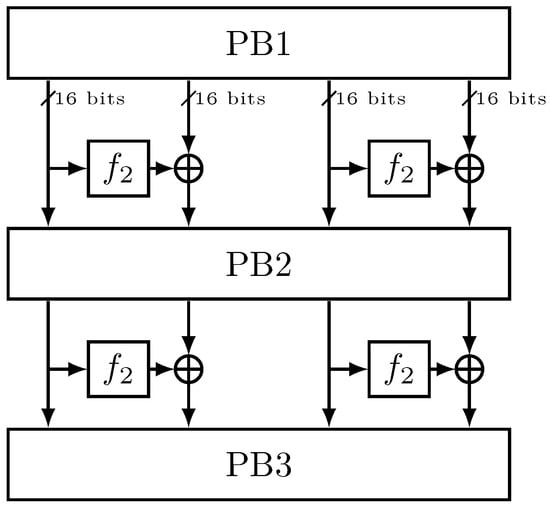
Figure 3.
The encryption process of IIoTBC-B.
A notable feature is its reliance on bit-slice technology. Each of the four branches in IIoTBC-B is represented as a matrix. The 64-bit input data are transformed into four slices, setting the stage for branch-specific processing. PB1 is to rearrange the 64-bit data and convert them to the input of four branches.
The function is applied to each branch, with its operation process adding to the cipher’s complexity and security, as shown in Figure 4. Different permutation functions (PB2 and PB3) are used for processing in odd and even rounds, individually. These operation processes of PB1, PB2, and PB3 are shown in Figure 5.
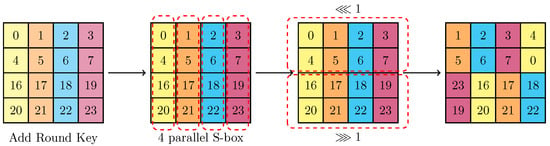
Figure 4.
The round function of IIoTBC-B.
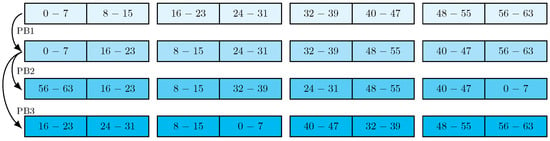
Figure 5.
The PB1, PB2, and PB3 of IIoTBC-B.
2.3. Bit-Based Division Property
The division property, as introduced in [], represents an advanced form of the integral property. Its primary function is to leverage the underlying relationships between traditional integral properties like ALL and BALANCE, thereby serving as a potent tool for developing enhanced integral distinguishers. In this subsection, we aim to succinctly revisit the concepts of the division property and outline the key propagation rules associated with the bit-based division property.
Definition 2
(Division Property). Let be a multiset whose elements take values from and let denote a set of m-dimensional vectors whose i-th element takes a value between 0 and ; this fulfills the following conditions:
If two vectors and in satisfy that , then is redundant and will be removed from . It is worth noting that, for the bit-based division property, are restricted to 1.
Propagation Rules of Bit-Based Division Property
For the bit-based division property, the rules governing operations such as COPY, XOR, AND, and Rotation are described as follows [].
Proposition 1
(COPY []). Let F be a COPY function, where the input is and the output is calculated as . Let and be the input multiset and output multiset, respectively. Assuming that the multiset has the division property , then the multiset has the division property , where is computed as
Proposition 2
(XOR []). Let F be an XOR function, where the input is and the output is calculated as . Let and be the input multiset and output multiset, respectively. Assuming that the multiset has the division property , then the multiset has the division property , where is computed as
Proposition 3
(AND []). Let F be an AND function, where the input is and the output is calculated as . Let and be the input multiset and output multiset, respectively. Assuming that the multiset has the division property , then the multiset has the division property , where is computed as
Proposition 4
(Rotation). Let F be a Left Rotation function, where the input is and the output is calculated as . Let and be the input multiset and output multiset, respectively. Assuming that the multiset has the division property , then the multiset has the division property , where is computed as
Todo, in [], posited that analyzing the propagation of the division property through a block cipher essentially involves the transition of vectors. Let represent the round function of a block cipher and denote a given initial division property. Following the rules detailed in [], the initial division property propagates through the round function to yield the division property , where comprises a set of vectors in . Therefore, the process of division property propagation through fundamentally constitutes a transition from to the vectors within .
Definition 3
(Division Trail). Let denote the round function of an iterated block cipher. Assume that the input multiset to the block cipher has initial division property , and denote the division property after i-round propagation through by . Thus, we have the following chain of division property propagations:
Moreover, for any vector in (), there must exist a vector in such that can propagate to by division property propagation rules. Furthermore, for , if can propagate to for all , we call an r-round division trail.
2.4. MILP Automatic Cryptanalysis
MILP automates the process of identifying weak points in cryptographic algorithms. It can efficiently handle large, complex systems, making it an invaluable tool in assessing modern cryptographic methods, which are often too complex for manual analysis. Central to MILP are the following key elements:
- Objective Function: The cornerstone of any MILP problem is its objective function, a linear expression that the solution process seeks to maximize or minimize. This function encapsulates the goal of the optimization, such as cost minimization or profit maximization.Maximize:
- Decision Variables: These are the variables whose values need to be determined. In MILP problems, these variables can be integers, binary (0 or 1), or continuous.
- Constraints: Constituting the backbone of the problem, constraints are linear equations or inequalities that limit the values of decision variables. They ensure that the solution adheres to practical conditions or business rules., and
- Parameters: These are known numerical values within the problem, used to define the constraints and the objective function. Variable Bounds: These define the permissible range (upper and lower limits) for the decision variables.and are integers
Together, these components form the basis of MILP, enabling it to tackle a wide range of optimization problems by finding the best possible solution under given constraints. Within the domain of MILP, Gurobi 10.0.3 http://www.gurobi.com/ (accessed on 10 December 2023) stands out as a pivotal optimization solver, offering a robust and efficient platform for tackling MILP problems. Solving an MILP problem using Gurobi involves a structured process. An outline of the typical workflow is given as follows
- Setup and Initialization
- Import the Gurobi library in your programming environment:from gurobipy import Model, GRB.
- Initialize a new model:m = Model("model_name").
- Define variables with types (integer, binary, continuous) and bounds:x = m.addVar(vtype=GRB.INTEGER, name="x"),y = m.addVar(vtype=GRB.INTEGER, name="y").
- Objective Function
- Set the objective (maximization or minimization):m.setObjective(20*x + 30*y, GRB.MAXIMIZE).
- Adding Constraints
- Formulate and add constraints to the model:m.addConstr(2*x + 3*y <= 100, "constraint_name1"),m.addConstr(x + 2*y <= 40, "constraint_name2").
- Optimization
- Optimize the model using: m.optimize().
- Optionally, tune parameters for complex problems.
- Solution Extraction and Analysis
- Check the solution status and ensure an optimal solution is found:m.status == GRB.Status.OPTIMAL
- Retrieve and analyze the results ("x.x", "y.x", the objective function value "m.objVal").
.
MILP provides the theoretical and practical framework for complex optimization problems, while Gurobi offers the technological prowess and computational efficiency to solve these problems effectively. This synergy is integral to the field of optimization, driving both academic research and practical applications forward.
3. Automatic Search Model for IIoTBC
3.1. Initial Bit-Based Division Property and Stop Rules
3.1.1. Initial Division Property
In the context of integral distinguisher search algorithms, an initial division property denoted as , symbolized by a vector , is often provided. Consider a division trail over r rounds, expressed as
Here, represents a system of linear inequalities defined on the variables (where and ) along with some auxiliary variables. It is necessary to incorporate the conditions (for ) into the system . Consequently, all feasible solutions of are division trails commencing from the vector .
In the case of ciphers, the data complexity of the cipher should be lower than . To ascertain the longest integral distinguisher within the framework, we commence by initializing the vector . This vector is configured such that its Hamming weight, denoted by , is precisely 63. This initialization results in an initial division property comprising 64 distinct vectors.
3.1.2. Stop Rule
Consider a set with the division property . If does not exhibit any integral property, for any , the projection remains unknown for any unit vector . Since has the division property , there must exist a vector such that . Given that u is a unit vector, we have , which implies that the set contains all n unit vectors.
Given a specific initial division vector , our analysis focuses on the division property , which describes the output divisions after r rounds in a cryptographic cipher. If includes all n unit vectors, it signals the point at which the algorithm should be terminated. This implies that, under the stipulated conditions, an r-round distinguisher is not found. Consequently, the longest possible integral distinguisher, based on the initial division vector , is confined to a maximum of rounds.
Thus, the objective function is
3.2. Modeling Division Propagation Using Linear Inequalities
The IIoTBC algorithm incorporates several fundamental operations, including COPY, XOR, rotation, and S-box. In the following subsections, we introduce models for the propagation of the bit-based division property associated with S-box operations.
Model S-Box
To construct the linear inequality system for an S-box, we first apply the table-aided bit-based division property, generating the S-box’s propagation table. Following this, the inequality_generator() function within the Sage 10.2 http://www.sagemath.org/ (accessed on 10 December 2023) framework is employed to derive a set of linear inequalities []. It is noteworthy, however, that the resultant number of linear inequalities can be substantial, occasionally to the extent that their complete integration into the MILP model leads to computational impracticality.
To mitigate this challenge, Sun et al. [] introduced a method termed the greedy algorithm, aimed at reducing the size of this inequality set. In the context of the S-box analyzed using Sage, the initial count of linear inequalities stands at 84. Application of the greedy algorithm (as described in Algorithm 1 of []) effectively reduces this number to 10. The following inequalities are 10 inequalities used to describe the S-box, where denotes a division trial.
3.3. Model and Distinguisher of IIoTBC-A and IIoTBC-B
Up to this point, for block ciphers based on the three operations (COPY, AND, XOR) and S-boxes, we can construct a set of linear inequalities that characterize the division property propagation for one round. By iterating this process r times, a linear inequality system L can be formulated, describing r rounds of division property propagation. All feasible solutions of L correspond to all possible r-round division trails. Let , , , and represent ACTIVE, CONSTANT, BALANCE, and UNKNOWN bits, respectively.
3.3.1. 1-Round Description of IIoTBC-A
Consider a one-round division trail of IIoTBC-A, denoted as . IIoTBC-A utilizes an eight-branch generalized Feistel structure, and thus the first modeling step addresses the COPY operation for the four left branches. The outputs of this COPY operation serve as inputs to the round function and the permutations (PA1 or PA2), guiding the division property propagation. This is represented by the set of following equations:
Here, and correspond to the inputs for the round function and the permutations, respectively. The function in IIoTBC-A consists of two parallel S-boxes coupled with a left rotation. The division trails for these S-boxes are calculated as detailed in Section 3.2 and modeled through a series of linear inequalities. Considering the presence of four parallel instances of in IIoTBC-A, we introduce 10 inequalities for each S-box, leading to a total of inequalities for the eight S-boxes, collectively denoted as . The output of the S-boxes is denoted by , and the division trails for these eight S-boxes are defined as
Post-processing through four instances of involves an XOR operation with the four right branches, integrated with the left rotation of . The output of this XOR operation then becomes the input for the permutation, leading to the following division propagation model:
The permutation layers in IIoTBC-A (PA1 and PA2) simply permute the bits, thereby transforming the vector coordinates .
Consequently, we have formulated a linear inequality system to characterize the division propagation in one round of IIoTBC-A. Iteratively applying this model for r rounds constructs a comprehensive linear inequality system. Integrating a given initial division property into this system allows us to use Gurobi to assess the potential existence of an integral distinguisher.
3.3.2. Distinguisher of IIoTBC-A
The longest integral distinguisher that we found for IIoTBC-A is 14 rounds, and the number of chosen plaintexts is . Some distinguishers are listed as follows, where represents that there is a one-bit CONSTANT in an arbitrary position of these eight bits and that the other seven bits are ACTIVE.
3.3.3. 1-Round Description of IIoTBC-B
Consider the scenario of a one-round division trail in IIoTBC-B. Analogous to IIoTBC-A, IIoTBC-B is structured upon a four-branch Feistel architecture. The initial phase involves the modeling of the COPY operation, which is represented by the set of following equations:
Here, and correspond to the inputs for the round function and the permutations, respectively. The function in IIoTBC-B consists of four parallel S-boxes coupled with a left rotation and a right rotation. Considering the presence of two parallel instances of in IIoTBC-B, we introduce 10 inequalities for each S-box, leading to a total of inequalities for the eight S-boxes, collectively denoted as . The output of the S-boxes is denoted by , and the division trails for these eight S-boxes are defined as
Post-processing through two instances of involves an XOR operation with the two right branches, integrated with the left rotation and right rotation of . The output of this XOR operation then becomes the input for the permutation, leading to the following division propagation model:
The permutation layers in IIoTBC-B transform the vector coordinates . Consequently, we have formulated a linear inequality system to characterize the division propagation in one round of IIoTBC-B.
3.3.4. Distinguisher of IIoTBC-B
Initially, the data complexity was set to to identify the longest possible distinguisher. Subsequent experimentation, however, revealed a noteworthy observation: regardless of the number of rounds, even extending to as many as 100, integral distinguishers were consistently discovered. This led to a strategic adjustment in our approach, where the data complexity was reduced to . This alteration in methodology culminated in the identification of several distinguishers. Selected results from this investigative process are presented below.
It was observed that when the 16th to 23rd bits remained continuously active, integral distinguishers were invariably identified. This consistent finding underscores the significance of these particular bit positions in the context of the distinguisher’s effectiveness. A comprehensive explanation for this phenomenon is elaborated in Section 5, where we delve into the specifics of this observation and its implications.
4. Key Recovery of IIoTBC-A
In this section, we focus on key recovery attacks for 22-round IIoTBC-A based on the 14-round distinguisher described in Section 3.
- Integral Distinguisher Utilization. For a set of plaintexts, denoted as P, with the form , the intermediate state after 14 rounds, denoted as , is of the form .
It is well established that once an integral characteristic is identified, it can be employed for a key recovery attack. Let f be the Boolean function representing the mapping from the ciphertext of IIoTBC-A to one of the balanced intermediate bits of (the output of the integral distinguisher). Our focus is on the following equation:
where is any one balanced bit and C is the corresponding set of ciphertexts encrypted from P. In evaluating this equation, we guess the involved subkey bits used in f and check whether the equation holds. Subkey values that violate this equation are filtered out and discarded, leaving the remaining candidates for the correct subkeys.
- Data Preparation We selected a set P of plaintexts from the structure . Each plaintext (for ) undergoes encryption under the 22-round IIoTBC-A algorithm, yielding the corresponding ciphertext denoted as . The output, corresponding to these specific inputs after 14 rounds of the encryption process, manifests a distinct characteristic , wherein 24 bits maintain a balanced state. Capitalizing on this phenomenon, particularly the equilibrium observed in the final 4 bits, we advance into the phases of subkey guessing and recovery.
- Subkey Guessing. We initiate our analysis from the starting point of [28–30] and continue to trace forward to determine the positions where key guessing is required. The process of deduction is illustrated in Figure 6, where all the yellow-colored functions represent the computations required for reverse decryption. The subkeys used in these functions must either be guessed or deduced.
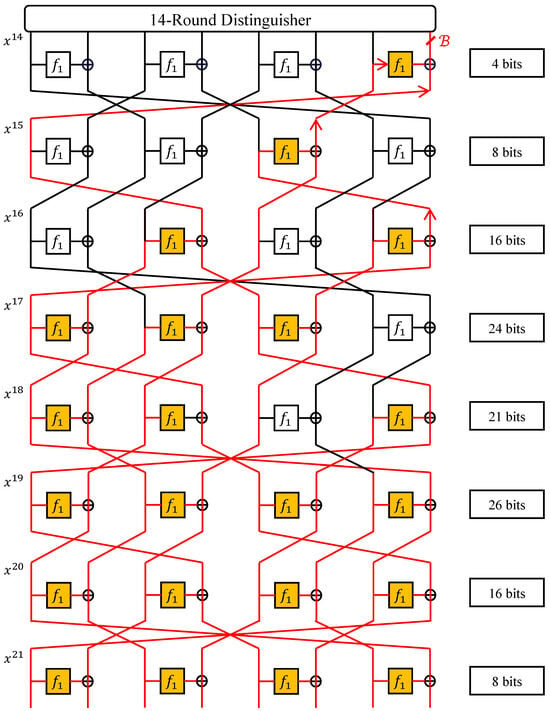 Figure 6. Key recovery of 22-round System A.
Figure 6. Key recovery of 22-round System A.
This process is complemented by considering the structure of the key generation algorithm, and we halt our examination at the round where the total number of guessed key bits is less than 128. The subkey generation is detailed in Appendix A. For rounds 5 to r, the subkey generation method satisfies the following equation:
where is the subkey for the i-th round.
Consequently, the subkeys required for subsequent rounds can be inferred from the subkeys guessed in earlier rounds, implying that not all necessary subkeys require independent guessing. The subkeys for rounds 15, 16, 17, and 18 necessitate guessing. However, starting from round 19, some subkeys can be computed based on those deduced in previous rounds. By integrating the subkey generations algorithm, we start our deduction from round 15 and proceed to identify the subkeys that need to be guessed. The specific subkeys required for each round, along with the positions of the subkeys that need to be guessed, are detailed in Table 2.

Table 2.
The position of guessing subkey in 15 to 22 rounds.
For instance, in the case of the 20th round, it is necessary to conjecture the following set of register values:
whereas the remaining values in the set
can be derived using certain subkeys from and , as explained in the following:
The aggregate number of subkeys that require guessing amounts to 126 bits. Specifically, for the 21-round and 20-round scenarios, the bit counts for the guessed subkeys are 118 and 102, respectively. In the context of the 22-round key, 46 subkeys can be computed based on previously guessed keys, necessitating the use of 46 S-boxes.
- Verification and Elimination. Let be the Boolean function representing the mapping from the 22-round ciphertext of IIoTBC-A to the partially balanced intermediate bits of . After that partial decryption, the , , and should be balanced.where .
For each ciphertext , the procedure involves using the guessed keys to partially decrypt the ciphertexts, transforming the 22-round ciphertext back to its state after the 14th round. This process requires executing 22 instances of .
The integrity of the decrypted data is then assessed against the expected integral property. Should this property be observed, it suggests the possibility of the guessed key bits being correct. Conversely, if the property does not hold, those key bits are discarded, prompting a new set of guesses. The key space under consideration entails a 126-bit guess.
- Complexity Analysis. The number of plaintext–ciphertext pairs required to reliably observe the integral property is , and the complexity is calculated as 22-round IIoTBC-A. Each decryption operation, translating the 22-round ciphertext back to its state after the 14th round, necessitates 22 invocations of . In comparison, a full 22-round encryption process requires 88 instances of . For the last four rounds, we can conjecture the round key and execute partial decryption, storing the results in a table. The numbers of guessed key bits for these rounds are 32, 32, 32, and 24, with the corresponding requirements of four, four, four, and three instances of , respectively. Thus, the complexity is calculated as IIoTBC-A encryptions. This part can be managed using four tables.
For the remaining four rounds, it is only necessary to guess bits; the rest of the 46 subkeys can be computed from the subkeys above. The number of instances in these rounds is seven, resulting in a complexity of IIoTBC-A encryptions. Therefore, the total complexity is calculated as
5. Integral Cryptanalysis of Full IIoTBC-B
In Section 3.3, we present our experimental results, which indicate that when the 16th to 23rd bits of the input are ACTIVE, a distinguisher can invariably be found, irrespective of the number of rounds.
To theoretically elucidate and substantiate these results, we will next describe the propagation through two rounds of the IIoTBC-B round function. Here, we denote an 8-bit ACTIVE input as x and an 8-bit constant as .
- Input: Denote the initial input as .
- After S-box and XOR: The output of the first round function iswhere , , , and .
- Permutation: The output after permutation becomes
- Second Round—S-box and XOR: The output after the second-round S-box and XOR operation iswhere , , , and .
- Final Output: The final output after the second permutation step is
After two rounds of encryption, the third branch becomes , which can be expressed as
Notably, apart from x, all operations within this branch involve constants or operations between constants, thereby ensuring that the third branch exhaustively explores all possible scenarios. As for the other branches, they persistently engage in operations amongst constants, which implies that their outputs also remain CONSTANT. This phenomenon is depicted in Figure 7, where the red lines illustrate the diffusion pattern of the third branch. It is observed that even after two rounds involving PB2 and PB3 operations, the third branch does not diffuse into other branches. Consequently, as long as the eight bits of the third branch are ACTIVE at the input, a distinguisher can consistently be identified, regardless of the number of encryption rounds.
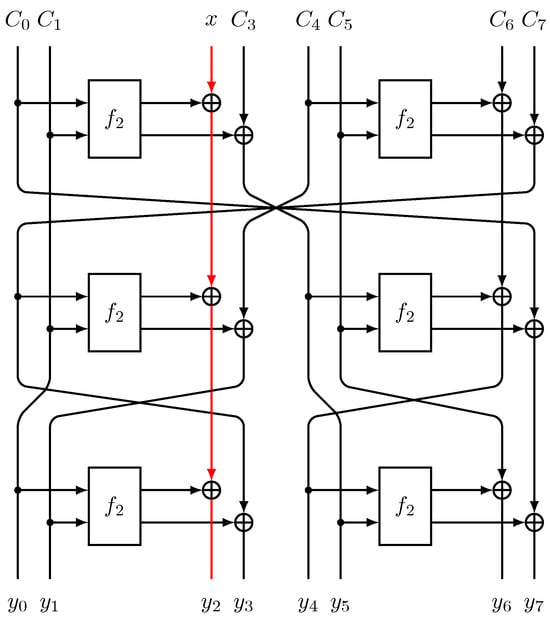
Figure 7.
Two-round encryption process of IIoTBC-B.
6. Conclusions
This paper has presented a comprehensive cryptanalysis of the IIoTBC algorithm, a cipher paramount in securing industrial IoT environments. Through meticulous research and application of MILP-based automated cryptanalysis, we have successfully unveiled integral distinguishers for both IIoTBC-A and System B, highlighting their respective cryptographic strengths and vulnerabilities.
For IIoTBC-A, the discovery of a 14-round integral distinguisher, followed by a successful 22-round key recovery attack, marks a significant achievement. This finding not only demonstrates the cipher’s susceptibilities but also emphasizes the need for continued vigilance in the design and analysis of cryptographic solutions for IoT systems. The 14-round distinguisher indicates potential weaknesses in the cipher’s structure, which could be exploited in real-world attacks. The subsequent 22-round key recovery further underscores the necessity of evaluating and enhancing the robustness of IIoTBC-A to safeguard sensitive industrial data.
In the case of IIoTBC-B, our identification of a full-round distinguisher represents a substantial advancement in understanding this variant’s security profile. The full-round distinguisher signifies that the entire cipher can be analyzed in a manner that reveals underlying patterns or correlations, which could compromise its security. This discovery is crucial for informing future designs and updates to the IIoTBC-B algorithm, ensuring that it remains a reliable component in IoT security frameworks.
The use of the division property method and MILP-based cryptanalysis in this study has proven to be highly effective. These techniques have allowed for a deeper exploration of the block cipher’s structure and potential security issues, illustrating the power of modern cryptanalytic methods in assessing and enhancing cipher security. By leveraging these advanced methods, we have provided a thorough evaluation of the IIoTBC algorithm, contributing valuable insights that can guide the development of more secure cryptographic solutions for industrial IoT environments.
Moreover, our findings have broader implications for the field of cryptography. They underscore the importance of continuous and rigorous cryptanalysis in the lifecycle of cryptographic algorithms. As the landscape of IoT continues to evolve, so too must the cryptographic methods used to protect it. Our research highlights the necessity for ongoing assessment and innovation to pre-emptively address potential vulnerabilities and ensure the robustness of encryption methods in increasingly complex digital ecosystems.
Author Contributions
Conceptualization, F.L. and Z.S.; data curation, X.L.; formal analysis, F.L. and Z.S.; funding acquisition, C.L.; investigation, J.W.; resources, C.L.; software, F.L. and X.L.; writing—original draft, F.L.; writing—review and editing, F.L., Z.S., X.L. and J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the Major Research plan of the National Natural Science Foundation of China, grant number 92167203; in part by the National Natural Science Foundation of China, grant number 62002077; in part by Guangdong Basic and Applied Basic Research Foundation, grant number 2024A1515011492; in part by Guangzhou Science and Technology Plan Project, grant number 2023A03J0119; in part by Guangxi Key Laboratory of Trusted Software, grant number KX202313.
Data Availability Statement
The detailed code for our analysis is available at https://github.com/YoLaughing/integral-attack-for-IIoTBC (accessed on 1 March 2024).
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Subkey Generation
The key size of is 128 bits. For the convenience of description, we represent the primary 128-bit keys as .
The relationship between the registers and the 128-bit keys can be expressed as follows:
where ‖ denotes the concatenation of bits.
Registers , and are used sequentially for rounds 1 to 4 of the AddRoundkey operation. For rounds 5 to r, the subkey generation method satisfies the following equation:
where is the subkey for the i-th round, and ⊕ denotes the bitwise XOR operation.
The function, which is part of the subkey generation process, includes a permutation and a S-box permutation.
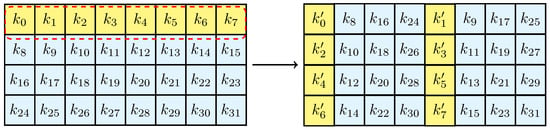
Figure A1.
The operation process of .
References
- Wilamowski, B.M.; Irwin, J.D. Industrial Communication Systems; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Khalid, H.; Hashim, S.J.; Ahmad, S.M.S.; Hashim, F.; Chaudhary, M.A. SELAMAT: A new secure and lightweight multi-factor authentication scheme for cross-platform industrial IoT systems. Sensors 2021, 21, 1428. [Google Scholar] [CrossRef] [PubMed]
- Yitian, G.; Liquan, C.; Tianyang, T.; Yuan, G.; Qianye, C. Post-quantum encryption technology based on BRLWE for internet of things. Chin. J. Netw. Inf. Secur. 2022, 8, 140. [Google Scholar] [CrossRef]
- Smith, J.; Doe, J. Advances in Industrial IoT Security. IEEE Trans. Ind. Inform. 2018, 14, 3550–3561. [Google Scholar]
- Johnson, M.; Lee, R. A Survey on IIoT Architectures and Applications. J. Netw. Comput. Appl. 2020, 150, 102481. [Google Scholar]
- Wang, A.; Zhang, B. Machine Learning in IIoT Systems. In Proceedings of the International Conference on IoT, Changsha, China, 21–23 August 2022; ACM: New York, NY, USA, 2019; pp. 765–770. [Google Scholar]
- Brown, D.; Green, E. IIoT and the Future of Smart Manufacturing. In Emerging Trends in IoT; Springer: Berlin/Heidelberg, Germany, 2021; pp. 101–120. [Google Scholar]
- Lee, K. IIoT in Industry 4.0: Challenges and Opportunities. In Technical Report IIC-WP-07-2017; Industrial Internet Consortium: Boston, MA, USA, 2017. [Google Scholar]
- Kuang, J.; Guo, Y.; Li, L. IIoTBC: A Lightweight Block Cipher for Industrial IoT Security. KSII Trans. Internet Inf. Syst. 2023, 17, 97–119. [Google Scholar]
- Daemen, J.; Knudsen, L.R.; Rijmen, V. The Block Cipher Square. In FSE’97; Biham, E., Ed.; Springer: Berlin/Heidelberg, Germany, 1997; Volume 1267, pp. 149–165. [Google Scholar] [CrossRef]
- Knudsen, L.R.; Wagner, D. Integral Cryptanalysis. In FSE 2002; Daemen, J., Rijmen, V., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2365, pp. 112–127. [Google Scholar] [CrossRef]
- Cui, T.; Sun, L.; Chen, H.; Wang, M. Statistical Integral Distinguisher with Multi-structure and Its Application on AES. In ACISP 17, Part I; Pieprzyk, J., Suriadi, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; Volume 10342, pp. 402–420. [Google Scholar]
- Wang, M.; Cui, T.; Chen, H.; Sun, L.; Wen, L.; Bogdanov, A. Integrals Go Statistical: Cryptanalysis of Full Skipjack Variants. In FSE 2016; Peyrin, T., Ed.; Springer: Berlin/Heidelberg, Germany, 2016; Volume 9783, pp. 399–415. [Google Scholar] [CrossRef]
- Xiang, Z.; Zhang, W.; Lin, D. On the Division Property of Simon48 and Simon64. In IWSEC 16; Ogawa, K., Yoshioka, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; Volume 9836, pp. 147–163. [Google Scholar] [CrossRef]
- Wang, Q.; Hao, Y.; Todo, Y.; Li, C.; Isobe, T.; Meier, W. Improved Division Property Based Cube Attacks Exploiting Algebraic Properties of Superpoly. In CRYPTO 2018, Part I; Shacham, H., Boldyreva, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; Volume 10991, pp. 275–305. [Google Scholar] [CrossRef]
- Hao, Y.; Leander, G.; Meier, W.; Todo, Y.; Wang, Q. Modeling for Three-Subset Division Property Without Unknown Subset—Improved Cube Attacks Against Trivium and Grain-128AEAD. In EUROCRYPT 2020, Part I; Canteaut, A., Ishai, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; Volume 12105, pp. 466–495. [Google Scholar] [CrossRef]
- Todo, Y. Structural Evaluation by Generalized Integral Property. In EUROCRYPT 2015, Part I; Oswald, E., Fischlin, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9056, pp. 287–314. [Google Scholar] [CrossRef]
- Boura, C.; Canteaut, A. Another View of the Division Property. In CRYPTO 2016, Part I; Robshaw, M., Katz, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; Volume 9814, pp. 654–682. [Google Scholar] [CrossRef]
- Todo, Y.; Morii, M. Bit-Based Division Property and Application to Simon Family. In FSE 2016; Peyrin, T., Ed.; Springer: Berlin/Heidelberg, Germany, 2016; Volume 9783, pp. 357–377. [Google Scholar] [CrossRef]
- Sun, L.; Wang, W.; Wang, M. Automatic Search of Bit-Based Division Property. In ASIACRYPT 2017, Part I; Takagi, T., Peyrin, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; Volume 10624, pp. 128–157. [Google Scholar] [CrossRef]
- Zhang, W.; Rijmen, V. Division cryptanalysis of block ciphers with a binary diffusion layer. IET Inf. Secur. 2019, 13, 87–95. [Google Scholar] [CrossRef]
- Sun, L.; Wang, W.; Wang, M.Q. MILP-aided bit-based division property for primitives with non-bit-permutation linear layers. IET Inf. Secur. 2020, 14, 12–20. [Google Scholar] [CrossRef]
- Hu, K.; Wang, Q.; Wang, M. Finding Bit-Based Division Property for Ciphers with Complex Linear Layer. Cryptology ePrint Archive, Report 2020/547. 2020. Available online: https://eprint.iacr.org/2020/547 (accessed on 10 October 2023).
- Hebborn, P.; Lambin, B.; Leander, G.; Todo, Y. Lower Bounds on the Degree of Block Ciphers. In ASIACRYPT 2020, Part I; Moriai, S., Wang, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; Volume 12491, pp. 537–566. [Google Scholar] [CrossRef]
- Xu, Z. Further accelerating the search of differential characteristics based on the SAT method. Chin. J. Netw. Inf. Secur. 2022, 8, 129. [Google Scholar]
- Hebborn, P.; Lambin, B.; Leander, G.; Todo, Y. Strong and Tight Security Guarantees Against Integral Distinguishers. In ASIACRYPT 2021, Part I; Tibouchi, M., Wang, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2021; Volume 13090, pp. 362–391. [Google Scholar] [CrossRef]
- Fu, K.; Wang, M.; Guo, Y.; Sun, S.; Hu, L. MILP-Based Automatic Search Algorithms for Differential and Linear Trails for Speck. In FSE 2016; Peyrin, T., Ed.; Springer: Berlin/Heidelberg, Germany, 2016; Volume 9783, pp. 268–288. [Google Scholar] [CrossRef]
- Sajadieh, M.; Vaziri, M. Using MILP in Analysis of Feistel Structures and Improving Type II GFS by Switching Mechanism. In INDOCRYPT 2018; Chakraborty, D., Iwata, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; Volume 11356, pp. 265–281. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, S.; Cai, J.; Hu, L. Speeding up MILP Aided Differential Characteristic Search with Matsui’s Strategy. In ISC 2018; Chen, L., Manulis, M., Schneider, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; Volume 11060, pp. 101–115. [Google Scholar] [CrossRef]
- Liu, Y.; Xiang, Z.; Chen, S.; Zhang, S.; Zeng, X. A Novel Automatic Technique Based on MILP to Search for Impossible Differentials. In ACNS 23, Part I; Tibouchi, M., Wang, X., Eds.; Springer: Berlin/Heidelberg, Germany, 2023; Volume 13905, pp. 119–148. [Google Scholar] [CrossRef]
- Zhou, C.; Zhang, W.; Ding, T.; Xiang, Z. Improving the MILP-based Security Evaluation Algorithm against Differential/Linear Cryptanalysis Using A Divide-and-Conquer Approach. IACR Trans. Symm. Cryptol. 2019, 2019, 438–469. [Google Scholar] [CrossRef]
- Rohit, R.; AlTawy, R.; Gong, G. MILP-Based Cube Attack on the Reduced-Round WG-5 Lightweight Stream Cipher. In Proceedings of the 16th IMA International Conference on Cryptography and Coding, Oxford, UK, 12–14 December 2017; O’Neill, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2017; Volume 10655, pp. 333–351. [Google Scholar]
- ElSheikh, M.; Youssef, A.M. On MILP-Based Automatic Search for Bit-Based Division Property for Ciphers with (Large) Linear Layers. In ACISP 21; Baek, J., Ruj, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2021; Volume 13083, pp. 111–131. [Google Scholar] [CrossRef]
- ElSheikh, M.; Abdelkhalek, A.; Youssef, A.M. On MILP-Based Automatic Search for Differential Trails Through Modular Additions with Application to Bel-T. In AFRICACRYPT 19; Buchmann, J., Nitaj, A., Rachidi, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; Volume 11627, pp. 273–296. [Google Scholar] [CrossRef]
- Wang, S.; Hu, B.; Guan, J.; Zhang, K.; Shi, T. MILP-aided Method of Searching Division Property Using Three Subsets and Applications. In ASIACRYPT 2019, Part III; Galbraith, S.D., Moriai, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; Volume 11923, pp. 398–427. [Google Scholar] [CrossRef]
- Zhu, B.; Dong, X.; Yu, H. MILP-Based Differential Attack on Round-Reduced GIFT. In CT-RSA 2019; Matsui, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2019; Volume 11405, pp. 372–390. [Google Scholar] [CrossRef]
- Todo, Y. Integral Cryptanalysis on Full MISTY1. In CRYPTO 2015, Part I; Gennaro, R., Robshaw, M.J.B., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9215, pp. 413–432. [Google Scholar] [CrossRef]
- Xiang, Z.; Zhang, W.; Bao, Z.; Lin, D. Applying MILP Method to Searching Integral Distinguishers Based on Division Property for 6 Lightweight Block Ciphers. In ASIACRYPT 2016, Part I; Cheon, J.H., Takagi, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; Volume 10031, pp. 648–678. [Google Scholar] [CrossRef]
- Todo, Y. Integral Cryptanalysis on Full MISTY1. J. Cryptol. 2017, 30, 920–959. [Google Scholar] [CrossRef]
- Sun, S.; Hu, L.; Wang, M.; Wang, P.; Qiao, K.; Ma, X.; Shi, D.; Song, L.; Fu, K. Towards Finding the Best Characteristics of Some Bit-oriented Block Ciphers and Automatic Enumeration of (Related-Key) Differential and Linear Characteristics with Predefined Properties. Cryptology ePrint Archive, Report 2014/747. 2014. Available online: https://eprint.iacr.org/2014/747 (accessed on 10 October 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).