Oceanic Shallow-Water Investigations on a Variable-Coefficient Davey–Stewartson System
Abstract
1. Introduction
2. Painlevé Test
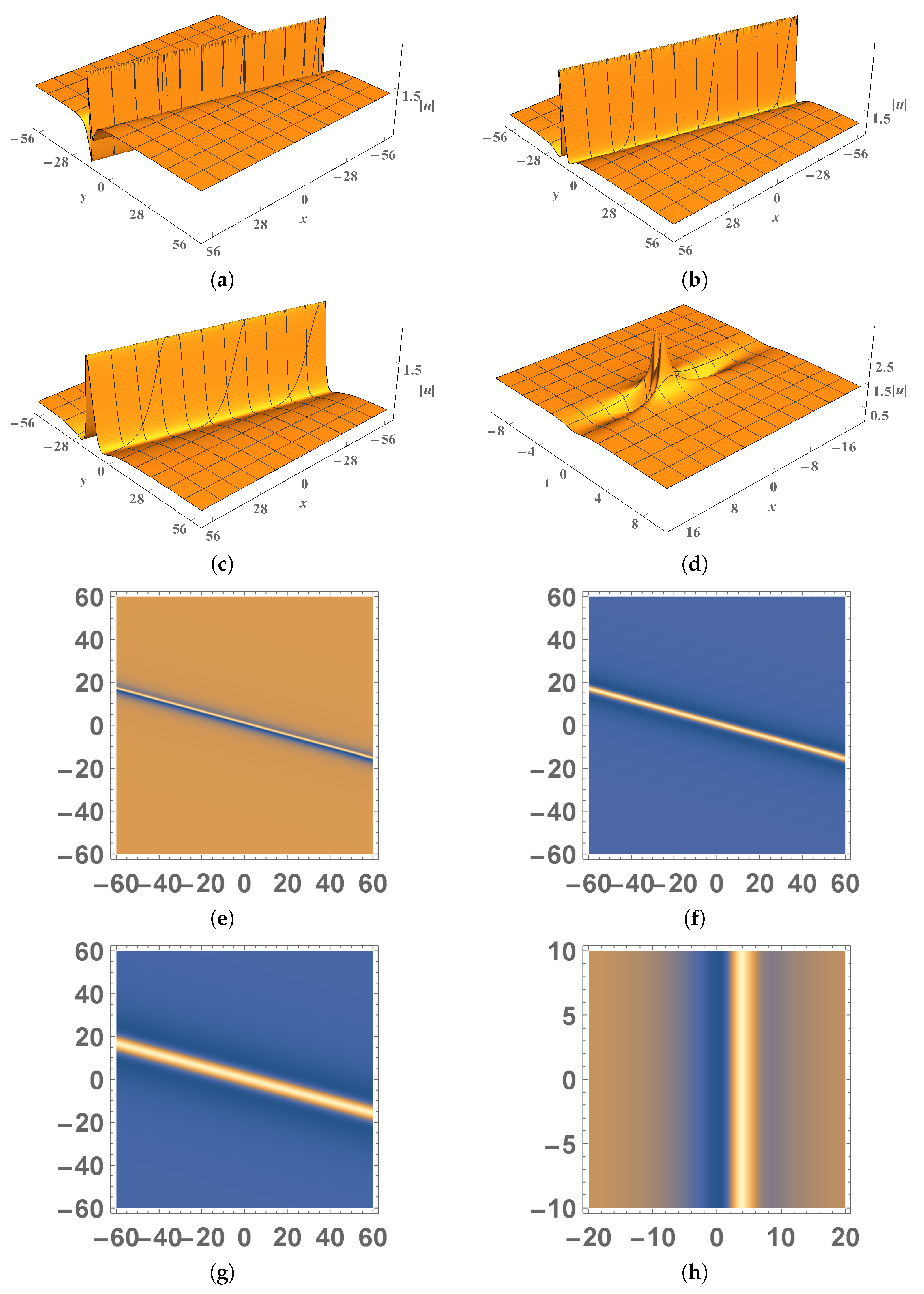
3. Rational Solutions
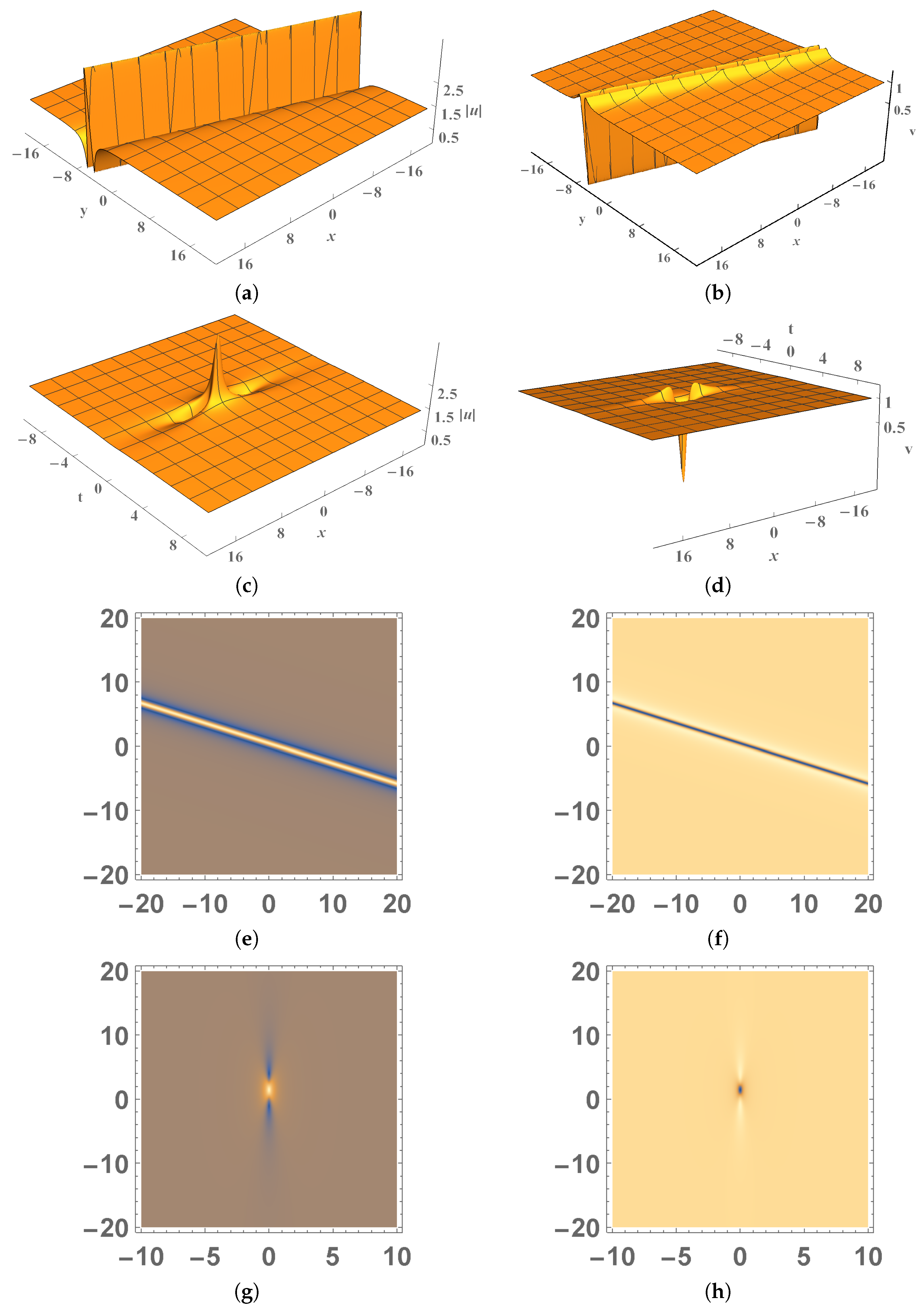
4. Rogue Wave Solutions
4.1. Fundamental Rational Solution
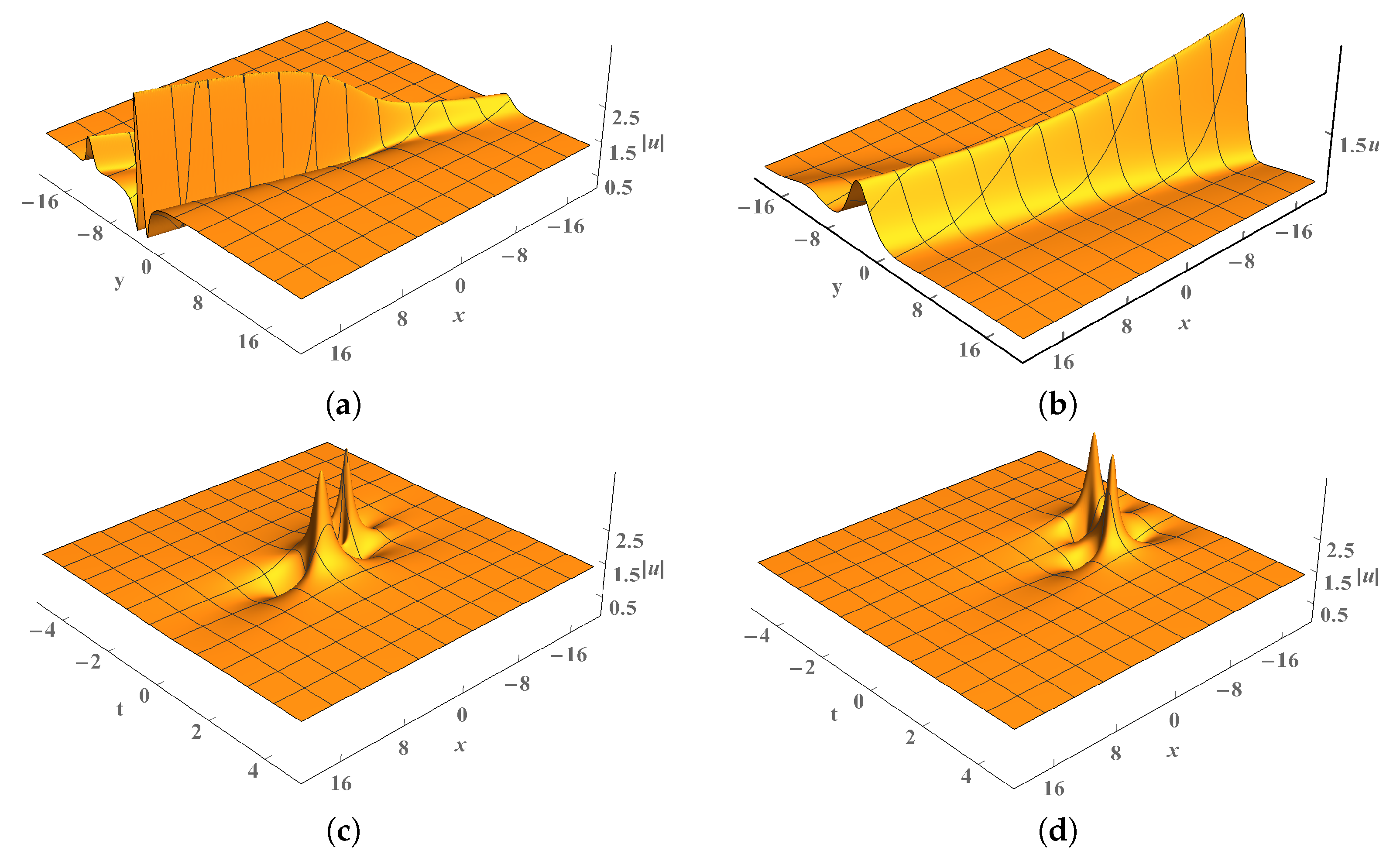
4.2. Multi-Rogue Wave Solution
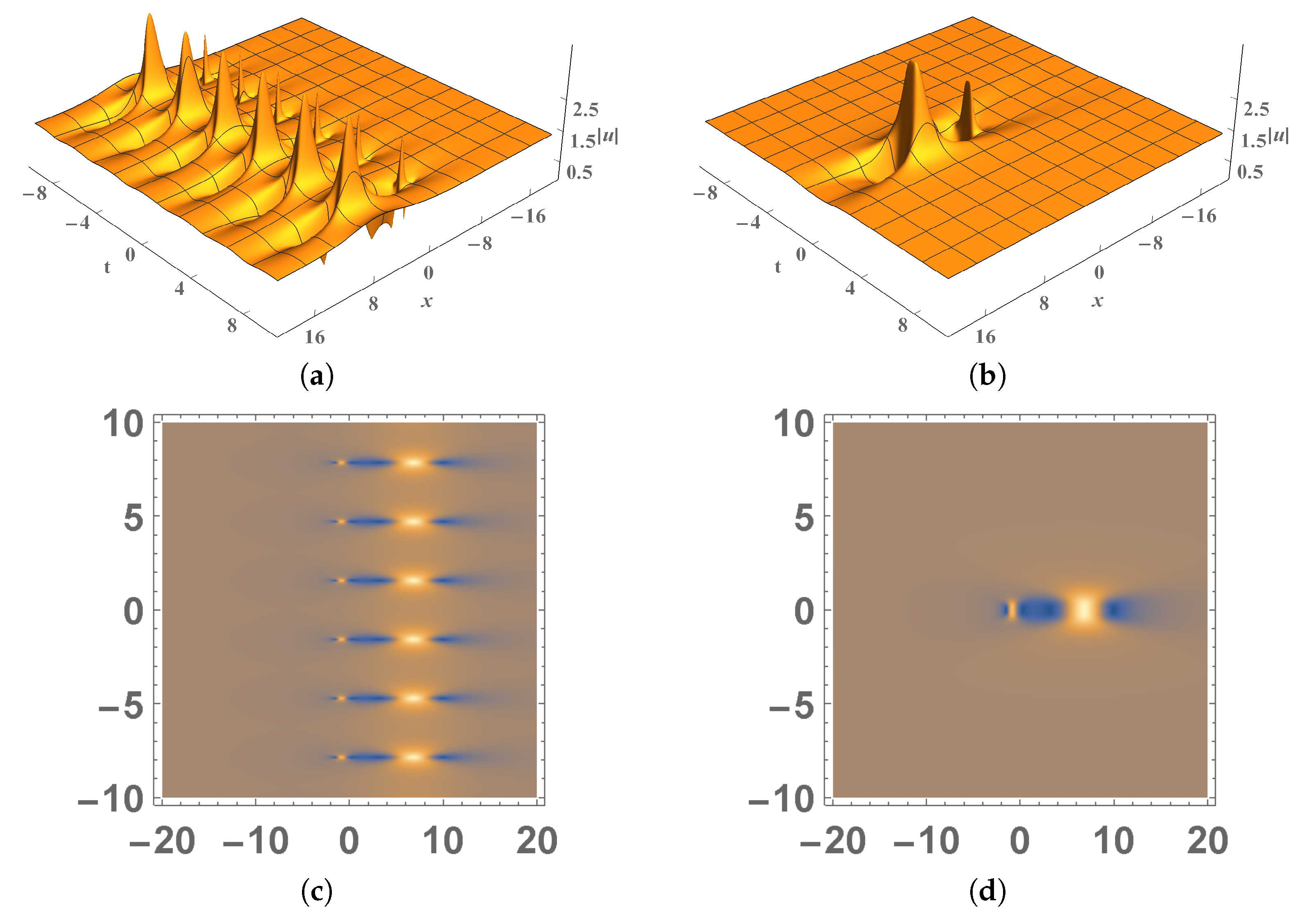
4.3. Higher-Order Rogue Wave Solution
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alqahtani, R.T.; Kaplan, M. Analyzing Soliton Solutions of the Extended (3 + 1)-Dimensional Sakovich Equation. Mathematics 2024, 12, 720. [Google Scholar] [CrossRef]
- Evans, L.C. Partial Differential Equations; American Mathematical Society: Providence, RI, USA, 2010. [Google Scholar]
- Pinelas, S.; Selvam, A.; Sabarinathan, S. Ulam–Hyers stability of linear differential equation with general transform. Symmetry 2023, 15, 2023. [Google Scholar] [CrossRef]
- Selvam, A.; Sabarinathan, S.; Nisar, K.S.; Ravichandran, C.; Senthil Kumar, B.V. Results on Ulam-type stability of linear differential equation with integral transform. Math. Method Appl. Sci. 2024, 47, 2311–2323. [Google Scholar] [CrossRef]
- Sivashankar, M.; Sabarinathan, S.; Govindan, V.; Fernandez-Gamiz, U.; Noeiaghdam, S. Stability analysis of COVID-19 outbreak using Caputo-Fabrizio fractional differential equation. AIMS Math. 2023, 8, 2720–2735. [Google Scholar] [CrossRef]
- Selvam, A.; Sabarinathan, S.; Senthil Kumar, B.V.; Byeon, H.; Guedri, K.; Eldin, S.M.; Khan, M.I.; Govindan, V. Ulam-Hyers stability of tuberculosis and COVID-19 co-infection model under Atangana-Baleanu fractal-fractional operator. Sci. Rep. 2023, 13, 9012. [Google Scholar] [CrossRef] [PubMed]
- Miah, M.M.; Seadawy, A.R.; Ali, H.S.; Akbar, M. Further investigations to extract abundant new exact traveling wave solutions of some NLEEs. J. Ocean Eng. Sci. 2019, 4, 387–394. [Google Scholar] [CrossRef]
- Barman, H.K.; Roy, R.; Mahmud, F.; Akbar, M.; Osman, M. Harmonizing wave solutions to the Fokas-Lenells model through the Kudryashov method. Optik 2021, 229, 166294. [Google Scholar] [CrossRef]
- Gao, X.Y. Two-layer-liquid and lattice considerations through a (3 + 1)-dimensional generalized Yu-Toda-Sasa-Fukuyama system. Appl. Math. Lett. 2024, 152, 109018. [Google Scholar] [CrossRef]
- Gao, X.Y. Auto-Bäcklund transformation with the solitons and similarity reductions for a generalized nonlinear shallow water wave equation. Qual. Theory Dyn. Syst. 2024, 23, 181. [Google Scholar] [CrossRef]
- Gao, X.Y. In the shallow water: Auto-Bäcklund, hetero-Bäcklund and scaling transformations via a (2+1)-dimensional generalized Broer-Kaup system. Qual. Theory Dyn. Syst. 2024, 23, 184. [Google Scholar] [CrossRef]
- Dong, H.N.; Zha, Q.L. Hybrid rogue wave and breather solutions for the nonlinear coupled dispersionless evolution equations. Wave Motion 2024, 125, 103259. [Google Scholar] [CrossRef]
- Zhang, H.W.; Zong, J.; Tian, G.; Wei, G.M. Analysis of High-Order Bright–Dark Rogue Waves in (2+1)-D Variable-Coefficient Zakharov Equation via Self-Similar and Darboux Transformations. Mathematics 2024, 12, 1359. [Google Scholar] [CrossRef]
- Smith, R. Giant waves. Fluid Mech. 1976, 77, 417–431. [Google Scholar] [CrossRef]
- Heller, E.J. Bound-state eigenfunctions of classically chaotic hamiltonian systems: Scars of periodic orbits. Phys. Rev. Lett. 1984, 53, 1515. [Google Scholar] [CrossRef]
- Arranz, F.J.; Borondo, F.; Benito, R.M. Scar formation at the edgeof the chaotic region. Phys. Rev. Lett. 1998, 80, 944–947. [Google Scholar] [CrossRef]
- Gao, X.Y. Oceanic shallow-water investigations on a generalized Whitham-Broer-Kaup-Boussinesq-Kupershmidt system. Phys. Fluids 2023, 35, 127106. [Google Scholar] [CrossRef]
- Osborne, A. Rogue waves: Classification, measurement and data analysis, and hyperfast numerical modeling. Eur. Phys. J. Spec. Top. 2010, 185, 225–245. [Google Scholar] [CrossRef]
- Yan, Z. Vector financial rogue waves. Phys. Lett. A 2011, 375, 4274–4279. [Google Scholar] [CrossRef]
- Ling, L.M.; Su, H.J. Rogue waves and their patterns for the coupled Fokas–Lenells equations. Phys. D Nonlinear Phenom. 2024, 461, 134111. [Google Scholar] [CrossRef]
- Davey, A.; Stewartson, K. On three-dimensional packets of surface waves. Proc. R. Soc. Lond. A 1974, 338, 101–110. [Google Scholar]
- Matveev, V.B.; Salle, M.A. Darboux Transformations and Solitons; Springer: Berlin, Germany, 1991. [Google Scholar]
- Ohta, Y.; Yang, J.K. Rogue waves in the Davey-Stewarton I equation. Phys. Rev. E 2012, 86, 036604. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.P.; Tian, B.; Mo, H.X.; Li, M.; Wang, P. Bäcklund transformation, Lax pair and solitons of the (2 + 1)-dimensional Davey-Stewartsonlike equations with variable coefficients for the electrostatic wave packets. J. Nonlinear Math. Phys. 2013, 20, 94–105. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Segur, H. On the transition from two-dimensional to three-dimensional water waves. Stud. Appl. Math. 2000, 104, 91–127. [Google Scholar]
- Zhang, Y.P.; Wang, J.Y.; Wei, G.M. The Painlevé property, Bäcklund transformation, Lax pair and new analytic solutions of a variable-coefficient KdV equation from fluids and plasmas. Phys. Scr. 2015, 90, 065203. [Google Scholar]
- Tajiri, M.; Arai, T. Growing-and-decaying mode solution to the Davey-Stewartson equation. Phys. Rev. E 1999, 60, 2297. [Google Scholar] [CrossRef] [PubMed]
- Guo, L.; He, J.; Mihalache, D. Rational and semi-rational solutions to the asymmetric Nizhnik Novikov-Veselov system. J. Phys. A Math. Theor. 2021, 54, 095703. [Google Scholar] [CrossRef]
- Guo, L.J.; Chen, L.; Mihalache, D.; He, J.S. Dynamics of soliton interaction solutions of the Davey-Stewartson I equation. Phys. Rev. E 2022, 105, 014218. [Google Scholar] [CrossRef]
- Wei, G.M.; Lu, Y.L.; Xie, Y.Q.; Zheng, W.X. Lie symmetry analysis and conservation law of variable-coefficient Davey–Stewartson equation. Comput. Math. Appl. 2018, 75, 3420–3430. [Google Scholar] [CrossRef]
- Wang, R.J.; Huang, Y.C. Exact solutions and excitations for the Davey–Stewartson equations with nonlinear and gain terms. Eur. Phys. J. D 2010, 57, 395–401. [Google Scholar] [CrossRef]
- Wei, G.M.; Gao, Y.T.; Xv, T.; Meng, X.H.; Zhang, C.Y. Painlevé property and new analytic solutions for a variable-coefficient Kadomtsev-Petviashvili equation with symbolic computation. Chin. Phys. Lett. 2008, 25, 1599–1602. [Google Scholar]
- Srivastava, S.; Kumar, M. Nonclassical symmetries, optimal classification, and dynamical behavior of similarity solutions of (3 + 1)-dimensional Burgers equation. Chin. J. Phys. 2024, 89, 404–416. [Google Scholar] [CrossRef]
- Weiss, J.; Tabor, M.; Carnevale, G. Carnevale, The Painlevé property for partial dierential equations. J. Math. Phys. 1983, 24, 522–526. [Google Scholar] [CrossRef]
- Weiss, J.; Tabor, M.; Carnevale, G. The Painlevé property for partial differential equations II: Bäcklund transformation, Lax pairs, and the Schwarzian derivative. J. Math. Phys. 1983, 24, 1405–1413. [Google Scholar] [CrossRef]
- Xu, G.Q. A note on the Painlevé test for nonlinear variable-coefficient PDEs. Comput. Phys. Commun. 2009, 180, 1137–1144. [Google Scholar] [CrossRef]
- Hirota, R. The Direct Method in Soliton Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Wei, G.; Song, Y.; Xie, Y. Oceanic Shallow-Water Investigations on a Variable-Coefficient Davey–Stewartson System. Mathematics 2024, 12, 1732. https://doi.org/10.3390/math12111732
Chen H, Wei G, Song Y, Xie Y. Oceanic Shallow-Water Investigations on a Variable-Coefficient Davey–Stewartson System. Mathematics. 2024; 12(11):1732. https://doi.org/10.3390/math12111732
Chicago/Turabian StyleChen, Haoqing, Guangmei Wei, Yuxin Song, and Yaqin Xie. 2024. "Oceanic Shallow-Water Investigations on a Variable-Coefficient Davey–Stewartson System" Mathematics 12, no. 11: 1732. https://doi.org/10.3390/math12111732
APA StyleChen, H., Wei, G., Song, Y., & Xie, Y. (2024). Oceanic Shallow-Water Investigations on a Variable-Coefficient Davey–Stewartson System. Mathematics, 12(11), 1732. https://doi.org/10.3390/math12111732




