Stability Analysis of the Credit Market in Supply Chain Finance Based on Stochastic Evolutionary Game Theory
Abstract
:1. Introduction
2. Construction and Analysis of Evolutionary Game Models
2.1. Description of the Problem
2.2. Model Assumptions
2.3. Analysis of the Game Model
2.4. Payment Matrix Construction
3. Construction of SEG Models and Analysis of Stabilization Strategies
3.1. Construction of SEG Systems
3.2. Stability Theory of Stochastic Dynamical Systems
3.2.1. Overview of the Lemma
3.2.2. Stability Theorem and Proof for Stochastic Dynamical Systems
- (I)
- When , ;
- (II)
- When ,
4. Numerical Simulation Analysis and Parameter Sensitivity Analysis
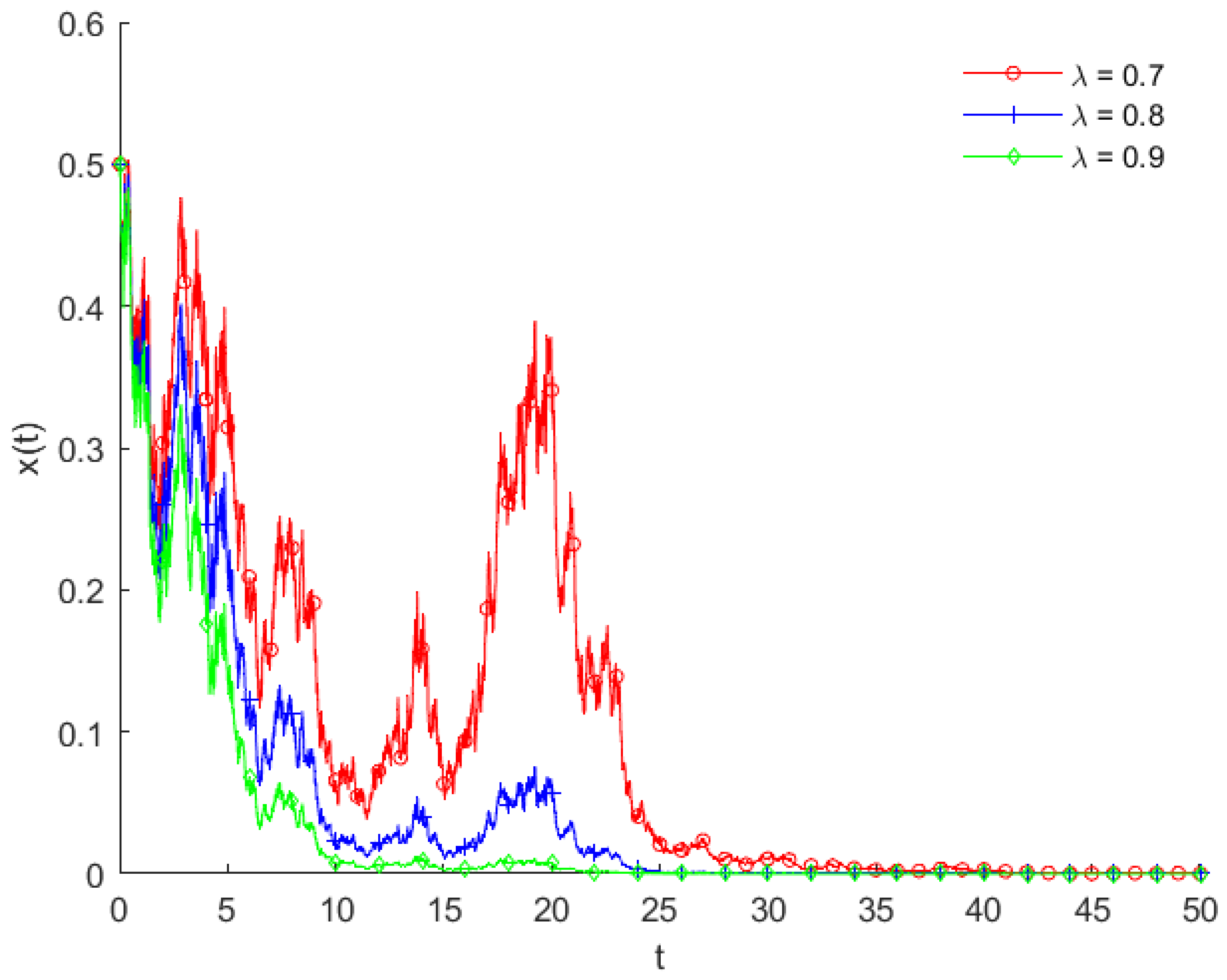
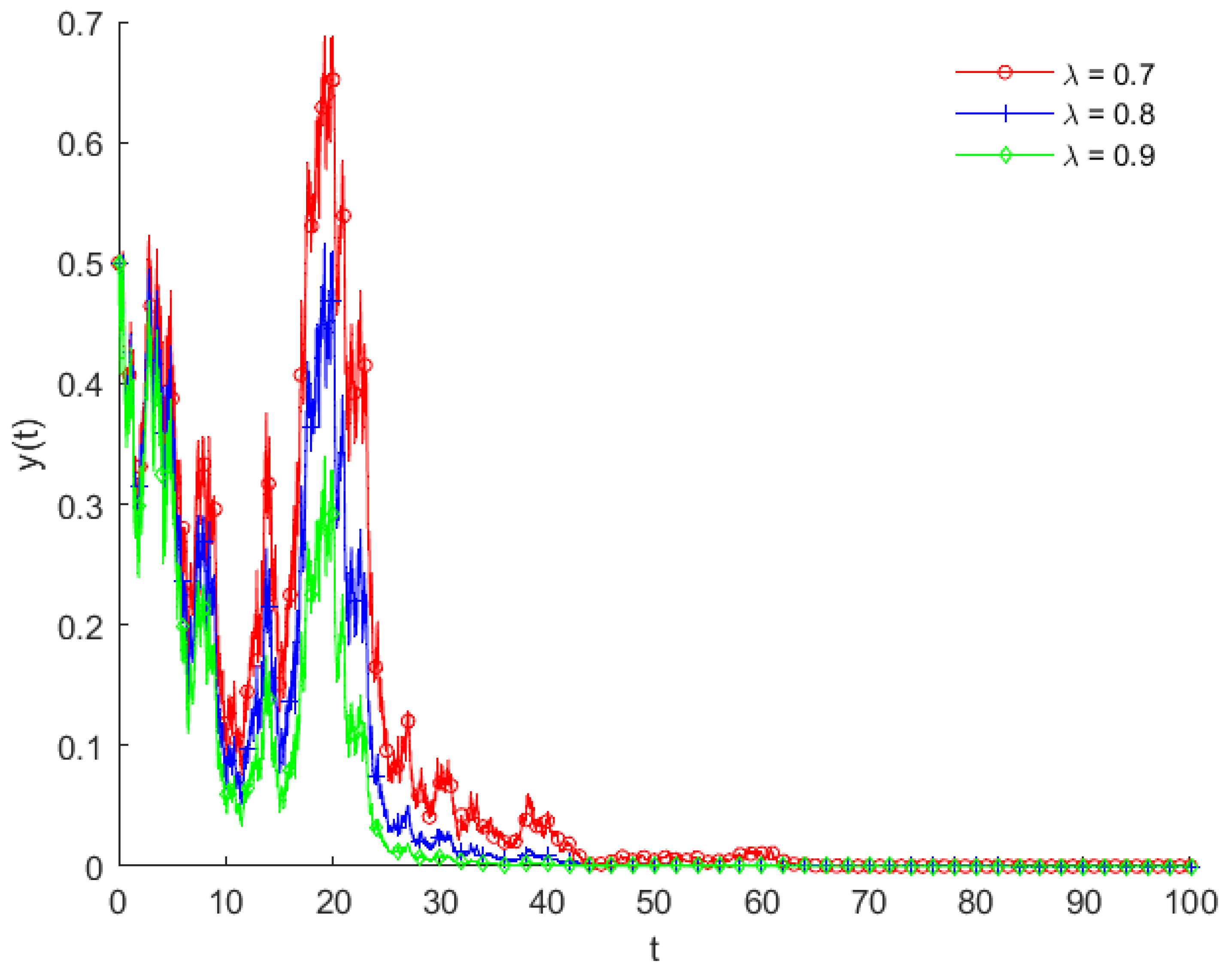
4.1. Credit Ratio Factor
- (A.1)
- (A.2)
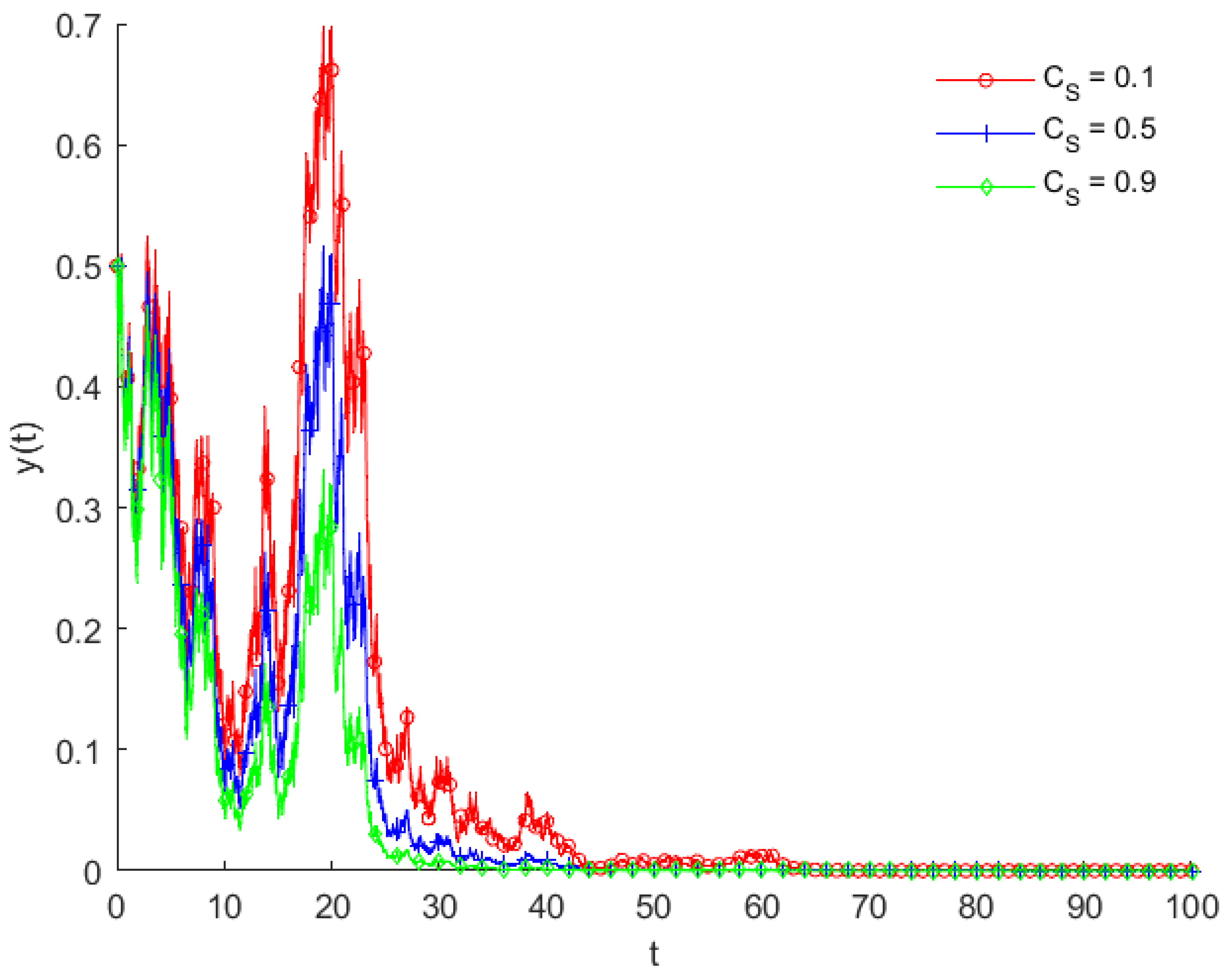
4.2. Penalty Intensity Factor
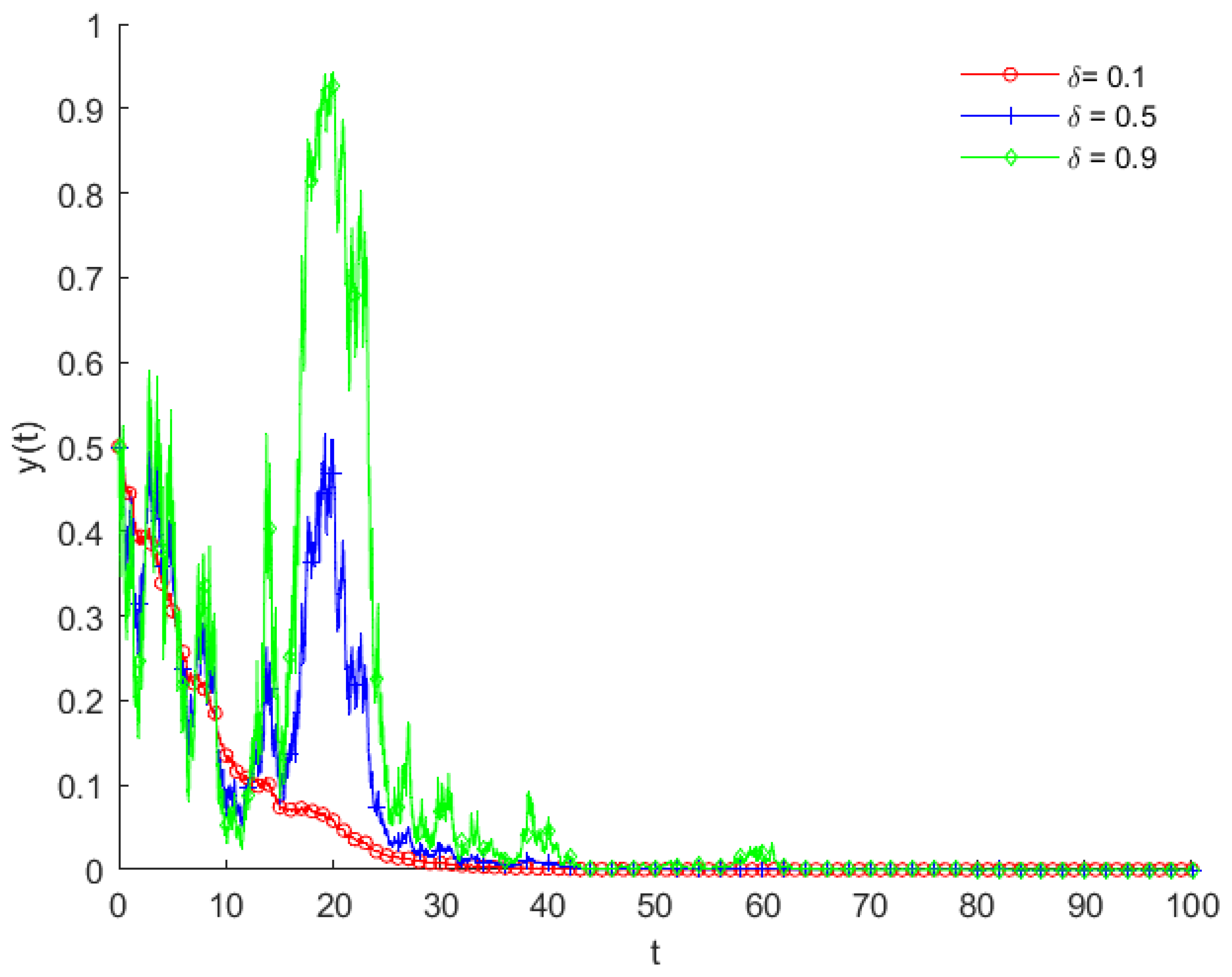
4.3. Intensity of the Random Disturbance Factor
- (B.1)
- (B.2)
5. Conclusions and Discussions
5.1. Conclusions
5.2. Suggestions
5.3. Limitations
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Benmelech, E.; Meisenzahl, R.R.; Ramcharan, R. The real effects of liquidity during the financial crisis: Evidence from automobiles. Q. J. Econ. 2017, 132, 317–365. [Google Scholar] [CrossRef]
- DeYoung, R.; Gron, A.; Torna, G.; Winton, A. Risk overhang and loan portfolio decisions: Small business loan supply before and during the financial crisis. J. Financ. 2015, 70, 2451–2488. [Google Scholar] [CrossRef]
- Lee, N.; Sameen, H.; Cowling, M. Access to finance for innovative SMEs since the financial crisis. Res. Policy 2015, 44, 370–380. [Google Scholar] [CrossRef]
- Wuttke, D.A.; Blome, C.; Heese, H.S.; Protopappa-Sieke, M. Supply chain finance: Optimal introduction and adoption decisions. Int. J. Prod. Econ. 2016, 178, 72–81. [Google Scholar] [CrossRef]
- Chakuu, S.; Masi, D.; Godsell, J. Exploring the relationship between mechanisms, actors and instruments in supply chain finance: A systematic literature review. Int. J. Prod. Econ. 2019, 216, 35–53. [Google Scholar] [CrossRef]
- Randall, W.; Theodore, F. Supply chain financing: Using cash-to-cash variables to strengthen the supply chain. Int. J. Phys. Distrib. Logist. Manag. 2009, 39, 669–689. [Google Scholar] [CrossRef]
- Chakuu, S.; Donato, M.; Godsell, J. A systematic literature review on supply chain finance actors, instruments and processes. In Proceedings of the 24th International Conference on Production Research, Posnan, Poland, 30 July–3 August 2017. [Google Scholar]
- Hu, Y.; Huang, S. Supply Chain Finance: Background, innovation and concept definition. J. Financ. Res. 2009, 8, 194–206. [Google Scholar]
- Gelsomino, L.; Mangiaracina, R.; Perego, A.; Tumino, A. Supply chain finance: A literature review. Int. J. Phys. Distrib. Logist. Manag. 2016, 46, 348–366. [Google Scholar] [CrossRef]
- Ross, S.A. The economic theory of agency: The principal’s problem. Am. Econ. Rev. 1973, 63, 134–139. [Google Scholar]
- Michael, J.; William, M. Theory of the Firm: Managerial Behavior, Agency Costs and Ownership Structure. In Corporate Governance; Gower: London, UK, 2019. [Google Scholar]
- Zhu, Q.; Zheng, K.; Wei, Y. Three-Party Stochastic Evolutionary Game Analysis of Reward and Punishment Mechanism for Green Credit. Discret. Dyn. Nat. Soc. 2021, 2021, 12. [Google Scholar] [CrossRef]
- Xu, M.; Ma, S.; Wang, G. Differential Game Model of Information Sharing among Supply Chain Finance Based on Blockchain Technology. Sustainability 2022, 14, 7139. [Google Scholar] [CrossRef]
- Li, X.; Xin, Y. Evolutionary Analysis of SME Credit Market Based on Supply Chain Finance. Oper. Manag. 2017, 10, 101–105. [Google Scholar]
- Tang, D.; He, P. Evolutionary game study on the financing enabling mechanism of family farms: Based on the financial perspective of e-commerce supply chain. Financ. Theory Pract. 2022, 8, 44–54. [Google Scholar]
- Geng, Z.; Du, H.; Wang, X.; Zhuang, W. Analysis of accounts receivable financing strategies in agricultural supply chain. Financ. Theory Pract. 2022, 8, 55–65. [Google Scholar]
- Xu, L.; Cong, X. Evolutionary game study of supply chain finance between commercial banks and third-party logistics companies. Financ. Theory Pract. 2022, 4, 10–18. [Google Scholar]
- Xu, Y.; Bao, H. FinTech regulation: Evolutionary game model, numerical simulation, and recommendations. Expert Syst. Appl. 2023, 211, 118327. [Google Scholar] [CrossRef]
- Wang, X.; Gu, C.; He, Q.; Zhao, J. The dynamics of the three-party evolutionary game in the supply chain finance and credit market. Logist. Manag. 2022, 1, 30–37. [Google Scholar]
- Foster, D.; Young, P. Stochastic Evolutionary Game Dynamics. Theor. Popul. Biol. 1990, 38, 219–232. [Google Scholar] [CrossRef]
- Shan, S.N.; Zhang, Z.C.; Ji, W.Y.; Wang, H. Analysis of collaborative urban public crisis governance in complex system: A multi-agent stochastic evolutionary game approach. Sustain. Cities Soc. 2023, 91, 104418. [Google Scholar] [CrossRef]
- Dong, C.; Liu, J.; Mi, J. How to enhance data sharing in digital government construction: A tripartite stochastic evolutionary game approach. Systems 2023, 11, 212. [Google Scholar] [CrossRef]
- Du, J.; Li, J.; Li, J.; Li, W. Competition–cooperation mechanism of online supply chain finance based on a stochastic evolutionary game. Oper. Res. 2023, 23, 55. [Google Scholar] [CrossRef]
- Evstigneev, I.V.; Hens, T.; Vanaei, M.J. Evolutionary finance: A model with endogenous asset payoffs. J. Bioecon. 2023, 25, 117–143. [Google Scholar] [CrossRef]
- Saha, I.; Kavitha, V. Systemic-risk and evolutionary stable strategies in a financial network. Dyn. Games Appl. 2023, 13, 897–928. [Google Scholar] [CrossRef]
- Su, L.; Cao, Y. Dynamic Evolutionary Game Approach for Blockchain-Driven Incentive and Restraint Mechanism in Supply Chain Financing. Systems 2023, 11, 406. [Google Scholar] [CrossRef]
- Feng, B.; Feng, C.; Zhao, S. Green Supply Chain Finance Credit Market under Government Regulation: An Evolutionary Game Theory Analysis. Pol. J. Environ. Stud. 2023, 32, 3999–4010. [Google Scholar] [CrossRef] [PubMed]
- Emtehani, F.; Nahavandi, N.; Rafiei, F.M. Trade credit financing for supply chain coordination under financial challenges: A multi-leader–follower game approach. Financ. Innov. 2023, 9, 6. [Google Scholar] [CrossRef]
- Wu, C.; Xu, C.; Zhao, Q.; Zhu, J. Research on financing strategy under the integration of green supply chain and blockchain technology. Comput. Ind. Eng. 2023, 184, 109598. [Google Scholar] [CrossRef]
- Zhang, C. Small and medium-sized enterprises closed-loop supply chain finance risk based on evolutionary game theory and system dynamics. J. Shanghai Jiaotong Univ. (Sci.) 2016, 21, 355–364. [Google Scholar] [CrossRef]
- Kang, K.; Bai, L.; Zhang, J. A tripartite stochastic evolutionary game model of complex technological products in a transnational supply chain. Comput. Ind. Eng. 2023, 186, 109690. [Google Scholar] [CrossRef]
- Li, H.; Wang, F.; Wang, L.; Su, L.; Zhang, C. The stochastic evolution game of knowledge sharing in the infrastructure PPP supply chain network. Complexity 2020, 2020, 1–17. [Google Scholar] [CrossRef]
- Rafail, K. Stability Analysis of Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Luo, J. Fixed points and stability of neutral stochastic delay differential equations. J. Math. Anal. Appl. 2007, 334, 431–440. [Google Scholar] [CrossRef]
- Burton, T. Stability and Periodic Solutions of Ordinary and Functional Differential Equations; Academic Press: New York, NY, USA, 1985. [Google Scholar]
- Wang, C. Stability of neutral volterra stochastic dynamical systems with multiple delays. Appl. Math. Mech. 2021, 42, 1190–1202. [Google Scholar]
- Wang, C.; Chen, H.; Lin, R.; Sheng, Y.; Jiao, F. New generalized Halanay inequalities and relative applications to neural networks with variable delays. Bound Value Probl. 2023, 2023, 95. [Google Scholar] [CrossRef]
- Wang, C.; Li, Y. Three kinds of fixed points and stability of stochastic dynamical systems. J. Control Theory Appl. 2017, 34, 677–682. [Google Scholar] [CrossRef]
- Zhang, B. Fixed points and stability in differential equations with variable delays. Nonlinear Anal. Theory Methods Appl. 2005, 63, e233–e242. [Google Scholar] [CrossRef]
- Ardjouni, A.; Djoudi, A. Fixed points and stability in neutral nonlinear differential equations with variable delays. Opusc. Math. 2012, 32, 5–19. [Google Scholar] [CrossRef]
- Raffoul, Y. Stability in neutral nonlinear differential equations with functional delays using fixed-point theory. Math. Comput. Model. 2004, 40, 691–700. [Google Scholar] [CrossRef]
- Kabak, K.E.; Hinckeldeyn, J.; Dekkers, R. A systematic literature review into simulation for building operations management theory: Reaching beyond positivism? J. Simul. 2024, 3, 1–29. [Google Scholar] [CrossRef]
- Gao, G.; Feng, Y. Game analysis of factoring financing of accounts receivable from the perspective of limited rationality. Manuf. Autom. 2020, 42, 33–38+78. [Google Scholar]
- Sun, R.; He, D.; Su, H. Application of blockchain technology to preventing supply chain finance based on evolutionary game. Chin. J. Manag. Sci. 2022, 2022, 11–17. [Google Scholar]
- Chen, H.; Lu, W.; Du, L. Analysis of stochastic evolution scenarios of neighbor-avoidance conflict events in risky agglomeration classes. China Manag. Sci. 2020, 28, 131–141. [Google Scholar]
- Zhou, X.; Zhong, S. Fixed point and exponential p-stability of neutral stochastic delay differential equations. J. Math. 2011, 31, 238–242. [Google Scholar]

| Parameters | Clarification |
|---|---|
| x | Probability of not lending by financial institutions |
| y | Probability of default for SMEs |
| M | Level of accounts receivable, currency unit |
| Accounts receivable factoring credit rate (lending ratio) | |
| The probability that SMEs choose not to engage in joint fraudulent loans with CEs | |
| r1 | Interest rates on loans from financial institutions |
| r2 | Deposit rates for financial institutions |
| r3 | Rate of return on SME financing used for normal production |
| C | Production costs for SMEs, currency unit |
| CS | Punitive intensity (penalty from CEs), currency unit |
| CF | Cost of credit to financial institutions, currency unit |
| Distribution ratio of benefits to SMEs in case of joint fraudulent loans |
| Strategic Combination | FI | SME |
|---|---|---|
| (Provide loans, not joint) | ||
| (Provide loans, Joint) | ||
| (Provide loans, Not default) | ||
| (Not provide loans, not joint) | ||
| (Not provide loans, joint) | 0 | |
| (Not provide loans, not default) | M − C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Weng, J.; He, J.; Wang, X.; Ding, H.; Zhu, Q. Stability Analysis of the Credit Market in Supply Chain Finance Based on Stochastic Evolutionary Game Theory. Mathematics 2024, 12, 1764. https://doi.org/10.3390/math12111764
Wang C, Weng J, He J, Wang X, Ding H, Zhu Q. Stability Analysis of the Credit Market in Supply Chain Finance Based on Stochastic Evolutionary Game Theory. Mathematics. 2024; 12(11):1764. https://doi.org/10.3390/math12111764
Chicago/Turabian StyleWang, Chunsheng, Jiatong Weng, Jingshi He, Xiaopin Wang, Hong Ding, and Quanxin Zhu. 2024. "Stability Analysis of the Credit Market in Supply Chain Finance Based on Stochastic Evolutionary Game Theory" Mathematics 12, no. 11: 1764. https://doi.org/10.3390/math12111764
APA StyleWang, C., Weng, J., He, J., Wang, X., Ding, H., & Zhu, Q. (2024). Stability Analysis of the Credit Market in Supply Chain Finance Based on Stochastic Evolutionary Game Theory. Mathematics, 12(11), 1764. https://doi.org/10.3390/math12111764







