Bias-Correction Methods for the Unit Exponential Distribution and Applications
Abstract
:1. Introduction
1.1. Literature Review
1.2. The Motivation and Organization
- An analytical procedure of the maximum likelihood bias-correction method is proposed.
- The implementation of the parametric bootstrap bias-correction method is proposed.
- The performance of the two proposed bias-correction methods is studied using Monte Carlo simulations. We find that the proposed maximum likelihood bias-correction method is more competitive than the other two competitors.
2. The Unit Exponential Distribution and Maximum Likelihood Estimation
3. Bias-Correction Methods
3.1. The Bias-Corrected Maximum Likelihood Estimation Method
3.2. The Bootstrap Bias-Correction Method
- Step 1:
- Generate a random sample, from the . Use the new generated random sample, , to obtain the MLE of and denote it by .
- Step 2:
- Repeat Step 1 M times. Denote the obtained MLEs by ). Evaluate the bias of byThen, the B-BCML estimate is evaluated by
4. Monte Carlo Simulations
- Set I:
- .
- Set II:
- .
- Set III:
- .
- Set IV:
- .
5. An Example
5.1. The Numerical Example
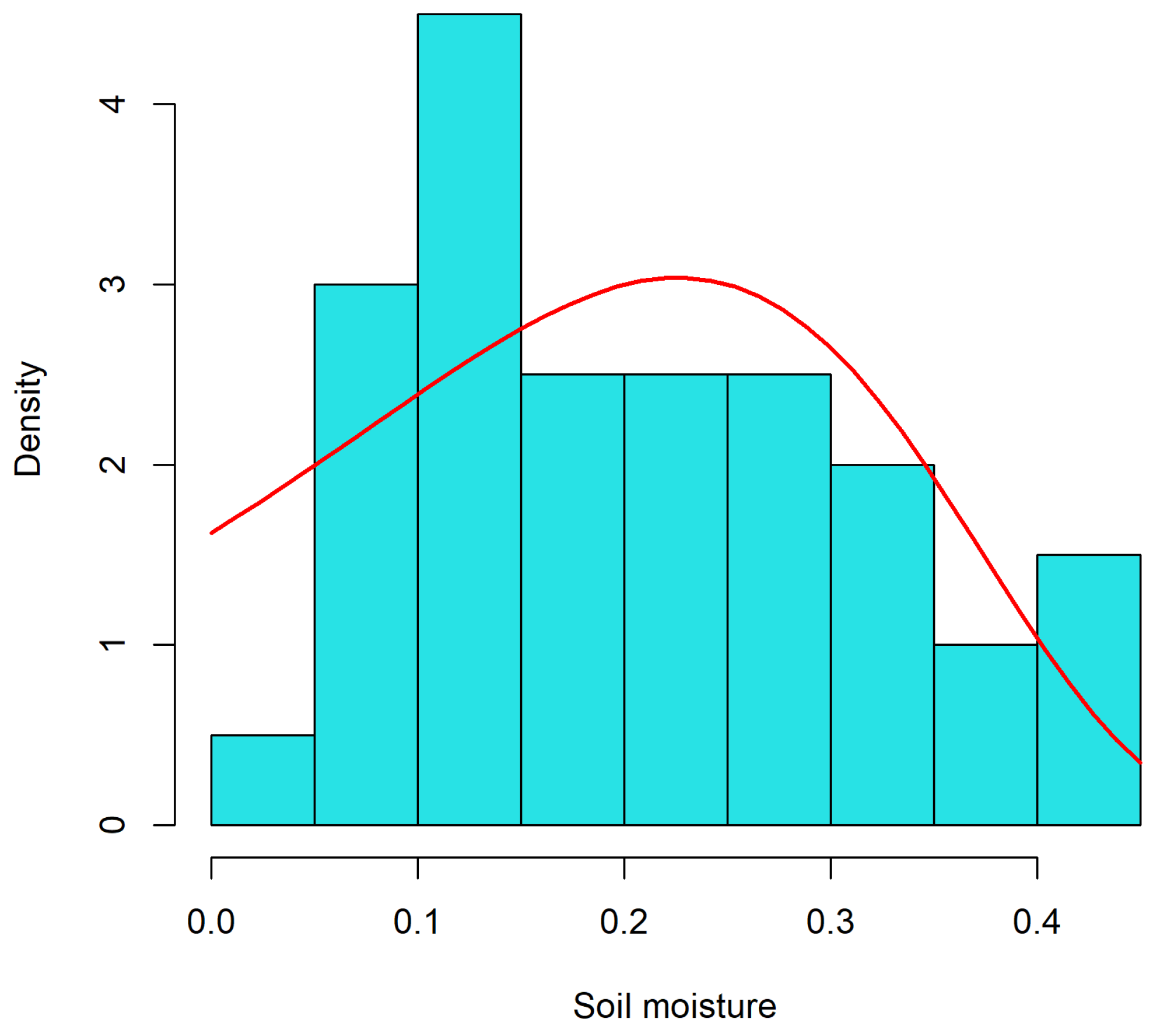
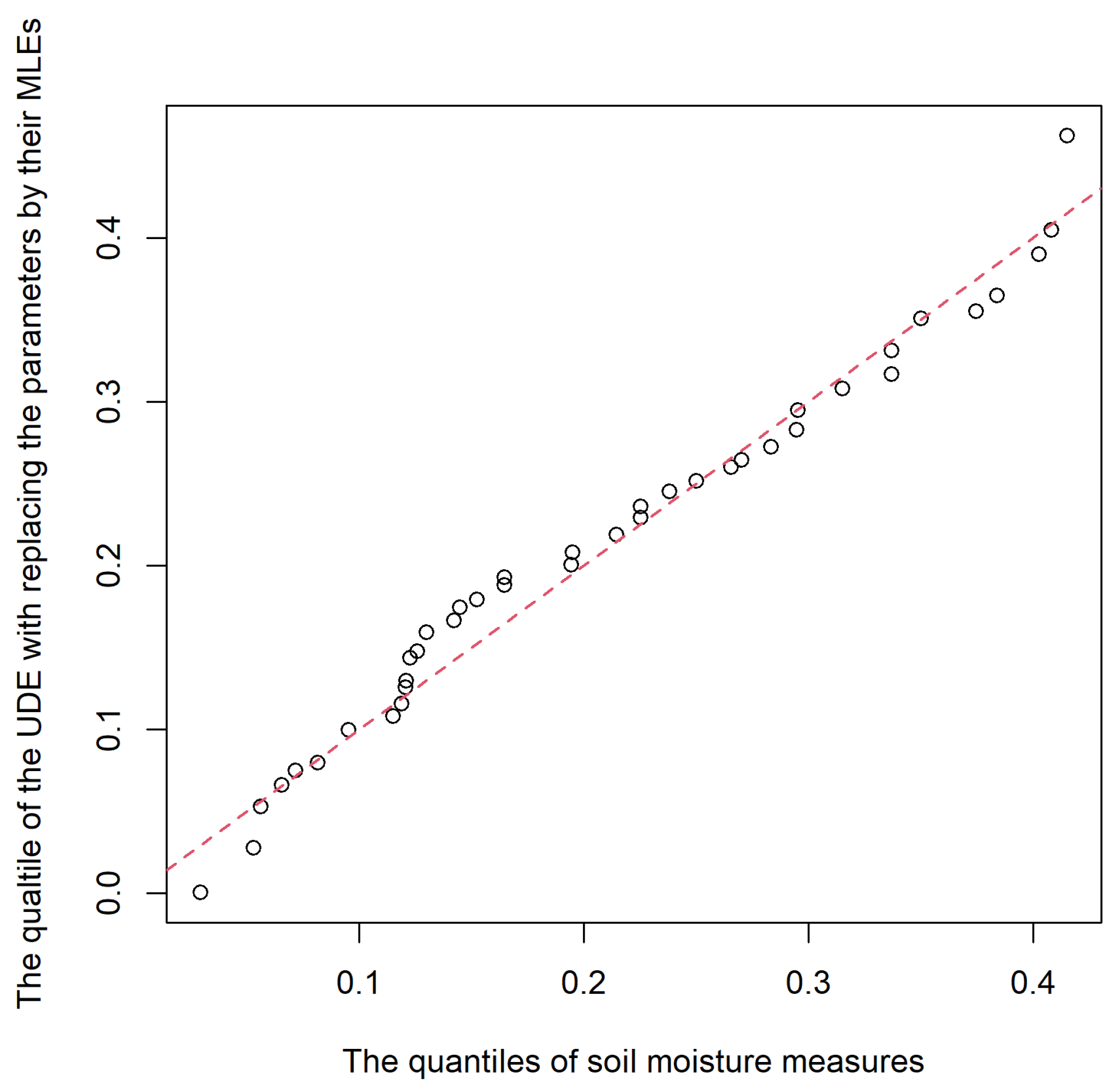
5.2. The Soil Moisture Example
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bayes, T. An Essay Towards Solving a Problem in the Doctrine of Chances. By the late Rev. Mr. Bayes, F.R.S. communicated by Mr. Price, in a letter to John Canton, A. M. F. R. S. Philos. Trans. R. Soc. 1763, 53, 370–418. [Google Scholar]
- Fleiss, J.L.; Levin, B.; Paik, M.C. Statistical Methods for Rates and Proportions, 3rd ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1993. [Google Scholar]
- Gilchrist, W. Statistical Modelling with Quantile Functions; CRC Press: Abingdon, UK, 2000. [Google Scholar]
- Seber, G.A.F. Statistical Models for Proportions and Probabilities; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Leipnik, R.B. Distribution of the Serial Correlation Coefficient in a Circularly Correlated Universe. Ann. Math. Stat. 1947, 18, 80–87. [Google Scholar] [CrossRef]
- Johnson, N. Systems of Frequency Curves Derived From the First Law of Laplace. Trab. Estad. 1955, 5, 283–291. [Google Scholar] [CrossRef]
- Topp, C.W.; Leone, F.C. A Family of J-Shaped Frequency Functions. J. Am. Stat. Assoc. 1955, 50, 209–219. [Google Scholar] [CrossRef]
- Consul, P.C.; Jain, G.C. On the Log-Gamma Distribution and Its Properties. Stat. Hefte 1971, 12, 100–106. [Google Scholar] [CrossRef]
- Kumaraswamy, P. A Generalized Probability Density Function for Double-Bounded Random Processes. J. Hydrol. 1980, 46, 79–88. [Google Scholar] [CrossRef]
- Jøørgensen, B. Proper Dispersion Models. Braz. J. Probab. Stat. 1997, 11, 89–128. [Google Scholar]
- Smithson, M.; Shou, Y. CDF-Quantile. Distributions for Modelling RVs on the Unit Interval. Br. J. Math. Stat. Psychol. 2017, 70, 412–438. [Google Scholar] [CrossRef] [PubMed]
- Altun, E.; Hamedani, G. The Log-X gamma Distribution with Inference and Application. J. Soc. Fr. Stat. 2018, 159, 40–55. [Google Scholar]
- Nakamura, L.R.; Cerqueira, P.H.R.; Ramires, T.G.; Pescim, R.R.; Rigby, R.A.; Stasinopoulos, D.M. A New Continuous Distribution the Unit Interval Applied to Modelling the Points Ratio of Football Teams. J. Appl. Stat. 2019, 46, 416–431. [Google Scholar] [CrossRef]
- Ghitany, M.E.; Mazucheli, J.; Menezes, A.F.B.; Alqallaf, F. The Unit-Inverse Gaussian Distribution: A New Alternative to Two-Parameter Distributions on the Unit Interval. Commun. Stat. Theory Methods. 2019, 48, 3423–3438. [Google Scholar] [CrossRef]
- Mazucheli, J.; Menezes, A.F.; Dey, S. Unit-Gompertz Distribution with Applications. Statistica 2019, 79, 25–43. [Google Scholar]
- Mazucheli, J.; Menezes, A.F.B.; Chakraborty, S. On the One Parameter Unit-Lindley Distribution and Its Associated Regression Model for Proportion Data. J. Appl. Stat. 2019, 46, 700–714. [Google Scholar] [CrossRef]
- Mazucheli, J.; Menezes, A.F.B.; Fernandes, L.B.; de Oliveira, R.P.; Ghitany, M.E. The Unit-Weibull Distribution as an Alternative to the Kumaraswamy Distribution for the Modeling of Quantiles Conditional on Covariates. J. Appl. Stat. 2019, 47, 954–974. [Google Scholar] [CrossRef]
- Altun, E. The Log-Weighted Exponential Regression Model: Alternative to the Beta Regression Model. Commun. Stat. Theory Methods 2020, 50, 2306–2321. [Google Scholar] [CrossRef]
- Gündüz, S.; Mustafa, Ç.; Korkmaz, M.C. A New Unit Distribution Based on the Unbounded Johnson Distribution Rule: The Unit Johnson SU Distribution. Pak. J. Stat. Oper. Res. 2020, 16, 471–490. [Google Scholar] [CrossRef]
- Biswas, A.; Chakraborty, S. A New Method for Constructing Continuous Distributions on the Unit Interval. arXiv 2021, arXiv:2101.04661. [Google Scholar]
- Afify, A.Z.; Nassar, M.; Kumar, D.; Cordeiro, G.M. A New Unit Distribution: Properties and Applications. Electron. J. Appl. Stat. 2022, 15, 460–484. [Google Scholar]
- Krishna, A.; Maya, R.; Chesneau, C.; Irshad, M.R. The Unit Teissier Distribution and Its Applications. Math. Comput. Appl. 2022, 27, 12. [Google Scholar] [CrossRef]
- Korkmaz, M.Ç.; Korkmaz, Z.S. The Unit Log–log Distribution: A New Unit Distribution with Alternative Quantile Regression Modeling and Educational Measurements Applications. J. Appl. Stat. 2023, 50, 889–908. [Google Scholar] [CrossRef] [PubMed]
- Fayomi, A.; Hassan, A.S.; Baaqeel, H.; Almetwally, E.M. Bayesian Inference and Data Analysis of the Unit–Power Burr X Distribution. Axioms 2023, 12, 297. [Google Scholar] [CrossRef]
- Bakouch, H.S.; Hussain, T.; Tošić, M.; Stojanović, V.S.; Qarmalah, N. Unit Exponential Probability Distribution: Characterization and Applications in Environmental and Engineering Data Modeling. Mathematics 2023, 11, 4207. [Google Scholar] [CrossRef]
- Dombi, J.; Jónás, T.; Tóth, Z.E. The Epsilon Probability Distribution and its Application in Reliability Theory. Acta Polytech. Hung. 2018, 15, 197–216. [Google Scholar]
- Cordeiro, G.M.; Klein, R. Bias correction in ARMA models. Stat. Probab. Lett. 1994, 19, 169–176. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An introduction to the bootstrap. In Monographs on Statistics and Applied Probability; Chapman & Hall: New York, NY, USA, 1993. [Google Scholar]
- Tsai, T.-R.; Xin, H.; Fan, Y.-Y.; Lio, Y.L. Bias-Corrected Maximum Likelihood Estimation and Bayesian Inference for the Process Performance Index Using Inverse Gaussian Distribution. Stats 2022, 5, 1079–1096. [Google Scholar] [CrossRef]
- Maity, R. Statistical Methods in Hydrology and Hydroclimatology; Springer Nature Singapore Pte Ltd.: Singapore, 2018. [Google Scholar]

| Methods | n | RB () | RSM () | RB () | RSM () | Updated Rate | ||
|---|---|---|---|---|---|---|---|---|
| MLE | 15 | 0.44 | 1.51 | −0.0676 | 0.7533 | 0.2746 | 0.5620 | 1 |
| BC | 15 | 0.44 | 1.51 | 0.1258 | 1.2614 | 0.1510 | 0.5474 | 0.887 |
| Boot-BC | 15 | 0.44 | 1.51 | 0.0330 | 1.0603 | 0.1443 | 0.6652 | 0.614 |
| MLE | 15 | 0.99 | 0.22 | −0.0201 | 0.9730 | 0.4363 | 0.8581 | 1 |
| BC | 15 | 0.99 | 0.22 | 0.1026 | 1.2209 | 0.2488 | 0.7746 | 0.901 |
| Boot-BC | 15 | 0.99 | 0.22 | −0.0274 | 1.0825 | 0.3053 | 0.9211 | 0.461 |
| MLE | 15 | 1.9 | 0.32 | −0.1249 | 0.9468 | 0.7639 | 1.3320 | 1 |
| BC | 15 | 1.9 | 0.32 | 0.0971 | 0.9999 | 0.4216 | 1.1163 | 0.675 |
| Boot-BC | 15 | 1.9 | 0.32 | −0.1626 | 1.0010 | 0.6201 | 1.3651 | 0.364 |
| MLE | 15 | 2.44 | 2.51 | 0.0414 | 1.2697 | 0.4551 | 0.7416 | 1 |
| BC | 15 | 2.44 | 2.51 | 0.0403 | 1.3476 | 0.3602 | 0.6710 | 0.978 |
| Boot-BC | 15 | 2.44 | 2.51 | −0.0314 | 1.3319 | 0.4308 | 0.8683 | 0.399 |
| Methods | n | RB () | RSM () | RB () | RSM () | Updated Rate | ||
|---|---|---|---|---|---|---|---|---|
| MLE | 20 | 0.44 | 1.51 | −0.0719 | 0.6375 | 0.2110 | 0.4549 | 1 |
| BC | 20 | 0.44 | 1.51 | 0.0910 | 1.0245 | 0.1069 | 0.4625 | 0.906 |
| Boot-BC | 20 | 0.44 | 1.51 | 0.0455 | 1.0274 | 0.0972 | 0.5808 | 0.715 |
| MLE | 20 | 0.99 | 0.22 | −0.0488 | 0.7719 | 0.3335 | 0.6828 | 1 |
| BC | 20 | 0.99 | 0.22 | 0.0549 | 0.9577 | 0.1812 | 0.6318 | 0.93 |
| Boot-BC | 20 | 0.99 | 0.22 | −0.0357 | 0.9505 | 0.2143 | 0.7738 | 0.579 |
| MLE | 20 | 1.9 | 0.32 | −0.1081 | 0.8218 | 0.5766 | 1.0468 | 1 |
| BC | 20 | 1.9 | 0.32 | 0.1093 | 0.8498 | 0.2696 | 0.8783 | 0.72 |
| Boot-BC | 20 | 1.9 | 0.32 | −0.1368 | 0.9076 | 0.4437 | 1.1027 | 0.464 |
| MLE | 20 | 2.44 | 2.51 | 0.0038 | 1.0083 | 0.4056 | 0.6994 | 1 |
| BC | 20 | 2.44 | 2.51 | 0.0174 | 1.1412 | 0.3347 | 0.6516 | 0.98 |
| Boot-BC | 20 | 2.44 | 2.51 | −0.0568 | 1.0974 | 0.3699 | 0.8383 | 0.471 |
| Methods | n | RB () | RSM () | RB () | RSM () | Updated Rate | ||
|---|---|---|---|---|---|---|---|---|
| MLE | 30 | 0.44 | 1.51 | −0.0583 | 0.5239 | 0.1422 | 0.3411 | 1 |
| BC | 30 | 0.44 | 1.51 | 0.0786 | 0.8206 | 0.0603 | 0.3664 | 0.936 |
| Boot-BC | 30 | 0.44 | 1.51 | 0.0440 | 0.9250 | 0.0606 | 0.4837 | 0.815 |
| MLE | 30 | 0.99 | 0.22 | −0.0441 | 0.6210 | 0.2241 | 0.5064 | 1 |
| BC | 30 | 0.99 | 0.22 | 0.0385 | 0.7694 | 0.1161 | 0.4852 | 0.968 |
| Boot-BC | 30 | 0.99 | 0.22 | −0.0004 | 0.8937 | 0.1268 | 0.6391 | 0.713 |
| MLE | 30 | 1.9 | 0.32 | −0.1094 | 0.6452 | 0.4033 | 0.7705 | 1 |
| BC | 30 | 1.9 | 0.32 | 0.0853 | 0.6386 | 0.1474 | 0.6408 | 0.793 |
| Boot-BC | 30 | 1.9 | 0.32 | −0.1175 | 0.7918 | 0.2932 | 0.8654 | 0.592 |
| MLE | 30 | 2.44 | 2.51 | −0.0515 | 0.7310 | 0.3438 | 0.6310 | 1 |
| BC | 30 | 2.44 | 2.51 | −0.0349 | 0.8658 | 0.2961 | 0.6046 | 0.981 |
| Boot-BC | 30 | 2.44 | 2.51 | −0.0953 | 0.8694 | 0.3015 | 0.7907 | 0.572 |
| Methods | n | RB () | RSM () | RB () | RSM () | Updated Rate | ||
|---|---|---|---|---|---|---|---|---|
| MLE | 40 | 0.44 | 1.51 | −0.0545 | 0.4607 | 0.1120 | 0.2896 | 1 |
| BC | 40 | 0.44 | 1.51 | 0.0630 | 0.7153 | 0.0446 | 0.3181 | 0.956 |
| Boot-BC | 40 | 0.44 | 1.51 | 0.0204 | 0.8298 | 0.0543 | 0.4333 | 0.862 |
| MLE | 40 | 0.99 | 0.22 | −0.0445 | 0.5338 | 0.1749 | 0.4267 | 1 |
| BC | 40 | 0.99 | 0.22 | 0.0160 | 0.6398 | 0.0941 | 0.4156 | 0.986 |
| Boot-BC | 40 | 0.99 | 0.22 | 0.0125 | 0.8710 | 0.0941 | 0.5846 | 0.796 |
| MLE | 40 | 1.9 | 0.32 | −0.1004 | 0.5536 | 0.3090 | 0.6252 | 1 |
| BC | 40 | 1.9 | 0.32 | 0.0777 | 0.5231 | 0.0807 | 0.5078 | 0.865 |
| Boot-BC | 40 | 1.9 | 0.32 | −0.0893 | 0.7729 | 0.2125 | 0.7612 | 0.704 |
| MLE | 40 | 2.44 | 2.51 | −0.0662 | 0.6151 | 0.2954 | 0.5739 | 1 |
| BC | 40 | 2.44 | 2.51 | −0.0637 | 0.6814 | 0.2606 | 0.5562 | 0.99 |
| Boot-BC | 40 | 2.44 | 2.51 | −0.0903 | 0.8032 | 0.2447 | 0.7495 | 0.654 |
| Methods | n | RB () | RSM () | RB () | RSM () | Updated Rate | ||
|---|---|---|---|---|---|---|---|---|
| MLE | 50 | 0.44 | 1.51 | −0.0409 | 0.4102 | 0.0859 | 0.246 | 1 |
| BC | 50 | 0.44 | 1.51 | 0.0641 | 0.6434 | 0.0279 | 0.2771 | 0.977 |
| Boot-BC | 50 | 0.44 | 1.51 | 0.0198 | 0.7505 | 0.0409 | 0.3892 | 0.898 |
| MLE | 50 | 0.99 | 0.22 | −0.0351 | 0.472 | 0.1359 | 0.3608 | 1 |
| BC | 50 | 0.99 | 0.22 | 0.0097 | 0.5463 | 0.0723 | 0.3545 | 0.994 |
| Boot-BC | 50 | 0.99 | 0.22 | 0.0301 | 0.833 | 0.0643 | 0.5352 | 0.857 |
| MLE | 50 | 1.9 | 0.32 | −0.0833 | 0.5045 | 0.2496 | 0.5418 | 1 |
| BC | 50 | 1.9 | 0.32 | 0.0688 | 0.4656 | 0.0588 | 0.4243 | 0.91 |
| Boot-BC | 50 | 1.9 | 0.32 | −0.0557 | 0.7629 | 0.161 | 0.7056 | 0.773 |
| MLE | 50 | 2.44 | 2.51 | −0.0576 | 0.5621 | 0.2529 | 0.5301 | 1 |
| BC | 50 | 2.44 | 2.51 | −0.0606 | 0.5975 | 0.226 | 0.5171 | 0.995 |
| Boot-BC | 50 | 2.44 | 2.51 | −0.0654 | 0.7776 | 0.1953 | 0.7176 | 0.715 |
| 0.1450 | 0.5176 | 0.2730 | 0.2337 | 0.3614 | 0.5350 | 0.1658 | 0.3711 | 0.3477 | 0.3108 |
| 0.4370 | 0.5852 | 0.5271 | 0.6111 | 0.2983 | 0.1238 | 0.6071 | 0.3384 | 0.3813 | 0.1458 |
| 0.2082 | 0.0228 | 0.2861 | 0.2319 | 0.0515 | 0.0210 | 0.5242 | 0.7207 | 0.2820 | 0.0737 |
| 0.0816 | 0.2253 | 0.1944 | 0.3370 | 0.1208 | 0.0954 | 0.0562 | 0.2382 | 0.1949 | 0.3500 |
| 0.4080 | 0.3745 | 0.1647 | 0.2654 | 0.1300 | 0.2703 | 0.3837 | 0.3152 | 0.1448 | 0.1152 |
| 0.0717 | 0.2253 | 0.4149 | 0.3370 | 0.2500 | 0.1423 | 0.1258 | 0.1228 | 0.2948 | 0.4024 |
| 0.2834 | 0.2953 | 0.1647 | 0.1190 | 0.0655 | 0.0532 | 0.0296 | 0.2145 | 0.1526 | 0.1210 |
| MLE | = 0.2706 | = 2.9962 |
| BC | = 0.2697 | = 2.9847 |
| Boot-BC | = 0.2613 | = 2.7608 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, H.; Lio, Y.; Fan, Y.-Y.; Tsai, T.-R. Bias-Correction Methods for the Unit Exponential Distribution and Applications. Mathematics 2024, 12, 1828. https://doi.org/10.3390/math12121828
Xin H, Lio Y, Fan Y-Y, Tsai T-R. Bias-Correction Methods for the Unit Exponential Distribution and Applications. Mathematics. 2024; 12(12):1828. https://doi.org/10.3390/math12121828
Chicago/Turabian StyleXin, Hua, Yuhlong Lio, Ya-Yen Fan, and Tzong-Ru Tsai. 2024. "Bias-Correction Methods for the Unit Exponential Distribution and Applications" Mathematics 12, no. 12: 1828. https://doi.org/10.3390/math12121828







