A Complex-Valued Stationary Kalman Filter for Positive and Negative Sequence Estimation in DER Systems

Abstract

In medium- and low-voltage three-phase distribution networks, the load imbalance among the phases may compromise the network voltage symmetry. Inverter-interfaced distributed energy resources (DERs) can contribute to compensating for such imbalances by sharing the required negative sequence current while providing active power synchronized with the positive sequence voltage. However, positive and negative sequences are conventionally defined in a steady state and are not directly observed from the instantaneous voltage and current measurements at the DER unit’s point of connection. In this article, an estimation algorithm for sequence separation based on the Kalman filter is proposed. Furthermore, the proposed filter uses a complex vector representation of the asymmetric three-phase signals in synchronous coordinates to allow for the implementation of the Kalman filter in its stationary form, resulting in a simple dynamic filter able to estimate positive and negative sequences even during transient operation. The proposed stationary complex Kalman filter performs better than state-of-the-art techniques like DSOGI and very similarly to other Kalman filter implementations found in the literature but at a fraction of its computational cost (23.5%).

1. Introduction

Inverter-interfaced distributed energy resources (DERs) are increasingly common in three-phase distribution networks, forming microgrids at medium or low voltage. The microgrid concept offers numerous benefits, including the capacity to integrate renewable energy sources near the loads, the integration of energy storage devices, and the possibility of islanded operation [1]. The DER units in a microgrid also can provide support for a host of power quality issues. For example, when the microgrid operates in a grid-connected mode, the sharing of reactive power by the DERs contributes to the local voltage regulation [2]. Among the challenges in power quality management, the compensation of imbalance is a significant one where DERs can make a substantial contribution. Unbalanced loads are characteristic of low-voltage networks and demand asymmetric currents that, in turn, can considerably affect the symmetry of the microgrid’s voltage. This may be exacerbated during asymmetric faults. In such cases, the DER units are required to remain in operation, at least temporarily, compensating some of the imbalance [3]. In [4], a current reference strategy including an explicit negative sequence component is suggested to contribute to voltage equalization during asymmetric fault ride-through. The compensation of imbalance is particularly important in the islanded mode of operation [5,6,7,8] where the DERs must supply the whole of the imbalance currents.

The implementation of appropriate control algorithms for unbalanced voltage support in unbalanced grids requires the decoupling of the so-called positive and negative sequences of asymmetrical three-phase voltages and currents. Typically, the voltage sequence components are used for current reference generation, and the current sequence components are used directly for feedback in the inner current control loop; see, e.g., [8]. Thus, the dynamic response of the current sequence separation algorithm influences the system’s response and should be considered in the control design for optimal performance. However, this aspect is, to the best of our knowledge, overlooked in the literature.

The concept of positive and negative sequence components in asymmetric three-phase systems was introduced by Fortescue [9] more than one hundred years ago, and stems from the fact that real sinusoidal signals can be expressed in terms of two complex exponentials of positive and negative frequencies, i.e., $e^{j\omega }$ and $e^{-j\omega }$ via Fourier series. Hence, one of the main characteristics of the Fortescue transformation is that it only applies to the steady-state regime. Afterwards, Clarke [10] introduced the idea of instantaneous complex vector transformation applicable to time-domain signals in transient regimes. Although this transformation does not include an explicit sequence separation, both Fortescue and Clarke transformations are strongly interconnected [11,12]; the former is applicable to signals in phasor representation, whereas the latter in the time domain. As a matter of fact, the Clarke transformation [10] yields a representation of the three three-phase signals in a coordinate system aligned with the direction of its average (or common mode) and a plane orthogonal to this common mode, the so-called $\alpha \beta$ plane [13]. The electrical quantities of interest can then be represented as a vector, ${\left[s_{\alpha }{s}_{\beta }\right]}^T\in {\mathbb{R}}^2$, or in complex representation ${\mathbf{s}}_{\alpha \beta }\in \mathbb{C}$. In this plane, the pure positive and negative sequences of a stationary three-phase system would be fixed magnitude complex signals that rotate in opposite directions at a fixed (synchronous) frequency. However, in this representation, both positive and negative sequences are condensed in a single quantity. The Clarke transformation leads to a more general representation of arbitrary signals that may include transients, harmonics, and noise. Unfortunately, there is no bijective transformation that separates the positive and negative sequence components from the resulting complex signal. Therefore, the positive and negative sequences can only be estimated by a dynamic algorithm, such as filters or observers.

Possibly the best-known algorithm for sequence separation is the delayed signal cancellation method [14]. This method uses a linear combination of the complex representation of the electrical quantities of interest ${\mathbf{s}}_{\alpha \beta }$ with a version of itself delayed by a quarter of its fundamental period ($T/4$). The only dynamic element on this filter is delay, and the rest are algebraic calculations. Therefore, this algorithm does not perform well with distorted signals or during transients. A family of methods that do incorporate filtering in the classical sense stems from the synchronous reference frame phase-locked loop (SRF-PLL) of [15]. To better handle unbalance, the use of two synchronous rotating frames (in opposite directions) and a decoupling network has been proposed in the double synchronous reference frame PLL (DSRF-PLL) [16]. The decoupled double synchronous reference frame (DDSRF) algorithm can be used for sequence separation [4]. Another family of synchronization methods is based on the second-order generalized integrator (SOGI-PLL) [17], originally devised to make use of the advantages of complex signal processing on single-phase (real) signals. The second-order generalized integrator is an adaptive band-pass filter centered at the fundamental frequency, providing additional filtering with respect to SRF-based methods and improving its handling of distorted signals. By applying the SOGI method to both components $(\alpha ,\beta )$ in an unbalanced system and using a decoupling network, the double second-order generalized integrator PLL (DSOGI-PLL) [18] and its frequency-locked loop variant DSOGI-FLL [19] can separate the positive and negative sequences effectively. For these reasons, the DSOGI has become a well-established method for sequence separation and synchronization in distorted and weak grids [20] and can be used as a benchmark for other methods. However, all the DDSRF- and DSOGI-based methods rely on coordinate rotations, filters, and linear combinations of the signals, resulting in deterministic implementations. The random nature of the sequence separation problem has been acknowledged in [21], which has led to the utilization of stochastic estimation techniques. In [21], a complex-valued Kalman filter is used to estimate the positive sequence and negative sequences. Moreover, the order of the model is expanded to estimate harmonic components. In [22,23], the problem of sequence separation is tackled together with the frequency estimation problem by implementing an extended Kalman filter (EKF). The idea of utilizing a complex-valued model was further explored in [24], where an extended model was developed and the estimation was carried out using a complex-valued EKF. However, the EKF approach in real-time closed-loop applications presents a high computational load and results in an uncertain dynamic response.

In many of the techniques described above, the real and imaginary components of the complex variables that arise from the transformations are treated separately, favoring vector ${\left[s_{\alpha }{s}_{\beta }\right]}^T$ (real) representation. This approach disregards the compactness and analytical advantages of dealing directly with complex-valued variables. The processing of complex signals ($\mathbf{s}\in \mathbb{C}$) has many advantages over the processing of real signals and this fact is used extensively in many sub-fields of electrical and electronic engineering, for example, in signal processing and communications (see, e.g., [25] and the references therein) and in drive control [26]. On the other hand, the advantage of using complex signals in sequence separation has been recognized in [21], where the real and imaginary parts of the process noise and measurement noise are assumed mutually independent. In this paper, the solution of the sequence estimation by a complex time-varying Kalman filter (KF) proposed in [21] is reviewed in detail in terms of the statistical properties of the process noise and measurement noise allowing for a straightforward implementation of the complex-valued Kalman filter, in which the transpose operator is simply replaced by the hermitian (conjugated transpose) operator. Moreover, in this paper, a linear transformation of the state variable is proposed, resulting in a stationary solution of the Kalman filter [27]. This complex-valued stationary KF for sequence separation is the main contribution of the article and leads to a sequence estimation algorithm with similar performance to the conventional (real valued) time-varying KF, but at a fraction of the computational cost. Additionally, this stationary filter results in a constant and predictable dynamic performance, facilitating its incorporation into the control design. The benefits of this property for modern control design are illustrated in a numerical example.

2. Problem Statement

2.1. Asymmetrical Three-Phase Signals in Stationary Coordinates

The discrete-time sampled signals in a three-phase unbalanced electrical network (the voltages or the currents) can be expressed as

$$\begin{array}{c}\hfill {\mathbf{s}}_{abc}\left[k\right]=\left[\begin{array}{c}{s}_a\left[k\right]cos({\theta }_s\left[k\right]+{\phi }_a\left[k\right])\\ s_b\left[k\right]cos({\theta }_s\left[k\right]-2\pi /3+{\phi }_b\left[k\right])\\ s_c\left[k\right]cos({\theta }_s\left[k\right]+2\pi /3+{\phi }_c\left[k\right])\end{array}\right],\end{array}$$

(1)

where amplitudes $s_a,s_b,s_c$ and phases ${\phi }_a,{\phi }_b,{\phi }_c$, in general, are different from each other in asymmetric systems and may be time-varying, i.e., they are a function of k (the discrete-time index), to include the description of transient operations. However, in grid applications, the frequency of these signals (${\omega }_s$) is nearly constant and known by the local controllers. Therefore, considering sampling time $T_s$, the phase of the corresponding sinusoidal waves at time instant k can be estimated as ${\theta }_s\left[k\right]={\theta }_s[k-1]+{\omega }_s{T}_s$.

The Clarke transformation maps the three-phase asymmetrical signals into a complex variable ${\mathbf{s}}_{\alpha \beta }\in \mathbb{C}$, plus a real common mode ${\mathbf{s}}_{\gamma }\in \mathbb{R}$ or a zero-sequence component. The trajectory of complex variable ${\mathbf{s}}_{\alpha \beta }$ is said to be in a stationary $\alpha \beta$ reference frame. The $\gamma$ or the zero-sequence component, by definition, does not contribute to the positive or negative components and is consequently disregarded hereinafter. Hence, the Clarke transformation from ${\mathbf{s}}_{abc}\in {\mathbb{R}}^3$ to ${\mathbf{s}}_{\alpha \beta }\in \mathbb{C}$ can be expressed as

$$\begin{array}{cc}\hfill {\mathbf{s}}_{\alpha \beta }& =\underset{\mathbf{T}}{\underbrace{\frac{2}{3}\left[\begin{array}{ccc}1& a& a^2\end{array}\right]}}{\mathbf{s}}_{abc}.\hfill \end{array}$$

(2)

with $a=e^{j\frac{2\pi }{3}}$. Before advancing to the Clarke transformation of the signals of (1), it is convenient to express this equation using the Euler form of the cosine function, $cos\eta =\frac{e^{j\eta }+e^{-j\eta }}{2}$. Thus,

$$\begin{array}{c}\hfill {\mathbf{s}}_{abc}\left[k\right]=\frac{1}{2}\left[\begin{array}{ccc}{s}_a\left[k\right]& 0& 0\\ 0& s_b\left[k\right]& 0\\ 0& 0& s_c\left[k\right]\end{array}\right]\left[\begin{array}{cc}{e}^{j{\phi }_a\left[k\right]}& e^{-j{\phi }_a\left[k\right]}\\ e^{j({\phi }_b\left[k\right]-\frac{2\pi }{3})}& e^{-j({\phi }_b\left[k\right]-\frac{2\pi }{3})}\\ e^{j({\phi }_c\left[k\right]+\frac{2\pi }{3})}& e^{-j({\phi }_c\left[k\right]+\frac{2\pi }{3})}\end{array}\right]\left[\begin{array}{c}{e}^{j{\theta }_s\left[k\right]}\\ e^{-j{\theta }_s\left[k\right]}\end{array}\right].\end{array}$$

(3)

Applying (2) to (3), obtain the asymmetrical three-phase signal in the complex $\alpha \beta$ frame as

$${\mathbf{s}}_{\alpha \beta }\left[k\right]=\underset{{\mathbf{s}}_{\alpha \beta }^{+}\left[k\right]}{\underbrace{\frac{1}{3}\left(s_a\left[k\right]e^{j{\phi }_a\left[k\right]}+s_b\left[k\right]e^{j{\phi }_b\left[k\right]}+s_c\left[k\right]e^{j{\phi }_c\left[k\right]}\right)e^{j{\theta }_s\left[k\right]}}}+\underset{{\mathbf{s}}_{\alpha \beta }^{-}\left[k\right]}{\underbrace{\frac{1}{3}\left(s_a\left[k\right]e^{-j{\phi }_a\left[k\right]}+s_b\left[k\right]e^{-j({\phi }_b\left[k\right]+\frac{2\pi }{3})}+s_c\left[k\right]e^{-j({\phi }_c\left[k\right]-\frac{2\pi }{3})}\right)e^{-j{\theta }_s\left[k\right]}}}$$

(4)

The expression in (4) corresponds to a single complex variable that can be written as the sum of two complex components rotating at synchronous frequency, one in the counter-clockwise direction (conventionally known as the positive sequence) and the other clockwise (the negative sequence). Even though Equation (4) is rigorously valid for steady-state conditions, i.e., with constant amplitudes $\{s_a,s_b,s_c\}$ and phases $\{{\phi }_a,{\phi }_b,{\phi }_c\}$, it does not describe exactly the sequence separation in transient conditions. When a causally changing event occurs in any of the variables (amplitudes $\{s_a\left[k\right],s_b\left[k\right],s_c\left[k\right]\}$ and/or of the phases $\{{\phi }_a\left[k\right],{\phi }_b\left[k\right],{\phi }_c\left[k\right]\}$), it introduces additional frequency components. To account for this, it is assumed that there is uncertainty in the components of ${\mathbf{s}}_{\alpha \beta }\left[k\right]$. Furthermore, it is considered that this uncertainty can be grouped in error signal ${\mathit{\epsilon }}_{\alpha \beta }$ with known stochastic properties. Therefore, Equation (4) can be expressed as

$$\begin{array}{c}\hfill {\mathbf{s}}_{\alpha \beta }\left[k\right]={\mathbf{s}}_{\alpha \beta }^{+}\left[k\right]+{\mathbf{s}}_{\alpha \beta }^{-}\left[k\right]+{\mathit{\epsilon }}_{\alpha \beta }\left[k\right],\end{array}$$

(5)

where ${\mathbf{s}}_{\alpha \beta }^{+},{\mathbf{s}}_{\alpha \beta }^{-}\in \mathbb{C}$. In addition, the simplifying assumption that ${\mathit{\epsilon }}_{\alpha \beta }\in \mathbb{C}$ is a circularly symmetric complex-valued Gaussian random variable is made, such that ${\mathit{\epsilon }}_{\alpha \beta }\sim \mathcal{CN}\left(\mathbf{0},{\mathbf{R}}_{\alpha \beta }\right)$, with ${\mathbf{R}}_{\alpha \beta }={\sigma }^2$. For details on complex-valued Gaussian random variables, see Appendix B.

Given that the asymmetrical signal (1) can now be expressed in the $\alpha \beta$ frame as (5), and that the statistical properties of ${\mathit{\epsilon }}_{\alpha \beta }$ are defined, the estimation of ${\mathbf{s}}_{\alpha \beta }^{+}$ and ${\mathbf{s}}_{\alpha \beta }^{-}$ could be solved in this reference frame. Nevertheless, it may be convenient to express the variables on a synchronous reference frame.

2.2. An Asymmetrical Three-Phase Signal Expressed on a Synchronous $dq$ Reference Frame

The original Park transformation [28] expresses the electrical variables measured in their natural $abc$ per-phase coordinates into a $dq$ reference frame that rotates synchronously with the positive sequence of the electrical variables. The same result is obtained by applying the previously discussed Clarke transformation and a coordinate rotation [13], and this procedure is employed hereinafter. As the frequency is known to be ${\omega }_s$, and the orientation angle can be arbitrarily chosen, without loss of generality, the orientation angle can be assumed to be ${\theta }_s\left[k\right]$. To rotate the signal (5) to the $dq$ frame, rotation ${\mathbf{s}}_{dq}\left[k\right]={\mathbf{s}}_{\alpha \beta }\left[k\right]e^{-j{\theta }_s\left[k\right]}$ is performed, leading to

$${\mathbf{s}}_{dq}\left[k\right]={\mathbf{s}}_{dq}^{+}\left[k\right]+{\mathbf{s}}_{dq}^{-}\left[k\right]e^{-j2{\theta }_s\left[k\right]}+{\mathit{\epsilon }}_{dq}\left[k\right],$$

(6)

where the noise in $dq$ is

$${\mathit{\epsilon }}_{dq}\left[k\right]={\mathit{\epsilon }}_{\alpha \beta }\left[k\right]e^{-j{\theta }_s\left[k\right]}.$$

(7)

As stochastic variable ${\mathit{\epsilon }}_{\alpha \beta }$ was assumed to be circularly symmetric, the stochastic properties remain invariant under rotations, that is,

$$\begin{array}{cc}\hfill \mathbb{E}\left\{{\mathit{\epsilon }}_{dq}\right\}& =0,{\mathbf{R}}_{dq}={\mathbf{R}}_{\alpha \beta }.\hfill \end{array}$$

(8)

It is worth noting that quantities ${\mathbf{s}}_{dq}^{+}$ and ${\mathbf{s}}_{dq}^{-}$ from (4), in steady state, are constant complex numbers, akin to conventional phasors. With the signals expressed in the synchronous $dq$ reference frame as given by (6), the estimation problem determines the positive (${\mathbf{s}}_{dq}^{+}\left[k\right]$) and negative (${\mathbf{s}}_{dq}^{-}\left[k\right]$) complex-valued sequence components from observed variable ${\mathbf{s}}_{dq}$, even during transient conditions.

3. Modeling and Estimation of the Complex Positive and Negative Sequence Components

The asymmetrical three-phase signals have been expressed as a complex variable in a $dq$ reference frame in (6). Here, ${\mathbf{s}}_{dq}\in \mathbb{C}$ is the observed or output variable, and ${\mathbf{s}}_{dq}^{+}$, ${\mathbf{s}}_{dq}^{-}\in \mathbb{C}$ are its positive and negative sequence components to be estimated, i.e., the state of the system to be estimated. In other words, (6) can be thought of as the output equation of a dynamic system. Unfortunately, the term $e^{-j2{\theta }_s}$ provides a time-varying characteristic to the dynamic model. Another difficulty to overcome is that the sequence components, i.e., the state of the system, depend on unknown conditions, like load imbalance, for example. Therefore, it may be concluded that an accurate dynamic model is not readily available for the system of interest. However, it can be safely assumed that $\mathbf{x}\left[k\right]={\left[{\mathbf{s}}_{dq}^{+}{\mathbf{s}}_{dq}^{-}\right]}^T$ is a constant variable at steady state. Hence, its dynamic behavior may be modeled as an uncorrelated Gaussian random walk:

$$\begin{array}{c}\hfill \mathbf{x}[k+1]=\mathbf{x}\left[k\right]+\mathbf{w}\left[k\right],\end{array}$$

(9)

with $\mathbf{x}\left[k\right]={\left[\begin{array}{cc}{\mathbf{s}}_{dq}^{+}\left[k\right]& {\mathbf{s}}_{dq}^{-}\left[k\right]\end{array}\right]}^T\in {\mathbb{C}}^2$, and $\mathbf{w}\left[k\right]\in {\mathbb{C}}^2$ a zero mean circularly symmetric (i.e., proper) complex Gaussian random variable with variance $\mathbf{Q}$, $\mathbf{w}\left[k\right]\sim \mathcal{CN}\{\mathbf{0},\mathbf{Q}\}$.

In the following, estimation algorithms that consider both the simplified dynamic model (9) and its time-varying output Equation (6) are proposed. Since the original problem is formulated in the complex plane, the use of the complex-valued Kalman filter (CKF) [21,29] is also considered in this section as a more compact alternative. Finally, based on the representation of the system in complex form, a linear transformation is used, assigning the time-varying term to the actual signal to be estimated, resulting in a time-invariant model. By applying this transformation, the stationary complex-valued Kalman filter (SCKF) is deduced. This implementation greatly reduces the computational load of the sequence separation without loss of accuracy. These two algorithms are detailed next.

3.1. Complex-Valued Kalman Filter (CKF)

The dynamic model (9) and the output Equation (6) correspond to a complex-valued state-space formulation. This representation can be used, for instance, in the formulation of a time-varying linear quadratic estimator problem, with the well-known time-varying KF as the optimal solution [30]. For complex linear systems, the CKF can be formulated using the well-known structure of the real-valued KF [31] when the initial condition. The process noise and the measurement noise are all proper complex random variables. In this case, the transpose operator from the real-valued KF is simply replaced by the hermitian (conjugate transpose) operator; see e.g., [29]. More details about the derivation of the KF and the complex-valued KF are provided in Appendix A and Appendix B, respectively.

For implementation, the output Equation (6) can be written as

$$\begin{array}{c}\hfill \underset{\mathbf{y}\left[k\right]}{\underbrace{{\mathbf{s}}_{dq}\left[k\right]}}=\underset{{\mathbf{C}}_{\theta }\left[k\right]}{\underbrace{\left[\begin{array}{cc}1& e^{-j2{\theta }_s\left[k\right]}\end{array}\right]}}\underset{\mathbf{x}\left[k\right]}{\underbrace{\left[\begin{array}{c}{\mathbf{s}}_{dq}^{+}\left[k\right]\\ {\mathbf{s}}_{dq}^{-}\left[k\right]\end{array}\right]}}+{\mathit{\epsilon }}_{dq}\left[k\right].\end{array}$$

(10)

With the state and output equations in (9) and (10), respectively, the corresponding CKF is obtained:

$$\begin{array}{cc}\hfill \mathbf{K}\left[k\right]& =\mathbf{P}\left[k\right|k-1]{\mathbf{C}}_{\theta }^H\left[k\right]{\left(\mathbf{R}+{\mathbf{C}}_{\theta }\left[k\right]\mathbf{P}\left[k\right|k-1]{\mathbf{C}}_{\theta }^H\left[k\right]\right)}^{-1},\hfill \\ \hfill \mathbf{x}\left[k\right|k]& =\mathbf{x}\left[k\right|k-1]+\mathbf{K}\left[k\right]\left(\mathbf{y}\left[k\right]-{\mathbf{C}}_{\theta }\left[k\right]\mathbf{x}\left[k\right|k-1]\right),\hfill \\ \hfill \mathbf{P}\left[k\right|k]& =\left(\mathbb{I}-\mathbf{K}\left[k\right]{\mathbf{C}}_{\theta }\left[k\right]\right)\mathbf{P}\left[k\right|k-1],\hfill \end{array}$$

(11)

In the algorithm, the time-variant part of ${\mathbf{C}}_{\theta }$, $e^{-2j{\theta }_s\left[k\right]}$ can be assumed to be known as the grid frequency is known by the local controllers, and the phase of the ${\mathbf{s}}_{dq}$ frame is arbitrary.

3.2. Stationary Complex Kalman Filter (SCKF)

In this section, the main results of the article are presented. Here, a change in variables to the positive and negative sequence in state vector $\mathbf{x}\left[k\right]$ is introduced, given by (9) and (10), that yields a time-invariant model. For estimation purposes, this model simplifies the implementation and reduces the computational load of the associated Kalman filter. To that end, a new complex-valued random variable $\tilde{\mathbf{x}}\left[k\right]$ is estimated instead of $\mathbf{x}\left[k\right]$. This new variable is defined as

$$\mathbf{x}\left[k\right]=\underset{{\mathbf{T}}_{\mathbf{x}}\left[k\right]}{\underbrace{\left[\begin{array}{cc}1& 0\\ 0& e^{j2{\theta }_s\left[k\right]}\end{array}\right]}}\tilde{\mathbf{x}}\left[k\right].$$

(12)

By inserting (12) to output Equation (10), the new output Equation (13) is obtained:

$$\mathbf{y}\left[k\right]=\underset{\tilde{\mathbf{C}}}{\underbrace{\left[\begin{array}{cc}1& 1\end{array}\right]}}\tilde{\mathbf{x}}\left[k\right]+{\mathit{\epsilon }}_{dq}\left[k\right].$$

(13)

Similarly, transformation (12) can be applied to the time-evolution of the variables to be estimated in (9), yielding

$$\begin{array}{c}\hfill {\mathbf{T}}_{\mathbf{x}}[k+1]\tilde{\mathbf{x}}[k+1]={\mathbf{T}}_{\mathbf{x}}\left[k\right]\tilde{\mathbf{x}}\left[k\right]+\mathbf{w}\left[k\right].\end{array}$$

(14)

As mentioned before, variable ${\theta }_s\left[k\right]$ is known for each time instant k and its time domain model is given by ${\theta }_s[k+1]={\theta }_s\left[k\right]+{\omega }_s{T}_s$. Therefore, the time evolution of transformation ${\mathbf{T}}_{\mathbf{x}}\left[k\right]$ can be written as

$$\begin{array}{c}\hfill {\mathbf{T}}_{\mathbf{x}}[k+1]=\left[\begin{array}{cc}1& 0\\ 0& e^{j2{\omega }_s{T}_s}\end{array}\right]{\mathbf{T}}_{\mathbf{x}}\left[k\right],\end{array}$$

(15)

and the time evolution of $\tilde{\mathbf{x}}\left[k\right]$ is given by

$$\begin{array}{c}\hfill \tilde{\mathbf{x}}[k+1]=\underset{\tilde{\mathbf{A}}}{\underbrace{\left[\begin{array}{cc}1& 0\\ 0& e^{-j2{\omega }_s{T}_s}\end{array}\right]}}\tilde{\mathbf{x}}\left[k\right]+\tilde{\mathbf{w}}\left[k\right],\end{array}$$

(16)

where $\tilde{\mathbf{w}}\left[k\right]={\mathbf{T}}_{\mathbf{x}}^{-1}[k+1]\mathbf{w}\left[k\right]$. Again, since $\mathbf{w}\left[k\right]$ is circularly symmetric and transformation ${\mathbf{T}}_{\mathbf{x}}\left[k\right]$ is a rotation in the complex plane, the vector of uncertainties preserves the original properties $\tilde{\mathbf{w}}\left[k\right]\sim \mathcal{CN}\{\mathbf{0},\mathbf{Q}\}$.

Finally, the CKF algorithm can be evaluated with state and output Equations (16) and (13), respectively, resulting in

$$\begin{array}{cc}\hfill \tilde{\mathbf{x}}\left[k\right|k-1]& =\tilde{\mathbf{A}}\tilde{\mathbf{x}}[k-1|k-1],\hfill \\ \hfill \mathbf{P}\left[k\right|k-1]& =\tilde{\mathbf{A}}\mathbf{P}[k-1|k-1]{\tilde{\mathbf{A}}}^H+\mathbf{Q},\hfill \\ \hfill \mathbf{K}\left[k\right]& =\mathbf{P}\left[k\right|k-1]{\tilde{\mathbf{C}}}^H{\left(\mathbf{R}+\tilde{\mathbf{C}}\mathbf{P}\left[k\right|k-1]{\tilde{\mathbf{C}}}^H\right)}^{-1},\hfill \\ \hfill \tilde{\mathbf{x}}\left[k\right|k]& =\tilde{\mathbf{x}}\left[k\right|k-1]+\mathbf{K}\left[k\right]\left(\mathbf{y}\left[k\right]-\tilde{\mathbf{C}}\tilde{\mathbf{x}}\left[k\right|k-1]\right),\hfill \\ \hfill \mathbf{P}\left[k\right|k]& =\left(\mathbb{I}-\mathbf{K}\left[k\right]\tilde{\mathbf{C}}\right)\mathbf{P}\left[k\right|k-1].\hfill \end{array}$$

(17)

The matrices $\tilde{\mathbf{A}}$ and $\tilde{\mathbf{C}}$ are time-invariant and the pair $\{\tilde{\mathbf{A}},\tilde{\mathbf{C}}\}$ is detectable; therefore, the convergence of the complex Riccati equation associated to the estimation problem is ensured. Consequently, one can implement the stationary solution of the CKF (SCKF) without loss of estimation accuracy and at low computational complexity. Here, the time index “k” is replaced by the symbol “∞” to denote the quantities that converge (i.e., the filtered covariance and the Kalman gain) for the stationary filter. In order to obtain the corresponding SCKF algorithm, the following discrete-time complex algebraic Riccati equation should be solved:

$$\begin{array}{c}\hfill \mathbf{P}[\infty ]=\mathbf{Q}+\tilde{\mathbf{A}}\left(\mathbf{P}[\infty ]-\mathbf{P}[\infty ]{\tilde{\mathbf{C}}}^H{\left(\mathbf{R}+\tilde{\mathbf{C}}\mathbf{P}[\infty ]{\tilde{\mathbf{C}}}^H\right)}^{-1}\tilde{\mathbf{C}}\mathbf{P}[\infty ]\right){\tilde{\mathbf{A}}}^H.\end{array}$$

(18)

To solve the algebraic Riccati equation, numerical packages are widely available. One alternative that can handle complex entries is MATLAB R2023b (The MathWorks, Inc., Natick, MA, USA), using command idare(·). Then, given the numerical value of $\mathbf{P}[\infty ]$, the stationary complex-valued Kalman gain can be found evaluating the following:

$$\mathbf{K}[\infty ]=\mathbf{P}[\infty ]{\tilde{\mathbf{C}}}^H{\left(\mathbf{R}+\tilde{\mathbf{C}}\mathbf{P}[\infty ]{\tilde{\mathbf{C}}}^H\right)}^{-1}.$$

(19)

With the stationary complex-valued Kalman gain obtained, the implementation of the SCKF for $\tilde{\mathbf{x}}\left[k\right|k]$ is straightforward, and can be written as

$$\begin{array}{c}\hfill \tilde{\mathbf{x}}\left[k\right|k]=\left(\tilde{\mathbf{A}}-\mathbf{K}[\infty ]\tilde{\mathbf{C}}\tilde{\mathbf{A}}\right)\tilde{\mathbf{x}}[k-1|k-1]+\mathbf{K}[\infty ]\mathbf{y}\left[k\right].\end{array}$$

(20)

This is a recursive time-invariant algorithm with constant matrices $\{\tilde{\mathbf{A}},\tilde{\mathbf{C}},\mathbf{K}[\infty ]\}$. Finally, solving (20) for each time instant k, the complex vector $\tilde{\mathbf{x}}\left[k\right|k]$ is found and the estimated positive and negative sequences are obtained by evaluating (12) for the estimated values. That is,

$$\begin{array}{c}\hfill \mathbf{x}\left[k\right|k]={\mathbf{T}}_{\mathbf{x}}\left[k\right]\tilde{\mathbf{x}}\left[k\right|k].\end{array}$$

(21)

For the sequence estimation problem, transformation (12) is a simple and effective way to express the time-varying nature of the problem. As a consequence, the estimation problem results to be time-invariant in the new state space. Hence, the stationary solution of the complex-valued Kalman filter can be obtained, simplifying the implementation and significantly reducing computational cost, without loss of accuracy. The straightforward SCKF for the sequence separation problem is expressed in Algorithm 1.

Algorithm 1: Proposed SCKF Algorithm.

4. Simulation Results

To evaluate the performance of the proposed SCKF and to compare it to the performance obtained by the well-established DSOGI method [18,19,20], an open-loop sequence separation problem is simulated. A brief explanation of the DSOGI algorithm is included in Appendix C, and the interested reader can find further details in [20].

The simulated system for this test is depicted in Figure 1. It consists of a symmetrical three-phase voltage source of 111 V phase—neutral, an islanding transformer connected in Delta–Delta, with turn ratio $1:\sqrt{3}$, and a three-phase resistive load with $R=47\Omega$ per phase. This load is intentionally unbalanced to produce asymmetrical three-phase current waveforms by disconnecting load phase b.

Figure 1. Case study 1: experimental prototype to produce the asymmetrical currents to be separated into its constituting positive and negative sequences by the proposed KF, CKF and SCKF.

For the implementation of the SCKF estimator, the values of the state and measurement noise covariance matrices, $\mathbf{Q}$ and $\mathbf{R}$ are required. These serve as tuning parameters for the simulation. In the interest of fairness, the same values used for the experimental testing discussed in the next section are also used in the simulation. These values can be found in Table 1. Noise covariance matrices were selected by trial and error. On the other hand, the DSOGI algorithm only has one tuning parameter, and value gain $k=\sqrt{2}$ used in [18,19,20] is considered.

Table 1. Estimation algorithm parameters; ${\mathbf{I}}_n$ denotes the identity matrix and ${\mathbf{0}}_{m\times n}$ denotes the zero matrix of size $m\times n$.

	$\mathbf{x}\left[0\right]$	$\mathbf{P}\left[0\right]$	Q	R	$\mathbf{K}\left[\mathbf{\infty }\right]$
KF	${\mathbf{0}}_{4\times 1}$	$0.01{\mathbf{I}}_4$	$0.01{\mathbf{I}}_4$	${\mathbf{I}}_2$	-
CKF	${\mathbf{0}}_{2\times 1}$	$0.01{\mathbf{I}}_2$	$0.01{\mathbf{I}}_2$	${\mathbf{I}}_1$	-
SCKF	${\mathbf{0}}_{2\times 1}$	-	$0.01{\mathbf{I}}_2$	${\mathbf{I}}_1$	$0.085\left[\begin{array}{c}{e}^{-j0.43}\\ e^{j0.43}\end{array}\right]$

A thousand Monte Carlo simulations were carried out, which is equivalent to measuring the same event a thousand times. Figure 2 shows the mean of the Monte Carlo simulation results. To examine and compare the estimation performance of each method, the separated sequence currents are presented in positive and negative rotating $dq$ frames, respectively. These results show that, although both algorithms are efective in achieving sequence separation, the SCKF has a faster response than DSOGI.

Figure 2. Simulated dynamic response of the proposed SCKF and the well-established DSOGI method to an abrupt change in the sequence content of a three-phase current set.

5. Experimental Validation

To confirm the aforementioned results, experimental tests are run in real time to evaluate the performance of the SCKF proposed in Section 3.2. Two different case studies are considered to validate the effectiveness of our proposal: an open-loop sequence separation problem and a closed-loop current control application. In the first case, a three-phase resistive load connected to the grid is severely unbalanced, resulting in a fast transition from symmetric to asymmetric currents replicating experimentally the simulation of the previous section using a balanced star-connected resistive load of $47\Omega$, 1 kW per phase and a circuit breaker in phase b to produce the imbalance. A resistive load is chosen because it demands the fastest change in load current, making it the most stringent test for assessing the performance of sequence separation algorithms. In this case, the grid is physically emulated by a three-phase $6\mathrm{kW}$ Chroma 61704 AC power supply (Chroma ATE Inc., Taoyuan, Taiwan) that produces very clean sinusoidal signals and an isolation transformer connected in Delta–Delta with turn ratio $1:\sqrt{3}$. The setup is instrumented with LEM current transducers, and the current measurement signals are sampled at $T_s=200\mathsf{\mu }$s by a dSPACE 1103 (dSPACE GmbH, Paderborn, Germanny) that performs all the calculations in real time. A general-purpose I/O signal of the dSPACE is used to control the circuit breaker via a chain of relays. For this experimental case study, the two discussed complex versions of the recursive algorithm (CKF and SCKF) are used to separate the positive and negative sequences of the currents to contrast their estimation performance and also their computational burden. In addition, the equivalent real-valued KF is used for comparison purposes. The description of the real-valued KF can be found in Appendix A. In the second case, the estimation of the SCKF-based algorithm is used as feedback in a positive and negative sequence control scheme of an $LC$-filtered DER unit, and the control performance is compared with the direct feedback of the asymmetrical variables. The DER consists of a 6 kW Semikron laboratory 2-level voltage source inverter (2L-VSC) (Semikron GmbH, Nuremberg, Germany) properly interfaced to be modulated by external signals. The primary energy resource (ER) is emulated using a programmable DC power supply (model N8762A of Agilent Technologies, Inc., Santa Clara, CA, USA), set at $v_{\mathrm{dc}}=540\mathrm{V}$. Finally, the same isolating transformer and three-phase load as in the previous case study are used. For this experimental case study, the estimation, the control and the space-vector PWM modulation are implemented in a dSPACE 1103 with a sampling time of $T_s=200\mathsf{\mu }$s, which is also the period of the PWM carrier for close loop control. Figure 3 shows a picture of this experimental setup.

Figure 3. Experimental Setup.

5.1. Case Study 1: Positive and Negative Sequence Estimation of an Asymmetrical Signal

This case study evaluates the estimation performance of the estimation algorithms described in Section 3. In particular, it is of interest to demonstrate that the proposed time-varying CKF exhibits performance similar to that of the conventional Kalman filter when the latter is implemented with an extended state vector of real variables (see Appendix A for details). These results help to validate the assumption of circular symmetric noises underlying the CKF formulation. Furthermore, it is of interest to show that the proposed SCKF exhibits almost identical estimates to the time-varying CKF after the initial transient of the Kalman gain matrix passes. As a result, the SCKF enables comparable performance with a significantly reduced computational load of the estimator. The experimental setup corresponds to the circuit depicted in Figure 1 and its parameters are the same as in the simulations of the previous section. In this experiment, the load is intentionally unbalanced to produce asymmetrical three-phase current waveforms by opening a single-phase breaker connected in phase b.

The implementation of CKF and SCKF estimators requires the knowledge of state and measurement noise covariance matrices, $\mathbf{Q}$ and $\mathbf{R}$. Additionally, these algorithms require to be initialized with the expected value of the initial state and covariance matrices at time instant $k=0$. The values used in each algorithm are given in Table 1. Notice that for the stationary filter, i.e., SCKF, the stationary Kalman gain $\mathbf{K}[\infty ]$ can be directly computed from matrices $\mathbf{Q}$, $\mathbf{R}$ and the matrices that define the dynamic system ($\tilde{\mathbf{A}}$ and $\tilde{\mathbf{C}}$, see (18) and (19)). Therefore, $\mathbf{K}[\infty ]$ does not depend on $\mathbf{P}\left[0\right]$. To examine and compare the estimation performance of each method, the separated sequence currents are presented in positive and negative rotating $dq$ frames, oriented with the supply voltage as $\pm \angle {\mathbf{v}}_s$, respectively.

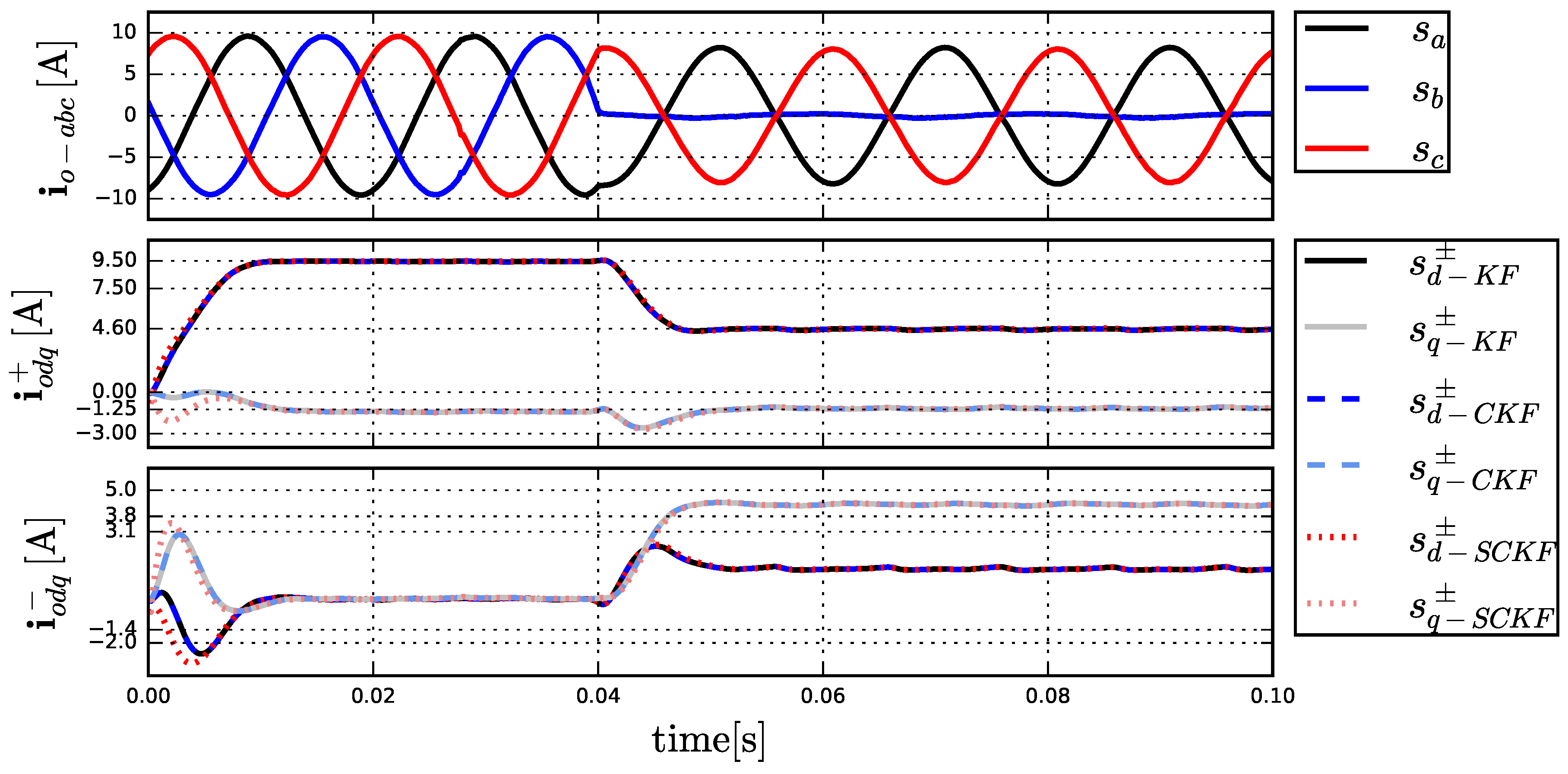
The experimental results are shown in Figure 4. The three-phase load is balanced, with Br₁ closed, hence demanding symmetric currents. The estimation is carried out using the three algorithms at $t=0$ s with the same initial value (either in real or complex form). For KF and CKF algorithms, the estimated states are almost identical, validating the assumption of circular symmetric complex noises in the CKF formulation. On the other hand, the dynamic response of the proposed SCKF differs slightly for the first few samples due to the difference in the initial Kalman gain of the time-varying algorithms (KF and CKF) with respect to the steady state $\mathbf{K}[\infty ]$ used in the SCKF. The three algorithms converge to the same Kalman gains after $t=7$ ms, making their time responses almost indistinguishable. At $t=0.04$ s, the breaker Br₁ is opened and the load in phase-b is disconnected, resulting in a considerable imbalance. As shown in Figure 4, the three implementations of the KF yield almost identical state estimates during this large transient, converging to the same steady-state values within (approximately) a third of the fundamental period. Therefore, the use of the proposed SCKF for sequence estimation can effectively replace the time-varying algorithms, KF and CKF. Consequently, positive and negative sequence estimation can be easily and efficiently implemented without loss of performance. In terms of computational complexity, first, the structure of the problem of interest is considered. That is, it is taking into account that some elements are equal to 1 when involved in multiplications, that some elements are real when involved in additions and multiplications, and that some matrices are symmetric or Hermitian when computed. In addition, it is considered that a real sum and a real multiplication are both equivalent to one floating point operation (FLOP), a complex sum equals 2 FLOPs and a complex multiplication equals 6 FLOPs. Then, the real-valued KF (see [21]) results in 213 FLOPs per iteration, the complex-valued KF in 74 FLOPs, whilst the proposed stationary CKF in only 50 FLOPs, which corresponds to a reduction of $76.5\%$ of the complexity with respect to the real-valued KF and a reduction of $32.4\%$ of the complexity with respect to the complex-valued KF.

Figure 4. Experimental dynamic response of the KF, CKF and the proposed SCKF to an abrupt change in the sequence content of a three-phase current set.

5.2. Case Study 2: The Use of the Estimated Sequences on a Closed-Loop Strategy

This case study explores the application of the proposed SCKF in a closed-loop control strategy that uses the estimated positive and negative sequences as feedback variables. The system under study is shown in Figure 5, where the $LC$ filtered stand-alone DER is subjected to an unbalanced load disturbance. The main goal of this case study is to confirm that the utilization of the state estimations (i.e., positive and negative sequences) that are obtained from the proposed SCKF in a real closed-loop application can yield good control performance in the presence of unbalanced loads. For comparison purposes, a closed-loop strategy based on the direct feedback of the asymmetrical measured variables, and otherwise similar control strategy, is used. The experimental set-up in Figure 5 has the following parameters: $R_f=0.1\Omega$, $L_f=5\mathrm{mH}$ and $C_f=12\mathsf{\mu }\mathrm{F}$. A second output filter inductance is provided by the leakage inductance of the transformer, approximately $0.6\mathrm{mH}$, but for control purposes, it can be considered part of the load of the system.

Figure 5. Case study 2: experimental prototype.

The two control strategies that are compared in this case study are based on state feedback. These are briefly described in the following paragraph.

The first control strategy uses the estimated positive and negative sequences from the proposed SCKF as feedback, and it can be summarized by the control diagram in Figure 6. In this scheme, the proposed SCKF algorithm follows the design presented in Table 1. In Figure 6, ${\mathbf{x}}^{+}={\left[\begin{array}{cc}{\mathbf{i}}_{fdq}^{+}& {\mathbf{v}}_{sdq}^{+}\end{array}\right]}^T$ and ${\mathbf{x}}^{-}={\left[\begin{array}{cc}{\mathbf{i}}_{fdq}^{-}& {\mathbf{v}}_{sdq}^{-}\end{array}\right]}^T$ are the positive and negative sequence state variables, ${\mathbf{u}}^{+}={\mathbf{v}}_{tdq}^{+}$ and ${\mathbf{u}}^{-}={\mathbf{v}}_{tdq}^{-}$ are the positive and negative sequences of voltage ${\mathbf{v}}_t$ modulated by the VSC. Currents ${\mathbf{d}}^{+}={\mathbf{i}}_{odq}^{+}$ and ${\mathbf{d}}^{-}={\mathbf{i}}_{odq}^{-}$ are demanded by the load and are considered as disturbances for the system. Finally, ${\mathbf{z}}^{+}={\mathbf{v}}_{sdq}^{+}$, ${\mathbf{z}}^{-}={\mathbf{v}}_{sdq}^{-}$ are the voltages at the shunt capacitor which are the output variables to be controlled. On the other hand, a direct or naive control strategy, without the sequence separation, is illustrated in Figure 7. Here, the state is given by $\mathbf{x}={\left[\begin{array}{cc}{\mathbf{i}}_{fdq}& {\mathbf{v}}_{sdq}\end{array}\right]}^T$, the control action is $\mathbf{u}={\mathbf{v}}_{tdq}$, the disturbance is given by load current $\mathbf{d}={\mathbf{i}}_{odq}$ and the output to be controlled is $\mathbf{z}={\mathbf{v}}_{sdq}$.

Figure 6. Proposed control strategy for positive and negative sequence control.

Figure 7. Control scheme for a DER unit’s output filter that uses asymmetrical variables as feedback.

Both control strategies follow a scheme based on state feedback that includes the set point of the variable to be controlled (${\mathbf{v}}_s$) and the compensation of the measured disturbance (${\mathbf{i}}_o$). It is worth noting that in this case study, where the capacitor voltage is the controlled variable, orientation angle ${\theta }_s\left[k\right]$ is directly obtained using the integration of frequency, and its phase is automatically adjusted by controlling the imaginary component $v_{sq}$ to a zero value. Feedback gains $\{{\mathbf{K}}_{\mathbf{c}},{\mathbf{K}}_{\mathbf{c}}^{+},{\mathbf{K}}_{\mathbf{c}}^{-}\}$ are designed as a linear quadratic regulator, and the matrices that map the set point (${\mathbf{H}}_{\mathbf{r}}$) and disturbance (${\mathbf{H}}_{\mathbf{d}}$) to the input variable are obtained following the analytical results in [27,32]. For the separated sequence control, the gain matrices differ only in the signs of some of its entries as summarized in Table 2. For direct control, the gain matrices are given by ${\mathbf{K}}_{\mathbf{c}}={\mathbf{K}}_{\mathbf{c}}^{+}$, ${\mathbf{H}}_{\mathbf{r}}={\mathbf{H}}_{\mathbf{r}}^{+}$ and ${\mathbf{H}}_{\mathbf{d}}={\mathbf{H}}_{\mathbf{d}}^{+}$. Note that this controller, shown in the scheme of Figure 7, is similar to the control of the positive sequence in the scheme of Figure 6, but the asymmetrical signal is used as feedback. Consequently, it is expected that the main difference between the closed-loop performances of both control methods would be manifested in the negative sequence of the variable to be controlled, ${\mathbf{v}}_{sdq}$.

Table 2. Implemented matrices in the strategies of Figure 6 and Figure 7.

${\mathbf{K}}_{\mathbf{c}}^{\pm }$	$\left[\begin{array}{cccc}3.9& \pm 0.12& -0.06& \mp 0.0019\\ \mp 0.12& 3.9& \pm 0.0019& -0.06\end{array}\right]$
${\mathbf{H}}_{\mathbf{r}}^{\pm }$	$\left[\begin{array}{cc}0.93& \mp 0.017\\ \pm 0.017& 0.93\end{array}\right]$
${\mathbf{H}}_{\mathbf{d}}^{\pm }$	$\left[\begin{array}{cc}4& \mp 1.45\\ \pm 1.45& 4\end{array}\right]$

The experimental response of the closed-loop current control in response to a step change from balanced to unbalanced load is shown in Figure 8, where the magnitude of the current and voltage vectors, ${\mathbf{i}}_{fdq}$ and ${\mathbf{v}}_{sdq}$, and the actual currents and voltages in $abc$ coordinates are shown for both methods. The set-ups of Figure 6 and Figure 7 start with the balanced three-phase load connected, and the voltages references are ${\mathbf{z}}_{\mathbf{ref}}^{+}=160+0j$ and ${\mathbf{z}}_{\mathbf{ref}}^{-}=0+0j$. At $t=0.04$ s, the phase b load is disconnected, resulting in an asymmetrical output current, ${\mathbf{i}}_{odq}$. Consequently, the DER unit’s output filter is subject to asymmetrical disturbance ${\mathbf{i}}_o$ that should be properly compensated at input $\mathbf{u}$. As it can be seen in Figure 8, the effect of load imbalance appears as an oscillation at the double of the fundamental frequency in the $dq$ frame for both methods, but the benefit of actively regulating both sequences is evident in the results shown in Figure 8f. The impact of the imbalance on the controlled variable, ${\mathbf{v}}_{sabc}$, is significantly reduced in this case. This confirms that the proposed SCKF can be used for sequence separation in closed-loop control, reducing the impact of the load imbalance on control performance.

Figure 8. Improvement of the control of an LC-filtered stand-alone DER by the feedback of separated sequences using the SCKF. (a) Magnitude of the filter current. (b) Magnitude of the filter output voltage. (c) Filter current in $abc$ with asymmetric feedback. (d) Filter output voltage in $abc$ with asymmetric feedback. (e) Filter current in $abc$ with sequence separation by SCKF. (f) Filter output voltage in $abc$ with sequence separation by SCKF.

The second closed-loop experimental result shows that by using the feedback of both estimated sequences, as shown in Figure 6, the negative sequence of the voltage can be regulated with independent reference ${\mathbf{z}}_{\mathbf{ref}}^{-}$. This is of particular importance in applications where a DER unit is required to share the imbalance of the loads. The result is shown in Figure 9, where the initial condition corresponds to the same steady state as that at the end of the previous result, i.e., with ${\mathbf{z}}_{\mathbf{ref}}^{+}=160+j0$ and ${\mathbf{z}}_{\mathbf{ref}}^{-}=0+j0$ and unbalanced load. At $t=0.04$ s, the reference of the negative voltage sequence is changed to ${\mathbf{z}}_{\mathbf{ref}}^{-}=20+j0$ and an intentional imbalance at the voltage reference is introduced. As it can be seen in the measurement of ${\mathbf{v}}_{sdq}$ in Figure 9d, both voltage sequences follow the change on demand with good dynamic response and high level of decoupling, showing that the proposed SCKF is useful for separate sequence control. It is important to note that the response exhibits a steady-state tracking error, which is an inherent characteristic of the proportional control utilized for testing and not a consequence of the proposed sequence separation algorithm.

Figure 9. Experimental response of the control of an LC-filtered stand-alone DER with feedback of separated sequences using the SCKF to change on the negative sequence reference. (a) Magnitude of the filter current. (b) Magnitude of filter voltage. (c) Magnitude of $dq$ components of the filter current. (d) Magnitude of $dq$ components of the filter voltage. (e) Filter current in $abc$. (f) Filter voltage in $abc$.

In the above experimental results, the output filter parameters are assumed to be accurately known and the nonlinearities of the inverter are neglected. Those assumptions may be questionable for applications requiring high-performance closed-loop control. However, one significant advantage of the proposed SCKF is its predictable frequency response, which can be considered in the control design process. This allows for a systematic way of dealing with the above-mentioned modeling errors, for example, limiting the closed-loop bandwidth, performing sensitivity analysis or including integral action in the controller. Nevertheless, such control-tuning procedures are out of the scope of this paper.

6. Conclusions

In this paper, the positive and negative sequence estimation problem is formulated through a time-varying complex variable model with suitable stochastic properties. However, the estimation problem for a model with such characteristics can be solved by the time-varying complex Kalman filter. The implementation of such an algorithm is computationally demanding. Hence, a suitable transformation of the complex state vector is proposed to achieve an alternative time-invariant complex model. Consequently, the stationary solution of the complex Kalman filter is proposed to simplify the implementation and reduce its computational cost, without loss of accuracy. The effectiveness of the proposal is tested in a $5 \mathrm{kW}$ experimental prototype. The dynamic performance of the proposal is compared with its time-varying counterparts, KF and CKF, showing estimations just as accurate and similar dynamics performance, except for the first few milliseconds. While this initial difference has no practical significance, the proposed technique, in contrast, achieves a five-fold improvement in computational efficiency. Lastly, as an illustrative example of its application, the proposed stationary complex Kalman filter for sequence separation is integrated into a positive and negative sequence voltage control strategy based on state feedback. The results demonstrate the effective independent control of each sequence.

Appendix B.1. Stochastic Complex-Valued Signals

The study of complex-valued signal arises from the necessity of handling compact expressions in a two-dimensional signal space that provides insight into an underlying physical phenomenon. In fact, the study of complex-valued signals arises from phasors (e.g., magnitude and phase of voltages and currents) and complex communication signals (in-phase and quadrature channels) [25,33], which in turn yield complex-valued linear and nonlinear systems, particularly in (modern) communication systems; see, e.g., [34] and the references therein.

To understand complex-valued random variables, let us consider two real-valued and possibly correlated random variables, x and y. For this kind of bivariate signal, it is customary to define a real-valued vector that includes both real-valued signals as $\mathbf{v}={\left[xy\right]}^{\mathrm{T}}$. Hence, the joint probability density function (pdf) of x and y can be defined as $p\left(\mathbf{v}\right)=p(x,y)$, which contains all the relevant information about x and y. On the other hand, all the relevant information of $\mathbf{v}={\left[xy\right]}^{\mathrm{T}}$ could be included in a complex-valued random variable $z=x+jy$. This would imply that $p\left(z\right)=p\left(\mathbf{v}\right)=p(x,y)$. However, as shown next, this is not always true.

When dealing with random variables, it is usual to characterize their second-order statistical properties. From this point of view, when considering $p\left(\mathbf{v}\right)$, there are five quantities that describe those second-order characteristics, that is, $E\left[x\right]={\mu }_x,E\left[y\right]={\mu }_y,E\left[{(x-{\mu }_x)}^2\right]={\sigma }_x^2,E\left[{(y-{\mu }_y)}^2\right]={\sigma }_y^2,E\left[(x-{\mu }_x)(y-{\mu }_y)\right]={\sigma }_{xy}$. When considering $p\left(z\right)$, the definition of expected value applies directly since the real-part and imaginary-part operators, $\mathfrak{Re}\{·\}$ and $\mathfrak{Im}\{·\}$, respectively, are linear. Hence, $E\left[z\right]={\mu }_z={\mu }_x+j{\mu }_y$.

However, the second-order moment of z cannot always be obtained straightforwardly. In general, with complex numbers, ${\left|z\right|}_2^2=z{z}^{*}$ is utilized, where ${\left(\right)}^{*}$ represents the complex conjugate, instead of $z^2$. If this definition is applied, $E\left[(z-{\mu }_z){(z-{\mu }_z)}^{*}\right]={\sigma }_z^2={\sigma }_x^2+{\sigma }_y^2$ is obtained. Clearly, this definition yields one real-valued term that is composed of two terms. In addition, cross-correlation term ${\sigma }_{xy}$ is missing from this second-order statistic. On the other hand, if $E\left[{(z-{\mu }_z)}^2\right]={\tilde{\sigma }}_z^2={\sigma }_x^2-{\sigma }_y^2+j2{\sigma }_{xy}$ is considered, a real and an imaginary term are obtained. However, not all the second-order statistics from $\mathbf{v}$ are contained in $E\left[z^2\right]$, since the real term contains both $E\left[{(x-{\mu }_x)}^2\right]$ and $E\left[{(y-{\mu }_y)}^2\right]$. Thus, the definition of the second-order statistics of complex-valued random variables comprises variance $E\left[(z-{\mu }_z){(z-{\mu }_z)}^{*}\right]$ and complementary covariance$E\left[{(z-{\mu }_z)}^2\right]$ [25,33,35]. To this end, augmented variable $\underline{\mathbf{z}}={\left[z{z}^{*}\right]}^{\mathrm{T}}$ is defined, from which the augmented covariance matrix $E[(\underline{\mathbf{z}}-{\underline{\mathit{\mu }}}_z){(\underline{\mathbf{z}}-{\underline{\mathit{\mu }}}_z)}^{\mathrm{H}}]=\left[\begin{array}{cc}{\sigma }_z^2& {\tilde{\sigma }}_z^2\\ {\left({\tilde{\sigma }}_z^2\right)}^{*}& {\left({\sigma }_z^2\right)}^{*}\end{array}\right]$ is defined. Clearly, this representation does not provide a very compact and simple expression. However, there is a special case where it does.

In many applications, such as Wireless Communications (see, e.g., [34] and the references therein) and System Identification (see, e.g., [36] and the references therein), the real and imaginary parts of complex random variables are independent and identically distributed. That is, ${\sigma }_x^2={\sigma }_y^2={\sigma }^2$ and ${\sigma }_{xy}=0$. In this particular case, the signals are considered proper, therefore, ${\sigma }_z^2=2{\sigma }^2$ and ${\tilde{\sigma }}_z^2=0$. Further, a special case of proper signals corresponds to circular symmetric signals, where random variables z and $v=e^{j\theta }z$ have the same pdf for any given $\theta \in \mathbb{R}$. This implies that ${\mu }_z=0$. In particular, a complex-valued zero-mean Gaussian random variable is proper if and only if it is circular [25]. The case where ${\sigma }_x^2\ne {\sigma }_y^2$ or ${\sigma }_{xy}\ne 0$ corresponds to improper signals, and to fully describe its second-order moments, the augmented covariance matrix is needed [25,35].

Appendix B.2. Complex-Valued Kalman Filter for Proper Signals

Appendix B.2.1. Proper (Complex-Valued) Gaussian Distributions

In the previous section, it was shown that proper complex-valued random variable $z=x+jy$ satisfies $E\left[{(x-{\mu }_x)}^2\right]=E\left[{(y-{\mu }_y)}^2\right]={\sigma }^2$ and $E\left[(x-{\mu }_x)(y-{\mu }_y)\right]=0$. If z is a proper complex Gaussian random variable, it is denoted by $z\sim \mathcal{CN}({\mu }_z,{\sigma }_z^2)$. Moreover, the pdf of z is given by

$$p\left(z\right)=\frac{1}{\pi {\sigma }_z^2}{e}^{-\frac{1}{{\sigma }_z^2}{(z-{\mu }_z)}^{\mathrm{H}}(z-{\mu }_z)}.$$

It can be shown that by replacing $z=x+jy$ with $x\sim \mathcal{N}(\mathfrak{Re}\left\{{\mu }_z\right\},{\sigma }_z^2/2)$ and $y\sim \mathcal{N}(\mathfrak{Im}\left\{{\mu }_z\right\},{\sigma }_z^2/2)$, $p\left(z\right)=p(x,y)=p\left(x\right)p\left(y\right)$ can be obtained.

For multivariate proper (complex-valued) Gaussian distributions,

$$p\left(\mathbf{z}\right)=\frac{1}{\det \left(\pi {\Sigma }_z\right)}{e}^{-{(\mathbf{z}-{\mathit{\mu }}_z)}^{\mathrm{H}}{\Sigma }_z^{-1}(\mathbf{z}-{\mathit{\mu }}_z)},$$

where ${\Sigma }_z$ is the covariance matrix and $\det (·)$ is the determinant. Notice that different elements of vector $\mathbf{z}$ can be correlated, but their real and imaginary parts cannot be, i.e., $E\left[\mathfrak{Re}\left\{z_l\right\}\mathfrak{Im}\left\{z_m\right\}\right]=0\forall l,m$. This yields a real-valued, positive-definite covariance matrix that admits complex-valued eigenvectors.

Appendix B.2.2. Complex-Valued Kalman Filter for Proper Signals

One of the main consequences of properness is the fact that any expression that includes the transpose of a vector or a matrix from real-valued signals and systems can be directly replaced by a Hermitian (conjugate transpose).

Let us consider the following state-space system:

$$\begin{array}{cc}\hfill \mathbf{x}[k+1]& =\mathbf{A}\left[k\right]\mathbf{x}\left[k\right]+\mathit{\eta }\left[k\right]\hfill \end{array}$$

(A5)

$$\begin{array}{cc}\hfill \mathbf{y}\left[k\right]& =\mathbf{C}\left[k\right]\mathbf{x}\left[k\right]+\mathbf{e}\left[k\right],\hfill \end{array}$$

(A6)

where $\mathit{\eta }\left[k\right]\sim \mathcal{CN}(\mathbf{0},\mathbf{Q}[k\left]\right)$ and $\mathbf{e}\left[k\right]\sim \mathcal{CN}(\mathbf{0},\mathbf{R}[k\left]\right)$. Thus, the complex-valued Kalman filter (CKF) for the linear system-defined proper signals is described in Algorithm A2 (see, e.g., [29]).

Algorithm A2: CKF Algorithm for Proper Signals.