A Hybrid Reproducing Kernel Particle Method for Three-Dimensional Helmholtz Equation
Abstract
1. Introduction
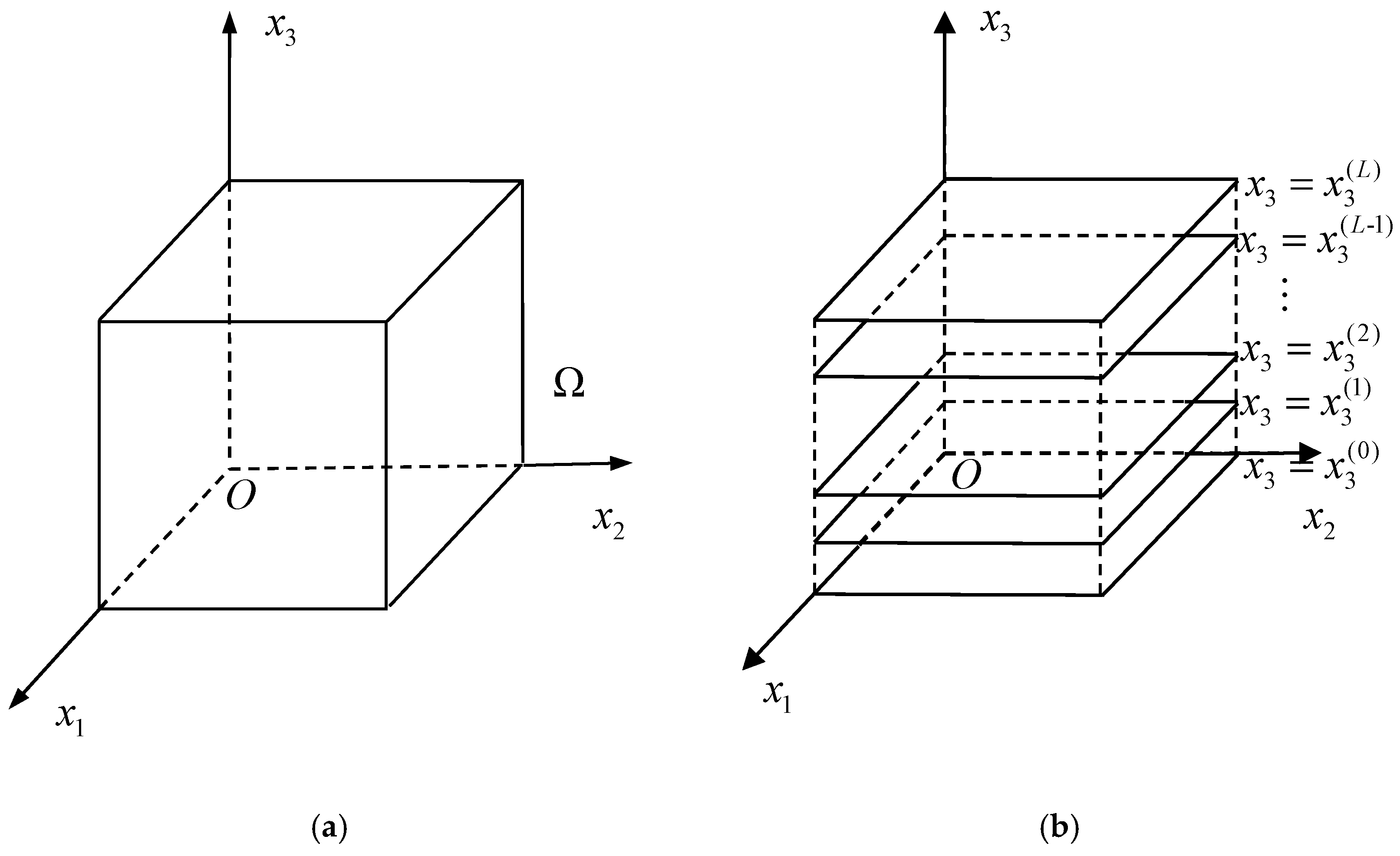
2. The Dimension-Splitting-Governing Equation of 3D Helmholtz Equation
3. The HRKPM Scheme for 3D Helmholtz Equation
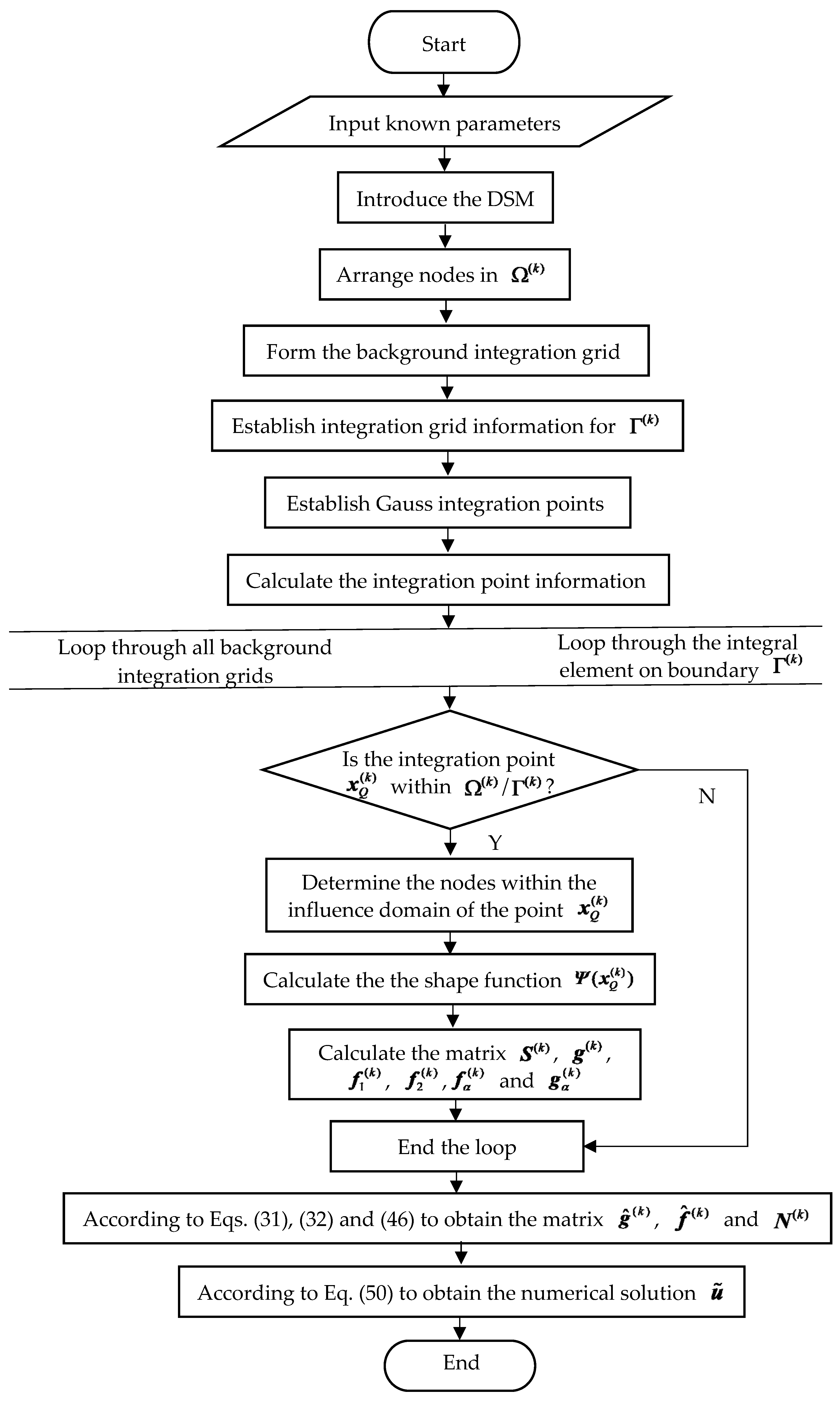
4. Algorithm Implementation Process
- (1)
- Input known parameters;
- (2)
- Select the dimension-splitting direction;
- (3)
- For the splitting 2D Helmholtz equation, determine its variables and coordinate system, arrange nodes on the subdomain and boundary , then record node information and node coordinates;
- (4)
- Establishing the background grid for integration;
- (5)
- Forming integral element information on boundary ;
- (6)
- Using the background grid and boundary information, establish Gauss integration points and calculate the corresponding integration point information (integration point coordinates, integration weights, and );
- (7)
- Generate matrices , and the first term of array ;
- (1)
- Loop through all background integration grids;
- (a)
- Loop through all Gaussian integration points within each background grid;
- (b)
- If the integration point is within , run steps (c) to (f); otherwise, run directly to step (f);
- (c)
- Determine the nodes within the influence domain of the current Gaussian integral point ;
- (d)
- Calculate the numerical values of the shape function and derivative at the Gauss integral point ;
- (e)
- Calculate the contribution of the current Gaussian integral point to matrices , and using Equations (24), (25) and (26), respectively;
- (f)
- End the point loop.
- (2)
- End the background grid loop;
- (8)
- Numerical integration on boundary : similar to the process in step (7), calculate the second term of the array using Equation (27);
- (9)
- Numerical integration on boundary : similar to the process in step (7), calculate the third term of the array and matrix using Equations (29) and (28);
- (10)
- According to Equation (32), obtain the final array ;
- (11)
- According to Equation (31), obtain the final matrix ;
- (12)
- According to Equation (46), obtain the final matrix ;
- (13)
- Based on the matrices , , and obtained above, obtain matrices and from Equations (47) and (49), respectively;
- (14)
- Substitute matrices and into the equation system (50) to obtain the numerical solution .
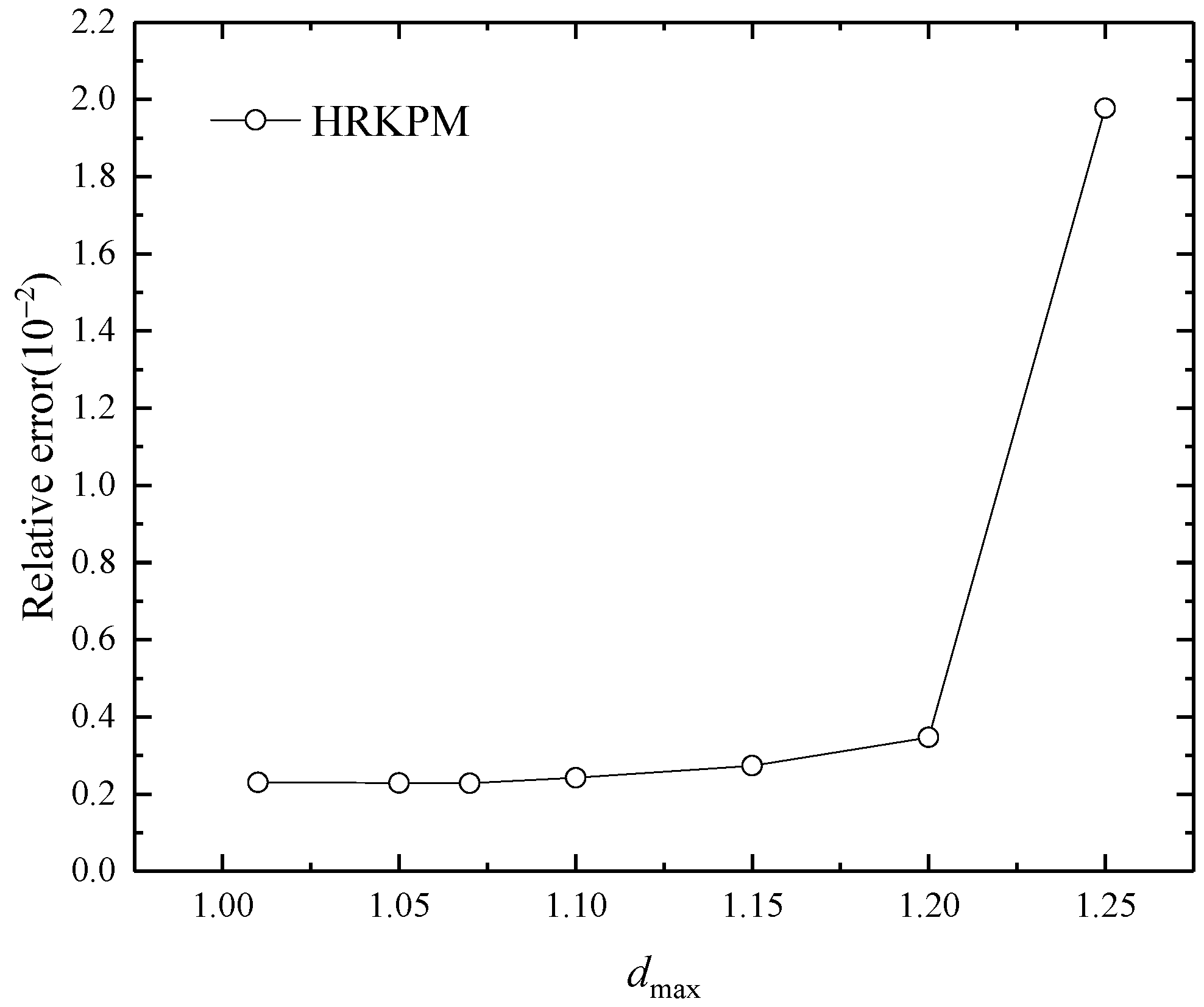
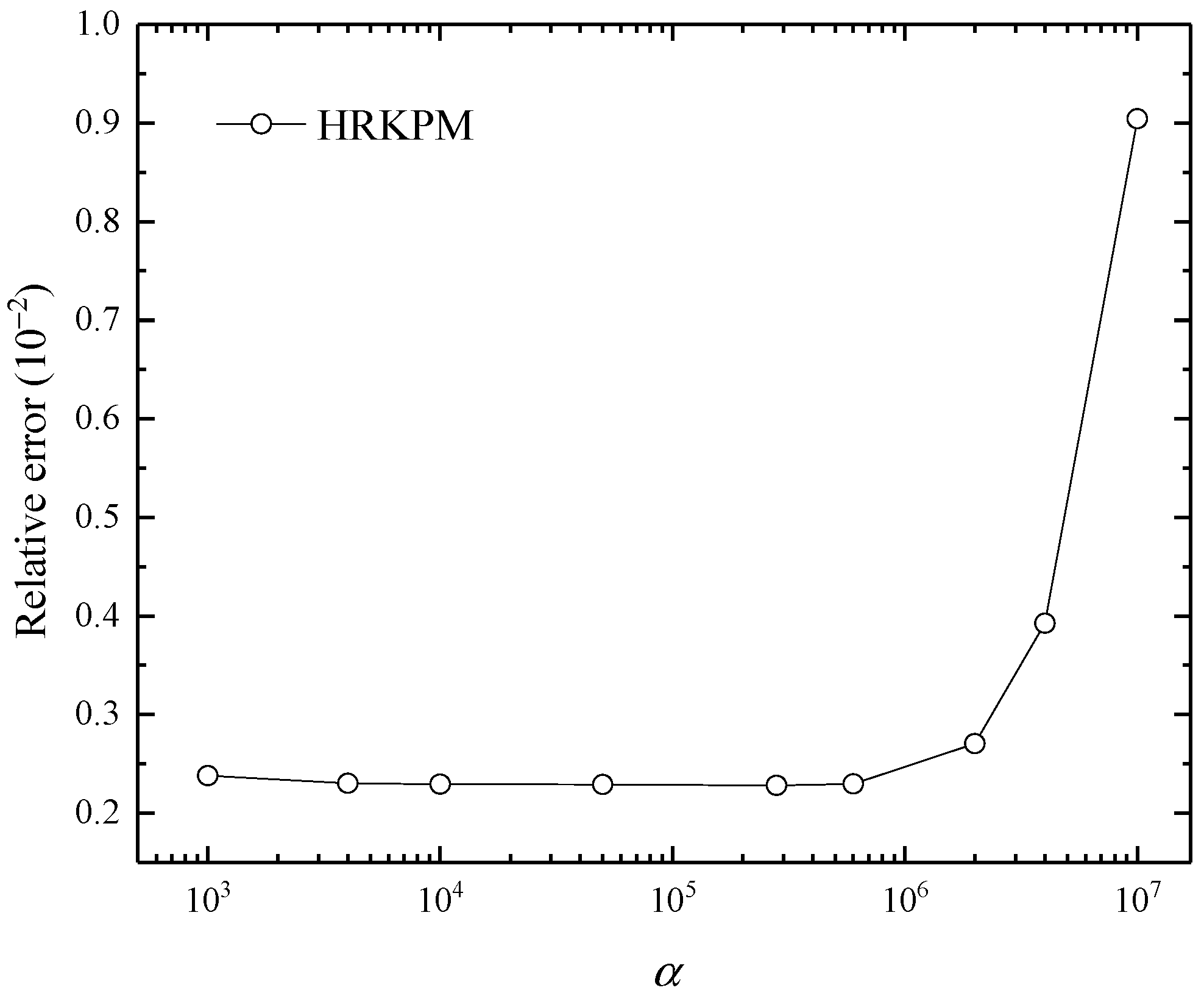
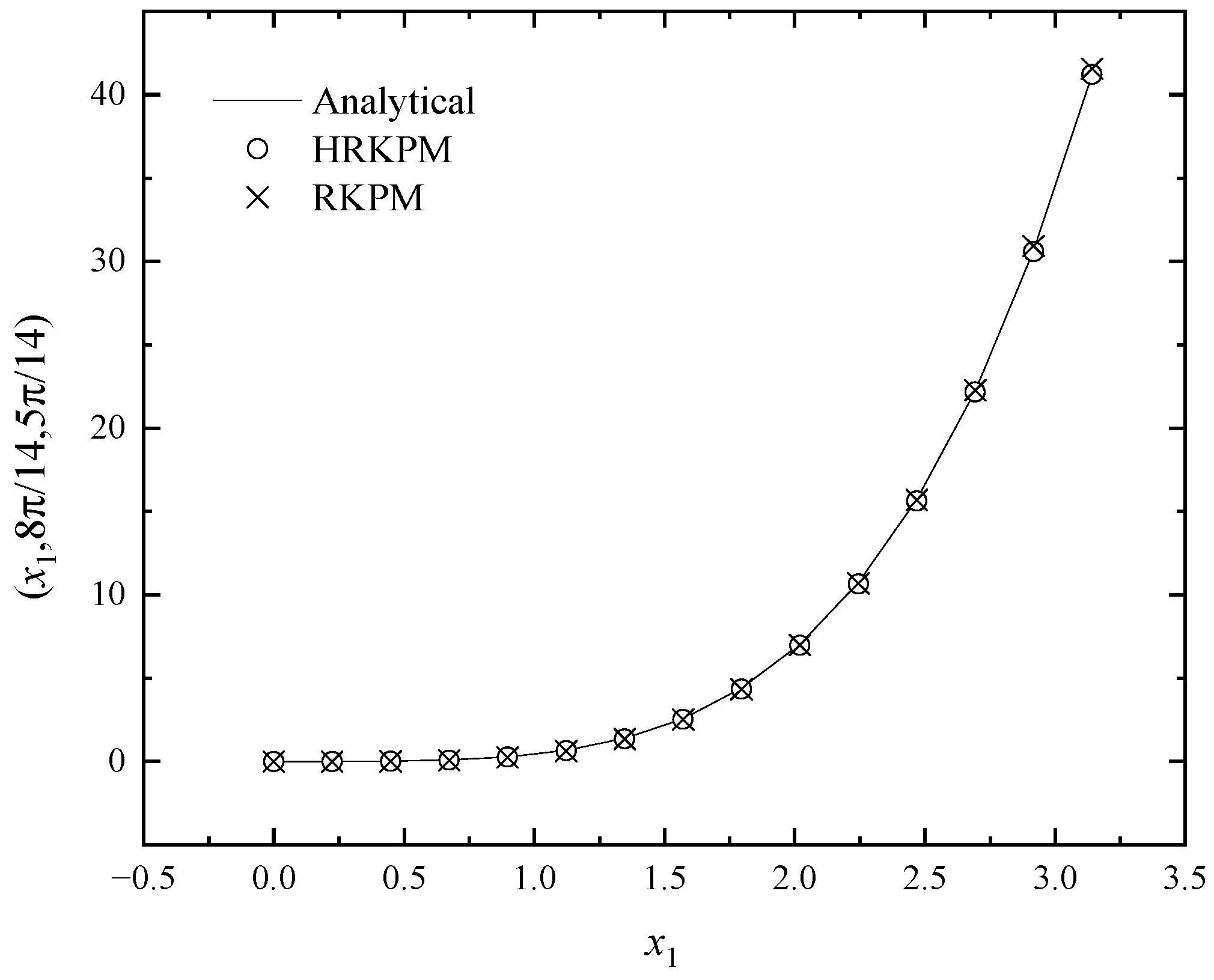
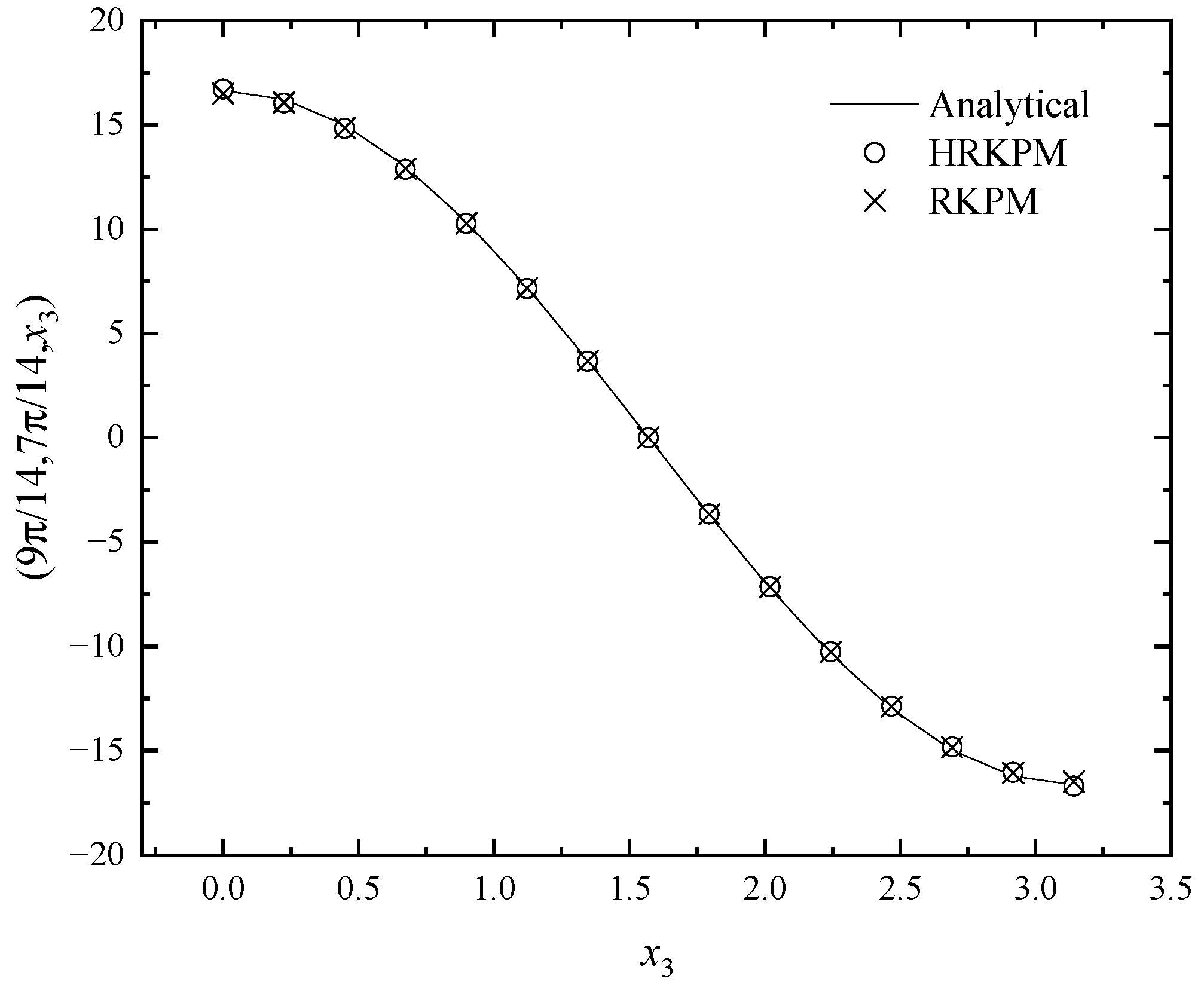
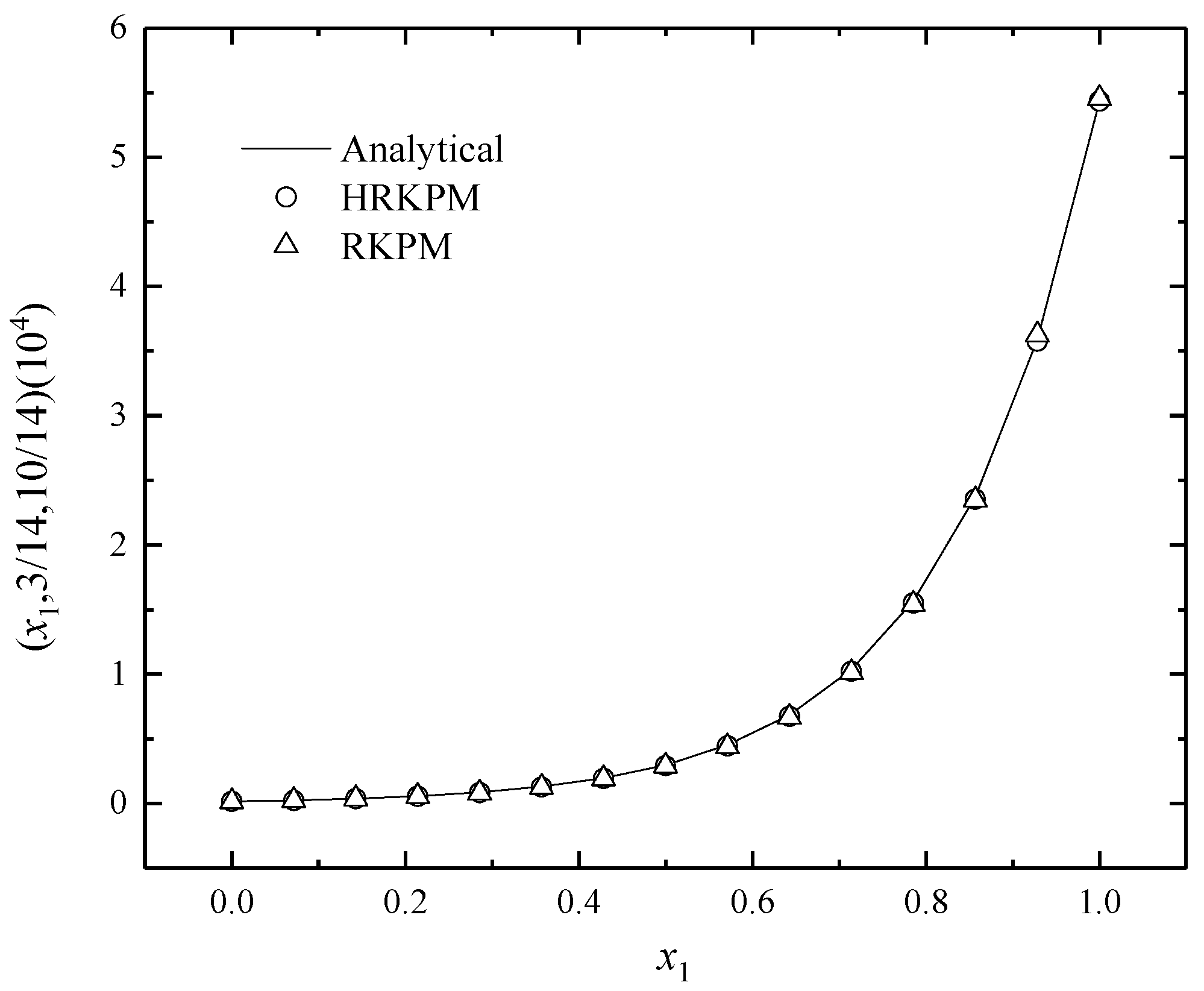
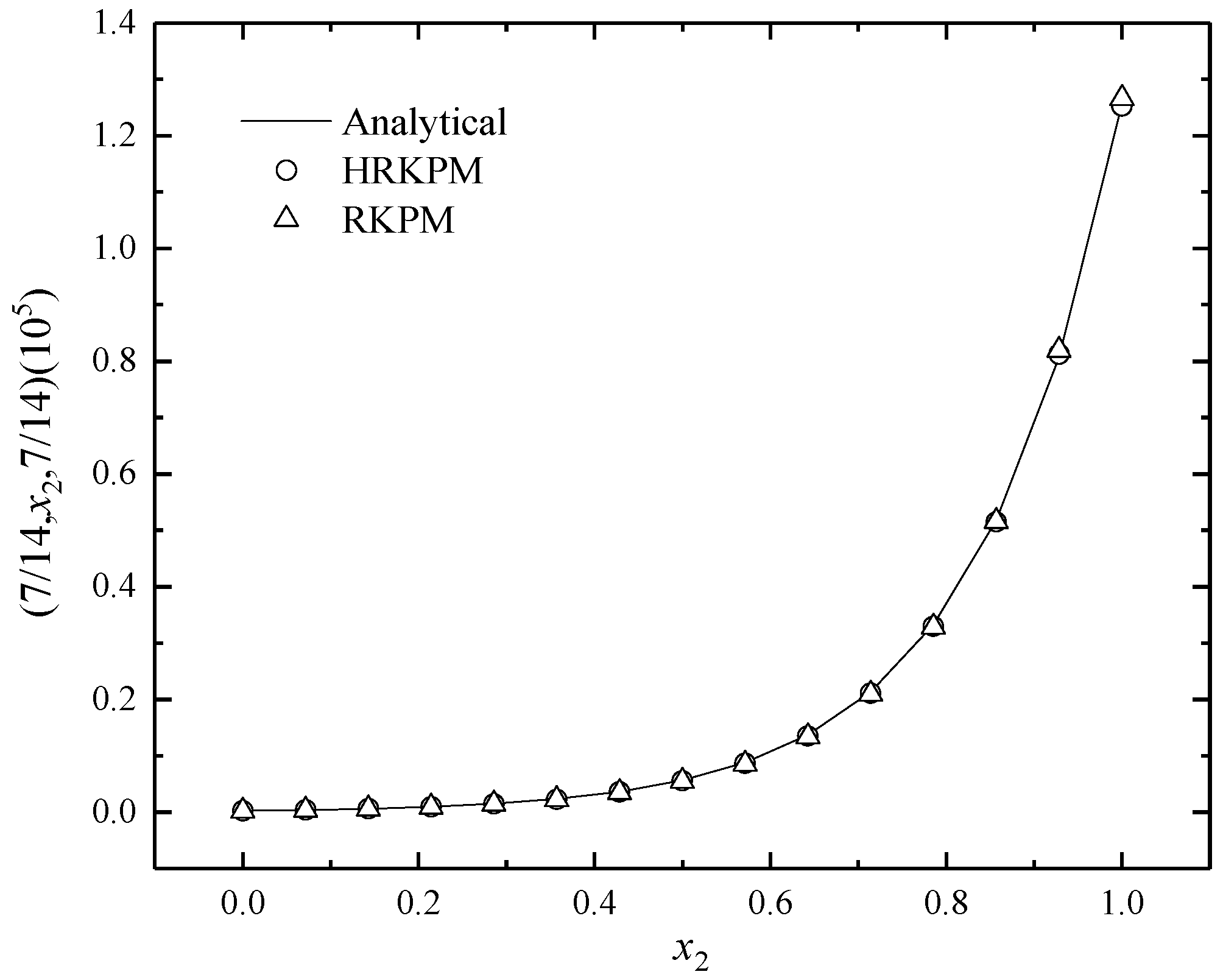
5. Numerical Examples
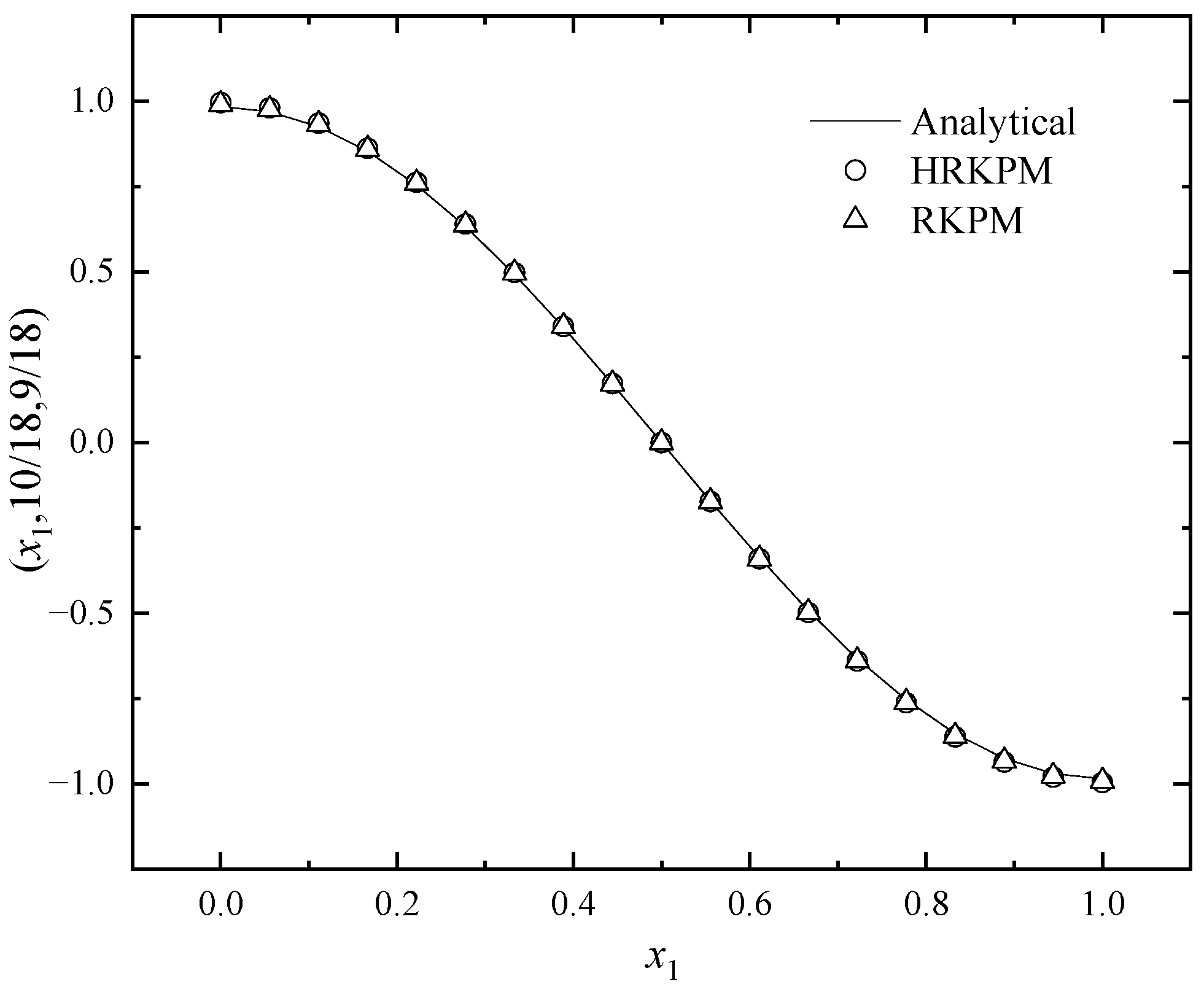
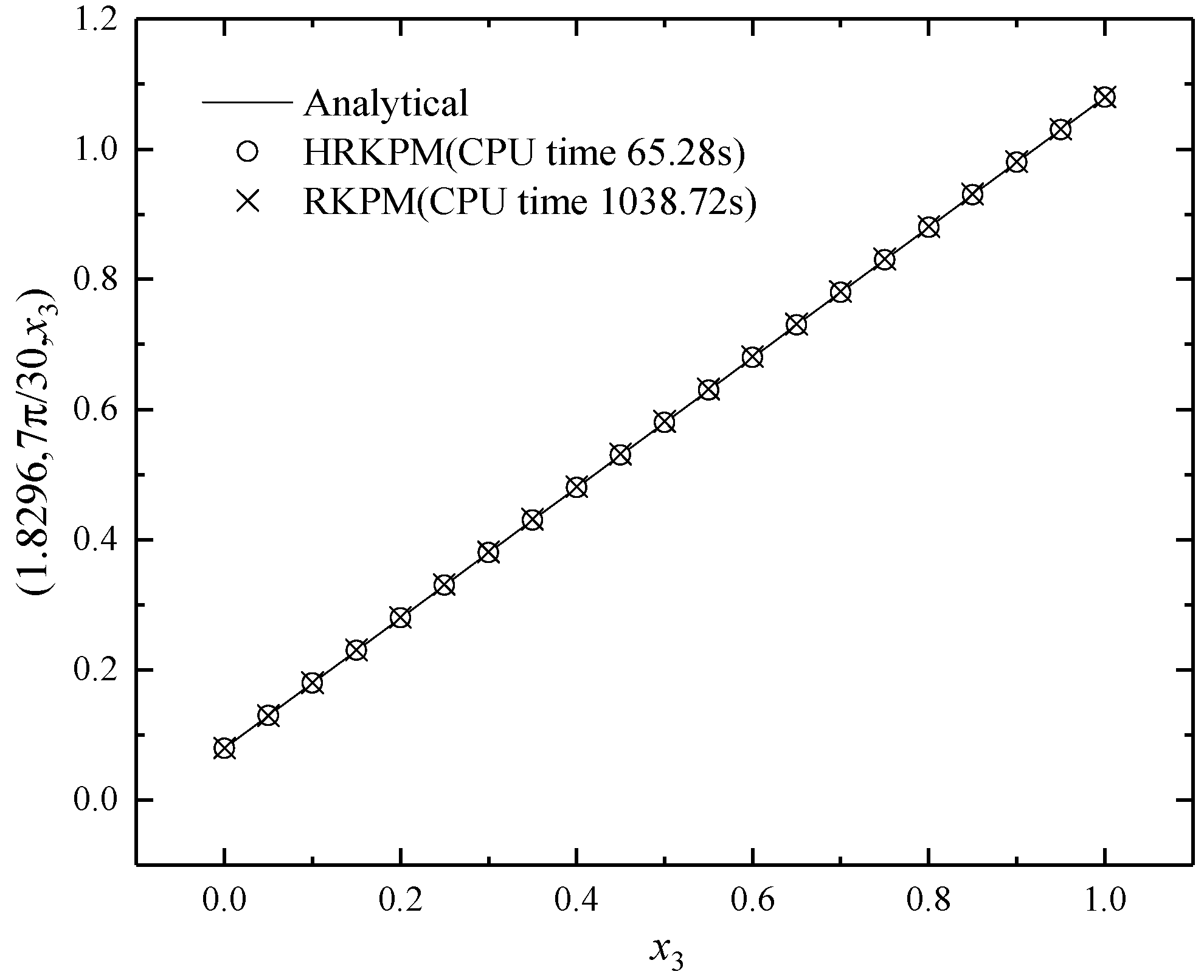
5.1. Example 1
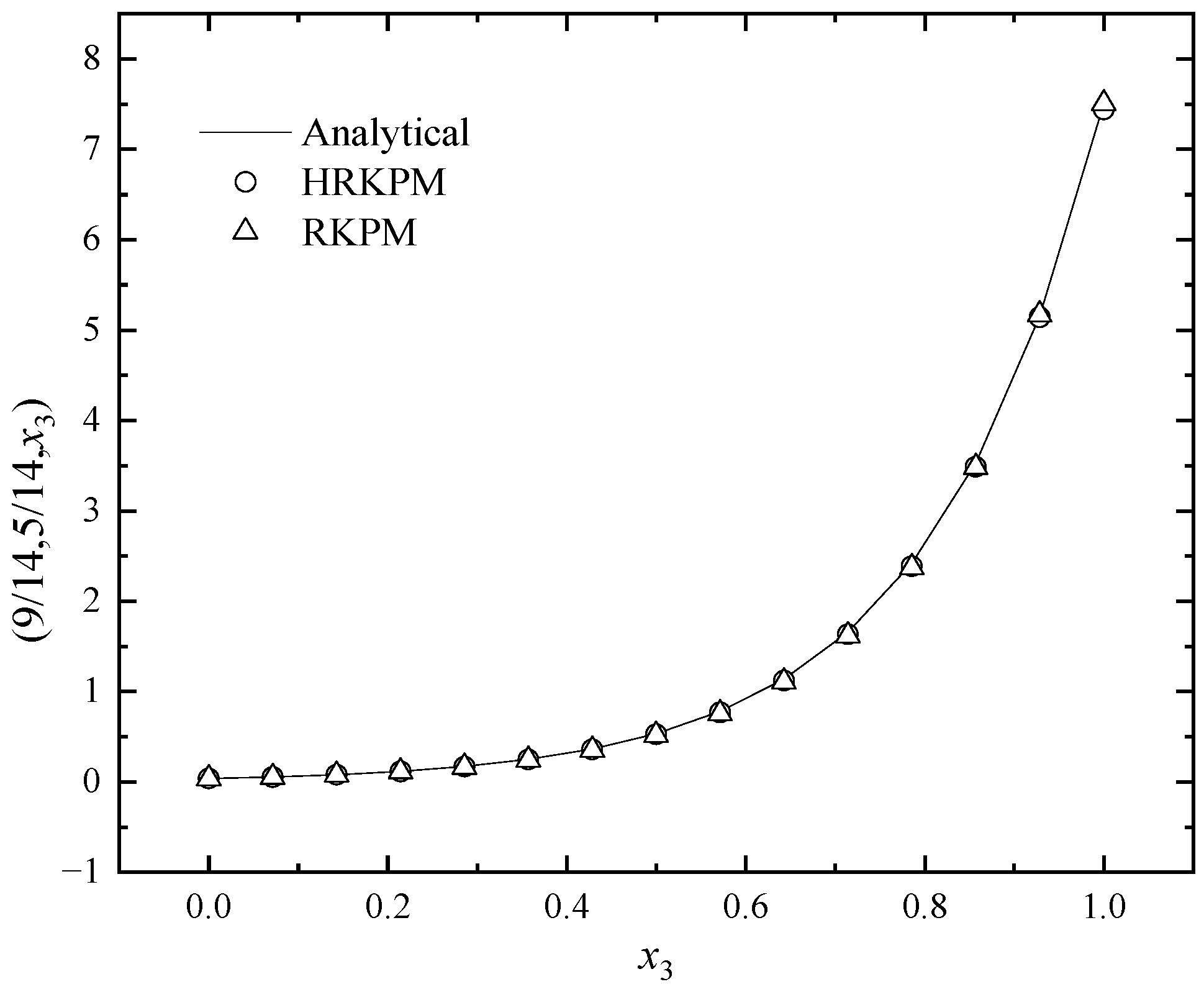
5.2. Example 2
5.3. Example 3
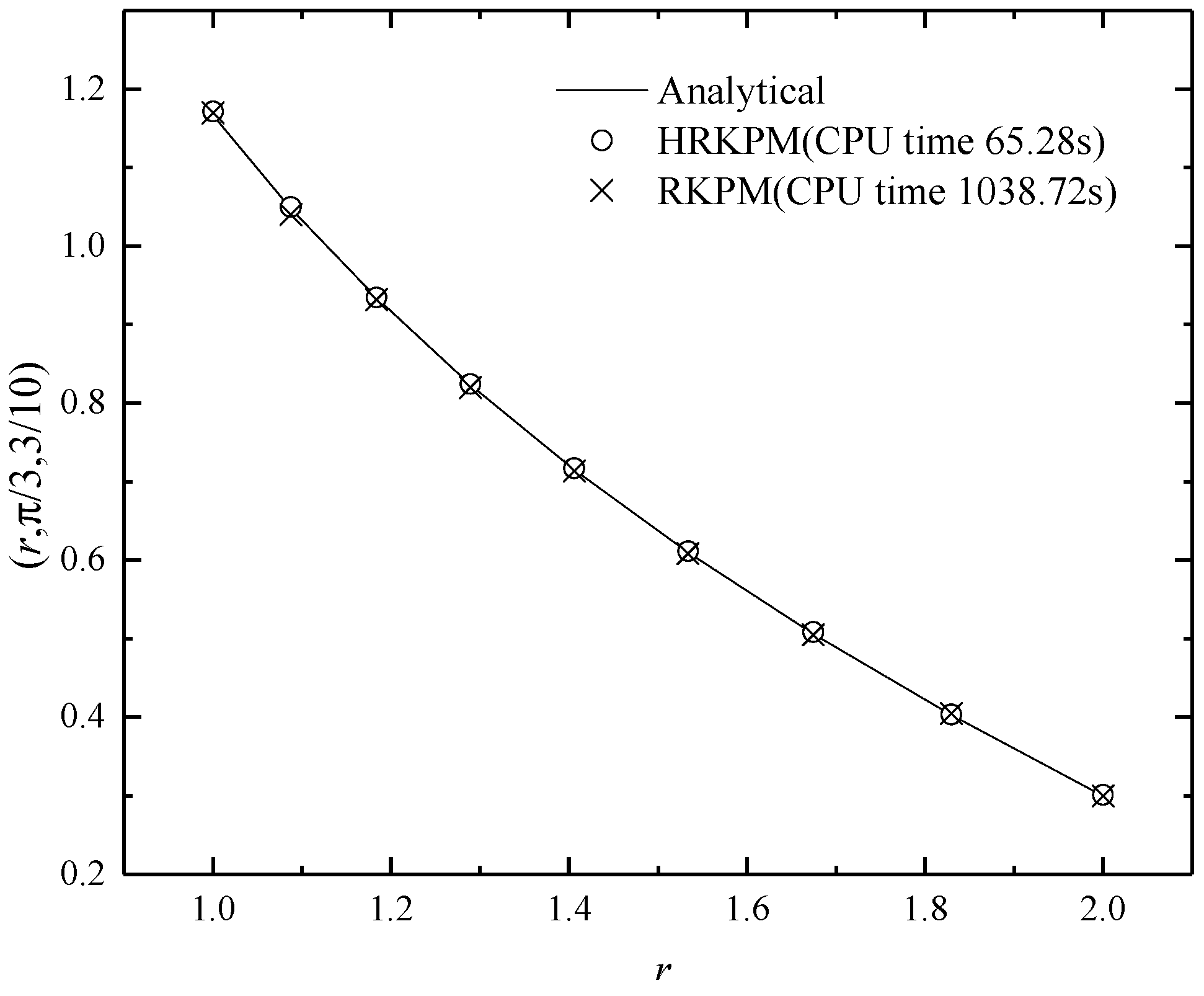
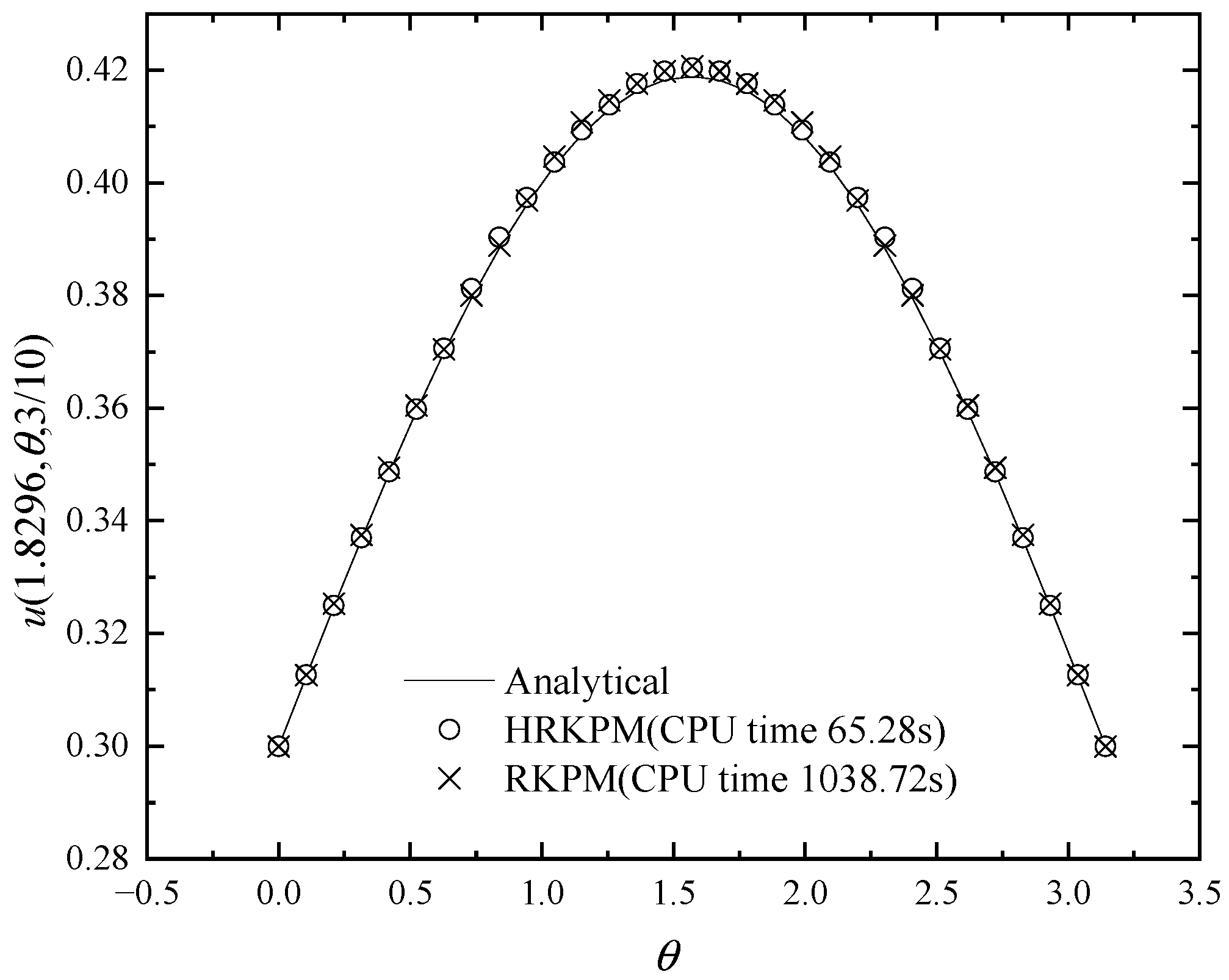
5.4. Example 4
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Oberai, A.A.; Pinsky, P.M. Residual-based finite element method for the Helmholtz equation. Int. J. Numer. Methods Eng. 2000, 49, 399–419. [Google Scholar] [CrossRef]
- Harari, I. A survey of finite element methods for time-harmonic acoustics. Comput. Methods Appl. Mech. Eng. 2006, 195, 1594–1607. [Google Scholar] [CrossRef]
- Thompson, L.L. A review of finite-element methods for time-harmonic acoustics. J. Acoust. Soc. Am. 2006, 119, 1315–1330. [Google Scholar] [CrossRef]
- Cheng, Y.M.; Li, R.X.; Peng, M.J. Complex variable element-free Galerkin method for viscoelasticity problems. Chin. Phys. B 2012, 21, 090205. [Google Scholar] [CrossRef]
- Oruc, O. Two meshless methods based on local radial basis function and barycentric rational interpolation for solving 2D viscoelastic wave equation. Comput. Math. Appl. 2020, 12, 79. [Google Scholar]
- Hidayat, M.I.P. Meshless finite difference method with B-splines for numerical solution of coupled advection-diffusion-reaction problems. Int. J. Therm. Sci. 2021, 165, 106933. [Google Scholar] [CrossRef]
- Singh, R.; Trobec, R. Analysis of the MLS variants in the meshless local Petrov-Galerkin method for a solution to the 2D Laplace equation. Eng. Anal. Bound. Elem. 2022, 135, 115–131. [Google Scholar] [CrossRef]
- Hosseinzadeh, H.; Shirzadi, A. A new meshless local integral equation method. Appl. Numer. Math. 2023, 194, 44–58. [Google Scholar] [CrossRef]
- Nguyen, V.P.; Rabczuk, T.; Bordas, S.; Duflot, M. Meshless methods: A review and computer implementation aspects. Math. Comput. Simul. 2008, 79, 763–813. [Google Scholar] [CrossRef]
- Li, S.; Liu, W.K. Meshfree and particle methods and their applications. Appl. Mech. Rev. 2002, 55, 1–34. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of the fission hypothesis. Astron. J. 1977, 82, 1013–1024. [Google Scholar] [CrossRef]
- Liu, W.K.; Jun, S.; Zhang, Y.F. Reproducing kernel particle methods. Int. J. Numer. Methods Fluids 1995, 20, 1081–1106. [Google Scholar] [CrossRef]
- Belytschko, T.; Lu, Y.Y.; Gu, L. Element-free Galerkin methods. Int. J. Numer. Methods Eng. 1994, 37, 229–256. [Google Scholar] [CrossRef]
- Suleau, S.; Deraemaeker, A.; Bouillard, P. Dispersion and pollution of meshless solutions for the Helmholtz equation. Comput. Methods Appl. Mech. Eng. 2000, 190, 639–657. [Google Scholar] [CrossRef]
- Uras, R.A.; Chang, C.T.; Chen, Y.; Liu, W.K. Multiresolution reproducing kernel particle methods in acoustics. J. Comput. Acoust. 1997, 5, 71–94. [Google Scholar] [CrossRef]
- Wenterodt, C.; Estorff, O.V. Dispersion analysis of the meshless radial point interpolation method for the Helmholtz equation. Int. J. Numer. Methods Eng. 2009, 77, 1670–1689. [Google Scholar] [CrossRef]
- Breitkopf, P.; Rassineux, A.; Touzot, G.; Villon, P. Explicit form and efficient computation of MLS shape functions and their derivatives. Int. J. Numer. Methods Eng. 2000, 48, 451–466. [Google Scholar] [CrossRef]
- Krysl, P.; Belytschko, T. ESFLIB: A library to compute the element free Galerkin shape functions. Comput. Methods Appl. Mech. Eng. 2001, 190, 2181–2205. [Google Scholar] [CrossRef][Green Version]
- Zhou, J.X.; Wang, X.M.; Zhang, Z.Q.; Zhang, L. Explicit 3-D RKPM shape functions in terms of kernel function moments for accelerated computation. Comput. Methods Appl. Mech. Eng. 2005, 194, 1027–1035. [Google Scholar] [CrossRef]
- Chen, J.S.; Yoon, S.; Wang, H.P.; Liu, W.K. An improved reproducing kernel particle method for nearly incompressible finite elasticity. Comput. Methods Appl. Mech. Eng. 2000, 181, 117–145. [Google Scholar] [CrossRef]
- Li, K.T.; Huang, A.X.; Zhang, W.L. A dimension split method for the 3D compressible Navier Stokes equations in turbomachine. Commun. Numer. Methods Eng. 2002, 18, 1–14. [Google Scholar] [CrossRef]
- Li, K.T.; Liu, D.M. Dimension splitting method for 3D rotating compressible Navier-Stokes equations in the turbomachinery. Int. J. Numer. Anal. Model. 2009, 6, 420–439. [Google Scholar]
- Li, K.T.; Shen, X.Q. A dimensional splitting method for the linearly elastic shell. Int. J. Comput. Math. 2007, 84, 807–824. [Google Scholar] [CrossRef]
- Cheng, J. Analyzing the factors influencing the choice of the government on leasing different types of land uses: Evidence from Shanghai of China. Land Use Policy 2020, 90, 104303. [Google Scholar] [CrossRef]
- Cheng, J. Analysis of commercial land leasing of the district governments of Beijing in China. Land Use Policy 2021, 100, 104881. [Google Scholar] [CrossRef]
- Cheng, J. Residential land leasing and price under public land ownership. J. Urban Plan. Dev. 2021, 147, 05021009. [Google Scholar] [CrossRef]
- Cheng, J.; Luo, X. Analyzing the land leasing behavior of the government of Beijing, China, via the multinomial logit model. Land 2022, 11, 376. [Google Scholar] [CrossRef]
- Cheng, J. Analysis of the factors influencing industrial land leasing in Beijing of China based on the district-level data. Land Use Policy 2022, 122, 106389. [Google Scholar] [CrossRef]
- Peng, P.P.; Wu, Q.; Cheng, Y.M. The dimension splitting reproducing kernel particle method for three-dimensional potential problems. Int. J. Numer. Methods Eng. 2020, 121, 146–164. [Google Scholar] [CrossRef]
- Peng, P.P.; Cheng, Y.M. Analyzing three-dimensional transient heat conduction problems with the dimension splitting reproducing kernel particle method. Eng. Anal. Bound. Elem. 2020, 121, 180–191. [Google Scholar] [CrossRef]
- Peng, P.P.; Cheng, Y.M. Analyzing three-dimensional wave propagation with the hybrid reproducing kernel particle method based on the dimension splitting method. Eng. Comput. 2022, 38, 1131–1147. [Google Scholar] [CrossRef]
- Peng, P.P.; Cheng, Y.M. A hybrid reproducing kernel particle method for three-dimensional advection-diffusion problems. Int. J. Appl. Mech. 2021, 13, 2150085. [Google Scholar] [CrossRef]
- Peng, P.P.; Cheng, H.; Cheng, Y.M. A hybrid reproducing kernel particle method for three-dimensional elasticity problems. Int. J. Appl. Mech. 2023, 15, 2350080. [Google Scholar] [CrossRef]





| Number of Nodes | Relative Error | CPU Time (s) | ||
|---|---|---|---|---|
| HRKPM | RKPM | HRKPM | RKPM | |
| 9 × 9 × 9 | 0.0084 | 0.021 | 1.63 | 33.59 |
| 11 ×11 × 11 | 0.005 | 0.0137 | 2.81 | 75.79 |
| 13 ×13 × 13 | 0.0032 | 0.0096 | 6.92 | 139.69 |
| 15 ×15 × 15 | 0.0023 | 0.007 | 12.21 | 193.5 |
| 17 × 17 × 17 | 0.0017 | 0.0052 | 28.56 | 426.42 |
| (x1, 5/9, 1/2) | Analytical Solution | Numerical Solution | ||
|---|---|---|---|---|
| HRKPM | RKPM | IEFG | ||
| 0 | 0.984807753 | 0.991521371 | 0.99044884 | 0.993332402 |
| 0.055555556 | 0.96984631 | 0.976371218 | 0.977304607 | 0.978241394 |
| 0.111111111 | 0.925416578 | 0.931618359 | 0.933103453 | 0.933427074 |
| 0.166666667 | 0.852868532 | 0.858555631 | 0.860636497 | 0.860251044 |
| 0.222222222 | 0.754406507 | 0.759408923 | 0.761959042 | 0.760936722 |
| 0.277777778 | 0.633022222 | 0.637196053 | 0.639936846 | 0.638501723 |
| 0.333333333 | 0.492403877 | 0.495633861 | 0.498190136 | 0.496666172 |
| 0.388888889 | 0.336824089 | 0.339024452 | 0.341004318 | 0.339739671 |
| 0.444444444 | 0.171010072 | 0.172124262 | 0.173205041 | 0.172490351 |
| 0.5 | 6.03 × 10−17 | 3.05 × 10−14 | 7.47 × 10−14 | −1.91 × 10−11 |
| 0.555555556 | −0.171010072 | −0.172124262 | −0.173205041 | −0.172490351 |
| 0.611111111 | −0.336824089 | −0.339024452 | −0.341004318 | −0.339739671 |
| 0.666666667 | −0.492403877 | −0.495633861 | −0.498190136 | −0.496666172 |
| 0.722222222 | −0.633022222 | −0.637196053 | −0.639936846 | −0.638501723 |
| 0.777777778 | −0.754406507 | −0.759408923 | −0.761959042 | −0.760936722 |
| 0.833333333 | −0.852868532 | −0.858555631 | −0.860636497 | −0.860251044 |
| 0.888888889 | −0.925416578 | −0.931618359 | −0.933103453 | −0.933427074 |
| 0.944444444 | −0.96984631 | −0.976371218 | −0.977304607 | −0.978241394 |
| 1 | −0.984807753 | −0.991521371 | −0.99044884 | −0.993332402 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, P.; Wang, N.; Cheng, Y. A Hybrid Reproducing Kernel Particle Method for Three-Dimensional Helmholtz Equation. Mathematics 2024, 12, 1900. https://doi.org/10.3390/math12121900
Peng P, Wang N, Cheng Y. A Hybrid Reproducing Kernel Particle Method for Three-Dimensional Helmholtz Equation. Mathematics. 2024; 12(12):1900. https://doi.org/10.3390/math12121900
Chicago/Turabian StylePeng, Piaopiao, Ning Wang, and Yumin Cheng. 2024. "A Hybrid Reproducing Kernel Particle Method for Three-Dimensional Helmholtz Equation" Mathematics 12, no. 12: 1900. https://doi.org/10.3390/math12121900
APA StylePeng, P., Wang, N., & Cheng, Y. (2024). A Hybrid Reproducing Kernel Particle Method for Three-Dimensional Helmholtz Equation. Mathematics, 12(12), 1900. https://doi.org/10.3390/math12121900







