Exploring the Therapeutic Potential of Defective Interfering Particles in Reducing the Replication of SARS-CoV-2
Abstract
1. Introduction
2. Materials and Methods
2.1. Sensitivity Analysis
2.2. Model Development and Calibration
2.3. Stochastic Simulation Algorithm
2.4. Software
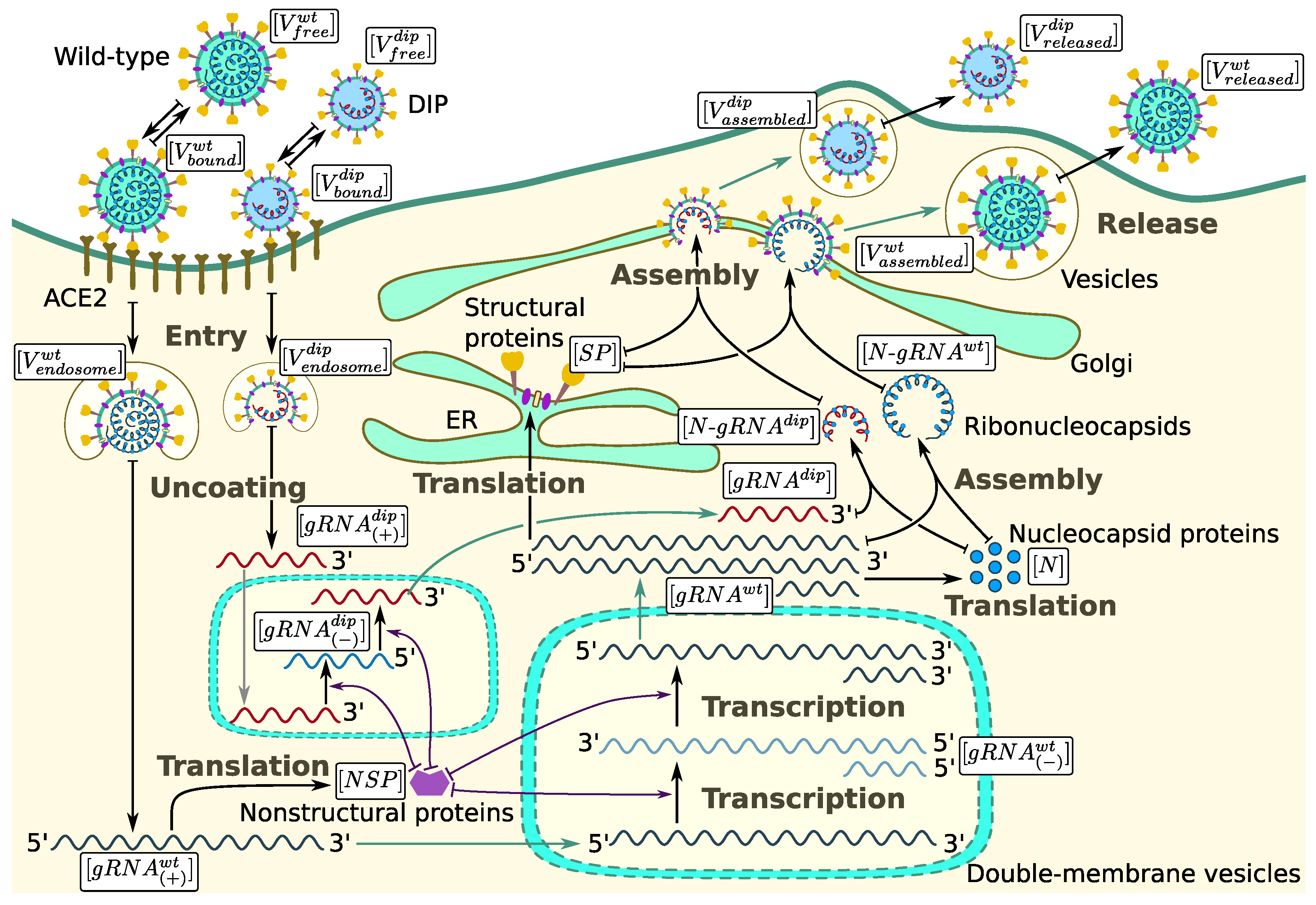
3. Mathematical Model of WT and DIP Infection
3.1. Cell Entry and RNA Release
3.2. RNA Transcription and DIP Parasitism
3.3. Translation and Competition for Nucleocapsid Protein and Other Structural Proteins
3.4. Assembly and Release of WT SARS-CoV-2 and DIPs
3.5. Stochastic Markov Chain Model
4. Results
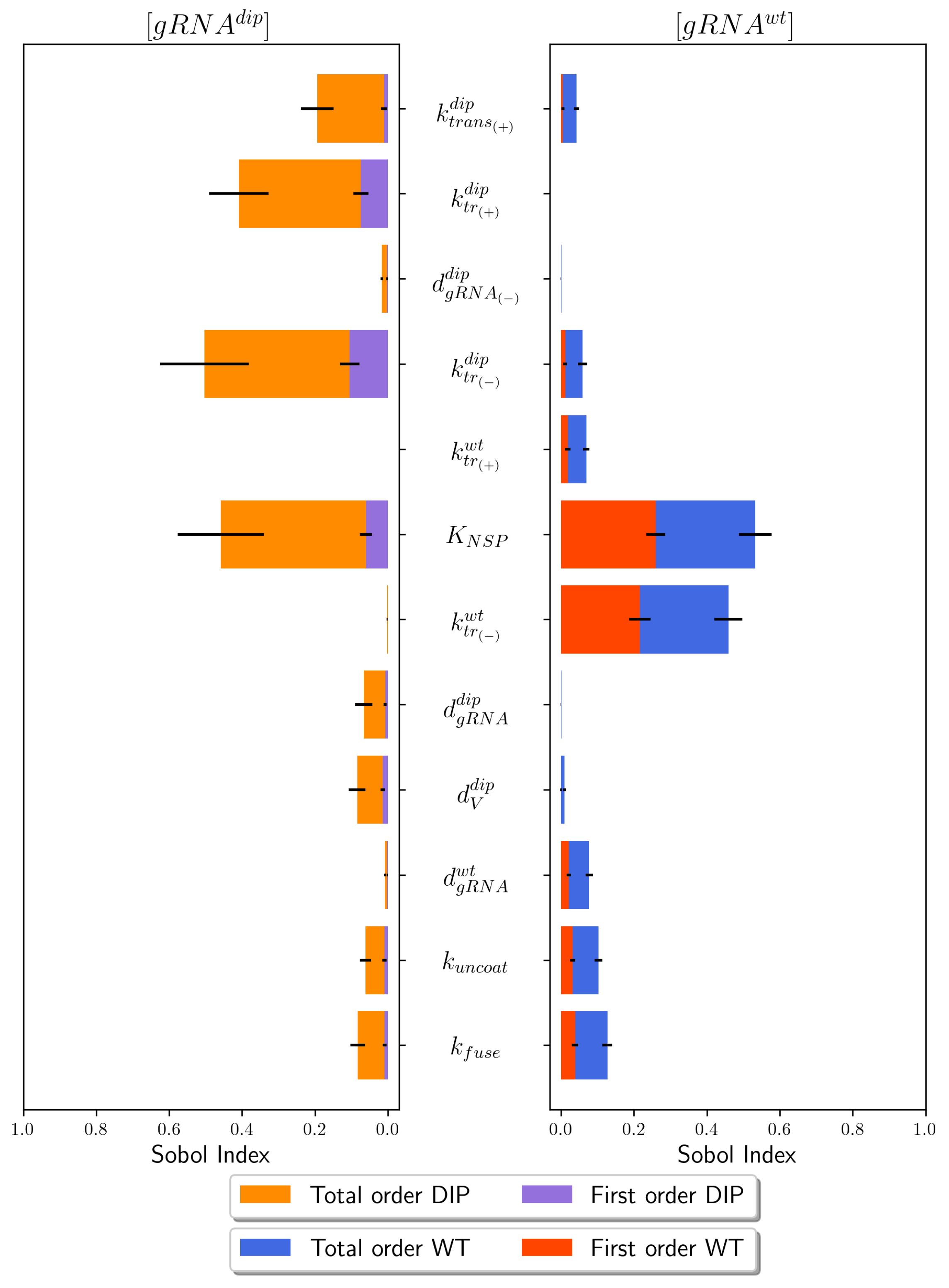
4.1. Sensitivity Analysis
4.2. Parameter Calibration
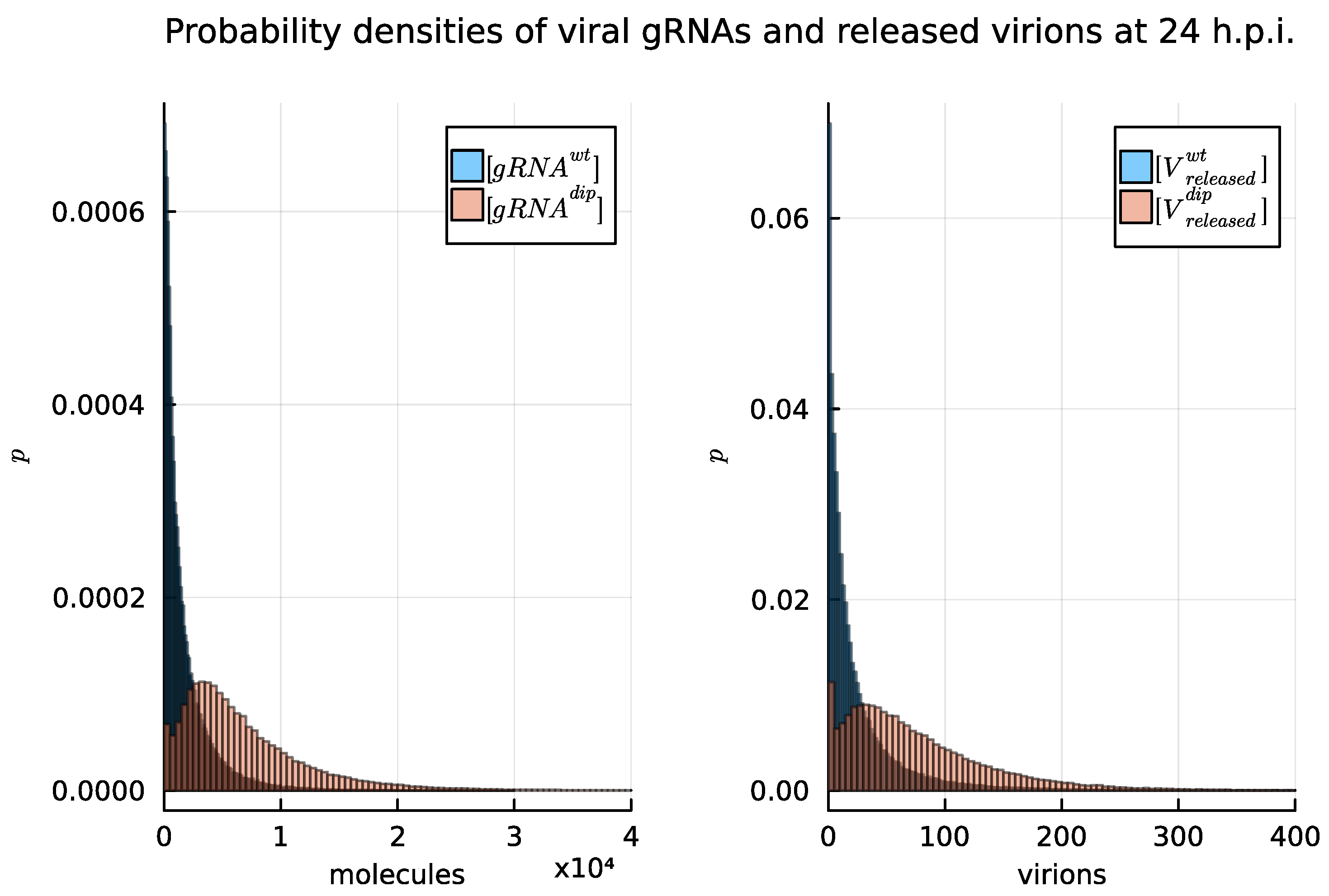
4.3. Stochastic Model Results
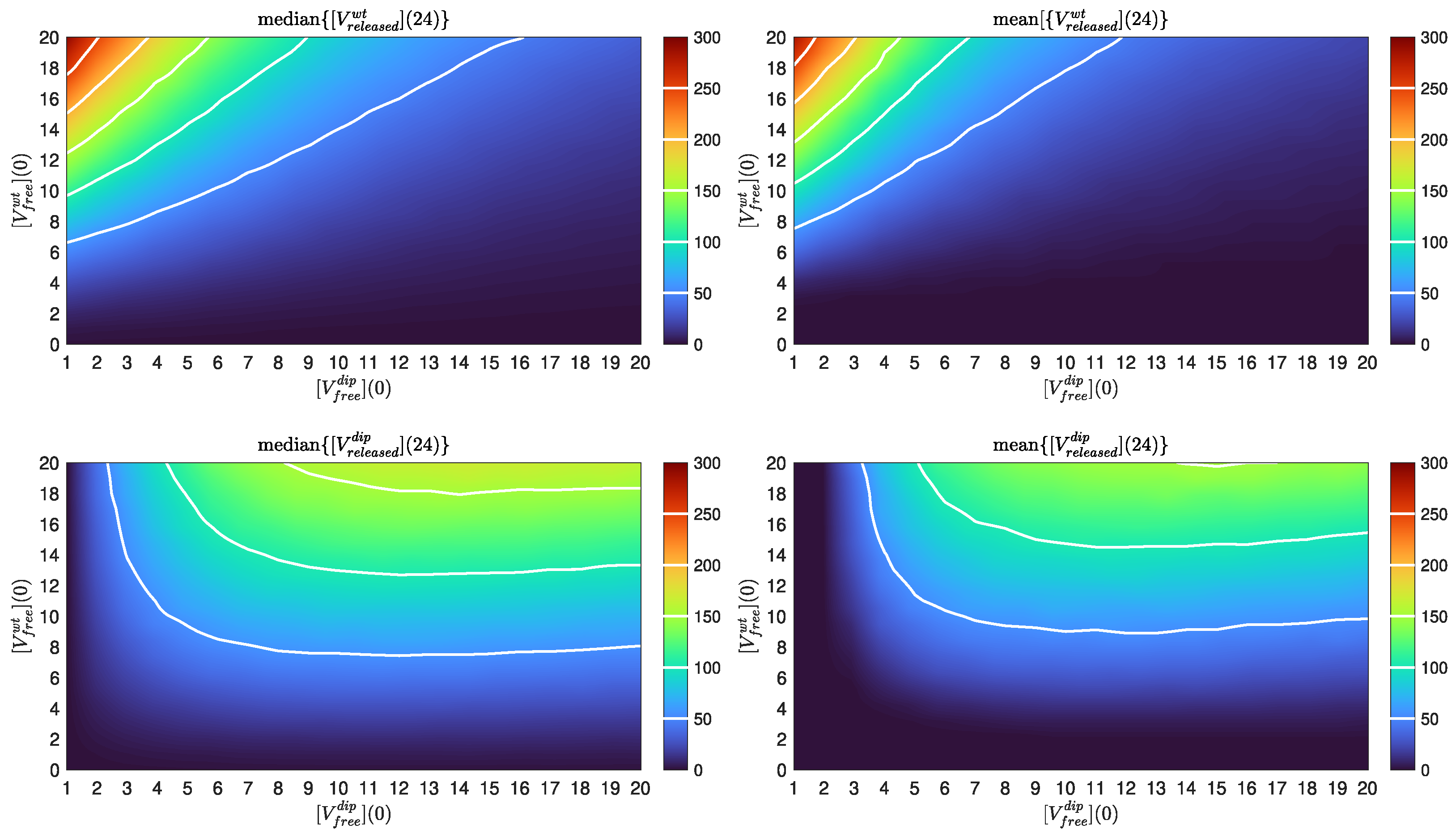
4.4. Dose Response Analysis
4.5. DIP Dose Effect on WT Virion Production
5. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ABC | Approximate Bayesian computation |
| MC | Markov chain |
| MOI | Multiplicity of infection |
| ODE | Ordinary differential equation |
| SDE | Stochastic differential equation |
| RSSA | Rejection stochastic simulation algorithm |
| TIP | Therapeutic interfering particle |
| DIP | Defective interfering particle |
| WT | Wild-type |
Appendix A

References
- Wu, D.; Wu, T.; Liu, Q.; Yang, Z. The SARS-CoV-2 outbreak: What we know. Int. J. Infect. Dis. 2020, 94, 44–48. [Google Scholar] [CrossRef]
- Li, X.; Wang, W.; Zhao, X.; Zai, J.; Zhao, Q.; Li, Y.; Chaillon, A. Transmission dynamics and evolutionary history of 2019-nCoV. J. Med. Virol. 2020, 92, 501–511. [Google Scholar] [CrossRef]
- Martellucci, C.A.; Flacco, M.E.; Cappadona, R.; Bravi, F.; Mantovani, L.; Manzoli, L. SARS-CoV-2 pandemic: An overview. Adv. Biol. Regul. 2020, 77, 100736. [Google Scholar] [CrossRef]
- World Health Organization. Coronavirus Disease 2019 (COVID-19): Situation Report, 73; World Health Organization: Geneva, Switzerland, 2020.
- Colson, P.; Rolain, J.M.; Raoult, D. Chloroquine for the 2019 novel coronavirus SARS-CoV-2, 2020. Int. J. Antimicrob. Agents 2020, 55, 105923. [Google Scholar] [CrossRef]
- Morse, J.S.; Lalonde, T.; Xu, S.; Liu, W.R. Learning from the past: Possible urgent prevention and treatment options for severe acute respiratory infections caused by 2019-nCoV. Chembiochem 2020, 21, 730–738. [Google Scholar] [CrossRef]
- Castells, M.C.; Phillips, E.J. Maintaining safety with SARS-CoV-2 vaccines. N. Engl. J. Med. 2021, 384, 643–649. [Google Scholar] [CrossRef]
- Boehm, E.; Kronig, I.; Neher, R.A.; Eckerle, I.; Vetter, P.; Kaiser, L. Novel SARS-CoV-2 variants: The pandemics within the pandemic. Clin. Microbiol. Infect. 2021, 27, 1109–1117. [Google Scholar] [CrossRef]
- Jangra, S.; Ye, C.; Rathnasinghe, R.; Stadlbauer, D.; Alshammary, H.; Amoako, A.A.; Awawda, M.H.; Beach, K.F.; Bermúdez-González, M.C.; Chernet, R.L.; et al. SARS-CoV-2 spike E484K mutation reduces antibody neutralisation. Lancet Microbe 2021, 2, e283–e284. [Google Scholar] [CrossRef]
- Naqvi, A.A.T.; Fatima, K.; Mohammad, T.; Fatima, U.; Singh, I.K.; Singh, A.; Atif, S.M.; Hariprasad, G.; Hasan, G.M.; Hassan, M.I. Insights into SARS-CoV-2 genome, structure, evolution, pathogenesis and therapies: Structural genomics approach. Biochim. Biophys. Acta Mol. Basis Dis. 2020, 1866, 165878. [Google Scholar] [CrossRef]
- Fu, Y.; Cheng, Y.; Wu, Y. Understanding SARS-CoV-2-mediated inflammatory responses: From mechanisms to potential therapeutic tools. Virol. Sin. 2020, 35, 266–271. [Google Scholar] [CrossRef]
- Alnaji, F.G.; Brooke, C.B. Influenza virus DI particles: Defective interfering or delightfully interesting? PloS Pathog. 2020, 16, e1008436. [Google Scholar] [CrossRef]
- Fatehi, F.; Bingham, R.J.; Dechant, P.P.; Stockley, P.G.; Twarock, R. Therapeutic interfering particles exploiting viral replication and assembly mechanisms show promising performance: A modelling study. Sci. Rep. 2021, 11, 23847. [Google Scholar] [CrossRef]
- Bdeir, N.; Arora, P.; Gärtner, S.; Hoffmann, M.; Reichl, U.; Pöhlmann, S.; Winkler, M. A system for production of defective interfering particles in the absence of infectious influenza A virus. PLoS ONE 2019, 14, e0212757. [Google Scholar] [CrossRef]
- Chaturvedi, S.; Vasen, G.; Pablo, M.; Chen, X.; Beutler, N.; Kumar, A.; Tanner, E.; Illouz, S.; Rahgoshay, D.; Burnett, J.; et al. Identification of a therapeutic interfering particle—A single-dose SARS-CoV-2 antiviral intervention with a high barrier to resistance. Cell 2021, 184, 6022–6036. [Google Scholar] [CrossRef]
- Smither, S.J.; Garcia-Dorival, I.; Eastaugh, L.; Findlay, J.S.; O’Brien, L.M.; Carruthers, J.; Williamson, E.D.; Molina-París, C.; Hiscox, J.A.; Laws, T.R. An Investigation of the Effect of Transfected Defective, Ebola Virus Genomes on Ebola Replication. Front. Cell. Infect. Microbiol. 2020, 10, 159. [Google Scholar] [CrossRef]
- Rouzine, I.M.; Weinberger, L.S. Design requirements for interfering particles to maintain coadaptive stability with HIV-1. J. Virol. 2013, 87, 2081–2093. [Google Scholar] [CrossRef]
- Grebennikov, D.; Karsonova, A.; Loguinova, M.; Casella, V.; Meyerhans, A.; Bocharov, G. Predicting the Kinetic Coordination of Immune Response Dynamics in SARS-CoV-2 Infection: Implications for Disease Pathogenesis. Mathematics 2022, 10, 3154. [Google Scholar] [CrossRef]
- Perelson, A.S.; Ke, R. Mechanistic modeling of SARS-CoV-2 and other infectious diseases and the effects of therapeutics. Clin. Pharmacol. Ther. 2021, 109, 829–840. [Google Scholar] [CrossRef]
- Zhao, Y.; Xing, Y. A delayed dynamical model for COVID-19 therapy with defective interfering particles and artificial antibodies. Discret. Contin. Dyn.-Syst.-B 2021, 27, 5367. [Google Scholar] [CrossRef]
- Grebennikov, D.; Kholodareva, E.; Sazonov, I.; Karsonova, A.; Meyerhans, A.; Bocharov, G. Intracellular Life Cycle Kinetics of SARS-CoV-2 Predicted Using Mathematical Modelling. Viruses 2021, 13, 1735. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Trame, M.N.; Lesko L, J.; Schmidt, S. Sobol Sensitivity Analysis: A Tool to Guide the Development and Evaluation of Systems Pharmacology Models. Pharmacometrics Syst. Pharmacol. 2015, 4, 69–79. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis. The Primer, 1st ed.; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Sobol, I.M. Sensitivity analysis for non-linear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Saltelli, A.; Tarantola, S.; Campolongo, F.; Ratto, M. Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Ozono, S.; Zhang, Y.; Ode, H.; Sano, K.; Tan, T.S.; Imai, K.; Miyoshi, K.; Kishigami, S.; Ueno, T.; Iwatani, Y.; et al. SARS-CoV-2 D614G spike mutation increases entry efficiency with enhanced ACE2-binding affinity. Nat. Commun. 2021, 12, 848. [Google Scholar] [CrossRef]
- Walls, A.C.; Park, Y.J.; Tortorici, M.A.; Wall, A.; McGuire, A.T.; Veesler, D. Structure, function, and antigenicity of the SARS-CoV-2 spike glycoprotein. Cell 2020, 181, 281–292. [Google Scholar] [CrossRef]
- Baggen, J.; Persoons, L.; Vanstreels, E.; Jansen, S.; Van Looveren, D.; Boeckx, B.; Geudens, V.; De Man, J.; Jochmans, D.; Wauters, J.; et al. Genome-wide CRISPR screening identifies TMEM106B as a proviral host factor for SARS-CoV-2. Nat. Genet. 2021, 53, 435–444. [Google Scholar] [CrossRef]
- Bocharov, G.; Romanyukha, A. Mathematical model of antiviral immune response III. Influenza A virus infection. J. Theor. Biol. 1994, 167, 323–360. [Google Scholar] [CrossRef]
- Baccam, P.; Beauchemin, C.; Macken, C.A.; Hayden, F.G.; Perelson, A.S. Kinetics of influenza A virus infection in humans. J. Virol. 2006, 80, 7590–7599. [Google Scholar] [CrossRef]
- Zhu, Y.; Yu, D.; Yan, H.; Chong, H.; He, Y. Design of potent membrane fusion inhibitors against SARS-CoV-2, an emerging coronavirus with high fusogenic activity. J. Virol. 2020, 94, e00635-20. [Google Scholar] [CrossRef]
- Heldt, F.S.; Kupke, S.Y.; Dorl, S.; Reichl, U.; Frensing, T. Single-cell analysis and stochastic modelling unveil large cell-to-cell variability in influenza A virus infection. Nat. Commun. 2015, 6, 8938. [Google Scholar] [CrossRef]
- Irigoyen, N.; Firth, A.E.; Jones, J.D.; Chung, B.Y.W.; Siddell, S.G.; Brierley, I. High-resolution analysis of coronavirus gene expression by RNA sequencing and ribosome profiling. PLoS Pathog. 2016, 12, e1005473. [Google Scholar] [CrossRef]
- Buccitelli, C.; Selbach, M. mRNAs, proteins and the emerging principles of gene expression control. Nat. Rev. Genet. 2020, 21, 630–644. [Google Scholar] [CrossRef]
- Kim, D.; Lee, J.Y.; Yang, J.S.; Kim, J.W.; Kim, V.N.; Chang, H. The architecture of SARS-CoV-2 transcriptome. Cell 2020, 181, 914–921. [Google Scholar] [CrossRef]
- Gasteiger, E.; Gattiker, A.; Hoogland, C.; Ivanyi, I.; Appel, R.D.; Bairoch, A. ExPASy: The proteomics server for in-depth protein knowledge and analysis. Nucleic Acids Res. 2003, 31, 3784–3788. [Google Scholar] [CrossRef]
- Nelson, D.L.; Lehninger, A.L.; Cox, M.M. Lehninger Principles of Biochemistry; Macmillan: New York, NY, USA, 2008. [Google Scholar]
- Adelman, K.; La Porta, A.; Santangelo, T.J.; Lis, J.T.; Roberts, J.W.; Wang, M.D. Single molecule analysis of RNA polymerase elongation reveals uniform kinetic behavior. Proc. Natl. Acad. Sci. USA 2002, 99, 13538–13543. [Google Scholar] [CrossRef]
- Klein, S.; Cortese, M.; Winter, S.L.; Wachsmuth-Melm, M.; Neufeldt, C.J.; Cerikan, B.; Stanifer, M.L.; Boulant, S.; Bartenschlager, R.; Chlanda, P. SARS-CoV-2 structure and replication characterized by in situ cryo-electron tomography. Nat. Commun. 2020, 11, 5885. [Google Scholar] [CrossRef]
- Zinzula, L.; Basquin, J.; Bohn, S.; Beck, F.; Klumpe, S.; Pfeifer, G.; Nagy, I.; Bracher, A.; Hartl, F.U.; Baumeister, W. High-resolution structure and biophysical characterization of the nucleocapsid phosphoprotein dimerization domain from the COVID-19 severe acute respiratory syndrome coronavirus 2. Biochem. Biophys. Res. Commun. 2021, 538, 54–62. [Google Scholar] [CrossRef]
- Chen, I.J.; Yuann, J.M.P.; Chang, Y.M.; Lin, S.Y.; Zhao, J.; Perlman, S.; Shen, Y.Y.; Huang, T.H.; Hou, M.H. Crystal structure-based exploration of the important role of Arg106 in the RNA-binding domain of human coronavirus OC43 nucleocapsid protein. Biochim. Biophys. Acta Proteins Proteom. 2013, 1834, 1054–1062. [Google Scholar] [CrossRef]
- Spencer, K.A.; Hiscox, J.A. Characterisation of the RNA binding properties of the coronavirus infectious bronchitis virus nucleocapsid protein amino-terminal region. FEBS Lett. 2006, 580, 5993–5998. [Google Scholar] [CrossRef]
- Spencer, K.A.; Dee, M.; Britton, P.; Hiscox, J.A. Role of phosphorylation clusters in the biology of the coronavirus infectious bronchitis virus nucleocapsid protein. Virology 2008, 370, 373–381. [Google Scholar] [CrossRef]
- Bar-On, Y.M.; Flamholz, A.; Phillips, R.; Milo, R. Science Forum: SARS-CoV-2 (COVID-19) by the numbers. elife 2020, 9, e57309. [Google Scholar] [CrossRef]
- Jack, A.; Ferro, L.S.; Trnka, M.J.; Wehri, E.; Nadgir, A.; Nguyenla, X.; Fox, D.; Costa, K.; Stanley, S.; Schaletzky, J.; et al. SARS-CoV-2 nucleocapsid protein forms condensates with viral genomic RNA. PLoS Biol. 2021, 19, e3001425. [Google Scholar] [CrossRef]
- Cubuk, J.; Alston, J.J.; Incicco, J.J.; Singh, S.; Stuchell-Brereton, M.D.; Ward, M.D.; Zimmerman, M.I.; Vithani, N.; Griffith, D.; Wagoner, J.A.; et al. The SARS-CoV-2 nucleocapsid protein is dynamic, disordered, and phase separates with RNA. Nat. Commun. 2021, 12, 1–17. [Google Scholar] [CrossRef]
- Viehweger, A.; Krautwurst, S.; Lamkiewicz, K.; Madhugiri, R.; Ziebuhr, J.; Hölzer, M.; Marz, M. Direct RNA nanopore sequencing of full-length coronavirus genomes provides novel insights into structural variants and enables modification analysis. Genome Res. 2019, 29, 1545–1554. [Google Scholar] [CrossRef]
- Neuman, B.W.; Kiss, G.; Kunding, A.H.; Bhella, D.; Baksh, M.F.; Connelly, S.; Droese, B.; Klaus, J.P.; Makino, S.; Sawicki, S.G.; et al. A structural analysis of M protein in coronavirus assembly and morphology. J. Struct. Biol. 2011, 174, 11–22. [Google Scholar] [CrossRef]
- Yao, H.; Song, Y.; Chen, Y.; Wu, N.; Xu, J.; Sun, C.; Zhang, J.; Weng, T.; Zhang, Z.; Wu, Z.; et al. Molecular architecture of the SARS-CoV-2 virus. Cell 2020, 183, 730–738. [Google Scholar] [CrossRef]
- Gordon, D.E.; Hiatt, J.; Bouhaddou, M.; Rezelj, V.V.; Ulferts, S.; Braberg, H.; Jureka, A.S.; Obernier, K.; Guo, J.Z.; Batra, J.; et al. Comparative host-coronavirus protein interaction networks reveal pan-viral disease mechanisms. Science 2020, 370, eabe9403. [Google Scholar] [CrossRef]
- Shcherbatova, O.; Grebennikov, D.; Sazonov, I.; Meyerhans, A.; Bocharov, G. Modeling of the HIV-1 life cycle in productively infected cells to predict novel therapeutic targets. Pathogens 2020, 9, 255. [Google Scholar] [CrossRef]
- Mooney, J.; Thakur, S.; Kahng, P.; Trapani, J.G.; Poccia, D. Quantification of exocytosis kinetics by DIC image analysis of cortical lawns. J. Chem. Biol. 2014, 7, 43–55. [Google Scholar] [CrossRef]
- Toni, T.; Welch, D.; Strelkowa, N.; Ipsen, A.; Stumpf, M.P. Approximate Bayesian computation scheme for parameter inference and model selection in dynamical systems. J. R. Soc. Interface 2009, 6, 187–202. [Google Scholar] [CrossRef]
- Gillespie, D.T. Stochastic Simulation of Chemical Kinetics. Annu. Rev. Phys. Chem. 2007, 58, 35–55. [Google Scholar] [CrossRef]
- Marchetti, L.; Priami, C.; Thanh, V.H. Simulation Algorithms for Computational Systems Biology; Texts in Theoretical Computer Science; An EATCS Series; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Sazonov, I.; Grebennikov, D.; Meyerhans, A.; Bocharov, G. Markov Chain-Based Stochastic Modelling of HIV-1 Life Cycle in a CD4 T Cell. Mathematics 2021, 9, 2025. [Google Scholar] [CrossRef]
- V’kovski, P.; Kratzel, A.; Steiner, S.; Stalder, H.; Thiel, V. Coronavirus biology and replication: Implications for SARS-CoV-2. Nat. Rev. Microbiol. 2021, 19, 155–170. [Google Scholar] [CrossRef]
- Mendonça, L.; Howe, A.; Gilchrist, J.B.; Sheng, Y.; Sun, D.; Knight, M.L.; Zanetti-Domingues, L.C.; Bateman, B.; Krebs, A.S.; Chen, L.; et al. Correlative multi-scale cryo-imaging unveils SARS-CoV-2 assembly and egress. Nat. Commun. 2021, 12, 4629. [Google Scholar] [CrossRef]
- Sazonov, I.; Grebennikov, D.; Meyerhans, A.; Bocharov, G. Sensitivity of SARS-CoV-2 Life Cycle to IFN Effects and ACE2 Binding Unveiled with a Stochastic Model. Viruses 2022, 14, 403. [Google Scholar] [CrossRef]
- Rand, U.; Kupke, S.Y.; Shkarlet, H.; Hein, M.D.; Hirsch, T.; Marichal-Gallardo, P.; Cicin-Sain, L.; Reichl, U.; Bruder, D. Antiviral activity of influenza A virus defective interfering particles against SARS-CoV-2 replication in vitro through stimulation of innate immunity. Cells 2021, 10, 1756. [Google Scholar] [CrossRef]
- Roux, L.; Simon, A.E.; Holland, J.J. Effects of defective interfering viruses on virus replication and pathogenesis in vitro and in vivo. Adv. Virus Res. 1991, 40, 181–211. [Google Scholar]
- Li, D.; Lin, M.H.; Rawle, D.J.; Jin, H.; Wu, Z.; Wang, L.; Lor, M.; Hussain, M.; Aaskov, J.; Harrich, D. Dengue virus-free defective interfering particles have potent and broad anti-dengue virus activity. Commun. Biol. 2021, 4, 557. [Google Scholar] [CrossRef]
- Dempsey, P.; Vaidya, S.; Cheng, G. The art of war: Innate and adaptive immune responses. Cell. Mol. Life Sci. 2003, 60, 2604–2621. [Google Scholar] [CrossRef]
- tenOever, B. The Evolution of Antiviral Defense Systems. Cell Host Microbe 2016, 19, 142–149. [Google Scholar] [CrossRef]
- Katze, M.G.; He, Y.; Gale, M. Viruses and interferon: A fight for supremacy. Nat. Rev. Immunol. 2002, 2, 675–687. [Google Scholar]
- Alalhareth, F.K.; Atta, U.; Ali, A.H.; Ahmad, A.; Alharbi, M.H. Analysis of Leptospirosis transmission dynamics with environmental effects and bifurcation using fractional-order derivative. Alex. Eng. J. 2023, 80, 372–382. [Google Scholar] [CrossRef]
- Dayan, F.; Ahmed, N.; Ali, A.H.; Rafiq, M.; Raz, A. Numerical investigation of a typhoid disease model in fuzzy environment. Sci. Rep. 2023, 13, 21993. [Google Scholar] [CrossRef]
- Lin, M.H.; Li, D.; Tang, B.; Li, L.; Suhrbier, A.; Harrich, D. Defective Interfering Particles with Broad-Acting Antiviral Activity for Dengue, Zika, Yellow Fever, Respiratory Syncytial and SARS-CoV-2 Virus Infection. Microbiol. Spectr. 2022, 10, e03949-22. [Google Scholar] [CrossRef]
- Wu, M.; Zhou, E.; Sheng, R.; Fu, X.; Li, J.; Jiang, C.; Su, W. Defective Interfering Particles of Influenza Virus and Their Characteristics, Impacts, and Use in Vaccines and Antiviral Strategies: A Systematic Review. Viruses 2022, 14, 2773. [Google Scholar] [CrossRef]
- Welch, S.R.; Spengler, J.R.; Harmon, J.R.; Coleman-McCray, J.D.; Scholte, F.E.M.; Genzer, S.C.; Lo, M.K.; Montgomery, J.M.; Nichol, S.T.; Spiropoulou, C.F. Defective Interfering Viral Particle Treatment Reduces Clinical Signs and Protects Hamsters from Lethal Nipah Virus Disease. mBio 2022, 13, e03294-21. [Google Scholar] [CrossRef]
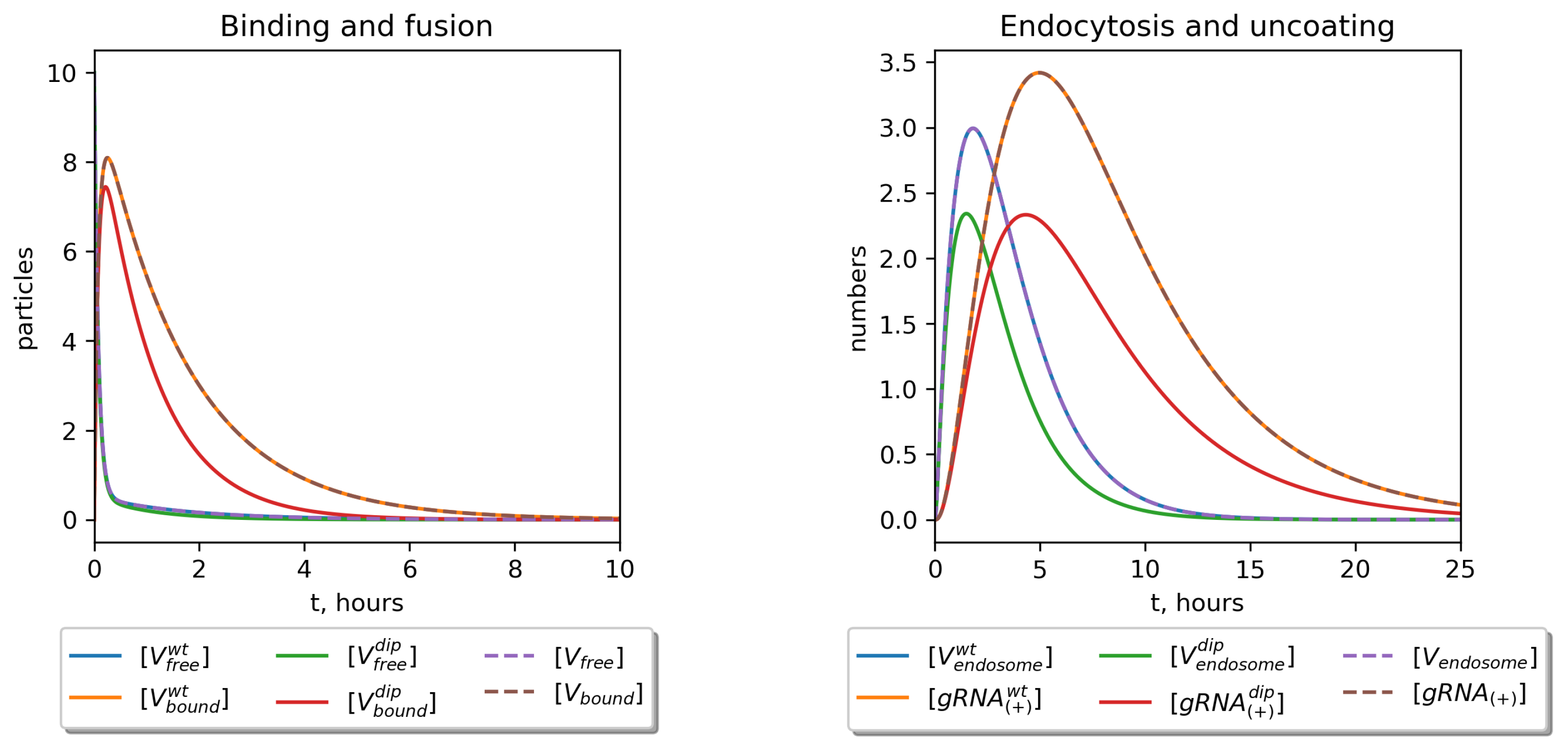
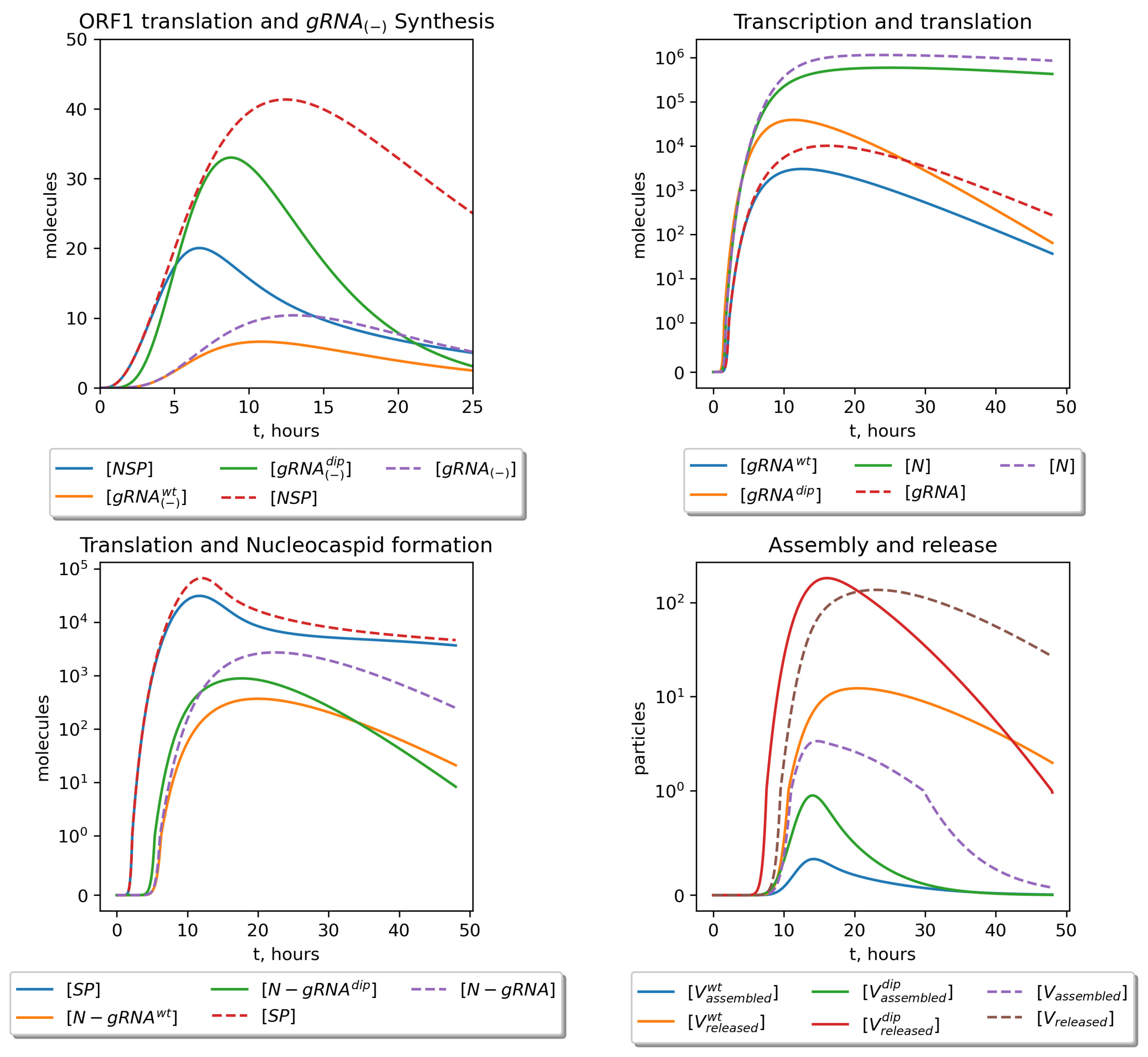
| Variable | Definition | Value |
|---|---|---|
| Number of free infectious (i.e., wild-type) virions outside the cell membrane | 10 | |
| Number of infectious virions bound to ACE2 and activated by TMPRSS2 | 1–10 | |
| Number of infectious virions in endosomes | 1–10 | |
| Number of free non-infectious (i.e., defective interfering particles) virions outside the cell membrane | ||
| Number of non-infectious virions bound to ACE2 and activated by TMPRSS2 | ||
| Number of non-infectious virions in endosomes | ||
| Single strand positive sense genomic RNA | 1–5 | |
| Single strand positive sense DIP genomic RNA | ||
| Population of non-structural proteins | ||
| Negative sense genomic and subgenomic RNAs of infectious virus | 10 | |
| Positive sense genomic and subgenomic RNAs of infectious virus | ||
| Negative sense subgenomic RNAs of DIPs | ||
| Positive sense subgenomic RNAs of DIPs | ||
| Total number of structural proteins per virion | ||
| N proteins per virion | 456; | |
| Ribonucleocapsid molecules for infectious virions | ||
| Ribonucleocapsid molecules for non-infectious virions | ||
| Assembled infectious virions in endosomes | ||
| Released infectious viruses | 10– virions in 7 to 24 h | |
| Assembled non-infectious virions in endosomes | ||
| Released non-infectious virions |
| Parameter | Description, Units | Value | Range [References] |
|---|---|---|---|
| Rate of virion binding to ACE2 receptor, h | 12 | (3.6, 12) [26,27] | |
| Clearance rate of WT extracellular virions, h | 0.12 | (0.06, 3.5) [28,29,30] | |
| Dissociation rate constant of bound virions, h | 0.61 | (0.32, 1.08) [26,27] | |
| Fusion rate constant, h | 0.5 | (0.33, 1) [31] | |
| Uncoating rate constant, h | 0.5 | (0.33, 1) [31] | |
| Degradation rate of WT virions in endosomes, h | 0.06 | (0.0001, 0.12) [28,32], | |
| Translation rate, nt/mRNA h | 45,360 | (40,000, 50,000) [33,34] | |
| Length of ORF1 of the RNA genome coding s, nt | 21,000 | fixed [35] | |
| Degradation rate of proteins in the cell, h | 0.069 | (0.023, 0.69) [34,36], | |
| tuned to (0.023, 0.1) | |||
| Transcription rate of WT negative sense | 3 | (1, 100) [34], | |
| Genomic and subgenomic RNAs, copies/mRNA h | tuned to (1, 20) | ||
| Threshold number of s | 100 | (10, 150) | |
| enhancing vRNA transcription, molecules | |||
| Degradation rate of WT positive sense RNAs in cell, h | 0.2 | (0.069, 0.69) [34,37], | |
| tuned to (0.069, 0.4) | |||
| Degradation rate of WT negative sense RNAs | 0.1 | (0.05, 0.2) | |
| in double-membrane vesicles, h | |||
| Replication rate of positive sense WT RNAs, copies/mRNA/h | 1000 | (620, 1380) [38] | |
| Rate of the WT nucleocapsid formation [N-], h | 0.4 | (0.02, 0.4) [39,40,41,42,43] | |
| Threshold number of N proteins at which | [44,45,46] | ||
| nucleocapsid formation slows down, molecules | |||
| Length of RNA genome coding N protein, nt | 1200 | fixed [47] | |
| Length of genome coding structural proteins S, E, M, nt | fixed [47] | ||
| Degradation rate of N protein, h | 0.023 | (0.023, 0.069) [36] | |
| Mean degradation rate of the pool of E, S, M proteins, h | 0.044 | (0.023, 0.36) [36] | |
| Total number of structural proteins S, M, E per WT virion, molecules | (1125, 2230) [39,48,49] | ||
| Number of N protein per WT virion, molecules | 456 | fixed [39] | |
| threshold number of WT virions at which | (10, ) [44,50] | ||
| the virion assembly process slows down, virions | |||
| Rate of WT virion assembling, h | 1 | (0.01, 10) [32,51] | |
| Degradation rate of WT ribonucleoprotein, h | 0.2 | (0.069, 0.69) [34,37] | |
| Rate of WT virion release via exocytosis, h | 8 | (8, 7200) [51,52] | |
| Assembled WT virion degradation rate, h | 0.06 | (, 0.12) [28] |
| Time (Hours) | Fold Log Reduction (2 d.p.) |
|---|---|
| 24 | 1.20 |
| 48 | 1.14 |
| Parameter | Description, Units | Value | Range [References] |
|---|---|---|---|
| Clearance rate of DIP extracellular virions, h | [28,29,30] | ||
| Degradation rate of DIP virions in endosomes, h | [28,32], | ||
| Transcription rate of DIP negative sense | 34 | [34], | |
| Genomic and subgenomic RNAs, copies/mRNA h | |||
| Degradation rate of DIP positive sense RNAs in cell, h | [34,37], | ||
| Degradation rate of DIP negative sense RNAs | |||
| in double-membrane vesicles, h | |||
| Replication rate of positive sense DIP RNAs, copies/mRNA/h | 2540 | [38] | |
| Rate of the DIP nucleocapsid formation [N-], h | [39,40,41,42,43] | ||
| Total number of structural proteins | 112 | [39,48,49] | |
| S, M, E per DIP virion, molecules | |||
| Number of N protein per DIP virion, molecules | 53 | ||
| Threshold number of DIP virions at which | 380 | [44,50] | |
| the virion assembly process slows down, virions | |||
| Rate of DIP virion assembling, h | [32,51] | ||
| Degradation rate of DIP ribonucleoprotein, h | [34,37] | ||
| Rate of DIP virion release via exocytosis, h | 105 | [51,52] | |
| Assembled DIP virion degradation rate, h | [28] | ||
| Rate of loss of s by trans elements | |||
| from negative sense WT RNA, h | |||
| Rate of loss of s by trans elements | |||
| from positive sense WT RNA, h | |||
| Rate of loss of s by trans elements | |||
| from negative sense WT RNA, h | |||
| Rate of loss of s by trans elements | |||
| from positive sense WT RNA, h |
| m | Transition | Propensity, |
|---|---|---|
| Entry and RNA release (WT): | ||
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| Entry and RNA release (DIPs): | ||
| 9 | ||
| 10 | ||
| 11 | ||
| 12 | ||
| 13 | ||
| 14 | ||
| 15 | ||
| 16 | ||
| ORF1 translation and competitive viral RNA replication: | ||
| 17 | ||
| 18 | ||
| 19 | ||
| 20 | ||
| 21 | ||
| 22 | ||
| 23 | ||
| 24 | ||
| 25 | ||
| 26 | ||
| 27 | ||
| 28 | ||
| 29 | ||
| 30 | ||
| Translation and ribonucleocapsid formation: | ||
| 31 | ||
| 32 | ||
| 33 | ||
| 34 | ||
| 35 | ||
| 36 | ||
| Assembly and release: | ||
| 37 | ||
| 38 | ||
| 39 | ||
| 40 | ||
| 41 | ||
| 42 | ||
| 43 | ||
| 44 | ||
| 45 | ||
| 46 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Locke, M.; Grebennikov, D.; Sazonov, I.; López-García, M.; Loguinova, M.; Meyerhans, A.; Bocharov, G.; Molina-París, C. Exploring the Therapeutic Potential of Defective Interfering Particles in Reducing the Replication of SARS-CoV-2. Mathematics 2024, 12, 1904. https://doi.org/10.3390/math12121904
Locke M, Grebennikov D, Sazonov I, López-García M, Loguinova M, Meyerhans A, Bocharov G, Molina-París C. Exploring the Therapeutic Potential of Defective Interfering Particles in Reducing the Replication of SARS-CoV-2. Mathematics. 2024; 12(12):1904. https://doi.org/10.3390/math12121904
Chicago/Turabian StyleLocke, Macauley, Dmitry Grebennikov, Igor Sazonov, Martín López-García, Marina Loguinova, Andreas Meyerhans, Gennady Bocharov, and Carmen Molina-París. 2024. "Exploring the Therapeutic Potential of Defective Interfering Particles in Reducing the Replication of SARS-CoV-2" Mathematics 12, no. 12: 1904. https://doi.org/10.3390/math12121904
APA StyleLocke, M., Grebennikov, D., Sazonov, I., López-García, M., Loguinova, M., Meyerhans, A., Bocharov, G., & Molina-París, C. (2024). Exploring the Therapeutic Potential of Defective Interfering Particles in Reducing the Replication of SARS-CoV-2. Mathematics, 12(12), 1904. https://doi.org/10.3390/math12121904









