Exact Periodic Wave Solutions for the Perturbed Boussinesq Equation with Power Law Nonlinearity
Abstract
:1. Introduction
- The exact periodic wave solutions for the perturbed Boussinesq equation with power law nonlinearity are studied. To the best of the authors’ knowledge, it is the first time to explore periodic wave solutions for the perturbed Boussinesq equation. Moreover, the periodic traveling wave solutions of the perturbed Boussinesq equation are obtained for general n, not just for a specific value of n [21,22].
- Different from the existing periodic wave solutions [15,16,17] for nonlinear evolution equations, which are expressed in trigonometric functions [15,17] and exponential functions [16]. The periodic solutions for the perturbed Boussinesq equation in this paper are expressed in terms of Jacobian elliptic functions. The Jacobian elliptic function is more suitable for engineering applications than other functions, such as the Duffing system, which is often used to describe oscillations in circuit systems [23].
- Furthermore, we investigate the limiting case where the periodicity of the periodic traveling wave solution vanishes and derive the soliton solution with a single-peaked waveform.
2. Preliminaries
3. Exact Periodic Wave Solutions for the Perturbed BE
3.1. n = 1 in Equation (3)
3.2. n ≥ 1 in Equation (3)
3.2.1. Details of the Extended Trial Equation Method
- Step 1.
- Substitute the following transformation into (19)
- Step 2.
- Denote the trial equation in the form
- Step 3.
- Balancing the highest derivative term with the nonlinear term, the relations between , p, and can be derived.
- Step 4.
- Step 5.
- Equation (23) can be simplified to the elementary integral form
- Case 1:
- , , has two distinct real roots with multiplicities one and two, respectively; that is, ;
- Case 2:
- , , has only one real root with multiplicity three; that is, ;
- Case 3:
- , has only one real root; that is, , where ;
- Case 4:
- , , has three different real roots ; that is, .
3.2.2. Application
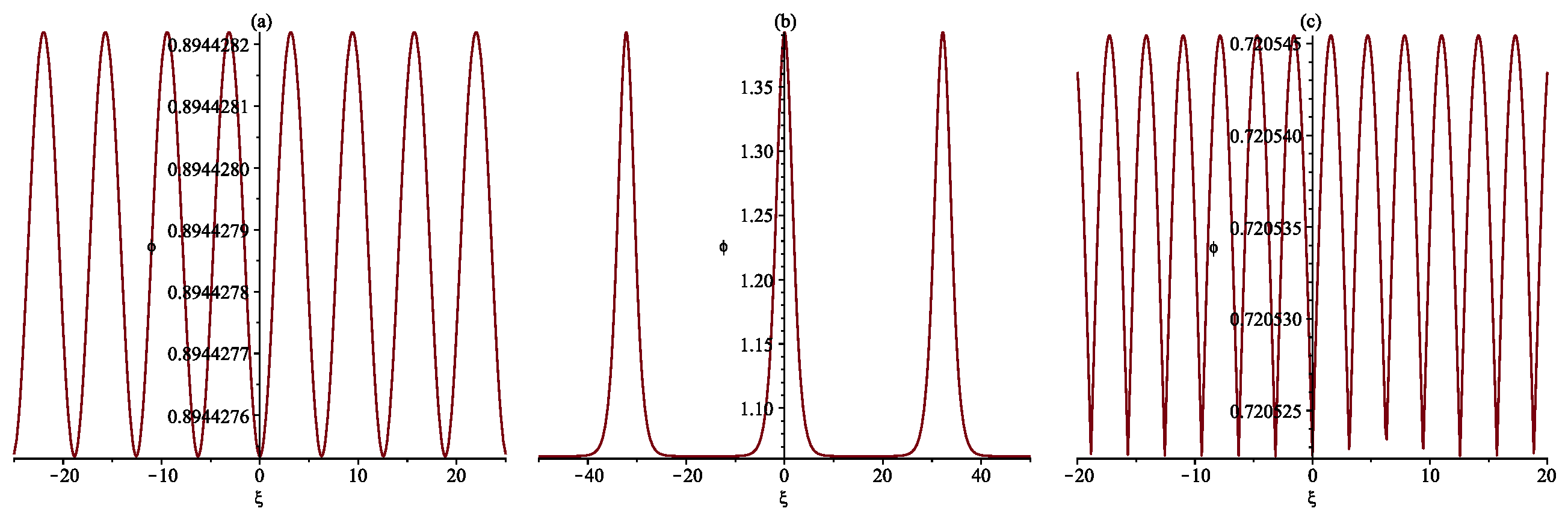
4. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Boussinesq, J. Theorie des ondes et des remous qui se propagent le long d’un canal rectangulaire horizontal, en communiquant au liquide contenu dans ce canal des vitesses sensiblement pareilles de la surface au fond. J. Math. Pures Appl. 1872, 2, 55–108. [Google Scholar]
- Anjan, B.; Daniela, M.; Arjuna, R. Solitary waves of Boussinesq equation in a power law media. Commun. Nonlinear Sci. Numer. Simulat. 2009, 14, 3738–3742. [Google Scholar]
- Liu, Y. Instability of solitary wave for generalized Boussinesq equations. J. Dyn. Differ. Equ. 1993, 5, 537–558. [Google Scholar] [CrossRef]
- Linares, F. Global existence of small solutions for a generalized Boussinesq equation. J. Differ. Equ. 1993, 106, 257–293. [Google Scholar] [CrossRef]
- Yang, Z.J. On local existence of solutions of initial boundary value problems for the bad Boussinesq-type equation. Nonlinear Anal. 2002, 51, 1259–1271. [Google Scholar]
- Xu, R.Z.; Yang, Y.B.; Liu, B.W.; Shen, J.H.; Huang, S.B. Global existence and blowup of solutions for the multidimensional sixth-order good Boussinesq equation. Z. Angew. Math. Phys. 2015, 66, 955–976. [Google Scholar]
- Charlier, C.; Lenells, J.; Wang, D. The “good” Boussinesq equation: Long-time asymptotics. Anal. PDE 2023, 16, 1351–1388. [Google Scholar] [CrossRef]
- Luigi, B.; Gianmarco, G.; Chengjian, Z. Spectrally accurate energy-preserving methods for the numerical solution of the good Boussinesq equation. Numer. Methods Partial. Differ. 2019, 35, 1343–1362. [Google Scholar]
- Kalantarov, V.K.; Ladyzhenskaya, O.A. The occurrence of collapse for quasilinear equations of parabolic and hyperbolic type. J. Sov. Math. 1978, 10, 53–70. [Google Scholar] [CrossRef]
- Levine, H.A. A note on the non-existence of global solutions of initial boundary value problems for the Boussinesq equation utt=uxx+3uxxxx − 12(u)xx. J. Math. Anal. 1985, 107, 206–210. [Google Scholar] [CrossRef]
- Dai, Z.D.; Huang, J.; Jiang, M.R.; Wang, S.H. Homoclinic orbits and periodic solitons for Boussinesq equation with even constraint. Chaos Soliton Fract. 2005, 26, 1189–1194. [Google Scholar] [CrossRef]
- Yang, Z.J.; Wang, X. Blowup of solutions for the bad Boussinesq-type equation. J. Math. Anal. Appl. 2003, 285, 282–298. [Google Scholar] [CrossRef]
- Kong, Y.; Xin, L.; Qiu, Q.R.; Han, L.J. Exact periodic wave solutions for the modified Zakharov equations with a quantum correction. Appl. Math. Lett. 2019, 94, 104–148. [Google Scholar] [CrossRef]
- Benjamin, T.B. Solitary and periodic waves of a new kind. Philos. Trans. R. Soc. Lond. Ser. A 1996, 354, 1775–1806. [Google Scholar]
- Zhang, L.-H. Traveling wave solutions for the generalized Zakharov-Kuznetsov equation with higher-order nonlinear terms. Appl. Math. Comput. 2009, 208, 144–155. [Google Scholar]
- Wang, K.-J. Traveling wave solutions of the Gardner equation in dusty plasmas. Results Phys. 2022, 33, 105207. [Google Scholar] [CrossRef]
- Hulya, D. Different types analytic solutions of the (1 + 1)-dimensional resonant nonlinear Schrodinger’s equation using (G′/G)-expansion method. Mod. Phys. Lett. B 2020, 34, 2050036. [Google Scholar]
- Yin, Y.-H.; Lv, X.; Ma, W.-X. Bäcklund transformation, exact solutions and diverse interaction phenomena to a (3 + 1)-dimensional nonlinear evolution equation. Nonlinear Dyn. 2022, 108, 4181–4194. [Google Scholar] [CrossRef]
- Sivalingam, S.M.; Pushpendra, K.; Govindaraj, V. A novel optimization-based physics-informed neural network scheme for solving fractional differential equations. Eng. Comput. 2024, 40, 855–865. [Google Scholar]
- Sivalingam, S.M.; Pushpendra, K.; Govindaraj, V. A Chebyshev neural network-based numerical scheme to solve distributed-order fractional differential equations. Comput. Math. Appl. 2024, 164, 150–165. [Google Scholar] [CrossRef]
- Krishnan, E.V.; Sachin, K.; Anjan, B. Solitons and other nonlinear waves of the Boussinesq equation. Nonlinear Dyn. 2012, 70, 1213–1221. [Google Scholar] [CrossRef]
- Akbar, M.A.; Norhashidah, H.; Mohd, A.; Tasnim, T. Adequate soliton solutions to the perturbed Boussinesq equation and the KdV-Caudrey-Dodd-Gibbon equation. J. King Saud Univ. Sci. 2020, 32, 2777–2785. [Google Scholar] [CrossRef]
- Okabe, T.; Kondou, T. Improvement to the averaging method using the Jacobian elliptic function. J. Sound Vib. 2009, 320, 339–364. [Google Scholar] [CrossRef]
- Pava, J.A. Nonlinear Dispersive Equations: Existence and Stability of Solitary and Periodic Travelling Wave Solutions; American Mathematical Society: Providence, RI, USA, 2009; Volume 156. [Google Scholar]
- Khaled, A. Extended trial equation method for nonlinear coupled Schrodinger Boussinesq partial differential equations. J. Egypt. Math. Soc. 2016, 24, 381–391. [Google Scholar]
- Liu, C.-S. Applications of complete discrimination system for polynomial for classifications of traveling wave solutions to nonlinear differential equations. Comput. Phys. Commun. 2010, 181, 317–324. [Google Scholar] [CrossRef]
- Byrd, P.F.; Friedman, M.D. Handbook of Elliptic Integrals for Engineers and Scientists, 2nd ed.; Springer: New York, NY, USA, 1971. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, Y.; Geng, J. Exact Periodic Wave Solutions for the Perturbed Boussinesq Equation with Power Law Nonlinearity. Mathematics 2024, 12, 1958. https://doi.org/10.3390/math12131958
Kong Y, Geng J. Exact Periodic Wave Solutions for the Perturbed Boussinesq Equation with Power Law Nonlinearity. Mathematics. 2024; 12(13):1958. https://doi.org/10.3390/math12131958
Chicago/Turabian StyleKong, Ying, and Jia Geng. 2024. "Exact Periodic Wave Solutions for the Perturbed Boussinesq Equation with Power Law Nonlinearity" Mathematics 12, no. 13: 1958. https://doi.org/10.3390/math12131958
APA StyleKong, Y., & Geng, J. (2024). Exact Periodic Wave Solutions for the Perturbed Boussinesq Equation with Power Law Nonlinearity. Mathematics, 12(13), 1958. https://doi.org/10.3390/math12131958