Production Planning Optimization in a Two-Echelon Multi-Product Supply Chain with Discrete Delivery and Storage at Manufacturer’s Warehouse
Abstract
:1. Introduction
- (1)
- Developing a model with discrete delivery to retailers and the storage of surplus production in a manufacturer’s warehouse;
- (2)
- Optimizing the proposed model.
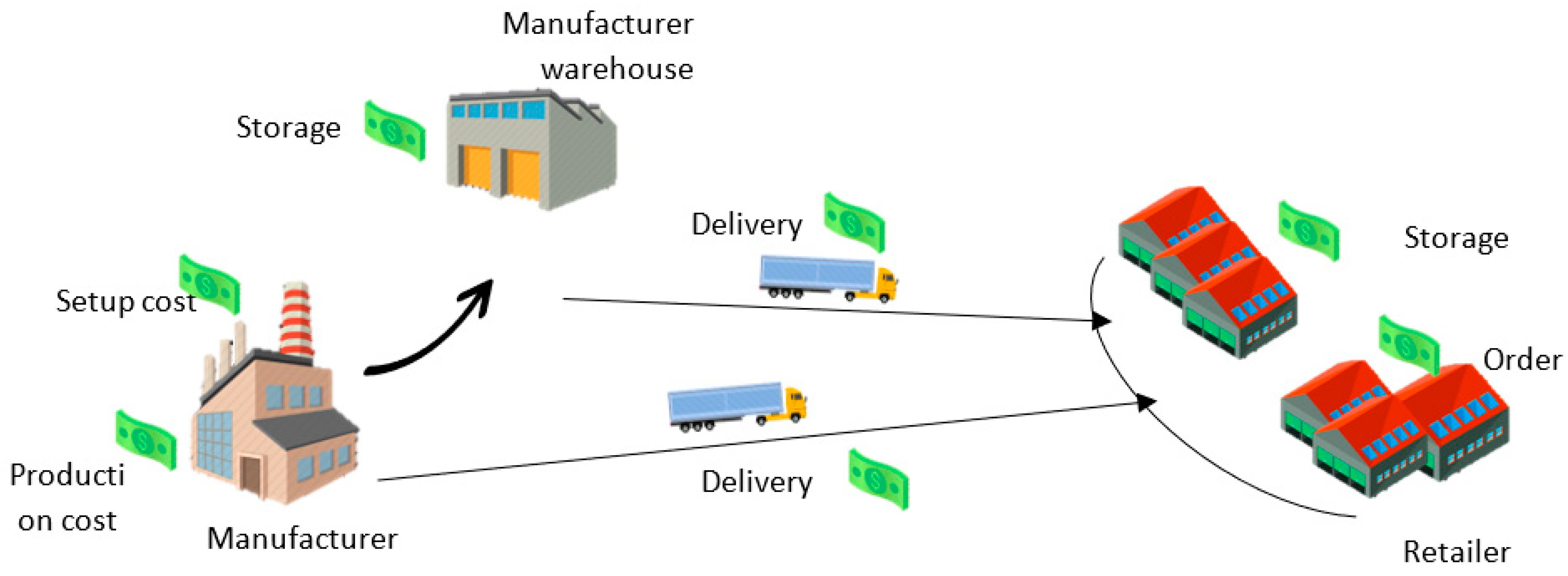
2. Problem Statement
- (1)
- Each of the retailers’ customers have fixed demands.
- (2)
- The retailers always have customers and must fulfill their demands.
- (3)
- Each retailer buys a different type of product from the manufacturer.
- (4)
- Each of the manufacturer’s products has a different production rate.
- (5)
- The transportation time from manufacturer to retailer is insignificant and therefore ignored.
- (6)
- The retailers place new orders when their inventory level drops to zero.
- (7)
- The manufacturer starts the production process and delivery of orders simultaneously.
- (8)
- Surplus items are stored in the manufacturer’s warehouse and delivered to retailers at specific intervals.
- (9)
- The manufacturer has an unlimited budget and warehouse space.
- (10)
- The idle and setup times to switch the machinery from one product to another are insignificant and considered as zero.
- (11)
- The time horizon is unlimited.
- (12)
- The manufacturer’s setup time is fixed.
- (13)
- The cost of delivering each retailers’ orders is a different but fixed value.
- (14)
- The warehousing cost is different for each product type in the manufacturer’s central warehouse and the retailers’ warehouses but remains fixed throughout the planning horizon.
3. Mathematical Model
3.1. Supplier–Retailer Relationship Modes
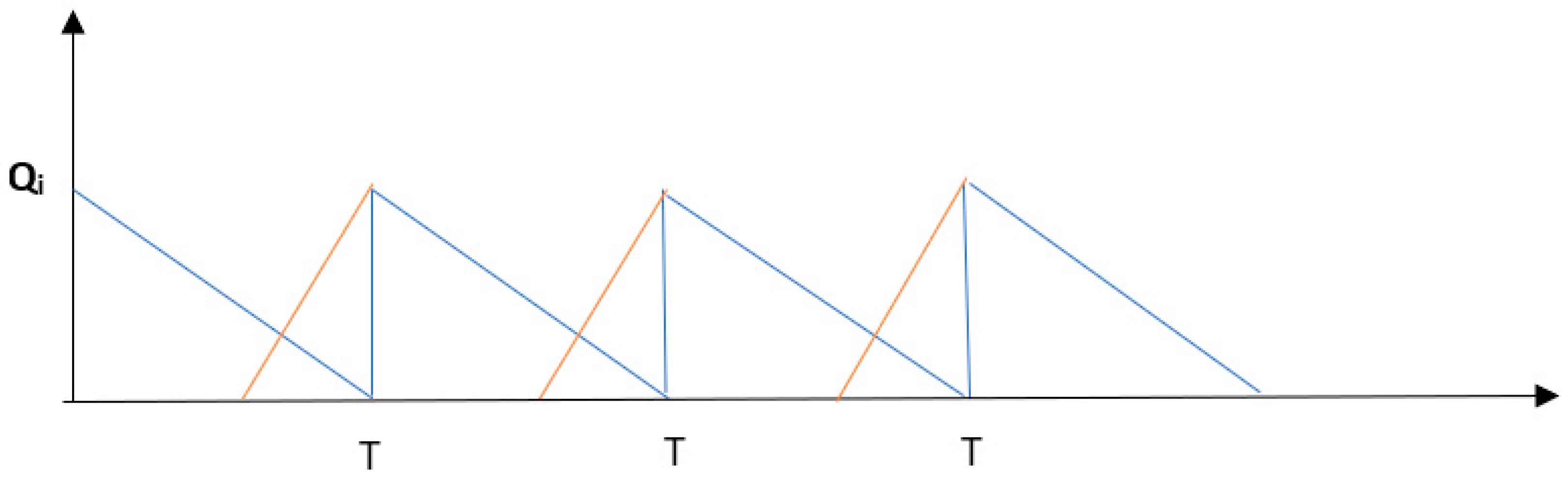
3.1.1. Equal Production and Consumption
3.1.2. Two Productions Per One Consumption
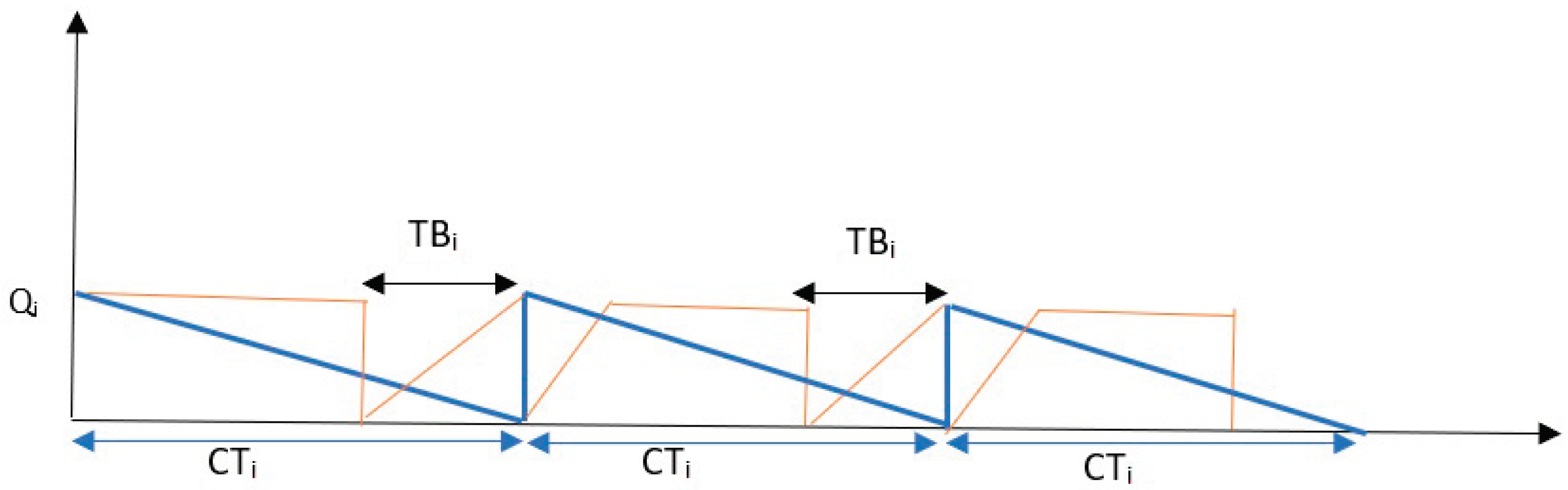
3.1.3. B Deliveries Per n Production Cycles of Q-Product Batches
(fixed + storage) (fixed + storage)
4. Computational Instances and Data Analysis
4.1. Theory Analysis
4.2. Numerical Scenario
5. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sales-Navarro, K.; Romero-Montes, M.; Acevedo-chedid, J.; Ospina-Mateus, H.; Florez, W.; Cardenas-Barron, L.E. Vendor managed inventory system considering deteriorating items and probabilistic demand for a three-layer supply chain. Expert. Syst. Appl. 2023, 218, 119608. [Google Scholar] [CrossRef]
- Berghman, L.; Kergosien, Y.; Billaut, J. A review on integrated scheduling and outbound vehicle routing problems. Eur. J. Oper. Res. 2023, 311, 1–23. [Google Scholar] [CrossRef]
- Ganji, M.; Kazemipoor, H.; Molana, S.M.H.; Sajadi, S.M. A green multi-objective integrated scheduling of production and distribution with heterogeneous fleet vehicle routing and time windows. J. Clean. Prod. 2020, 259, 120824. [Google Scholar] [CrossRef]
- Sabzevari, M.; Sajadi, S.M.; Molana, S.M.H. Supply chain Reconfiguration for a New Product Development with Risk Management Approach. Int. J. Sci. Technol. Sci. Iran. 2019, 27, 2108–2126. [Google Scholar] [CrossRef]
- Amelian, S.S.; Sajadi, S.M.; Navabakhsh, M.; Esmaelian, M. Multi-objective optimization for stochastic failure-prone job shop scheduling problem via hybrid of NSGA-II and simulation method. WILEY Expert. Syst. 2019, 39, e12455. [Google Scholar] [CrossRef]
- Pasandideh, S.H.R.; Niaki, S.T.A. Optimizing the Economic Production Quantity model with discrete delivery orders. J. Econ. Comput. 2010, 44, 49–62. [Google Scholar]
- Nobil, A.H.; Niaki, S.T.A.; Nobil, E. An Effective and simple algorithm to solve the discrete multi-product economic production quantity model. Econ. Comput. Econ. Cybern. Stud. Res. 2017, 51, 252. [Google Scholar]
- Afghah, M.; Sajadi, S.M.; Razavi, S.M.; Taghizadeh-Yazdi, M. Hard dimensions evaluation in sustainable supply chain management for environmentally adaptive and mitigated adverse eco-effect environmental policies. Bus. Strategy Environ. 2023, 32, 5044–5067. [Google Scholar] [CrossRef]
- Shokouhifar, M.; Sohrabi, M.; Rabbani, M.; Molana, S.M.H.; Werner, F. Sustainable Phosphorus Fertilizer Supply Chain Management to Improve Crop Yield and P Use Efficiency Using an Ensemble Heuristic–Metaheuristic Optimization Algorithm. Agronomy 2023, 13, 565. [Google Scholar] [CrossRef]
- Shokouhifar, M. Fuzzy heuristic-based ant colony optimization for joint virtual network function placement and routing. Appl. Soft Comput. 2021, 107, 107401. [Google Scholar] [CrossRef]
- Shaabani, H.; Hoff, A.; Hvattum, L.M.; Laporte, G. A matheuristic for the multi-product maritime inventory routing problem. Comput. Oper. Res. 2023, 154, 106214. [Google Scholar] [CrossRef]
- Ganji, M.; Rabet, R.; Sajadi, S.M. A new coordinating model for green supply chain and batch delivery scheduling with satisfaction customers. Environ. Dev. Sustain. 2021, 24, 4566–4601. [Google Scholar] [CrossRef]
- Viswanthan, S. Optimal strategy for the integrated vendor-buyer inventory model. Eur. J. Oper. Res. 1998, 105, 38–42. [Google Scholar] [CrossRef]
- Sajadi, S.M.; Kashan, A.H.; Khaledan, S. A new approach for permutation flow-shop scheduling problem using league championship algorithm. In Proceedings of the CIE44 and IMSS, Istanbul, Turkey, 14–16 October 2014. [Google Scholar]
- Hatami-Marbini, A.; Varzgani, N.; Sajadi, S.M.; Kamali, A. An emergency medical services system design using mathematical modeling and simulation-based optimization approaches. Decis. Anal. J. 2022, 3, 100059. [Google Scholar] [CrossRef]
- Pasandideh, S.H.R.; Niaki, S.T.A. A genetic algorithm approach to optimize a multi-products EPQ model with discrete delivery orders and constrained space. Appl. Math. Comput. 2008, 195, 506–514. [Google Scholar] [CrossRef]
- Amelian, S.; Sajadi, S.M.; Alinaghian, M. Optimal production and preventive maintenance rate in a failure-prone manufacturing system using discrete event simulation. Int. J. Ind. Syst. Eng. 2015, 20, 483–496. [Google Scholar] [CrossRef]
- Widyadana, G.A.; Wee, H.M. A multi-products EPQ model with discrete delivery order: A lagrangean solution approach. In Global Perspective for Competitve Enterprise, Economy and Ecology; Springer: London, UK, 2009. [Google Scholar]
- Pasandideh, S.H.R.; Niaki, S.T.A.; Yeganeh, J.A. A parameter-tuned genetic algorithm for multi-product economic production quantity model with space constraint, discrete delivery orders and shortages. Adv. Eng. Softw. 2009, 41, 306–314. [Google Scholar] [CrossRef]
- Taleizadeh, A.A.; Widyadana, G.A.; Wee, H.M.; Biabani, J. Multi products single machine economic production quantity model with multiple batch size. Int. J. Ind. Eng. Comput. 2011, 2, 213–224. [Google Scholar] [CrossRef]
- Rad, M.H.; Sajadi, S.M.; Tavakoli, M.M. The efficiency analysis of a manufacturing system by TOPSIS technique and simulation. Int. J. Ind. Syst. Eng. 2014, 18, 222–236. [Google Scholar] [CrossRef]
- Sajadi, S.M.; Alizadeh, A.; Zandieh, M.; Tavan, F. Robust and stable flexible job shop scheduling with random machine breakdowns: Multi-objectives genetic algorithm approach. Int. J. Math. Oper. Res. 2019, 132, 279–291. [Google Scholar] [CrossRef]
- Cárdenas-Barrón, L.E.; Treviño-Garza, G.; Wee, H.M. A simple and better algorithm to solve the vendor managed inventory control system of multi-product multi-constraint economic order quantity model. Expert. Syst. Appl. 2012, 39, 3888–3895. [Google Scholar] [CrossRef]
- Jha, J.K.; Shanker, K. Single-vendor multi-buyer integrated production-inventory model with controllable lead time and service level constraints. Appl. Math. Model. 2013, 37, 1753–1767. [Google Scholar] [CrossRef]
- Cárdenas-Barrón, L.E.; Treviño-Garza, G.; Widyadana, G.A.; Wee, H.M. A constrained multi-products EPQ inventory model with discrete delivery order and lotsize. Appl. Math. Comput. 2014, 230, 359–370. [Google Scholar]
- Ziaei, M.; Sajadi, S.M.; Tavakoli, M.M. The performance improvement of water pump manufacturing system via multi-criteria decision-making and simulation (a case study: Iran Godakht Company). Int. J. Product. Qual. Manag. 2016, 17, 1–15. [Google Scholar] [CrossRef]
- Sanej, K.D.; Zareh, M.E.; Moghadam, R.T.; Sajadi, S.M.; Sadjadi, S.J. Solving a new robust reverse job shop scheduling problem by meta-heuristic algorithms. Eng. Appl. Artif. Intell. 2021, 101, 104207. [Google Scholar] [CrossRef]
- Glock, C.H.; Kim, T. Shipment consolidation in a multiple-vendor single-buyer integrated inventory model. Comput. Ind. Eng. 2014, 70, 31–42. [Google Scholar] [CrossRef]
- Aiassi, R.; Sajadi, S.M.; Molana, S.M.H.; Babgohari, A.Z. Designing a stochastic multi-objective simulation-based optimization model for sales and operations planning in built-to-order environment with uncertain distant outsourcing. Simul. Model. Pract. Theory 2020, 104, 102103. [Google Scholar] [CrossRef]
- Rabbani, M.; Molana, S.M.H.; Sajadi, S.M.; Davoodi, M.H. Sustainable fertilizer supply chain network design using evolutionary-based resilient robust stochastic programming. Comput. Ind. Eng. 2022, 174, 108770. [Google Scholar] [CrossRef]
- Nobil, A.H.; Seifbarghy, M.; Sedigh, A.H.A.; Pishva, D. Considering discrete delivery ordering and shipment consolidation in a three-echelon supply chain with failure. Int. J. Adv. Oper. Manag. 2016, 8, 247–275. [Google Scholar] [CrossRef]
- Shafiee-Gol, S.; Nasiri, M.M.; Taleizadeh, A.A. Pricing and Production decision in multi-product single machine manufacturing system with discrete delivery and rework. Oper. Res. Soc. India 2016, 53, 873–888. [Google Scholar] [CrossRef]
- Malekpour, H.; Sajadi, S.M.; Vahdani, H. Using discrete-event simulation and the Taguchi method for optimizing the production rate of network failure-prone manufacturing systems with perishable goods. Int. J. Serv. Oper. Manag. 2016, 23, 387–406. [Google Scholar]
- Marbini, A.H.; Sajadi, S.M.; Malekpour, H. Optimal control and simulation for production planning of network failureprone manufacturing systems with perishable goods. Comput. Ind. Eng. 2020, 146, 106614. [Google Scholar] [CrossRef]
- Amelian, S.S.; Sajadi, S.M.; Navabakhsh, M.; Esmaelian, M. Multi-objective optimization of stochastic failure-prone manufacturing system with consideration of energy consumption and job sequences. Int. J. Environ. Sci. Technol. 2018, 16, 3389–3402. [Google Scholar] [CrossRef]
- Afzalabadi, M.; Haji, A.; Haji, R. Vendor’s optimal inventory policy with dynamic and discrete demands in an infinit time horizon. Comput. Ind. Eng. 2016, 102, 368–373. [Google Scholar] [CrossRef]
- Zandieh, M.; Sajadi, S.M.; Behnoud, R. Integrated production scheduling and maintenance planning in a hybrid flow shop system: A multi-objective approach. Int. J. Syst. Assur. Eng. Manag. 2017, 8, 1630–1642. [Google Scholar] [CrossRef]
- Sajadi, S.M.; Esfahani, M.M.S.; Sorensen, K. Production control in a failure-prone manufacturing network using discrete event simulation and automated response surface methodology. Int. J. Adv. Manuf. Technol. 2011, 53, 35–46. [Google Scholar] [CrossRef]
- Seifbarghy, M.; Kalani, M.M.; Hemmati, M. A discrete particle swarm optimization algorithm with local search for a production-based two-echelon single-vendor multiple-buyer supply chain. J. Ind. Eng. Int. 2016, 12, 29–43. [Google Scholar] [CrossRef]
- Nobil, A.H.; Sedigh, A.H.A.; Cárdenas-Barrón, L.E. A multi-product single machine economic production quantity (EPQ) inventory model with discrete delivery order, joint production policy and budget constraints. Ann. Oper. Res. 2017, 286, 265–301. [Google Scholar] [CrossRef]
- Nobil, A.H.; Nobil, E.; Cárdenas-Barrón, L.E. Some observations to:lot sizing with Non-zero setup time for rework. Int. J. Appl. Comput. Math. 2017, 3, 1511–1517. [Google Scholar] [CrossRef]
- Jonrinaldi, J.; Rahman, T.; Henmaidi, H.; Wirdianto, E.; Zhang, D.Z. A multiple items EPQ/EOQ model for a vendor and multiple buyers system with considering continuous and discrete demand simultaneously. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: New York, NY, USA, 2018. [Google Scholar]
- Amiri, S.A.H.S.; Zahedi, A.; Kazemi, M.; Soroor, J.; Keshteli, M.H. Determination of the optimal sales level of perishable goods in a two-echelons supply chain network. Comput. Ind. Eng. 2020, 139, 106156. [Google Scholar] [CrossRef]
- Afshar-Bakeshloo, M.B.; Bozorgi-Amiri, A.; Sajadi, S.M.; Jolai, F. A multi-objective Environmental Hedging Point Policy with customer satisfaction criteria. J. Clean. Prod. 2018, 179, 478–494. [Google Scholar] [CrossRef]

| Symbol | Description |
|---|---|
| Indices | |
| i | Number of products |
| Decision variables | |
| Qi | Quantity of product i delivered to a retailer |
| ni | Factor number of Qi products per each production cycle |
| Ni | Number of setup times to manufacture product i |
| Parameters | |
| Production rate of product i | |
| Demand for product i | |
| Cost of each time product i starts being manufactured | |
| Cost of each time product i is delivered to a retailer | |
| Time it takes to manufacture | |
| Time it takes to manufacture a batch of Qi products | |
| Time of rest period after manufacturing | |
| Time it takes to consume a batch of Qi products | |
| Total time of a production cycle and a rest period | |
| Cost of storing product i at manufacturer’s warehouse | |
| Cost of storing product i at retailers’ warehouse | |
| B | Number of breaks in the production |
| Scenario No. | Parameters | |||||
|---|---|---|---|---|---|---|
| 1 | Hmi = 1 | Ai = 20 | Hri = 5 | Ci = 10 | Ri = 4000 | Di = 1000 |
| Min TC = 470 | Ni = 6 | ni = 2 | ||||
| 2 | Hmi = 1 | Ai = 20 | Hri = 5 | Ci = 10 | Ri = 12,000 | Di = 3000 |
| Min TC = 813 | Ni = 10 | ni = 2 | ||||
| 3 | Hmi = 1 | Ai = 20 | Hri = 5 | Ci = 10 | Ri = 15,000 | Di = 6000 |
| Min TC = 1140 | Ni = | ni = 4 | ||||
| 4 | Hmi = 2.5 | Ai = 20 | Hri = 5 | Ci = 10 | Ri = 4000 | Di = 1000 |
| Min TC = 502 | Ni = 6 | ni = 2 | ||||
| 5 | Hmi = 2.5 | Ai = 20 | Hri = 5 | Ci = 10 | Ri = 12,000 | Di = 3000 |
| Min TC = 867 | Ni = 11 | ni = 2 | ||||
| 6 | Hmi = 2.5 | Ai = 20 | Hri = 5 | Ci = 10 | Ri = 15,000 | Di = 6000 |
| Min TC = 1226 | Ni = 15 | ni = 2 | ||||
| 7 | Hmi = 1 | Ai = 15 | Hri = 5 | Ci = 10 | Ri = 4000 | Di = 1000 |
| Min TC = 440 | Ni = 6 | ni = 2 | ||||
| 8 | Hmi = 1 | Ai = 15 | Hri = 5 | Ci = 10 | Ri = 12,000 | Di = 3000 |
| Min TC = 761 | Ni = 11 | ni = 2 | ||||
| 9 | Hmi = 1 | Ai = 15 | Hri = 5 | Ci = 10 | Ri = 15,000 | Di = 6000 |
| Min TC = 1076 | Ni = | ni = 2 | ||||
| 10 | Hmi = 1 | Ai = 20 | Hri = 5 | Ci = 8 | Ri = 4000 | Di = 1000 |
| Min TC = 442 | Ni = 4 | ni = 4 | ||||
| 11 | Hmi = 1 | Ai = 20 | Hri = 5 | Ci = 8 | Ri = 12,000 | Di = 3000 |
| Min TC = 766 | Ni = 7 | ni = 4 | ||||
| 12 | Hmi = 1 | Ai = 20 | Hri = 5 | Ci = 8 | Ri = 15,000 | Di = 6000 |
| Min TC = 1060 | Ni = | ni = | ||||
| Scenario No. | Parameters | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Hm1 | Hm2 | A1 | A2 | Hr1 | Hr2 | C1 | C2 | R1 | R2 | D1 | D2 |
| 1 | 2.5 | 20 | 15 | 5 | 5 | 10 | 8 | 4000 | 12,000 | 1000 | 3000 | |
| MinTC1 = 513 | N1 = 9 | n1 = 2 | ||||||||||
| MinTC2 = 801 | N2 = 9 | n2 = 2 | ||||||||||
| 2 | Hm1 | Hm2 | A1 | A2 | Hr1 | Hr2 | C1 | C2 | R1 | R2 | D1 | D2 |
| 1 | 2.5 | 20 | 15 | 5 | 5 | 10 | 8 | 12,000 | 15,000 | 3000 | 6000 | |
| MinTC1 = 726 | N1 = 15 | n1 = 2 | ||||||||||
| MinTC2 = 1091 | N2 = 15 | n2 = 2 | ||||||||||
| 3 | Hm1 | Hm2 | A1 | A2 | Hr1 | Hr2 | C1 | C2 | R1 | R2 | D1 | D2 |
| 1 | 2.5 | 20 | 15 | 5 | 5 | 3 | 2.5 | 4000 | 12,000 | 1000 | 3000 | |
| MinTC1 = 412,427 | N1 = 11, 12 | n1 = 2 | ||||||||||
| MinTC2 = 647,632 | N2 = 11, 12 | n2 = 2 | ||||||||||
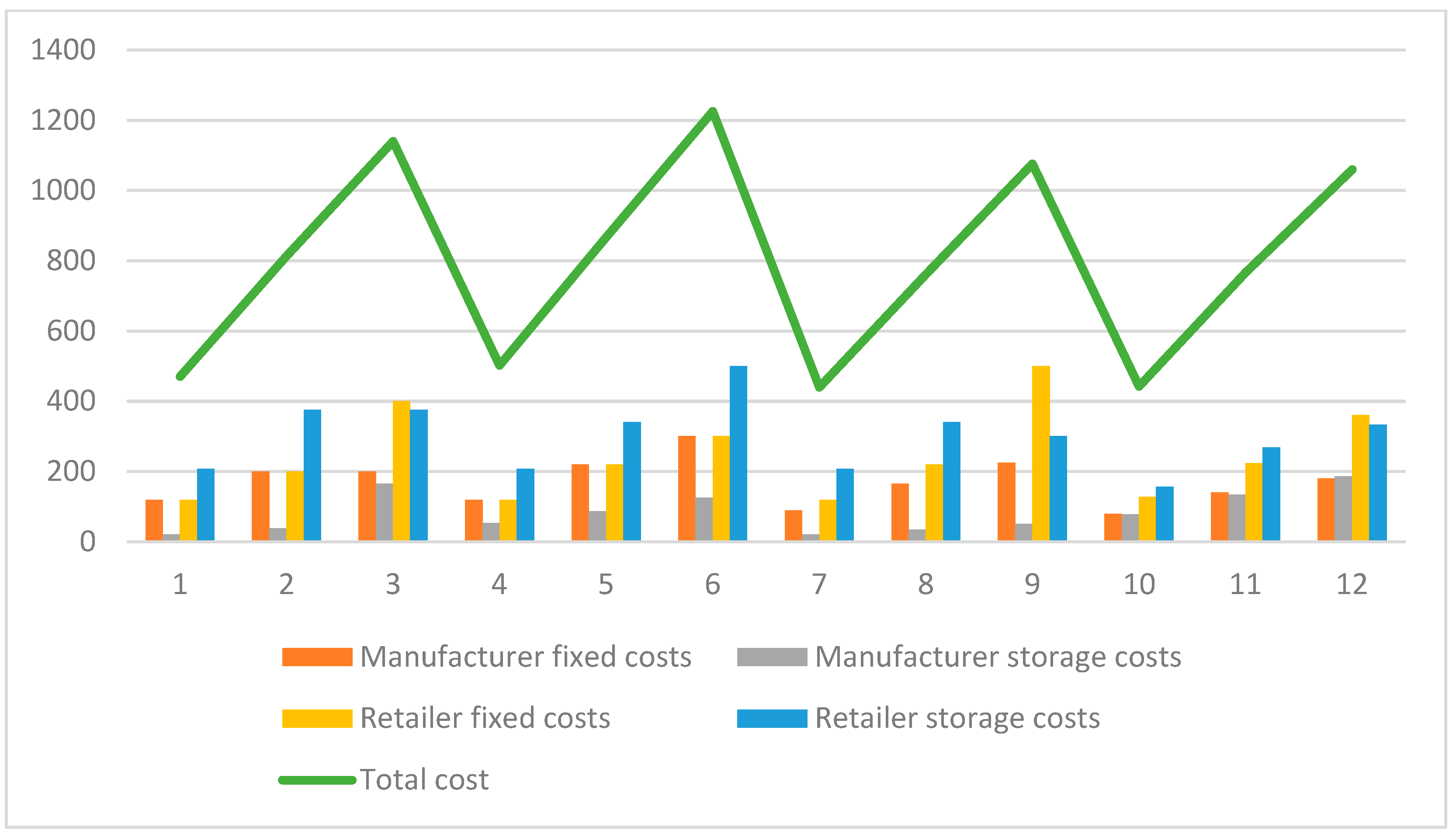
| Scenario No. | Manufacturer Fixed Costs | Manufacturer Storage Costs | Retailer Fixed Costs | Retailer Storage Costs | Total Cost |
|---|---|---|---|---|---|
| 1 | 120 | 21.3333 | 120 | 208.3333 | 470 |
| 2 | 200 | 38 | 200 | 375 | 813 |
| 3 | 200 | 165 | 400 | 375 | 1140 |
| 4 | 120 | 53.3333 | 120 | 208.3333 | 502 |
| 5 | 220 | 86.4773 | 220 | 340.9091 | 867 |
| 6 | 300 | 126.25 | 300 | 500 | 1226 |
| 7 | 90 | 21.3333 | 120 | 208.3333 | 440 |
| 8 | 165 | 34.5909 | 220 | 340.9091 | 761 |
| 9 | 225 | 50.5 | 500 | 300 | 1076 |
| 10 | 80 | 78.125 | 128 | 156.25 | 442 |
| 11 | 140 | 133.9286 | 224 | 267.8571 | 766 |
| 12 | 180 | 186.6667 | 360 | 333.3333 | 1060 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tajik, M.; Hajimolana, S.M.; Daneshvar Kakhki, M. Production Planning Optimization in a Two-Echelon Multi-Product Supply Chain with Discrete Delivery and Storage at Manufacturer’s Warehouse. Mathematics 2024, 12, 1986. https://doi.org/10.3390/math12131986
Tajik M, Hajimolana SM, Daneshvar Kakhki M. Production Planning Optimization in a Two-Echelon Multi-Product Supply Chain with Discrete Delivery and Storage at Manufacturer’s Warehouse. Mathematics. 2024; 12(13):1986. https://doi.org/10.3390/math12131986
Chicago/Turabian StyleTajik, Maedeh, Seyed Mohammad Hajimolana, and Mohammad Daneshvar Kakhki. 2024. "Production Planning Optimization in a Two-Echelon Multi-Product Supply Chain with Discrete Delivery and Storage at Manufacturer’s Warehouse" Mathematics 12, no. 13: 1986. https://doi.org/10.3390/math12131986
APA StyleTajik, M., Hajimolana, S. M., & Daneshvar Kakhki, M. (2024). Production Planning Optimization in a Two-Echelon Multi-Product Supply Chain with Discrete Delivery and Storage at Manufacturer’s Warehouse. Mathematics, 12(13), 1986. https://doi.org/10.3390/math12131986






