Exponential Synchronization of Coupled Neural Networks with Hybrid Delays and Stochastic Distributed Delayed Impulses
Abstract
:1. Introduction
- (1)
- Different from the deterministic distributed delayed impulses in the literature [26,27,28,29,30,31], in this paper, the intensities of distributed delayed impulses are supposed to be random. Two types of stochastic impulses including stochastic distributed delayed impulses with independent property and Markov property have been explored, respectively.
- (2)
- Based on the average impulsive interval method, total probability formula and ergodic theory, two novel impulsive Halanay differential inequalities are established, which generalize the findings in the literature [34,35] since time-varying delays, distributed delays and stochastic distributed delayed impulses are introduced simultaneously. Parameter c can be arbitrarily chosen. In view of invariant distribution theory, the stochastic impulses with Markov property are tackled.
- (3)
- By utilizing the established inequalities and graph theory, some criteria for exponential synchronization of CNNs with stochastic distributed delayed impulses are derived. In [36], impulses can only be regarded as outer disturbances for coupled inertial NNs with hybrid delays. Compared with the work [36], in this paper, impulses may also be viewed as outer perturbations or stabilizing sources, and the case of stochastic impulses with Markov property is also discussed.
2. Preliminaries
3. Main Results
- (i)
- , where , , , , , and .
- (ii)
- , where , , , , and is the unique solution of .
- (i)
- , where , , , , , and ;
- (ii)
- , where , , , , , , , is a sufficient small positive constant and is the unique solution of ;
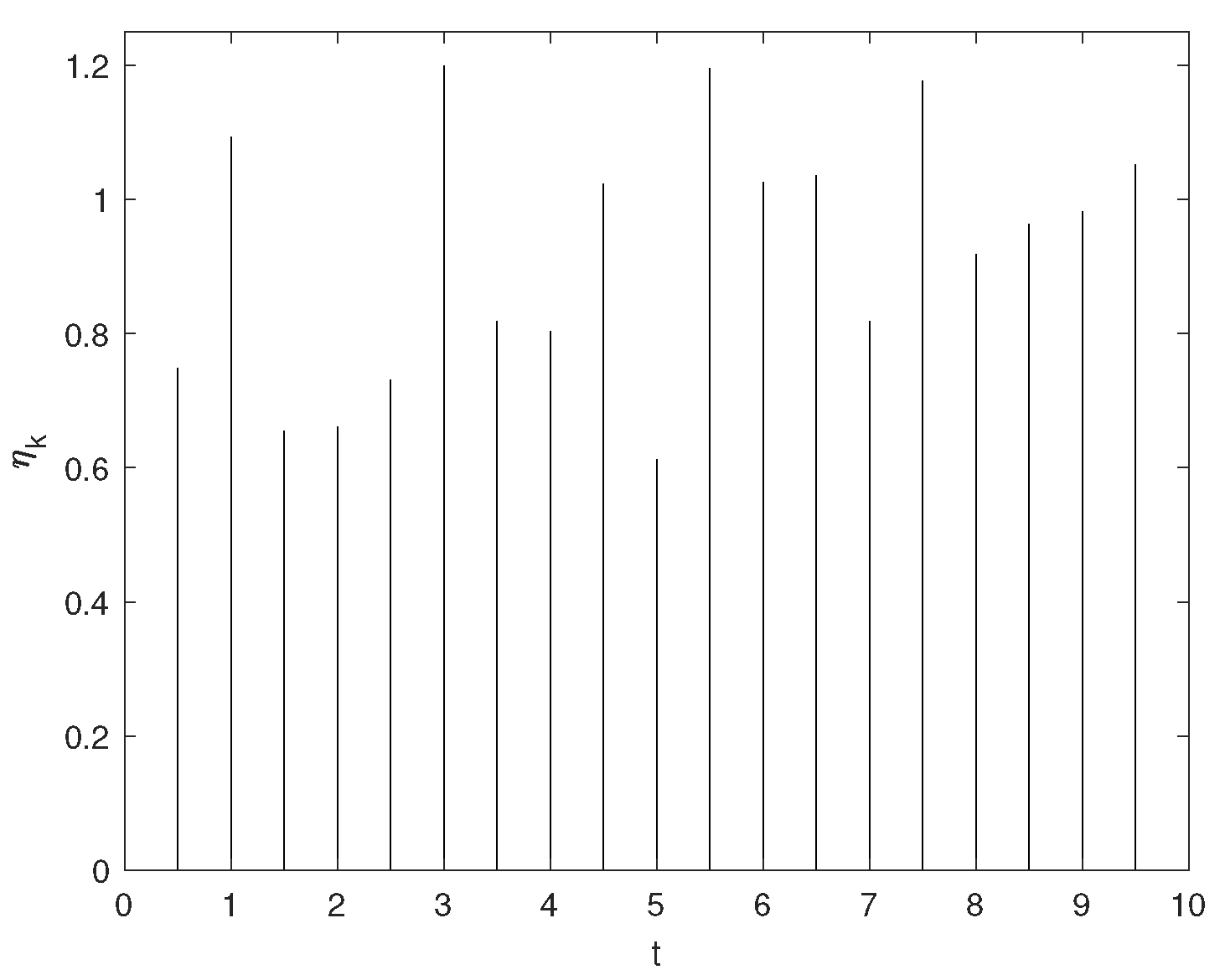
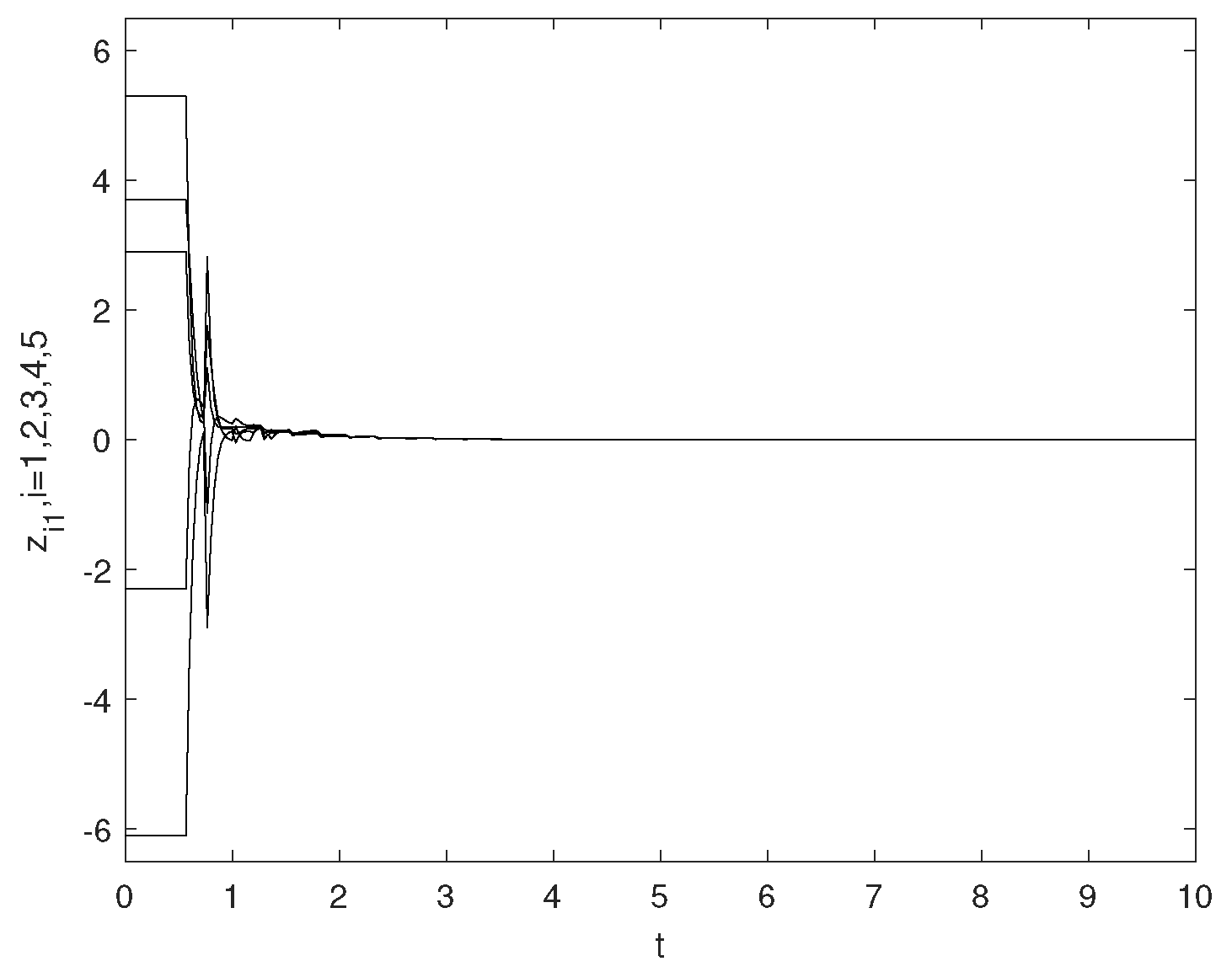
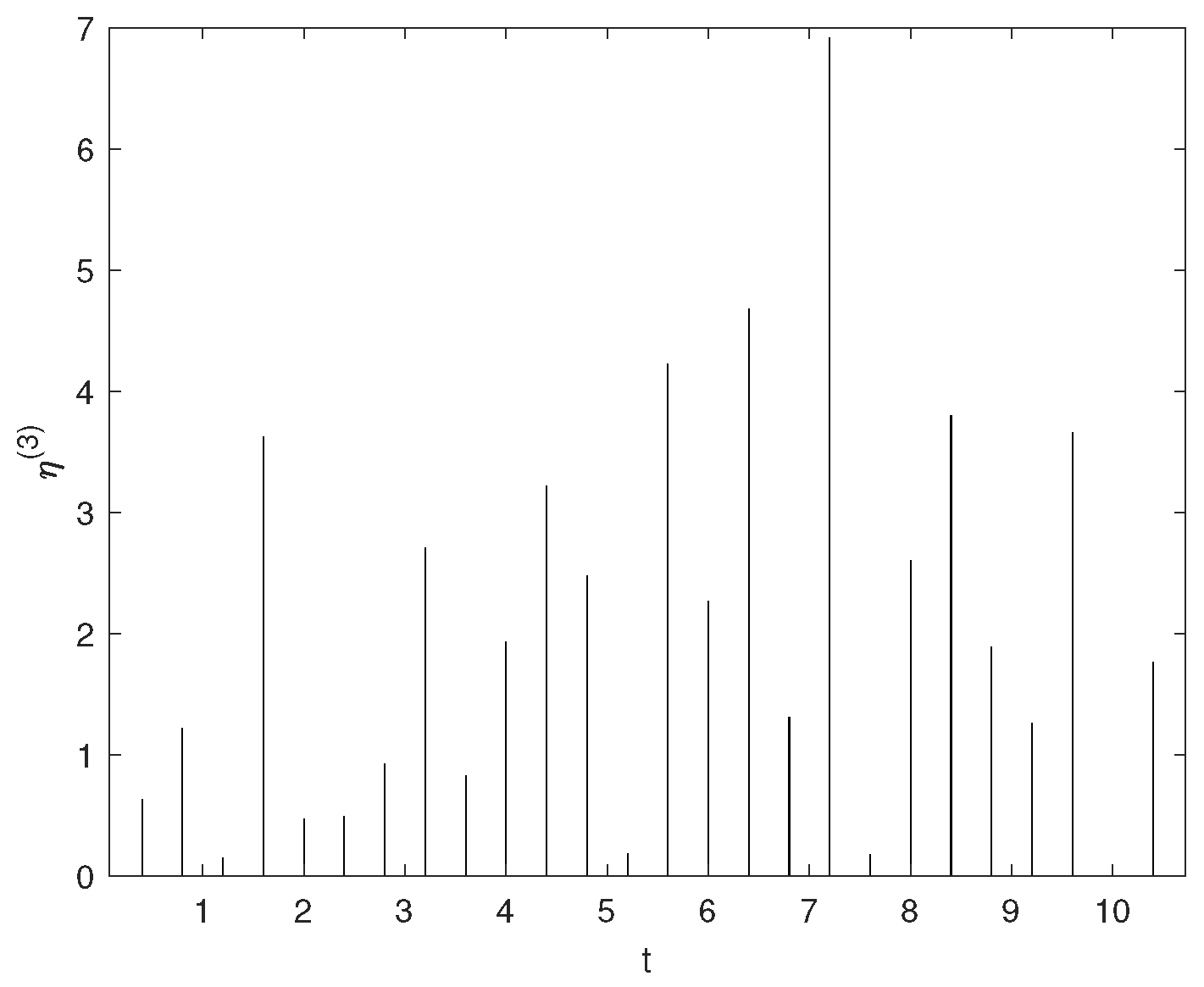
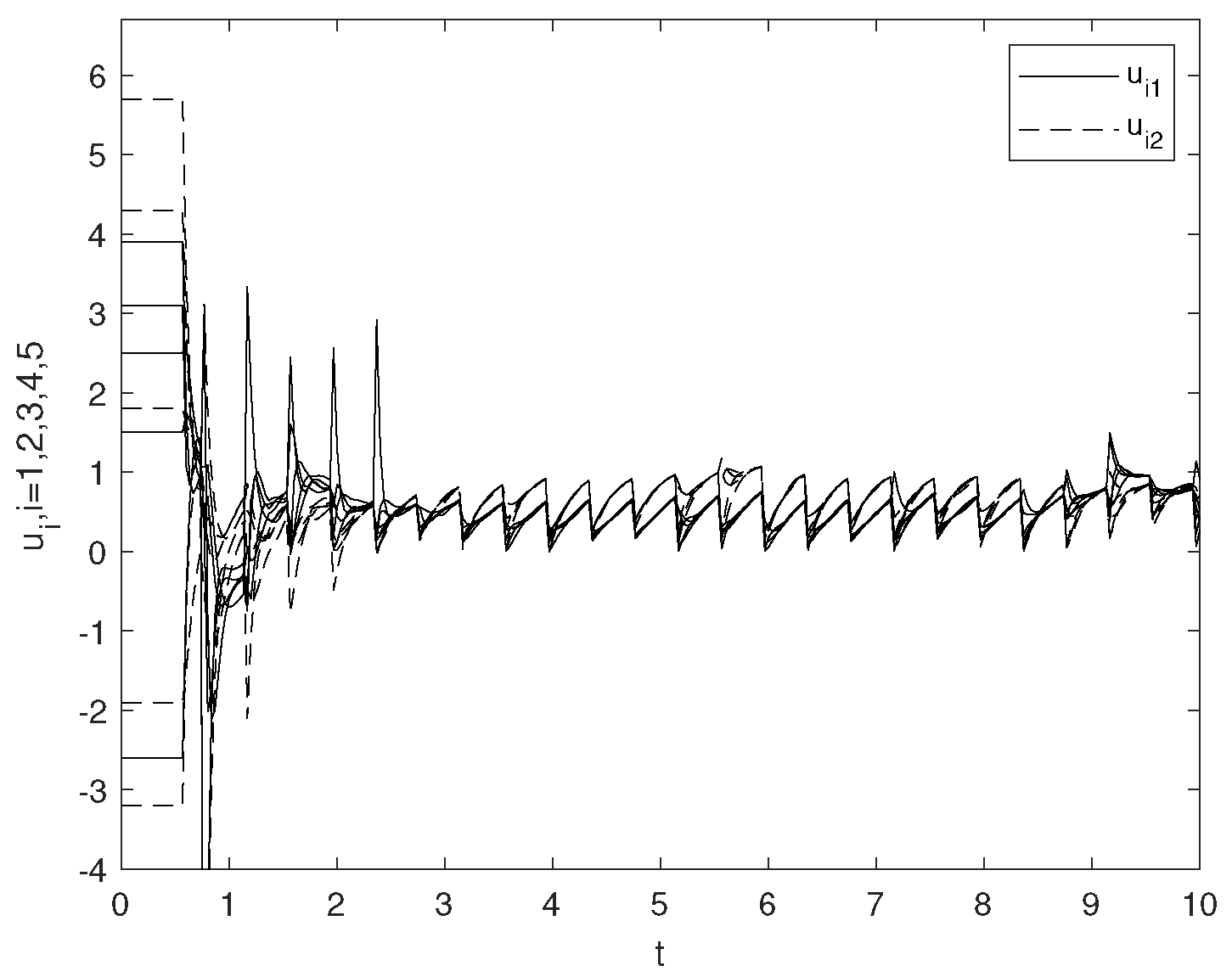
4. Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nishio, Y.; Ushida, A. Spatio-temporal chaos in simple coupled chaotic circuits. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1995, 42, 678–686. [Google Scholar] [CrossRef]
- Perez-Munuzuri, V.; Perez-Villar, V.; Chua, O.L. Autowaves for image processing on a two-dimensional CNN array of excitable nonlinear circuits:Flat and wrinkled labyrinths. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1993, 40, 174–181. [Google Scholar] [CrossRef]
- Xiu, R.; Zhang, W.; Zhou, Z. Synchronization issue of coupled neural networks based on flexible impulse control. Neural Netw. 2022, 149, 57–65. [Google Scholar] [CrossRef] [PubMed]
- Mao, X.; Wang, Z. Stability switches and bifurcation in a system of four coupled neural networks with multiple time delays. Nonlinear Dyn. 2015, 82, 1551–1567. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821–824. [Google Scholar] [CrossRef] [PubMed]
- Liang, J.; Wang, Z.; Liu, Y.; Liu, X. Robust synchronization of an array of coupled stochastic discrete-time delayed neural networks. IEEE Trans. Neural Netw. 2008, 19, 1910–1921. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.L.; Wu, H.N.; Huang, T. Pinning control strategies for synchronization of linearly coupled neural networks with reaction-diffusion terms. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 749–761. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Shi, P.; Lim, C.C. Exponential synchronization for Markovian stochastic coupled neural networks of neutral-type via adaptive feedback control. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 1618–1632. [Google Scholar] [CrossRef]
- Wen, S.; Zeng, Z.; Chen, M.Z.Q.; Huang, T. Synchronization of switched neural networks with communication delays via the event-triggered control. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2334–2343. [Google Scholar] [CrossRef]
- Gao, C.; Wang, Z.; He, X.; Yue, D. Sampled-data-based fault-tolerant consensus control for multi-agent systems: A data privacy preserving scheme. Automatica 2021, 133, 109–847. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, J. Exponential synchronization for delayed coupled systems on networks via graph-theoretic method and periodically intermittent control. Phys. A 2020, 545, 123–733. [Google Scholar] [CrossRef]
- Zhang, G.; Xia, Y.; Li, X.; He, S. Multievent-triggered sliding-Mode control for a class of complex dynamic network. IEEE Trans. Control Netw. Syst. 2022, 9, 835–844. [Google Scholar] [CrossRef]
- Fan, H.; Rao, Y.; Shi, K.; Wen, H. Global synchronization of fractional-order multi-delay coupled neural networks with multi-link complicated structures via hybrid impulsive control. Mathematics 2023, 11, 3051. [Google Scholar] [CrossRef]
- Rao, R.; Zhu, Q. Synchronization for reaction–diffusion switched delayed feedback epidemic systems via impulsive control. Mathematics 2024, 12, 447. [Google Scholar] [CrossRef]
- Xiao, Q.; Liu, H.; Wang, Y. An improved finite-time and fixed-time stable synchronization of coupled discontinuous neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 3516–3526. [Google Scholar] [CrossRef]
- Li, P.; Cao, J.; Wang, Z. Robust impulsive synchronization of coupled delayed neural networks with uncertainties. Phys. A 2007, 373, 261–272. [Google Scholar] [CrossRef]
- Lu, J.; Ho, D.W.; Cao, J.; Kurths, J. Exponential synchronization of linearly coupled neural networks with impulsive disturbances. IEEE Trans. Neural Netw. 2011, 22, 329–335. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Li, X.; Song, S. Finite-time synchronization for delayed complex dynamical networks with synchronizing or desynchronizing impulses. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 736–746. [Google Scholar] [CrossRef]
- Wang, N.; Li, X.; Lu, J.; Alsaadi, F.E. Unified synchronization criteria in an array of coupled neural networks with hybrid impulses. Neural Netw. 2018, 101, 25–32. [Google Scholar] [CrossRef]
- Xu, H.; Zhu, Q.; Zheng, W.X. Exponential stability of stochastic nonlinear delay systems subject to multiple periodic impulses. IEEE Trans. Autom. Control 2023, 69, 2621–2628. [Google Scholar] [CrossRef]
- Hu, W.; Zhu, Q.; Karimi, H.R. Some improved Razumikhin stability criteria for impulsive stochastic delay differential systems. IEEE Trans. Autom. Control 2019, 64, 5207–5213. [Google Scholar] [CrossRef]
- Li, X.; Wu, J. Stability of nonlinear differential systems with state-dependent delayed impulses. Automatica 2016, 64, 63–69. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, K. Synchronization of linear dynamical networks on time scales: Pinning control via delayed impulses. Automatica 2016, 72, 147–152. [Google Scholar] [CrossRef]
- Huang, Z.; Cao, J.; Li, J.; Bin, H. Quasi-synchronization of neural networks with parameter mismatches and delayed impulsive controller on time scales. Nonlinear Anal. Hybri. 2019, 33, 104–115. [Google Scholar] [CrossRef]
- Gao, K.; Lu, J.; Zheng, W.X.; Chen, X. Synchronization in coupled neural networks with hybrid delayed impulses: Average impulsive delay-gain method. IEEE Trans. Neural Netw. Learn. Syst. 2024; in press. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, K. Stabilization of nonlinear time-delay systems: Distributed-delay dependent impulsive control. Syst. Control Lett. 2018, 120, 17–22. [Google Scholar] [CrossRef]
- Xu, Z.; Peng, D.; Li, X. Synchronization of chaotic neural networks with time delay via distributed delayed impulsive control. Neural Netw. 2019, 118, 332–337. [Google Scholar] [CrossRef]
- Zhang, X.; Li, C.; Li, H.; Cao, Z. Synchronization of uncertain coupled neural networks with time-varying delay of unknown bound via distributed delayed impulsive control. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 3624–3635. [Google Scholar] [CrossRef] [PubMed]
- Fang, Q.; Wang, M.; Li, X. Event-triggered distributed delayed impulsive control for nonlinear systems with applications to complex networks. Chaos Soliton Fract. 2023, 175, 113–943. [Google Scholar] [CrossRef]
- Hu, W.; Zhu, Q. Stability criteria for impulsive stochastic functional differential systems with distributed-delay dependent impulsive effects. IEEE Trans. Syst. Man, Cybern. 2021, 51, 2027–2032. [Google Scholar] [CrossRef]
- Li, J.; Zhu, Q. Stability of neutral stochastic delayed systems with switching and distributed-delay dependent impulses. Nonlinear Anal. Hybri. 2023, 47, 101–279. [Google Scholar] [CrossRef]
- Tang, Y.; Wu, X.; Shi, P.; Qian, F. Input-to-state stability for nonlinear systems with stochastic impulses. Automatica 2020, 113, 108–766. [Google Scholar] [CrossRef]
- Liu, J.; Zhu, Q. Finite time stability of time-varying stochastic nonlinear systems with random impulses. Int. J. Control 2023. [Google Scholar] [CrossRef]
- Sun, Y.; Li, L.; Liu, X. Exponential synchronization of neural networks with time-varying delays and stochastic impulses. Neural Netw. 2020, 132, 342–352. [Google Scholar] [CrossRef]
- Cui, Q.; Li, L.; Cao, J. Stability of inertial delayed neural networks with stochastic delayed impulses via matrix measure method. Neurocomputing 2022, 471, 70–78. [Google Scholar] [CrossRef]
- Li, L.; Cui, Q.; Cao, J.; Qiu, J.; Sun, Y. Exponential synchronization of coupled inertial neural networks with hybrid delays and stochastic impulses. IEEE Trans. Neural Netw. Learn. Syst. 2023; in press. [Google Scholar] [CrossRef]
- Ling, G.; Liu, X.; Guan, Z.H.; Ge, M.F.; Tong, Y.H. Input-to-state stability for switched stochastic nonlinear systems with mode-dependent random impulses. Inf. Sci. 2022, 596, 588–607. [Google Scholar] [CrossRef]
- Zhang, N.; Huang, S.; Li, W. Stability of stochastic delayed semi-Markov jump systems with stochastic mixed impulses: A novel stochastic impulsive differential inequality. J. Franklin Inst. Eng. Appl. Math. 2022, 359, 10785–10812. [Google Scholar] [CrossRef]
- Ross, S.M. Stochastic Processes; John Wiley & Sons: New York, NY, USA, 1996. [Google Scholar]
- Lu, J.; Ho, D.W.C.; Cao, J. A unified synchronization criterion for impulsive dynamical networks. Automatica 2010, 46, 1215–1221. [Google Scholar] [CrossRef]
- Dong, S.; Shi, K.; Wen, S.; Shen, Y.; Zhong, S. Almost surely synchronization of directed coupled neural networks via stochastic distributed delayed impulsive control. Chaos Soliton Fract. 2023, 174, 113–742. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Song, Y.; Liu, X. Exponential Synchronization of Coupled Neural Networks with Hybrid Delays and Stochastic Distributed Delayed Impulses. Mathematics 2024, 12, 1995. https://doi.org/10.3390/math12131995
Zhang G, Song Y, Liu X. Exponential Synchronization of Coupled Neural Networks with Hybrid Delays and Stochastic Distributed Delayed Impulses. Mathematics. 2024; 12(13):1995. https://doi.org/10.3390/math12131995
Chicago/Turabian StyleZhang, Gang, Yinfang Song, and Xiaoyou Liu. 2024. "Exponential Synchronization of Coupled Neural Networks with Hybrid Delays and Stochastic Distributed Delayed Impulses" Mathematics 12, no. 13: 1995. https://doi.org/10.3390/math12131995





