Modal Discontinuous Galerkin Simulations of Richtmyer–Meshkov Instability at Backward-Triangular Bubbles: Insights and Analysis
Abstract
1. Introduction
2. Problem Description
3. Mathematical Formulation
3.1. Physical Conservation Laws for Compressible Two-Component Flow
3.2. Initial Conditions
3.3. Description of Physical Parameters
3.3.1. Atwood Number
3.3.2. Vorticity
3.3.3. Vorticity Transport Equation (VTE)
3.3.4. Enstrophy
3.3.5. Kinetic Energy
4. Numerical Method and Validations
4.1. Numerical Method Based on Modal DG Scheme
4.1.1. Spatial Discretization
4.1.2. Numerical Fluxes
4.1.3. Temporal Discretization
4.1.4. Higher-Order Moment Limiter
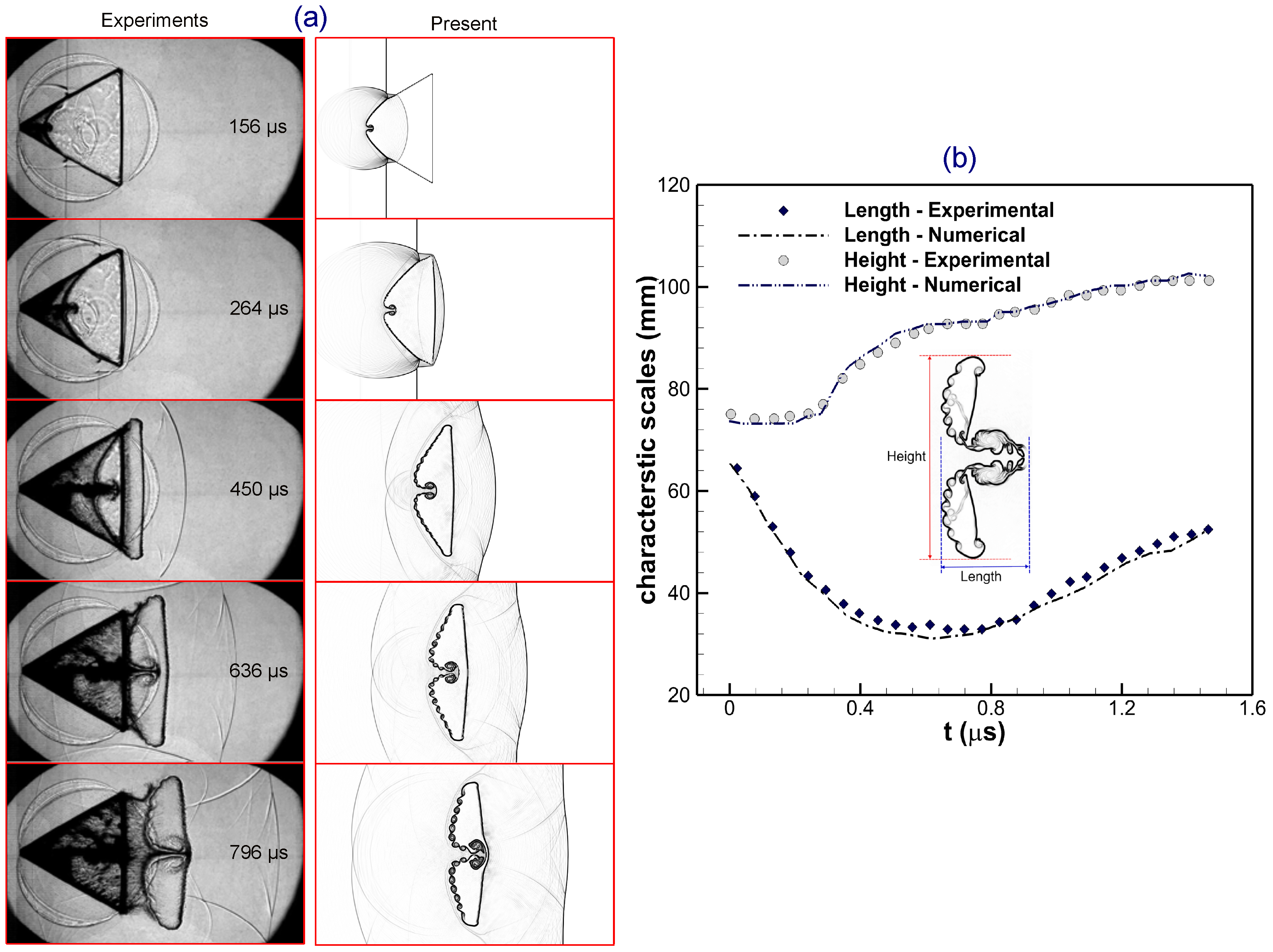
4.2. Validations
5. Results and Discussion
5.1. Mesh Convergence
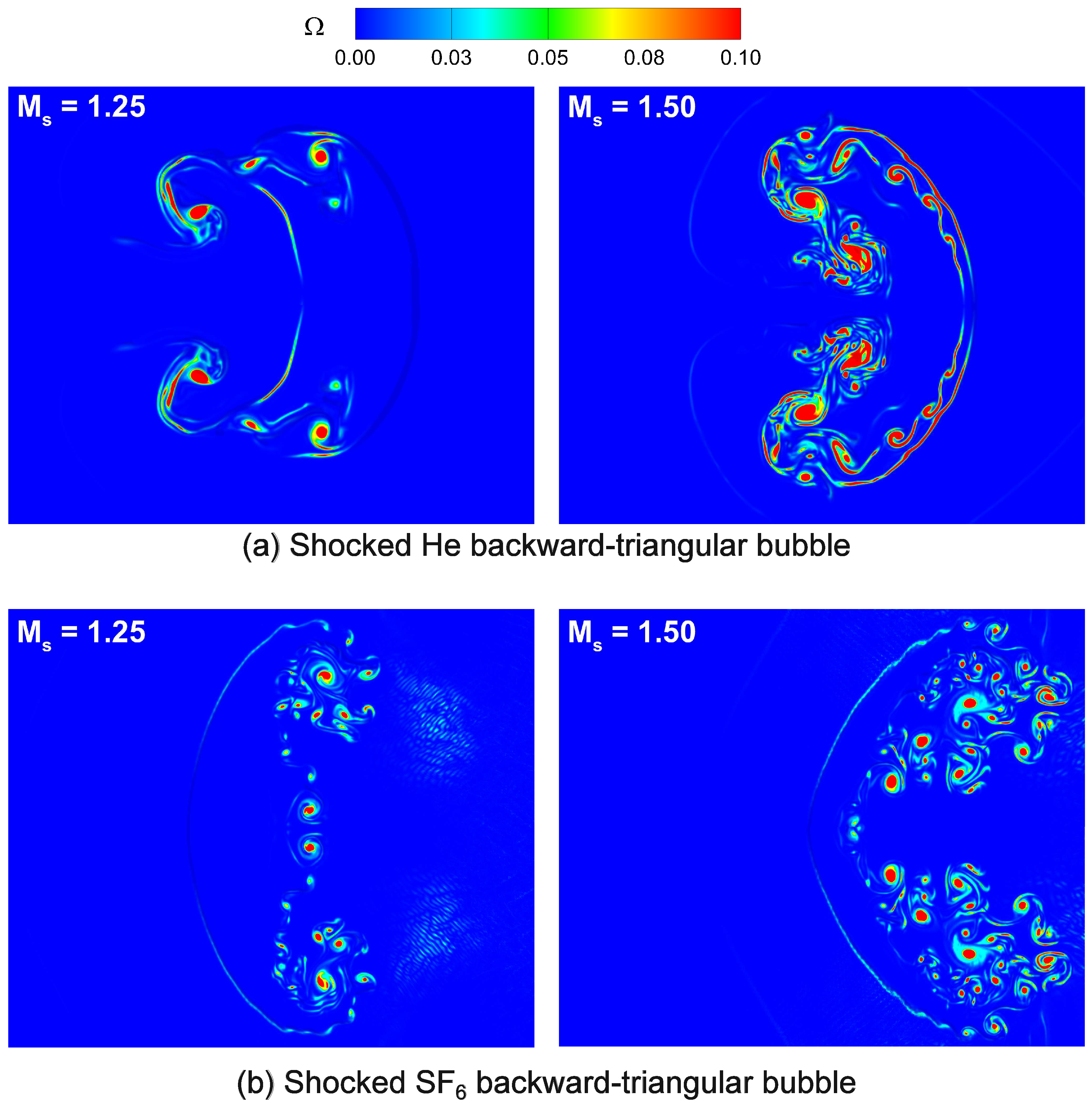
5.2. Flow Structures and Wave Patterns
5.3. Vorticity Generation and Transport Mechanisms
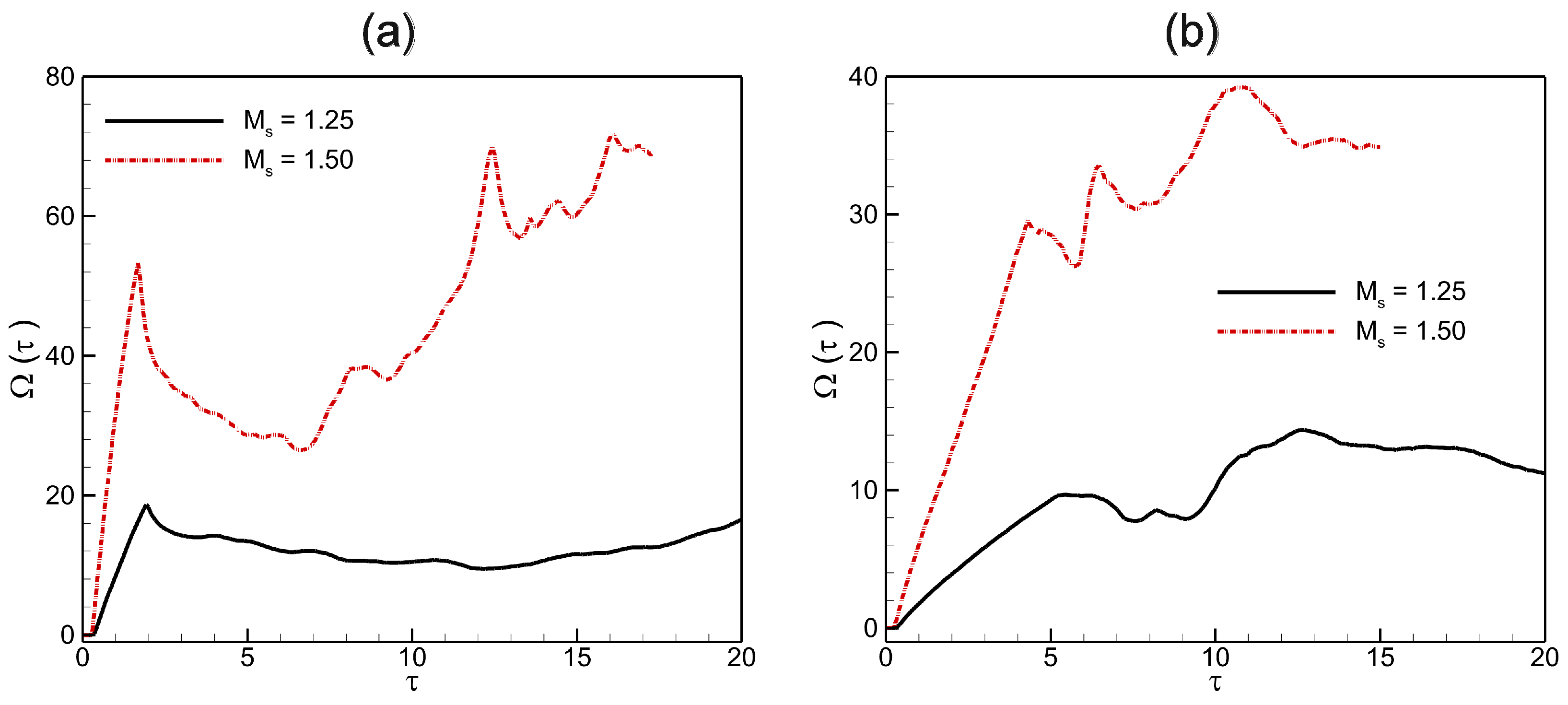
5.4. Enstrophy Generation Mechanism
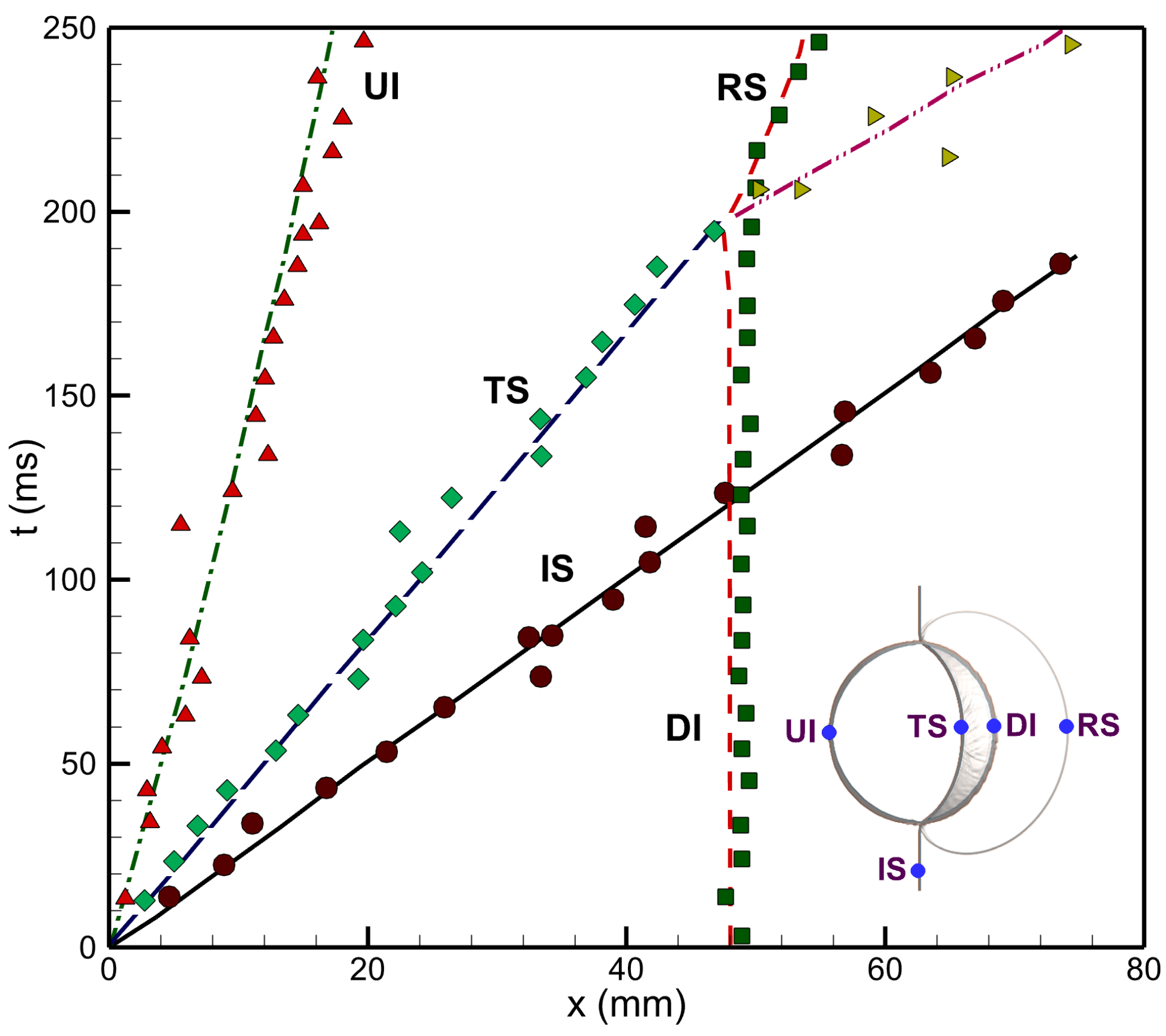
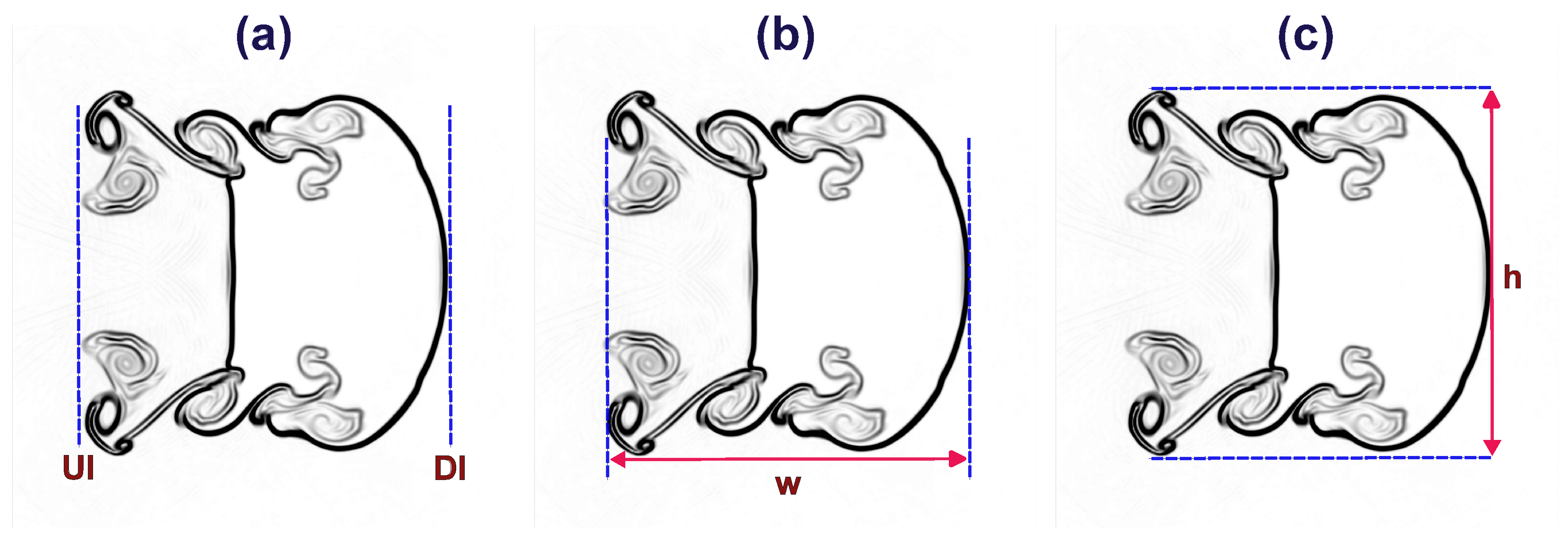
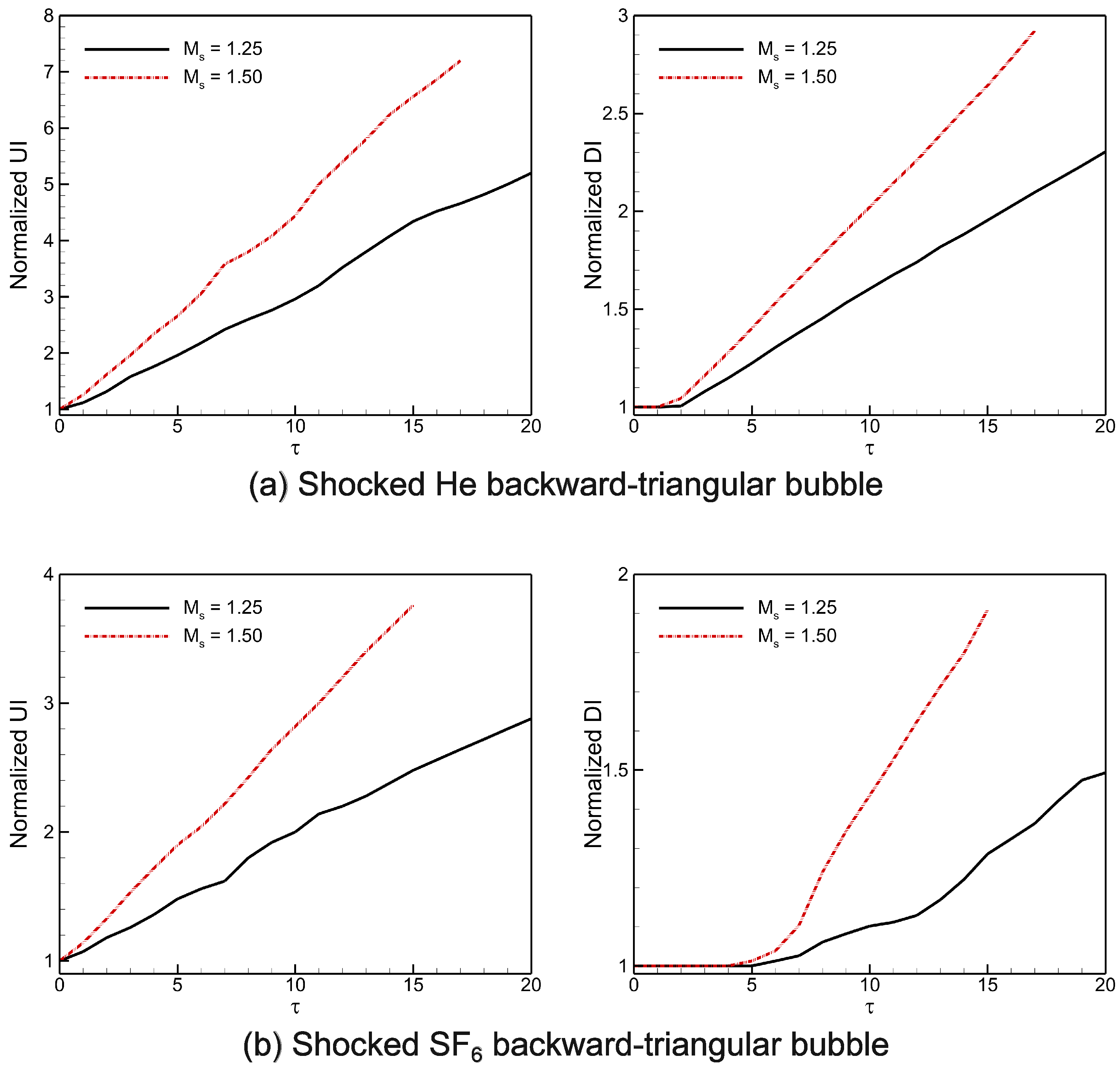
5.5. Interface Characteristics
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Richtmyer, R.D. Taylor instability in shock acceleration of compressible fluids. Commun. Pure. Appl. Math. 1960, 13, 297–319. [Google Scholar] [CrossRef]
- Meshkov, E.E. Instability of the interface of two gases accelerated by a shock wave. Fluid Dyn. 1969, 4, 101. [Google Scholar] [CrossRef]
- Brouillette, M. The Richtmyer-Meshkov instability. Annu. Rev. Fluid Mech. 2002, 34, 445. [Google Scholar] [CrossRef]
- Zhou, Y. Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing-I. Phys. Rep. 2017, 720, 1–136. [Google Scholar]
- Zhou, Y. Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing-II. Phys. Rep. 2017, 723, 1–160. [Google Scholar]
- Zhou, Y.; Williams, R.J.; Ramaprabhu, P.; Groom, M.; Thornber, B.; Hillier, A.; Mostert, W.; Rollin, B.; Balachandar, S.; Powell, P.D.; et al. Rayleigh–Taylor and Richtmyer-Meshkov instabilities: A journey through scales. Phys. D 2021, 423, 132838. [Google Scholar] [CrossRef]
- Arnett, W.D.; Bahcall, J.N.; Kirshner, R.P.; Woosley, S.E. Supernova 1987A. Ann. Rev. Astron. Astrophys. 1989, 2, 629–700. [Google Scholar] [CrossRef]
- Kuranz, C.C.; Park, H.S.; Huntington, C.M.; Miles, A.R.; Remington, B.A.; Plewa, T.; Trantham, M.R.; Robey, H.F.; Shvarts, D.; Shimony, A.; et al. How high energy fluxes may affect Rayleigh–Taylor instability growth in young supernova remnants. Nat. Commun. 2018, 9, 1564. [Google Scholar] [CrossRef] [PubMed]
- Lindl, J.D.; McCrory, R.L.; Campbell, E.M. Progress toward ignition and burn propagation in inertial confinement fusion. Phys. Today 1992, 45, 32–40. [Google Scholar] [CrossRef]
- Lindl, J.; Landen, O.; Edwards, J.; Moses, E.; Team, N. Review of the national ignition campaign 2009–2012. Phys. Plasmas 2014, 21, 020501. [Google Scholar] [CrossRef]
- Yang, J.; Kubota, T.; Zukoski, E.E. Applications of shock-induced mixing to supersonic combustion. AIAA J. 1993, 31, 854–862. [Google Scholar] [CrossRef]
- Yang, Q.; Chang, J.; Bao, W. Richtmyer-Meshkov instability induced mixing enhancement in the scramjet combustor with a central strut. Adv. Mech. Eng. 2014, 6, 614189. [Google Scholar] [CrossRef]
- Markstein, G.H. A shock-tube study of flame front-pressure wave interaction. Symp. (Int.) Combust. 1957, 6, 387. [Google Scholar] [CrossRef]
- Rudinger, G.; Somers, L.M. Behaviour of small regions of different gases carried in accelerated gas flows. J. Fluid Mech. 1960, 7, 161–176. [Google Scholar] [CrossRef]
- Haas, J.F.; Sturtevant, B. Interaction of weak shock waves with cylindrical and spherical gas inhomogeneities. J. Fluid Mech. 1987, 181, 41–76. [Google Scholar] [CrossRef]
- Ranjan, D.; Niederhaus, J.H.J.; Oakley, J.G.; Anderson, M.H.; Bonazza, R.; Greenough, J.A. Shock-bubble interactions: Features of divergent shock-refraction geometry observed in experiments and simulations. Phys. Fluids 2008, 20, 036101. [Google Scholar] [CrossRef]
- Jacobs, J.W. Shock-induced mixing of a light-gas cylinder. J. Fluid Mech. 1992, 234, 629. [Google Scholar] [CrossRef]
- Layes, G.; Jourdan, G.; Houas, L. Distortion of a spherical gaseous interface accelerated by a plane shock wave. Phys. Rev. Lett. 2003, 91, 174502. [Google Scholar] [CrossRef] [PubMed]
- Guillaume, L.; Georges, J.; Lazhar, H. Experimental investigation of the shock wave interaction with a spherical gas inhomogeneity. Phys. Fluids 2005, 17, 028103. [Google Scholar]
- Hosseini, S.H.R.; Takayama, K. Experimental study of Richtmyer-Meshkov instability induced by cylindrical shock waves. Phys. Fluids 2005, 17, 084101. [Google Scholar] [CrossRef]
- Ding, J.; Si, T.; Chen, M.; Zhai, Z.; Lu, X.; Luo, X. On the interaction of a planar shock with a three-dimensional light gas cylinder. J. Fluid Mech. 2017, 828, 289–317. [Google Scholar] [CrossRef]
- Quirk, J.J.; Karni, S. On the dynamics of a shock-bubble interaction. J. Fluid Mech. 1996, 318, 129–163. [Google Scholar] [CrossRef]
- Bagabir, A.; Drikakis, D. Mach number effects on shock-bubble interaction. Shock Waves 2001, 11, 209. [Google Scholar] [CrossRef]
- Shankar, S.K.; Kawai, S.; Lele, S.K. Two-dimensional viscous flow simulation of a shock accelerated heavy gas cylinder. Phys. Fluids 2011, 23, 024102. [Google Scholar] [CrossRef]
- Zhu, Y.; Gao, L.; Yang, Z. Sulfur hexafluoride bubble evolution in shock accelerated flow with a transverse density gradient. Phys. Fluids 2020, 32, 026101. [Google Scholar] [CrossRef]
- Singh, S.; Battiato, M.; Myong, R.S. Impact of the bulk viscosity on flow morphology of shock-bubble interaction in diatomic and polyatomic gases. Phys. Fluids 2021, 33, 066103. [Google Scholar] [CrossRef]
- Singh, S.; Msmali, A.H.; Nelson, M.I. Unfolding of shocked hydrodynamic instability at SF6 elliptical interface: Physical insights from numerical simulations. Comput. Fluids 2024, 277, 106304. [Google Scholar] [CrossRef]
- Picone, J.M.; Boris, J.P. Vorticity generation by shock propagation through bubbles in a gas. J. Fluid Mech. 1988, 189, 23–51. [Google Scholar] [CrossRef]
- Yang, J.; Kubota, T.; Zukoski, E.E. A model for characterization of a vortex pair formed by shock passage over a light-gas inhomogeneity. J. Fluid Mech. 1994, 258, 217–244. [Google Scholar] [CrossRef]
- Samtaney, R.; Zabusky, N.J. Circulation deposition on shock-accelerated planar and curved density-stratified interfaces: Models and scaling laws. J. Fluid Mech. 1994, 269, 45–78. [Google Scholar] [CrossRef]
- Niederhaus, J.H.J.; Greenough, J.A.; Oakley, J.G.; Ranjan, D.; Anderson, M.H.; Bonazza, R.A. A computational parameter study for the three-dimensional shock-bubble interaction. J. Fluid Mech. 2008, 594, 85. [Google Scholar] [CrossRef]
- Bates, K.R.; Nikiforakis, N.; Holder, D. Richtmyer-Meshkov instability induced by the interaction of a shock wave with a rectangular block of SF6. Phys. Fluids 2007, 19, 036101. [Google Scholar] [CrossRef]
- Zhai, Z.; Wang, M.; Si, T.; Luo, X. On the interaction of a planar shock with a light polygonal interface. J. Fluid Mech. 2014, 757, 800. [Google Scholar] [CrossRef]
- Luo, X.; Wang, M.; Si, T.; Zhai, Z. On the interaction of a planar shock with an SF6 polygon. J. Fluid Mech. 2015, 773, 366. [Google Scholar] [CrossRef]
- Igra, D.; Igra, O. Numerical investigation of the interaction between a planar shock wave with square and triangular bubbles containing different gases. Phys. Fluids 2018, 30, 056104. [Google Scholar] [CrossRef]
- Igra, D.; Igra, O. Shock wave interaction with a polygonal bubble containing two different gases, a numerical investigation. J. Fluid Mech. 2020, 88, A26. [Google Scholar] [CrossRef]
- Singh, S. Role of Atwood number on flow morphology of a planar shock-accelerated square bubble: A numerical study. Phys. Fluids 2020, 32, 126112. [Google Scholar] [CrossRef]
- Singh, S.; Battiato, M. Numerical investigation of shock Mach number effects on Richtmyer–Meshkov instability in a heavy square bubble. Phys. D Nonlinear Phenom. 2023, 453, 133844. [Google Scholar] [CrossRef]
- Singh, S.; Battiato, M. Numerical simulations of Richtmyer-Meshkov instability of SF6 square bubble in diatomic and polyatomic gases. Comput. Fluids 2022, 242, 105502. [Google Scholar] [CrossRef]
- Singh, S.; Torrilhon, M. On the shock-driven hydrodynamic instability in square and rectangular light gas bubbles: A comparative study from numerical simulations. Phys. Fluids 2023, 35, 012117. [Google Scholar] [CrossRef]
- Latini, M.; Schilling, O.; Don, W.S. Effects of WENO flux reconstruction order and spatial resolution on reshocked two-dimensional Richtmyer–Meshkov instability. J. Comput. Phys. 2007, 221, 805–836. [Google Scholar] [CrossRef]
- Movahed, P.; Johnsen, E. A solution-adaptive method for efficient compressible multifluid simulations, with application to the Richtmyer–Meshkov instability. J. Comput. Phys. 2013, 239, 166–186. [Google Scholar] [CrossRef]
- Pandare, A.K.; Waltz, J.; Li, W.; Luo, H.; Bakosi, J. On the design of stable, consistent, and conservative high-order methods for multi-material hydrodynamics. J. Comput. Phys. 2023, 490, 112313. [Google Scholar] [CrossRef]
- Maltsev, V.; Skote, M.; Tsoutsanis, P. High-order methods for diffuse-interface models in compressible multi-medium flows: A review. Phys. Fluids 2022, 34, 021301. [Google Scholar] [CrossRef]
- He, Z.; Liu, H.; Li, L. Generic five-equation model for compressible multi-material flows and its corresponding high-fidelity numerical algorithms. J. Comput. Phys. 2023, 487, 112154. [Google Scholar] [CrossRef]
- Singh, S.; Karchani, A.; Chourushi, T.; Myong, R.S. A three-dimensional modal discontinuous Galerkin method for the second-order Boltzmann-Curtiss-based constitutive model of rarefied and microscale gas flows. J. Comput. Phys. 2022, 457, 111052. [Google Scholar] [CrossRef]
- Cockburn, B.; Shu, C.-W. The Runge–Kutta discontinuous Galerkin method for conservation laws V: Multidimensional systems. J. Comput. Phys. 1998, 141, 199–224. [Google Scholar] [CrossRef]
- Liu, H.; Xu, K. A Runge–Kutta discontinuous Galerkin method for viscous flow equations. J. Comput. Phys. 2007, 224, 1223–1242. [Google Scholar] [CrossRef]
- Kontzialis, K.; Ekaterinaris, J.A. High order discontinuous Galerkin discretizations with a new limiting approach and positivity preservation for strong moving shocks. Comput. Fluids 2013, 71, 98–112. [Google Scholar] [CrossRef]
- Park, J.S.; You, H.; Kim, C. Higher-order multi-dimensional limiting process for DG and FR/CPR methods on tetrahedral meshes. Comput. Fluids 2017, 154, 322–334. [Google Scholar] [CrossRef]
- You, H.; Kim, C. High-order multi-dimensional limiting strategy with subcell resolution I. Two-dimensional mixed meshes. J. Comput. Phys. 2018, 375, 1005–1032. [Google Scholar] [CrossRef]
- Chan, J.; Lin, Y.; Warburton, T. Entropy stable modal discontinuous Galerkin schemes and wall boundary conditions for the compressible Navier-Stokes equations. J. Comput. Phys. 2022, 448, 110723. [Google Scholar] [CrossRef]
- Hesthaven, J.S.; Warburton, T. Nodal Discontinuous Galerkin Methods: Algorithms, Analysis, and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Hindenlang, F.; Gassner, G.J.; Altmann, C.; Beck, A.; Staudenmaier, M.; Munz, C. Explicit discontinuous Galerkin methods for unsteady problems. Comput. Fluids 2012, 61, 86–93. [Google Scholar] [CrossRef]
- Huerta, A.; Casoni, E.; Peraire, J. A simple shock-capturing technique for high-order discontinuous Galerkin methods. Int. J. Numer. Methods Fluids 2016, 69, 1614–1632. [Google Scholar] [CrossRef]
- Krank, B.; Fehn, N.; Wall, W.A.; Kronbichler, M. A high-order semi-explicit discontinuous Galerkin solver for 3D incompressible flow with application to DNS and LES of turbulent channel flow. J. Comput. Phys. 2017, 348, 634–659. [Google Scholar] [CrossRef]
- Ferrer, E.; Willden, R.H.J. A high order discontinuous Galerkin finite element solver for the incompressible Navier–Stokes equations. Comput. Fluids. 2011, 46, 224–230. [Google Scholar] [CrossRef]
- Kronbichler, M.; Wall, W.A. A performance comparison of continuous and discontinuous Galerkin methods with fast multigrid solvers. SIAM J. Sci. Comput. 2018, 40, A3423–A3448. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Sherwin, S. Spectral/hp Element Methods for Computational Fluid Dynamics; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Johnsen, E.; Colonius, T. Implementation of WENO schemes in compressible multicomponent flow problems. J. Comput. Phys. 2006, 219, 715–732. [Google Scholar] [CrossRef]
- Ketcheson, D.I. Highly efficient strong stability-preserving Runge–Kutta methods with low-storage implementations. SIAM J. Sci. Comput. 2008, 30, 2113–2136. [Google Scholar] [CrossRef]
- Krivodonova, L. Limiters for high-order discontinuous Galerkin methods. J. Comput. Phys. 2007, 226, 879–896. [Google Scholar] [CrossRef]










| Gases | Density | Heat Ratio | Sound Velocity | Atwood Number |
|---|---|---|---|---|
| 1.25 | 1.40 | 352 | ambient | |
| He | 0.16 | 1.66 | 1007 | −0.773 |
| 6.03 | 1.09 | 135 | 0.667 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsaeed, S.S.; Singh, S. Modal Discontinuous Galerkin Simulations of Richtmyer–Meshkov Instability at Backward-Triangular Bubbles: Insights and Analysis. Mathematics 2024, 12, 2005. https://doi.org/10.3390/math12132005
Alsaeed SS, Singh S. Modal Discontinuous Galerkin Simulations of Richtmyer–Meshkov Instability at Backward-Triangular Bubbles: Insights and Analysis. Mathematics. 2024; 12(13):2005. https://doi.org/10.3390/math12132005
Chicago/Turabian StyleAlsaeed, Salman Saud, and Satyvir Singh. 2024. "Modal Discontinuous Galerkin Simulations of Richtmyer–Meshkov Instability at Backward-Triangular Bubbles: Insights and Analysis" Mathematics 12, no. 13: 2005. https://doi.org/10.3390/math12132005
APA StyleAlsaeed, S. S., & Singh, S. (2024). Modal Discontinuous Galerkin Simulations of Richtmyer–Meshkov Instability at Backward-Triangular Bubbles: Insights and Analysis. Mathematics, 12(13), 2005. https://doi.org/10.3390/math12132005







