Synergistic Exploration of Heat Transfer for Integration Magnetohydrodynamics of Nanofluids Peristaltic Transport within Annular Tubes
Abstract
:1. Introduction
2. Materials and Analytical Method
2.1. Mathematical Modeling
2.2. Non-Dimensional Analysis
2.3. Solution Procedure
3. Results and Discussion
3.1. Problem Validation
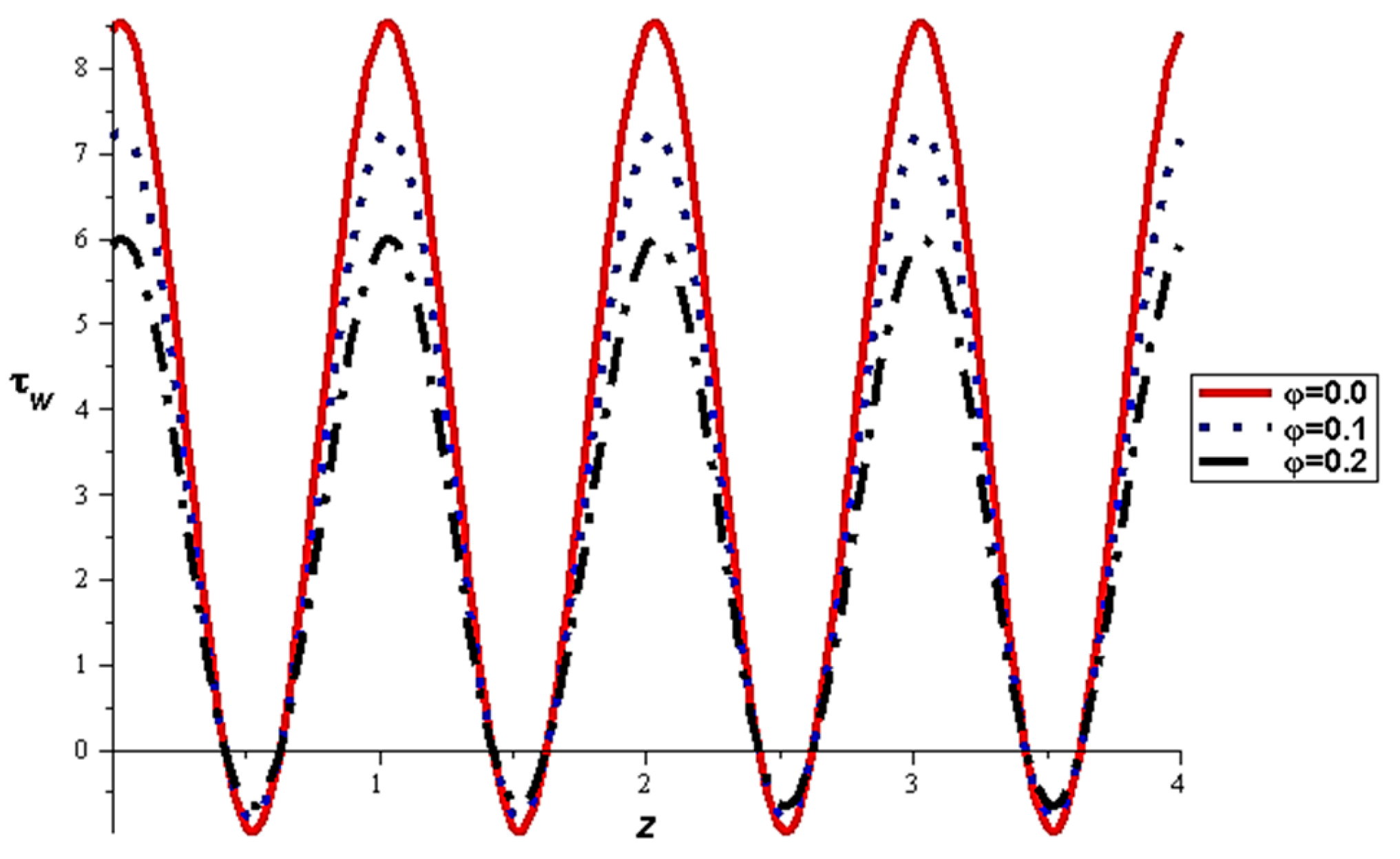
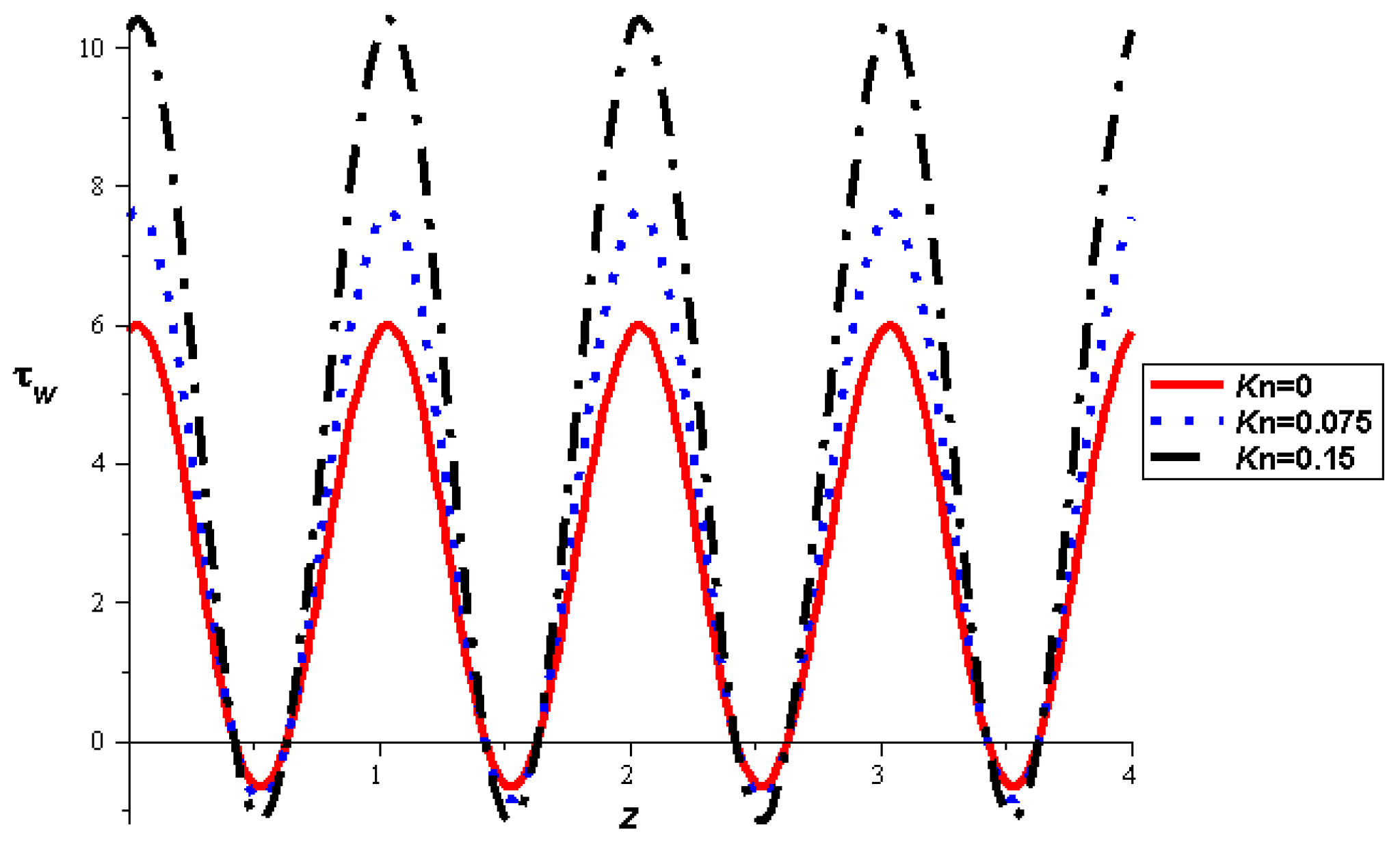
3.2. Analysis and Discussion
4. Conclusions
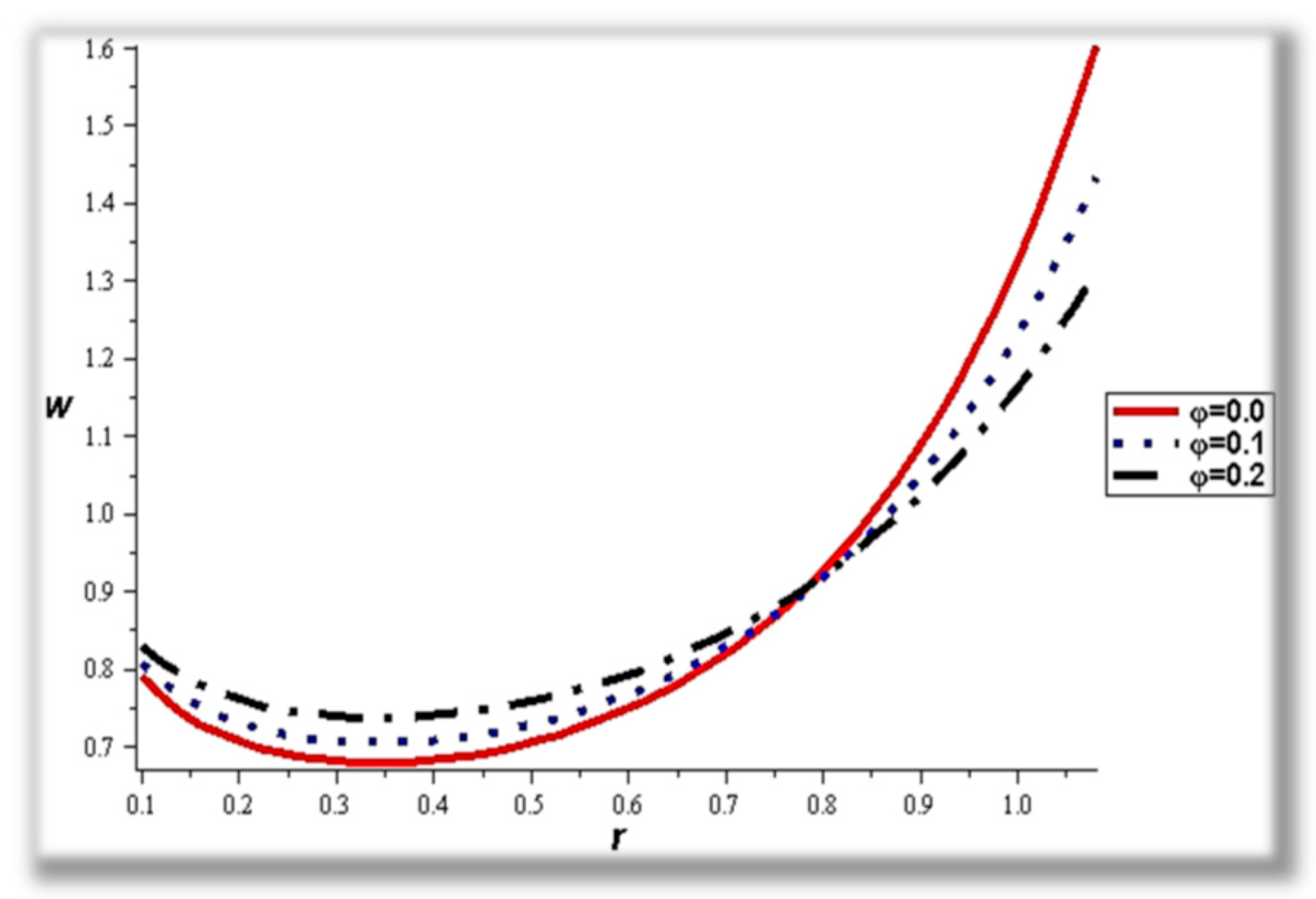
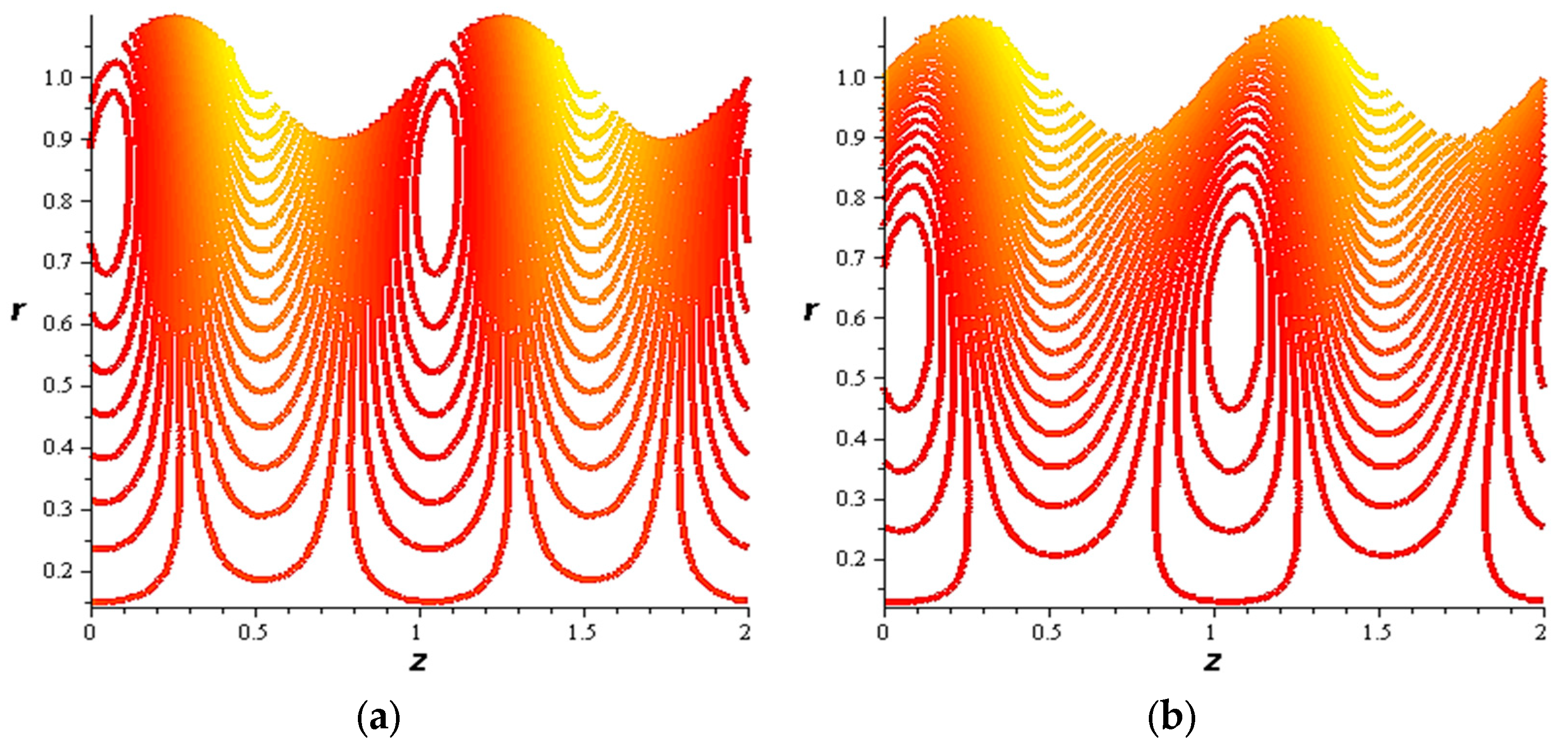
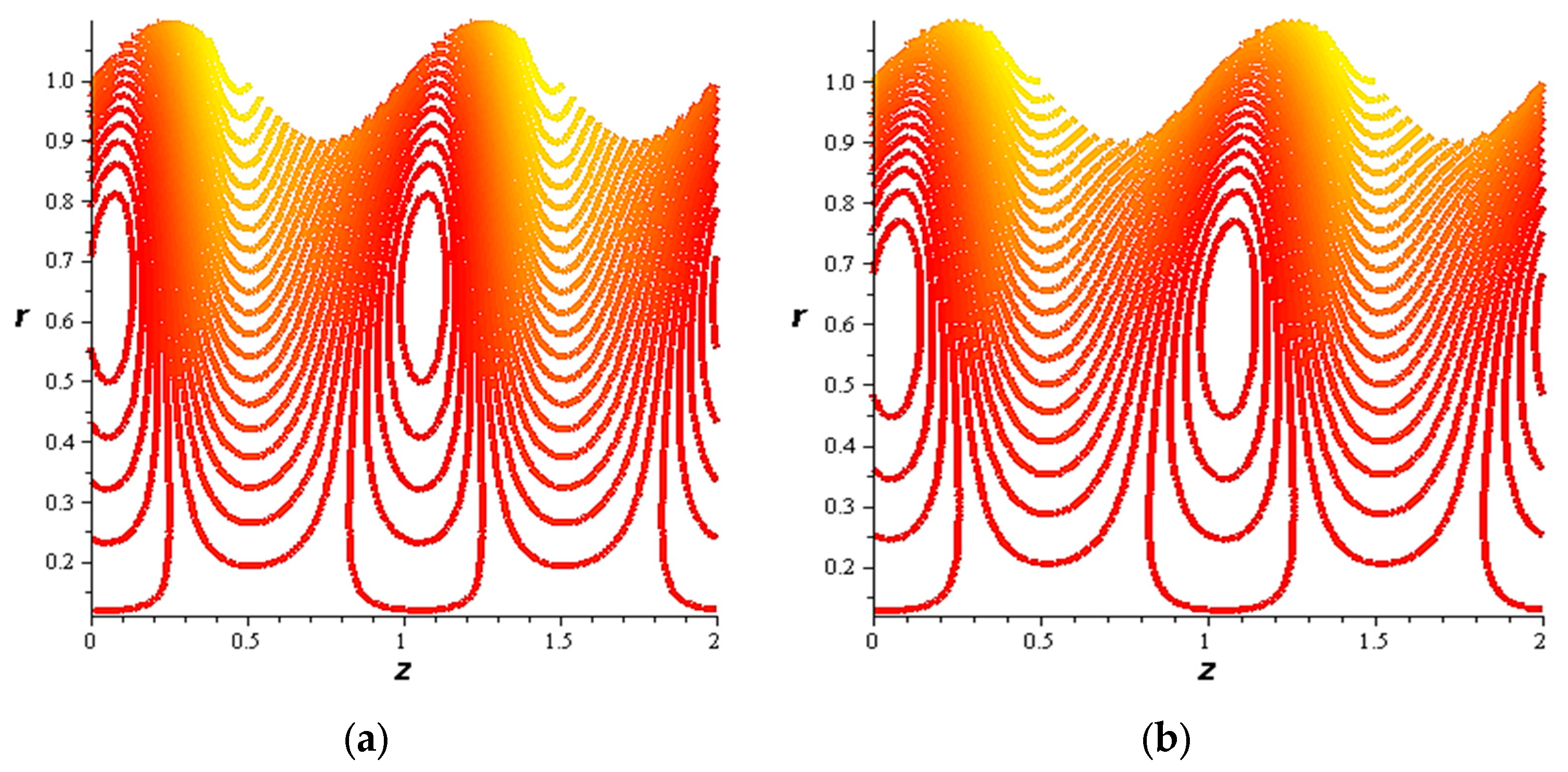
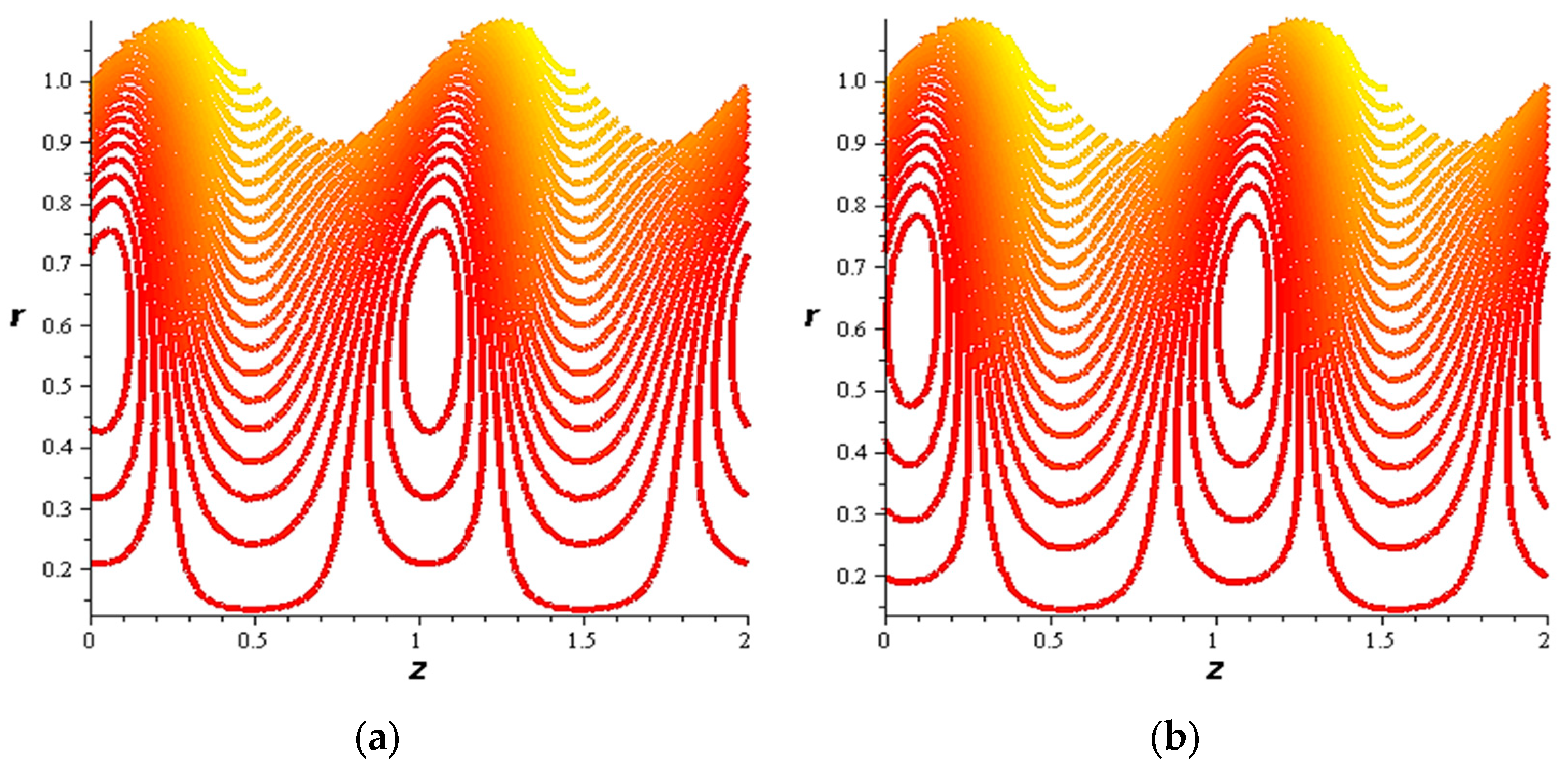
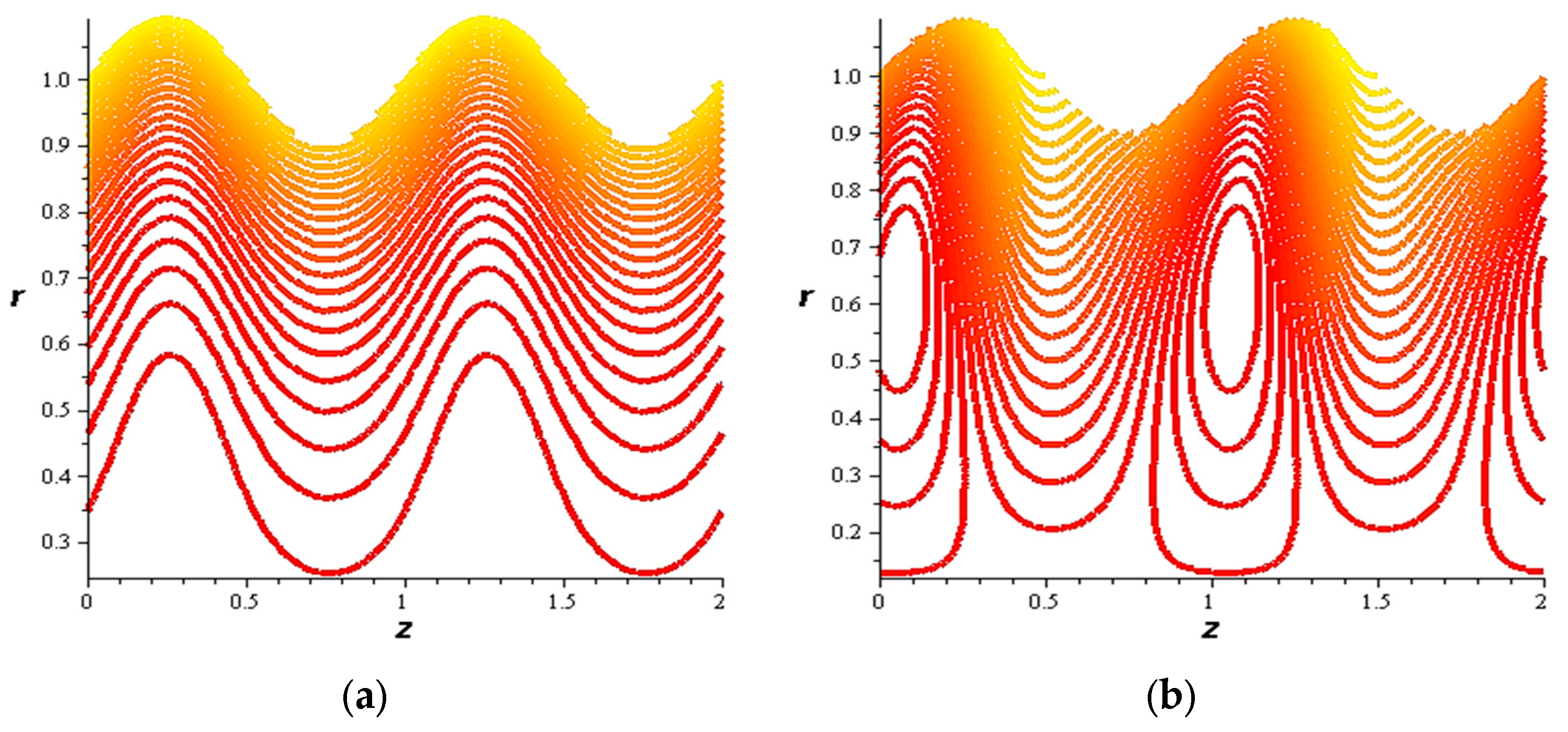
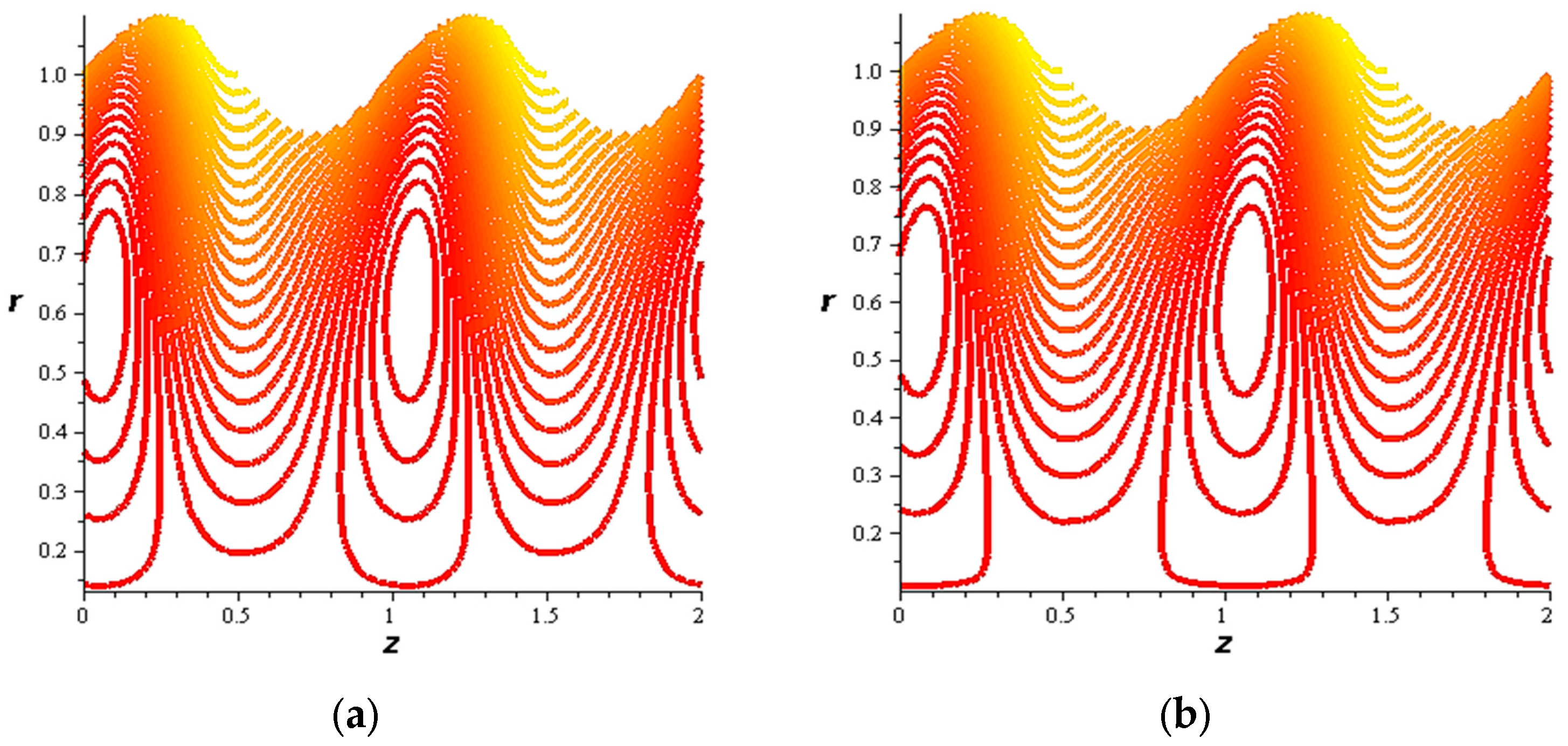
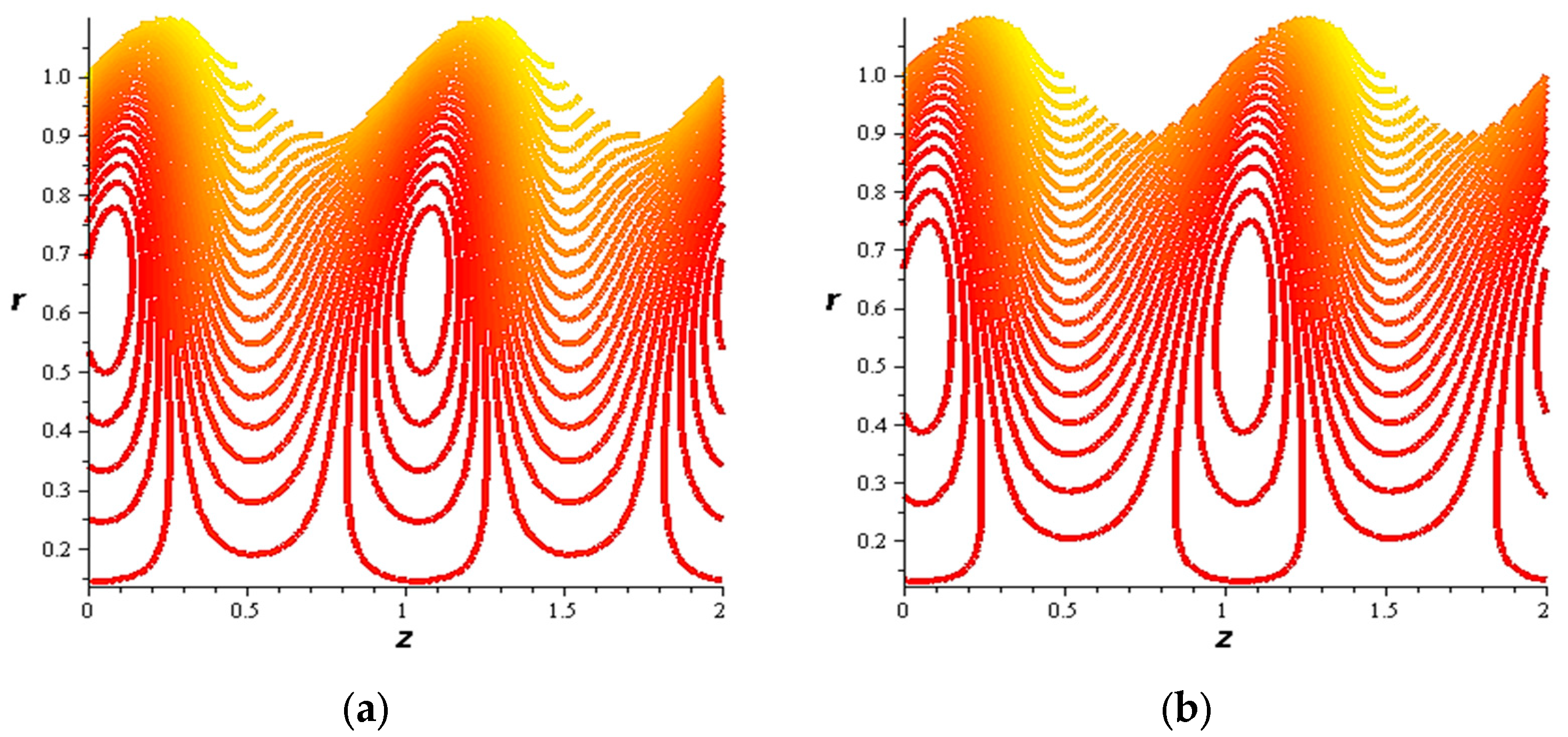
- For both slipping and without slipping, the magnitude of the velocity increases at the artery wall and diminishes at the catheter with nanoparticle concentration, φ, and with catheter size and the amplitude ratio. This effect is evident in the streamlines, as in the presence of nanoparticles, the fluid lines decrease.
- Increasing velocity with increasing amplitude ratio occurs at most of the interface points between the artery wall and the catheter.
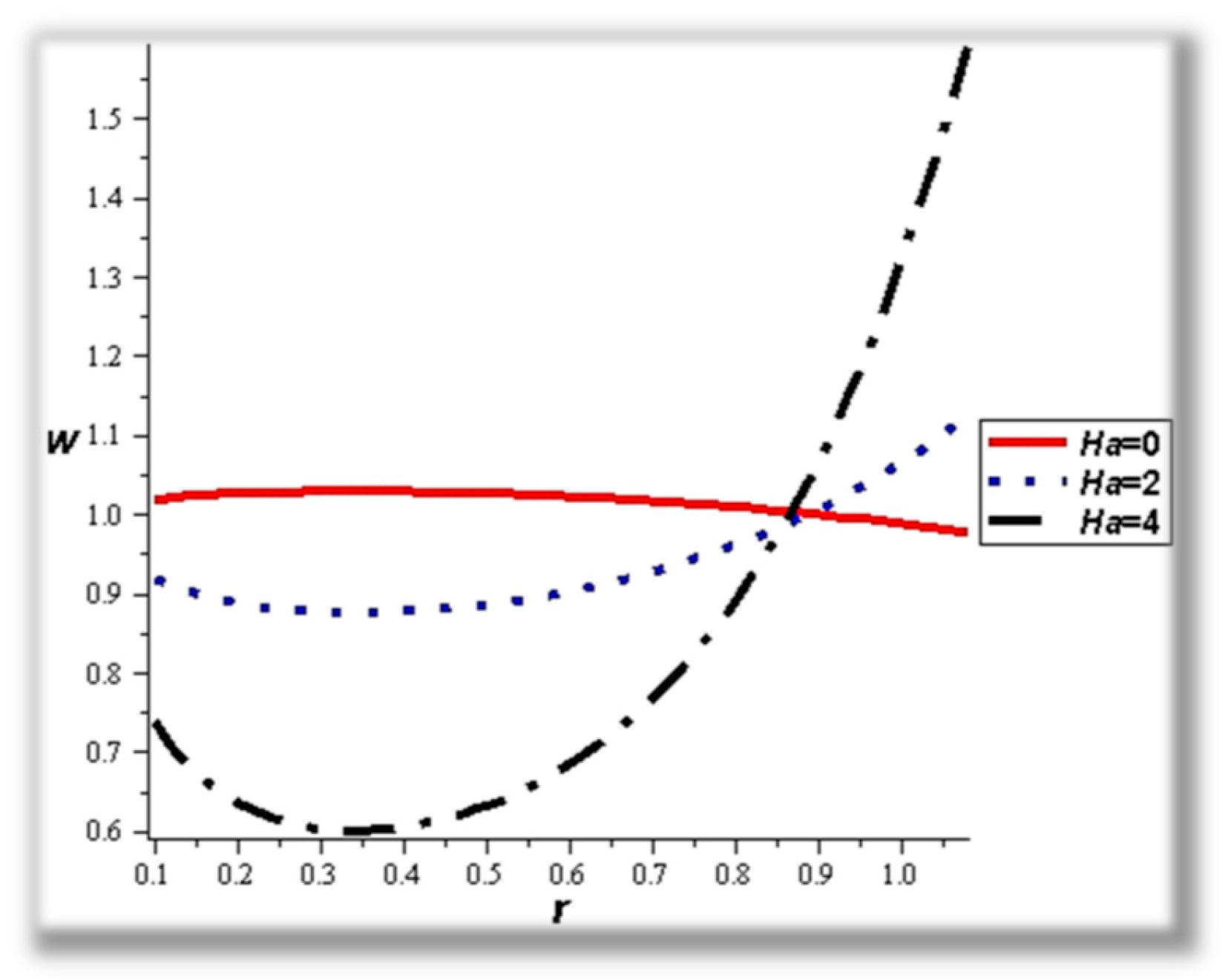
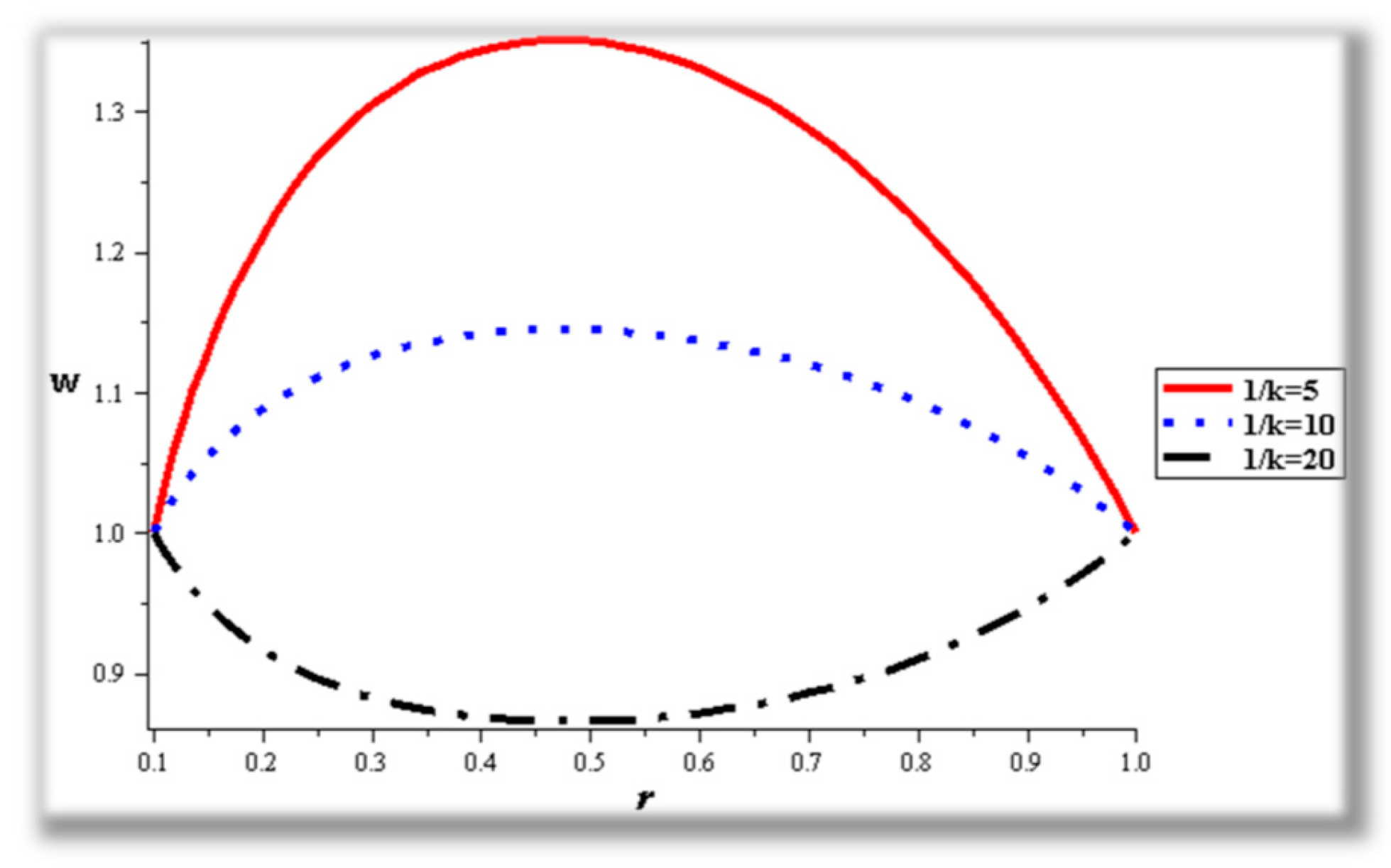
- The strength of the magnetic field works to obstruct the flow movement and, therefore, it reduces the flow speed in most areas of the artery, but the distribution of speeds increases next to the wall as it depends on the occurrence of slipping. The streamlines are affected by the magnetic field, as increasing the influencing magnetic field leads to a decrease in the flow lines, which leads to an increase in the speed of the fluid layers.
- The velocity also increases with the presence of a catheter. It is also observed that the slipping on the tube wall increases the velocity, while the slip condition at the catheter decreases the velocity. The sliding that occurs on the artery wall leads to a reduction in vortices on this wall and streamlines the flow lines. The kinetic and thermal energy of the fluid decreases when the catheter moves.
- By studying the effect of wall properties on flow behavior, it was found that the damping affecting the artery wall, as well as the mass of the cells relative to their area, have the same effect on flow performance, in contrast to tension between the artery wall cells.
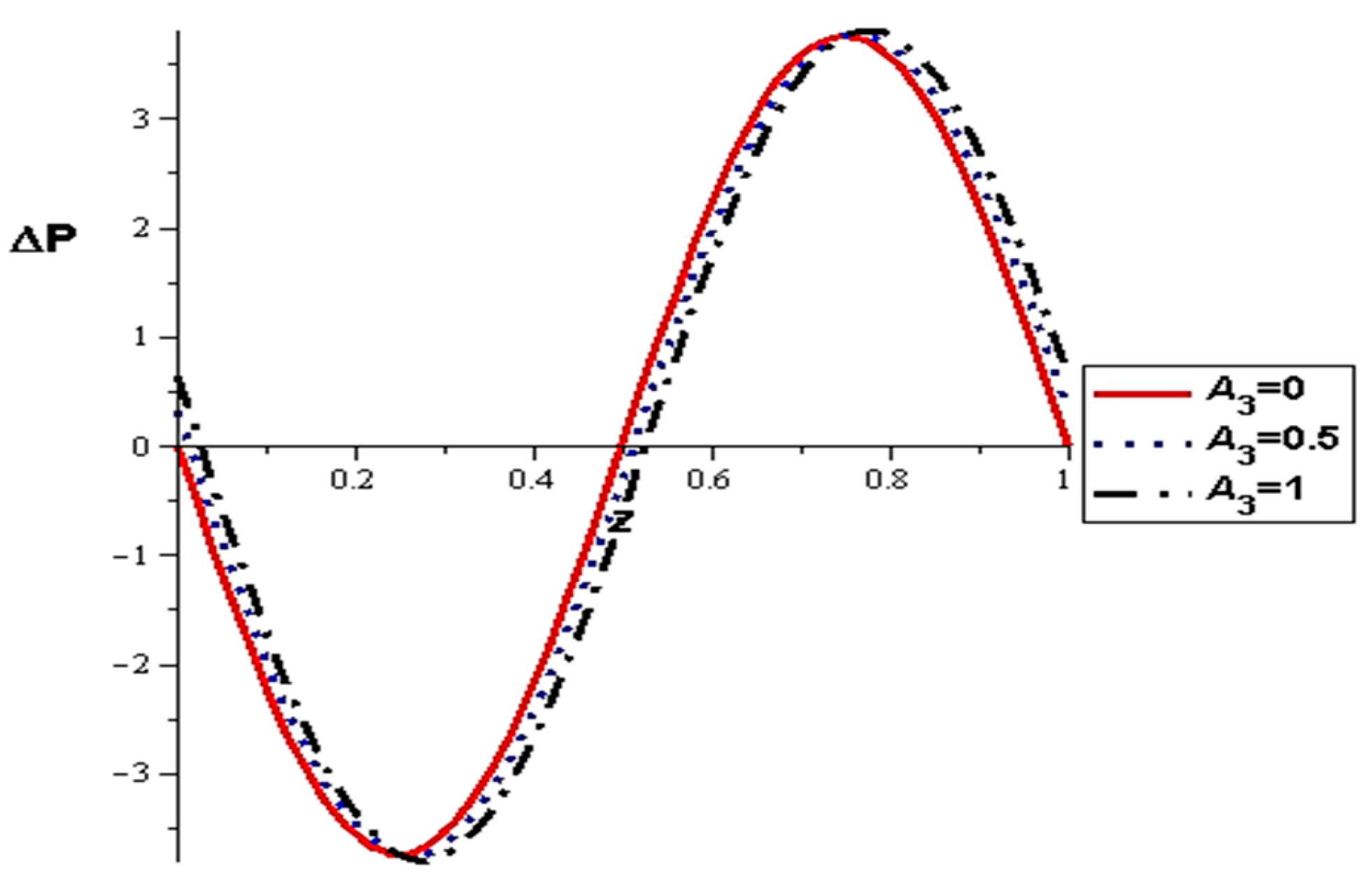
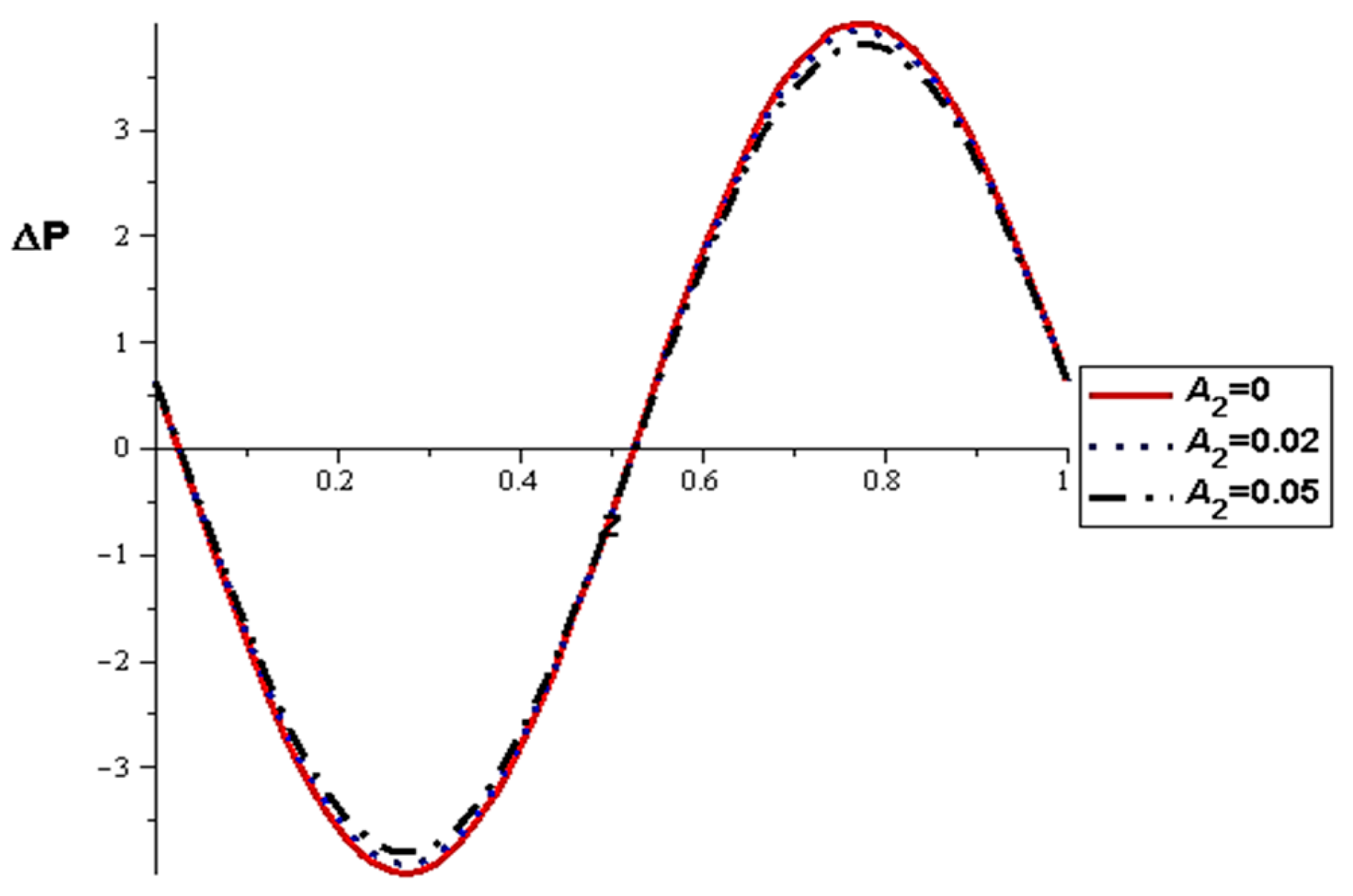
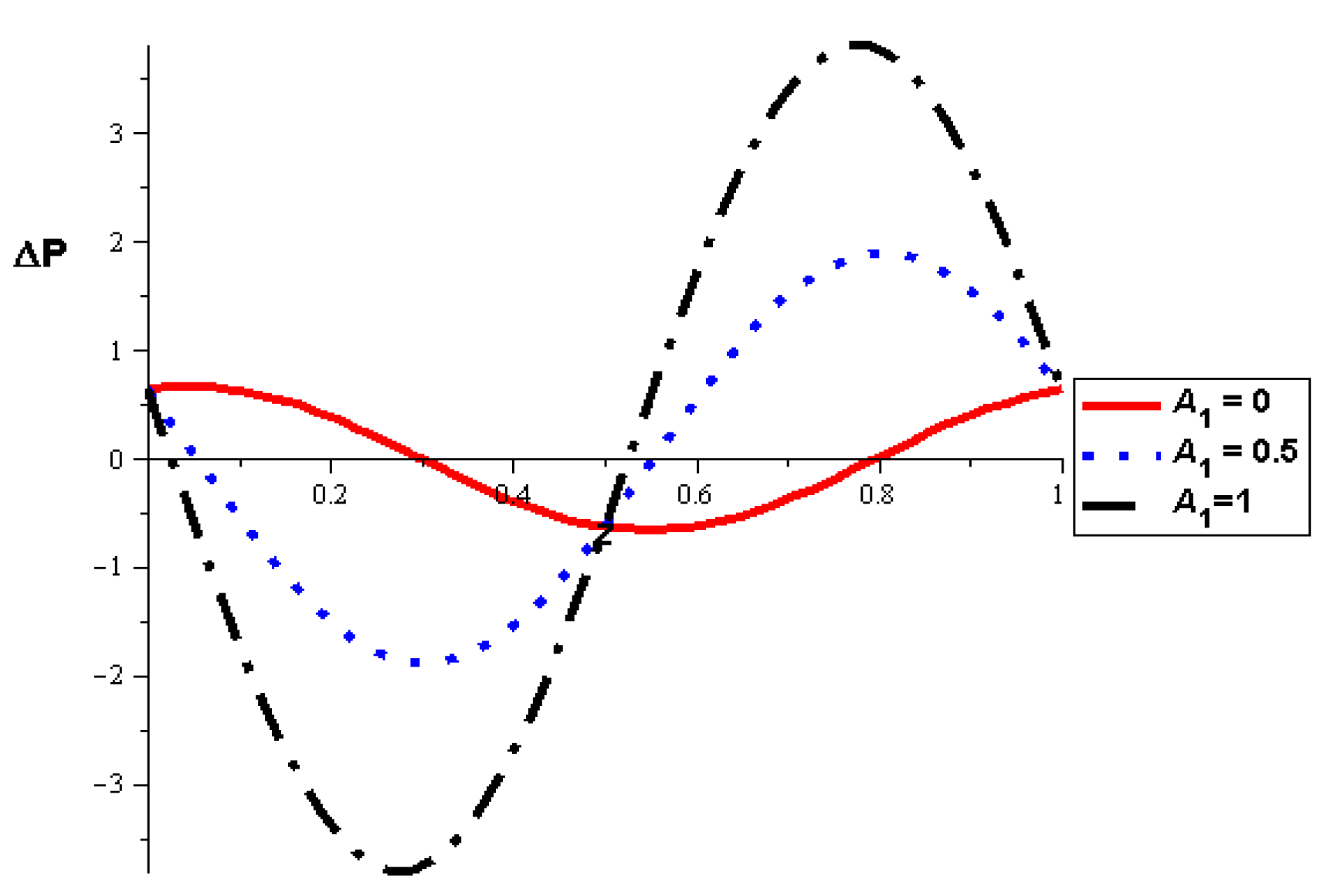
- The pressure difference depends on the wall properties. It was found that the mass of the wall cells relative to their area decreases the pressure difference, in contrast to the tension between those cells, which increases the pressure difference. Intercellular damping depends on the peristaltic movement of the artery, which determines the increase or decrease in the pressure difference.
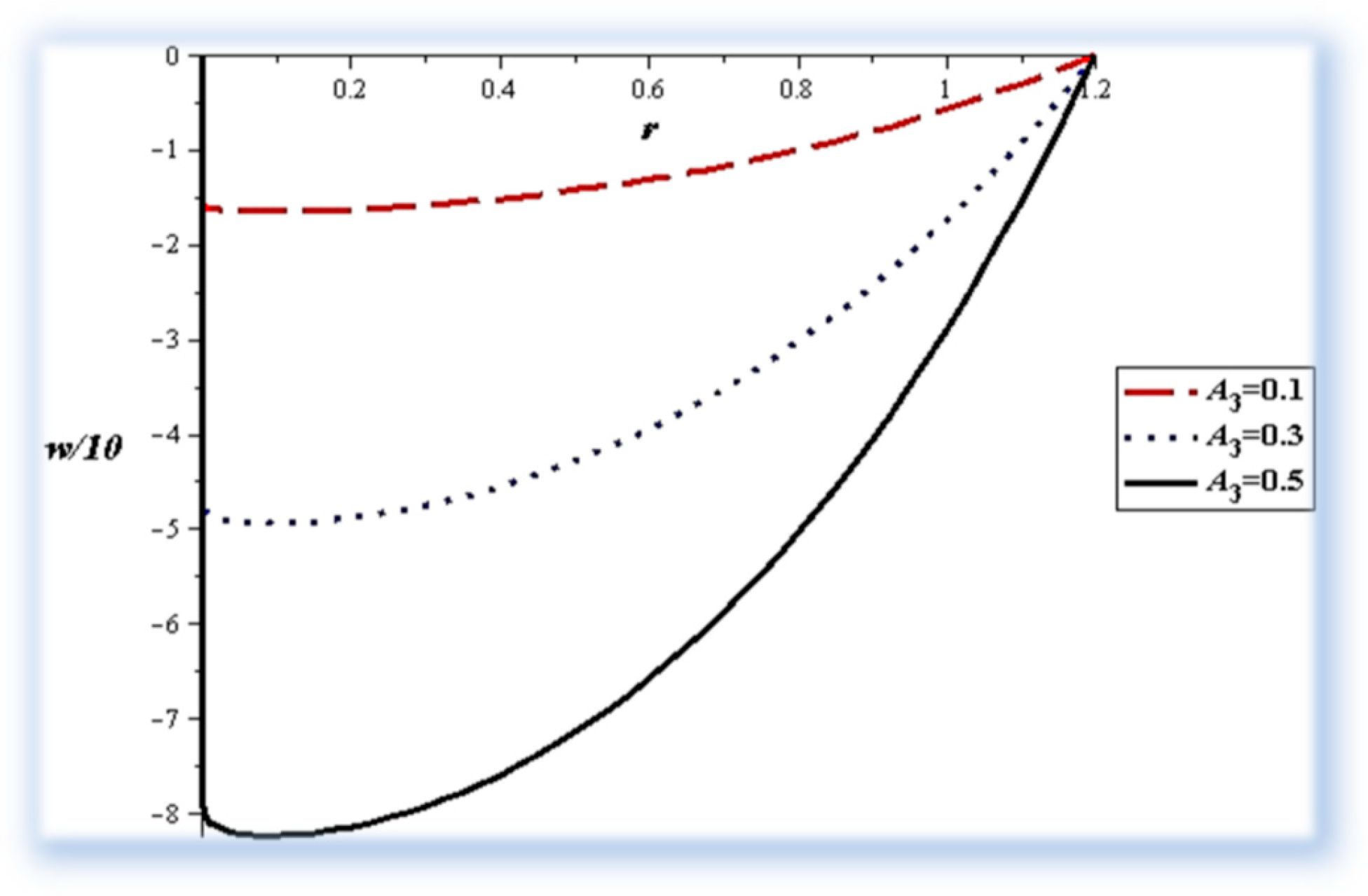
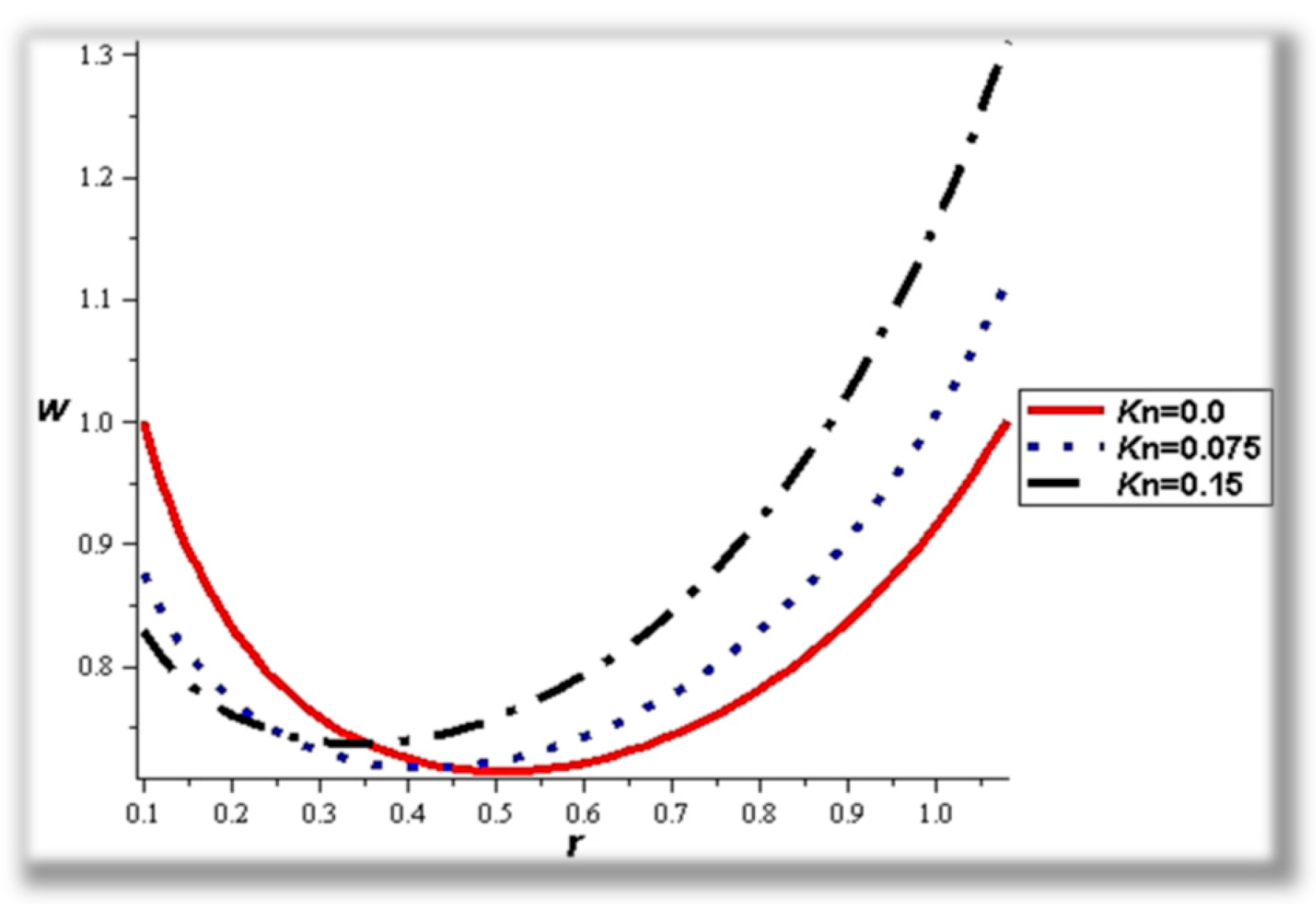
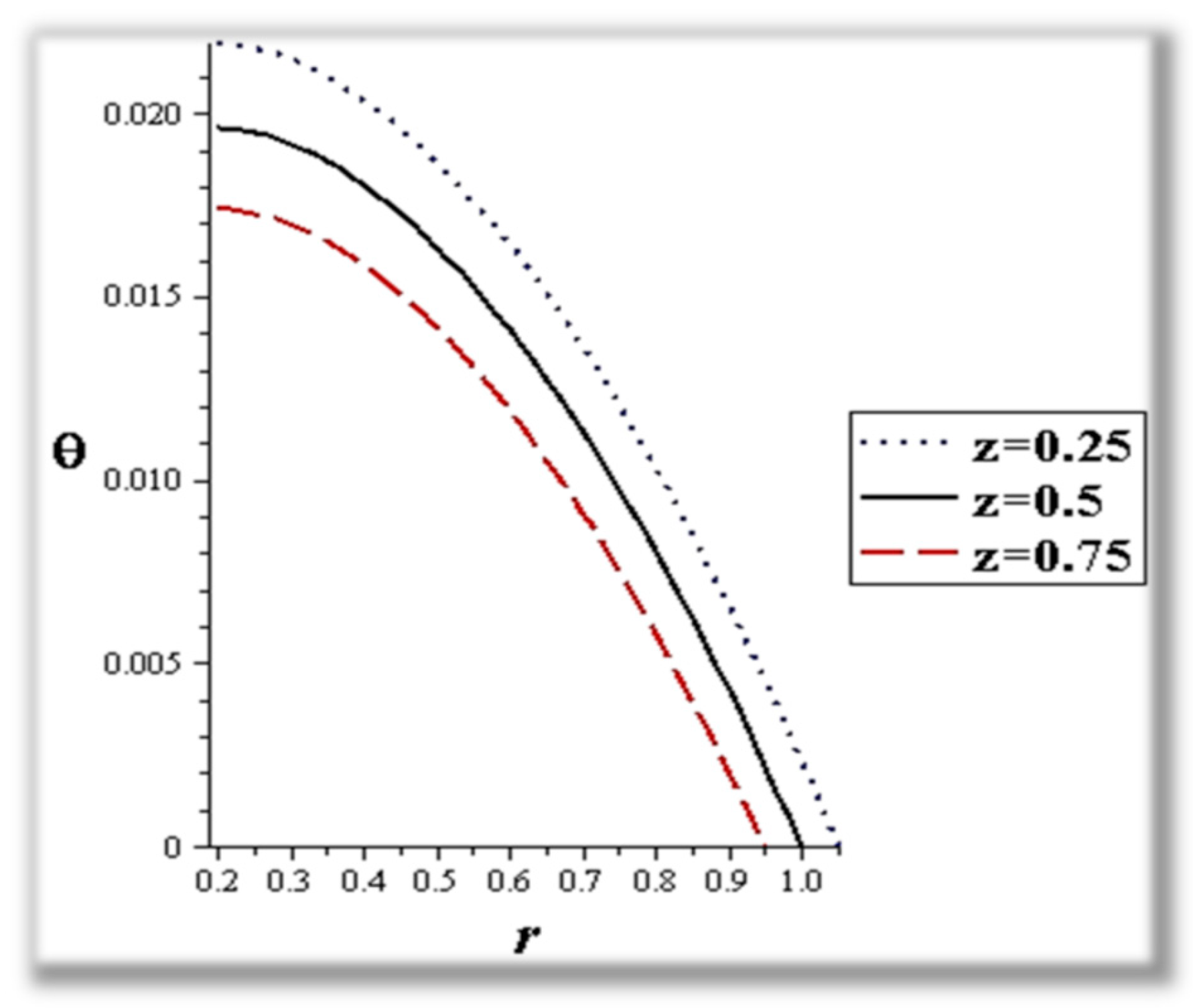
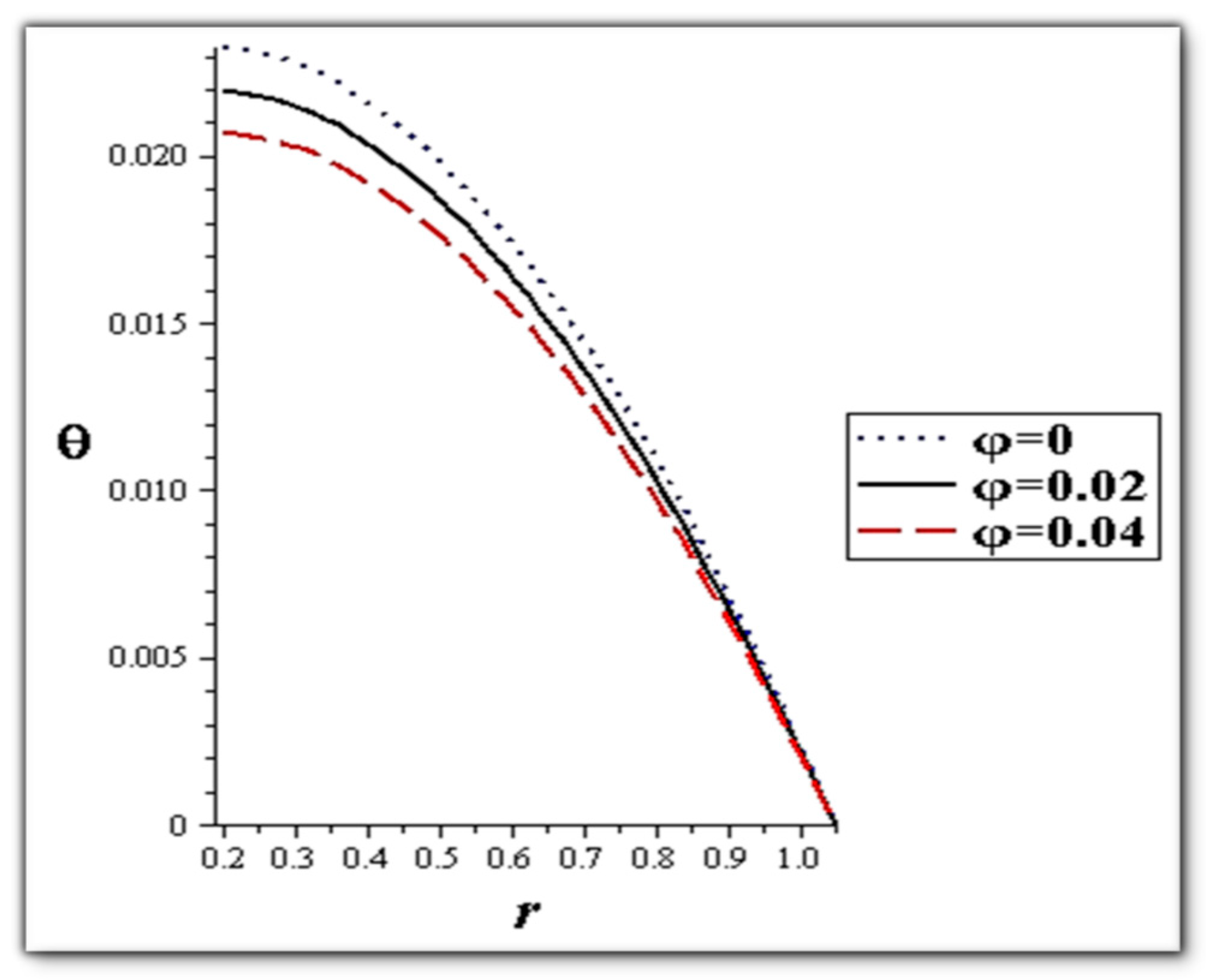
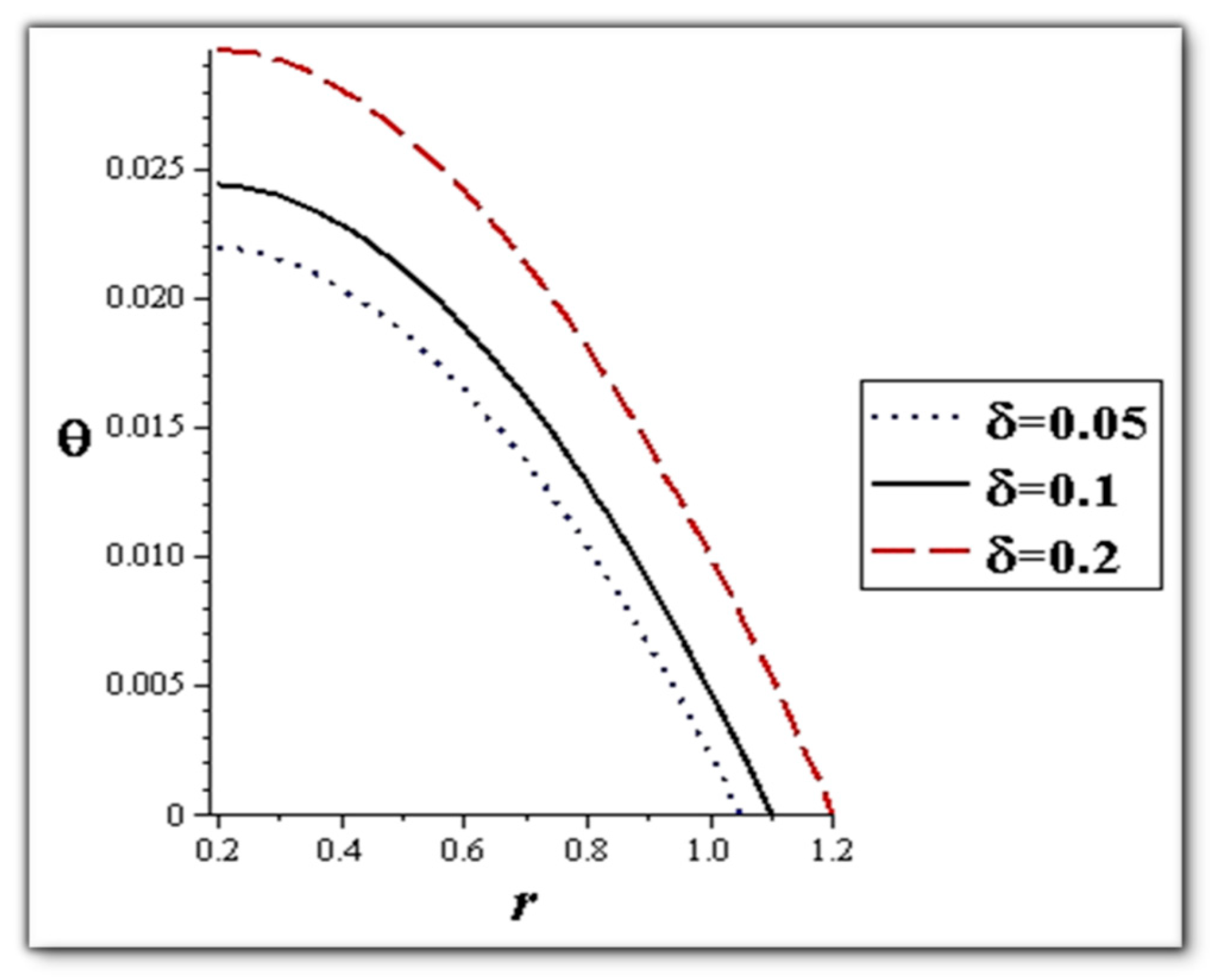
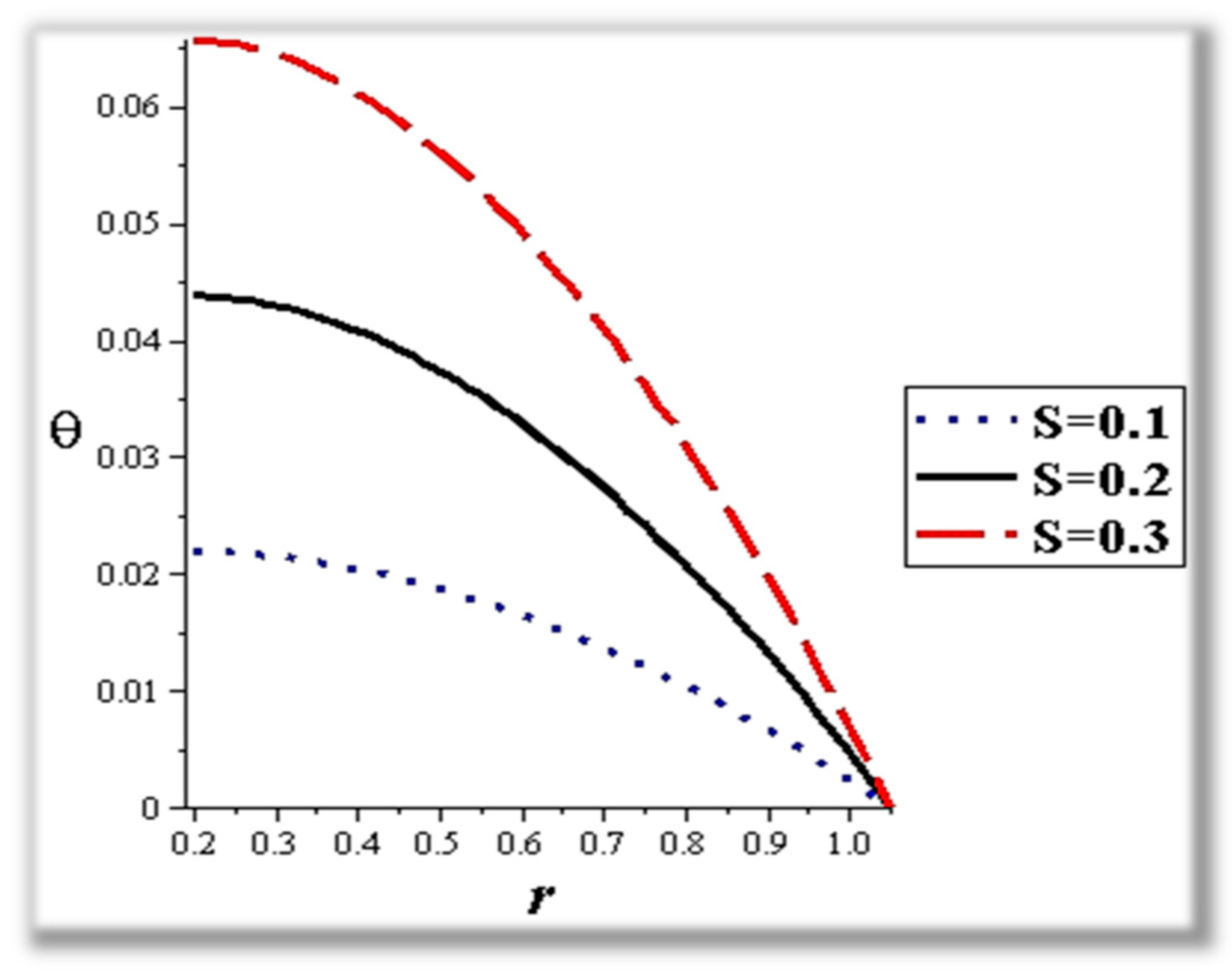
- The flow rate and amplitude ratio increase the temperature, while the temperature decreases with slip conditions and increasing fluid suspension concentration.
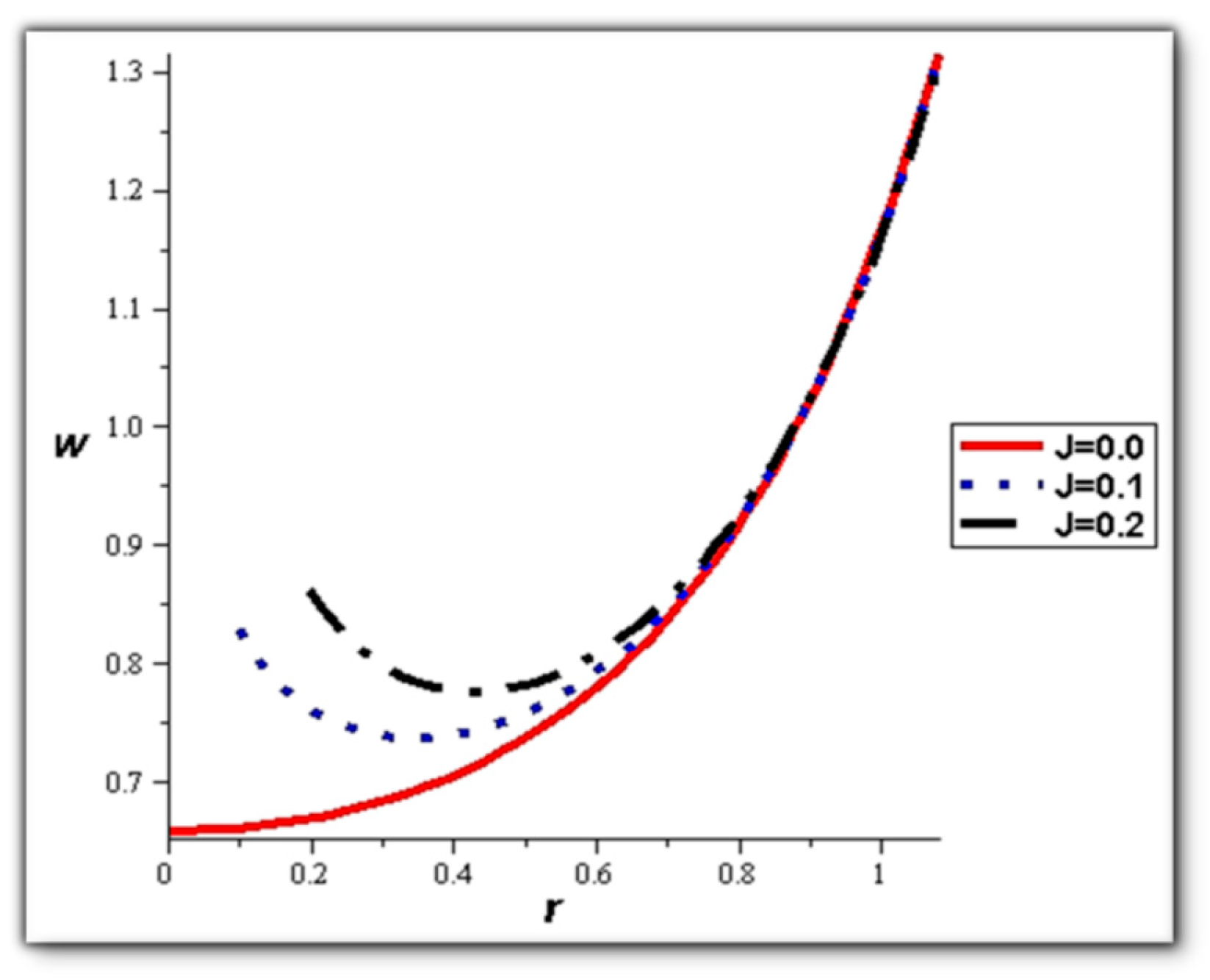
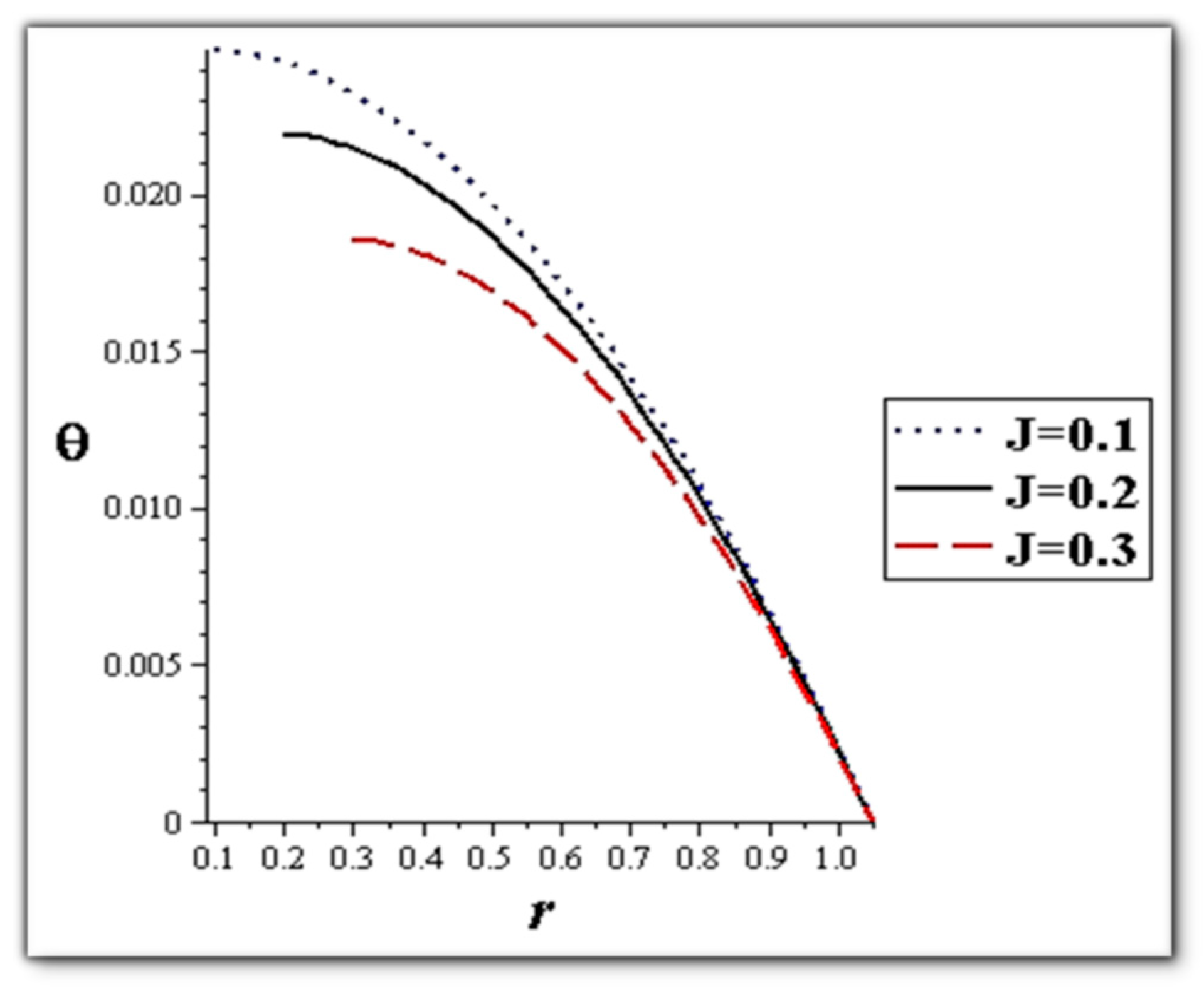
- Catheter size enhances the thermal effect.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Definition | Unit |
| a1 | Catheter radius | cm |
| Specific heat at constant pressure | Joule/kg.K | |
| D | Source term of heat | Joule |
| Ha | Hartmann number | Dimensionless |
| J = a1/ | Catheter size | Dimensionless |
| Knf | Nanofluid thermal conductivity | W/(m·K) |
| 1/k` | Permeability parameter | cm2 |
| Kn = Ω/ | Knudsen number | Dimensionless |
| λ | Wave length | cm |
| Pressure | N/cm2 | |
| r׳, z׳ | Polar coordinates | cm |
| Re = / | Reynolds number | Dimensionless |
| Main tube radius | cm | |
| S | Source term of heat | Dimensionless |
| T׳ | Temperature | K |
| To | Ambient temperature | K |
| t` | Time | sec |
| u׳, w׳ | Velocity components | cm/s |
| uo | Wave propagation velocity | cm/s |
| Constant applied magnetic field | Tesla (T) | |
| Amplitude of the peristaltic wave | cm | |
| δ = / | Amplitude ratio in tube | Dimensionless |
| ε = | Wave number | Dimensionless |
| θ | Dimensionless temperature | Dimensionless |
| Ω | Mean free path | cm |
| μ f | Coefficient of dynamic viscosity of the fluid | Pa.s |
| μ nf | Coefficient of dynamic viscosity of the nanofluid mixture | Pa.s |
| ρ | Density | Kg/cm3 |
| σ | Electrical conductivity | Simens/cm |
| φ | Nanoparticle concentration | Dimensionless |
| Stream function | cm2/s | |
| m1 | Wall tension of the artery | Kg.cm/s2 |
| m2 | Mass per unit area of the artery | Kg/cm2 |
| m3 | Viscous damping coefficient of the artery | Kg/s |
References
- Pandey, A.; Teixeira, J.A.C. Current Developments in Biotechnology and Bioengineering. In Foundations of Biotechnology and Bioengineering; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Huang, Y.; Lan, Y.; Thomson, Y.S.; Fang, J.A.; Hoffmann, W.C.; Lacey, R.E. Development of soft computing and applications in agricultural and biological engineering. Comput. Electron. Agric. 2010, 71, 107–127. [Google Scholar] [CrossRef]
- Norotte, C.; Marga, F.S.; Niklason, L.E.; Forgacs, G. Scaffold-free vascular tissue engineering using bioprinting. Biomaterials 2009, 30, 5910–5917. [Google Scholar] [CrossRef]
- Pettet, G.J.; Malda, J. Mathematicians in Biologists. Clothes: A Clarion Call for collaboration. In Biotechnology and Bioengineering; Nova Science Publishers: New York, NY, USA, 2008. [Google Scholar]
- Marieb, E.N.; Hoehn, K. Human Anatomy and Physiology, 8th ed.; Benjamin Cummings/Pearson: San Francisco, CA, USA, 2010. [Google Scholar]
- Tripathi, D. Peristaltic transport of fractional Maxwell fluids in uniform tubes: Applications in endoscopy. Comput. Math. Appl. 2011, 62, 1116–1126. [Google Scholar] [CrossRef]
- Sobh, A.M. Slip flow in peristaltic transport of a Carreau fluid in an asymmetric channel. Can. J. Phys. 2009, 87, 957–965. [Google Scholar] [CrossRef]
- Medhavi, A.; Singh, U.K. A two-layered suspension flow induced by peristaltic waves. Int. J. Fluid Mech. 2008, 35, 258–272. [Google Scholar] [CrossRef]
- Abd Elnaby, M.A.; Haroun, M.H. Influence of compliant wall properties on peristaltic motion in two-dimensional channel. Commun. Nonlinear Sci. Numer. Simul. 2008, 13, 738–752. [Google Scholar]
- El-Desoky, I.M. Influence of slip condition on peristaltic transport of a compressible Maxwell fluid through porous medium in a tube. Int. J. Appl. Math. Mech. 2012, 2, 99–117. [Google Scholar]
- Liu, J.; Lu, Y. Preparation of aptamer-linked gold nanoparticle purple aggregates for colorimetric sensing of analytes. Nat. Protoc. 2006, 1, 246–252. [Google Scholar] [CrossRef] [PubMed]
- Lassoued, A.; Lassoued, M.S.; Dkhil, B.; Ammar, S.; Gadri, A. Synthesis, structural, morphological, optical and magnetic characterization of iron oxide (α-Fe2O3) nanoparticles by precipitation method: Effect of varying the nature of precursor. Phys. E Low-Dimens. Syst. Nanostruct. 2018, 97, 328–334. [Google Scholar] [CrossRef]
- Khan, S.; Dewang, Y.; Raghuwanshi, J.; Shrivastava, A.; Sharma, V. Nanoparticles as fuel additive for improving performance and reducing exhaust emissions of internal combustion engines. Int. J. Environ. Anal. Chem. 2022, 102, 319–341. [Google Scholar] [CrossRef]
- Khorramshokouh, S.; Pirouzfar, V.; Kazerouni, Y.; Fayyazbakhsh, A.; Abedini, R. Improving the properties and engine performance of diesel–methanol–nanoparticle blend fuels via optimization of the emissions and engine performance. Energy Fuels 2016, 30, 8200–8208. [Google Scholar] [CrossRef]
- Sarma, C.J.; Sharma, P.; Bora, B.J.; Bora, D.K.; Senthilkumar, N.; Balakrishnan, D.; Ayesh, A.I. Improving the combustion and emission performance of a diesel engine powered with mahua biodiesel and TiO2 nanoparticles additive. Alex. Eng. J. 2023, 72, 387–398. [Google Scholar] [CrossRef]
- Beg, O.A.; Akbar, N.S.; Huda, A.B.; Khan, M.Y. Dynamics of variable-viscosity nanofluid flow with heat transfer in a flexible vertical tube under peristaltic waves. Results Phys. 2017, 7, 413–425. [Google Scholar]
- Nicolle, L.E. Catheter associated urinary tract infections. Antimicrob. Resist. Infect. Control 2014, 3, 23. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, V.P.; Rastogi, R. Blood flow through a stenosed catheterized artery: Effects of hematocrit and stenosis shape. Comput. Math. Appl. 2010, 59, 1377–1385. [Google Scholar] [CrossRef]
- Cho, S.A.; Jang, Y.E.; Ji, S.H.; Kim, E.H.; Lee, J.H.; Kim, H.S.; Kim, J.T. Ultrasound-guided arterial catheterization. Anesth. Pain Med. 2021, 16, 119. [Google Scholar] [CrossRef] [PubMed]
- Dolui, S.; Bhaumik, B.; De, S. Combined effect of induced magnetic field and thermal radiation on ternary hybrid nanofluid flow through an inclined catheterized artery with multiple stenosis. Chem. Phys. Lett. 2023, 811, 140209. [Google Scholar] [CrossRef]
- Sher Akbar, N.; Nadeem, S. Simulation of peristaltic flow of chyme in small intestine for couple stress Fluid. Meccanica 2014, 49, 325–334. [Google Scholar] [CrossRef]
- Ellahi, R.; Bhatti, M.M.; Vafai, K. Effects of heat and mass transfer on peristaltic flow in a non-uniform rectangular duct. Int. J. Heat Mass Transf. 2014, 71, 706–719. [Google Scholar] [CrossRef]
- Vajravelu, K.; Sreenadh, S.; Lakshminarayana, P. The influence of heat transfer on peristaltic transport of a Jeffrey fluid in a vertical porous stratum. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 3107–3125. [Google Scholar] [CrossRef]
- Akbar, N.S.; Nadeem, S.; Hayat, T.; Hendi, A.A. Effects of heat and mass transfer on the peristaltic flow of hyperbolic tangent fluid in an annulus. Int. J. Heat Mass Transf. 2011, 54, 4360–4369. [Google Scholar] [CrossRef]
- Nadeem, S.; Akbar, N.S. Influence of heat and mass transfer on the peristaltic flow of a Johnson Segalman fluid in a vertical asymmetric channel with induced MHD. J. Taiwan Inst. Chem. Eng. 2011, 42, 58–66. [Google Scholar] [CrossRef]
- Khan, L.A.; Raza, M.; Mir, N.A.; Ellahi, R. Effects of different shapes of nanoparticles on peristaltic flow of MHD nanofluids filled in an asymmetric channel: A novel mode for heat transfer enhancement. J. Therm. Anal. Calorim. 2020, 140, 879–890. [Google Scholar] [CrossRef]
- Riaz, A.; Alolaiyan, H.; Razaq, A. Convective heat transfer and magnetohydrodynamics across a peristaltic channel coated with nonlinear nanofluid. Coatings 2019, 9, 816. [Google Scholar] [CrossRef]
- Abd-Alla, A.M.; Abo-Dahab, S.M.; Thabet, E.N.; Abdelhafez, M.A. Heat and mass transfer for MHD peristaltic flow in a micropolar nanofluid: Mathematical model with thermophysical features. Sci. Rep. 2022, 12, 21540. [Google Scholar] [CrossRef] [PubMed]
- Beavers, G.S.; Joseph, D.D. Boundary conditions at a naturally permeable wall. J. Fluid Mech. 1967, 30, 197–207. [Google Scholar] [CrossRef]
- Wang, C. Stagnation flows with slip: Exact solutions of the Navier-Stokes equations. Z. Angew. Math. Und Phys. ZAMP 2003, 54, 184–189. [Google Scholar] [CrossRef]
- Ahmed, M.M.; Eldesoky, I.M.; Abdelsalam, S.I.; El-askary, W.A. The integrated thermal effect in conjunction with slip conditions on peristaltically induced particle fluid transport in a catheterized pipe. J. Porous Media 2020, 23, 695–713. [Google Scholar]
- Zhu, Y.; Granick, S. Limits of the hydrodynamic no-slip boundary condition. Phys. Rev. Lett. 2002, 88, 106102. [Google Scholar] [CrossRef] [PubMed]
- Mishra, A. Thompson and Troian slip effects on ternary hybrid nanofluid flow over a permeable plate with chemical reaction. Numer. Heat Transf. Part B Fundam. 2024, 1–29.–29. [Google Scholar] [CrossRef]
- Eldesoky, I.M.; Abumandour, R.M.; Kamel, M.H.; Abdelwahab, E.T. The combined influences of heat transfer, compliant wall properties and slip conditions on the peristaltic flow through tube. SN Appl. Sci. 2019, 1, 897. [Google Scholar] [CrossRef]
- Khan, A.A.; Tariq, H. Influence of wall properties on the peristaltic flow of a dusty Walter’s B fluid. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 368. [Google Scholar] [CrossRef]
- Eldesoky, I.M.; Abdelsalam, S.I.; El-Askary, W.A.; Ahmed, M.M. Concurrent development of thermal energy with magnetic field on a particle-fluid suspension through a porous conduit. Bio Nanosci. 2019, 9, 186–202. [Google Scholar] [CrossRef]
- Hasany, S.; Ahmed, I.; Rajan, J.; Rehman, A. Systematic review of the preparation techniques of iron oxide magnetic nanoparticles. Nanosci. Nanotechnol. 2012, 2, 148–158. [Google Scholar] [CrossRef]
- Eldesoky, I.M.; Abdelsalam, S.I.; El-Askary, W.A.; El-Refaey, A.M.; Ahmed, M.M. Joint effect of magnetic field and heat transfer on particulate fluid suspension in a catheterized wavy tube. BioNanoScience 2019, 9, 723–739. [Google Scholar] [CrossRef]
- Akbar, N.S.; Maraj, E.; Butt, A.W. Copper nanoparticles impinging on a curved channel with compliant walls and peristalsis. Eur. Phys. J. Plus 2014, 129, 193. [Google Scholar] [CrossRef]
- Shapiro, A.H.; Jaffrin, M.Y.; Weinberg, S.L. Peristaltic pumping with long wavelengths at low Reynolds number. J. Fluid Mech. 1969, 37, 799–825. [Google Scholar] [CrossRef]
- Afifi, N.; Mahmoud, S.; Al-Isede, H. Effect of magnetic field and wall properties on peristaltic motion of micropolar fluid. Int. Math. Forum 2011, 6, 1345–1356. [Google Scholar]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magdy, M.; Abumandour, R.; Eldesoky, I.; Alotaibi, H. Synergistic Exploration of Heat Transfer for Integration Magnetohydrodynamics of Nanofluids Peristaltic Transport within Annular Tubes. Mathematics 2024, 12, 2024. https://doi.org/10.3390/math12132024
Magdy M, Abumandour R, Eldesoky I, Alotaibi H. Synergistic Exploration of Heat Transfer for Integration Magnetohydrodynamics of Nanofluids Peristaltic Transport within Annular Tubes. Mathematics. 2024; 12(13):2024. https://doi.org/10.3390/math12132024
Chicago/Turabian StyleMagdy, Muhammad, Ramzy Abumandour, Islam Eldesoky, and Hammad Alotaibi. 2024. "Synergistic Exploration of Heat Transfer for Integration Magnetohydrodynamics of Nanofluids Peristaltic Transport within Annular Tubes" Mathematics 12, no. 13: 2024. https://doi.org/10.3390/math12132024
APA StyleMagdy, M., Abumandour, R., Eldesoky, I., & Alotaibi, H. (2024). Synergistic Exploration of Heat Transfer for Integration Magnetohydrodynamics of Nanofluids Peristaltic Transport within Annular Tubes. Mathematics, 12(13), 2024. https://doi.org/10.3390/math12132024







