Quasi-Analytical Solution of Kepler’s Equation as an Explicit Function of Time
Abstract
:1. Introduction
The Orbit Equation
2. Methodology
2.1. Step 0
2.2. Step 1
2.3. Step 2
2.4. Step 3
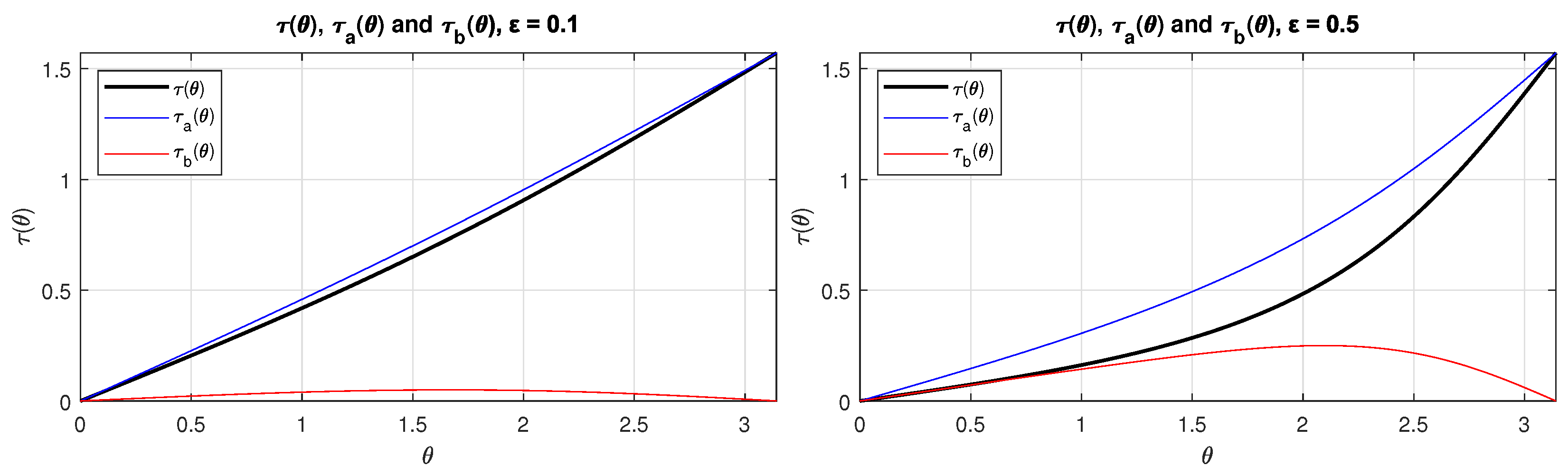
2.4.1. Method A
2.4.2. Method B
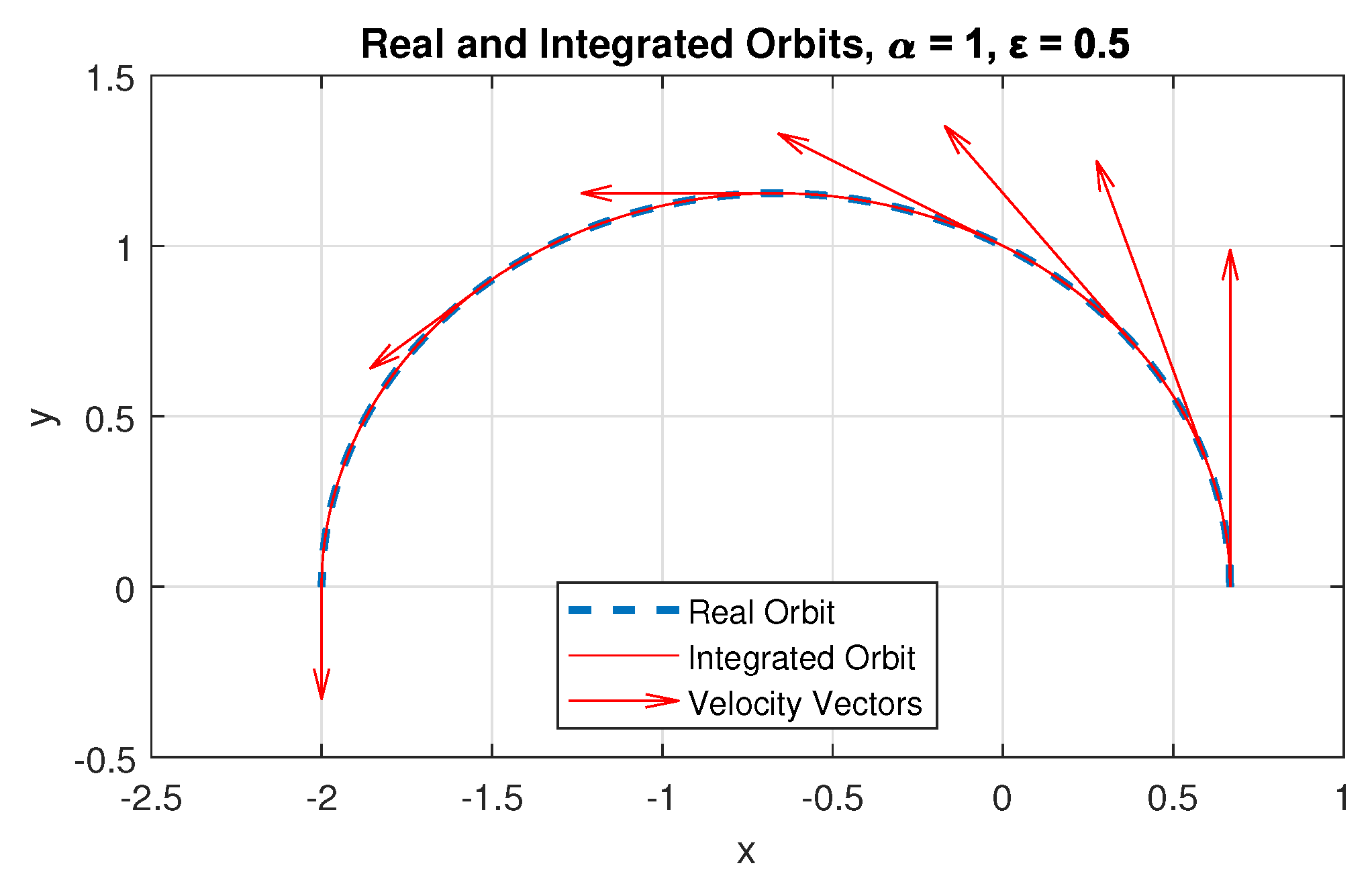
3. Results
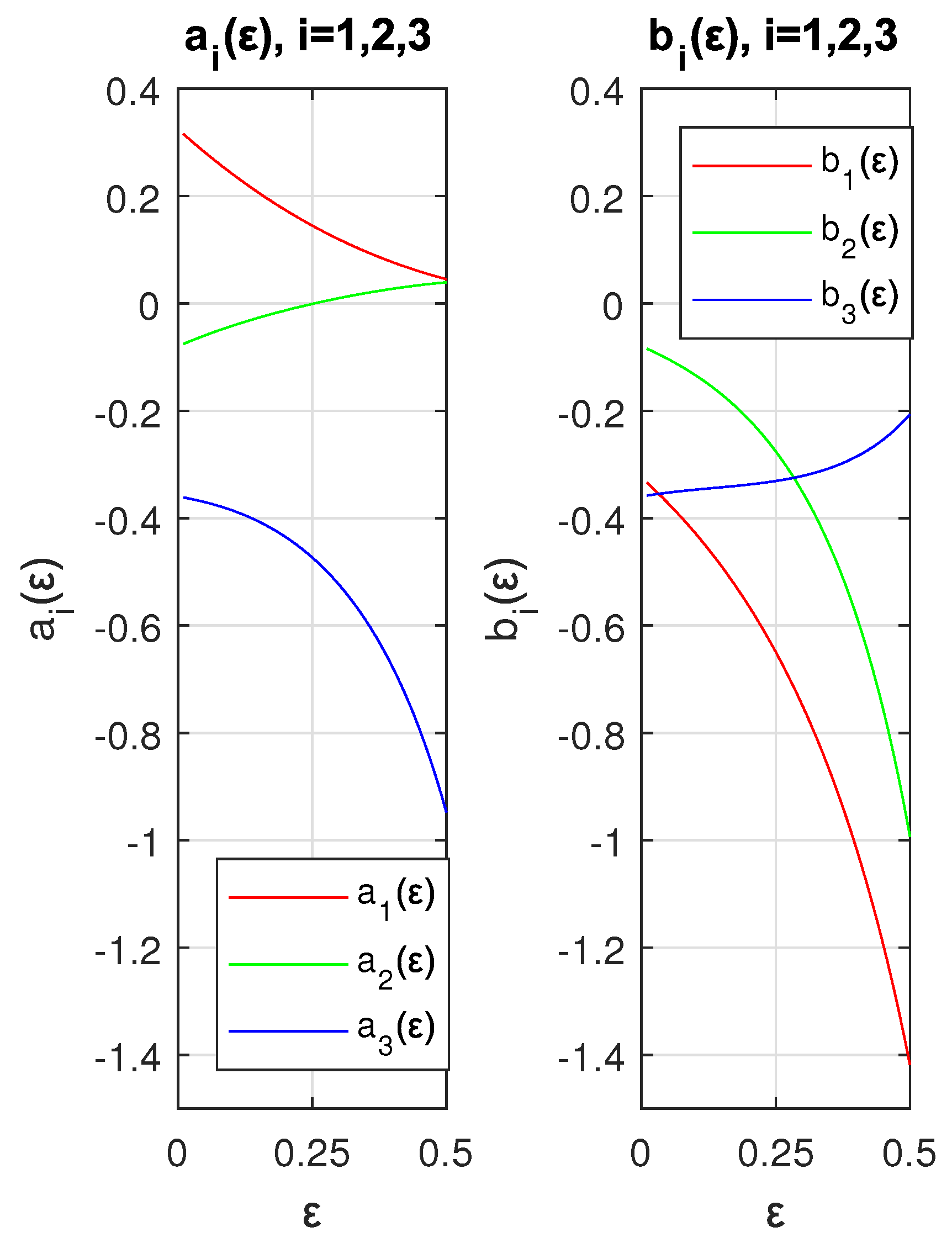
3.1. Method A
3.2. Method B
3.3. Equations of Motion for the Planets
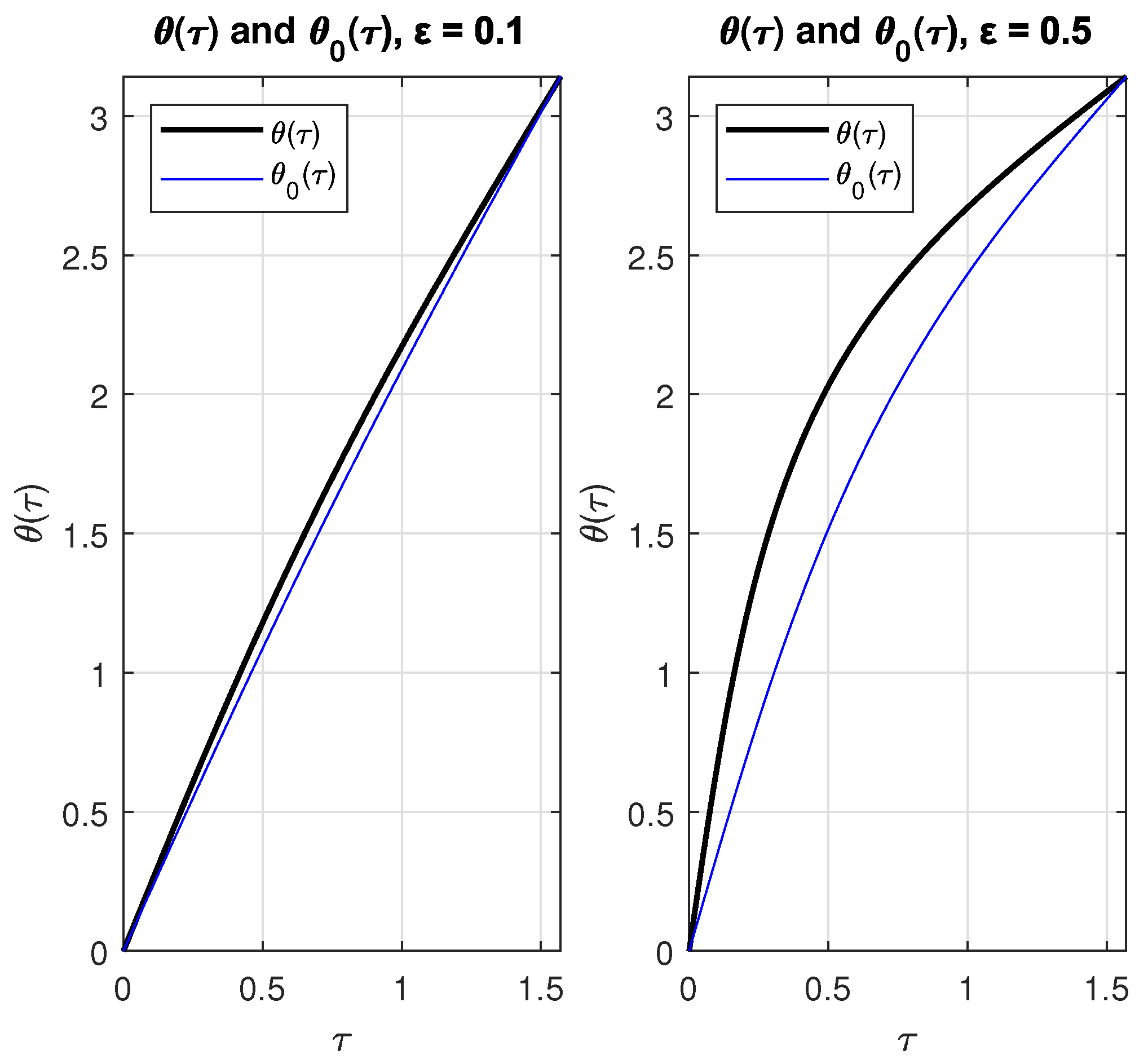
4. Solution to Kepler’s Equation
5. Remarks and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Integration of Equation (uid1)
Appendix B. Proofs of Limits Equations (18) and (19)
References
- Krisciunas, K. Demonstrating the elliptical orbit of Mars using naked eye data. Am. J. Phys. 2019, 87, 885–893. [Google Scholar] [CrossRef]
- Goldstein, H. Classical Mechanics, 2nd ed.; Addison-Wesley: Reading, UK, 2020. [Google Scholar]
- Baisheng, W.; Zhou, Y.; Lim, C.; Zhong, H. A new solution approach via analytical approximation of the elliptic kepler equation. Acta Astronaut. 2023, 202, 303–310. [Google Scholar] [CrossRef]
- Colwell, P. Solving Kepler’s Equation over Three Centuries; Willman-Bell, Inc.: Richmond, VA, USA, 1993. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Mechanics, 3rd ed.; Elsevier Butterworth-Heinemann: Burlington, NJ, USA, 1976. [Google Scholar]
- Hagihara, Y. Celestial Mechanics: Perturbation Theory, 1st ed.; MIT Press: Cambridge, MA, USA, 1970. [Google Scholar]
- Danby, J.M.A. Fundamentals of Celestial Mechanics: Perturbation Theory, 2nd ed.; Willmann-Bell: New York, NY, USA, 1988. [Google Scholar]
- Odell, A.W.; Gooding, R.H. Procedures for Solving Kepler’s Equation. Cel. Mech. 1986, 38, 307–334. [Google Scholar] [CrossRef]
- Sacchetti, A. Francesco Carlini: Kepler’s equation and the asymptotic solution to singular differential equations. Hist. Math. 2020, 53, 1–32. [Google Scholar] [CrossRef]
- González-Gaxiola, O.; Hernández-Linares, S. An Efficient Iterative Method for Solving the Elliptical Kepler’s Equation. Int. J. Appl. Comput. Math 2021, 7, 1–14. [Google Scholar] [CrossRef]
- Abubekerov, M.K.; Gostev, N.Y. Solution of Kepler’s equation with machine precision, Astr. Rep. 2020, 64, 1060–1066. [Google Scholar] [CrossRef]
- Dubinov, A.E.; Galidakis, I.N. Explicit solution of the Kepler equation. Phys. Part. Nuclei Lett. 2007, 4, 213–216. [Google Scholar] [CrossRef]
- Elenin, G.G.; Elenina, T.G. Parametrization of the Solution of the Kepler Problem and New Adaptive Numerical Methods Based on This Parametrization. Differ. Equ. 2018, 54, 911–918. [Google Scholar] [CrossRef]
- Markley, F.L. Kepler Equation solver. Celest. Mech. Dyn. Astron. 1995, 63, 101–111. [Google Scholar] [CrossRef]
- Simha, A. An algebra and trigonometry-based proof of Kepler’s first law. Am. J. Phys. 2021, 89, 1009–1011. [Google Scholar] [CrossRef]
- Easton, R.W.; Anderson, R.L.; Lo, M.W. Conic transfer arcs for Kepler’s problem. Am. J. Phys. 2022, 90, 666–671. [Google Scholar] [CrossRef]
- Calvo, M.; Elipe, A.; Rández, L. On the integral solution of elliptic Kepler’s equation. Celest. Mech. Dyn. Astron. 2023, 135, 26. [Google Scholar] [CrossRef]
- Borghi, R. On the Bessel solution of Kepler’s Equation. Mathematics 2024, 12, 154. [Google Scholar] [CrossRef]
- Orlando, F.; de Souza, C.F.; Zarro, C.; Terra, P. Kepler’s equation and some of its pearls. Am. J. Phys. 2018, 86, 849–858. [Google Scholar] [CrossRef]
- Zheng, M.; Luo, J.; Dang, Z. Machine Learning-Based Solution of Kepler’s Equation; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; SPIE: Bellingham, WA, USA, 2022. [Google Scholar] [CrossRef]
- Marion, J.B. Classical Dynamics, 1st ed.; Academic Press Inc.: Cambridge, MA, USA, 1965. [Google Scholar]
- Mikkola, S.A. A cubic approximation for Kepler’s equation. Cel. Mech. 2018, 86, 849–858. [Google Scholar] [CrossRef]




| Planet | ME | MAE | RMSE | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Earth | 0.0167 | 0.310 | −0.073 | −0.363 | −0.340 | −0.087 | −0.357 | |||
| Pluto | 0.2488 | 0.146 | −0.001 | −0.472 | −0.647 | −0.274 | −0.331 |
| Mercury | Venus | Earth | Mars | Jupiter | Saturn | Uranus | Neptune | Pluto | |
|---|---|---|---|---|---|---|---|---|---|
| 0.2056 | 0.0067 | 0.0167 | 0.0935 | 0.0489 | 0.0565 | 0.0457 | 0.0113 | 0.2488 | |
| 0.17053517 | 0.31862395 | 0.30977503 | 0.24694331 | 0.28234256 | 0.27609996 | 0.28499728 | 0.31453377 | 0.14561949 | |
| −0.01166110 | −0.07705003 | −0.0728542 | −0.04432541 | −0.06014655 | −0.05731287 | −0.06135776 | −0.07510434 | −0.0012376 | |
| −0.43861374 | −0.36086494 | −0.36274460 | −0.38289299 | −0.36985666 | −0.37179675 | −0.36907139 | −0.36171170 | −0.47217706 | |
| −0.57282655 | −0.33074668 | −0.34005421 | −0.42023391 | −0.37170483 | −0.37957121 | −0.36843946 | −0.33499871 | −0.64694223 | |
| −0.22240872 | −0.08288098 | −0.08742593 | −0.12920751 | −0.10334339 | −0.10741403 | −0.10166725 | −0.08494978 | −0.27396065 | |
| −0.33681377 | −0.35855961 | −0.35697508 | −0.34764211 | −0.35253989 | −0.35161930 | −0.35294044 | −0.35781706 | −0.33108759 | |
| ME | |||||||||
| MAE | |||||||||
| RMSE | |||||||||
| 208 | 0.11 | 0.92 | 80 | 52 | 131 | 163 | 12 | 39,000 |
| Range of | (0,0.1] | (0.1,0.25] | (0.25,0.5] | (0.5,0.7] | (0.7,1.0) |
|---|---|---|---|---|---|
| 0.32464090 | 0.32455984 | 0.32493519 | 0.33117795 | 0.34799892 | |
| −0.90342437 | −0.90136299 | −0.90443788 | −0.94434644 | −1.02378174 | |
| 0.79798292 | 0.77956682 | 0.78688870 | 0.87179816 | 0.99672027 | |
| −0.24897861 | −0.19074605 | −0.19470806 | −0.25486105 | −0.32027157 | |
| −0.07992819 | −0.07920359 | −0.07197522 | −0.06646582 | −0.11098658 | |
| 0.43404410 | 0.41648507 | 0.33665965 | 0.29615322 | 0.50088661 | |
| −0.64017363 | −0.49188569 | −0.19208276 | −0.09396227 | −0.40748236 | |
| 0.75341116 | 0.31132787 | −0.07256170 | −0.15093252 | 0.00894242 | |
| −0.35968044 | −0.35742442 | −0.15675162 | 6.29837377 | 154.50791377 | |
| −0.17220655 | −0.22278632 | −2.20357719 | −41.92862343 | −715.24316797 | |
| −0.64666864 | −0.26055305 | 6.28024901 | 87.40520959 | 1105.82612363 | |
| −1.78408496 | −2.80408480 | −10.06884121 | −65.08749455 | −577.96129585 | |
| −0.32463507 | −0.32142203 | −0.09294215 | 6.21933680 | 138.39317241 | |
| −0.90434048 | −0.97722350 | −3.24616805 | −42.18802414 | −643.15766068 | |
| −1.11071449 | −0.54525397 | 7.00356134 | 86.74796714 | 996.53861794 | |
| −1.63153199 | −3.15712303 | −11.61829996 | −65.86504267 | −524.44755555 | |
| −0.07992299 | −0.07527391 | 0.29080466 | 11.97863173 | 287.23614950 | |
| −0.43571269 | −0.54094614 | −4.16198706 | −76.07319110 | −1326.12648115 | |
| −0.78063318 | 0.03353877 | 12.02291626 | 158.84151291 | 2048.91985911 | |
| −2.10660888 | −4.29567159 | −17.65734989 | −117.20310761 | −1068.68369232 | |
| −0.35968350 | −0.36025835 | −0.44346730 | −3.54853992 | −81.17535211 | |
| 0.17171182 | 0.18402819 | 0.99888552 | 20.06864682 | 372.42195877 | |
| −0.59524043 | −0.68312683 | −3.34688052 | −42.20159066 | −574.67488149 | |
| 1.45594036 | 1.66666199 | 4.58818969 | 30.87266047 | 298.77577747 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beloiarov, A.N.; Beloiarov, V.A.; Cruz-Gómez, R.C.; Monzón, C.O.; Romero, J.L. Quasi-Analytical Solution of Kepler’s Equation as an Explicit Function of Time. Mathematics 2024, 12, 2108. https://doi.org/10.3390/math12132108
Beloiarov AN, Beloiarov VA, Cruz-Gómez RC, Monzón CO, Romero JL. Quasi-Analytical Solution of Kepler’s Equation as an Explicit Function of Time. Mathematics. 2024; 12(13):2108. https://doi.org/10.3390/math12132108
Chicago/Turabian StyleBeloiarov, A. N., V. A. Beloiarov, R. C. Cruz-Gómez, C. O. Monzón, and J. L. Romero. 2024. "Quasi-Analytical Solution of Kepler’s Equation as an Explicit Function of Time" Mathematics 12, no. 13: 2108. https://doi.org/10.3390/math12132108







