Optimal Investment for Defined-Contribution Pension Plans with the Return of Premium Clause under Partial Information
Abstract
:1. Introduction
2. Model and Assumptions
2.1. Financial Market and Filtered Estimation
2.2. Wealth Process
3. Solution of the Optimization Problem
3.1. HJB Equation and Verification Theorem
3.2. Optimal Strategy
3.3. Suboptimal Strategy
3.3.1. Ignoring Learning
3.3.2. Utility Loss
4. Numerical Illustration
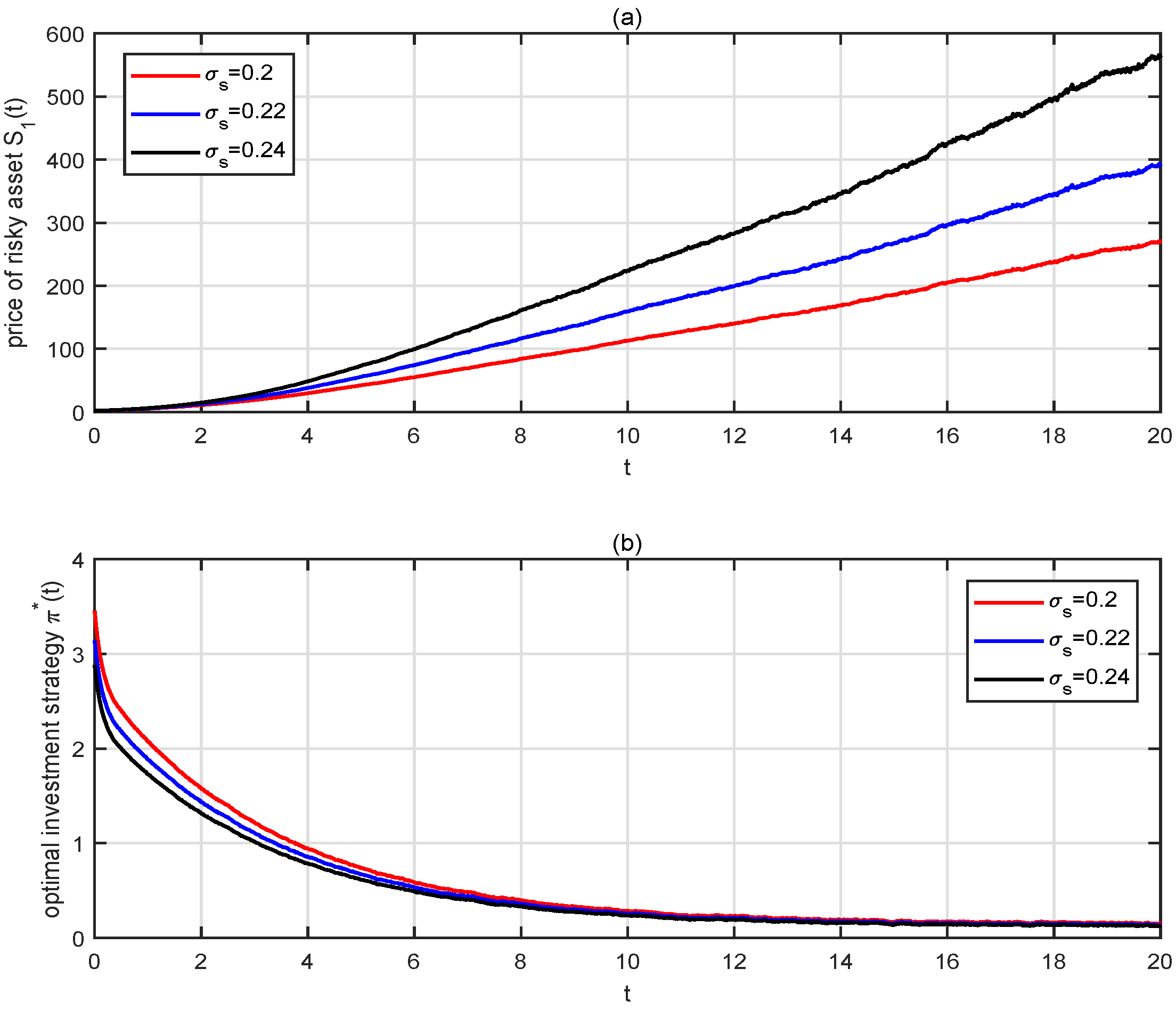
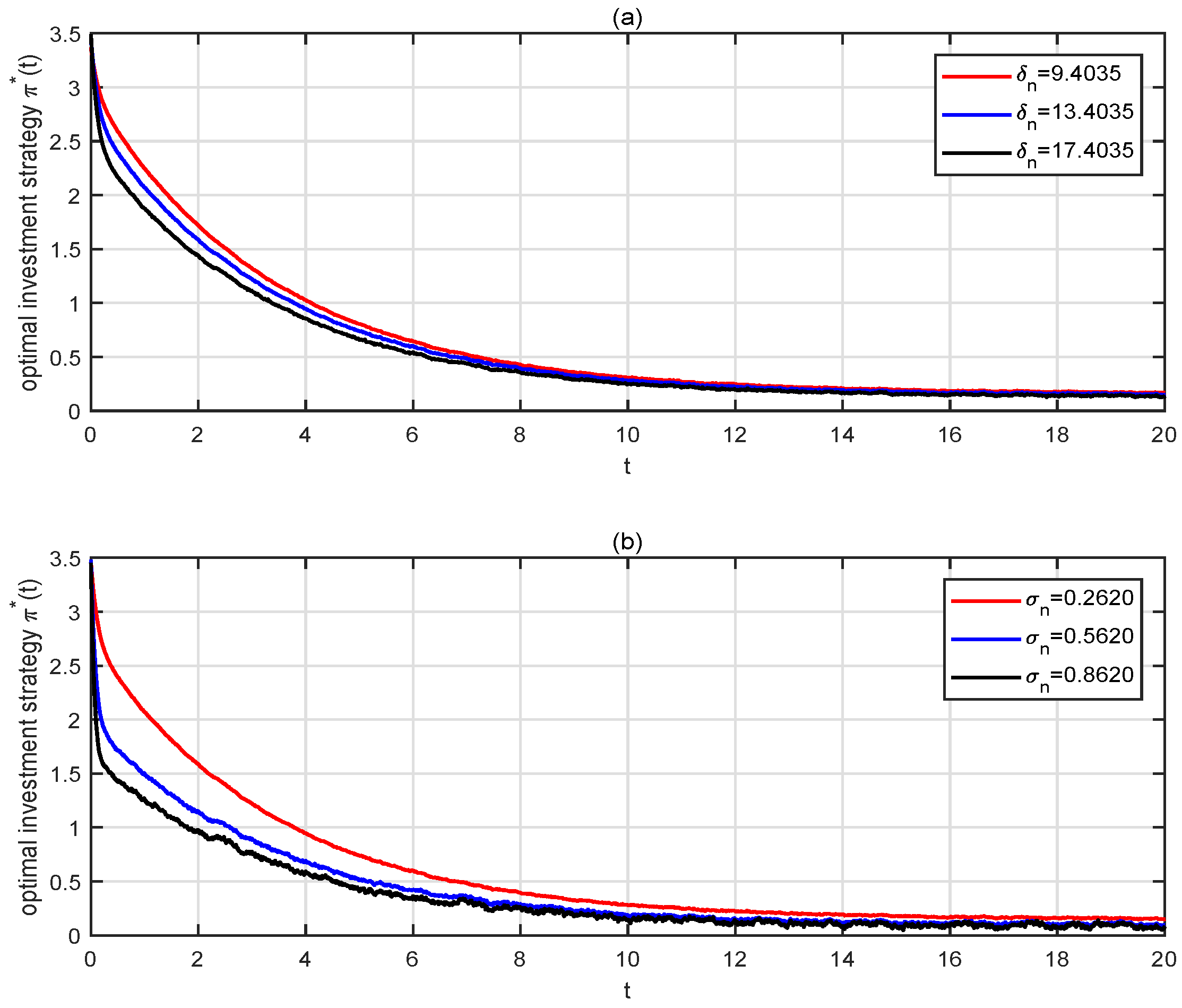
4.1. Numerical Results of the Optimal Investment Strategies
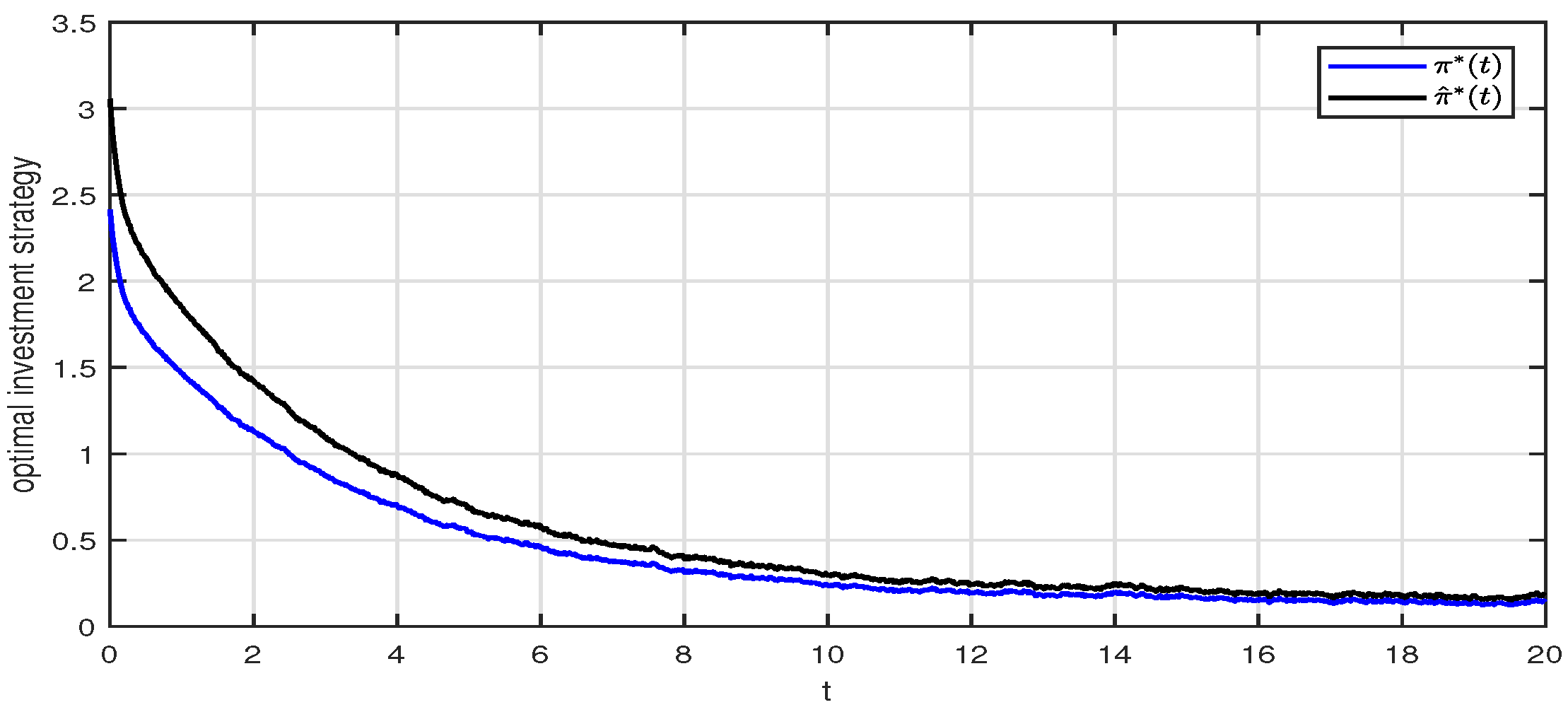
4.2. Comparison of the Optimal and Suboptimal Strategies
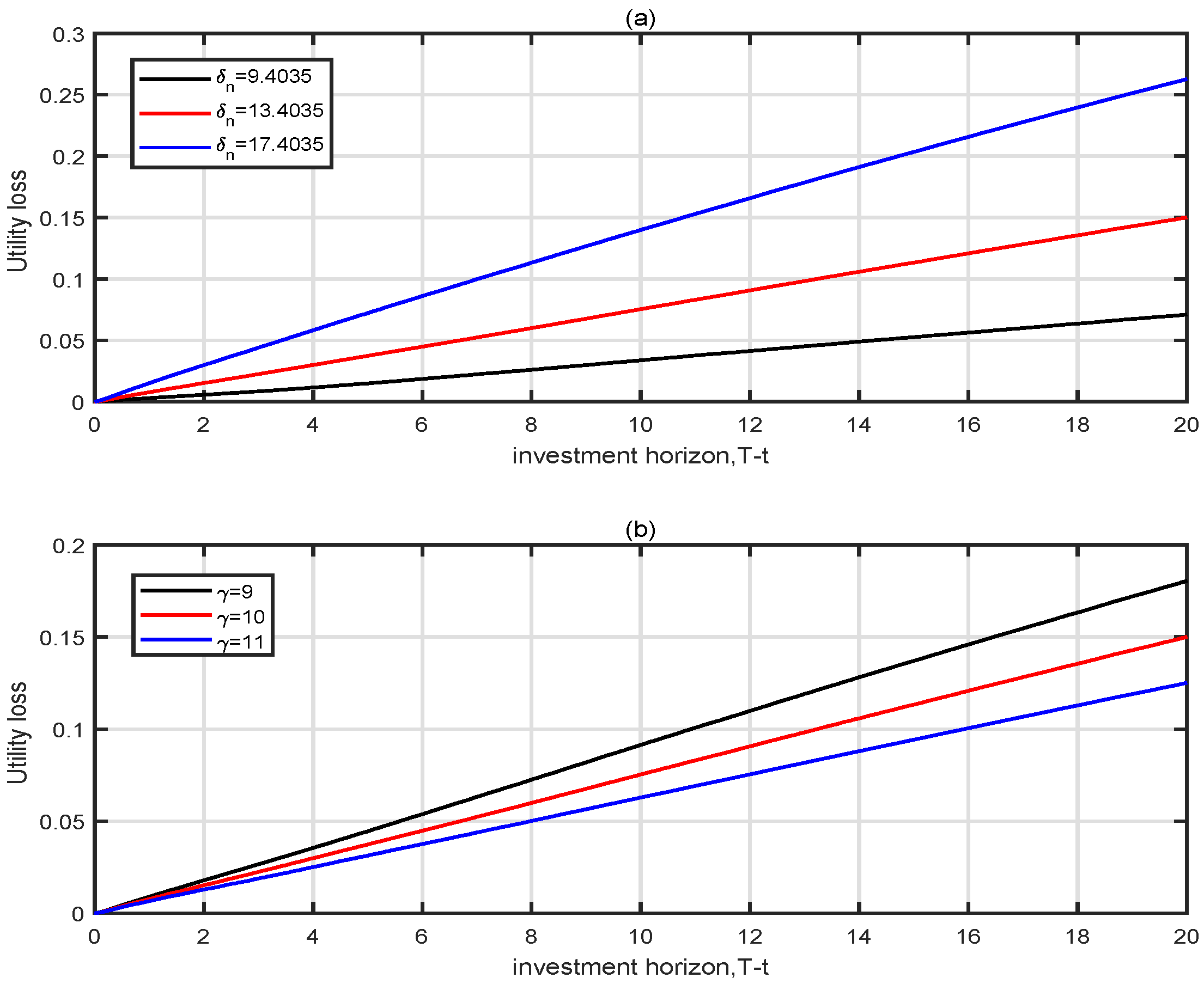
4.3. Analysis of Utility Losses from Ignoring Learning
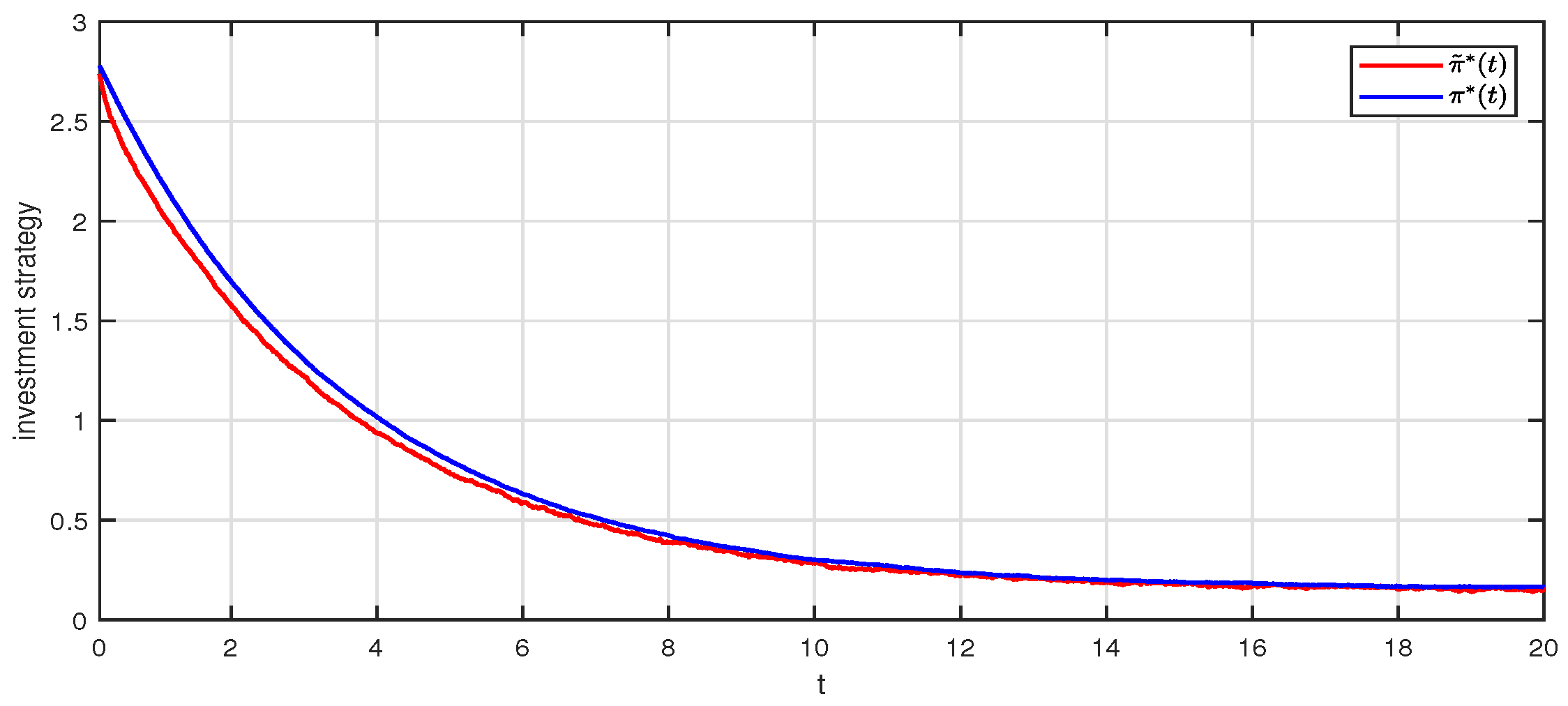
4.4. Effect of the Return of Premium Clause on the Optimal Investment Strategy
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Li, D.; Ng, W.L. Optimal dynamic portfolio selection: Multiperiod mean-variance formulation. Math. Financ. 2000, 10, 387–406. [Google Scholar] [CrossRef]
- Xiao, H.; Zhou, Z.; Ren, T.; Bai, Y.; Liu, W. Time-consistent strategies for multi-period mean-variance portfolio optimization with the serially correlated returns. Commun.-Stat.-Theory Methods 2020, 49, 2831–2868. [Google Scholar] [CrossRef]
- Battocchio, P.; Menoncin, F. Optimal pension management in a stochastic framework. Insur. Math. Econ. 2004, 34, 79–95. [Google Scholar] [CrossRef]
- Han, N.; Hung, M. Optimal asset allocation for DC pension plans under inflation. Insur. Math. Econ. 2012, 51, 172–181. [Google Scholar] [CrossRef]
- Zeng, Y.; Li, D.; Chen, Z.; Yang, Z. Ambiguity aversion and optimal derivative-based pension investment with stochastic income and volatility. J. Econ. Dyn. Control 2018, 88, 70–103. [Google Scholar] [CrossRef]
- Wang, P.; Li, Z.; Sun, J. Robust portfolio choice for a DC pension plan with inflation risk and mean-reverting risk premium under ambiguity. Optimization 2021, 70, 191–224. [Google Scholar] [CrossRef]
- Wang, P.; Li, Z. Robust optimal investment strategy for an AAM of DC pension plans with stochastic interest rate and stochastic volatility. Insur. Math. Econ. 2018, 80, 67–83. [Google Scholar] [CrossRef]
- Dong, Y.; Zheng, H. Optimal investment of DC pension plan under shortselling constraints and portfolio insurance. Insur. Math. Econ. 2019, 85, 47–59. [Google Scholar] [CrossRef]
- Lv, W.; Tian, L.; Zhang, X. Optimal Defined Contribution Pension Management with Jump Diffusions and Common Shock Dependence. Mathematics 2023, 11, 2954. [Google Scholar] [CrossRef]
- He, L.; Liang, Z. Optimal investment strategy for the DC plan with the return of premiums clauses in a mean–variance framework. Insur. Math. Econ. 2013, 53, 643–649. [Google Scholar] [CrossRef]
- Bian, L.; Li, Z.; Yao, H. Pre-commitment and equilibrium investment strategies for the DC pension plan with regime switching and a return of premiums clause. Insur. Math. Econ. 2018, 81, 78–94. [Google Scholar] [CrossRef]
- Chang, H.; Li, J. Robust equilibrium strategy for DC pension plan with the return of premiums clauses in a jump-diffusion model. Optimization 2023, 72, 463–492. [Google Scholar] [CrossRef]
- Li, D.; Rong, X.; Zhao, H.; Yi, B. Equilibrium investment strategy for DC pension plan with default risk and return of premiums clauses under CEV model. Insur. Math. Econ. 2017, 72, 6–20. [Google Scholar] [CrossRef]
- Lai, C.; Liu, S.; Wu, Y. Optimal portfolio selection for a defined-contribution plan under two administrative fees and return of premium clauses. J. Comput. Appl. Math. 2021, 398, 113694. [Google Scholar] [CrossRef]
- Nie, G.; Chen, X.; Chang, H. Time-consistent strategies between two competitive DC pension plans with the return of premiums clauses and salary risk. Commun. Stat.-Theory Methods 2023, 1–22. [Google Scholar] [CrossRef]
- Fama, E.; French, K. Permanent and temporary components of stock prices. J. Political Econ. 1988, 96, 246–273. [Google Scholar] [CrossRef]
- Boudoukh, J.; Michaely, R.; Richardson, M.; Roberts, M. On the importance of measuring payout yield: Implications for empirical asset pricing. J. Financ. 2007, 62, 877–915. [Google Scholar] [CrossRef]
- Brennan, M. The role of learning in dynamic portfolio decisions. Rev. Financ. 1998, 1, 295–306. [Google Scholar] [CrossRef]
- Van Binsbergen, J.; Koijen, R. Predictive regressions: A present-value approach. J. Financ. 2010, 65, 1439–1471. [Google Scholar] [CrossRef]
- Branger, N.; Larsen, L.; Munk, C. Robust portfolio choice with ambiguity and learning about return predictability. J. Bank. Financ. 2013, 37, 1397–1411. [Google Scholar] [CrossRef]
- Escobar, M.; Ferrando, S.; Rubtsov, A. Portfolio choice with stochastic interest rates and learning about stock return predictability. Int. Rev. Econ. Financ. 2016, 41, 347–370. [Google Scholar] [CrossRef]
- Wang, P.; Shen, Y.; Zhang, L.; Kang, Y. Equilibrium investment strategy for a DC pension plan with learning about stock return predictability. Insur. Math. Econ. 2021, 100, 384–407. [Google Scholar] [CrossRef]
- Xia, Y. Learning about predictability: The effects of parameter uncertainty on dynamic asset allocation. J. Financ. 2001, 56, 205–246. [Google Scholar] [CrossRef]
- Huang, J.; Chen, Z. Optimal risk asset allocation of a loss-averse bank with partial information under inflation risk. Financ. Res. Lett. 2021, 38, 101513. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, L.; Li, Z. Asset allocation for a DC pension plan with learning about stock return predictability. J. Ind. Manag. Optim. 2022, 18, 3847–3877. [Google Scholar] [CrossRef]
- Harvey, C. The specification of conditional expectations. J. Empir. Financ. 2001, 8, 573–637. [Google Scholar] [CrossRef]
- Whitelaw, R. Time variations and covariations in the expectation and volatility of stock market returns. J. Financ. 1994, 49, 515–541. [Google Scholar] [CrossRef]
- Chacko, G.; Viceira, L. Dynamic consumption and portfolio choice with stochastic volatility in incomplete markets. Rev. Financ. Stud. 2005, 18, 1369–1402. [Google Scholar] [CrossRef]
- Liptser, R.; Shiryaev, A. Statistics of Random Processes. Volume 2: Applications; Springer: Heidelberg/Berlin, Germany, 2001. [Google Scholar]
- Fleming, W.; Soner, H. Controlled Markov Processes and Viscosity Solutions; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2006; Volume 25. [Google Scholar]
- Heston, S. A closed-form solution for options with stochastic volatility with applications to bonds and currency options. Rev. Financ. Stud. 1993, 6, 327–343. [Google Scholar] [CrossRef]
- Larsen, L.S.; Munk, C. The costs of suboptimal dynamic asset allocation: General results and applications to interest rate risk, stock volatility risk and growth/value tilts. J. Econ. Dyn. Control. 2012, 36, 266–293. [Google Scholar] [CrossRef]
- Flor, C.; Larsen, L. Robust portfolio choice with stochastic interest rates. Ann. Financ. 2014, 10, 243–265. [Google Scholar] [CrossRef]


| c | r | ||||||
|---|---|---|---|---|---|---|---|
| 100 | 20 | 0.01 | 10 | 3.7816 | 1.6315 | 13.4035 | 0.0366 |
| 1 | 0.2935 | 4.0942 | −2.1493 | 0 | 0.2 | 0.1467 | 0.2620 |
| T | |||||||
| −0.2186 | −0.2164 | −0.4913 | 40 | 10 | 1 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Zhang, H.; Wang, Y.; Huang, Y. Optimal Investment for Defined-Contribution Pension Plans with the Return of Premium Clause under Partial Information. Mathematics 2024, 12, 2130. https://doi.org/10.3390/math12132130
Liu Z, Zhang H, Wang Y, Huang Y. Optimal Investment for Defined-Contribution Pension Plans with the Return of Premium Clause under Partial Information. Mathematics. 2024; 12(13):2130. https://doi.org/10.3390/math12132130
Chicago/Turabian StyleLiu, Zilan, Huanying Zhang, Yijun Wang, and Ya Huang. 2024. "Optimal Investment for Defined-Contribution Pension Plans with the Return of Premium Clause under Partial Information" Mathematics 12, no. 13: 2130. https://doi.org/10.3390/math12132130




