Sensitivity Analysis and Uncertainty of a Myocardial Infarction Model †
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mathematical Models
2.1.1. SIRS Model
2.1.2. Heart Infarction Model
- Necrotic phase: heart cells die rapidly (starts soon after after MI).
- Acute inflammatory phase: the immune system responds and starts eliminating dead cells (1–7 days).
- Sub-acute granulation phase: myofibroblasts proliferate to form granulation tissue to help stabilize the heart (1–3 weeks).
- Chronic scar phase: myofibroblast proliferation continues, leading to the generation of the final scar tissue (1 month).
2.2. Sensitivity Analysis
2.3. Stochastic Differential Equations
3. Results
3.1. SIRS Epidemic Model
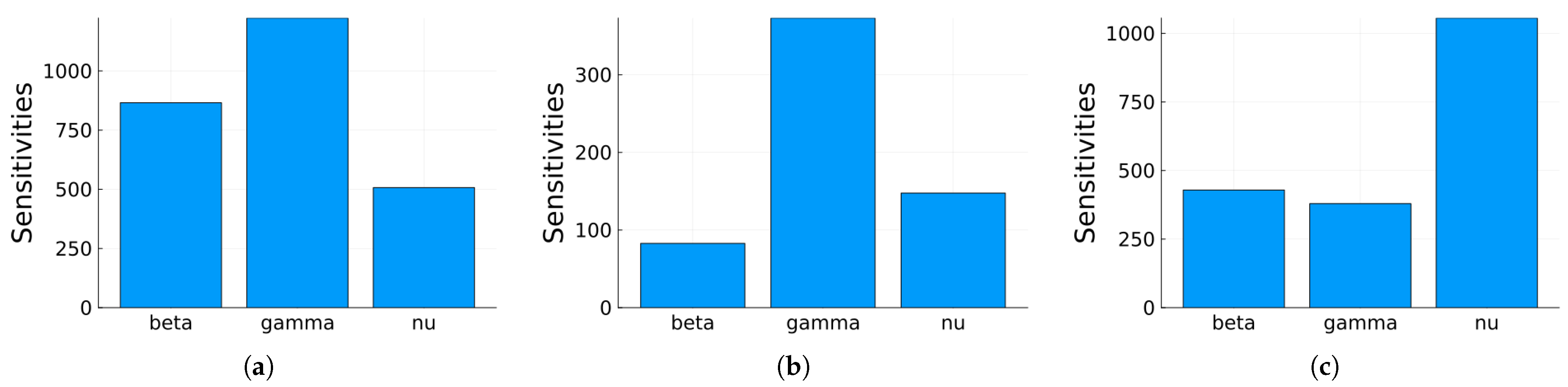
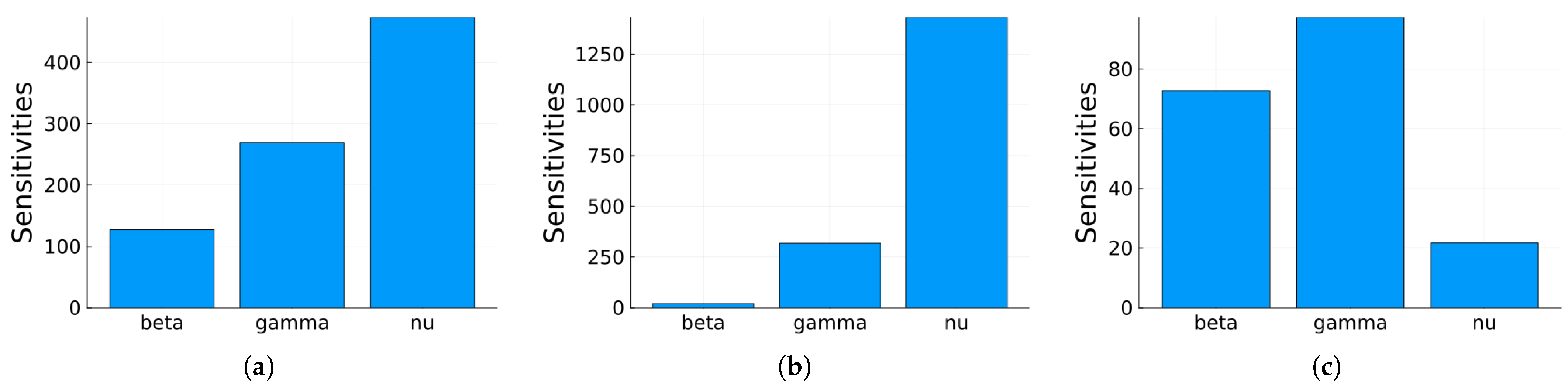
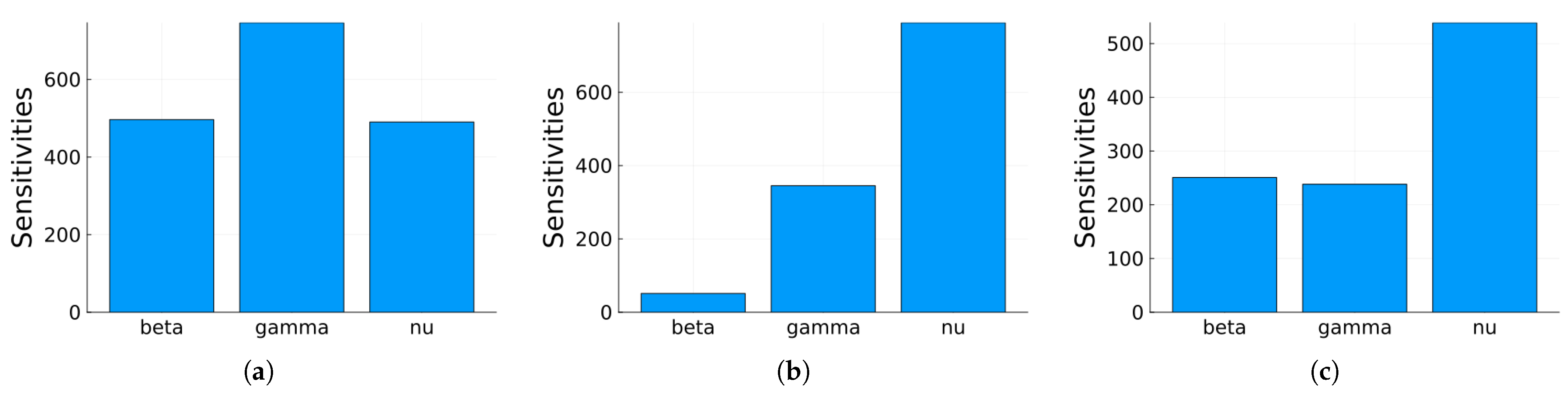
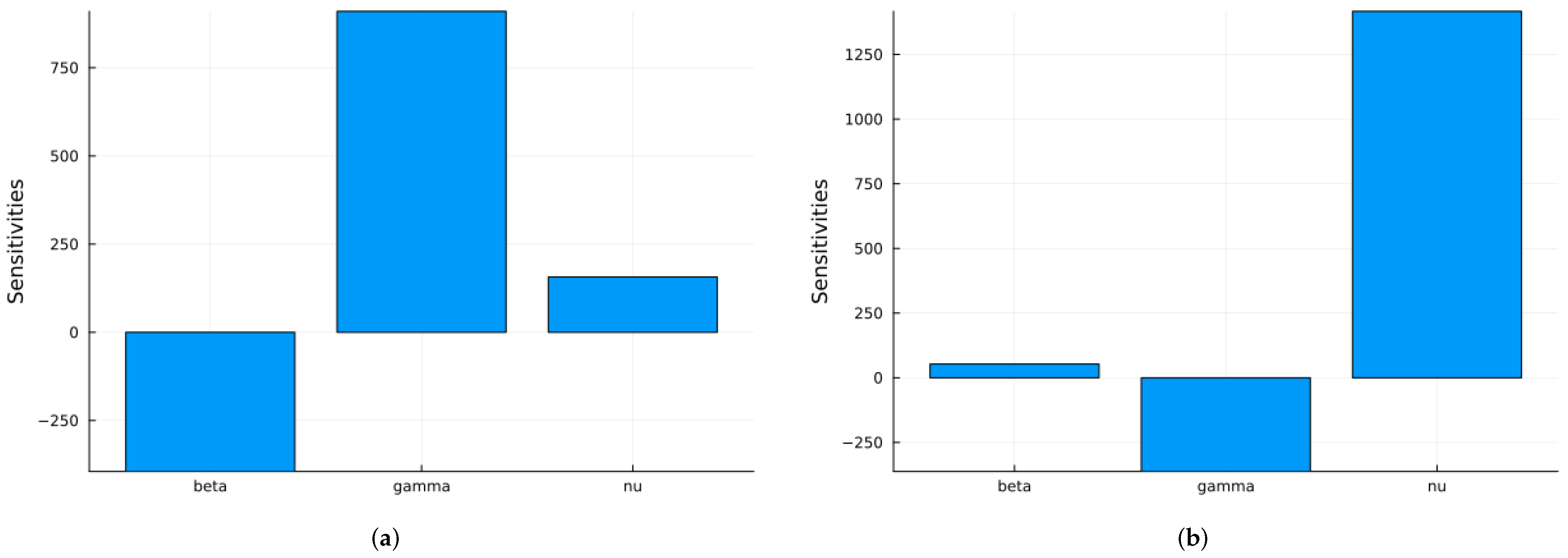
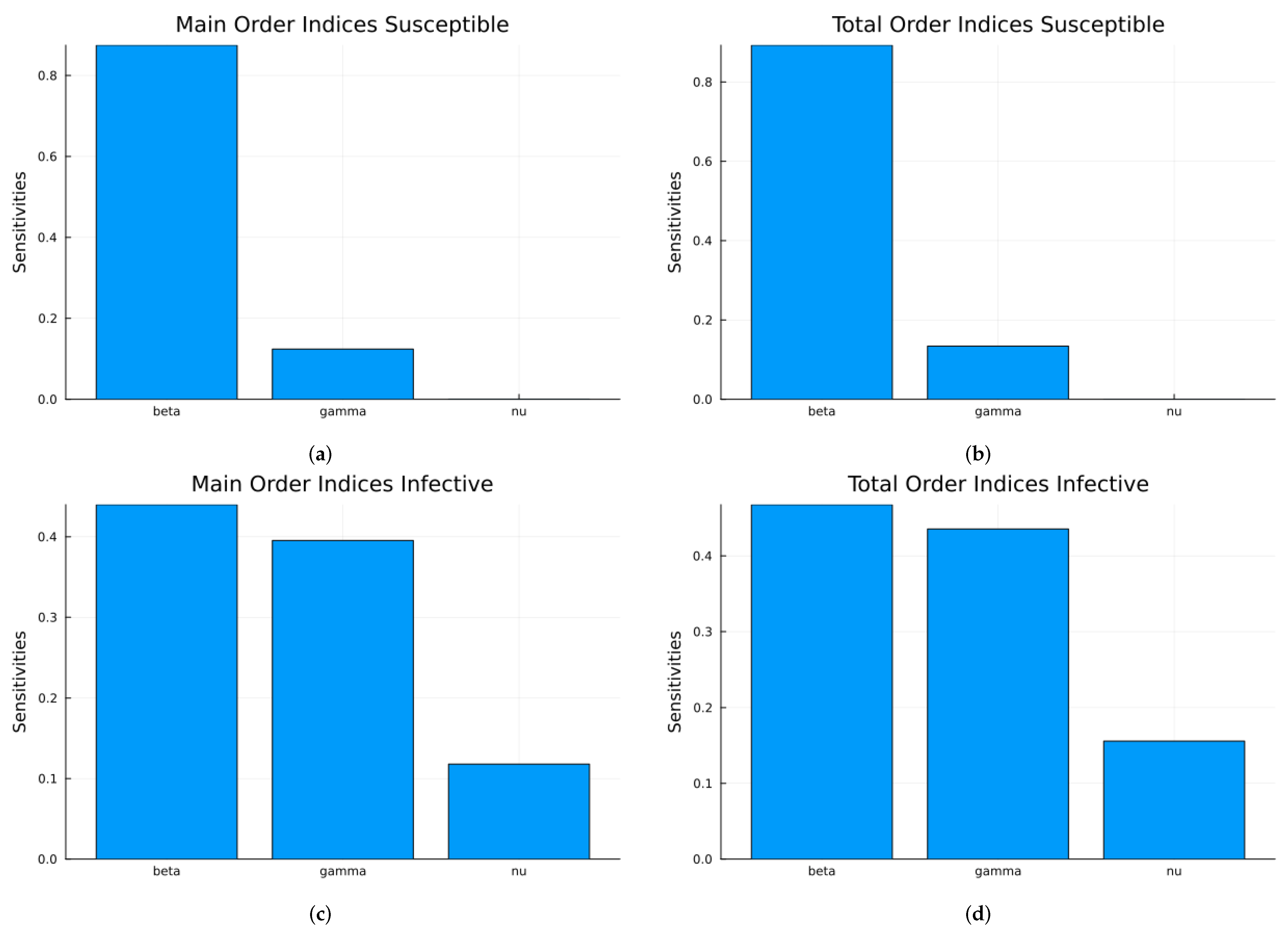
3.1.1. Sensitivity Analysis
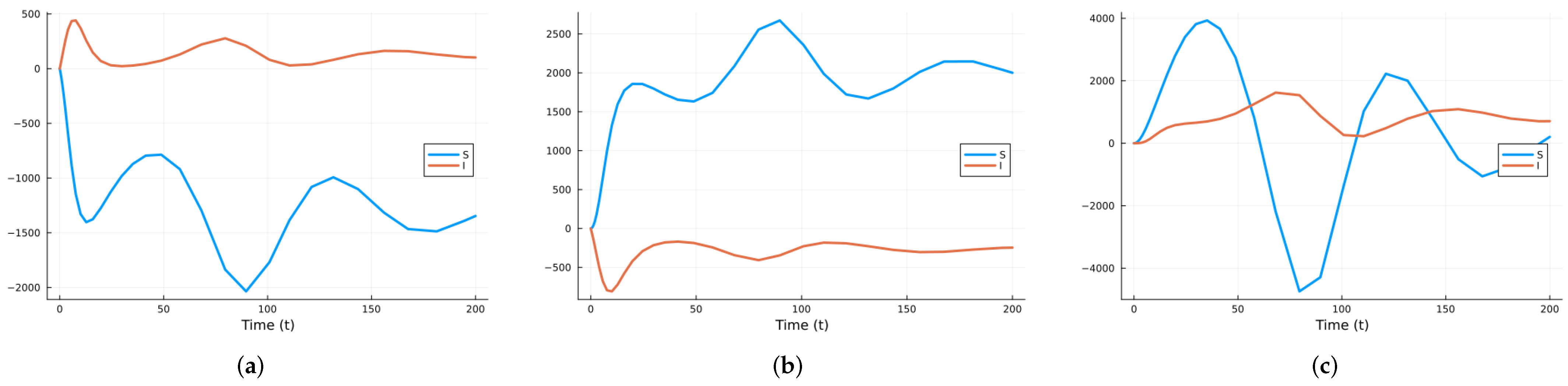
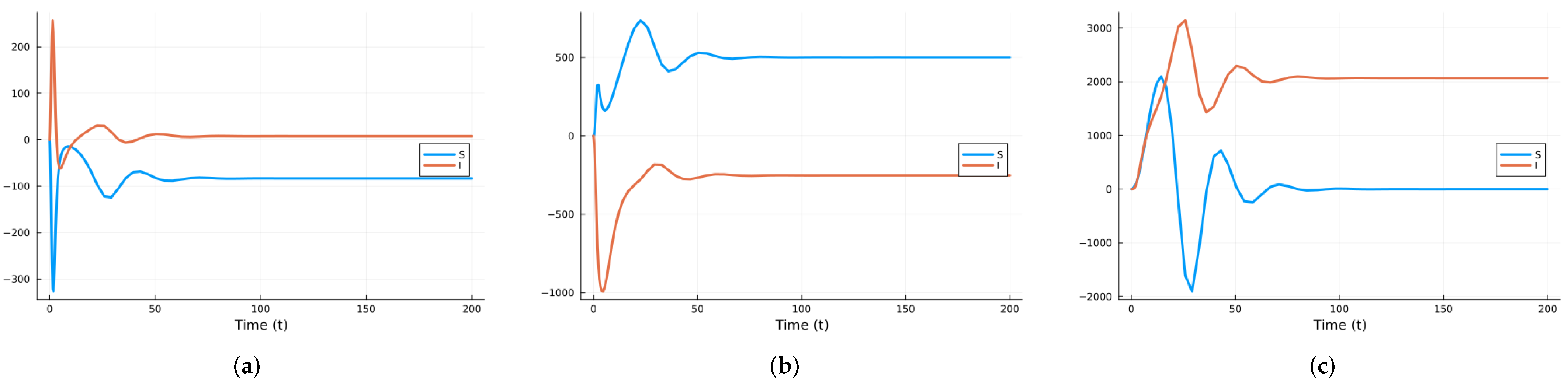
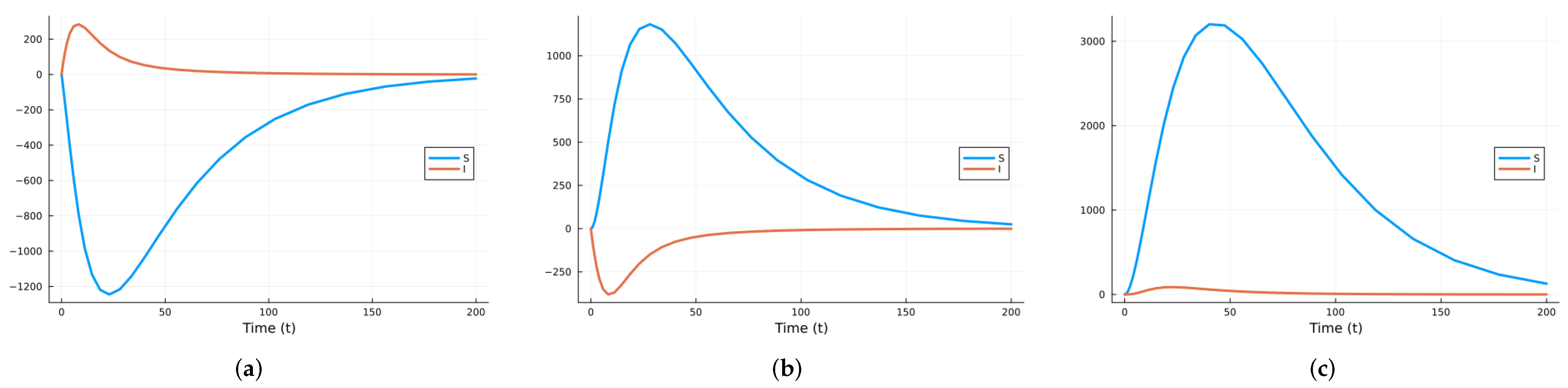
3.1.2. Stochastic and Random Differential Equations
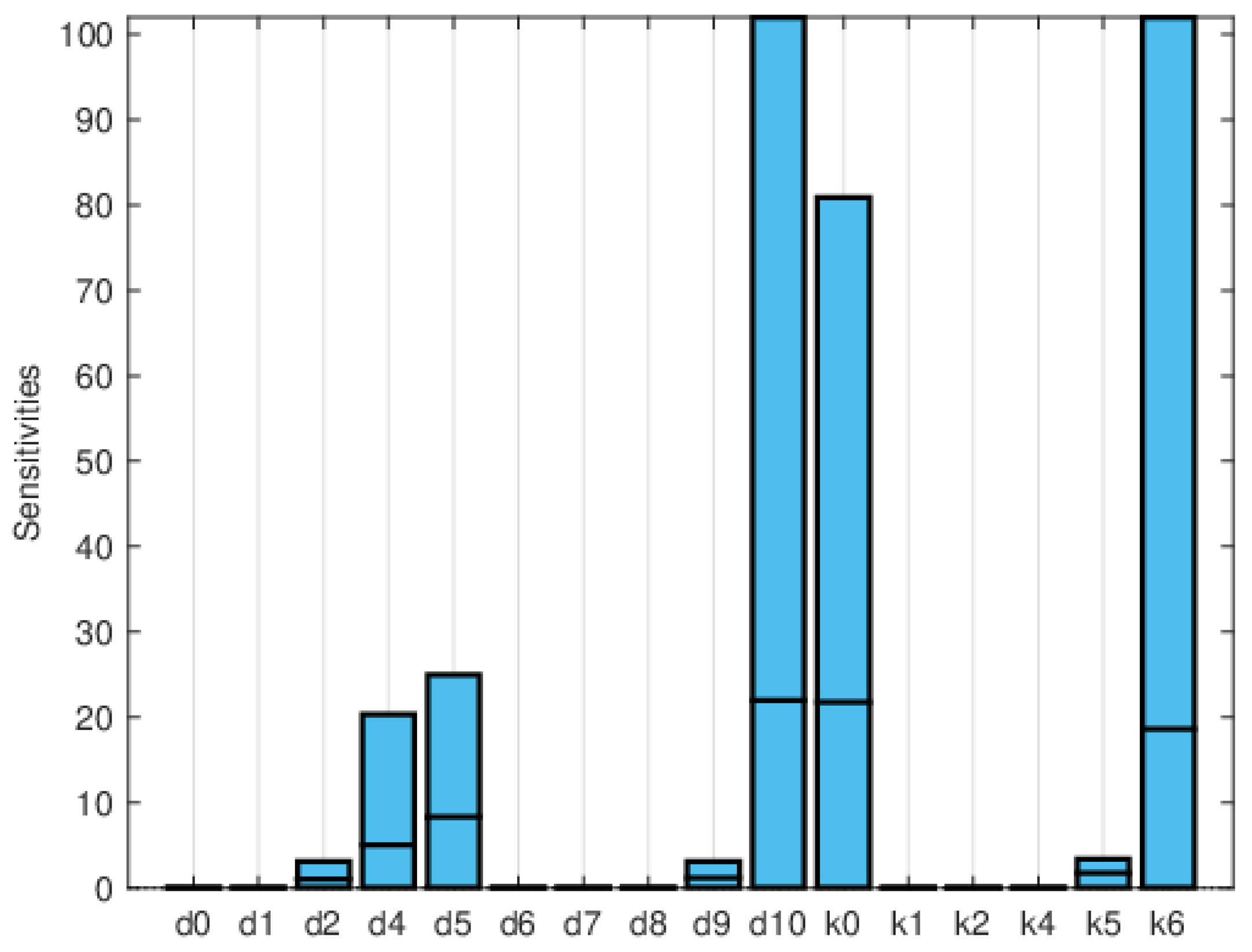
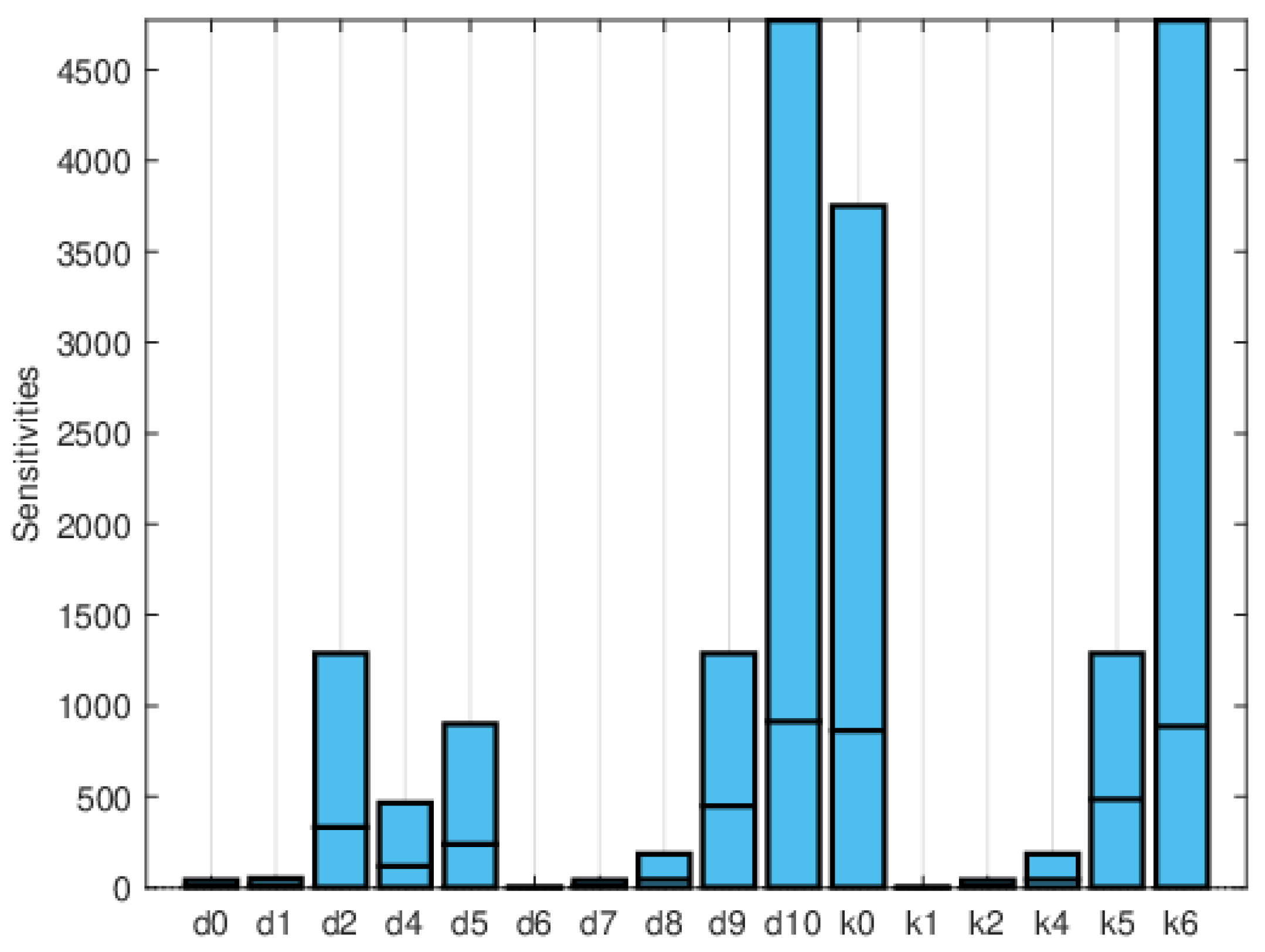
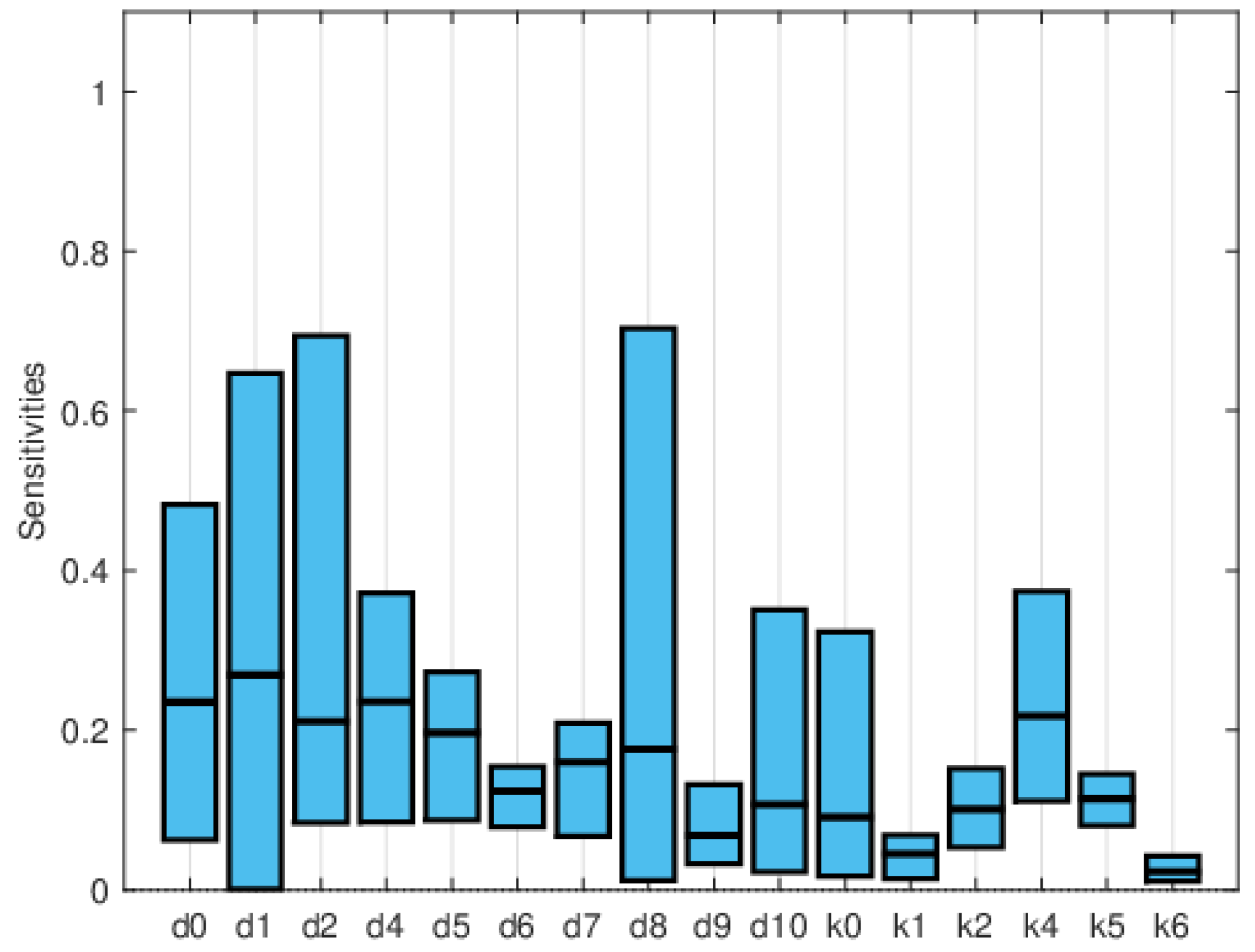
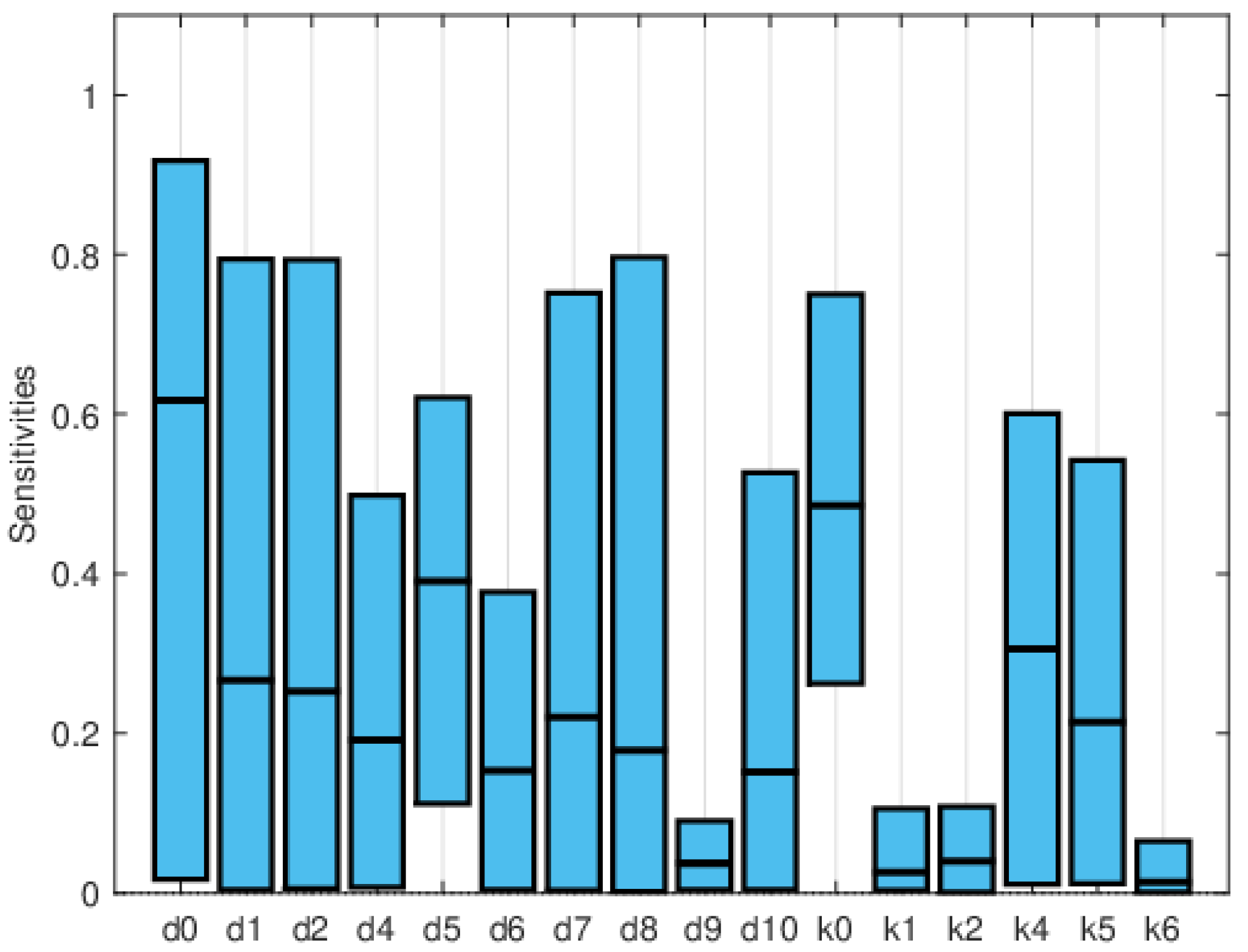
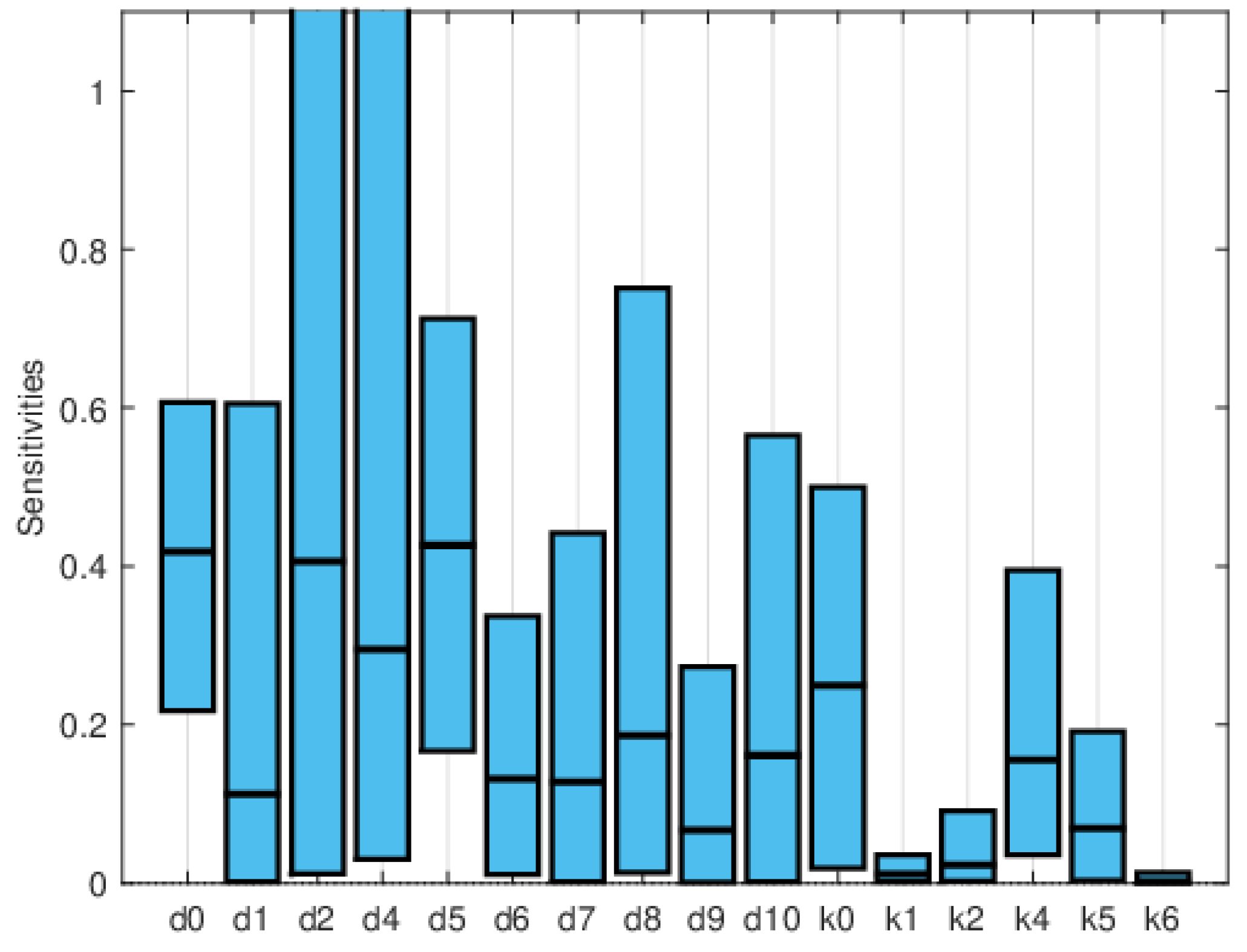
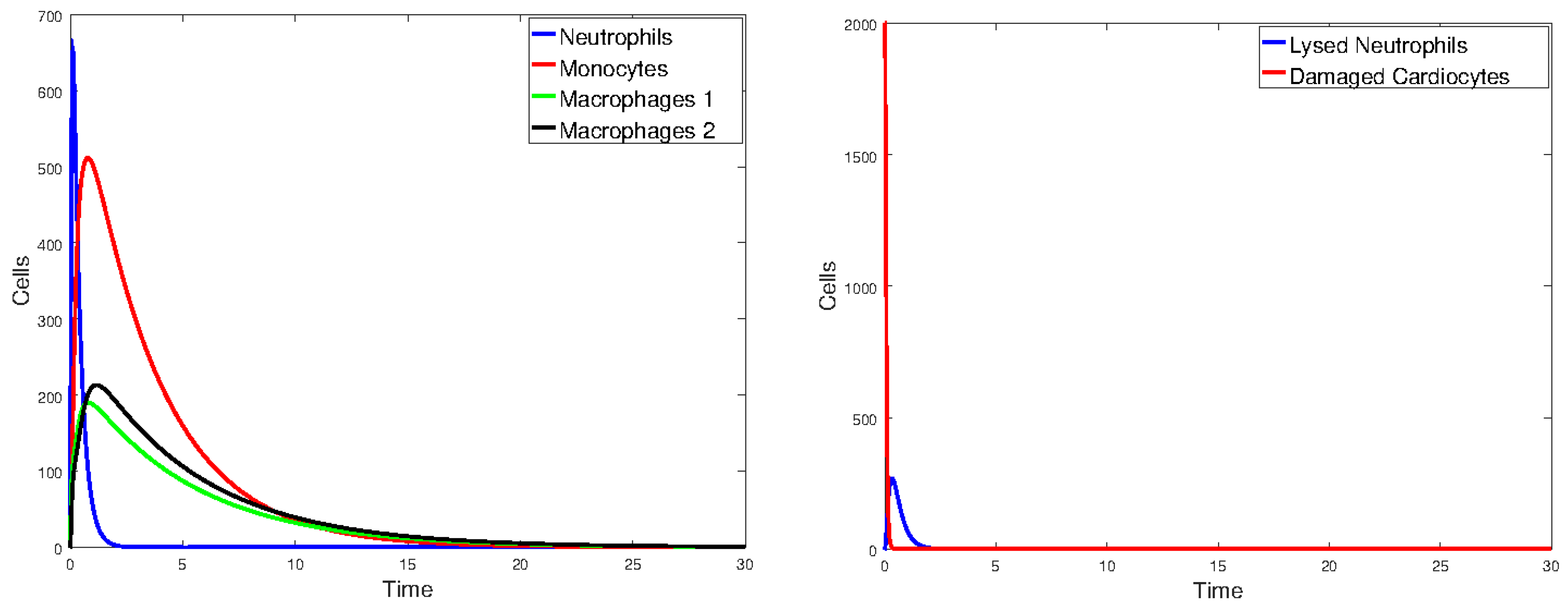
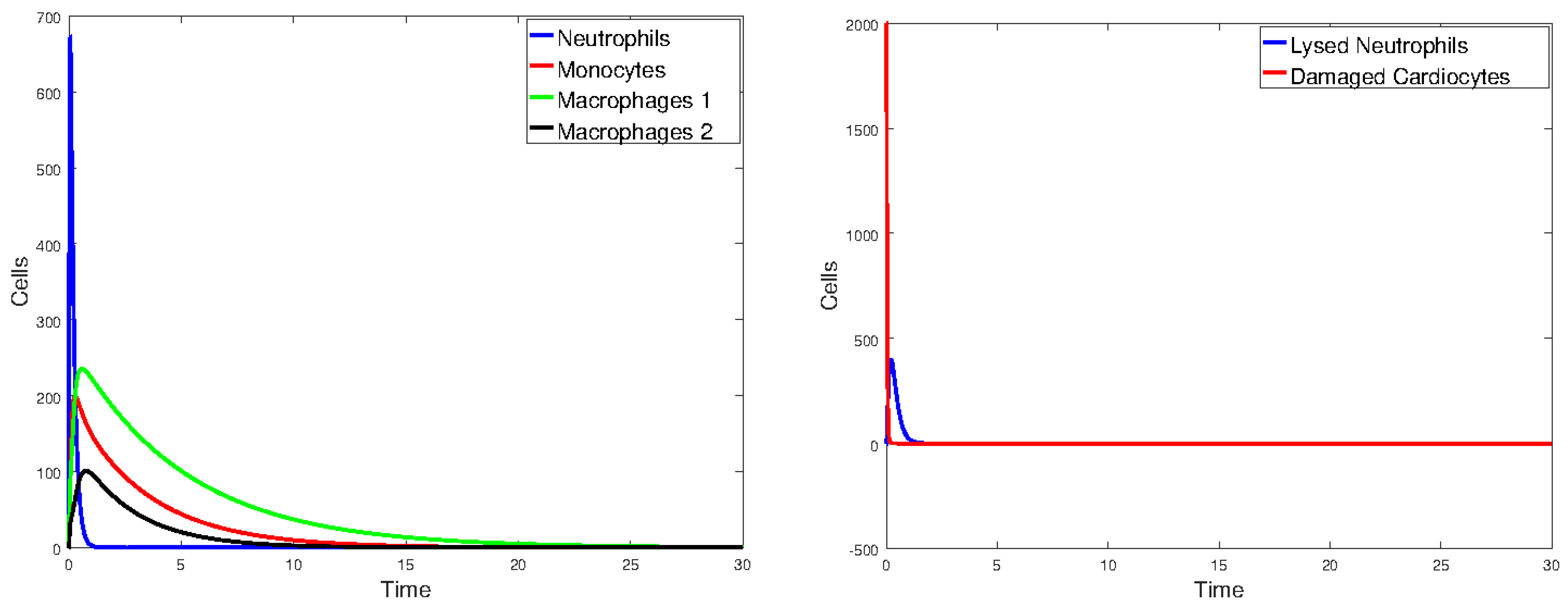
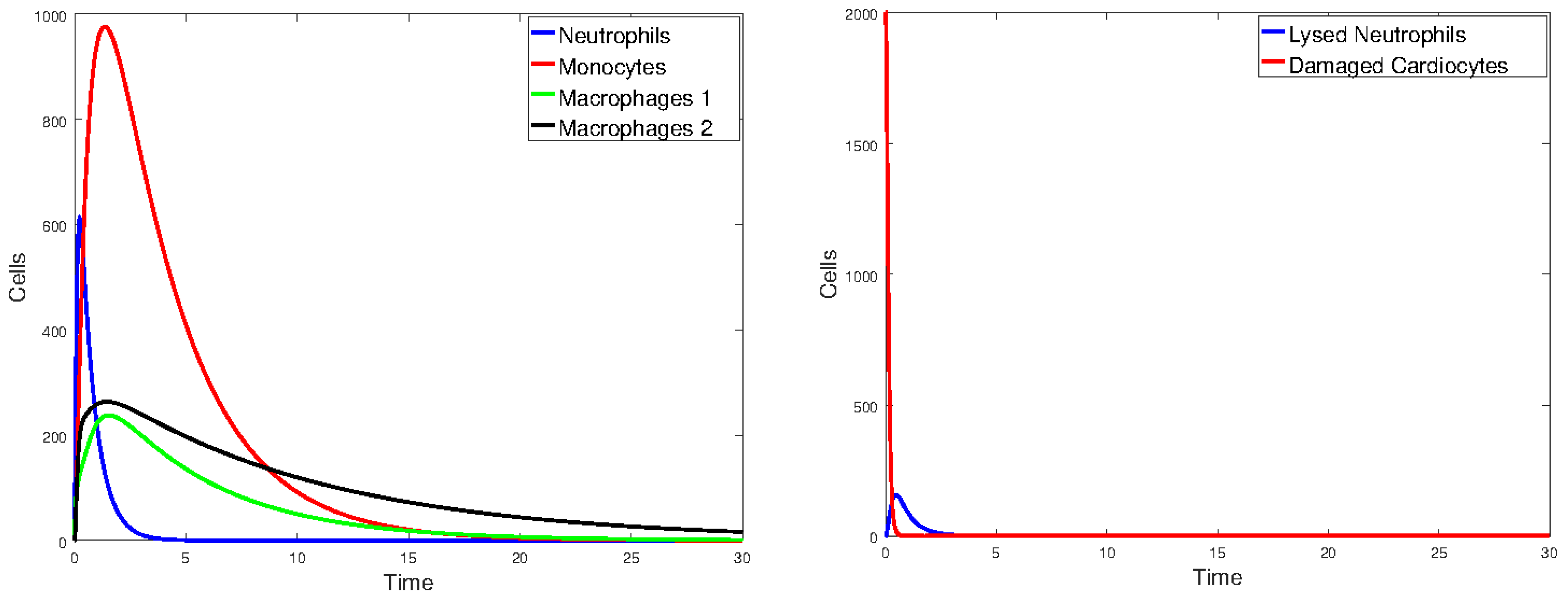
3.2. Heart Infarction Model
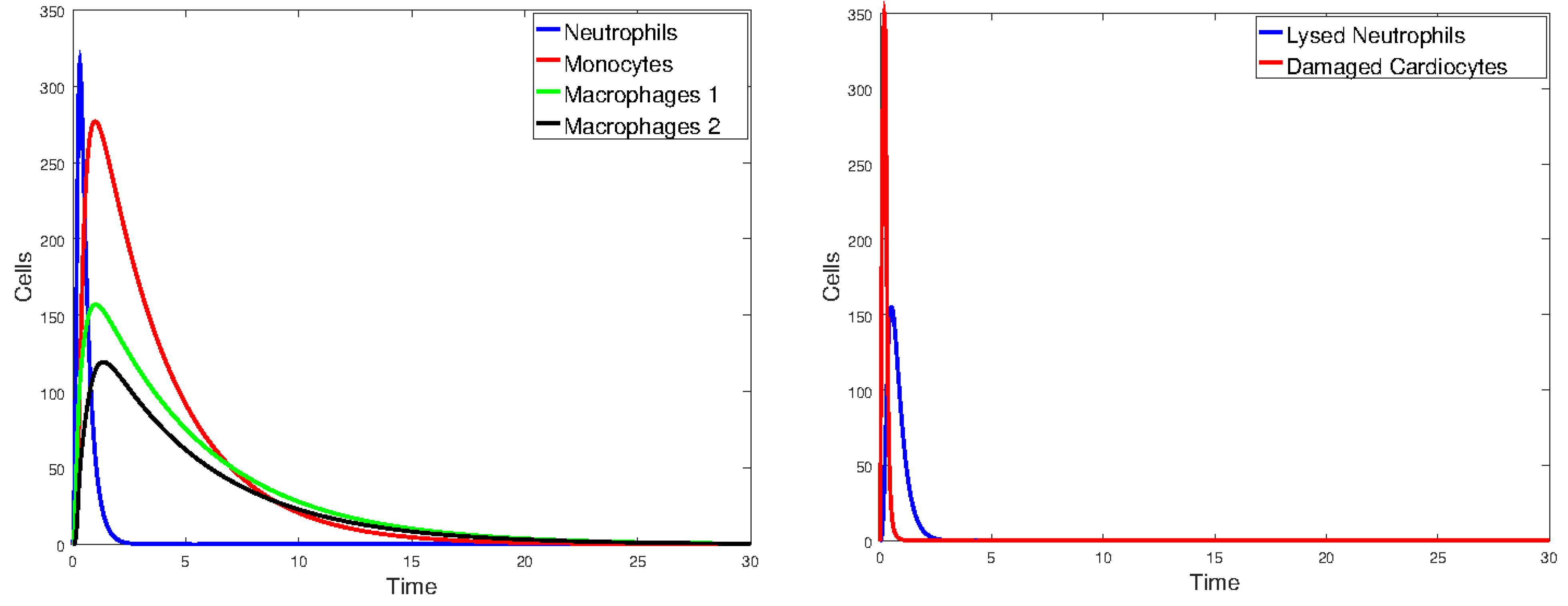
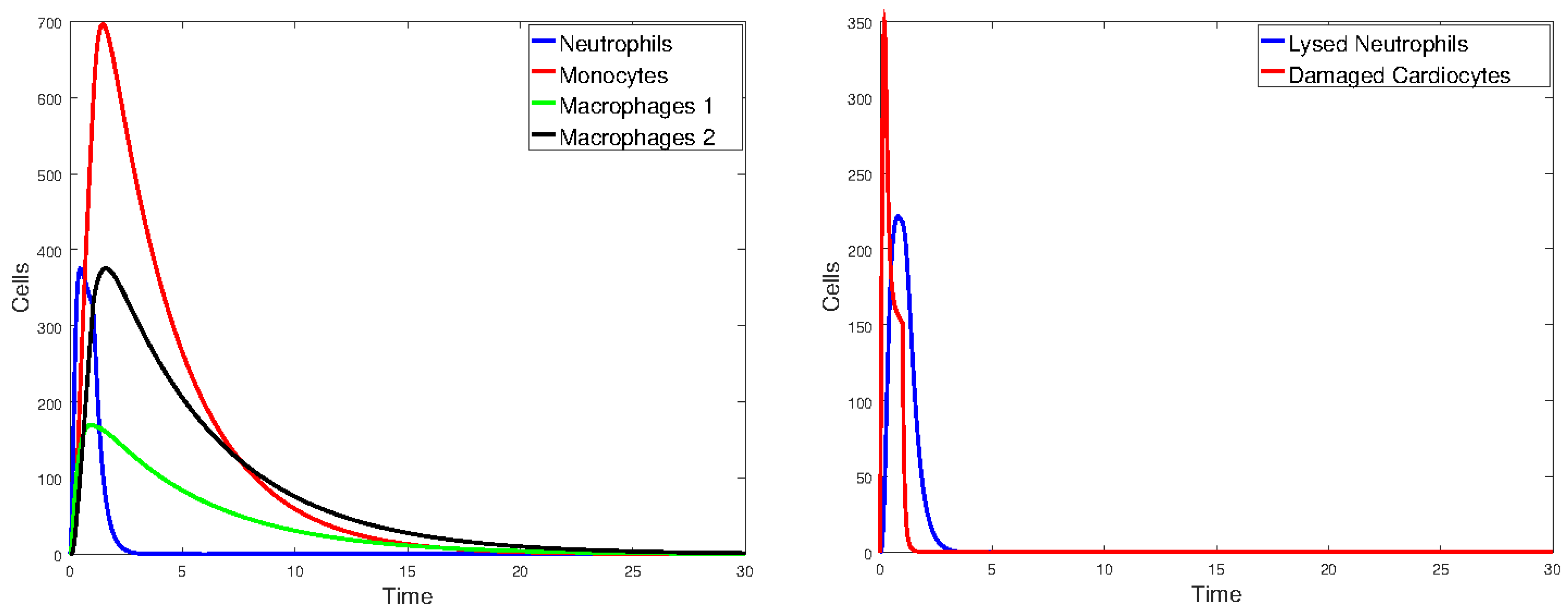
3.2.1. Numerical Simulations
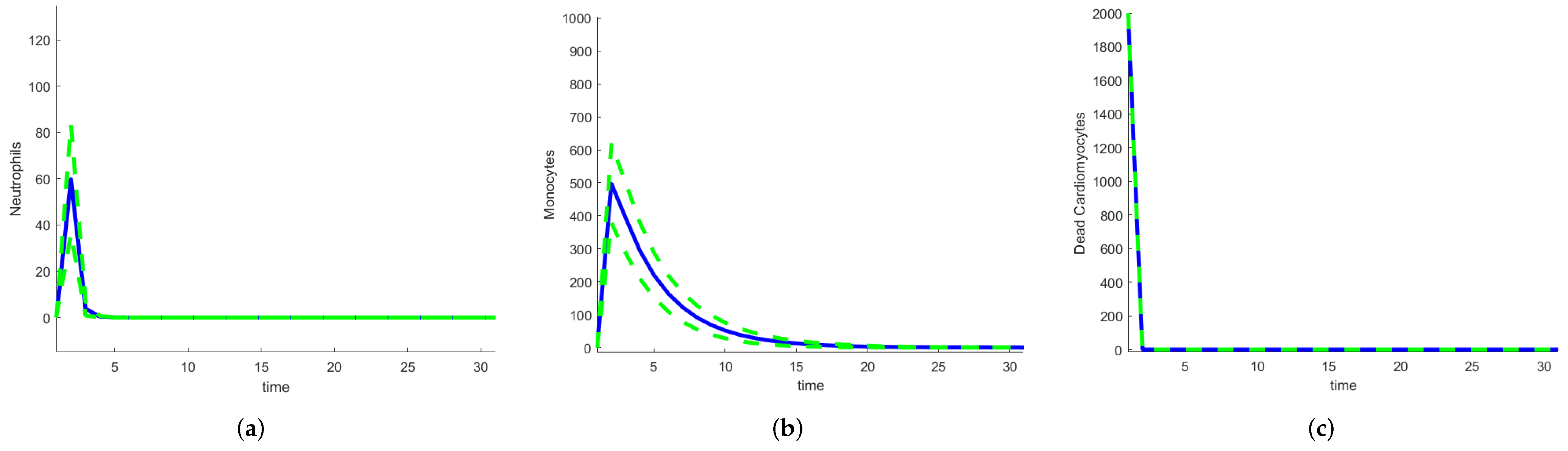
3.2.2. Stochastic and Random Differential Equations
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| ODE | ordinary differential equation |
| SDE | stochastic differential equation |
| RODE | random ordinary differential equation |
| SIRS | Susceptible–Infective–Recovered–Susceptible |
| MI | myocardial infarction |
| DFE | disease-free equilibrium |
| basic reproduction number | |
| PRCC | partial rank correlation coefficient |
| FAST | Fourier amplitude sensitivity test |
| EFAST | extended Fourier amplitude sensitivity test |
References
- Borgonovo, E.; Plischke, E. Sensitivity analysis: A review of recent advances. Eur. J. Oper. Res. 2016, 248, 869–887. [Google Scholar] [CrossRef]
- Christopher Frey, H.; Patil, S.R. Identification and review of sensitivity analysis methods. Risk Anal. 2002, 22, 553–578. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Campolongo, F.; Ratto, M. Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models; Wiley Online Library: Hoboken, NJ, USA, 2004; Volume 1. [Google Scholar]
- Pianosi, F.; Beven, K.; Freer, J.; Hall, J.W.; Rougier, J.; Stephenson, D.B.; Wagener, T. Sensitivity analysis of environmental models: A systematic review with practical workflow. Environ. Model. Softw. 2016, 79, 214–232. [Google Scholar] [CrossRef]
- Qian, G.; Mahdi, A. Sensitivity analysis methods in the biomedical sciences. Math. Biosci. 2020, 323, 108306. [Google Scholar] [CrossRef]
- Iwanaga, T.; Usher, W.; Herman, J. Toward SALib 2.0: Advancing the accessibility and interpretability of global sensitivity analyses. Socio-Environ. Syst. Model. 2022, 4, 18155. [Google Scholar] [CrossRef]
- Dai, H.; Liu, Y.; Guadagnini, A.; Yuan, S.; Yang, J.; Ye, M. Comparative assessment of two global sensitivity approaches considering model and parameter uncertainty. Water Resour. Res. 2024, 60, e2023WR036096. [Google Scholar] [CrossRef]
- Razavi, S.; Jakeman, A.; Saltelli, A.; Prieur, C.; Iooss, B.; Borgonovo, E.; Plischke, E.; Piano, S.L.; Iwanaga, T.; Becker, W.; et al. The future of sensitivity analysis: An essential discipline for systems modeling and policy support. Environ. Model. Softw. 2021, 137, 104954. [Google Scholar] [CrossRef]
- Meiler, S.; Ciullo, A.; Kropf, C.M.; Emanuel, K.; Bresch, D.N. Uncertainties and sensitivities in the quantification of future tropical cyclone risk. Commun. Earth Environ. 2023, 4, 371. [Google Scholar] [CrossRef]
- Vermeulen-Miltz, E.; Clifford-Holmes, J.K.; Scharler, U.M.; Lombard, A.T. A system dynamics model to support marine spatial planning in Algoa Bay, South Africa. Environ. Model. Softw. 2023, 160, 105601. [Google Scholar] [CrossRef]
- Moallemi, E.A.; Kwakkel, J.; de Haan, F.J.; Bryan, B.A. Exploratory modeling for analyzing coupled human-natural systems under uncertainty. Glob. Environ. Chang. 2020, 65, 102186. [Google Scholar] [CrossRef]
- Douglas-Smith, D.; Iwanaga, T.; Croke, B.F.; Jakeman, A.J. Certain trends in uncertainty and sensitivity analysis: An overview of software tools and techniques. Environ. Model. Softw. 2020, 124, 104588. [Google Scholar] [CrossRef]
- Rounsevell, M.D.; Arneth, A.; Brown, C.; Cheung, W.W.; Gimenez, O.; Holman, I.; Leadley, P.; Luján, C.; Mahevas, S.; Maréchaux, I.; et al. Identifying uncertainties in scenarios and models of socio-ecological systems in support of decision-making. One Earth 2021, 4, 967–985. [Google Scholar] [CrossRef]
- Puy, A.; Beneventano, P.; Levin, S.A.; Lo Piano, S.; Portaluri, T.; Saltelli, A. Models with higher effective dimensions tend to produce more uncertain estimates. Sci. Adv. 2022, 8, eabn9450. [Google Scholar] [CrossRef]
- Soong, T.T.; Bogdanoff, J. Random Differential Equations in Science and Engineering; Academic Press: Cambridge, MA, USA, 1974. [Google Scholar]
- Ghanem, R.G.; Spanos, P.D. Stochastic Finite Elements: A Spectral Approach; Courier Corporation: Washington, DC, USA, 2003. [Google Scholar]
- Xiu, D.; Karniadakis, G.E. The Wiener–Askey polynomial chaos for stochastic differential equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Chen-Charpentier, B.M.; Stanescu, D. Epidemic models with random coefficients. Math. Comput. Model. 2010, 52, 1004–1010. [Google Scholar] [CrossRef]
- Cortés, J.C.; Romero, J.V.; Roselló, M.D.; Santonja, F.J.; Villanueva, R.J. Solving continuous models with dependent uncertainty: A computational approach. Abstr. Appl. Anal. 2013, 2013, 983839. [Google Scholar]
- Oksendal, B. Stochastic Differential Equations: An Introduction with Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Friedman, A. Stochastic differential equations and applications. In Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 1975; pp. 75–148. [Google Scholar]
- Evans, L.C. An Introduction to Stochastic Differential Equations; American Mathematical Society: Rhode Island, RI, USA, 2012; Volume 82. [Google Scholar]
- Allen, L.J. An Introduction to Stochastic Processes with Applications to Biology; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Boettiger, C. From noise to knowledge: How randomness generates novel phenomena and reveals information. Ecol. Lett. 2018, 21, 1255–1267. [Google Scholar] [CrossRef]
- Constable, G.W.; Rogers, T.; McKane, A.J.; Tarnita, C.E. Demographic noise can reverse the direction of deterministic selection. Proc. Natl. Acad. Sci. USA 2016, 113, E4745–E4754. [Google Scholar] [CrossRef]
- Zaikin, A.; Kurths, J. Additive noise in noise-induced nonequilibrium transitions. Chaos Interdiscip. J. Nonlinear Sci. 2001, 11, 570–580. [Google Scholar] [CrossRef]
- Allen, E. Modeling with Itô Stochastic Differential Equations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007; Volume 22. [Google Scholar]
- Allen, E.J.; Allen, L.J.; Arciniega, A.; Greenwood, P.E. Construction of equivalent stochastic differential equation models. Stoch. Anal. Appl. 2008, 26, 274–297. [Google Scholar] [CrossRef]
- Edelstein-Keshet, L. Mathematical Models in Biology; SIAM: Philadelphia, PA, USA, 2005. [Google Scholar]
- Allen, L. An Introduction to Mathematical Biology; Pearson-Prentice Hall: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Chen-Charpentier, B.; Kojouharov, H. Mathematical Modeling of Myocardial Infarction. Model. Eng. Hum. Behav. 2019, 46, 1–216. [Google Scholar]
- WHO. The Atlas of Heart Disease and Stroke; WHO: Geneva, Switzerland, 2004. [Google Scholar]
- Anderson, J.L.; Morrow, D.A. Acute Myocardial Infarction. N. Engl. J. Med. 2017, 376, 2053–2064. [Google Scholar] [CrossRef] [PubMed]
- Terjung, R.; Frangogiannis, N.G. Pathophysiology of Myocardial Infarction; John Wiley and Sons: Hoboken, NJ, USA, 2013; pp. 313–1875. [Google Scholar]
- Ambrose, J.; Singh, M. Pathophysiology of coronary artery disease leading to acute coronary syndromes. F1000Prime Rep. 2015, 7, 8. [Google Scholar] [CrossRef] [PubMed]
- Betts, J.G. Anatomy and Physiology; OpenStax College, Rice University: Houston, TX, USA, 2013. [Google Scholar]
- Jackson, K.A.; Majka, S.M.; Wang, H.; Pocius, J.; Hartley, C.J.; Majesky, M.W.; Entman, M.L.; Michael, L.H.; Hirschi, K.K.; Goodell, M.A. Regeneration of ischemic cardiac muscle and vascular endothelium by adult stem cells. J. Clin. Investig. 2001, 107, 1395–1402. [Google Scholar] [CrossRef] [PubMed]
- Hethcote, H.W. The mathematics of infectious diseases. SIAM Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef] [PubMed]
- Gray, G.; Toor, I.; Castellan, R.; Crisan, M.; Meloni, M. Resident cells of the myocardium: More than spectators in cardiac injury, repair and regeneration. Curr. Opin. Physiol. 2018, 1, 46–51. [Google Scholar] [CrossRef] [PubMed]
- Nahrendorf, M.; Swirski, F.K. Monocyte and Macrophage Heterogeneity in the Heart. Circ. Res. 2013, 112, 1624–1633. [Google Scholar] [CrossRef] [PubMed]
- Roszer, T. Understanding the Mysterious M2 Macrophage through Activation Markers and Effector Mechanisms. Mediat. Inflamm. 2015, 2015, 816460. [Google Scholar] [CrossRef] [PubMed]
- Bonvini, R.F.; Hendiri, T.; Camenzind, E. Inflammatory response post-myocardial infarction and reperfusion: A new therapeutic target? Eur. Heart J. Suppl. 2005, 7, I27–I36. [Google Scholar] [CrossRef]
- Chen, B.; Frangogiannis, N.G. Immune cells in repair of the infarcted myocardium. Microcirculation 2017, 24, e12305. [Google Scholar] [CrossRef]
- Fang, L.; Moore, X.L.; Dart, A.M.; Wang, L.M. Systemic inflammatory response following acute myocardial infarction. J. Geriatr. Cardiol. JGC 2015, 12, 305. [Google Scholar] [PubMed]
- Saparov, A.; Ogay, V.; Nurgozhin, T.; Chen, W.C.W.; Mansurov, N.; Issabekova, A.; Zhakupova, J. Role of the immune system in cardiac tissue damage and repair following myocardial infarction. Inflamm. Res. 2017, 66, 739–751. [Google Scholar] [CrossRef] [PubMed]
- Swirski, F.K.; Nahrendorf, M. Cardioimmunology: The immune system in cardiac homeostasis and disease. Nat. Rev. Immunol. 2018, 18, 733–744. [Google Scholar] [CrossRef] [PubMed]
- Troidl, C.; Möllmann, H.; Nef, H.; Masseli, F.; Voss, S.; Szardien, S.; Willmer, M.; Rolf, A.; Rixe, J.; Troidl, K.; et al. Classically and alternatively activated macrophages contribute to tissue remodelling after myocardial infarction. J. Cell. Mol. Med. 2009, 13, 3485–3496. [Google Scholar] [CrossRef] [PubMed]
- Frangogiannis, N.G.; Mendoza, L.H.; Lindsey, M.L.; Ballantyne, C.M.; Michael, L.H.; Smith, C.W.; Entman, M.L. IL-10 Is Induced in the Reperfused Myocardium and May Modulate the Reaction to Injury. J. Immunol. 2000, 165, 2798–2808. [Google Scholar] [CrossRef] [PubMed]
- Patti, G.; D’Ambrosio, A.; Mega, S.; Giorgi, G.; Zardi, E.M.; Zardi, D.M.; Dicuonzo, G.; Dobrina, A.; Di Sciascio, G. Early interleukin-1 receptor antagonist elevation in patients with acute myocardial infarction. J. Am. Coll. Cardiol. 2004, 43, 35–38. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Yang, T.; Ma, Y.; Halade, G.V.; Zhang, J.; Lindsey, M.L.; Jin, Y.F. Mathematical modeling and stability analysis of macrophage activation in left ventricular remodeling post-myocardial infarction. BMC Genom. 2012, 13, S21. [Google Scholar] [CrossRef] [PubMed]
- Jin, Y.F.; Han, H.C.; Berger, J.; Dai, Q.; Lindsey, M.L. Combining experimental and mathematical modeling to reveal mechanisms of macrophage-dependent left ventricular remodeling. BMC Syst. Biol. 2011, 5, 60. [Google Scholar] [CrossRef] [PubMed]
- Dunster, J.L.; Byrne, H.M.; King, J.R. The Resolution of Inflammation: A Mathematical Model of Neutrophil and Macrophage Interactions. Bull. Math. Biol. 2014, 76, 1953–1980. [Google Scholar] [CrossRef]
- Dunster, J.L. The macrophage and its role in inflammation and tissue repair: Mathematical and systems biology approaches: Macrophage and its role in inflammation and tissue repair. Wiley Interdiscip. Rev. Syst. Biol. Med. 2016, 8, 87–99. [Google Scholar] [CrossRef]
- Yang, F.; Liu, Y.H.; Yang, X.P.; Xu, J.; Kapke, A.; Carretero, O.A. Myocardial Infarction and Cardiac Remodelling in Mice. Exp. Physiol. 2002, 87, 547–555. [Google Scholar] [CrossRef] [PubMed]
- Perko, L. Differential Equations and Dynamical Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Dickinson, R.P.; Gelinas, R.J. Sensitivity analysis of ordinary differential equation systems—A direct method. J. Comput. Phys. 1976, 21, 123–143. [Google Scholar] [CrossRef]
- Gustafson, P.; Srinivasan, C.; Wasserman, L. Local sensitivity analysis. Bayesian Stat. 1996, 5, 197–210. [Google Scholar]
- Arriola, L.; Hyman, J.M. Sensitivity analysis for uncertainty quantification in mathematical models. In Mathematical and Statistical Estimation Approaches in Epidemiology; Springer: Berlin/Heidelberg, Germany, 2009; pp. 195–247. [Google Scholar]
- Ma, Y.; Dixit, V.; Innes, M.J.; Guo, X.; Rackauckas, C. A comparison of automatic differentiation and continuous sensitivity analysis for derivatives of differential equation solutions. In Proceedings of the 2021 IEEE High Performance Extreme Computing Conference (HPEC), Virtual, 20–24 September 2021; pp. 1–9. [Google Scholar]
- Rabitz, H. General Sensitivity Analysis of Differential Equation Systems. In Proceedings of the Fluctuations and Sensitivity in Nonequilibrium Systems: Proceedings of an International Conference, Austin, TX, USA, 12–16 March 1984; Springer: Berlin/Heidelberg, Germany, 1984; pp. 196–203. [Google Scholar]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Saltelli, A. Sensitivity analysis: Could better methods be used? J. Geophys. Res. Atmos. 1999, 104, 3789–3793. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Trame, M.N.; Lesko, L.J.; Schmidt, S. Sobol sensitivity analysis: A tool to guide the development and evaluation of systems pharmacology models. CPT Pharmacomet. Syst. Pharmacol. 2015, 4, 69–79. [Google Scholar] [CrossRef] [PubMed]
- Savatorova, V. Exploring Parameter Sensitivity Analysis in Mathematical Modeling with Ordinary Differential Equations. CODEE J. 2023, 16, 4. [Google Scholar]
- Cukier, R.; Fortuin, C.; Shuler, K.E.; Petschek, A.; Schaibly, J.H. Study of the sensitivity of coupled reaction systems to uncertainties in rate coefficients. I Theory. J. Chem. Phys. 1973, 59, 3873–3878. [Google Scholar] [CrossRef]
- Pianosi, F.; Sarrazin, F.; Wagener, T. A Matlab toolbox for global sensitivity analysis. Environ. Model. Softw. 2015, 70, 80–85. [Google Scholar] [CrossRef]
- Dela, A.; Shtylla, B.; de Pillis, L. Multi-method global sensitivity analysis of mathematical models. J. Theor. Biol. 2022, 546, 111159. [Google Scholar] [CrossRef]
- Morris, M.D. Factorial sampling plans for preliminary computational experiments. Technometrics 1991, 33, 161–174. [Google Scholar]
- Marino, S.; Hogue, I.B.; Ray, C.J.; Kirschner, D.E. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 2008, 254, 178–196. [Google Scholar] [CrossRef] [PubMed]
- Alam, M.S.; Kamrujjaman, M.; Islam, M.S. Parameter sensitivity and qualitative analysis of dynamics of ovarian tumor growth model with treatment strategy. J. Appl. Math. Phys. 2020, 8, 941–955. [Google Scholar] [CrossRef]
- Li, D.; Jiang, P.; Hu, C.; Yan, T. Comparison of local and global sensitivity analysis methods and application to thermal hydraulic phenomena. Prog. Nucl. Energy 2023, 158, 104612. [Google Scholar] [CrossRef]
- Qin, C.; Jin, Y.; Tian, M.; Ju, P.; Zhou, S. Comparative Study of Global Sensitivity Analysis and Local Sensitivity Analysis in Power System Parameter Identification. Energies 2023, 16, 5915. [Google Scholar] [CrossRef]
- Rabitz, H.; Kramer, M.; Dacol, D. Sensitivity analysis in chemical kinetics. Annu. Rev. Phys. Chem. 1983, 34, 419–461. [Google Scholar] [CrossRef]
- Zheng, Y.; Rundell, A. Comparative study of parameter sensitivity analyses of the TCR-activated Erk-MAPK signalling pathway. IEE Proc.-Syst. Biol. 2006, 153, 201–211. [Google Scholar] [CrossRef] [PubMed]
- Serban, R.; Hindmarsh, A.C. CVODES: An ODE Solver with Sensitivity Analysis Capabilities; Technical Report; Technical Report UCRL-JP-200039; Lawrence Livermore National Laboratory: Livermore, CA, USA, 2003.
- Rackauckas, C.; Ma, Y.; Martensen, J.; Warner, C.; Zubov, K.; Supekar, R.; Skinner, D.; Ramadhan, A. Universal differential equations for scientific machine learning. arXiv 2020, arXiv:2001.04385. [Google Scholar]
- MathWorks. odeSensitivity. 2024. Available online: https://www.mathworks.com/help/matlab/ref/odesensitivity.html (accessed on 10 June 2012).
- McKay, M.D.; Beckman, R.J.; Conover, W.J. Comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 1979, 21, 239–245. [Google Scholar]
- Kucherenko, S.; Albrecht, D.; Saltelli, A. Exploring multi-dimensional spaces: A comparison of Latin hypercube and quasi Monte Carlo sampling techniques. arXiv 2015, arXiv:1505.02350. [Google Scholar]
- Renardy, M.; Joslyn, L.R.; Millar, J.A.; Kirschner, D.E. To Sobol or not to Sobol? The effects of sampling schemes in systems biology applications. Math. Biosci. 2021, 337, 108593. [Google Scholar] [CrossRef]
- Blower, S.M.; Hartel, D.; Dowlatabadi, H.; Anderson, R.M.; May, R.M. Drugs, sex and HIV: A mathematical model for New York City. Phil. Trans. R. Soc. Lond. B 1991, 331, 171–187. [Google Scholar]
- Xu, C.; Gertner, G. Understanding and comparisons of different sampling approaches for the Fourier Amplitudes Sensitivity Test (FAST). Comput. Stat. Data Anal. 2011, 55, 184–198. [Google Scholar] [CrossRef] [PubMed]
- Pianosi, F.; Sarrazin, F.; Wagener, T. How successfully is open-source research software adopted? Results and implications of surveying the users of a sensitivity analysis toolbox. Environ. Model. Softw. 2020, 124, 104579. [Google Scholar] [CrossRef]
- Dixit, V.K.; Rackauckas, C. GlobalSensitivity.jl: Performant and Parallel Global Sensitivity Analysis with Julia. J. Open Source Softw. 2022, 7, 4561. [Google Scholar] [CrossRef]
- Kloeden, P.E.; Platen, E.; Schurz, H. Numerical Solution of SDE through Computer Experiments; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Sauer, T. Computational solution of stochastic differential equations. Wiley Interdiscip. Rev. Comput. Stat. 2013, 5, 362–371. [Google Scholar] [CrossRef]
- Higham, D.; Kloeden, P. An Introduction to the Numerical Simulation of Stochastic Differential Equations; SIAM: Philadelphia, PA, USA, 2021. [Google Scholar]
- Colizza, V.; Barrat, A.; Barthelemy, M.; Valleron, A.J.; Vespignani, A. Modeling the worldwide spread of pandemic influenza: Baseline case and containment interventions. PLoS Med. 2007, 4, e13. [Google Scholar] [CrossRef] [PubMed]
- Centers for Disease Control. Influenza (Flu). 2024. Available online: https://www.cdc.gov/flu/about/keyfacts.htm#:~:text=Flu%20is%20a%20contagious%20respiratory,a%20flu%20vaccine%20each%20year (accessed on 24 April 2012).
- Rackauckas, C.; Nie, Q. DifferentialEquations.jl—A Performant and Feature-Rich Ecosystem for Solving Differential Equations in Julia. J. Open Res. Softw. 2017, 5, 15. [Google Scholar] [CrossRef]
- Olivetti, G. Aging, Cardiac Hypertrophy and Ischemic Cardiomyopathy Do Not Affect the Proportion of Mononucleated and Multinucleated Myocytes in the Human Heart. J. Mol. Cell. Cardiol. 1996, 28, 1463–1477. [Google Scholar] [CrossRef] [PubMed]
- Saltelli, A.; Aleksankina, K.; Becker, W.; Fennell, P.; Ferretti, F.; Holst, N.; Li, S.; Wu, Q. Why so many published sensitivity analyses are false: A systematic review of sensitivity analysis practices. Environ. Model. Softw. 2019, 114, 29–39. [Google Scholar] [CrossRef]
- Lafci Büyükkahraman, M.; Sabine, G.K.; Kojouharov, H.V.; Chen-Charpentier, B.M.; McMahan, S.R.; Liao, J. Using models to advance medicine: Mathematical modeling of post-myocardial infarction left ventricular remodeling. Comput. Methods Biomech. Biomed. Eng. 2022, 25, 298–307. [Google Scholar] [CrossRef]
- Moise, N.; Friedman, A. A mathematical model of immunomodulatory treatment in myocardial infarction. J. Theor. Biol. 2022, 544, 111122. [Google Scholar] [CrossRef] [PubMed]



| Symbol | Parameter Description | Value |
|---|---|---|
| Average number of contacts per unit of time | 0.5 /d | |
| Recovery rate | 1/3/d | |
| Loss of immunity rate | 1/30/d | |
| N | Total population | 1000 |
| Parameter Description | Value | |
|---|---|---|
| Maximal rate of neutrophil influx due to dead myocytes | 6 | |
| Rate of M/M1 monocyte conversion due to dead myocytes | 1 | |
| Rate of M/M1 monocyte conversion due to dead neutrophils | ||
| Maximal rate of monocyte recruitment due to neutrophils | ||
| Maximal rate of monocyte recruitment due to dead myocytes | ||
| Saturation constant | 1 | |
| Rate of neutrophil apoptosis | 3 | |
| Rate at which M1 macrophages exit the tissue | 0.2 | |
| Rate at which M2 macrophages exit the tissue | 0.2 | |
| Rate at which M1 macrophages engulf dead myocytes | 0.02 | |
| Rate at which neutrophils engulf dead myocytes | ||
| Rate of M1/M2 macrophage conversion due to dead myocytes | 0.01 | |
| Rate of M1/M2 macrophage conversion due to dead neutrophils | ||
| Rate at which monocytes exit the tissue | ||
| Rate at which M1 macrophages engulf lead neutrophils | 0.01 | |
| Rate of secondary necrosis of neutrophils | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen-Charpentier, B.; Kojouharov, H. Sensitivity Analysis and Uncertainty of a Myocardial Infarction Model. Mathematics 2024, 12, 2217. https://doi.org/10.3390/math12142217
Chen-Charpentier B, Kojouharov H. Sensitivity Analysis and Uncertainty of a Myocardial Infarction Model. Mathematics. 2024; 12(14):2217. https://doi.org/10.3390/math12142217
Chicago/Turabian StyleChen-Charpentier, Benito, and Hristo Kojouharov. 2024. "Sensitivity Analysis and Uncertainty of a Myocardial Infarction Model" Mathematics 12, no. 14: 2217. https://doi.org/10.3390/math12142217
APA StyleChen-Charpentier, B., & Kojouharov, H. (2024). Sensitivity Analysis and Uncertainty of a Myocardial Infarction Model. Mathematics, 12(14), 2217. https://doi.org/10.3390/math12142217






