Design and Analysis of a Novel Fractional-Order System with Hidden Dynamics, Hyperchaotic Behavior and Multi-Scroll Attractors
Abstract
:1. Introduction
2. Hidden Hyperchaotic Multi-Scroll Fractional-Order System
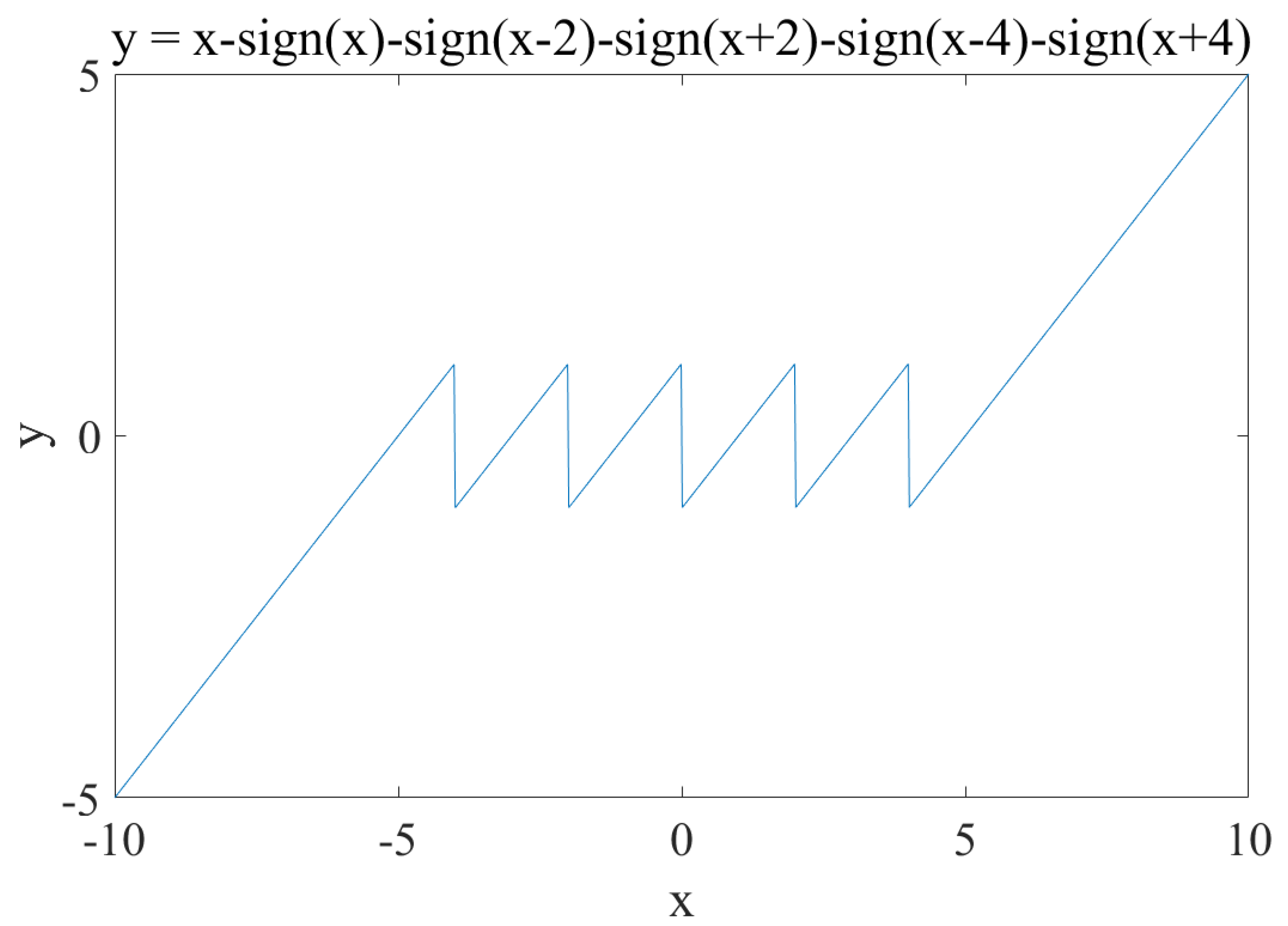
2.1. Design of System Model
2.2. Equilibrium Point Analysis
2.3. Adomian Decomposition
3. Dynamics Analysis
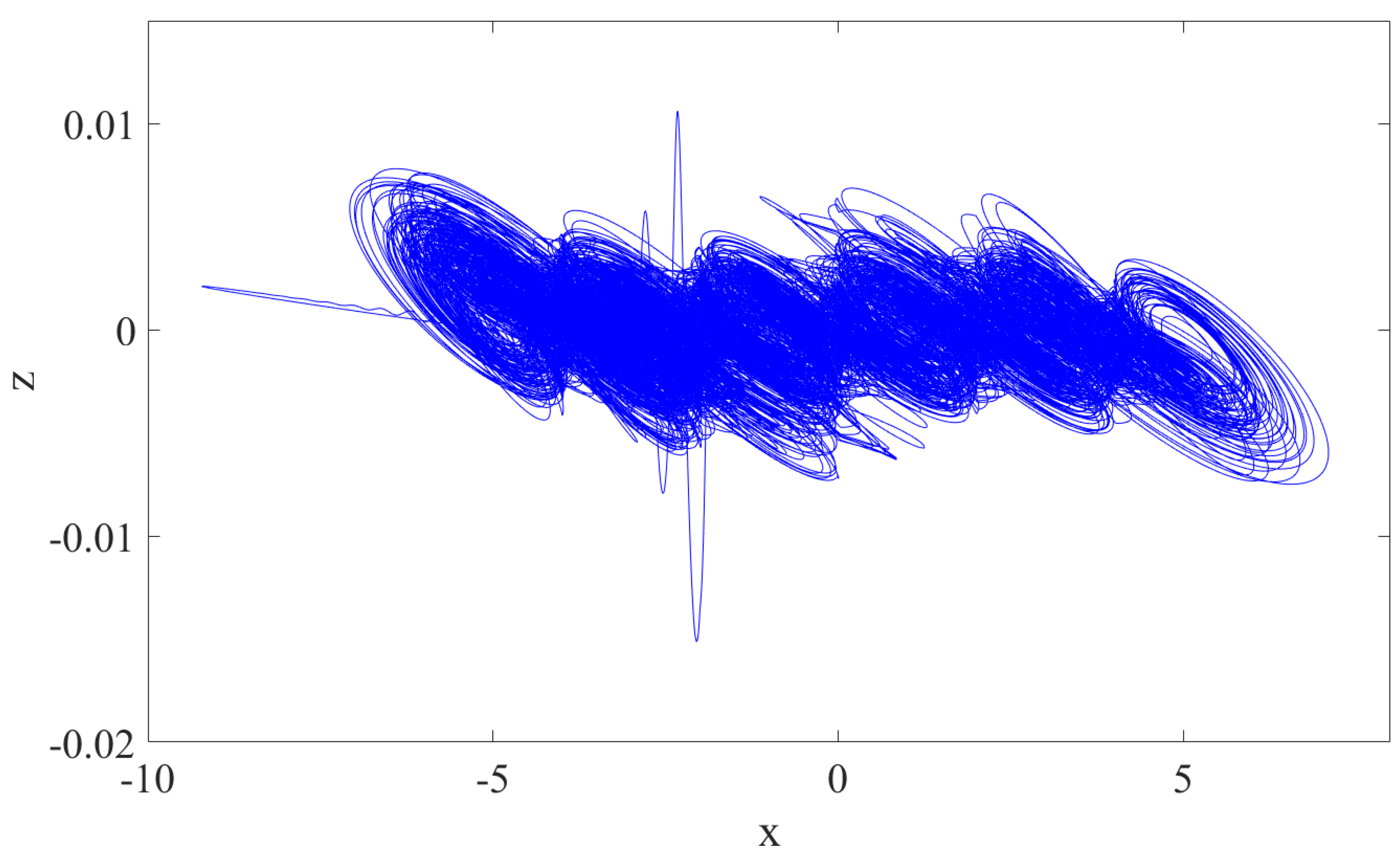
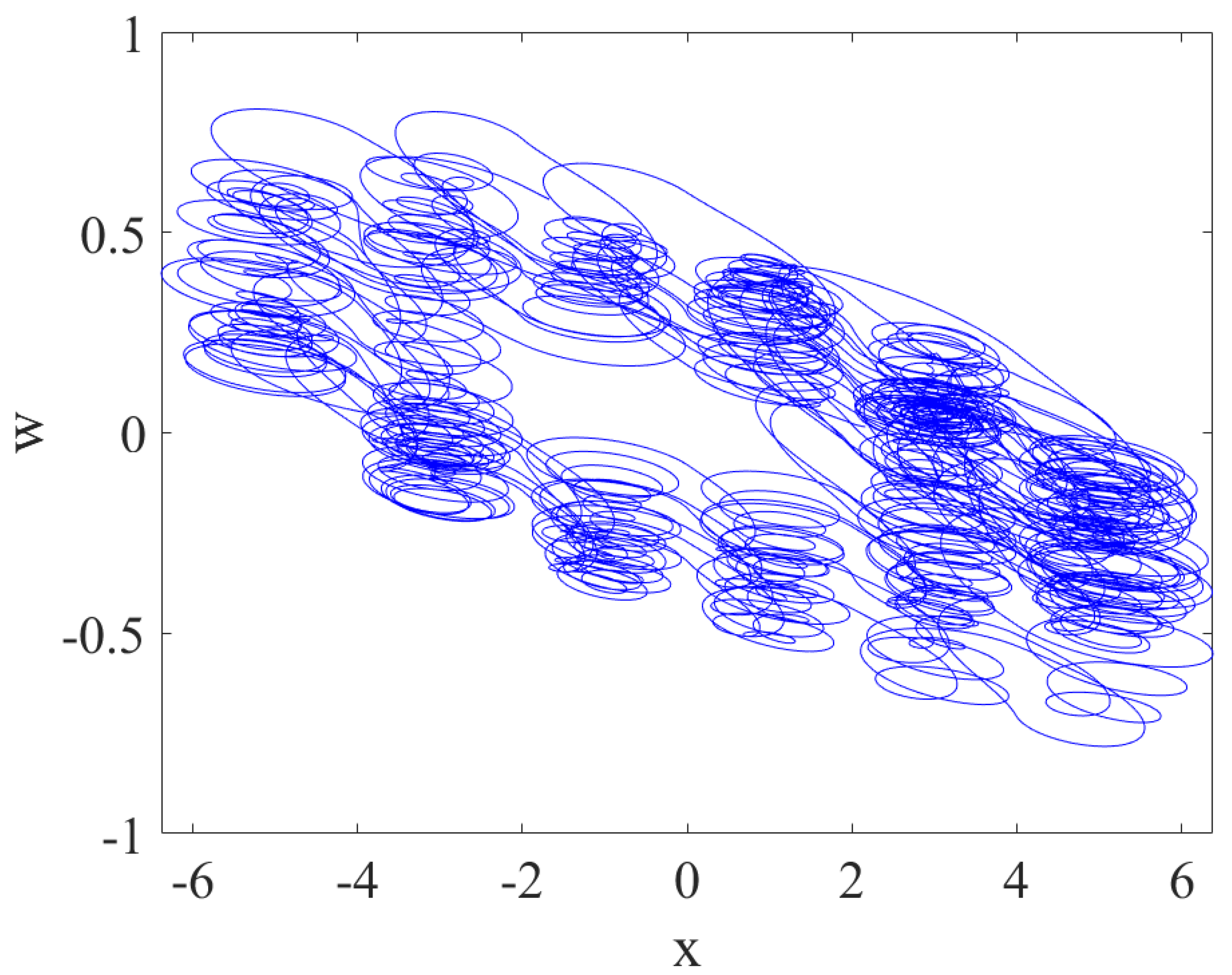
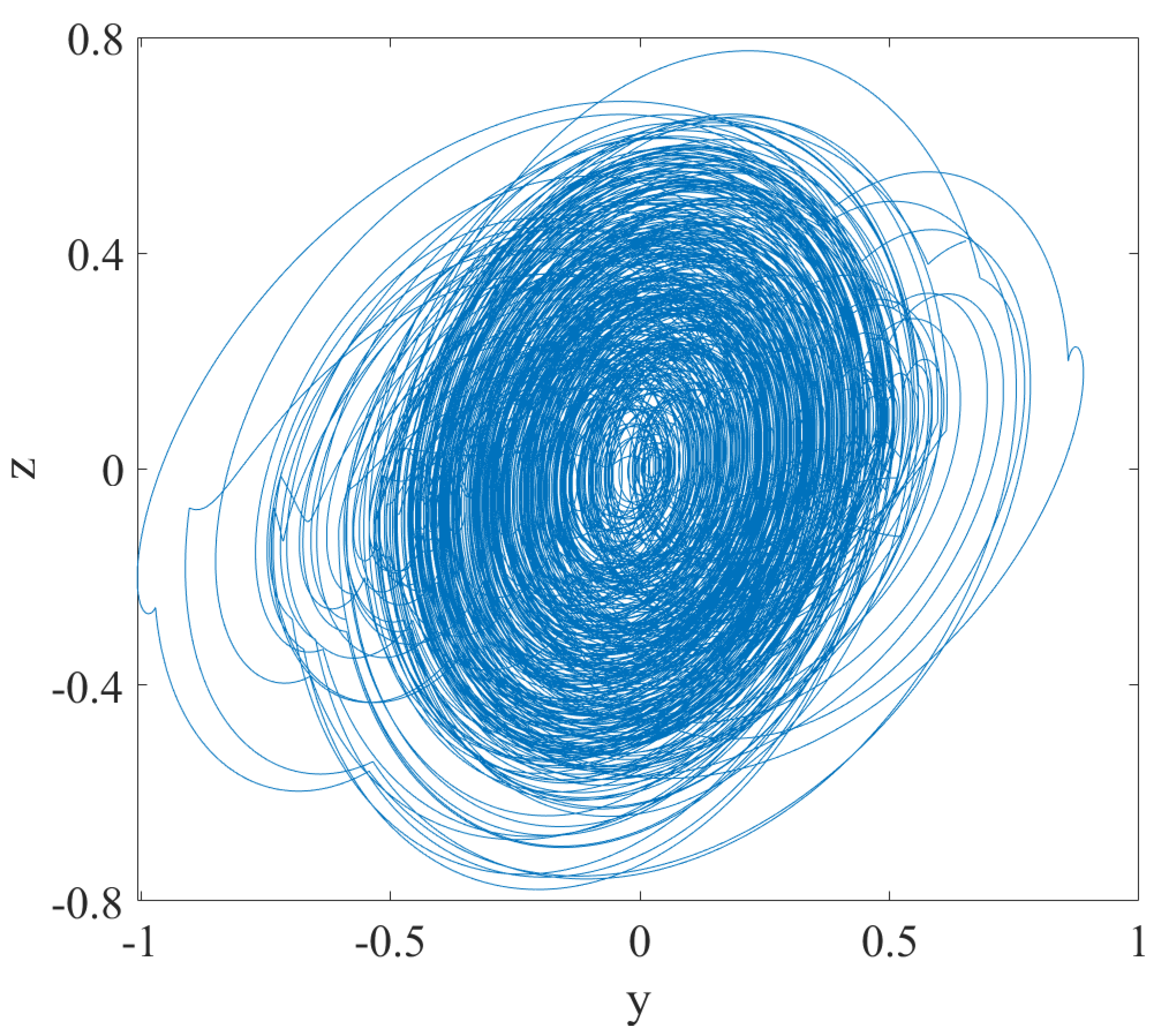
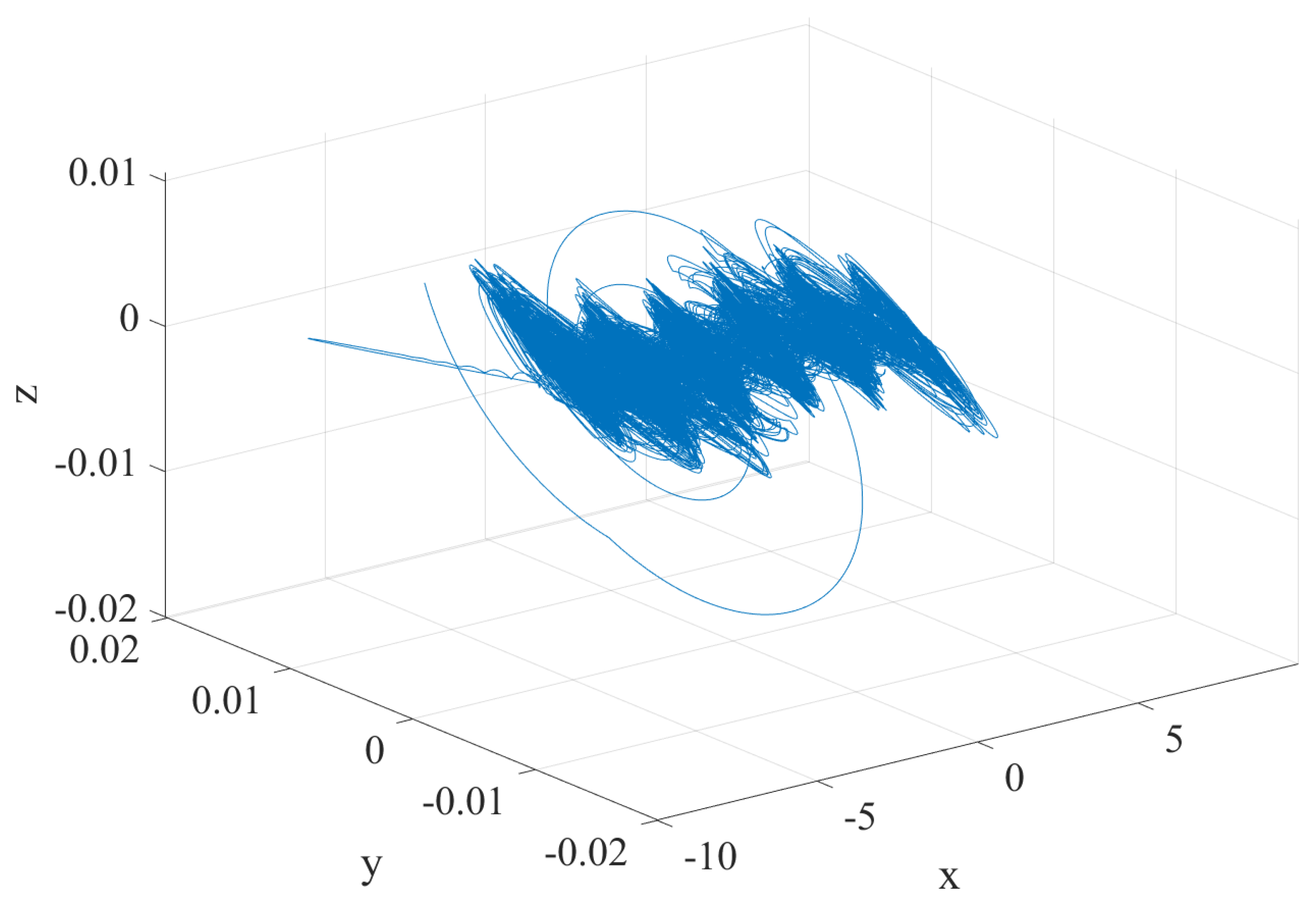
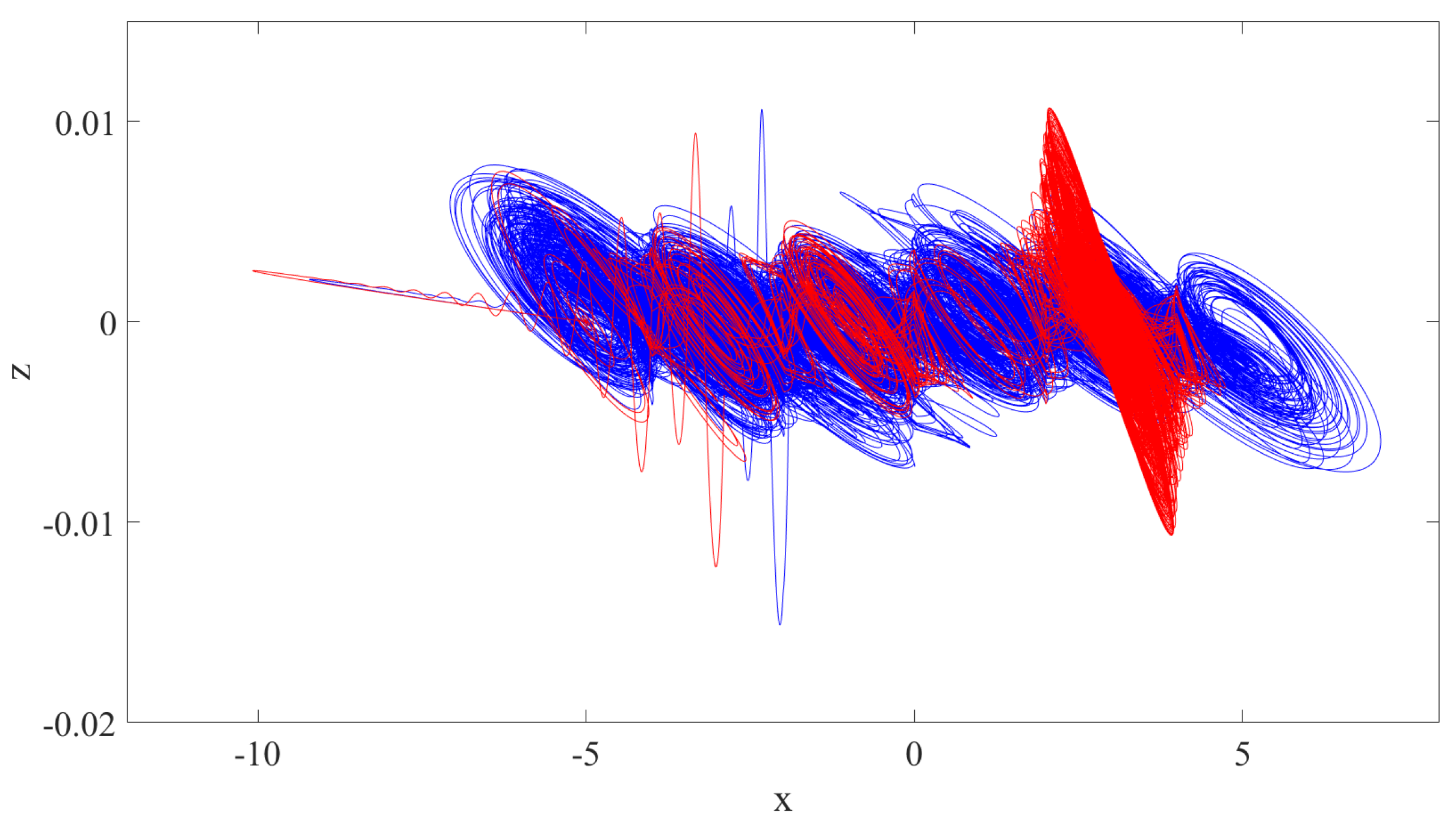
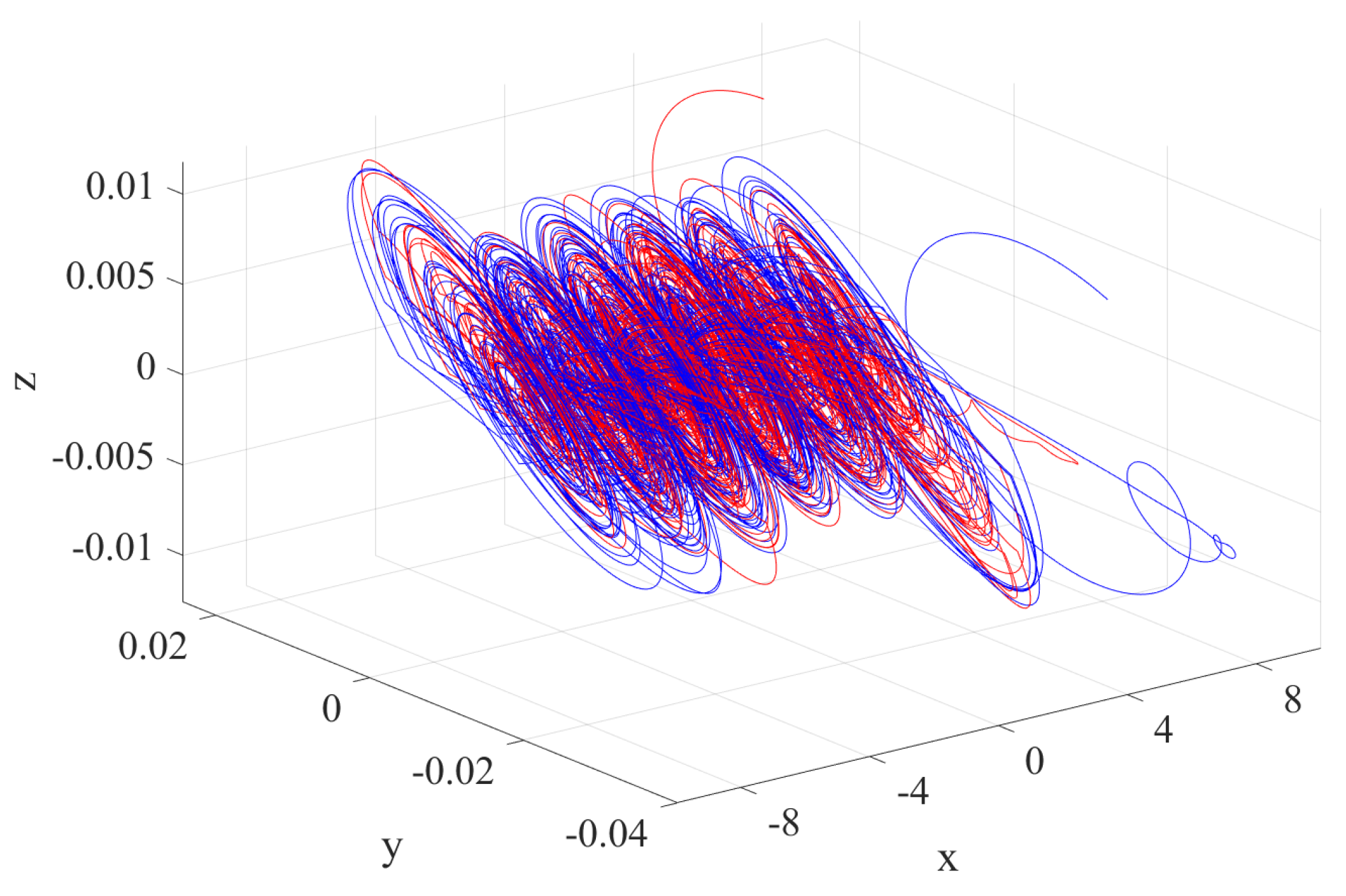
3.1. Phase Analysis
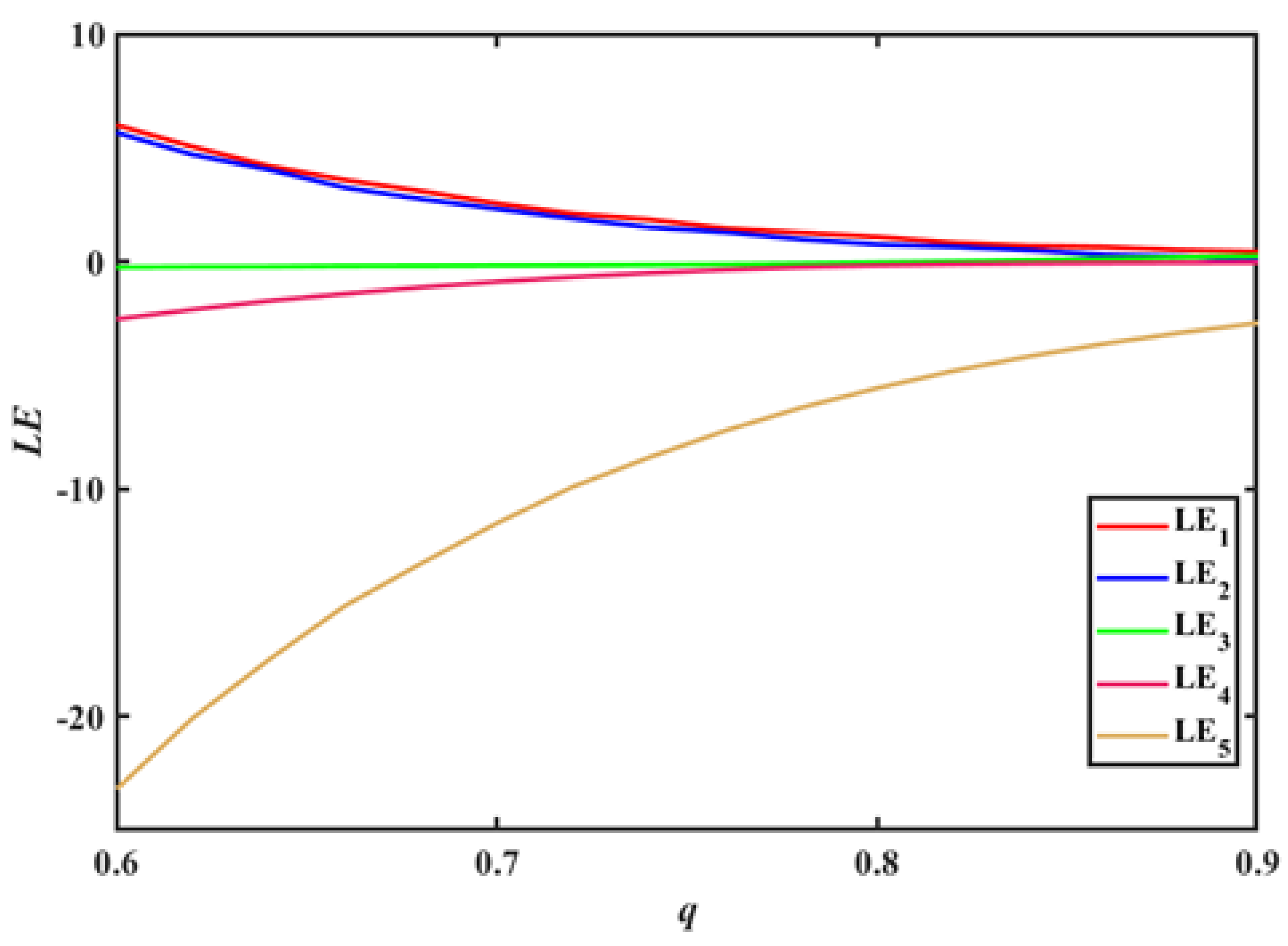
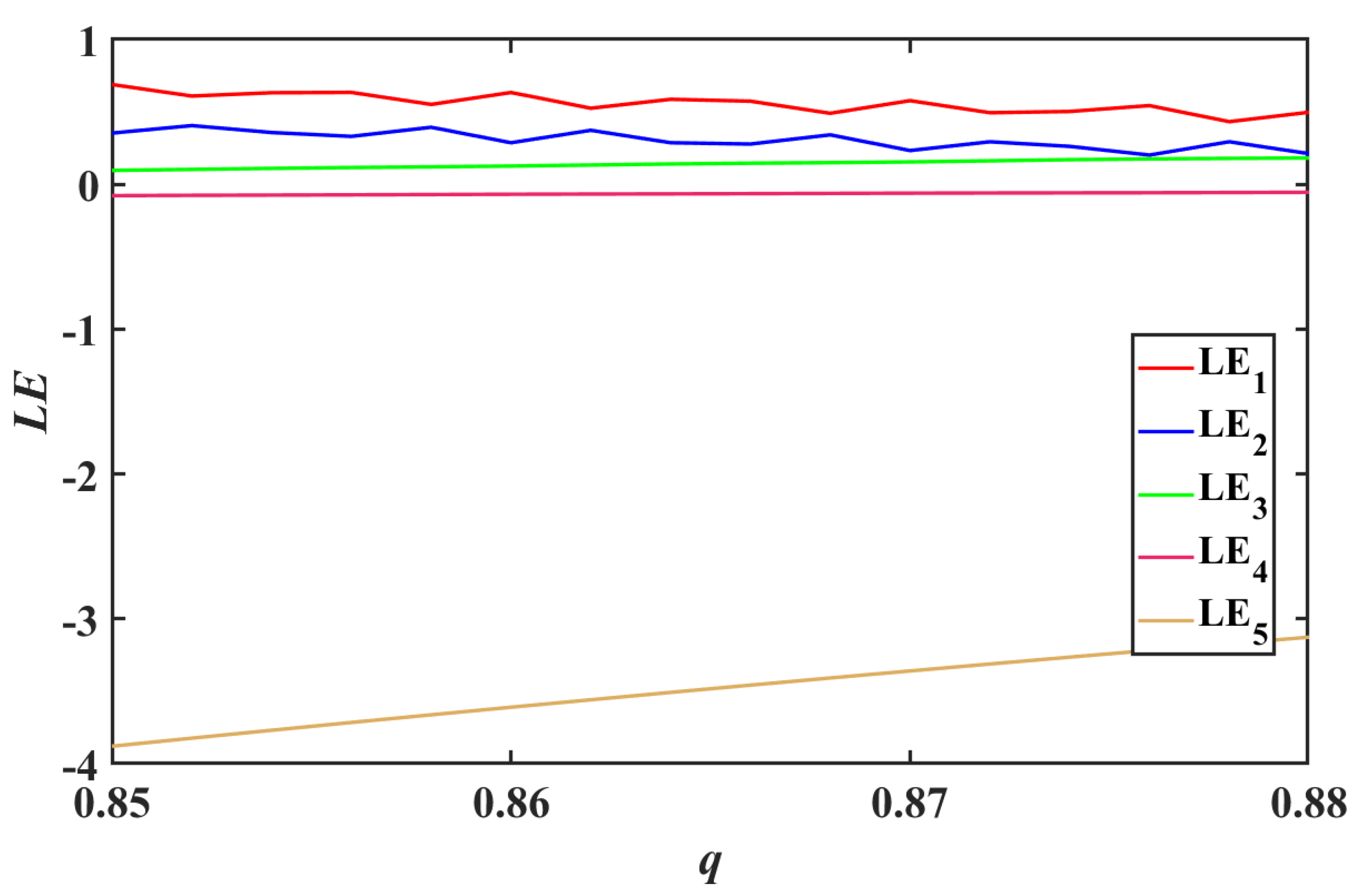
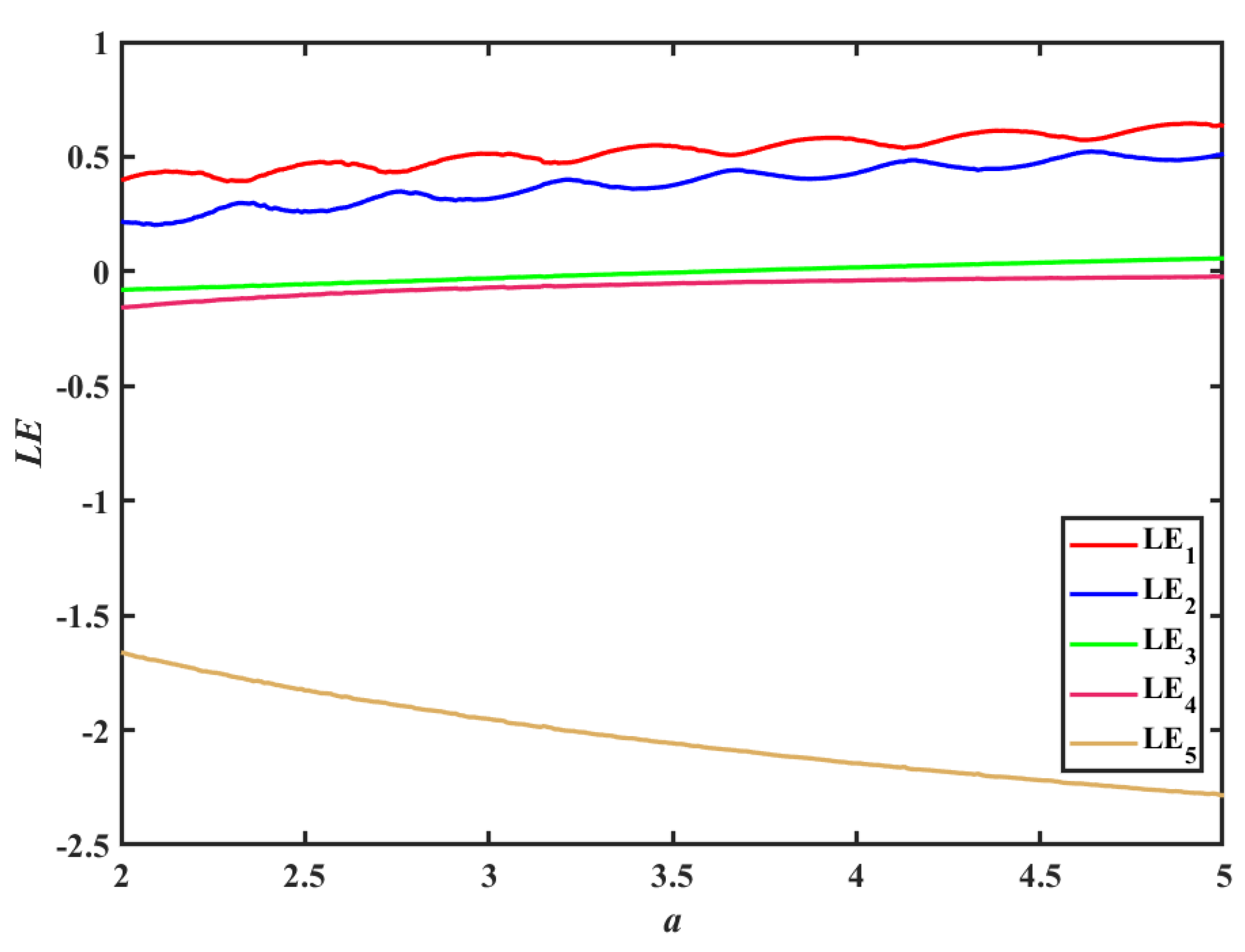
3.2. Lyapunov Exponents Analysis
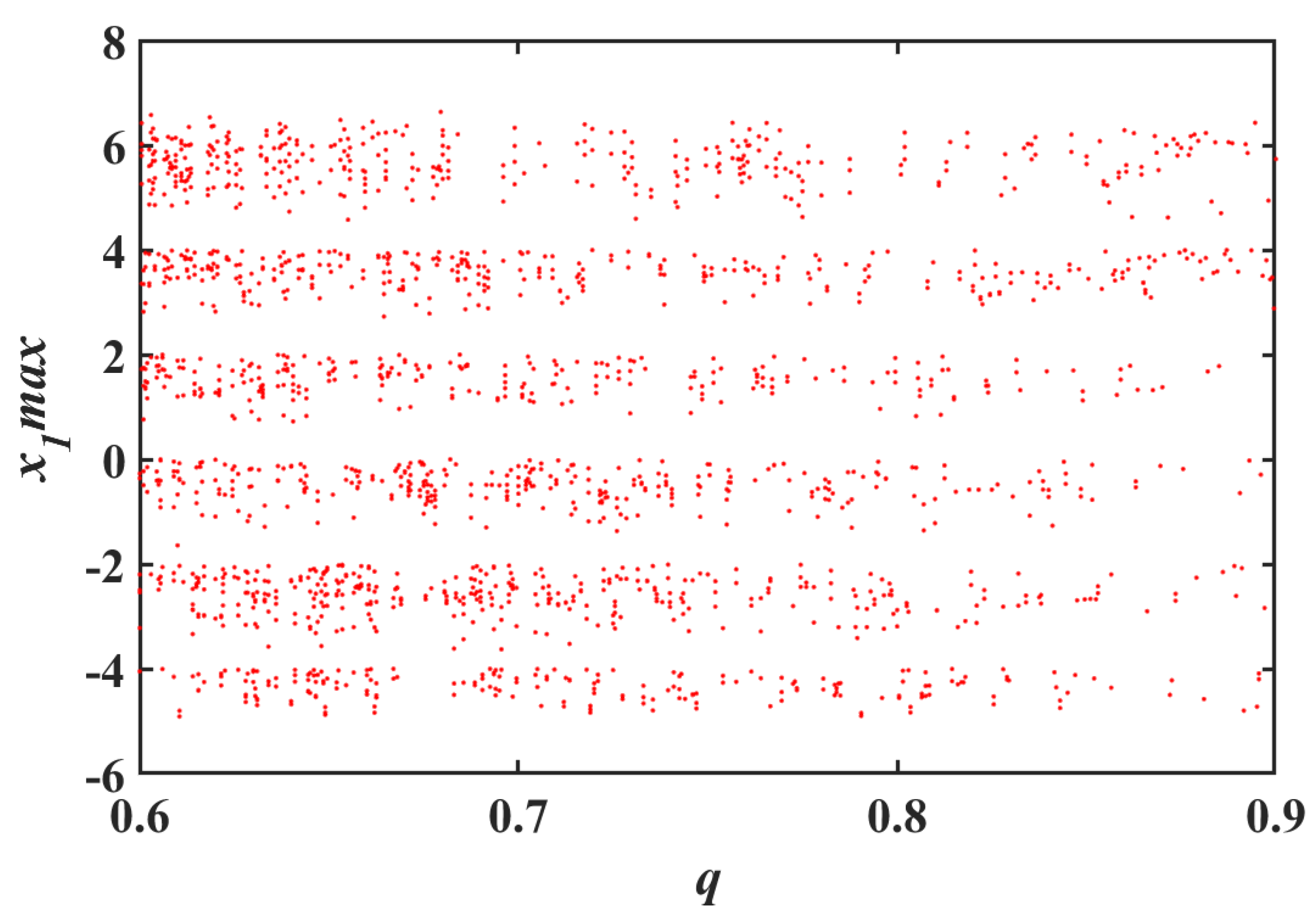
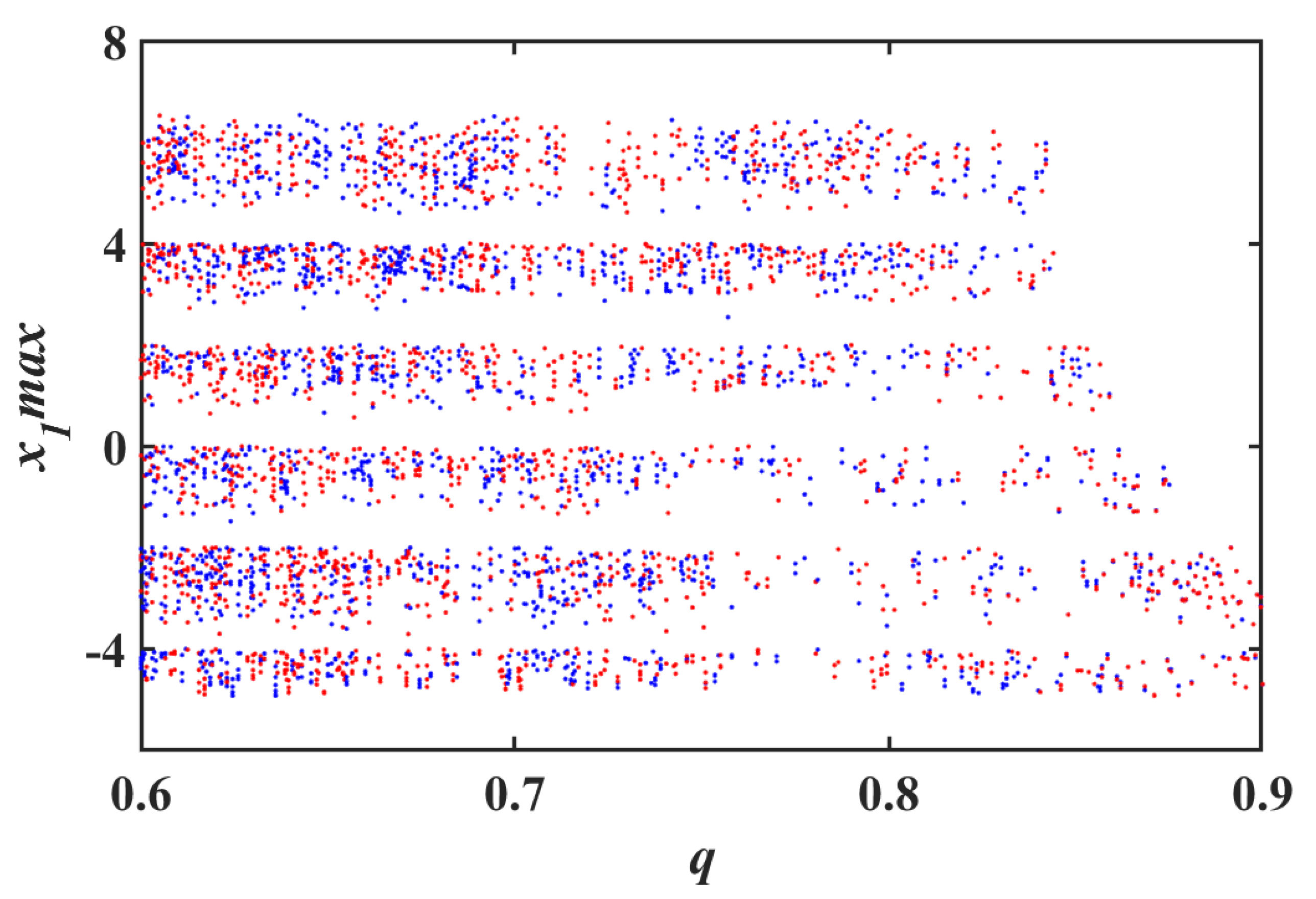
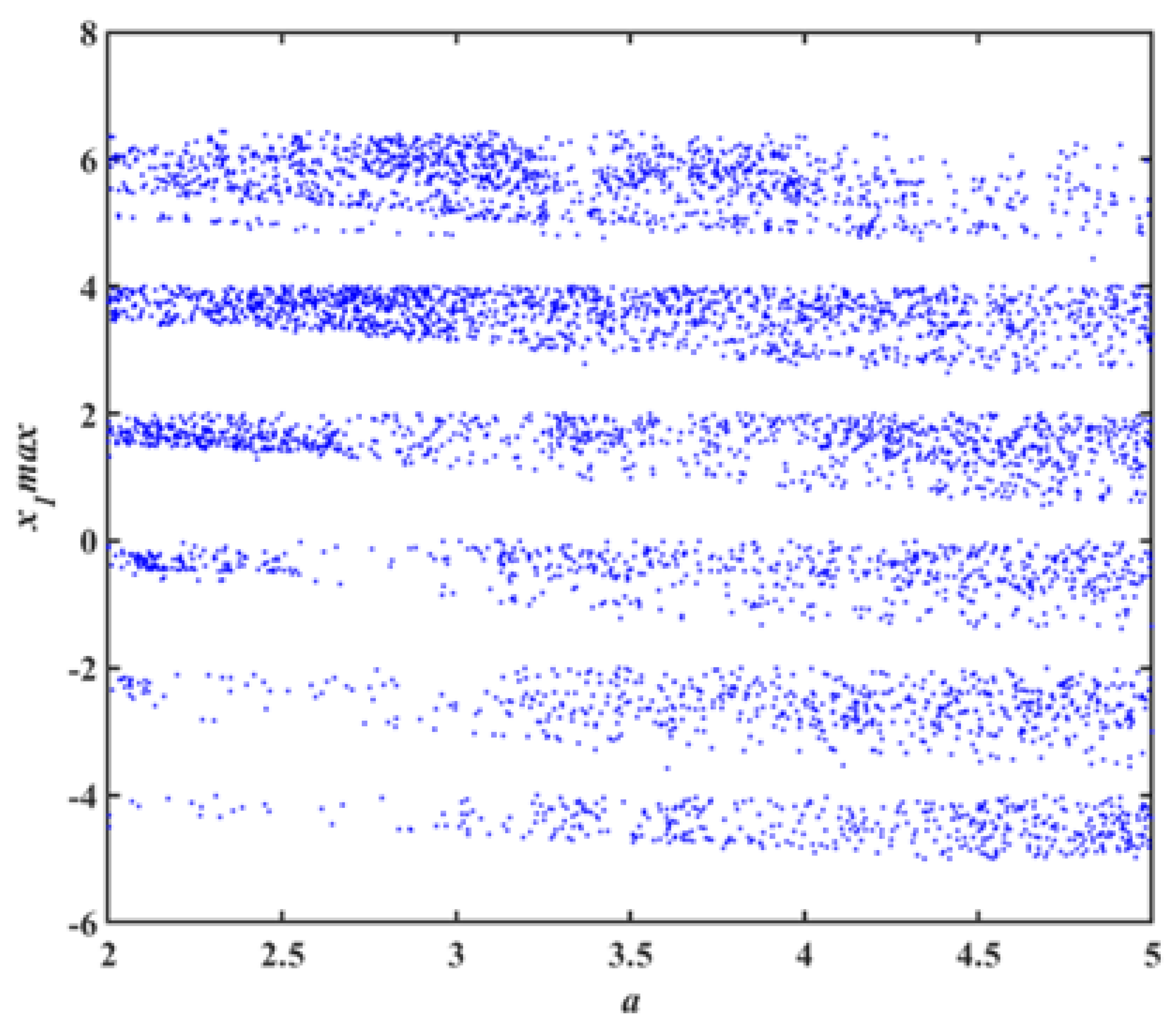
3.3. Bifurcation Analysis
4. Hardware Implementation
5. Application in Medical Image Encryption
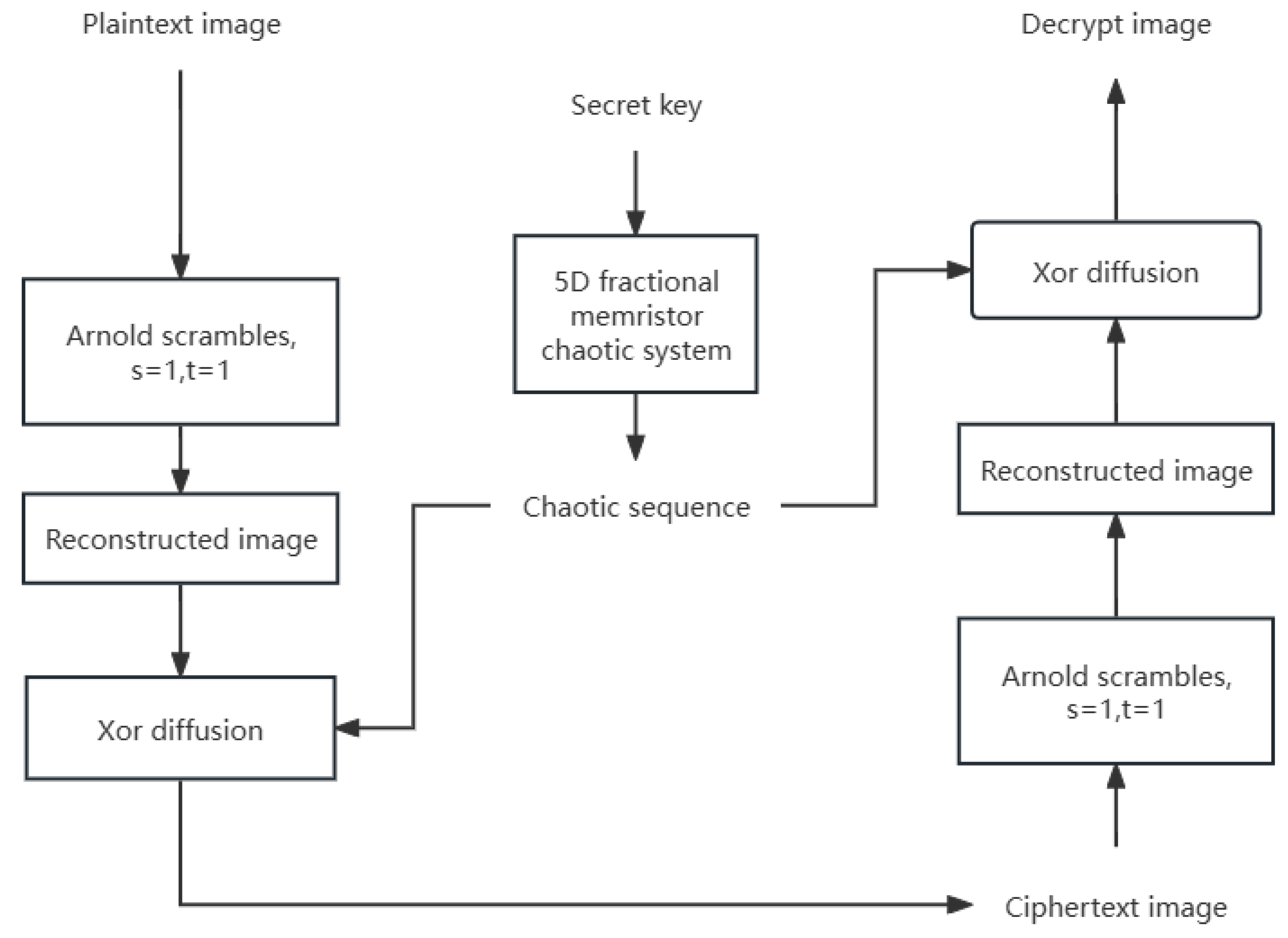
5.1. Encryption Scheme Design
5.2. Security Analysis
5.2.1. Histogram
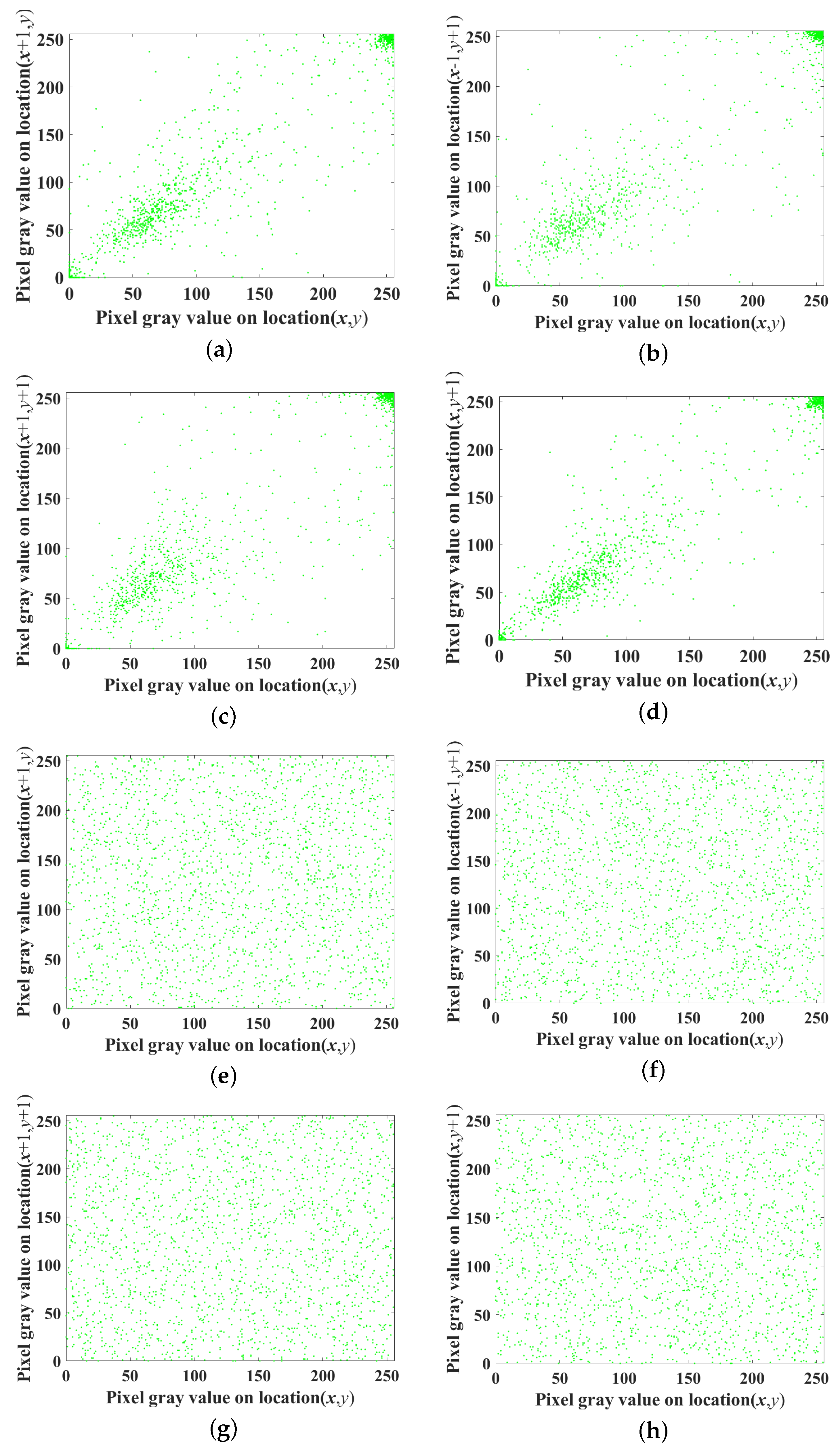
5.2.2. Correlation
5.2.3. Running Time
5.2.4. Information Entropy
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yu, F.; Kong, X.; Mokbel, A.A.M.; Yao, W.; Cai, S. Complex dynamics, hardware implementation and image encryption application of multiscroll memeristive Hopfield neural network with a novel local active memeristor. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 326–330. [Google Scholar] [CrossRef]
- Wang, C.; Liang, J.; Deng, Q. Dynamics of heterogeneous Hopfield neural network with adaptive activation function based on memristor. Neural Netw. 2024, 178, 106408. [Google Scholar] [CrossRef] [PubMed]
- Yu, F.; Kong, X.; Yao, W.; Zhang, J.; Cai, S.; Lin, H.; Jin, J. Dynamics analysis, synchronization and FPGA implementation of multiscroll Hopfield neural networks with non-polynomial memristor. Chaos Solitons Fractals 2024, 179, 114440. [Google Scholar] [CrossRef]
- Yao, W.; Liu, J.; Sun, Y.; Zhang, J.; Yu, F.; Cui, L.; Lin, H. Dynamics analysis and image encryption application of Hopfield neural network with a novel multistable and highly tunable memristor. Nonlinear Dyn. 2024, 112, 693–708. [Google Scholar] [CrossRef]
- Yu, F.; Shen, H.; Yu, Q.; Kong, X.; Sharma, P.K.; Cai, S. Privacy protection of medical data based on multi-scroll memristive Hopfield neural network. IEEE Trans. Netw. Sci. Eng. 2023, 10, 845–858. [Google Scholar] [CrossRef]
- Lin, H.; Deng, X.; Yu, F.; Sun, Y. Grid multi-butterfly memristive neural network with three memristive systems: Modeling, dynamic analysis, and application in police IoT. IEEE Internet Things J. 2024. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Y.; Liu, P.; Wen, S.; Wang, Y. Memristor-based neural network circuit with multimode generalization and differentiation on pavlov associative memory. IEEE Trans. Cybern. 2022, 53, 3351–3362. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Yu, F.; Hong, Q.; Xu, C.; Sun, Y. A triple-memristor Hopfield neural network with space multistructure attractors and space initial-offset behaviors. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2023, 42, 4948–4958. [Google Scholar] [CrossRef]
- Gao, X.; Mou, J.; Banerjee, S.; Zhang, Y. Color-gray multi-image hybrid compression–encryption scheme based on BP neural network and knight tour. IEEE Trans. Cybern. 2023, 53, 3267785. [Google Scholar] [CrossRef] [PubMed]
- Kong, X.; Yu, F.; Yao, W.; Cai, S.; Zhang, J.; Lin, H. Memristor-induced hyperchaos, multiscroll and extreme multistability in fractional-order HNN: Image encryption and FPGA implementation. Neural Netw. 2024, 171, 85–103. [Google Scholar] [CrossRef]
- Yu, F.; Xu, S.; Xiao, X.; Yao, W.; Huang, Y.; Cai, S.; Li, Y. Dynamics analysis, FPGA realization and image encryption application of a 5D memristive exponential hyperchaotic system. Integration 2023, 90, 58–70. [Google Scholar] [CrossRef]
- Deng, Q.; Wang, C.; Lin, H. Chaotic dynamical system of Hopfield neural network influenced by neuron activation threshold and its image encryption. Nonlinear Dyn. 2024, 112, 6629–6646. [Google Scholar] [CrossRef]
- Kong, X.; Yu, F.; Yao, W.; Xu, C.; Zhang, J.; Cai, S.; Wang, C. A class of 2n+1 dimensional simplest hamiltonian conservative chaotic systems and fast image encryption schemes. Appl. Math. Model. 2024, 125, 351–374. [Google Scholar] [CrossRef]
- Ma, X.; Wang, C. Hyper-chaotic image encryption system based on N+2 ring Joseph algorithm and reversible cellular automata. Multimed. Tools Appl. 2023, 82, 38967–38992. [Google Scholar] [CrossRef]
- Wang, M.; Ding, J.; Li, J.; He, S.; Zhang, X.; Iu Herbert, H.-C.; Li, Z. A novel multistable chaotic system with 2 m-scroll attractor and its application. Eur. Phys. J. Plus 2024, 139, 64. [Google Scholar] [CrossRef]
- Yu, F.; Zhang, Z.; Liu, L.; Shen, H.; Huang, Y.; Shi, C.; Cai, S.; Song, Y.; Du, S.; Xu, Q. Secure communication scheme based on a new 5D multistable four-wing memristive hyperchaotic system with disturbance inputs. Complexity 2020, 2020, 5859273. [Google Scholar] [CrossRef]
- Gokyildirim, A.; Kocamaz, U.E.; Uyaroglu, Y.; Calgan, H. A novel five-term 3D chaotic system with cubic nonlinearity and its microcontroller-based secure communication implementation. AEU-Int. J. Electron. Commun. 2023, 160, 154497. [Google Scholar] [CrossRef]
- Jin, J.; Chen, W.; Ouyang, A.; Yu, F.; Liu, H. A time-varying fuzzy parameter zeroing neural network for the synchronization of chaotic systems. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 8, 364–376. [Google Scholar] [CrossRef]
- Yao, W.; Wang, C.; Sun, Y.; Gong, S.; Lin, H. Event-triggered control for robust exponential synchronization of inertial memristive neural networks under parameter disturbance. Neural Netw. 2023, 164, 67–80. [Google Scholar] [CrossRef]
- Ma, M.L.; Xie, X.H.; Yang, Y.; Li, Z.J.; Sun, Y.C. Synchronization coexistence in a Rulkov neural network based on locally active discrete memristor. Chin. Phys. B 2023, 32, 058701. [Google Scholar] [CrossRef]
- Xu, Q.; Wang, Y.; Iu, H.H.C.; Wang, N.; Bao, H. Locally active memristor-based neuromorphic circuit: Firing pattern and hardware experiment. IEEE Trans. Circuits Syst. Regul. Pap. 2023, 70, 3276983. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Y.; Liu, P.; Wen, S.; Wang, Y. Memristor-based circuit design of PAD emotional space and its application in mood congruity. IEEE Internet Things J. 2023, 10, 16332–16342. [Google Scholar] [CrossRef]
- Lai, Q.; Wan, Z.; Kuate, P.D.K.; Fotsin, H. Coexisting attractors, circuit implementation and synchronization control of a new chaotic system evolved from the simplest memristor chaotic circuit. Commun. Nonlinear Sci. Numer. Simul. 2020, 89, 105341. [Google Scholar] [CrossRef]
- Yu, F.; Yuan, Y.; Wu, C.; Yao, W.; Xu, C.; Cai, S.; Wang, C. Modeling and hardware implementation of a class of Hamiltonian conservative chaotic systems with transient quasi-period and multistability. Nonlinear Dyn. 2024, 112, 2331–2347. [Google Scholar] [CrossRef]
- Murillo-Escobar, D.; Murillo-Escobar, M.Á.; Cruz-Hernández, C.; Arellano-Delgado, A.; López-Gutiérrez, R.M. Pseudorandom number generator based on novel 2D Hénon-Sine hyperchaotic map with microcontroller implementation. Nonlinear Dyn. 2023, 111, 6773–6789. [Google Scholar] [CrossRef] [PubMed]
- Yu, F.; Zhang, Z.; Shen, H.; Huang, Y.; Cai, S.; Jin, J.; Du, S. Design and FPGA implementation of a pseudo-random number generator based on a Hopfield neural network under electromagnetic radiation. Front. Phys. 2021, 9, 690651. [Google Scholar] [CrossRef]
- Li, S.; Liu, Y.; Ren, F.; Yang, Z. Design of a high throughput pseudorandom number generator based on discrete hyper-chaotic system. IEEE Trans. Circuits Syst. II Express Briefs 2022, 70, 806–810. [Google Scholar] [CrossRef]
- Yu, F.; Zhang, W.; Xiao, X.; Yao, W.; Cai, S.; Zhang, J.; Li, Y. Dynamic analysis and FPGA implementation of a new, simple 5D memristive hyperchaotic Sprott-C system. Mathematics 2023, 11, 701. [Google Scholar] [CrossRef]
- Muthuswamy, B.; Kokate, P.P. Memristor-based chaotic circuits. IETE Tech. Rev. 2009, 26, 417–429. [Google Scholar] [CrossRef]
- Hu, X.; Liu, C.; Liu, L.; Yao, Y.; Zheng, G. Multi-scroll hidden attractors and multi-wing hidden attractors in a 5-dimensional memristive system. Chin. Phys. 2017, 26, 110502. [Google Scholar] [CrossRef]
- Wang, M.; Deng, Y.; Liao, X.; Li, Z.; Ma, M.; Zeng, Y. Dynamics and circuit implementation of a four-wing memristive chaotic system with attractor rotation. Int. J. -Non-Linear Mech. 2019, 111, 149–159. [Google Scholar] [CrossRef]
- Gu, J.; Li, C.; Chen, Y.; Iu, H.H.; Lei, T. A conditional symmetric memristive system with infinitely many chaotic attractors. IEEE Access 2020, 8, 12394–12401. [Google Scholar] [CrossRef]
- Wan, Q.; Zhou, Z.; Ji, W.; Wang, C.; Yu, F. Dynamic analysis and circuit realization of a novel no-equilibrium 5D memristive hyperchaotic system with hidden extreme multistability. Complexity 2020, 2020, 7106861. [Google Scholar] [CrossRef]
- Li, H.; Yang, Y.; Li, W.; He, S.; Li, C. Extremely rich dynamics in a memristor-based chaotic system. Eur. Phys. J. Plus 2020, 135, 579. [Google Scholar] [CrossRef]
- Qiu, J.; Ding, D.; Weng, Y.; Qian, X. A fractional-order memristive system with time-delay and no equilibrium points. In Proceedings of the 2018 5th International Conference on Information Science and Control Engineering (ICISCE), Zhengzhou, China, 20–22 July 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1025–1029. [Google Scholar]
- Qiu, L.; Zhang, J.; Dai, Y.; Ding, Z.; Li, S.; Wang, L. Characteristic analysis of a fractional-order memristive hyperchaotic system. In Proceedings of the 2023 International Conference on Neuromorphic Computing (ICNC), Wuhan, China, 15–17 December 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 189–194. [Google Scholar]
- Liu, T.; Yu, J.; Yan, H.; Mou, J. A fractional-order chaotic system with infinite attractor coexistence and its DSP implementation. IEEE Access 2020, 8, 199852–199863. [Google Scholar] [CrossRef]
- Higazy, M.; Hamed, Y.S. Dynamics, circuit implementation and control of new caputo fractional order chaotic 5-dimensions hyperjerk model. Alex. Eng. J. 2021, 60, 4177–4190. [Google Scholar] [CrossRef]
- Yu, F.; Zhang, W.; Xiao, X.; Yao, W.; Cai, S.; Zhang, J.; Li, Y. Dynamic analysis and field-programmable gate array implementation of a 5D fractional-order memristive hyperchaotic system with multiple coexisting attractors. Fractal Fract. 2024, 8, 271. [Google Scholar] [CrossRef]
- Cui, L.; Lu, M.; Ou, Q.; Duan, H.; Luo, W. Analysis and circuit implementation of fractional order multi-wing hidden attractors. Chaos Solitons Fractals 2020, 138, 109894. [Google Scholar] [CrossRef]
- Sahoo, S.; Roy, B.K. A new multi-wing chaotic attractor with unusual variation in the number of wings. Chaos Solitons Fractals 2022, 164, 112598. [Google Scholar] [CrossRef]
- Sahoo, S.; Roy, B.K. Design of multi-wing chaotic systems with higher largest Lyapunov exponent. Chaos Solitons Fractals 2022, 157, 111926. [Google Scholar] [CrossRef]
- Yang, Y.; Huang, L.; Yu, X.; Kuznetsov, N.V.; Lai, Q. Generating multi-wing hidden hyperchaotic attractors with a single stable equilibrium. IEEE Trans. Circuits Syst. II Express Briefs 2023, 71, 2374–2378. [Google Scholar] [CrossRef]
- Tang, Z.; Yu, S. Design and realization of digital image encryption and decryption based on multi-wing butterfly chaotic attractors. In Proceedings of the 2012 5th International Congress on Image and Signal Processing, Chongqing, China, 16–18 October 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1143–1147. [Google Scholar]
- Grassi, G.; Khennaoui, A.A.; Ouannas, A.; Pham, V.T. Three-dimensional chaotic fractional maps without fixed points: Dynamics, coexisting hidden attractors and hardware implementation. In Proceedings of the 2023 International Conference on Fractional Differentiation and Its Applications (ICFDA), Ajman, United Arab Emirates, 14–16 March 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar]
- Yu, H.; Dong, E.; Du, S.; Jia, C. Transient chaos analysis of a modified Sprott-C system with hidden attractor and multistability. In Proceedings of the 2021 China Automation Congress (CAC), Beijing, China, 22–24 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 808–813. [Google Scholar]
- Wen, J.; Feng, Y.; Tao, X.; Cao, Y. Dynamical analysis of a new chaotic system: Hidden attractor, coexisting-attractors, offset boosting, and DSP realization. IEEE Access 2021, 9, 167920–167927. [Google Scholar] [CrossRef]
- Chen, S.; Ding, D.; Yang, Z. Multistability and hidden attractors in a fractional-order memristive Tabu learning neuron model and its medical image encryption. In Proceedings of the 2023 IEEE International Conference on Memristive Computing and Applications (ICMCA), Jinan, China, 8–10 December 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–5. [Google Scholar]
- Lin, H.; Wang, C.; Sun, Y. A universal variable extension method for designing multiscroll/wing chaotic systems. IEEE Trans. Ind. Electron. 2024, 71, 7806–7818. [Google Scholar] [CrossRef]
- Lai, Q.; Wan, Z.; Kuate, P.D.K. Generating grid multi-scroll attractors in memristive neural networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 70, 1324–1336. [Google Scholar] [CrossRef]
- Wang, N.; Li, C.; Bao, H.; Chen, M.; Bao, B. Generating multi-scroll Chua’s attractors via simplified piecewise-linear Chua’s diode. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 4767–4779. [Google Scholar] [CrossRef]
- Yu, F.; Chen, H.; Kong, X.; Yu, Q.; Cai, S.; Huang, Y.; Du, S. Dynamic analysis and application in medical digital image watermarking of a new multi-scroll neural network with quartic nonlinear memristor. Eur. Phys. J. Plus 2022, 137, 434. [Google Scholar] [CrossRef] [PubMed]
- Yan, S.; Li, L.; Gu, B.; Cui, Y.; Wang, J.; Song, J. Design of hyperchaotic system based on multi-scroll and its encryption algorithm in color image. Integration 2023, 88, 203–221. [Google Scholar] [CrossRef]
- Zhang, J.; Lv, Y.; Tao, J.; Huang, F.; Zhang, J. A robust real-time anchor-free traffic sign detector with one-level feature. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 8, 1437–1451. [Google Scholar] [CrossRef]
- Deng, Z.; Zhou, B.; He, P.; Huang, J.; Alfarraj, O.; Tolba, A. A position-aware transformer for image captioning. Comput. Mater. Contin. 2021, 70, 2005–2021. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Y.; He, S.; Sharma, P.K.; Yu, X.; Alfarraj, O.; Tolba, A. Lightweight single image super-resolution convolution neural network in portable device. KSII Trans. Internet Inf. Syst. 2021, 15, 4065–4083. [Google Scholar]
- Zhang, J.; He, Y.; Chen, W.; Kuang, L.D.; Zheng, B. CorrFormer: Context-aware tracking with cross-correlation and transformer. Comput. Electr. Eng. 2024, 114, 109075. [Google Scholar] [CrossRef]
- Gui, Y.; Zeng, G. Joint learning of visual and spatial features for edit propagation from a single image. Vis. Comput. 2020, 36, 469–482. [Google Scholar] [CrossRef]
- Liu, H.; Teng, L.; Zhang, Y.; Si, R.; Liu, P. Mutil-medical image encryption by a new spatiotemporal chaos model and DNA new computing for information security. Expert Syst. Appl. 2024, 235, 121090. [Google Scholar] [CrossRef]
- El-Shafai, W.; Khallaf, F.; El-Rabaie, E.S.M.; El-Samie, F.E.A. Proposed 3D chaos-based medical image cryptosystem for secure cloud-IoMT eHealth communication services. J. Ambient. Intell. Humaniz. Comput. 2024, 15, 1–28. [Google Scholar] [CrossRef]
- Pankaj, S.; Dua, M. Chaos based medical image encryption techniques: A comprehensive review and analysis. Inf. Secur. J. Glob. Perspect. 2024, 33, 332–358. [Google Scholar] [CrossRef]
- Jamal, S.S.; Hazzazi, M.M.; Khan, M.F.; Bassfar, Z.; Aljaedi, A.; ul Islam, Z. Region of interest-based medical image encryption technique based on chaotic S-boxes. Expert Syst. Appl. 2024, 238, 122030. [Google Scholar] [CrossRef]
- Ye, G.; Wong, K.W. An efficient chaotic image encryption algorithm based on a generalized Arnold map. Nonlinear Dyn. 2012, 69, 2079–2087. [Google Scholar] [CrossRef]
- Mirzaei, O.; Yaghoobi, M.; Irani, H. A new image encryption method: Parallel sub-image encryption with hyper chaos. Nonlinear Dyn. 2012, 67, 557–566. [Google Scholar] [CrossRef]
- Yavuz, E.; Yazıcı, R.; Kasapbaşı, M.C.; Yamaç, E. A chaos-based image encryption algorithm with simple logical functions. Comput. Electr. Eng. 2016, 54, 471–483. [Google Scholar] [CrossRef]
- Natiq, H.; Al-Saidi, N.M.G.; Said, M.R.M.; Kilicman, A. A new hyperchaotic map and its application for image encryption. Eur. Phys. J. Plus 2018, 133, 6. [Google Scholar] [CrossRef]
- Saljoughi, S.; Ahmad; Mirvaziri, H. A new method for image encryption by 3D chaotic map. Pattern Anal. Appl. 2019, 22, 243–257. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, D.; Nkapkop, J.D.D.; Njitacke, Z.T.; Ahmad, M.; Zhu, L.; Tsafack, N. A memristive autapse-synapse neural network: Application to image encryption. Phys. Scr. 2023, 98, 035222. [Google Scholar] [CrossRef]



| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0.001 | 0.0013 | 0.0013 | 0.0012 | 0.0012 |
| −1.001 | −1.0013 | −1.0013 | −1.0012 | −1.0012 |
| Resource | Utilization | Available | Utilization |
|---|---|---|---|
| LUT | 31,347 | 53,200 | 58.92 |
| LUTRAM | 1413 | 17,400 | 8.12 |
| FF | 37.452 | 106,440 | 35.18 |
| DSP | 136 | 220 | 61.81 |
| IO | 35 | 125 | 28 |
| FF | 1 | 32 | 3.13 |
| Direction | Horizontal | Diagonal | Vertical |
|---|---|---|---|
| Encrypted | 0.9735 | 0.9636 | 0.9622 |
| Decrypted | 0.0323 | −0.0029 | −0.0031 |
| Ref. [63] | 0.0770 | −0.0615 | −0.0724 |
| Ref. [64] | −0.0893 | 0.0010 | 0.0034 |
| Ref. [65] | −0.0289 | 0.0366 | 0.0146 |
| Encryption Time (s) | Decrypted Time (s) |
|---|---|
| 0.18832 | 0.18874 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, F.; Xu, S.; Lin, Y.; He, T.; Wu, C.; Lin, H. Design and Analysis of a Novel Fractional-Order System with Hidden Dynamics, Hyperchaotic Behavior and Multi-Scroll Attractors. Mathematics 2024, 12, 2227. https://doi.org/10.3390/math12142227
Yu F, Xu S, Lin Y, He T, Wu C, Lin H. Design and Analysis of a Novel Fractional-Order System with Hidden Dynamics, Hyperchaotic Behavior and Multi-Scroll Attractors. Mathematics. 2024; 12(14):2227. https://doi.org/10.3390/math12142227
Chicago/Turabian StyleYu, Fei, Shuai Xu, Yue Lin, Ting He, Chaoran Wu, and Hairong Lin. 2024. "Design and Analysis of a Novel Fractional-Order System with Hidden Dynamics, Hyperchaotic Behavior and Multi-Scroll Attractors" Mathematics 12, no. 14: 2227. https://doi.org/10.3390/math12142227
APA StyleYu, F., Xu, S., Lin, Y., He, T., Wu, C., & Lin, H. (2024). Design and Analysis of a Novel Fractional-Order System with Hidden Dynamics, Hyperchaotic Behavior and Multi-Scroll Attractors. Mathematics, 12(14), 2227. https://doi.org/10.3390/math12142227








