Nonlinear SIRS Fractional-Order Model: Analysing the Impact of Public Attitudes towards Vaccination, Government Actions, and Social Behavior on Disease Spread
Abstract
1. Introduction
2. Preliminaries
- 1.
- for , the condition for (3) is ,
- 2.
- for , the conditions for (3) are either Routh–Hurwitz conditions or , ,
- 3.
- for , if the discriminant, of is positive, then Routh–Hurwitz conditions are the necessary and sufficient conditions for (3), that is, , , if ,
- 4.
- 5.
- if , , , then (3) is satisfied for all ,
- 6.
- for general n, , is necessary condition for (3).
3. Mathematical Model
4. Existence and Uniqueness
5. Equilibrium Points and Stability Analysis
- Disease free equilibrium point (DFE), :Here, , ,The basic reproduction number represents the number of newly infected people from a single infected individual in a susceptible environment. The procedure developed by van den Driessche and Watmough is usually used to obtain [38]. Let, . Then we have: whereHere, and contain the compartment with the new infection term and the rest of the terms, respectively. Then, at , we haveNow, is the spectral radius of the next generation matrix and is denoted by:
- Interior equilibrium point, :, ,and is the positive root of the given equation:
| Reproduction Number | Sign of Coefficients of (9) | Number of Positive Roots | ||
|---|---|---|---|---|
| 0 | ||||
| 2 (if ) 0 (if ) | ||||
| 0 | ||||
| 1 | ||||
| 1 | ||||
| 1 | ||||
Local Stability Analysis
- 1.
- If , , and are Routh–Hurwitz determinantsthen for , the necessary and sufficient conditions for the interior equilibrium point to be locally asymptotically stable are
- 2.
- If , , and , then is unstable.
- 3.
- If , , , , and , then is locally asymptotically stable. Also, if , , , , , then is unstable.
- 4.
- If , , , , and , then the equilibrium point is locally asymptotically stable, for all .
- 5.
- is the necessary condition for the equilibrium point to be locally asymptotically stable.
- 1.
- for , if ,
- 2.
- for , if and ,
- 3.
- for , if and .
- , if .
- all , if and
- , if and .
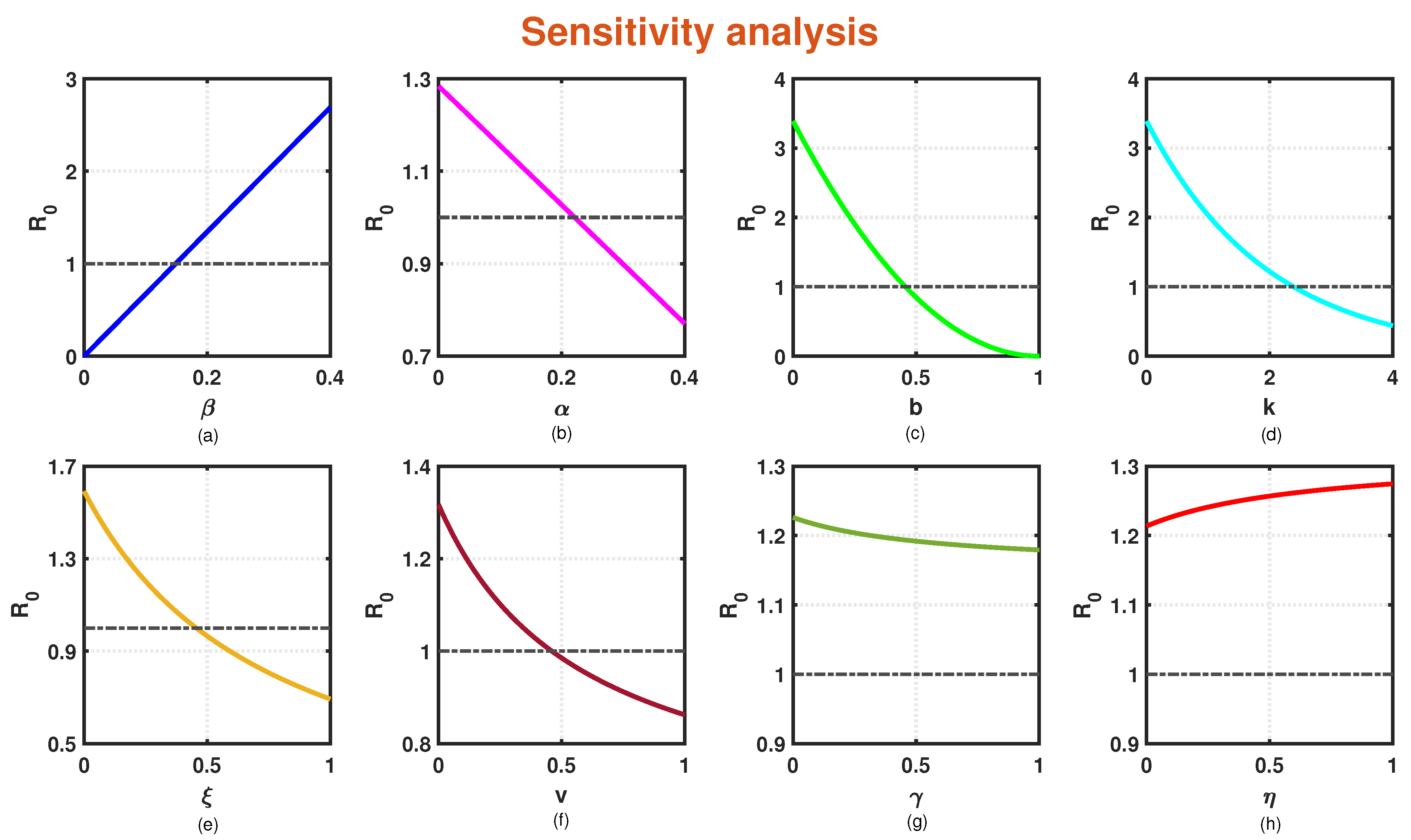
6. Sensitivity Analysis
7. Optimal Control
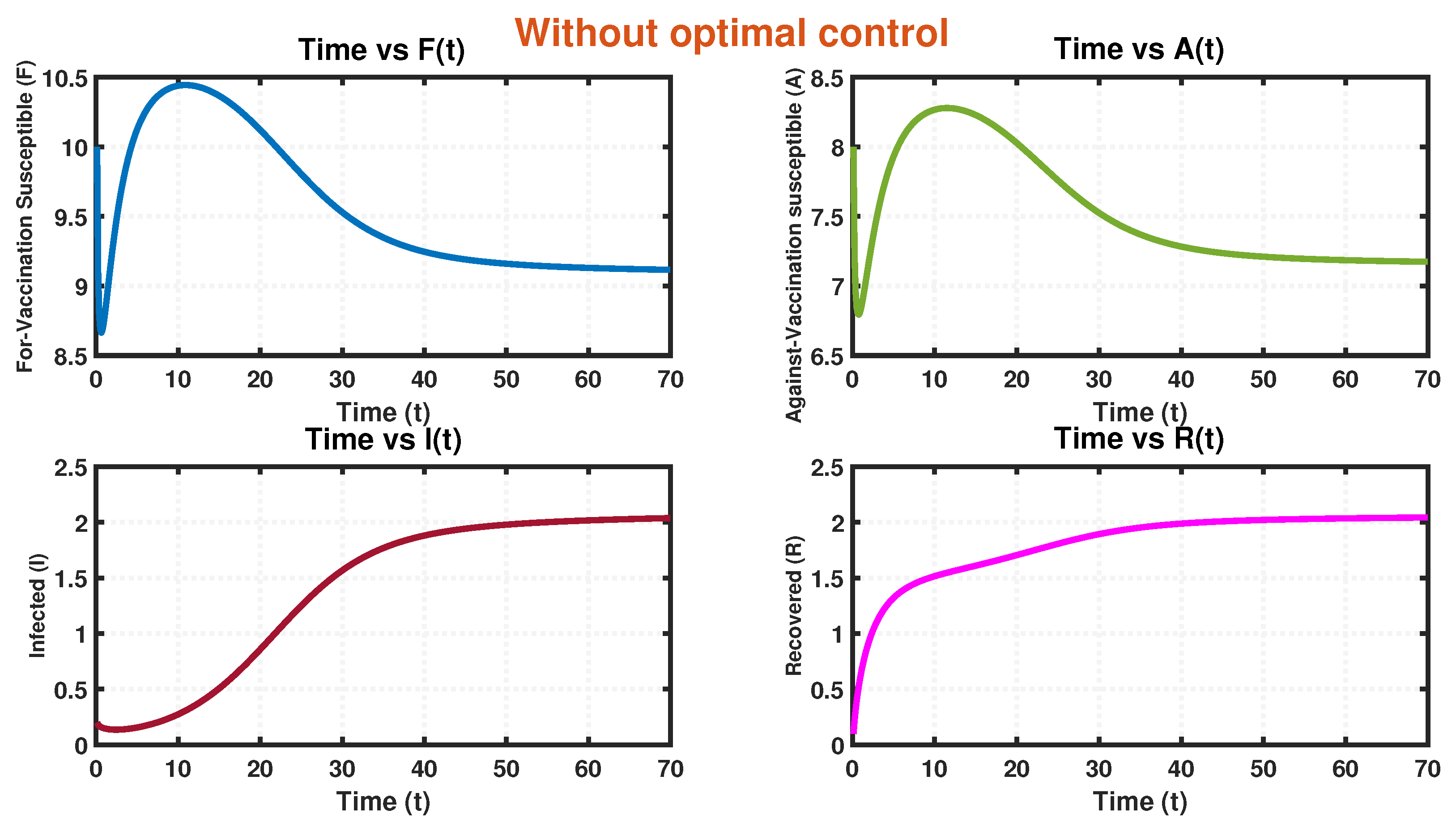
8. Numerical Simulation
9. Conclusions
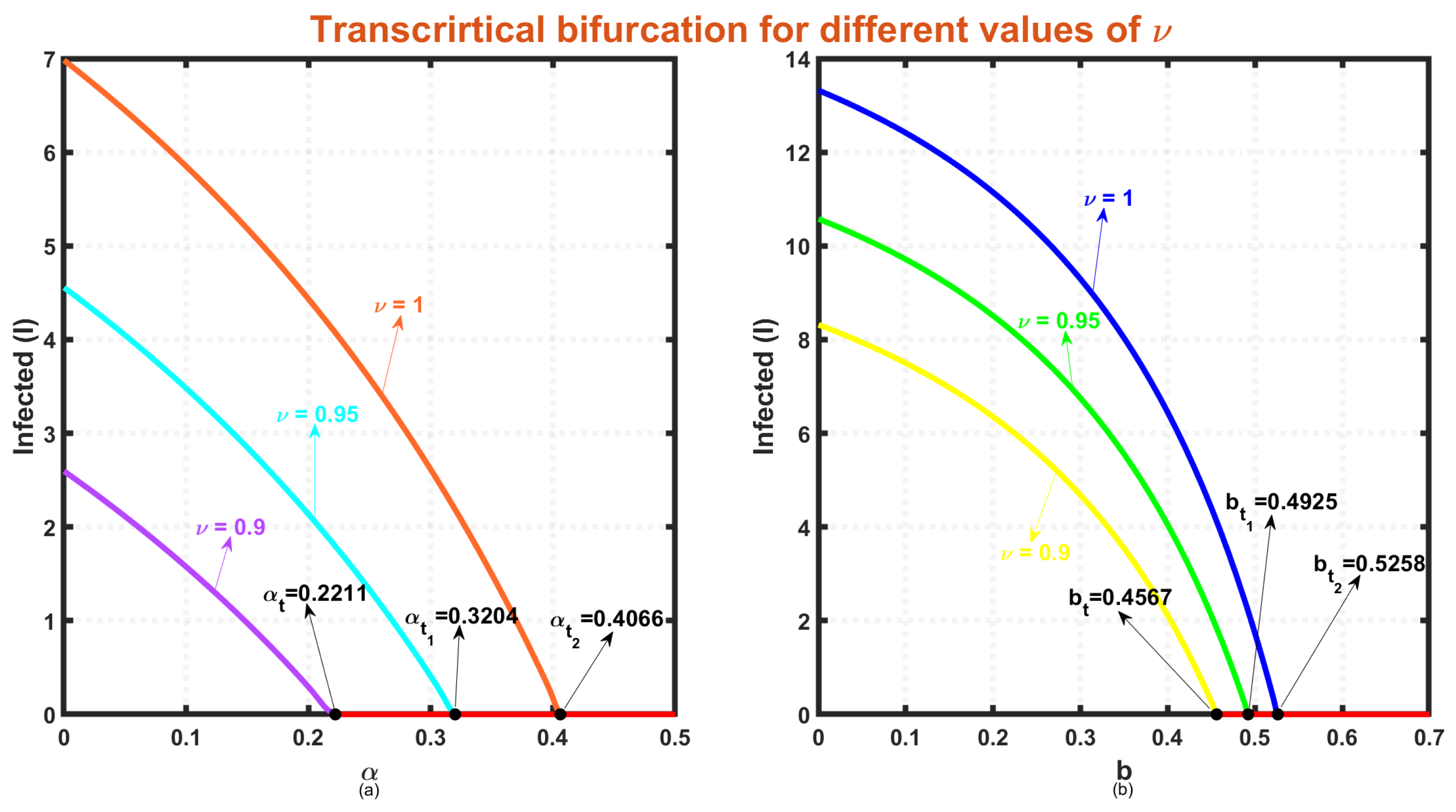
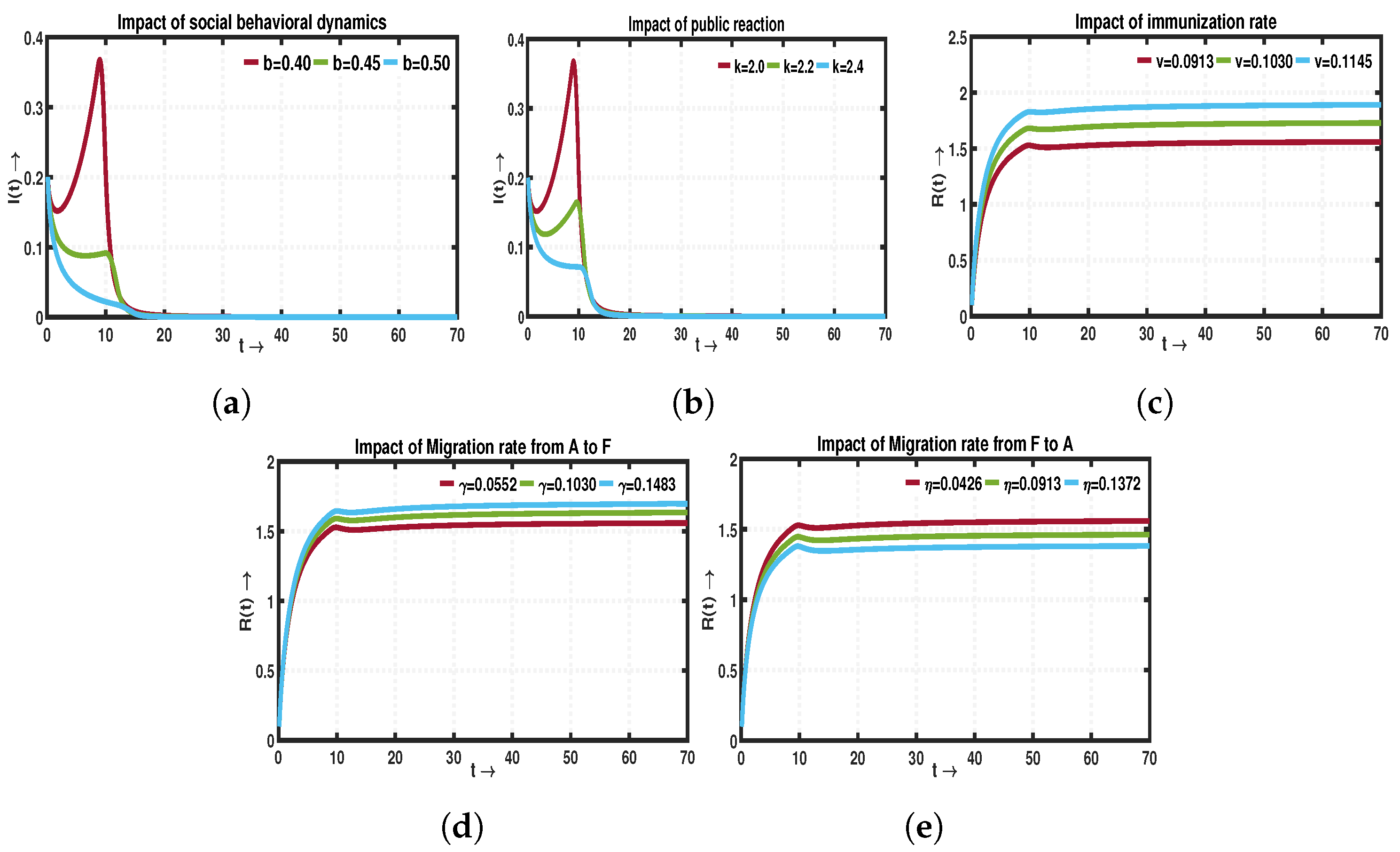
- Our findings demonstrate the better performance of the fractional-order model compared to the traditional integer-order model constructed using ordinary differential equations One limitation of integer-order systems is their inability to consider the historical information of the system, which is crucial in the context of disease transmission. When a disease spreads, the susceptible population relies on their past experiences and memory, to protect themselves from infection. In contrast, a dynamical system incorporating fractional-order derivatives encompasses not only the current state but also retains information about its previous states. Consequently, fractional-order systems provide a more comprehensive understanding of the underlying system dynamics compared to integer-order systems, as they take into account both present and past interactions and behaviors. In this study, a comprehensive investigation is conducted using a nonlinear SIRS compartmental framework to analyze the intricate dynamics of infectious diseases. The numerical section offers an in-depth analysis of various fractional and integer-order derivatives to gain insights into the complex dynamics of the proposed system. Figure 10a,b illustrate the variation in the level of infected individuals () as and b change for three different values of . In Figure 10a, when , a transcritical bifurcation occurs at . For , this bifurcation happens at . When , stability exchange is seen at , and the endemic equilibrium disappears after surpassing . These results indicate that using fractional differential equations results in stability exchange at a lower value. A similar observation is made for the model parameter b, as shown in Figure 10b.
- Moreover, we have derived the explicit expression for the basic reproduction number, denoted as . Additionally, our analysis reveals the existence of two feasible equilibriums within the system: the DFE and the EE. Notably, the disease-free state experiences a transcritical bifurcation when the basic reproduction number, represented by , reaches unity (). This critical point signifies a significant transition in the system’s behavior, where the disease-free state interacts with the endemic state, leading to fundamental changes in the dynamics of the system. Again, our observations indicate that both equilibria, namely DFE and EE, exhibit local asymptotic stability. This crucial property implies that the DFE serves as a threshold for the complete eradication of the disease, ensuring its elimination from the system. On the other hand, the local asymptotic stability of the EE signifies that the disease will persist within the system under specific parametric conditions. In the case of EE, complete eradication of the disease is not possible within the system.
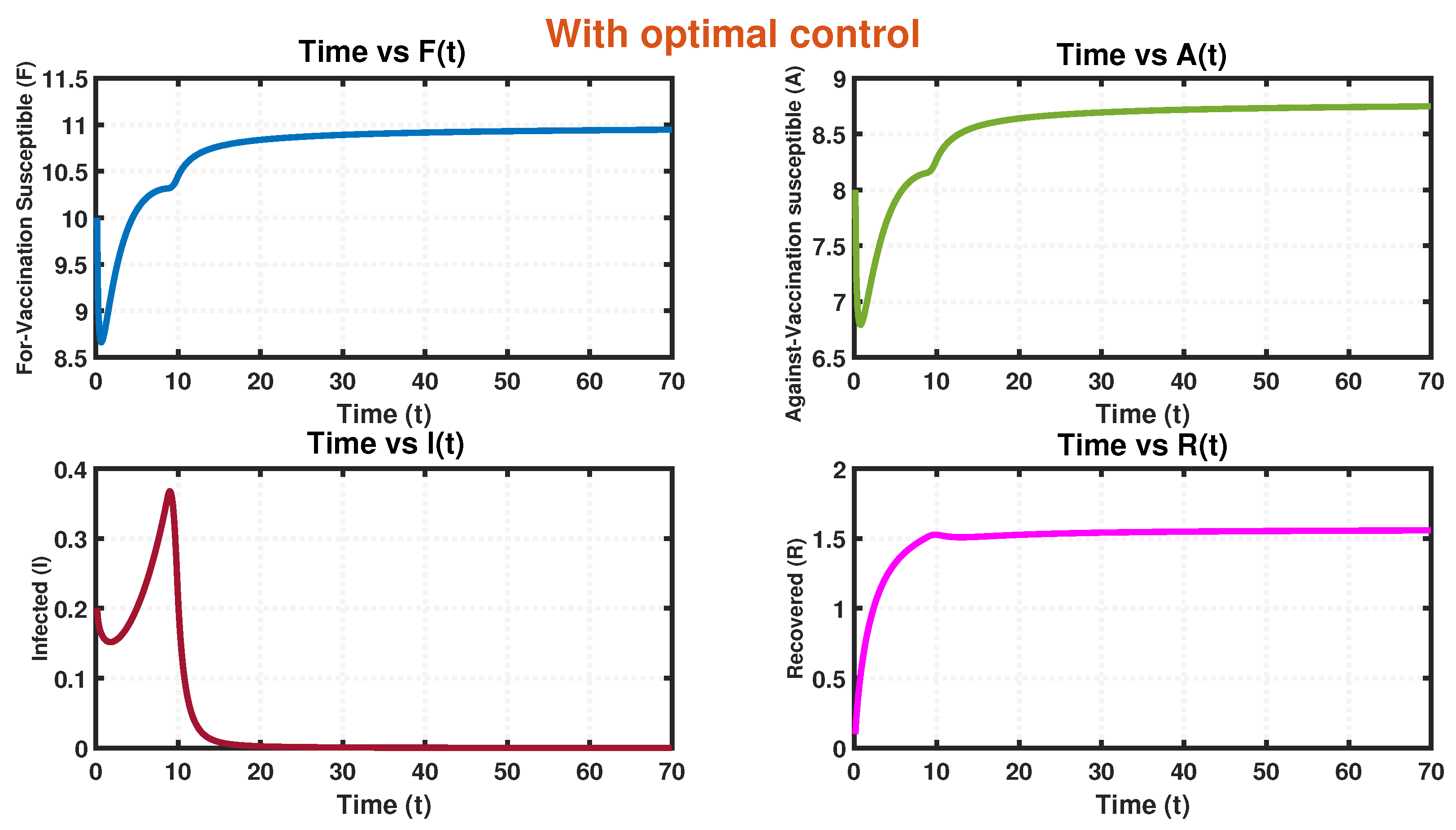
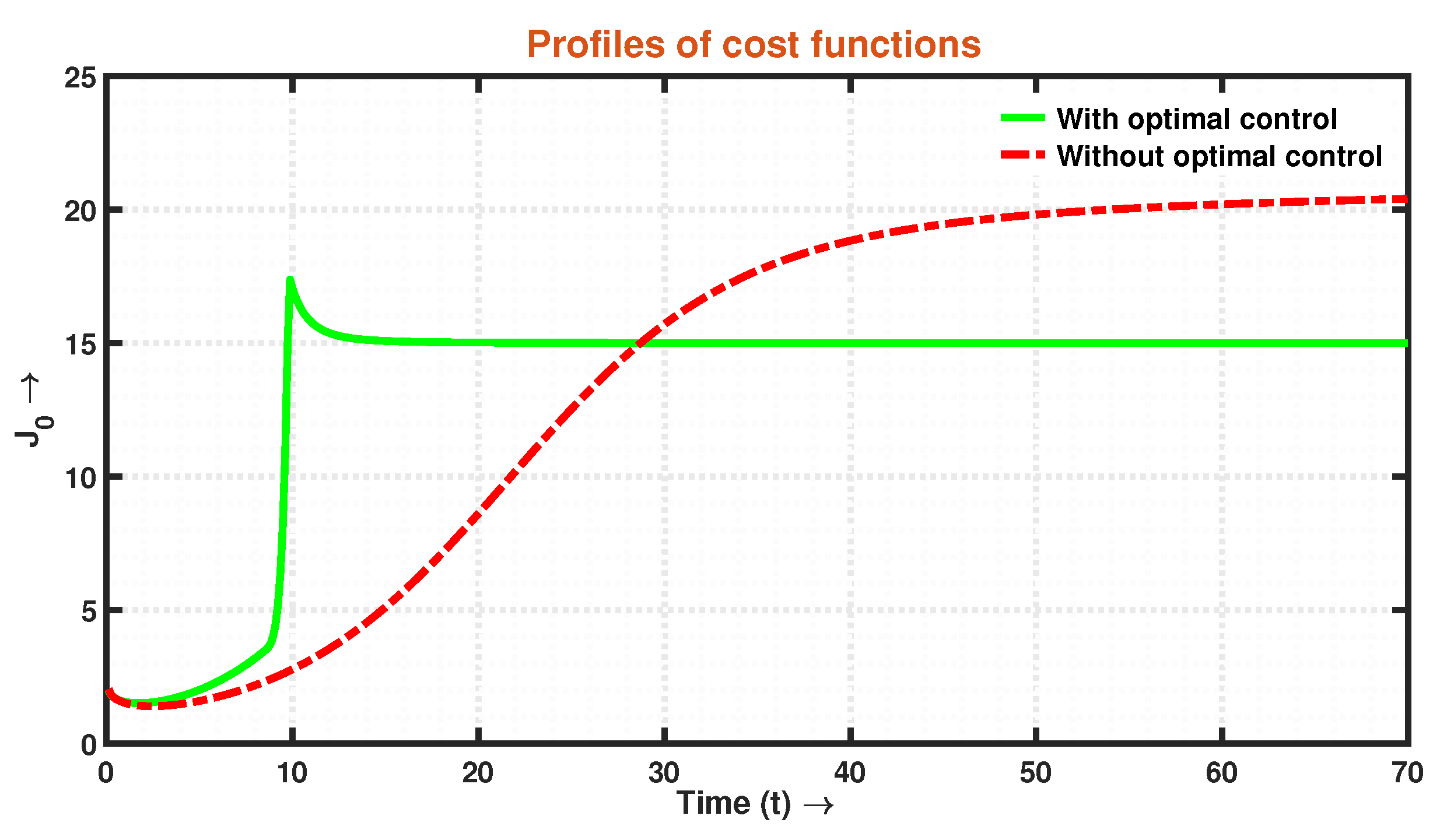
- Recognizing this challenge, we propose an associated optimal control problem to investigate the influence of governmental regulations on the dynamics of the system. The numerical simulations conducted in this study provide compelling evidence that the implementation of a control policy leads to a significant reduction in the size of infected individuals. This outcome implies that the adoption of control measures not only decreases the prevalence of the disease but also alleviates the economic burden associated with the epidemic. The findings highlight the effectiveness of the time-dependent control intervention in mitigating the spread of infection within a system during an epidemic outbreak. This control strategy proves to be instrumental in curbing infectivity, ultimately yielding positive outcomes in disease management and the overall well-being of the affected population.
10. Future Research Scope
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Podlubny, I. An introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. Math. Sci. Eng 1999, 198, 340. [Google Scholar]
- Petráš, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Teodoro, G.S.; Machado, J.T.; De Oliveira, E.C. A review of definitions of fractional derivatives and other operators. J. Comput. Phys. 2019, 388, 195–208. [Google Scholar] [CrossRef]
- Kai, Y.; Chen, S.; Zhang, K.; Yin, Z. Exact solutions and dynamic properties of a nonlinear fourth-order time-fractional partial differential equation. Waves Random Complex Media 2022, 2044541. [Google Scholar] [CrossRef]
- Li, M.; Wang, L.; Luo, C.; Wu, H. A new improved fractional Tikhonov regularization method for moving force identification. Structures 2024, 60, 105840. [Google Scholar] [CrossRef]
- Kumar, P.; Erturk, V.S.; Abboubakar, H.; Nisar, K.S. Prediction studies of the epidemic peak of coronavirus disease in Brazil via new generalised Caputo type fractional derivatives. Alex. Eng. J. 2021, 60, 3189–3204. [Google Scholar] [CrossRef]
- Zafar, Z.U.A.; Ali, N.; Baleanu, D. Dynamics and numerical investigations of a fractional-order model of toxoplasmosis in the population of human and cats. Chaos Solitons Fractals 2021, 151, 111261. [Google Scholar] [CrossRef]
- Zafar, Z.U.A.; Zaib, S.; Hussain, M.T.; Tunç, C.; Javeed, S. Analysis and numerical simulation of tuberculosis model using different fractional derivatives. Chaos Solitons Fractals 2022, 160, 112202. [Google Scholar] [CrossRef]
- Nisar, K.S.; Farman, M.; Abdel-Aty, M.; Cao, J. A review on epidemic models in sight of fractional calculus. Alex. Eng. J. 2023, 75, 81–113. [Google Scholar] [CrossRef]
- Azeem, M.; Farman, M.; Abukhaled, M.; Nisar, K.S.; AKGÜL, A. Epidemiological Analysis Of Human Liver Model with Fractional Operator. Fractals 2023, 31, 2340047. [Google Scholar] [CrossRef]
- Nisar, K.S.; Farman, M.; Abdel-Aty, M.; Abdel-Aty, M. Mathematical Epidemiology: A Review of the Singular and Non-Singular Kernels and their Applications. Prog. Fract. Differ. Appl. 2023, 9, 507–544. [Google Scholar] [CrossRef]
- Zafar, Z.U.A.; DarAssi, M.H.; Ahmad, I.; Assiri, T.A.; Meetei, M.Z.; Khan, M.A.; Hassan, A.M. Numerical simulation and analysis of the stochastic hiv/aids model in fractional order. Results Phys. 2023, 53, 106995. [Google Scholar] [CrossRef]
- Vitanov, N.K.; Ausloos, M.R. Knowledge epidemics and population dynamics models for describing idea diffusion. In Models of Science Dynamics: Encounters between Complexity Theory and Information Sciences; Springer: Berlin/Heidelberg, Germany, 2011; pp. 69–125. [Google Scholar] [CrossRef]
- Larson, H.J.; Jarrett, C.; Eckersberger, E.; Smith, D.M.; Paterson, P. Understanding vaccine hesitancy around vaccines and vaccination from a global perspective: A systematic review of published literature, 2007–2012. Vaccine 2014, 32, 2150–2159. [Google Scholar] [CrossRef]
- Lin, C.; Tu, P.; Beitsch, L.M. Confidence and receptivity for COVID-19 vaccines: A rapid systematic review. Vaccines 2020, 9, 16. [Google Scholar] [CrossRef]
- Piedrahita-Valdés, H.; Piedrahita-Castillo, D.; Bermejo-Higuera, J.; Guillem-Saiz, P.; Bermejo-Higuera, J.R.; Guillem-Saiz, J.; Sicilia-Montalvo, J.A.; Machío-Regidor, F. Vaccine hesitancy on social media: Sentiment analysis from June 2011 to April 2019. Vaccines 2021, 9, 28. [Google Scholar] [CrossRef]
- Reiter, P.L.; Pennell, M.L.; Katz, M.L. Acceptability of a COVID-19 vaccine among adults in the United States: How many people would get vaccinated? Vaccine 2020, 38, 6500–6507. [Google Scholar] [CrossRef]
- Bonte, J. The Continuum of Attitudes towards Vaccination A Qualitative Analysis of Arguments Used in Pro-, Anti-and Hesitant Tweets. Master’s Thesis, Utrecht University, Utrecht, The Netherlands, 2022. [Google Scholar]
- Lee, S.K.; Sun, J.; Jang, S.; Connelly, S. Misinformation of COVID-19 vaccines and vaccine hesitancy. Sci. Rep. 2022, 12, 13681. [Google Scholar] [CrossRef]
- Wang, Q.; Jiang, Q.; Yang, Y.; Pan, J. The burden of travel for care and its influencing factors in China: An inpatient-based study of travel time. J. Transp. Health 2022, 25, 101353. [Google Scholar] [CrossRef]
- Nisar, K.S.; Shoaib, M.; Raja, M.A.Z.; Tabassum, R.; Morsy, A. A novel design of evolutionally computing to study the quarantine effects on transmission model of Ebola virus disease. Results Phys. 2023, 48, 106408. [Google Scholar] [CrossRef]
- Dutta, P.; Saha, S.; Samanta, G. Assessing the influence of public behavior and governmental action on disease dynamics: A PRCC analysis and optimal control approach. Eur. Phys. J. Plus 2024, 139, 527. [Google Scholar] [CrossRef]
- Agrawal, O.P. A general formulation and solution scheme for fractional optimal control problems. Nonlinear Dyn. 2004, 38, 323–337. [Google Scholar] [CrossRef]
- Kheiri, H.; Jafari, M. Optimal control of a fractional-order model for the HIV/AIDS epidemic. Int. J. Biomath. 2018, 11, 1850086. [Google Scholar] [CrossRef]
- Al-Basir, F.; Elaiw, A.M.; Kesh, D.; Roy, P.K. Optimal control of a fractional-order enzyme kinetic model. Control. Cybern. 2015, 44, 443–461. [Google Scholar]
- Akman Yıldız, T. Optimal control problem of a non-integer order waterborne pathogen model in case of environmental stressors. Front. Phys. 2019, 7, 95. [Google Scholar] [CrossRef]
- Kada, D.; Kouidere, A.; Balatif, O.; Rachik, M.; Labriji, E.H. Mathematical modeling of the spread of COVID-19 among different age groups in Morocco: Optimal control approach for intervention strategies. Chaos Solitons Fractals 2020, 141, 110437. [Google Scholar] [CrossRef] [PubMed]
- Khajji, B.; Kada, D.; Balatif, O.; Rachik, M. A multi-region discrete time mathematical modeling of the dynamics of Covid-19 virus propagation using optimal control. J. Appl. Math. Comput. 2020, 64, 255–281. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.; Govindaraj, V.; Erturk, V.S.; Nisar, K.S.; Inc, M. Fractional mathematical modeling of the Stuxnet virus along with an optimal control problem. Ain Shams Eng. J. 2023, 14, 102004. [Google Scholar] [CrossRef]
- Hussain, T.; Ozair, M.; Faizan, M.; Jameel, S.; Nisar, K.S. Optimal control approach based on sensitivity analysis to retrench the pine wilt disease. Eur. Phys. J. Plus 2021, 136, 1–27. [Google Scholar] [CrossRef]
- Li, H.L.; Zhang, L.; Hu, C.; Jiang, Y.L.; Teng, Z. Dynamical analysis of a fractional-order predator-prey model incorporating a prey refuge. J. Appl. Math. Comput. 2017, 54, 435–449. [Google Scholar] [CrossRef]
- Ahmed, E.; Elgazzar, A. On fractional order differential equations model for nonlocal epidemics. Phys. A Stat. Mech. Its Appl. 2007, 379, 607–614. [Google Scholar] [CrossRef] [PubMed]
- Das, M.; Samanta, G.; De la Sen, M. A Fractional Order Model to Study the Effectiveness of Government Measures and Public Behaviours in COVID-19 Pandemic. Mathematics 2022, 10, 3020. [Google Scholar] [CrossRef]
- Saha, S.; Dutta, P.; Samanta, G. Dynamical behavior of SIRS model incorporating government action and public response in presence of deterministic and fluctuating environments. Chaos Solitons Fractals 2022, 164, 112643. [Google Scholar] [CrossRef]
- Dutta, S.; Dutta, P.; Samanta, G. Modelling disease transmission through asymptomatic carriers: A societal and environmental perspective. Int. J. Dyn. Control. 2024. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Podlubny, I. Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag–Leffler stability. Comput. Math. Appl. 2010, 59, 1810–1821. [Google Scholar] [CrossRef]
- Ghosh, U.; Pal, S.; Banerjee, M. Memory effect on Bazykin’s prey-predator model: Stability and bifurcation analysis. Chaos Solitons Fractals 2021, 143, 110531. [Google Scholar] [CrossRef]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef] [PubMed]
- Matouk, A. Stability conditions, hyperchaos and control in a novel fractional order hyperchaotic system. Phys. Lett. A 2009, 373, 2166–2173. [Google Scholar] [CrossRef]
- Guo, T.L. The necessary conditions of fractional optimal control in the sense of Caputo. J. Optim. Theory Appl. 2013, 156, 115–126. [Google Scholar] [CrossRef]
- Ndaïrou, F.; Torres, D.F. Distributed-Order Non-Local Optimal Control. Axioms 2020, 9, 124. [Google Scholar] [CrossRef]
- Das, M.; Samanta, G.P. Optimal control of a fractional order epidemic model with carriers. Int. J. Dyn. Control. 2022, 10, 598–619. [Google Scholar] [CrossRef]
- Das, M.; Samanta, G.; De la Sen, M. Stability analysis and optimal control of a fractional order synthetic drugs transmission model. Mathematics 2021, 9, 703. [Google Scholar] [CrossRef]
- Gaff, H.; Schaefer, E. Optimal control applied to vaccination and treatment strategies for various epidemiological models. Math. Biosci. Eng. 2009, 6, 469–492. [Google Scholar] [CrossRef] [PubMed]
- Kassa, S.M.; Ouhinou, A. The impact of self-protective measures in the optimal interventions for controlling infectious diseases of human population. J. Math. Biol. 2015, 70, 213–236. [Google Scholar] [CrossRef] [PubMed]
- Garrappa, R. On linear stability of predictor–corrector algorithms for fractional differential equations. Int. J. Comput. Math. 2010, 87, 2281–2290. [Google Scholar] [CrossRef]
- Du, M.; Wang, Z.; Hu, H. Measuring memory with the order of fractional derivative. Sci. Rep. 2013, 3, 3431. [Google Scholar] [CrossRef]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 42. [Google Scholar]
- Cao, X.; Datta, A.; Al Basir, F.; Roy, P.K. Fractional-order model of the disease psoriasis: A control based mathematical approach. J. Syst. Sci. Complex. 2016, 29, 1565–1584. [Google Scholar] [CrossRef]
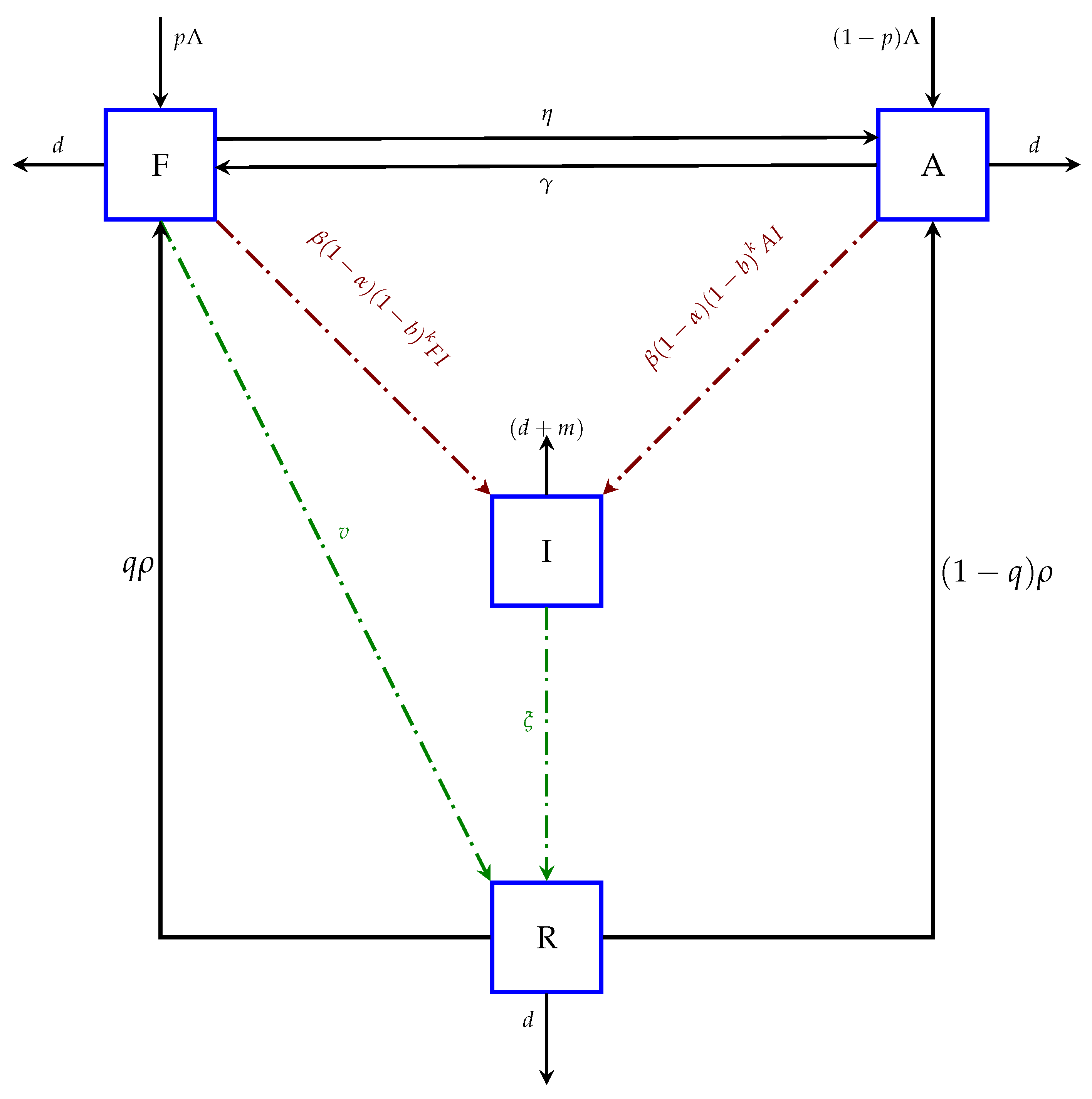






| Parameters/Variables | Biological Meaning of the Variables and Parameter |
|---|---|
| For-vaccination susceptible compartment | |
| Against-vaccination susceptible compartment | |
| Infected compartment | |
| Recovered compartment | |
| p | Portion of the recruitment goes in class |
| Portion of the recruitment goes in class | |
| The recruitment rate | |
| Coefficient of rate of propagation of infection for susceptible classes | |
| The effectiveness of governmental intervention | |
| b | The effectiveness of social behavioral dynamics |
| k | Strength of public reaction |
| Immunization rate of for-vaccination compartment | |
| Migration rate from against-vaccination to for-vaccination compartment through awareness | |
| Migration rate from for-vaccination to against-vaccination compartment through receiving false information about vaccines | |
| q | Portion of the recovered goes in class |
| Portion of the recovered goes in class | |
| Rate of chance of reinfection | |
| Natural death rate | |
| Recovery rate of infected class | |
| Disease related mortality rate |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dutta, P.; Santra, N.; Samanta, G.; De la Sen, M. Nonlinear SIRS Fractional-Order Model: Analysing the Impact of Public Attitudes towards Vaccination, Government Actions, and Social Behavior on Disease Spread. Mathematics 2024, 12, 2232. https://doi.org/10.3390/math12142232
Dutta P, Santra N, Samanta G, De la Sen M. Nonlinear SIRS Fractional-Order Model: Analysing the Impact of Public Attitudes towards Vaccination, Government Actions, and Social Behavior on Disease Spread. Mathematics. 2024; 12(14):2232. https://doi.org/10.3390/math12142232
Chicago/Turabian StyleDutta, Protyusha, Nirapada Santra, Guruprasad Samanta, and Manuel De la Sen. 2024. "Nonlinear SIRS Fractional-Order Model: Analysing the Impact of Public Attitudes towards Vaccination, Government Actions, and Social Behavior on Disease Spread" Mathematics 12, no. 14: 2232. https://doi.org/10.3390/math12142232
APA StyleDutta, P., Santra, N., Samanta, G., & De la Sen, M. (2024). Nonlinear SIRS Fractional-Order Model: Analysing the Impact of Public Attitudes towards Vaccination, Government Actions, and Social Behavior on Disease Spread. Mathematics, 12(14), 2232. https://doi.org/10.3390/math12142232












