Trajectory Tracking Control of an Autonomous Vessel in the Presence of Unknown Dynamics and Disturbances
Abstract
:1. Introduction
- The symbol , with , refers to the sign function of a real number and is defined as
- The symbol , with , refers to the sign function of a vector of real numbers and is defined as
- The symbol , with , refers to the linear saturation function defined as
- In similar form , with , refers to the vector of linear saturation function defined as
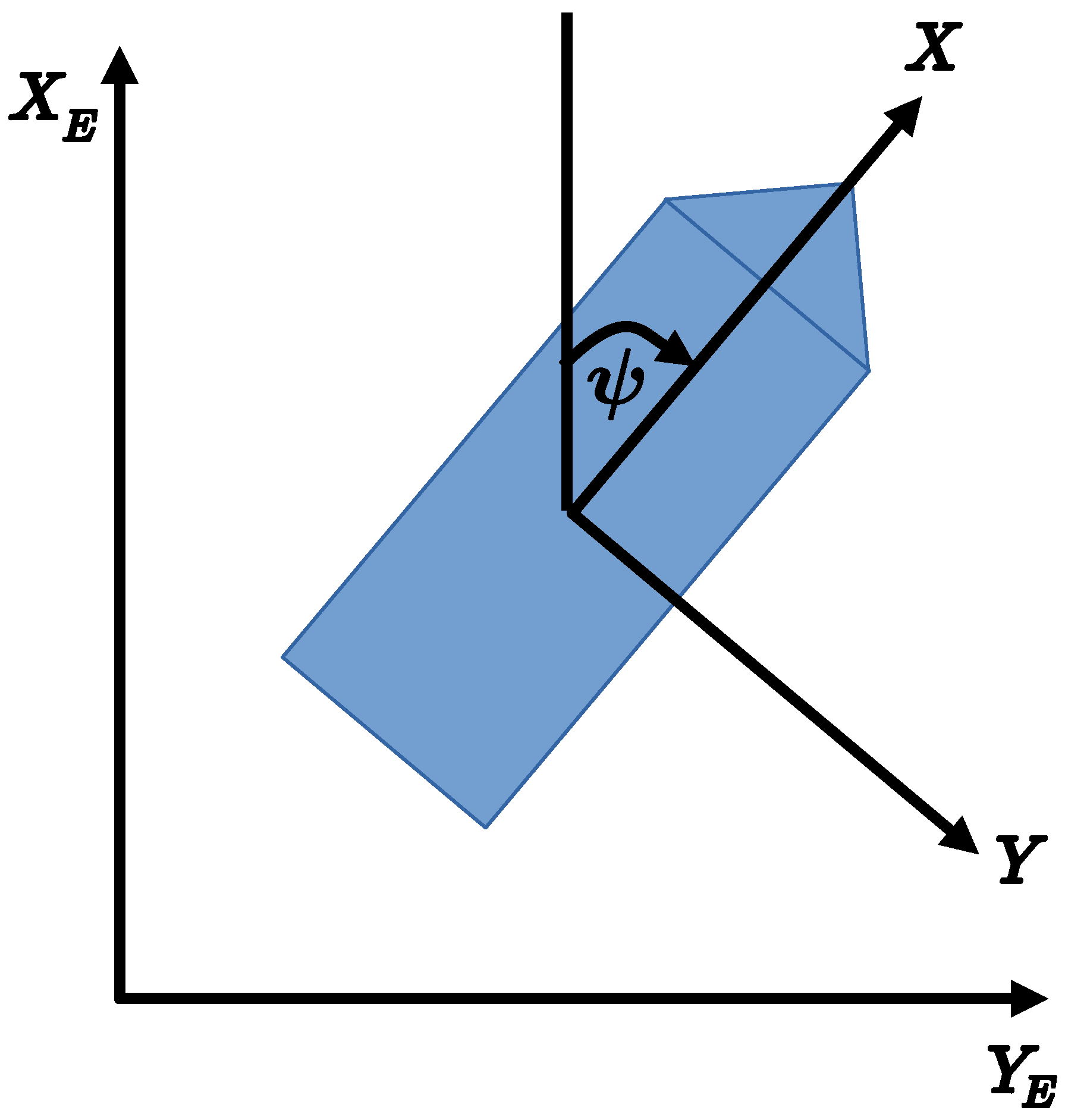
2. Dynamic Model and Problem Statement
- (A1)
- The perturbation satisfieswhere is an unknown parameter.
- (A2)
- the state variables and are measurable.
Limitations
3. Control Strategy
The Trajectory Control Law for the Vessel
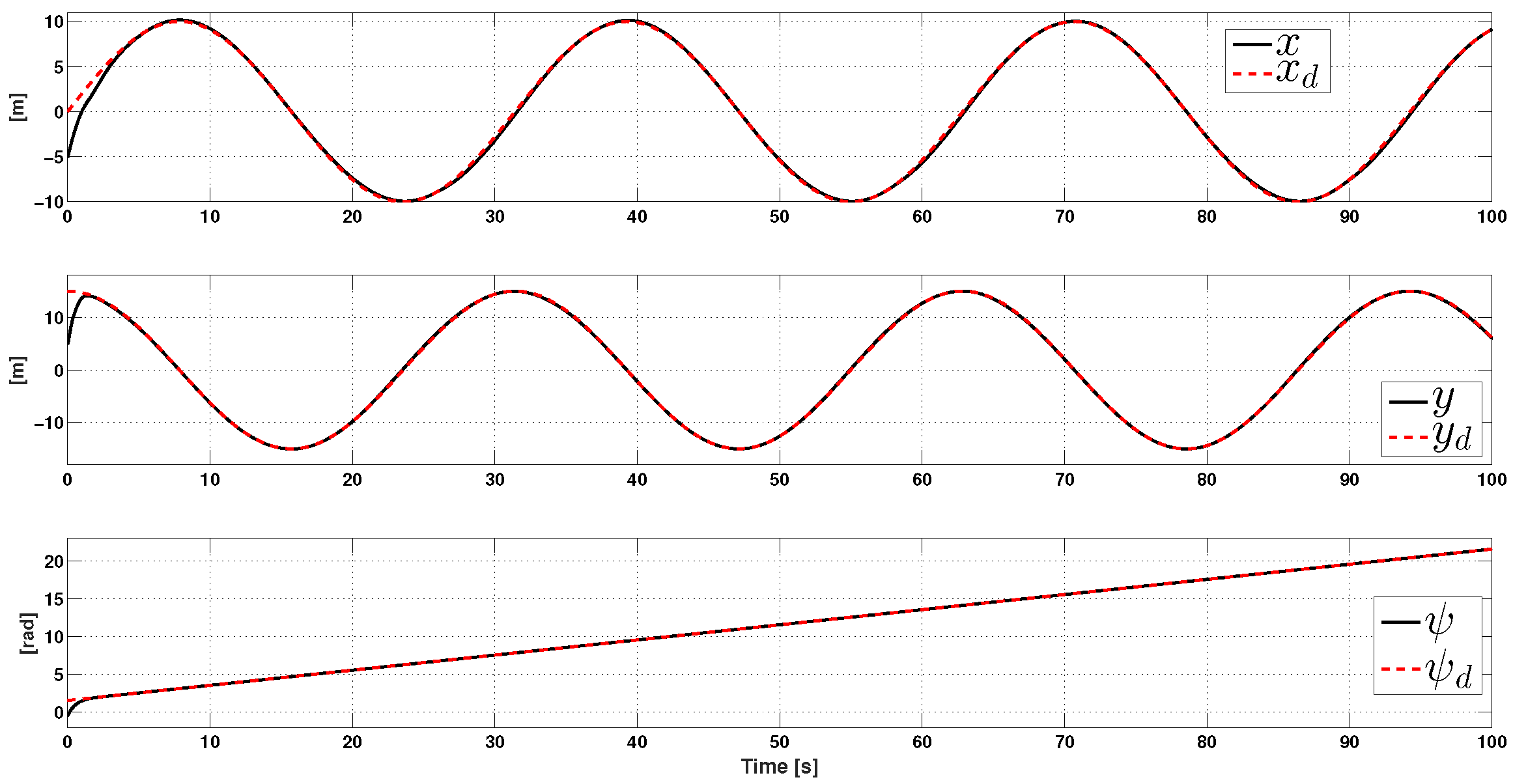
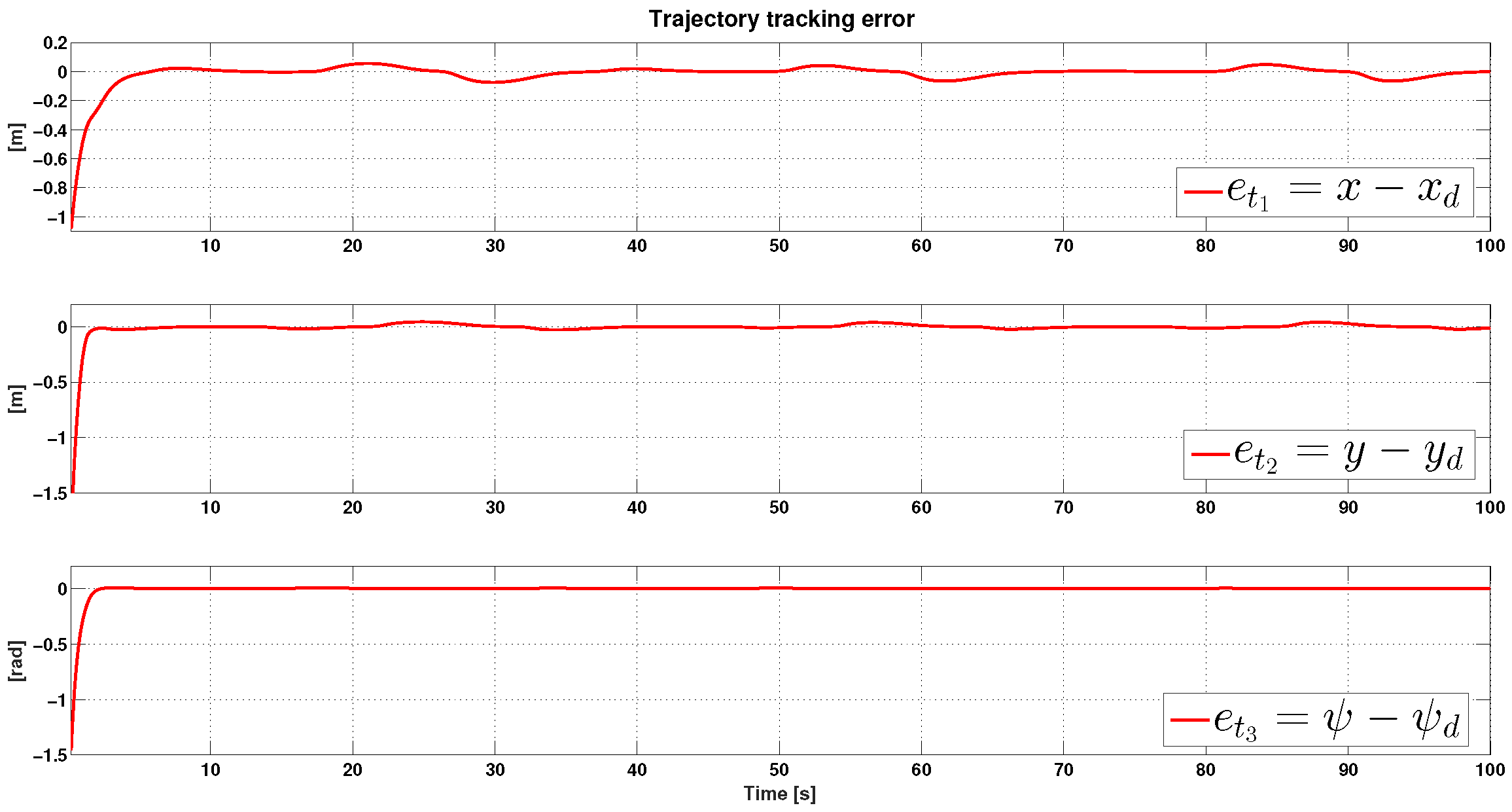
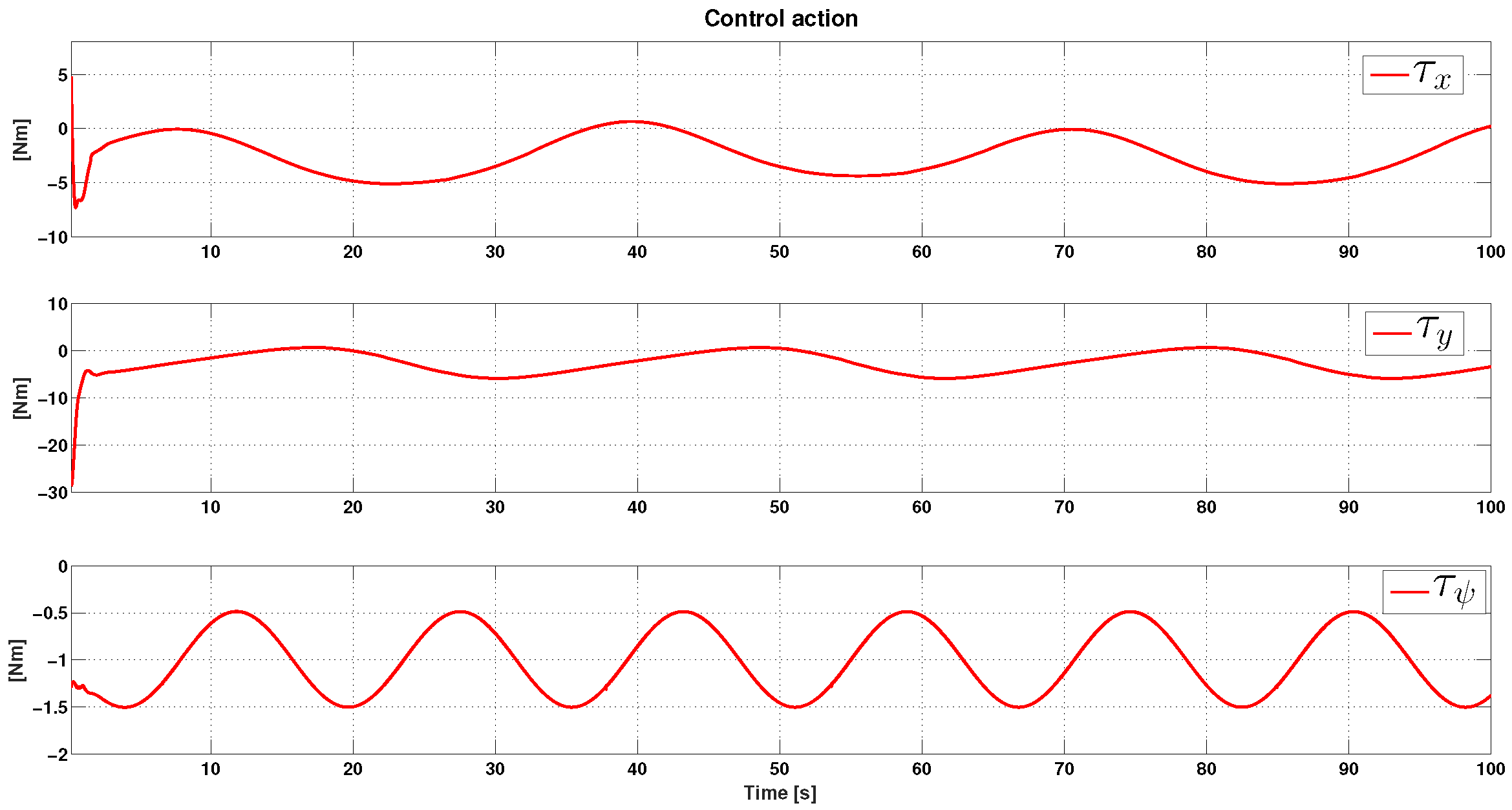
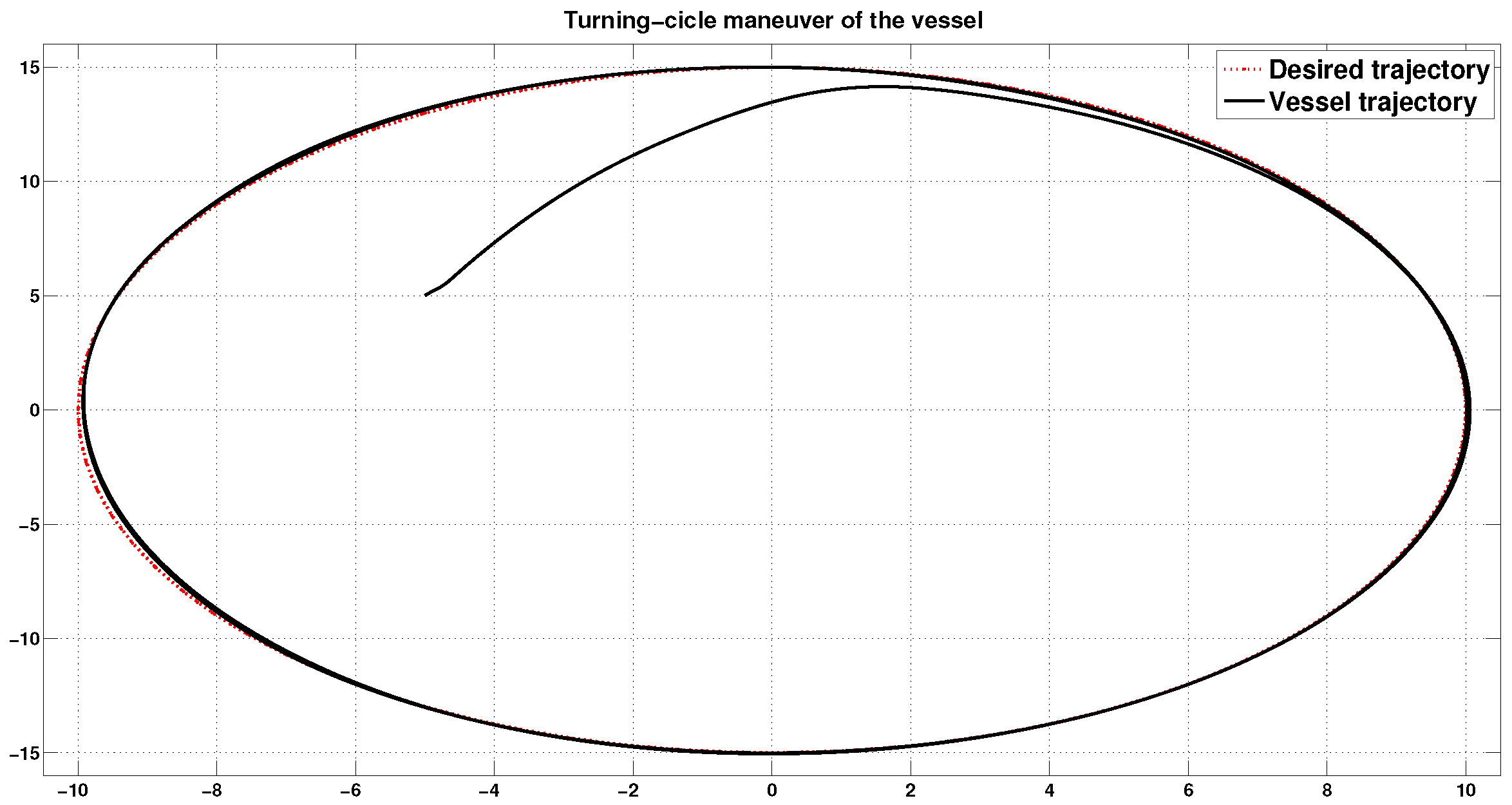
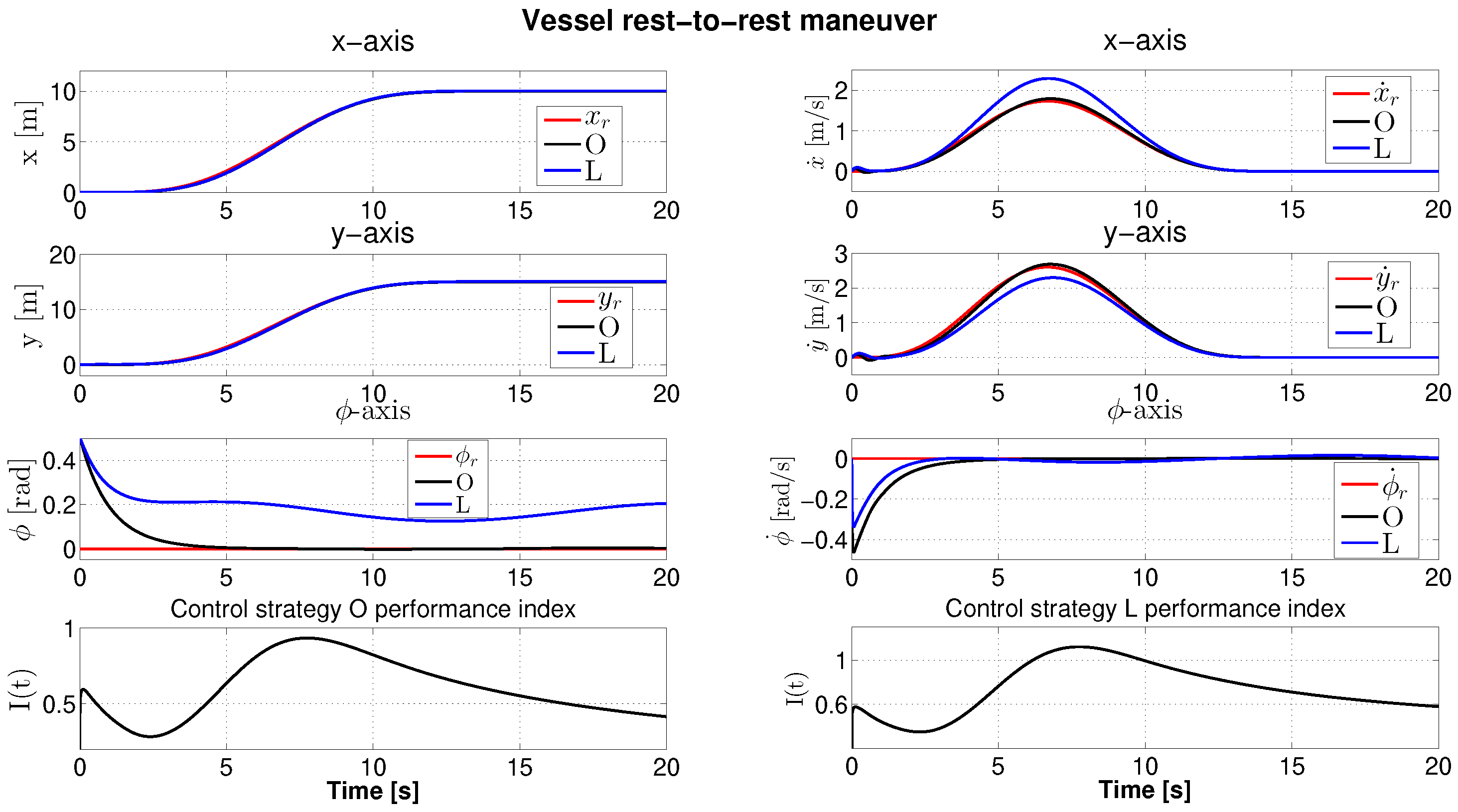
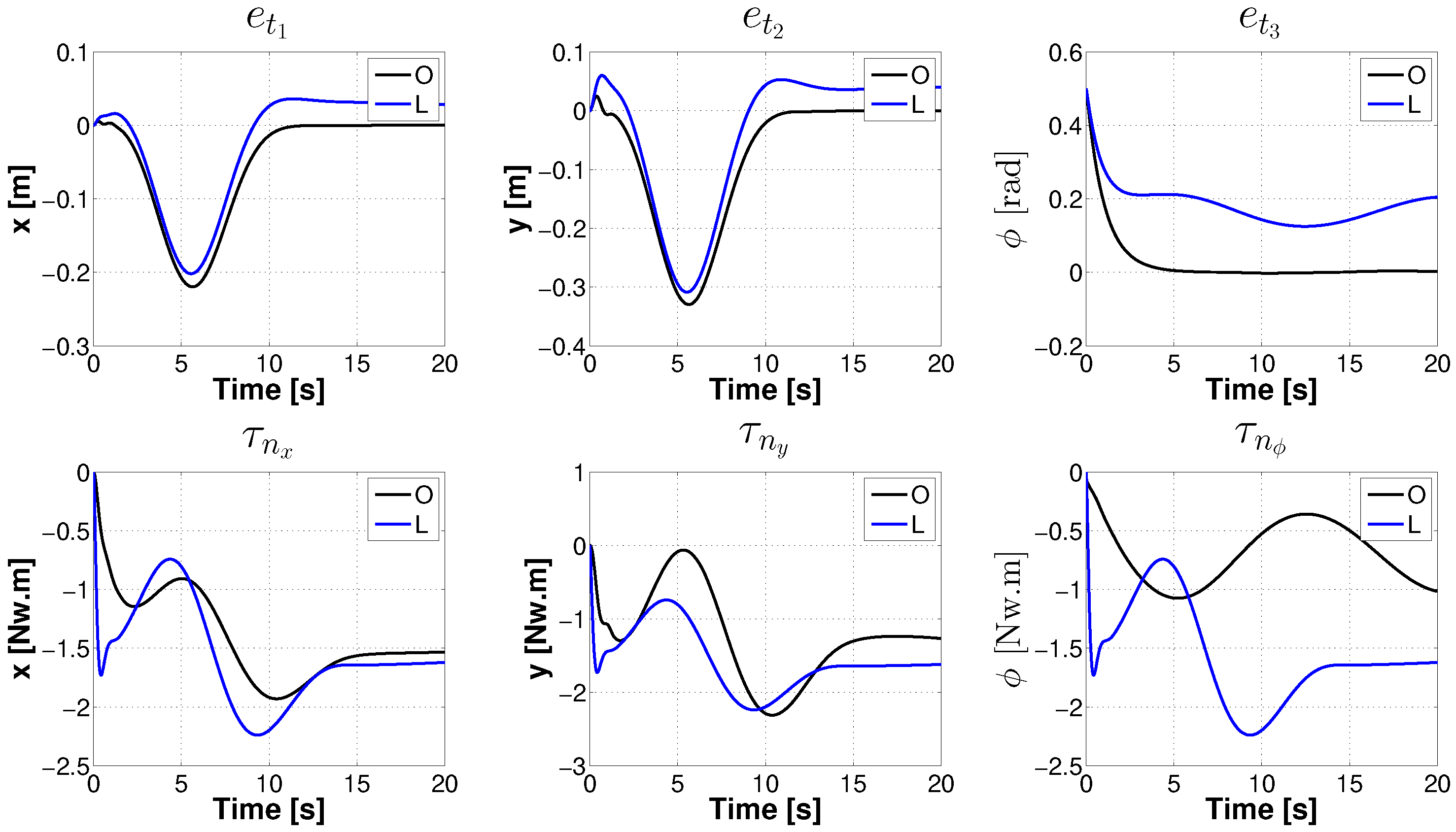
4. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Proof of Inequality (21)
References
- Fossen, T.I. Guidance and Control of Ocean Vehicles. Ph.D. Thesis, University of Trondheim, Trondheim, Norway, 1999. [Google Scholar]
- Yuh, J. Design and control of autonomous underwater robots: A survey. Auton. Robot. 2000, 8, 7–24. [Google Scholar] [CrossRef]
- Morales, R.; Sira-Ramírez, H.; Somolinos, J. Linear active disturbance rejection control of the hovercraft vessel model. Ocean Eng. 2015, 96, 100–108. [Google Scholar] [CrossRef]
- Fantoni, I.; Lozano, R.; Mazenc, F.; Pettersen, K. Stabilization of a nonlinear underactuated hovercraft. In Proceedings of the 38th IEEE Conference on Decision and Control (Cat. No. 99CH36304), Phoenix, AZ, USA, 7–10 December 1999; Volume 3, pp. 2533–2538. [Google Scholar]
- Soro, D.; Lozano, R. Stabilization of an underactuated ship using a linear time-varying control. In Proceedings of the 41st IEEE Conference on Decision and Control, Las Vegas, NV, USA, 10–13 December 2002; Volume 2, pp. 1693–1698. [Google Scholar]
- Sira-Ramírez, H. Dynamic second-order sliding mode control of the hovercraft vessel. IEEE Trans. Control Syst. Technol. 2002, 10, 860–865. [Google Scholar] [CrossRef]
- Loria, A.; Fossen, T.I.; Panteley, E. A separation principle for dynamic positioning of ships: Theoretical and experimental results. IEEE Trans. Control Syst. Technol. 2000, 8, 332–343. [Google Scholar] [CrossRef]
- Fang, Y.; Zergeroglu, E.; De Queiroz, M.; Dawson, D.M. Global output feedback control of dynamically positioned surface vessels: An adaptive control approach. Mechatronics 2004, 14, 341–356. [Google Scholar] [CrossRef]
- Tee, K.P.; Ge, S.S. Control of fully actuated ocean surface vessels using a class of feedforward approximators. IEEE Trans. Control Syst. Technol. 2006, 14, 750–756. [Google Scholar] [CrossRef]
- Skjetne, R.; Fossen, T.I.; Kokotović, P.V. Adaptive maneuvering, with experiments, for a model ship in a marine control laboratory. Automatica 2005, 41, 289–298. [Google Scholar] [CrossRef]
- Chen, M.; Ge, S.S.; How, B.V.E.; Choo, Y.S. Robust adaptive position mooring control for marine vessels. IEEE Trans. Control Syst. Technol. 2012, 21, 395–409. [Google Scholar] [CrossRef]
- Do, K.D. Global robust and adaptive output feedback dynamic positioning of surface ships. J. Mar. Sci. Appl. 2011, 10, 325–332. [Google Scholar] [CrossRef]
- Qin, H.; Li, C.; Sun, Y.; Deng, Z.; Liu, Y. Trajectory tracking control of unmanned surface vessels with input saturation and full-state constraints. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418808113. [Google Scholar] [CrossRef]
- Moreno-Valenzuela, J.; Acho-Zuppa, L. Dynamic positioning control of ships via relay observer design. Asian J. Control 2004, 6, 398–406. [Google Scholar] [CrossRef]
- Qiu, B.; Wang, G.; Fan, Y.; Mu, D.; Sun, X. Robust adaptive trajectory linearization control for tracking control of surface vessels with modeling uncertainties under input saturation. IEEE Access 2018, 7, 5057–5070. [Google Scholar] [CrossRef]
- Qin, H.; Li, C.; Sun, Y.; Wang, N. Adaptive trajectory tracking algorithm of unmanned surface vessel based on anti-windup compensator with full-state constraints. Ocean Eng. 2020, 200, 106906. [Google Scholar] [CrossRef]
- Reyes-Báez, R.; van der Schaft, A.; Jayawardhana, B.; Donaire, A.; Pérez, T. Tracking control of marine craft in the port-Hamiltonian framework: A virtual differential passivity approach. In Proceedings of the 2019 18th European Control Conference (ECC), Naples, Italy, 25–28 June 2019; pp. 1636–1641. [Google Scholar]
- Khaled, N.; Chalhoub, N. A dynamic model and a robust controller for a fully-actuated marine surface vessel. J. Vib. Control 2011, 17, 801–812. [Google Scholar] [CrossRef]
- Yu, X.N.; Hao, L.Y.; Wang, X.L. Fault tolerant control for an unmanned surface vessel based on integral sliding mode state feedback control. Int. J. Control. Autom. Syst. 2022, 20, 2514–2522. [Google Scholar] [CrossRef]
- Yao, Q. Fixed-time trajectory tracking control for unmanned surface vessels in the presence of model uncertainties and external disturbances. Int. J. Control 2022, 95, 1133–1143. [Google Scholar] [CrossRef]
- Wright, R.G. Intelligent autonomous ship navigation using multi-sensor modalities. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2019, 13, 503–510. [Google Scholar] [CrossRef]
- He, S.; Dai, S.L.; Luo, F. Asymptotic trajectory tracking control with guaranteed transient behavior for MSV with uncertain dynamics and external disturbances. IEEE Trans. Ind. Electron. 2018, 66, 3712–3720. [Google Scholar] [CrossRef]
- Shen, Z.; Bi, Y.; Wang, Y.; Guo, C. MLP neural network-based recursive sliding mode dynamic surface control for trajectory tracking of fully actuated surface vessel subject to unknown dynamics and input saturation. Neurocomputing 2020, 377, 103–112. [Google Scholar] [CrossRef]
- From, P.J.; Schjølberg, I.; Gravdahl, J.T.; Pettersen, K.Y.; Fossen, T.I. On the boundedness and skew-symmetric properties of the inertia and coriolis matrices for vehicle-manipulator systems. IFAC Proc. Vol. 2010, 43, 193–198. [Google Scholar] [CrossRef]
- Ortega, R.; Spong, M.W. Adaptive motion control of rigid robots: A tutorial. Automatica 1989, 25, 877–888. [Google Scholar] [CrossRef]
- Kelly, R.; Santibáñez, V.; Loría, A. Control of Robot Manipulators in Joint Space; Springer: Berlin/Heidelberg, Germany, 2005; Volume 693. [Google Scholar]
- Sira-Ramírez, H.; López-Uribe, C.; Velasco-Villa, M. Linear observer-based active disturbance rejection control of the omnidirectional mobile robot. Asian J. Control 2013, 15, 51–63. [Google Scholar] [CrossRef]
- Sira-Ramírez, H.; Luviano-Juárez, A.; Ramírez-Neria, M.; Zurita-Bustamante, E.W. Active Disturbance Rejection Control of Dynamic Systems: A Flatness Based Approach; Butterworth-Heinemann: Oxford, UK, 2018. [Google Scholar]
- Davila, J.; Fridman, L.; Poznyak, A. Observation and identification of mechanical systems via second order sliding modes. In Proceedings of the International Workshop on Variable Structure Systems, 2006. VSS’06, Alghero, Italy, 5–7 June 2006; pp. 232–237. [Google Scholar]
- Ferreira, A.; Bejarano, F.J.; Fridman, L.M. Robust control with exact uncertainties compensation: With or without chattering? IEEE Trans. Control Syst. Technol. 2010, 19, 969–975. [Google Scholar] [CrossRef]
- Ríos, H.; Rosales, A.; Ferreira, A.; Dávilay, A. Robust regulation for a 3-DOF helicopter via sliding-modes control and observation techniques. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 4427–4432. [Google Scholar]
- Küchler, S.; Pregizer, C.; Eberharter, J.K.; Schneider, K.; Sawodny, O. Real-time estimation of a ship’s attitude. In Proceedings of the 2011 American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011; pp. 2411–2416. [Google Scholar]
- Rogne, R.H.; Bryne, T.H.; Fossen, T.I.; Johansen, T.A. MEMS-based inertial navigation on dynamically positioned ships: Dead reckoning. IFAC-PapersOnLine 2016, 49, 139–146. [Google Scholar] [CrossRef]
- Roy, S.; Baldi, S.; Fridman, L.M. On adaptive sliding mode control without a priori bounded uncertainty. Automatica 2020, 111, 108650. [Google Scholar] [CrossRef]
- Parra-Vega, V.; Arimoto, S.; Liu, Y.H.; Hirzinger, G.; Akella, P. Dynamic sliding PID control for tracking of robot manipulators: Theory and experiments. IEEE Trans. Robot. Autom. 2003, 19, 967–976. [Google Scholar] [CrossRef]
- Ye, H.; Gui, W.; Liu, G.P. Stabilization of complex cascade systems using boundedness information in finite time. Int. J. Robust Nonlinear Control. IFAC-Affil. J. 2009, 19, 1150–1167. [Google Scholar] [CrossRef]
- Sira-Ramirez, H.; Agrawal, S.K. Differentially Flat Systems; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aguilar-Ibanez, C.; Suarez-Castanon, M.S.; García-Canseco, E.; Rubio, J.d.J.; Barron-Fernandez, R.; Martinez, J.C. Trajectory Tracking Control of an Autonomous Vessel in the Presence of Unknown Dynamics and Disturbances. Mathematics 2024, 12, 2239. https://doi.org/10.3390/math12142239
Aguilar-Ibanez C, Suarez-Castanon MS, García-Canseco E, Rubio JdJ, Barron-Fernandez R, Martinez JC. Trajectory Tracking Control of an Autonomous Vessel in the Presence of Unknown Dynamics and Disturbances. Mathematics. 2024; 12(14):2239. https://doi.org/10.3390/math12142239
Chicago/Turabian StyleAguilar-Ibanez, Carlos, Miguel S. Suarez-Castanon, Eloísa García-Canseco, Jose de Jesus Rubio, Ricardo Barron-Fernandez, and Juan Carlos Martinez. 2024. "Trajectory Tracking Control of an Autonomous Vessel in the Presence of Unknown Dynamics and Disturbances" Mathematics 12, no. 14: 2239. https://doi.org/10.3390/math12142239





