Stability Analysis, Modulation Instability, and Beta-Time Fractional Exact Soliton Solutions to the Van der Waals Equation
Abstract
:1. Introduction
1.1. -Time Derivative and Its Characteristics
1.2. Characteristics
2. Model Representation and Mathematical Analysis
3. Description of METhF Technique
Application to the METhF Technique
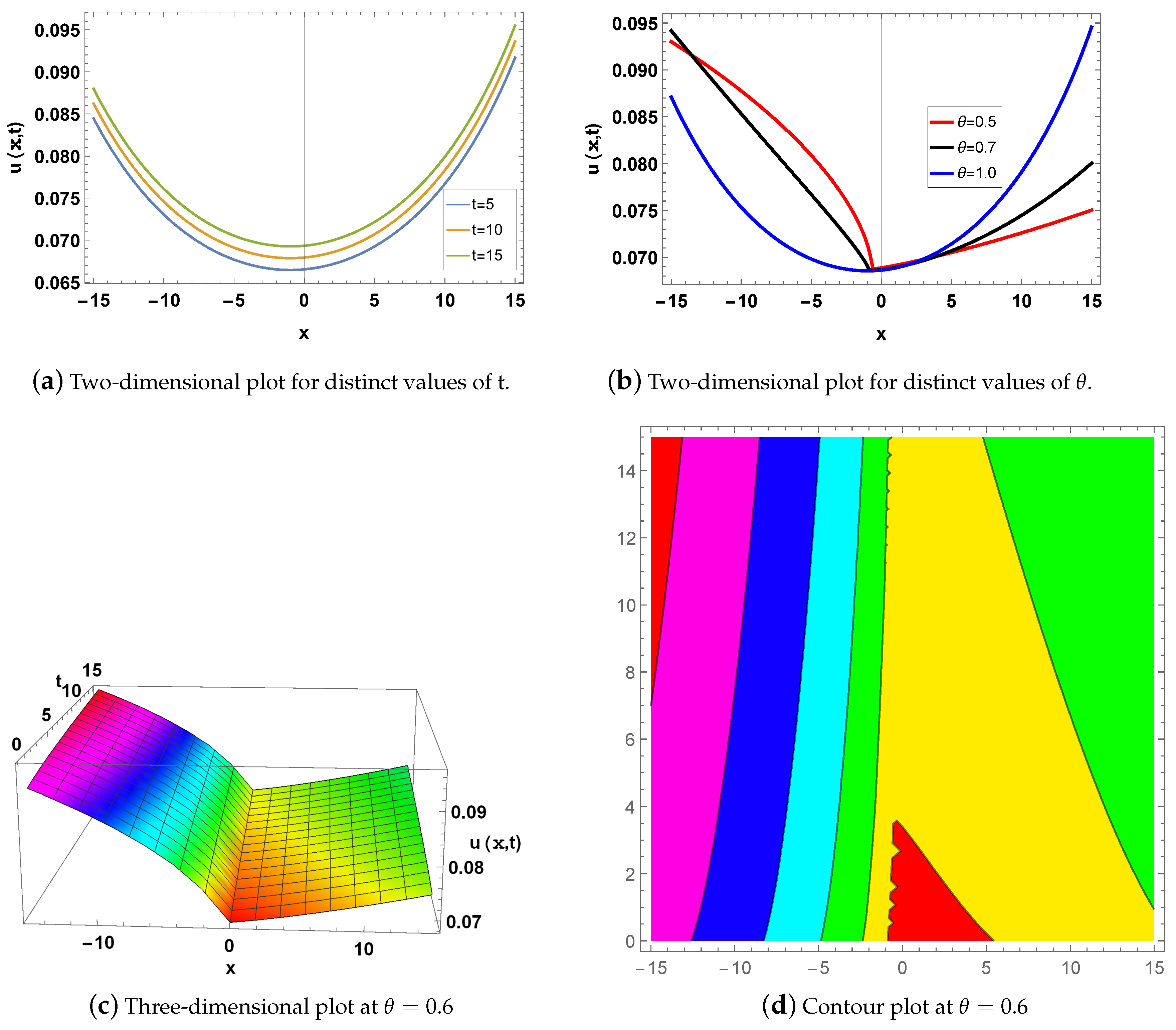
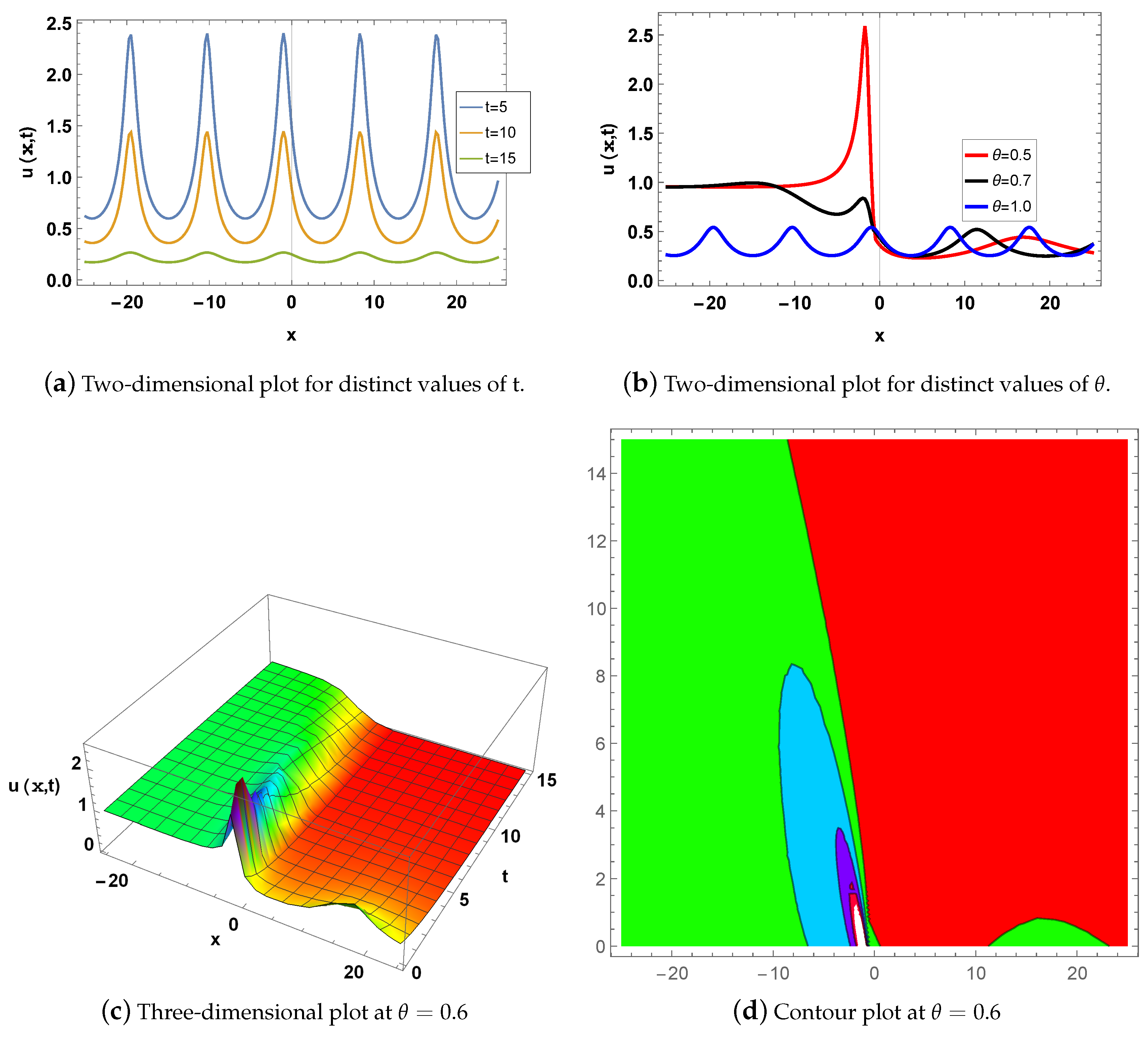
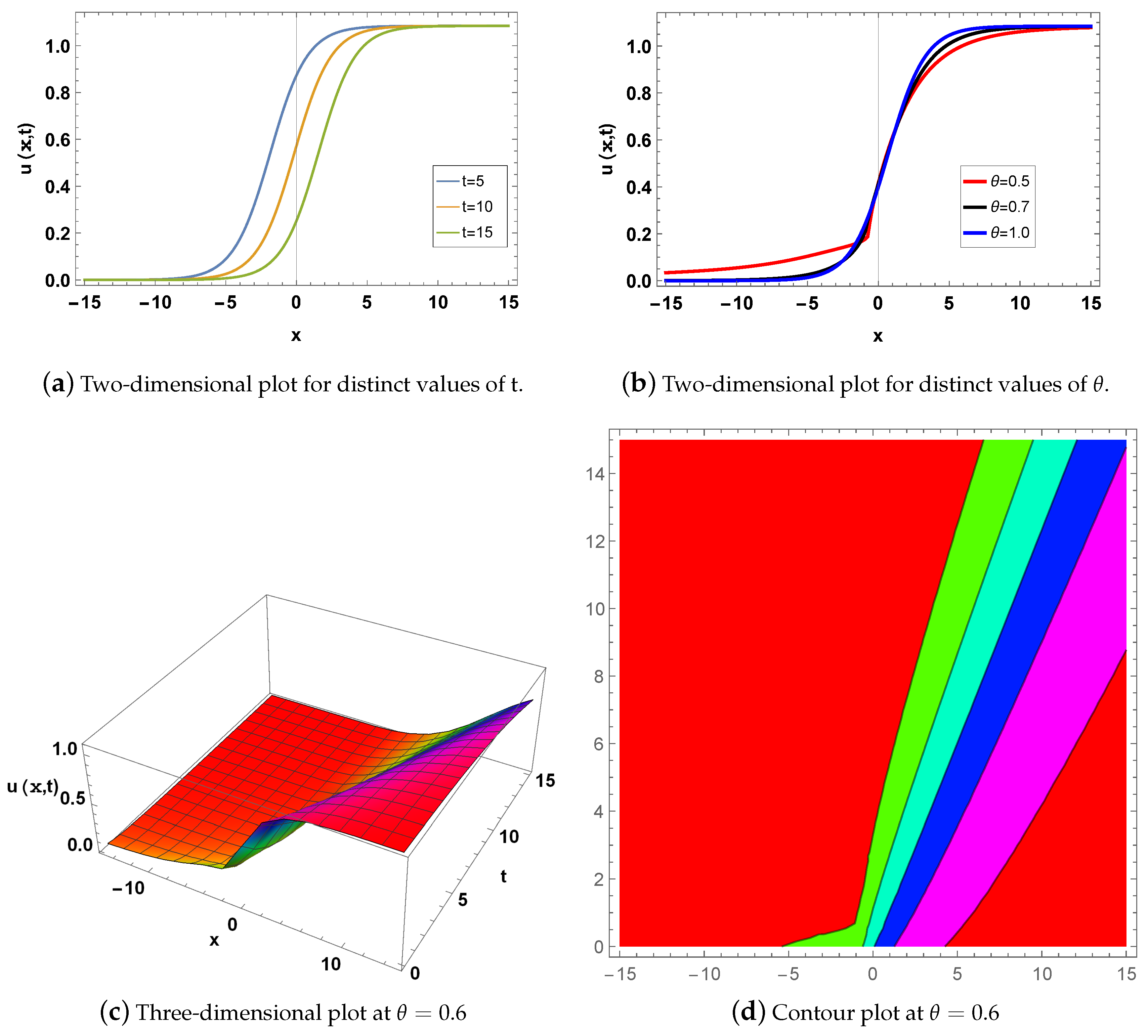
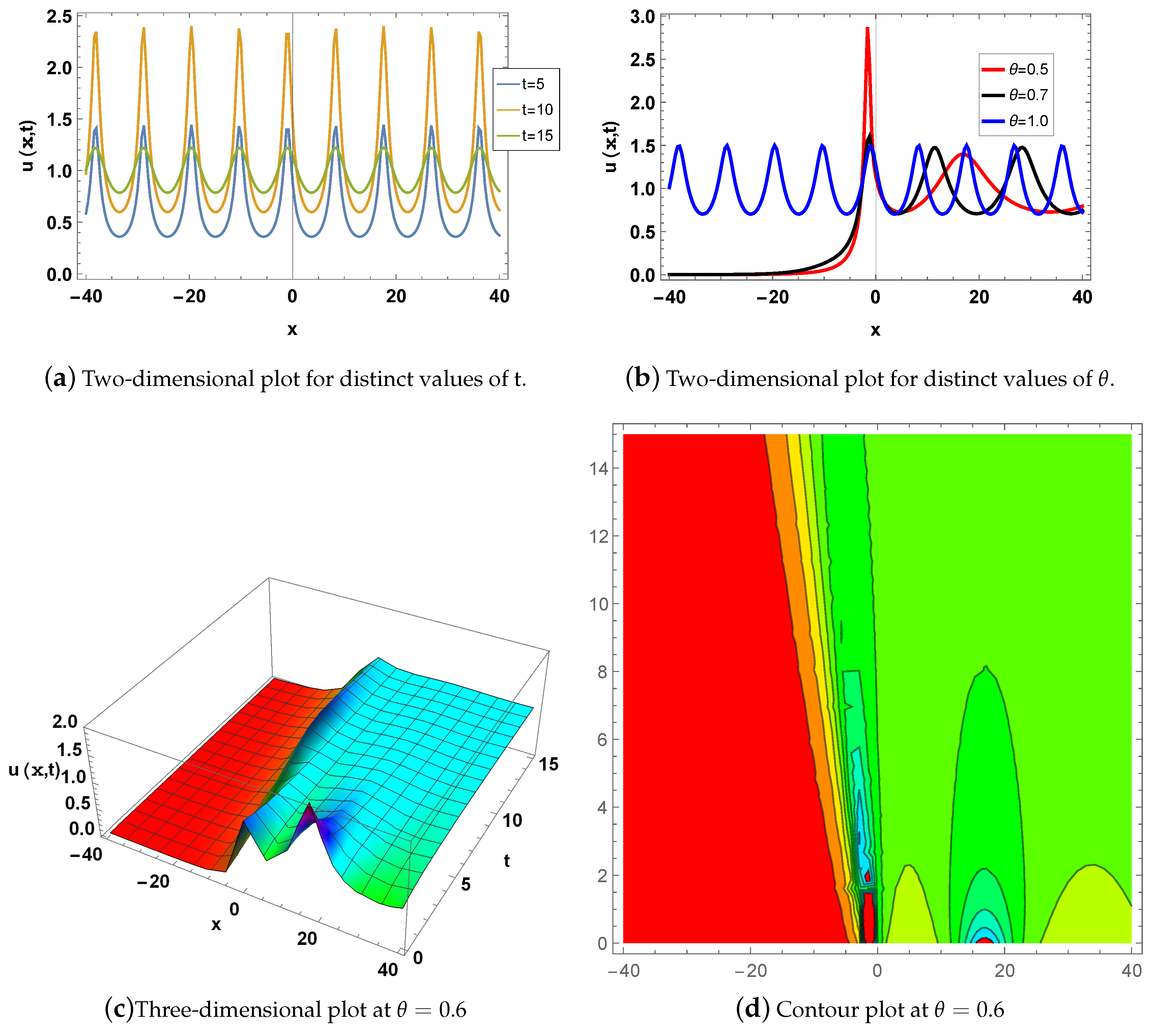
4. Graphical Description
5. Physical Interpretations
6. Stability Analysis
7. Modulation Instability Analysis
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Seadawy, A.R.; Ali, A.; Bekir, A. Exact wave solutions of new generalized Bogoyavlensky–Konopelchenko model in fluid mechanics. Mod. Phys. Lett. B 2024, 38, 2450262. [Google Scholar] [CrossRef]
- Durur, H. Exact Solutions of the Oskolkov Equation in Fluid Dynamics. Afyon Kocatepe Univ. J. Sci. Eng. 2023, 2, 355–361. [Google Scholar] [CrossRef]
- Dehghan, M.; Manafian, J.; Saadatmandi, A. Solving nonlinear fractional partial differential equations using the homotopy analysis method. Numer. Methods Partial. Differ. Equ. J. 2010, 26, 448–479. [Google Scholar] [CrossRef]
- Dehghan, M.; Manafian, J. The solution of the variable coefficients fourth–order parabolic partial differential equations by homotopy perturbation method. Z. Naturforsch. A 2009, 64a, 420–430. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Manafian, J. New soliton solution to the longitudinal wave equation in a magneto-electro-elastic circular rod. Results Phys. 2018, 8, 1158–1167. [Google Scholar] [CrossRef]
- Ullah, M.S.; Abdeljabbar, A.; Roshid, H.-O.; Ali, M.Z. Application of the unified method to solve the Biswas–Arshed model. Results Phys. 2022, 42, 105946. [Google Scholar] [CrossRef]
- Aydemir, T. Application of the generalized unified method to solve (2 + 1)-dimensional Kundu–Mukherjee–Naskar equation. Opt. Quantum Electron. 2023, 55, 534. [Google Scholar] [CrossRef]
- Batiha, I.M.; Njadat, S.A.; Batyha, R.M.; Zraiqat, A.; Dababneh, A.; Momani, S. Design Fractional-order PID Controllers for Single-Joint Robot Arm Model. Int. J. Adv. Soft Comput. Its Appl. 2022, 14, 96–114. [Google Scholar] [CrossRef]
- Ahmad, S.; Mahmoud, E.E.; Saifullah, S.; Ullah, A.; Ahmad, S.; Akgül, A.; El Din, S.M. New waves solutions of a nonlinear Landau–Ginzburg–Higgs equation: The Sardar-subequation and energy balance approaches. Results Phys. 2023, 51, 106736. [Google Scholar] [CrossRef]
- Jiang, H.; Li, S.M.; Wang, W.G. Moderate deviations for parameter estimation in the fractional ornstein-uhlenbeck processes with periodic mean. Acta Math. Sin. Engl. Ser. 2024, 40, 1308–1324. [Google Scholar] [CrossRef]
- Chen, D.; Zhao, T.; Han, L.; Feng, Z. Single-stage multi-input buck type high-frequency link’s inverters with series and simultaneous power supply. IEEE Trans. Power Electron. 2022, 37, 7411–7421. [Google Scholar] [CrossRef]
- Xie, G.; Fu, B.; Li, H.; Du, W.; Zhong, Y.; Wang, L.; Geng, H.; Zhang, J.; Si, L. A gradient-enhanced physics-informed neural networks method for the wave equation. Eng. Anal. Boundary Elements 2024, 166, 105802. [Google Scholar] [CrossRef]
- Li, X.; Hu, S.; He, J.; Li, D.; Xi, Y.; Lan, H.L.; Xu, L.; Mingliang Tan, M.; Xiao, M. Electric-feld-driven printed 3D highly ordered microstructure with cell feature size promotes the maturation of engineered cardiac tissues. Adv. Sci. 2023, 10, 2206264. [Google Scholar]
- Zhang, K.; Liu, Q.; Qian, H.; Xiang, B.; Cui, Q.; Zhou, J.; Chen, E. Eatn: An efficient adaptive transfer network for aspect-level sentiment analysis. IEEE Trans. Knowl. Data Eng. 2021, 35, 377–389. [Google Scholar] [CrossRef]
- Chen, D.; Zhao, T.; Xu, S. Single-stage multi-input buck type high-frequency link’s inverters with multiwinding and time-sharing power supply. IEEE Trans. Power Elec. 2022, 37, 12763–12773. [Google Scholar] [CrossRef]
- Chen, C.; Han, D.; Chang, C.C. MPCCT: Multimodal vision-language learning paradigm with context-based compact transformer. Pattern Recogn. 2024, 147, 110084. [Google Scholar] [CrossRef]
- Shi, S.; Han, D.; Cui, M. A multimodal hybrid parallel network intrusion detection model. Connect. Sci. 2023, 35, 2227780. [Google Scholar] [CrossRef]
- Wanh, H.; Han, D.; Cui, M.; Chen, C. NAS-YOLOX: A SAR ship detection using neural architecture search and multi-scale attention. Connect. Sci. 2023, 35, 1–32. [Google Scholar]
- Zhou, C.; Wang, C.; Zhang, B.; Li, B. Deep Learning-Based Coseismic Deformation Estimation From InSAR Interferograms. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5203610. [Google Scholar] [CrossRef]
- Fei, R.; Guo, Y.; Li, J.; Hu, B.; Yang, L. An improved BPNN method based on probability density for indoor location. IEICE Trans. Inf. Syst. 2023, 106, 773–785. [Google Scholar] [CrossRef]
- Mohammed, P.O.; Agarwal, R.P.; Brevik, I.; Abdelwahed, M.; Kashuri, A.; Yousif, M.A. On Multiple-Type Wave Solutions for the Nonlinear Coupled Time-Fractional Schrödinger Model. Symmetry 2024, 16, 553. [Google Scholar] [CrossRef]
- Ozkan, E.M. New exact solutions of some important nonlinear fractional partial differential Equations with beta derivative. Fractal Fract. 2022, 6, 173. [Google Scholar] [CrossRef]
- Qawaqneh, H.; Zafar, A.; Raheel, M.; Zaagan, A.A.; Zahran, E.H.M.; Cevikel, A.; Bekir, A. New soliton solutions of M-fractional Westervelt model in ultrasound imaging via two analytical techniques. Opt. Quantum Electron. 2024, 56, 737. [Google Scholar] [CrossRef]
- Gasmi, B.; Moussa, A.; Mati, Y.; Alhakim, L.; Baskonus, H.M. Bifurcation and exact traveling wave solutions to a conformable nonlinear Schrödinger equation using a generalized double auxiliary equation method. Opt. Quantum Electron. 2024, 56, 18. [Google Scholar] [CrossRef]
- Faridi, W.A.; Myrzakulova, Z.; Myrzakulov, R.; Akgül, A.; Osman, M.S. The construction of exact solution and explicit propagating optical soliton waves of Kuralay equation by the new extended direct algebraic and Nucci’s reduction techniques. Int. J. Modell. Simul. 2024, 1–20. [Google Scholar] [CrossRef]
- Nasreen, N.; Rafiq, M.N.; Younas, U.; Arshad, M.; Abbas, M.; Ali, M.R. Stability analysis and dynamics of solitary wave solutions of the (3+ 1)-dimensional generalized shallow water wave equation using the Ricatti equation mapping method. Results Phys. 2024, 56, 107226. [Google Scholar] [CrossRef]
- Faridi, W.A.; Wazwaz, A.-M.; Mostafa, A.M.; Myrzakulov, R.; Umurzakhova, Z. The Lie point symmetry criteria and formation of exact analytical solutions for Kairat-II equation: Paul-Painlevé approach, Chaos. Solitons Fractals 2024, 182, 114745. [Google Scholar] [CrossRef]
- Wang, H. Exact traveling wave solutions of the generalized fifth-order dispersive equation by the improved Fan subequation method. Math. Methods Appl. Sci. 2024, 47, 1701–1710. [Google Scholar] [CrossRef]
- Arnous, A.H.; Hashemi, M.S.; Nisar, K.S.; Shakeel, M.; Ahmad, J.; Ahmad, I.; Jan, R.; Ali, A.; Kapoor, M.; Shah, N.A. Investigating solitary wave solutions with enhanced algebraic method for new extended Sakovich equations in fluid dynamics. Results Phys. 2024, 57, 107369. [Google Scholar] [CrossRef]
- Ramya, S.; Krishnakumar, K.; Ilangovane, R. Exact solutions of time fractional generalized burgers–Fisher equation using exp and exponential rational function methods. Int. J. Dyn. Control 2024, 12, 292–302. [Google Scholar] [CrossRef]
- Eidinejad, Z.; Saadati, R.; Li, C.; Inc, M.; Vahidi, J. The multiple exp-function method to obtain soliton solutions of the conformable Date–Jimbo–Kashiwara–Miwa equations. Int. J. Mod. Phys. B 2024, 38, 2450043. [Google Scholar] [CrossRef]
- Feng, Y.; Bilige, S. Multiple rogue wave solutions of (2 + 1)-dimensional YTSF equation via Hirota bilinear method. Waves Random Complex Medium 2024, 34, 94–110. [Google Scholar] [CrossRef]
- Elsadany, A.A.; Elboree, M.K. Construction of shock, periodic and solitary wave solutions for fractional-time Gardner equation by Jacobi elliptic function method. Opt. Quantum Electron. 2024, 56, 481. [Google Scholar] [CrossRef]
- Eslami, M.; Heidari, S.; Abduridha, S.A.J.; Asghari, Y. Dynamic simulation of traveling wave solutions for the differential-difference Burgers’ equation utilizing a generalized exponential rational function approach. Opt. Quantum Electron. 2024, 56, 504. [Google Scholar] [CrossRef]
- Khan, M.I.; Farooq, A.; Nisar, K.S.; Shah, N.A. Unveiling new exact solutions of the unstable nonlinear Schrödinger equation using the improved modified Sardar sub-equation method. Results Phys. 2024, 59, 107593. [Google Scholar] [CrossRef]
- Samir, I.; Ahmed, H.M.; Darwish, A.; Hussein, H.H. Dynamical behaviors of solitons for NLSE with Kudryashov’s sextic power-law of nonlinear refractive index using improved modified extended tanh-function method. Ain Shams Eng. J. 2024, 15, 102267. [Google Scholar] [CrossRef]
- Ullah, N.; Asjad, M.I.; Awrejcewicz, J.; Muhammad, T.; Baleanu, D. On soliton solutions of fractional-order nonlinear model appears in physical sciences. AIMS Math. 2022, 7, 7421–7440. [Google Scholar] [CrossRef]
- Luo, N.; Peng, Z.; Hu, J.; Ghosh, B.K. Adaptive optimal control of affine nonlinear systems via identifier-critic neural network approximation with relaxed PE conditions. Neural Netw. 2023, 167, 588–600. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.; Al-Dossari, M.; Rezapour, S.; Alsallami, S.A.M.; Gunay, B. Bifurcations, chaotic behavior, and optical solutions for the complex Ginzburg-Landau equation. Results Phys. 2024, 59, 107601. [Google Scholar] [CrossRef]
- Zhu, C.; Al-Dossari, M.; Rezapour, S.; Gunay, B. On the exact soliton solutions and different wave structures to the (2+1) dimensional Chaffee-Infante equation. Results Phys. 2024, 57, 107431. [Google Scholar] [CrossRef]
- Zhu, C.; Al-Dossari, M.; Rezapour, S.; Shateyi, S.; Gunay, B. Analytical optical solutions to the nonlinear Zakharov system via logarithmic transformation. Results Phys. 2024, 56, 107298. [Google Scholar] [CrossRef]
- Kai, Y.; Ji, J.; Yin, Z. Study of the generalization of regularized long-wave equation. Nonlinear Dyn. 2022, 107, 2745–2752. [Google Scholar] [CrossRef]
- Kai, Y.; Yin, Z. Linear structure and soliton molecules of Sharma-Tasso-Olver-Burgers equation. Phys. Let. A 2022, 452, 128430. [Google Scholar] [CrossRef]
- Ali, T.A.A.; Xiao, Z.; Jiang, H.; Li, B. A Class of Digital Integrators Based on Trigonometric Quadrature Rules. IEEE Trans. Indus. Elec. 2024, 71, 6128–6138. [Google Scholar] [CrossRef]
- Mohammadzadeh, A.; Taghavifar, H.; Zhang, Y.; Zhang, W. A Fast Nonsingleton Type-3 Fuzzy Predictive Controller for Nonholonomic Robots Under Sensor and Actuator Faults and Measurement Errors. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 4175–4187. [Google Scholar] [CrossRef]
- Mohammadzadeh, A.; Zhang, C.; Alattas, K.A.; El-Sousy, F.F.; Vu, M.T. Fourier-based type-2 fuzzy neural network: Simple and effective for high dimensional problems. Neurocomput. 2023, 547, 126316. [Google Scholar] [CrossRef]
- Mohammadzadeh, A.; Taghavifar, H.; Zhang, C.; Alattas, K.A.; Liu, J.; Vu, M.T. A non-linear fractional-order type-3 fuzzy control for enhanced path-tracking performance of autonomous cars. IET Control Theo. Appl. 2024, 18, 40–54. [Google Scholar] [CrossRef]
- Yan, S.R.; Guo, W.; Mohammadzadeh, A.; Rathinasamy, S. Optimal deep learning control for modernized microgrids. Appl. Intelligence 2023, 53, 15638–15655. [Google Scholar] [CrossRef]
- Hui, Z.; Wu, A.; Han, D.; Li, T.; Li, L.; Gong, J.; Li, X. Switchable Single- to Multiwavelength Conventional Soliton and Bound-State Soliton Generated from a NbTe2 Saturable Absorber-Based Passive Mode-Locked Erbium-Doped Fiber Laser. ACS Appl. Mater. Interfaces 2024, 16, 22344–22360. [Google Scholar] [CrossRef]
- Gong, S.P.; Khishe, M.; Mohammadi, M. Niching chimp optimization for constraint multimodal engineering optimization problems. Expert Sys. Appl. 2022, 198, 116887. [Google Scholar] [CrossRef]
- Chen, F.; Yang, C.; Khishe, M. Diagnose parkinson’s disease and cleft lip and palate using deep convolutional neural networks evolved by ip-based chimp optimization algorithm. Biomed. Signal Proc. Cont. 2022, 77, 103688. [Google Scholar] [CrossRef]
- Shi, W.; Zhou, C.; Zhang, Y.; Li, K.; Ren, X.; Liu, H.; Ye, X. Hybrid modeling on reconstitution of continuous arterial blood pressure using finger photoplethysmography Biomed. Signal Proc. Cont. 2023, 85, 2023. [Google Scholar]
- Alazeb, A.; Chughtai, B.R.; Al Mudawi, N.; AlQahtani, Y.; Alonazi, M.; Aljuaid, H.; Jalal, A.; Liu, H. Remote intelligent perception system for multi-object detection Front. Neurorobotics 2024, 18, 1398703. [Google Scholar] [CrossRef] [PubMed]
- Bo, Q.; Cheng, W.; Khishe, M.; Mohammadi, M.; Mohammed, A.H. Solar photovoltaic model parameter identification using robust niching chimp optimization. Solar Energy 2022, 239, 179–197. [Google Scholar] [CrossRef]
- Khishe, M. Greedy opposition-based learning for chimp optimization algorithm. Artif. Intell. Rev. 2023, 56, 7633–7663. [Google Scholar] [CrossRef]
- Cai, C.F.; Gou, B.; Khishe, M.; Mohammadi, M.; Rashidi, S.; Moradpour, R.; Mirjalili, S. Improved deep convolutional neural networks using chimp optimization algorithm for covid19 diagnosis from the x-ray images. Expert Syst. Appl. 2023, 213, 119206. [Google Scholar] [CrossRef]
- Khishe, M.; Orouji, N.; Mosavi, M.R. Multi-objective chimp optimizer: An innovative algorithm for multi-objective problems. Expert Syst. Appl. 2023, 211, 118734. [Google Scholar] [CrossRef]
- Chen, C.; Han, D.; Shen, X. CLVIN: Complete language-vision interaction network for visual question answering. Knowl. Based Syst. 2023, 275, 110706. [Google Scholar] [CrossRef]
- Chen, X.; Yang, P.; Wang, M.; Hu, F.; Xu, J. Output voltage drop and input current ripple suppression for the pulse load power supply using virtual multiple quasi-notch-flters impedance. IEEE Trans. Power Electron. 2023, 38, 9552–9565. [Google Scholar] [CrossRef]
- Han, D.; Zhou, H.X.; Weng, T.H.; Wu, Z.; Han, B.; Li, K.C.; Pathan, A.S.K. LMCA: A lightweight anomaly network traffic detection model integrating adjusted mobilenet and coordinate attention mechanism for IoT. Telecommun. Syst. 2023, 84, 549–564. [Google Scholar] [CrossRef]
- Liao, L.; Guo, Z.; Gao, Q.; Wang, Y.; Yu, F.; Zhao, Q.; Maybank, S.J.; Liu, Z.; Li, C.; Li, L. Color image recovery using generalized matrix completion over higher-order finite dimensional algebra. Axioms 2023, 12, 954. [Google Scholar] [CrossRef]
- Meng, S.; Meng, F.; Chi, H.; Chen, H.; Pang, A. A robust observer based on the nonlinear descriptor systems application to estimate the state of charge of lithium-ion batteries. J. Frankl. Inst. 2023, 360, 11397–11413. [Google Scholar] [CrossRef]
- Chen, D.L.; Zhao, J.W.; Qin, S.R. SVM strategy and analysis of a three-phase quasi-Z-source inverter with high voltage transmission ratio. Sci. China Technol. Sci. 2023, 66, 29963010. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, Z.; Zheng, X.; Zhao, Y.; Wang, J. 3D path planning in threat environment based on fuzzy logic. J. Intell. Fuzzy Sys. 2024, 46, 7021–7034. [Google Scholar] [CrossRef]
- Hussein, H.H.; Ahmed, H.M.; Alexan, W. Analytical soliton solutions for cubic-quartic perturbations of the Lakshmanan-Porsezian-Daniel equation using the modified extended tanh function method. Ain Shams Eng. J. 2024, 15, 102513. [Google Scholar] [CrossRef]
- Akbulut, A.; Taşcan, F. Application of conservation theorem and modified extended tanh-function method to (1+ 1)-dimensional nonlinear coupled Klein–Gordon–Zakharov equation, Chaos. Solitons Fractals 2017, 104, 33–40. [Google Scholar] [CrossRef]
- Zahran, E.H.M.; Khater, M.M.A. Modified extended tanh-function method and its applications to the Bogoyavlenskii equation. Appl. Math. Modell. 2016, 40, 1769–1775. [Google Scholar] [CrossRef]
- El-Wakil, S.A.; Abdou, M.A. Modified extended tanh-function method for solving nonlinear partial differential equations, Chaos. Solitons Fractals 2007, 31, 1256–1264. [Google Scholar] [CrossRef]
- Zaman, U.H.M.; Arefin, M.A.; Akbar, M.A.; Uddin, M.H. Utilizing the extended tanh-function technique to scrutinize fractional order nonlinear partial differential equations. Partial Differ. Equ. Appl. Math. 2023, 8, 100563. [Google Scholar] [CrossRef]
- Chu, Y.; Shallal, M.A.; Mirhosseini-Alizamini, S.M.; Rezazadeh, H.; Javeed, S.; Baleanu, D. Application of modified extended Tanh technique for solving complex Ginzburg-Landau equation considering Kerr law nonlinearity. Comput. Mater. Contin. 2021, 66, 1369–1378. [Google Scholar] [CrossRef]
- Alam, L.M.B.; Jiang, X.; Al-Mamun, A. Exact and explicit traveling wave solution to the time-fractional phi-four and (2 + 1) dimensional CBS equations using the modified extended tanh-function method in mathematical physics. Partial Differ. Equ. Appl. Math. 2021, 4, 100039. [Google Scholar] [CrossRef]
- Rabie, W.B.; Ahmed, H.M.; Darwish, A.; Hussein, H.H. Construction of new solitons and other wave solutions for a concatenation model using modified extended tanh-function method. Alex. Eng. J. 2023, 74, 445–451. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D.; Alsaedi, A. Analysis of time-fractional Hunter–Saxton equation: A model of neumatic liquid crystal. Open Phys. 2016, 14, 145–149. [Google Scholar] [CrossRef]
- Uddin, M.F.; Hafez, M.G.; Hammouch, Z.; Baleanu, D. Periodic and rogue waves for Heisenberg models of ferromagnetic spin chains with fractional beta derivative evolution and obliqueness. Waves Random Complex Media 2021, 31, 2135–2149. [Google Scholar] [CrossRef]
- Ghanbari, B.; Gómez-Aguilar, J.F. The generalized exponential rational function method for Radhakrishnan–Kundu–Lakshmanan equation with Beta time derivative. Rev. Mex. Fís. 2019, 65, 503–518. [Google Scholar] [CrossRef]
- Altalbe, A.; Zaagan, A.A.; Bekir, A.; Cevikel, A. The nonlinear wave dynamics of the space-time fractional van der Waals equation via three analytical methods. Phys. Fluids 2024, 36, 2. [Google Scholar] [CrossRef]
- Bibi, S.; Ahmed, N.; Khan, U.; Mohyud-Din, S.T. Some new exact solitary wave solutions of the van der Waals model arising in nature. Results Phys. 2018, 9, 648–655. [Google Scholar] [CrossRef]
- Zafar, A.; Mushtaq, T.; Malik, A.; Bekir, A. New solitary wave and other exact solutions of the van der Waals normal form for granular materials. J. Ocean Eng. Sci. 2022, 7, 170–177. [Google Scholar] [CrossRef]
- Ali, N.H.; Mohammed, S.A.; Manafian, J. New explicit soliton and other solutions of the Van der Waals model through the EShGEEM and the IEEM. J. Modern Tech. Eng. 2023, 8, 5–18. [Google Scholar]
- Raslan, K.R.; Khalid, K.A.; Shallal, M.A. The modified extended tanh method with the Riccati equation for solving the space-time fractional EW and MEW equations, Chaos. Solitons Fractals 2017, 103, 404–409. [Google Scholar] [CrossRef]
- Tariq, K.U.; Wazwaz, A.M.; Javed, R. Construction of different wave structures, stability analysis and modulation instability of the coupled nonlinear Drinfel–Sokolov–Wilson model, Chaos. Solitons Fractals 2023, 166, 112903. [Google Scholar] [CrossRef]
- Zulfiqar, H.; Aashiq, A.; Tariq, K.U.; Ahmad, H.; Almohsen, B.; Aslam, M.; Rehman, H.U. On the solitonic wave structures and stability analysis of the stochastic nonlinear Schrödinger equation with the impact of multiplicative noise. Optik 2023, 289, 171250. [Google Scholar] [CrossRef]
- Ur Rehman, S.; Ahmad, J. Modulation instability analysis and optical solitons in birefringent fibers to RKL equation without four wave mixing. Alex. Eng. J. 2021, 60, 1339–1354. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qawaqneh, H.; Manafian, J.; Alharthi, M.; Alrashedi, Y. Stability Analysis, Modulation Instability, and Beta-Time Fractional Exact Soliton Solutions to the Van der Waals Equation. Mathematics 2024, 12, 2257. https://doi.org/10.3390/math12142257
Qawaqneh H, Manafian J, Alharthi M, Alrashedi Y. Stability Analysis, Modulation Instability, and Beta-Time Fractional Exact Soliton Solutions to the Van der Waals Equation. Mathematics. 2024; 12(14):2257. https://doi.org/10.3390/math12142257
Chicago/Turabian StyleQawaqneh, Haitham, Jalil Manafian, Mohammed Alharthi, and Yasser Alrashedi. 2024. "Stability Analysis, Modulation Instability, and Beta-Time Fractional Exact Soliton Solutions to the Van der Waals Equation" Mathematics 12, no. 14: 2257. https://doi.org/10.3390/math12142257




