Unveiling Malicious Network Flows Using Benford’s Law

Abstract

The increasing proliferation of cyber-attacks threatening the security of computer networks has driven the development of more effective methods for identifying malicious network flows. The inclusion of statistical laws, such as Benford’s Law, and distance functions, applied to the first digits of network flow metadata, such as IP addresses or packet sizes, facilitates the detection of abnormal patterns in the digits. These techniques also allow for quantifying discrepancies between expected and suspicious flows, significantly enhancing the accuracy and speed of threat detection. This paper introduces a novel method for identifying and analyzing anomalies within computer networks. It integrates Benford’s Law into the analysis process and incorporates a range of distance functions, namely the Mean Absolute Deviation (MAD), the Kolmogorov–Smirnov test (KS), and the Kullback–Leibler divergence (KL), which serve as dispersion measures for quantifying the extent of anomalies detected in network flows. Benford’s Law is recognized for its effectiveness in identifying anomalous patterns, especially in detecting irregularities in the first digit of the data. In addition, Bayes’ Theorem was implemented in conjunction with the distance functions to enhance the detection of malicious traffic flows. Bayes’ Theorem provides a probabilistic perspective on whether a traffic flow is malicious or benign. This approach is characterized by its flexibility in incorporating new evidence, allowing the model to adapt to emerging malicious behavior patterns as they arise. Meanwhile, the distance functions offer a quantitative assessment, measuring specific differences between traffic flows, such as frequency, packet size, time between packets, and other relevant metadata. Integrating these techniques has increased the model’s sensitivity in detecting malicious flows, reducing the number of false positives and negatives, and enhancing the resolution and effectiveness of traffic analysis. Furthermore, these techniques expedite decisions regarding the nature of traffic flows based on a solid statistical foundation and provide a better understanding of the characteristics that define these flows, contributing to the comprehension of attack vectors and aiding in preventing future intrusions. The effectiveness and applicability of this joint method have been demonstrated through experiments with the CICIDS2017 public dataset, which was explicitly designed to simulate real scenarios and provide valuable information to security professionals when analyzing computer networks. The proposed methodology opens up new perspectives in investigating and detecting anomalies and intrusions in computer networks, which are often attributed to cyber-attacks. This development culminates in creating a promising model that stands out for its effectiveness and speed, accurately identifying possible intrusions with an F1 of nearly $80\%$, a recall of $99.42\%$, and an accuracy of $65.84\%$.

1. Introduction

The increase in cyber-attacks poses various problems associated with security flaws in computer networks, whether physical or cloud-based, including vulnerabilities that allow attackers to exploit weaknesses in network protocols and carry out malware attacks, such as ransomware infections, compromising data integrity and confidentiality [1,2].

Network traffic flows encapsulate essential data, such as the source and destination IP addresses, the time intervals between server communications, the timestamps of each transaction, and the communication protocols used. A common vulnerability exploited in cyberattacks is unauthorized access to the network, which results in the theft of sensitive data and compromises the integrity of systems. By knowing IP addresses, attackers can identify potential targets within the network, devise attack strategies and, using spoofing techniques, hide or falsify their locations. Statistical analysis of IP addresses in traffic logs can reveal discrepancies that suggest manipulation or fabrication, indicative of malicious activity. In addition, analysis of communication times can expose periods of lower protection or higher activity on the network, allowing attackers to determine the ideal times to launch attacks. Accurate knowledge of these times can be crucial, allowing malicious actions during windows of opportunity when detection is unlikely [3,4].

These features are candidates to be analyzed using a set of statistical laws, namely the application of Benford’s Law, a mathematical principle that describes the frequency of occurrence of the first digit (from 1 to 9) in numerical datasets and makes it possible to detect anomalies in the distribution of digits. This law states that digits tend to follow a specific distribution pattern, with the digit 1 appearing with a frequency of $30.10\%$, followed by the digit 2 with 17.6%, and so on, in a pattern that resembles a negative exponential. This pattern has been observed in various datasets, including financial transactions and demographic statistics [5,6]. For example, if an attacker manipulates or creates log records to hide their activities, the distribution of the first digits of these records may not adhere to Benford’s Law.

Understanding the protocols used on the network is a crucial aspect of cybersecurity. It allows attackers to choose the best techniques and tools to exploit existing vulnerabilities in the network. The most common attacks include the abuse of TCP SYN packets, which indicate the intention to establish a connection, and PSH-ACK packets, which convey the urgency of data delivery and confirmation that it has been received by the recipient. These attacks can result in large volumes of transferred data, the analysis of which, using statistical laws such as Benford’s Law, can identify abnormal statistical distributions that deviate from the expected, suggesting illicit activity [7,8,9,10,11].

Flow analysis is a powerful network management and security tool. Each flow is identified by critical components, including the source and destination IP addresses and the protocol used, whether TCP or UDP. The real power of flow analysis lies in its ability to identify atypical traffic patterns, such as communications to suspicious destinations or excessive traffic volumes at certain times, indicating a security breach. Network administrators and security analysts can stay one step ahead of potential threats by analyzing these flows.

In network security, flow analysis plays a crucial role in identifying malware attacks in contrast to other types of attacks due to various factors. These include the rapid spread of this attack, often including methods to hide its presence in infected systems. In addition, the adaptive capacity of malware means that attackers continually develop new strategies to elude intrusion detection systems (IDSs). The complexity and diversity of malware attacks are also significant, ranging from simple viruses to sophisticated spyware or ransomware programs. Given the ability of malware to establish communications with command and control servers through unconventional ports or protocols, rapid detection of these communications is imperative to enable an agile and effective response to control the infection [12,13,14].

Although current systems, such as signature-based IDS, anomaly-based IDS, hybrid or behavior-based IDS, have high success rates in detecting intrusions, they face limitations, such as complex configurations, the need for vast computing resources, the inability to detect new or unknown threats (zero-day attacks), the need for constant updates of signature datasets, the high number of false negatives if the signature dataset is not comprehensive, and the dependence on large volumes of historical data to form a suitable basis for comparative analysis [15,16].

In contrast to traditional intrusion detection systems, Benford’s Law offers distinct advantages due to its simplicity of implementation and operational efficiency. This methodology allows for identifying digit divergences without the need for large computer resources or large volumes of historical data on which to base decisions, making it particularly useful in any attack scenario, whether previously known or unknown.

Benford’s Law can be effectively applied without resorting to statistical analysis mechanisms to detect abnormal or malicious activity in network flows by analyzing the patterns of the first digits of numerical metadata, such as inter-packet times or packet sizes. If the frequency of the first digits deviates significantly from the expectations of Benford’s Law, this can indicate malicious communications or cyber-attacks. Monitoring systems can periodically check these distributions and warn of persistent deviations. However, not all data will follow Benford’s Law, making validating and calibrating its use in security analyses essential. To improve the analysis of these deviations, studies recommend integrating Benford’s Law with statistical measures such as the calculation of Pearson, Spearman, and Kendall correlation coefficients, the Chi-square test, and the application of the Weibull distribution to assess the fit of statistical models to the observed data [17,18,19].

In addition to using such statistical methods, distance functions combined with Benford’s Law can significantly improve the detection of anomalies in network traffic flows. These functions make it possible to quantify the degree to which data deviate from what is expected by Benford’s Law, increasing sensitivity in identifying small deviations that could signal intrusion attempts or other malicious activities. In addition, they provide a standard method for comparing different datasets or periods within the same set, adapting to the specific context of the analysis. For example, the Euclidean distance may be suitable when the magnitude of the deviations is relevant. At the same time, other more subtle and non-linear patterns can be captured using other distance functions, notably when using the Kullback–Leibler divergence, which identifies small patterns that could be overlooked in simple frequency analyses. Functions such as the Chi-squared test, the mean absolute deviation (MAD), and the sum of squared deviations (SSD) are handy, providing an objective and quantitative measurement of anomalies, and are the most widely used. Compliance with Benford’s Law is usually proven when the value of a specific distance function is below a critical threshold, as indicated in Nigrini’s studies on accounting fraud. However, it is crucial to assess whether these thresholds are applicable in the context of network data, thus ensuring the effectiveness and relevance of the security analyses carried out [20,21].

This paper goes beyond analyzing network traffic data, employing an integrated approach that combines Benford’s Law with three distance metrics: the mean absolute deviation, the Kolmogorov–Smirnov test, and the Kullback–Leibler divergence. The developed methodology examines the data and identifies unnatural patterns in the first digit that could signal network vulnerability exploitation. By applying these three distance metrics, the study aims to identify significant distances between the frequencies of occurrence of the first digit and the empirical frequencies stipulated by Benford’s Law, thus making it possible to identify possible anomalies or intrusion attempts.

This approach enables rigorous data flow analysis, contributing to the proactive detection and mitigation of security risks in network environments. Combining these techniques allows for a deeper and more efficient analysis of network traffic, overcoming challenges such as the need for vast computing resources, dependence on large volumes of historical data, and difficulties detecting new or unknown threats. This methodology allows us to detect abnormal patterns in the initial digits of flows, which can indicate malicious activity. The integration of distance functions aims to enrich network flow analysis by quantifying anomalies, providing a robust assessment of data dispersion. The approach proposed in this paper incorporates the following three distance functions:

• Mean Absolute Deviation (MAD), where the dispersion of the data is calculated by averaging the absolute differences between the observed and expected frequencies, providing a precise measure of the variance about Benford’s Law.
• Kolmogorov–Smirnov (KS) test compares the cumulative distributions of the observed frequencies of the digits with those predicted by Benford’s Law, identifying significant discrepancies that may indicate anomalies.
• Kullback–Leibler (KL) divergence measures the information lost when the observed distribution is used to estimate the distribution expected by Benford’s Law. This metric quantifies the degree of divergence between the two distributions.

High values obtained from calculating the distances between the frequencies observed and those expected by Benford’s Law in any of the applied metrics may indicate substantial deviations between what is observed and what is expected by Benford’s Law, which suggests the possible occurrence of abnormal patterns or suspicious activity in the network data. This multidimensional approach allows for detailed and in-depth analysis, which is crucial for accurately identifying irregularities in network flows.

The research was conducted using the CIC-IDS2017 dataset, a comprehensive collection of network flows representing various types of attacks. This dataset, which includes network flows generated and analyzed by CICFlowMeter, covers many attacks, including brute force attacks on FTP and SSH, Heartbleed, web attacks, infiltrations, botnet activities and DDoS attacks.

To develop and evaluate the model based on Benford’s Law in conjunction with the three distance functions, we followed a systematic approach. This approach, similar to the one proposed by Nigrini, involved evaluating the compliance of the data with Benford’s Law for the first digit. This allowed us to implement the different distance functions, namely the Mean Absolute Deviation, the Komolgorov test, and the calculation of the Kullback–Leibler divergence. By following this approach, we were able to develop a robust model for detecting anomalies in network traffic data, contributing to the proactive detection and mitigation of security risks in network environments.

The methodology developed for detecting malicious flows was structured in two main phases. Initially, each distance function was assessed individually for its ability to detect malicious flows, analyzing the discrepancy between the observed frequencies of the first digits and those expected by Benford’s Law.

In the second phase, a specific version of Bayes’ Theorem was integrated and adjusted precisely to detect malicious flows. This integration made it possible to transform the p-values obtained by the distance functions into a new joint p-value, assuming that each flow could be malicious. This new p-value was then recalculated for each distance function and combined using recognized p-value aggregation methods, such as the Fisher and Tippett methods.

This approach aimed to enrich the model’s ability to make informed decisions based on the data derived from the deviations between the frequencies observed and those expected by Benford’s Law, making it possible to assess the significance and likelihood of the anomalies more effectively detected, indicating abnormal behavior, such as potential intrusions. Thus, classifying flows as benign or malicious made it possible to calculate the probability of each flow being correctly identified, leading to a new decision that enhances the accuracy and reliability of security systems in detecting potential intrusions.

Based on the adjusted probabilities and combined p-values produced in the second phase, this new decision was used to formulate an ensemble of the results generated by each distance function. This ensemble aims to provide a more comprehensive and accurate view of detecting malicious flows, significantly boosting the accuracy and reliability of the security system in network environments.

The results obtained with the experiments demonstrate an accuracy of around $65.85\%$, with an F1-Score score of approximately $80\%$. Although encouraging, the results emphasize the need for further studies to assess the model’s applicability in different contexts, especially in accounting crime. Furthermore, additional studies are essential to investigate the possibility of integrating the model with other fraud detection techniques, such as pattern analysis or machine learning. This integration could increase the model’s accuracy and reduce the false positive rate, providing a more robust and effective approach to identifying fraudulent activity. The wide range of existing studies on the application of Benford’s Law in this field will make it possible to consolidate and validate the proposed model. At the same time, developing the integrated model, which combines Benford’s Law with distance functions dedicated to analyzing malicious network flows, could provide indispensable information for security analysts in the fight against cybercrime in the future.

The paper describes the results obtained in the research:

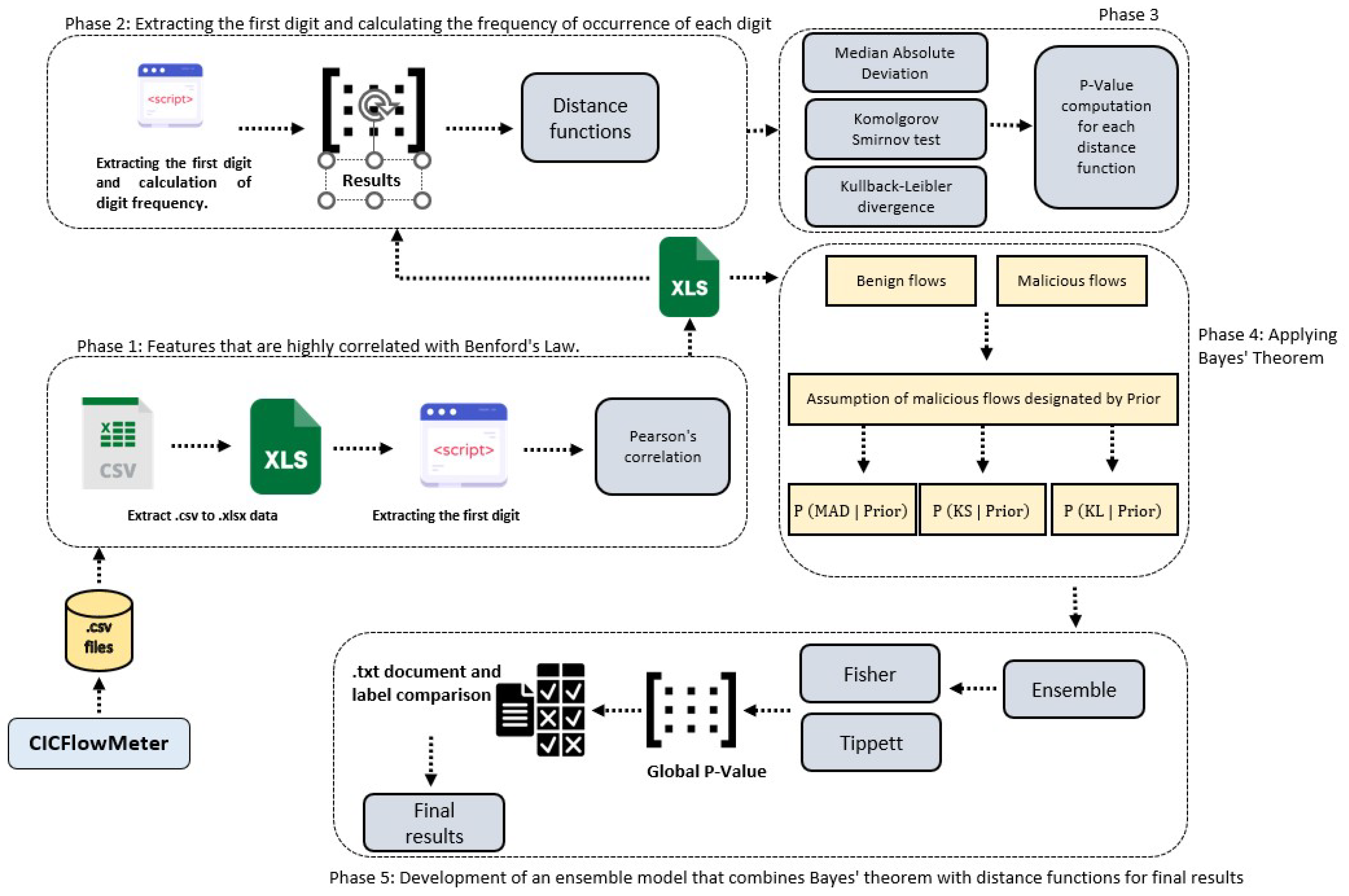
• A model based on the joint application of Benford’s Law and three distance functions, namely the Mean Absolute Deviation, the Kullback–Leibler divergence, and the Komolgorov–Smirnov test in analyzing and identifying anomalies in the flows obtained from a computer network.
• The development of a set of Matlab scripts that facilitated the implementation of Benford’s Law in conjunction with three distance functions. These scripts were used to extract the first digit, calculate each digit’s frequency of occurrence, and generate an ensemble that integrates the distance functions with Benford’s Law, applying Bayes’ Theorem, and can be found in https://github.com/pacfernandes/Unvelling-Network-Malicious-flows.git (1 July 2024).
• The comparison between the results obtained with this model and those attained with automatic learning-based methods.

This paper is structured in several different sections. Section 2 reviews the literature, highlighting the most relevant works that explore the application of Benford’s Law to detect anomalies and intrusions in computer networks. This includes a critical discussion of the methodologies employed, the results achieved, and their implications for cyber security. Section 3 deals mathematically with Benford’s Law, the distance functions used, their relevance and application in the domain under study. Section 4 sets out the general architecture of the proposed model, including the pre-processing and processing steps for extracting the features aligned with Benford’s Law, the evaluation of the model based on methods suggested by Nigrini, and the metrics used to obtain the overall evaluation results. Section 5 presents the experimental results and subsequent analysis. Finally, Section 6 discusses the research’s main conclusions and suggests directions for future work.

2. Benford’s Law and Distance Functions in the Detection of Malicious Flows

This section analyzes studies that apply Benford’s Law and other statistical techniques for detecting malicious flows in computer networks. At the end of this section, we summarize the main gaps identified in previous work and the motivation for this study.

2.1. Related Work

Computer network security has predominantly focused on using machine learning techniques to analyze and detect anomalies or intrusions. However, purely statistical approaches are often overlooked. This trend neglects valuable methods such as regression analysis, outlier detection, and Markov models, which offer complementary and usually more intuitive insights. These methods allow for the identification of hidden patterns, the prediction of security events, and a deeper understanding of attacker behavior, which are essential elements for a robust analysis of atypical behavior on the network [22,23,24,25].

However, Iorliam [26] has brought a fresh perspective by delving into the applicability of Benford’s Law in analyzing network traffic data. This unique study aimed to verify the compliance of network data with this statistical law and to differentiate the relationship between benign and malicious network traffic flows, offering a novel approach to network security. Iorliam’s study examined all the data collected, applying the Chi-squared statistical test to assess the correlation between the observed data and the expected distributions according to Benford’s and Zipf’s laws.

The Chi-squared test is widely used to test hypotheses about the independence of variables in contingency tables, allowing researchers to determine whether differences between categories are due to chance or a statistically significant relationship. In this case, it was used to assess the compliance of the network data with Benford’s Law and other natural laws, namely Zipf’s Law. The results showed that the p-values obtained by the Chi-squared test when applying Benford’s law are inversely proportional to the values obtained when applying Zipf’s law. This result suggests a variation in the effectiveness of the laws in different contexts of network traffic analysis. While Iorliam’s research laid the groundwork for applying Benford’s laws in network traffic analysis, it left a gap in addressing the practical aspects of differentiating between benign and malicious traffic flows using these statistical laws. It is crucial to note that applying these laws can face challenges in real-life scenarios, such as the need for large amounts of data and the possibility of false positives or negatives. Therefore, this study opens the door for future research that validates or improves these statistical laws as diagnostic tools in cybersecurity environments, emphasizing the potential impact of the contribution to advancing the field.

Recent studies have begun to unveil the potential of Benford’s Law as a tool for revolutionizing intrusion detection systems (IDSs) in high-volume network traffic scenarios. For instance, ref. [27] proposed a new feature extraction method based on this statistical law. The method, which extracted six features from the divergence values, focused mainly on the first three digits. The authors evaluated the model’s effectiveness using three machine learning classifiers, and the results were promising, hinting at a potential enhancement in the efficiency of IDS.

Furthermore, with the growing adoption of the Internet of Things (IoT) and the challenges associated with the limited resources of these devices, ref. [19] explored the applicability of an IDS adapted for resource-constrained environments. IoT devices are computationally limited in resources, memory space, and energy, making it challenging to implement robust security measures. The study proposed using Benford’s Law to differentiate the sizes of network flows and implemented linear regression to process this information. This approach can effectively identify abnormal traffic, even with limited resources, by taking advantage of the distribution patterns inherent in the sizes of network flows. The results showed that this approach could be practical for IoT systems, offering a viable solution that requires fewer computational resources, less memory space, and lower energy consumption.

These studies highlight the versatility and applicability of Benford’s Law in different contexts within cybersecurity, suggesting avenues for future research that could expand its use in intrusion detection systems adapted to contemporary digital security requirements. Distributed Denial of Service (DDoS) attacks, such as SYN flood or ICMP smurf, are often perpetrated using packets generated by malicious scripts or programs. In response to these challenges, Kemal Hajdarevic et al. [28] propose an innovative method based on Benford’s Law to detect abnormal network traffic packets by analyzing real-time data and focusing on packet size.

In addition, zero-day attacks, which refer to unknown vulnerabilities in software, remain a significant threat. These vulnerabilities, when exploited, can allow unauthorized access or destabilization of critical systems before patches or preventative measures can even be applied. These attacks are particularly dangerous because they are not yet known to the software vendor and can, therefore, be used by hackers to gain unauthorized access to systems. Traditionally, network traffic analysis (NTA) is performed by machine learning (ML)-based network intrusion detection systems (NIDSs), whose effectiveness is often compromised by redundant features such as IP addresses. Ref. [29] addressed this issue by using Benford’s Law to extract meaningful network features, assessing the relevance of a feature by whether it complies with or violates Benford’s Law in benign and malicious traffic, respectively. This study used a semi-supervised ML-based approach, comparing feature sets identified in the literature.

Historically, approaches that apply Benford’s Law to network intrusion detection have been restricted to limited features, often excluding negative or zero digits. The exclusion of zero digits, which is not applicable in logarithmic functions, and manipulating negative digits using the modulus are practices discussed in the literature [20]. However, these exclusions can result in the loss of critical information for detecting attacks. In addition, studies have mainly been limited to using the Chi-squared test and, occasionally, Euclidean distance for evaluation [30,31]. Considering a more comprehensive range of features and evaluation methods, these limitations emphasize the need for more comprehensive and robust research into applying Benford’s Law to network intrusion detection.

Our knowledge about the nature of flows in computer networks is limited and characterized by uncertainty. Incorporating Bayes’ Theorem and Benford’s Law and distance functions has facilitated inference based on the available flow data in the dataset. The combination of the p-values, calculated from the discrepancies between the observed and expected frequencies according to Benford’s Law and assuming prior knowledge about the proportion of malicious flows, aimed to refine the detection model to increase the accuracy of identifying these flows and minimize the rate of false positives and negatives. The main aim of integrating Bayes’ Theorem was to calculate the probability of a flow being malicious from the p-values obtained by the distance functions, generating a new p-value for each distance function and then combining them into a single global p-value. From a statistical point of view, the fusion of Benford’s Law with Bayesian updates has added a layer of mathematical rigor, seeking to increase precision and reliability in analyzing each network flow. This innovative model stands out for its scalability, which makes it capable of managing large volumes of data without significantly increasing computing resources, making it ideal for environments with expanding network traffic. In addition, the flexibility of the statistical models makes it possible to adjust the probability thresholds and criteria for identifying malicious flows according to Bayes’ Theorem, adapting to different operational contexts or specific security requirements.

2.2. Challenges and Strengths

Studies that apply Benford’s Law to detect malicious flows highlight several shortcomings. The first of these is the complexity of new attacks, which can alter or camouflage features in network flows, compromising the effectiveness of statistical analysis. In addition, the difficulty of adapting Benford’s Law to all types of data, especially in the massive presence of the zero digits, and the increased complexity of the model, with the inclusion of distance functions and Bayesian inference, can pose real challenges in validating the model and minimizing false positives and negatives. On the other hand, although adopting Benford’s Law, distance functions, and Bayesian inference to new attack patterns have not yet been fully explored, zero-day attacks and advanced evasion methods can be imperceptible to approaches based on traditional statistical patterns.

However, despite these shortcomings, integrating Benford’s Law with the various distance functions can strengthen the model, making it more robust in identifying malicious flows. This enhancement can result in significant benefits, such as the ability to detect subtle deviations in data patterns that may indicate malicious activity, noise filtering and accuracy in identifying malicious flows, providing a more solid basis for security decisions. Additionally, introducing Bayesian inference could allow the probabilities to be continuously updated as new data are received, making the model adaptable to new threats.

The exclusive use of the Chi-squared test can also be limited, especially in situations with subtle anomalies in network traffic. Incorporating Bayesian inference and other statistical methods could increase the model’s sensitivity to these anomalies.

Finally, Benford’s Law assumes a specific distribution of the first digits. In networks where data are manipulated or distorted by malicious activity in subtle ways, the empirical application of this law can be ineffective, resulting in false positives or negatives. Applying distance functions to detect distortions in frequencies and distances between them is crucial to overcoming this weakness.

3. Benford’s Law and Distance Functions

3.1. Benford’s Law

Benford’s law, known as the law of the first digit, is an empirical law that defines the frequency of distribution of digits in a non-uniform way, i.e., different from $1÷9=0.11\dots$, but states that the frequency of occurrence for the digit 1 is $30.10\%$, for the digit 2 it is $17.6\%$, and so on.

Let X be an independent and identically distributed (i.i.d.) random variable, such that $X=\left(X_1,X_2,\dots ,X_i\right),i=1,2,3,\dots ,n,\forall n\in \mathbb{N}$, and $D_i\left(X\right)$ represent the $i\mathrm{th}$ significant decimal digit of X. The probability mass function that describes Benford’s Law is given by Equation (1):

$$P\left(D_i\left(X\right)\right)=\log \left(1+{\displaystyle \frac{1}{d}}\right),\mathrm{if}d=\{1,2,3,\dots ,9\}$$

(1)

Definition 1 represents the basic notion governing Benford’s Law and is implicit in the meaning of the number, i.e., the value of the mantissa. Given a decimal number, the mantissa refers to the first significant digit. For example, if we have the number $0.014$, the mantissa is provided by the first significant digit, i.e., 1 [32].

Definition 1

(Mantissa). The mantissa represents the decimal part in the calculation of the logarithm of a number. The relation translates to $\log S\left(x\right)$. The only number r in $\left[{\displaystyle \frac{1}{10}},1\right[$ with $x=r\times {10}^n$ for some integer.

Benford’s Law is based on three fundamental properties:

• The distribution of significant digits is invariant concerning the change of scale.
• The distribution of significant digits is continuous and invariant concerning the change of base.
• The frequencies are uniformly distributed in the range of $\left]0,1\right[$, relative to the fractional parts of the logarithm.

Theorem 1 applies Benford’s Law to negative digits.

Theorem 1.

Given a sequence of real numbers $\left(x_n\right)$, with $n\in \mathbb{N}$, $\log |x_n|=\log |x_1|,$ $\log |x_2|,\dots$

Benford’s Law is not only defined for the first digit but can be extended to two or more digits. Thus, Theorem 2 defines the general Benford’s Law that allows obtaining the occurrence frequency of one or more digits [33].

Theorem 2

(General law). Let $k\in Z$, $d_1\in \{1,2,3,\dots ,9\}$ and $d_j\in \{0,1,2,\cdots ,9\}$, $j=2,\dots ,k$.

$$P\left(D_k=d_k\right)=\log \left(1+{\displaystyle \frac{1}{{\sum }_{i=1}^k{d}_i\times {10}^{k-i}}}\right)$$

(2)

We can find proof of the general Benford’s law, described in Theorem 2, in [33,34].

To meet the specifications of Benford’s Law for extracting the first digit, the number’s modulus operation was implemented to eliminate negative digits. In addition, the numbers were rounded to avoid decimals, thus allowing the most significant digit to be extracted from the data. The technique adopted for this extraction is based on the methodology proposed by [20], detailed in his study “Benford’s Law: Applications for Forensic Accounting, Auditing, and Fraud Detection”. Equation (3) describes the specific formula used:

$$D_{\mathrm{collapsed}}=\left|{\displaystyle \frac{10\times a}{{10}^{int\left(\log \left(a\right)\right)}}}\right|$$

(3)

where $D_{\mathrm{collapsed}}$ represents the digit of the collapsed number a and $int$ denotes the function that converts to an integer. To make the value positive, the modulus of the number was added.

3.2. Distance Functions

3.2.1. Kolmogorov–Smirnov Test

The Kolmogorov–Smirnov test is a non-parametric goodness-of-fit test often used to check whether two samples follow the same probability distribution. It is a test statistic that quantifies the absolute distance between the empirical distribution function and the reference distribution obtained from the reference sample. It is a test that is extremely sensitive to differences between the maximum deviations between the empirical distribution and the sample distribution, both locally and globally [35,36].

The reason we chose to use the KS test was because we needed to verify whether each network flow follows the same distribution as Benford’s Law, i.e., to decide between two hypotheses:

$$H_0:P=P_0 \mathrm{vs}. H_1:P\ne P_0$$

where $P_0$ refers to each data flow and P refers to the distribution of Benford’s Law.

The dataset, consisting of n network flows, comprises $X_i$ independent and identically distributed (i.i.d.) variables, whose empirical distribution function is usually given by Equation (4).

$$F_n\left(x\right)={\displaystyle \frac{1}{n}}\sum _{i=1}^n\mathit{I}\left(X_i\le X\right)$$

(4)

Contrary to what is stated in the literature, we will not derive the empirical distribution function from the original dataset. However, we will assume that Benford’s Law gives this function. The aim is to check whether deviations exist between the i.i.d. variables of each flow by comparing them with Benford’s Empirical Law. If the deviations observed for each network flow are considerable, we can assume we are dealing with a malicious flow.

These are important ideas to retain when using the K-S test in this research. From a distribution function $F_X\left(x\right)$, we can define an empirical cumulative distribution function (c.d.f.), given by Equation (4), which allows us to account for the proportion of sample points below the x level. For each $x\in \mathbb{R}$, the law implies that $F_n\left(x\right)=F_X\left(x\right)$, given by Equation (5).

$$F_n\left(x\right)={\displaystyle \frac{1}{n}}\sum _{i=1}^n\mathit{I}\left(X_i\le X\right)\to E\mathit{I}\left(X_i\le X\right)=F_X\left(x\right).$$

(5)

From Equations (4) and (5), we can conclude that the probability of the sample proportion in the dataset remains uniform over all $x\in \mathbb{R}$ and that when there are no large deviations between the distribution function and the empirical distribution function, the probability of the difference between the two functions usually tends to be zero.

Theorem 3.

If the distribution function $F_X\left(x\right)$ is continuous, then the distribution of

$$\underset{x\in \mathbb{R}}{\sup }|F_n\left(x\right)-F_X\left(x\right)|$$

(6)

does not depend on F.

In Equation (6), $sup$ refers to the maximum value of the set of distances.

This investigation used the KS test to check whether the probability distributions for the network flow and Benford’s Law differed. In this sense, the equation given by Theorem 3 can be changed to Equation (7).

$$\underset{x\in \mathbb{R}}{\sup }|F_{1,n}\left(x\right)-F_{2,m}X\left(x\right)|$$

(7)

with $F_{1,n}\left(x\right)$ and $F_{2,m}X\left(x\right)$ being the distribution functions of the set of network flows and Benford’s Law, respectively. In this particular case, if $F_{1,n}X\left(x\right)$ and $F_{2,m}X\left(x\right)$ are the corresponding c.d.f.s, then the test statistic is given by Equation (8).

$$D_{n,m}=\sqrt{{\displaystyle \frac{m\times n}{m+n}}}\times \underset{x\in \mathbb{R}}{\sup }|F_{1,n}\left(x\right)-F_{2,m}X\left(x\right)|$$

(8)

whose null hypothesis will be rejected at significance level $\alpha$ if

$$D_{n,m}>\sqrt{{\displaystyle \frac{-1}{2}}\ln \left({\displaystyle \frac{\alpha }{2}}\right)}\times \sqrt{{\displaystyle \frac{m\times n}{m+n}}}$$

(9)

Table 1. Observed and empirical cumulative frequencies, and the respective deviations between frequencies.

First Digit	Cumulative Frequency for Flow 14: ${\mathit{F}}_{\mathit{X}}\left(\mathit{x}\right)$	Cumulative Frequency for Benfords’ Law: ${\mathit{F}}_{\mathit{n}}\left(\mathit{x}\right)$	$\mathit{D}={\displaystyle \underset{\mathit{x}\in \mathbb{R}}{\sup }}|{\mathit{F}}_{\mathit{n}}\left(\mathit{x}\right)-{\mathit{F}}_{\mathit{X}}\left(\mathit{x}\right)|$
1	0.2222	0.3010	0.0788
2	0.2778	0.4771	0.1993
3	0.3889	0.6021	0.2132
4	0.4444	0.6990	0.2545
5	0.5556	0.7782	0.2226
6	0.7222	0.8451	0.1229
7	0.8889	0.9031	0.0142
8	0.9444	0.9542	0.0098
9	1	1	0

shows an example of applying the Kolmogorov–Smirnov test to a network flow, such as flow 14, following the procedure described in

Table 2. Kolmogorov–Smirnov test procedure based on the study of Benford’s Law applied to any network flow.

Calculation of the Cumulative Empirical Distribution Function for one flow in general;

Calculation of the Empirical Cumulative Distribution Function for Benford’s Law;

Calculation of the Kolmogorov–Smirnov Statistic using Equation (7);

$D_{\mathrm{test}}$ will be the largest value of the $D_i$ calculated in the previous step;

Compare $D_{\mathrm{test}}$ with a critical value of D;

If $D_{\mathrm{test}}<D_{\mathrm{critical}}$, there is not enough statistical evidence to reject $H_0$.

.

Based on the values obtained in Table 1, Figure 1 shows the highest value of the differences between the cumulative functions.

Following the procedure described in Table 2, the $D_{test}$ value $=0.2545$. To check whether the flow is malicious or benign, it is necessary to compare the value obtained in $D_{test}$ with a critical value. Considering a significance level of $0.05$ and using Equation (9), we obtain a critical value of $4.073$. As $D_{test}<D_{critical}$, there is not enough statistical evidence to reject $H_0$, so we conclude that the flow is not malicious.

3.2.2. Median Absolute Deviation

The Mean Absolute Deviation (MAD), given by Equation (10), is a measure of compliance with Benford’s Law that returns the value of the average deviation of the frequency with which each digit occurs from the empirical frequency of each digit [37]. Usually, the Mean Absolute Deviation Percentage Error (MAPE) is used, which, although an adaptation of the MAD, allows the accuracy of the adjusted time series values to be measured. The smaller the value returned by the difference between the real and empirical frequencies, the closer it is to the real values, producing forecasts with high certainty. The MAD makes it possible to graphically compare the average deviation between the heights of the bars, referring to the actual proportion of each digit and the proportion expected by Benford’s Law in a two-dimensional graphic. Figure 2 shows the MAD between Benford’s Law and flow 14.

This possibility meant that in this research, we only used the MAD to the detriment of the MAPE. More significant mean absolute deviations necessarily imply a more considerable mean difference between the actual and expected proportions, strongly suggesting the presence of anomalies in the data and, therefore, the presence of possible malicious flows [38].

$$MAD={\displaystyle \frac{{\sum }_{i=1}^N|F_r-E_f|}{N}}$$

(10)

where $F_r$ is the real frequency of each digit, $E_f$ is the empirical frequency of Benford’s Law, and N represents the number of bins, which equals 9 for the first digit.

3.2.3. Kullback–Leibler Divergence

The Kullback–Leibler (KL) divergence, usually known as relative entropy, is a fundamental metric in information theory and probability theory used to measure the discrepancy between two probability distributions over the same random variable x [21]. This non-symmetric metric quantifies how a probability distribution $q\left(x\right)$, which can represent an observed empirical frequency, deviates from a model distribution $p\left(x\right)$. In the context of our research, $p\left(x\right)$ corresponds to the theoretical frequency predicted by Benford’s Law for the occurrence of first digits. In line with the procedure carried out in the Kolmogorov–Smirnov test for flow 14, Figure 3 shows the Kullback–Leibler divergence between each digit’s occurrence frequency in flow 14 and the empirical frequency from Benford’s Law.

Specifically, the KL divergence from $q\left(x\right)$ to $p\left(x\right)$, denoted by $DKL\left(p\left(x\right)\Vert q\left(x\right)\right)$, provides a quantitative measure of the information lost when $q\left(x\right)$ is used to estimate $p\left(x\right)$. This analysis assumes that $p\left(x\right)$ and $q\left(x\right)$ are independent probability distributions of a discrete random variable x. Both distributions must be strictly positive $q\left(x\right)>0$ and $p\left(x\right)>0$ throughout the sample space X, with their sums approaching 1 [39].

For our research, we apply the continuous version of the KL divergence due to the continuous nature of the random variables observed in the frequencies. Equation (11) continuously defines the KL divergence $q\left(x\right)$ in $p\left(x\right)$.

$$D_{KL}\left(p\left(x\right),q\left(x\right)\right)=\sum _{x\in X}p\left(x\right)\times \ln {\displaystyle \frac{p\left(x\right)}{q\left(x\right)}}$$

(11)

where $p\left(x\right)$ and $q\left(x\right)$ are the probability densities of the distributions p and q, respectively. This approach provides a detailed analysis of the divergences in the frequencies of occurrence of the digits from the theoretical expectations of Benford’s Law, which is essential for understanding and quantifying the anomalies in the analyzed datasets [40].

Although the KL divergence is not a distance function, it does have several important properties.

• Non-symmetric, $D_{KL}\left(p\left(x\right),q\left(x\right)\right)\ne D_{KL}\left(q\left(x\right),p\left(x\right)\right)$;
• Non-negative measure, $D_{KL}\left(p\left(x\right),q\left(x\right)\right)\ge 0$ and $D_{KL}\left(p\left(x\right),q\left(x\right)\right)=0$ if $p=0$ or $q=0$.

Fisher’s method was implemented to integrate the p-values derived from the mean absolute deviation, the Kolmogorov–Smirnov test, and the Kullback–Leibler divergence. This approach calculated a more robust and sensitive p-value to minimize the number of false positives.

To summarize, the choice of the Mean Absolute Deviation, the Kolmogorov–Smirnov test, and the Kullback–Leibler divergence was based on various aspects that distinguish them from other functions:

Kolmogorov–Smirnov test (KS):

• Robustness of comparisons: The KS test is robust for comparisons between the empirical frequency of Benford’s Law and the frequency of occurrence of the digits.
• Sensitivity to deviations: This test shows greater sensitivity to distribution deviations.
• Non-Parametric Nature: Considering that data from a computer network can be irregular, the non-parametric nature of the KS test is advantageous, as it does not require the data to follow a specific distribution.

Comparison with other tests:

• Chi-Square Test: Unlike the chi-square test, the KS test does not rely on predefined data categories, thus avoiding information loss. In addition, the KS test can be applied when the null hypothesis is well defined, which is not always possible with the chi-square test.
• Anderson–Darling test: Although similar to the KS, the Anderson–Darling test is more complex and less intuitive, making the KS preferable for many applications.

Kullback–Leibler Divergence (KL):

• Assessment of Proximity between Distributions: The KL divergence is widely used in data mining literature to check the closeness between two distributions. The lower the value obtained, the closer the distributions are.
• Directed and Asymmetric Analysis: The asymmetric and directed nature of KL divergence allows for a detailed analysis of discrepancies between the frequency of digits and the empirical frequency of Benford’s Law.
• Sensitivity to Small Differences: KL divergence is particularly sensitive to slight differences between distributions, making it helpful in detecting subtle anomalies.

Comparison with other tests:

• Jensen–Shannon Divergence: Despite being a symmetrical version of KL, KL’s simplicity and sensitivity are preferable for many analyses.
• Mahalanobis distance: Although the Mahalanobis distance effectively detects multivariate anomalies, the KL is better suited to measuring differences in probability distributions.

Mean Absolute Deviation (MAD):

• Simplicity and straightforward interpretation: The Mean Absolute Deviation is simple to calculate and interpret, directly measuring the discrepancies between the observed frequencies and those expected by Benford’s Law.
• Less Sensitivity to Outliers: This method is less sensitive to outliers, especially in digit 1 of Benford’s Law, which makes it preferable to the mean square deviation.

Conclusion:

The choice of the Kolmogorov–Smirnov, Kullback–Leibler, and Mean Absolute Deviation distance functions considered each method’s robustness, sensitivity, and simplicity. These characteristics make them particularly useful for analyzing and evaluating network flows, providing more effective detection of flow anomalies and irregularities [41,42,43,44,45].

3.3. Fisher’s Method

The Fisher method facilitates the aggregation of multiple p-values from independent tests into a single composite value [46]. Given that the p-values are independent, derived from distance functions without any correlation, the employed formula culminates in Equation (12).

$$T=-2\times \sum _{i=1}^3{\log }_e\left(p_i\right)$$

(12)

where $p_i$ represents the p-values obtained from the three distance functions: the mean absolute deviation, the Kolmogorov–Smirnov test, and the Kullback–Leibler divergence. Finally, to combine these p-values, the resulting statistic, T, follows a Chi-squared distribution with $2k$ degrees of freedom, given by Equation (13).

$$P\left(X>T\right)=1-{\int }_0^{T}f\left(x;df\right)dx$$

(13)

where $f\left(x;df\right)$ represents the probability density function of the Chi-squared distribution with $df=6$ degrees of freedom [47].

3.4. Tippett’s Method

The Tippett test is another methodology used to generate a global set of p-values from the p-values derived from the distance functions. This test, denoted by $T_p$, is modelled by the beta distribution and is described by Equation (14). The resulting global p-value is defined by Equation (15), where the choice for each global p-value results from Equation (16). This test was chosen because of its similarity to the Bonferroni method, which minimizes false positives [48].

$$T_p=min\left(p_1,p_2,p_3\right)$$

(14)

$$p=1-{\left(1-p_{\left(1\right)}\right)}^n$$

(15)

where

$$p_{\left(1\right)}=min\left(p_{MAD},p_{KS},p_{KL}\right)$$

(16)

4. Model Architecture

This section details the architecture used to exploit Benford’s Law, distance functions, and Bayes’ Theorem to identify intrusions in computer networks by analyzing data flows.

4.1. Natural Law-Based Method

The proposed model uses Benford’s Law combined with three specific distance measurement methods: the mean absolute deviation, the Kolmogorov–Smirnov test, and the Kullback–Leibler divergence, described in Section 3.2. Each distance function was evaluated individually in terms of results and globally when integrated in applying Bayes’ Theorem, allowing for a holistic approach to assessing discrepancies in the data analyzed and possible improvements in minimizing false positives.

The process begins by examining the first digit of the data, which is extracted after a preliminary data reduction stage. The main application consists of using Benford’s Law on the first digit to identify abnormal patterns that may indicate the nature of the data flow. Based on these patterns, the model distinguishes between malicious and benign flows, enabling a subsequent evaluation of the model’s performance.

Figure 4 depicts the system’s architecture and comprises three main components: pre-processing, processing, and analyzing results. Each block plays a crucial role in data utilization and the overall effectiveness of network intrusion detection.

Figure 5 depicts the general architecture of the model, highlighting the three main blocks represented in Figure 4. It includes each stage of the model, based on Benford’s Law, distance functions, and Bayes’ Theorem. In addition, the ensemble developed to aggregate the p-values obtained through Bayes’ Theorem is detailed in Section 3.3, Section 3.4 and Section 5.4.

Given that the dataset used in the research is public, the only checks required were for the presence of non-numerical data and correct labelling. We implemented a set of scripts to develop a functional model based on Benford’s Law and distance functions. These scripts facilitated not only the extraction of the first digit but also the calculation of features aligned with Benford’s Law and the measurement of the distance between the frequencies of the flow features and the empirical frequencies of the law. Subsequently, it was essential to integrate the distance functions to generate a single p-value from the individual p-values, allowing network flows to be categorized as malicious or benign.

After initially analyzing the dataset used in the research, the pre-processing phase began, which involved reducing the data using Microsoft Excel for each characteristic presented in

Table 3. General features present in the dataset.

Destination Port	Bwd Packet Length Max	Fwd IAT Total	Fwd Flags
Flow Duration	Bwd Packet Length Min	Fwd IAT Mean	Bwd PSH Flags
Total Fwd Packets	Bwd Packet Length Mean	Fwd IAT Std	Fwd URG Flags
Total Backward Packets	Bwd Packet Length Std	Fwd IAT Max	Bwd URG Flags
Total Length of Fwd Packets	Flow Bytes/s	Fwd IAT Min	Fwd Header Length
Total Length of Bwd Packets	Flow Packets/s	Bwd IAT Total	Bwd Header Length
Fwd Packet Length Max	Flow IAT Mean	Bwd IAT Mean	Fwd Packets/s
Fwd Packet Length Min	Flow IAT Std	Bwd IAT Std	Bwd Packets/s
Fwd Packet Length Mean	Flow IAT Max	Bwd IAT Max	Min Packet Length
Fwd Packet Length Std	Flow IAT Min	Bwd IAT Min	Max Packet Length
Packet Length Mean	ECE Flag Count	Bwd Avg Packets/Bulk	Active Mean
Packet Length Std	Down/Up Ratio	Bwd Avg Bulk Rate	Active Std
Packet Length Variance	Average Packet Size	Subflow Fwd Packets	Active Max
FIN Flag Count	Avg Fwd Segment Size	Subflow Fwd Bytes	Active Min
SYN Flag Count	Avg Bwd Segment Size	Subflow Bwd Packets	Idle Mean
RST Flag Count	Fwd Header Length_1	Subflow Bwd Bytes	Idle Std
PSH Flag Count	Fwd Avg Bytes/Bulk	Init_Win_bytes_forward	Idle Max
ACK Flag Count	Fwd Avg Packets/Bulk	Init_Win_bytes_backward	Idle Min
URG Flag Count	Fwd Avg Bulk Rate	act_data_pkt_fwd
CWE Flag Count	Bwd Avg Bytes/Bulk	min_seg_size_forward

. Initially, and considering that the dataset is numerical, we chose not to carry out any data cleaning or normalization process to keep the dataset as close as possible to its original form. Subsequently, considering the heterogeneity of the values in the dataset, which comprises integer and decimal values, the number collapse module was carried out so that the dataset consisted only of positive integer values. It is important to emphasize that the zero digit was not removed, as its extraction could result in a significant loss of information. After transforming the numbers, the most significant digit of each characteristic was extracted for subsequent calculation of the Pearson correlation between the frequency of occurrence of each digit and the empirical frequency of Benford’s Law. This process generated a percentage indicating the degree of correlation between the variables. However, it was observed that specific characteristics with only two digits, such as 0 and 1, produced high values in the correlation, which could lead to erroneous conclusions as to the nature of these characteristics following Benford’s Law. This is a significant limitation when calculating the Pearson correlation between Benford’s Law and the frequency of occurrence of digits for traits with little distribution of occurrence. High values in the first digit could lead to errors in the classification of flows and thus affect the model’s accuracy, as seen in Table 9, Section 5.1.

Given the use of Benford’s Law to detect anomalies in the distribution of digits, it is unlikely that there will be a significant bias in the results relating to detecting malicious flows. However, applying the model to a predefined set of attacks could limit its effectiveness in detecting other types of anomalies. However, this limitation is irrelevant in this study, since what is analyzed is possible anomalies in the digits according to Benford’s Law.

On the other hand, the heterogeneity of the data, which include integer values or decimals, can introduce additional complexity to the processing. We must carefully consider how to convert the data to mitigate potential errors that could distort the characteristics of the flows, underscoring the importance of our role in the process. To mitigate possible biases in the data, it is essential to implement additional analyses, namely the analysis of variance (ANOVA) and analysis of outliers, using methods such as the interquartile range (IQR). Including these additional analyses could ensure that the anomaly detection results are more accurate, instilling the audience with a sense of reassurance and confidence.

Figure 6 schematically illustrates this pre-processing phase. The original dataset contained several captures of attacks that occurred on different days of the week, stored in .CSV format, with values separated by commas.

To centralize the information, a representative sample of network flows for each type of attack was selected and compiled into a new dataset called NetworkFlows. Subsequently, a Matlab script was developed to extract the first digit of each network flow, storing these data in a specific digit matrix.

After the data preparation and reduction phase, we begin the data processing process, which is divided into two main stages. The first involves calculating the frequency of occurrence of each digit, with the results stored in a frequency matrix. Using the data in the digit matrix, we developed a Matlab script to determine the frequency of each digit based on the features identified during the pre-processing phase. This process makes it possible to calculate the distance between the observed frequencies of each digit and the corresponding frequencies according to Benford’s Law. The procedure for calculating the frequency of occurrence of each digit in network flows is simple. It divides the number of occurrences of each digit by the total sum of occurrences of all flows. In the same way, we calculate the total frequency for all occurrences of the digits. The values obtained are stored in a matrix of digits and then used to calculate the p-value, which is essential for classifying each network flow as malicious or benign. In this stage, the distance functions are also implemented for the subsequent p-value calculation in the second processing stage. The second stage applies distance functions to compare these frequencies with the empirical frequencies predicted by Benford’s Law to classify each network flow. This approach is schematized in Figure 7.

The second processing stage includes applying specific distance functions—Mean Absolute Deviation, Kolmogorov–Smirnov test, and Kullback–Leibler divergence—and forming an ensemble to integrate these measures. The aim is to classify the dataset and ensure each network flows efficiently. The classification is carried out graphically and probabilistically, making it easier to visualize the discrepancies between the observed frequencies of each digit and the empirical frequencies predicted by Benford’s Law.

In addition to calculating the p-value from each distance function, statistical inference was used for classification, using Bayes’ Theorem. This method aggregated the distance functions to calculate the overall p-value for each flow. Both this method and the subsequent one made it possible to compare the results with different degrees of statistical significance through hypothesis tests. The calculated p-value indicates the probability of obtaining a test statistic as extreme as the one observed, assuming the null hypothesis is accurate, and defines the lowest significance level for rejecting the null hypothesis based on the data analyzed.

After calculating the distances and p-values for each network flow, these data are stored in a matrix of values and subjected to a comparative analysis with different degrees of statistical significance. The methodology for classifying each flow as malicious or benign is based on the following hypotheses:

• $H_0:$ “The network flow is benign”;
• $H_1:$ “The network flow is malicious”.

If the p-value is less than the established significance level, there is strong statistical evidence to reject the null hypothesis, indicating that the network flow is malicious. The significance levels adopted were $0.1$, $0.01$, and $0.05$, following the standards usually recognized in the literature.

Table 4. Parameter settings used for the statistical tests.

Statistical Test	Parameters	Settings	Threshold Setting	Settings
Kolmogorov–Smirnov test	The significance level used was $0.05,0.01,0.1$. Sample size: 29,000 flows	The distribution of digit occurrence frequencies was calculated and compared with the empirical distribution of Benford’s Law. The KS test was applied to verify the most significant difference between the empirical cumulative distributions of the observed data and Benford’s Law.	A threshold value was established for the 1%, 5%, and $10\%$ significance levels.	p-values obtained lower than the critical value were considered malicious.
Kullback–Leibler divergence	$\epsilon ={10}^{-10}$ was added to all observed probabilities to avoid division by zero. The probabilities were normalized to add up to 1.	We calculated the probability distributions for the first digit of each feature in the dataset and Benford’s Law. The KL divergence was calculated to measure the difference between the observed distribution of digits and the distribution expected by Benford’s Law.
Mean Absolute Deviation	The first digit of the dataset was considered.	The KL divergence was calculated to measure the difference between the observed distribution of digits and the distribution expected by Benford’s Law.

details the configurations used, including the parameter settings for the statistical tests applied and the threshold values set for anomaly detection.

The results of the classification of each flow are stored in a .txt document, labelled 1 for flows classified as malicious and 0 for benign. These data are then contrasted with the actual classifications of each flow, making it easier to draw up a confusion table to assess the model’s accuracy.

4.2. Dataset

The experiments analyzed 29,000 network flows, consisting of 10,000 benign and 19,000 malicious flows, extracted from the CICIDS2017 dataset. This dataset includes network flows covering various attacks and benign flows and is available for consultation at [50].

The use of the CICIDS2017 dataset instead of more recent versions was due to several factors:

• High data quality and controlled environment: CICIDS2017 offers high-quality data captured in a controlled environment, guaranteeing the reliability and consistency of the results.
• Well-defined variety of attack types: The dataset presents an apparent diversity of attack types and precise labelling of flows as malicious or benign, allowing the results obtained by applying Benford’s Law to be compared with the original results, facilitating the classification of flows.
• Extensive use in previous studies: Numerous studies using CICIDS2017 allow for directly comparing the results obtained with those of other investigations. One example is Mbona’s work, which used CICIDS2017 with Benford’s Law for feature selection.

These flows were analyzed using the CICFlowMeter tool, version 3.0. This open-source software generates bidirectional records from pcap files and extracts features from them, determining the direction of packets from the first packet between source and destination [49]. The research was based on an unbalanced dataset to reproduce what happens daily in computer systems.

The flows were categorized as benign or malicious based on the type of attack, date and time, source and destination IPs, ports used, and protocols. These flows were then stored in .csv files. The dataset was captured between 9 a.m. on Monday (3 July 2017) and 5 p.m. on Friday (7 July 2017). Except for Monday, which only recorded benign traffic, the remaining days included benign and malicious flows.

Table 5. Quantity of flows extracted according to the type of activity for each day of the week.

Week Date	Type of Activity	Flows Extracted
Monday	Only benign flows	2000	-
Tuesday	Benign flows	2000	-
	FTP-Patator	-	2000
	SSH-Patator	-	2000
Wednesday	Benign flows	2000	-
	DoS/DDoS	-	2000
	DoS slowloris	-	2000
	DoS Slowhttptest	-	2000
	DoS Hulk	-	2000
	DoS GoldenEye	-	2000
Thursday	Benign flows	2000	-
	Web Attack—Brute Force	-	1000
	Web Attack—XSS	-	1000
	Web Attack—Sql Injection	-	1000
	Infiltration	-	1000
Friday	Benign Flows	2000	-
	DDoS LOIT	-	1000
Total:		10,000	19,000

summarizes the days of the week, the types of attacks, and the number of flows analyzed to make up the dataset used in the experiments.

The feature selection process was meticulously carried out in two crucial phases. In the first phase, features were extracted from the network traffic packets, while the second phase focused on selecting these features for the various studies. The initial feature extraction phase was carried out using the CICFlowMeter tool, version 3.0, generating realistic traffic for constructing the dataset. Sharafaldin [49] proposed the B-Profile system to create a profile of the abstract behavior of human interactions and generate naturalistic and benign traffic. To build the dataset, the behavior of 25 users was modelled based on the HTTP, HTTPS, FTP, SSH, and email protocols. Eleven criteria were identified: complete network configuration, traffic, labelled dataset, complete interaction, complete capture, available protocols, attack diversity, heterogeneity, resource set, and metadata.

The process of extracting characteristics in the initial phase began with capturing the packets travelling on the network, which were then grouped into flows according to criteria such as source and destination IP addresses, source and destination ports, and transport protocols (UDP, TCP, among others). For each network flow, CICFlowMeter determined a set of features that allow a detailed and differentiated description of the flow, such as:

• Time features: flow duration, time between packets (minimum, average, maximum time, and standard deviation).
• Size features: smallest, average, largest, and total packet size.
• Count features: total number of packets in the flow and count of TCP, UDP, and ICMP packets.
• Header features: number of TCP flags.
• Statistical features include the calculation of flow entropy, packet per second rate, and byte per second rate.

After extraction, the features were organized into flow records structured in tables. Each flow record represents a single network flow and includes all the calculated features. Finally, the flow records were stored in .csv format. More details on the extracted features are available on the GitHub [51] project.

In the second phase, the selection of features was based on calculating the Pearson correlation between the frequencies of occurrence of the first most significant digit and the empirical frequency of Benford’s Law. The numbers in the dataset were adjusted using the digit collapse procedure to avoid decimal numbers with leading zeros. This procedure made it possible to transform any decimal number with leading zeros into a decimal number whose significant digit differs from 0. After this adjustment, the most significant digit was extracted, and Pearson’s correlation was calculated. After this procedure, the selection of features was based on the correlation values obtained, from which the features with values of $70\%$ or above, $80\%$ or above, and $90\%$ were selected. These correlation values indicate a strong relationship between the variables, showing their natural dependence.

Two fundamental aspects justify this imbalance between benign and malicious flows. Firstly, in a natural context, malicious and benign events are disproportionate in size and frequency. Thus, a dataset that reflects this disproportion offers a more realistic and challenging test environment for developing intrusion detection systems, ensuring that models can operate effectively in natural environments. Studies such as [52] on the ROC curve in unbalanced environments show that models trained under such conditions can achieve more representative accuracy in detecting minority classes, which are often of greater interest.

On the other hand, an unbalanced dataset favors improvement in evaluating anomalous behavior. A model developed from an unbalanced dataset makes it possible to identify and analyze features potentially indicative of malicious activity. This process increases sensitivity in detecting new or rare forms of attack. In fact, ML techniques, such as those discussed by [53], which include oversampling methods such as SMOTE (Synthetic Minority Over-sampling Technique) and undersampling techniques, can be applied to adjust the class distribution without compromising the integrity of the data, thus maintaining effectiveness in detecting anomalies. Inspired by these studies, we sought to apply this principle to malicious flow detection using a purely statistical model.

4.3. Evaluation Metrics for Classification

Applying Benford’s law to the model resulted in a binary classification, assigning 1 to malicious network flows and 0 to benign ones. In this context, 1 is interpreted as a true positive and 0 as a true negative, forming two distinct classes. However, there are cases where a malicious flow can be wrongly classified as benign (false negative) or a benign flow as malicious (false positive). It is essential to evaluate the model’s performance considering these discrepancies, which is accomplished through the confusion matrix.

Table 6. Confusion matrix.

		Predicted Observation
		Positive	Negative
Real observation	Positive	Malicious network flow True positive (TP)	Malicious network flow rated as benign False negative (FN)
	Negative	Benign network flow rated malicious False positive (FP)	Benign network flow True negative (TN)

shows the confusion matrix customized for our analysis, as described in [32].

The relationship between True Positives (TP), True Negatives (TN), False Positives (FP), and False Negatives (FN) allows the model to be evaluated using a set of widely documented metrics used in machine learning models, including Accuracy, Precision, Recall, and F1-score, as detailed in [54].

5. Results of the Proposed Model

This section describes and discusses the results obtained using the model based on Benford’s law and the distance functions by analyzing the p-value for each distance function and using Bayes’ Theorem combined, according to the metrics defined in Section 4.3. These results were obtained by comparing the original labels of each flow in the network with those received after the data processing phase. The classification of flows into benign and malicious was obtained by comparing the p-value with the previously defined significance levels.

This research focused on identifying malicious flows in computer networks. It analyzed a dataset of 29,000 flows, of which 10,000 were benign and 19,000 malicious, covering various attacks. During the pre-processing phase, an analysis was conducted to determine which features adhered to Benford’s Law, as detailed in Section 4. Of the 78 features evaluated, 41 showed compliance with the law, as shown in

Table 7. General features that are in line with Benford’s Law.

Bwd Packet Length Mean	Fwd IAT Total	Flow IAT Mean	Packet Length Std
Flow Duration	Fwd IAT Mean	Flow IAT Std	Packet Length Variance
Total Fwd Packets	Fwd IAT Std	Flow IAT Max	Down/Up Ratio
Total Backward Packets	Fwd IAT Max	Subflow Fwd Packets	Avg Fwd Segment Size
Total Length of Fwd Packets	Fwd IAT Min	Subflow Fwd Bytes	Avg Bwd Segment Size
Total Length of Bwd Packets	Bwd IAT Total	Subflow Bwd Packets	Max Packet Length
Fwd Packet Length Mean	Bwd IAT Std	Subflow Bwd Bytes	Packet Length Mean
Fwd Packet Length Std	Bwd IAT Max	act_data_pkt_fwd	Flow Packets/s
Fwd Packet’s	Bwd Packet Length Std	Active Mean	Idle Std
Bwd Packet’s	Flow Bytes/s	Active Std	Active Max
Active Min

. These features were correlated with Benford’s empirical distribution for each digit.

The experiment was structured in different stages, according to the two phases described in Section 1, and was based on the correlation of these features with the data:

• First phase:

  -

  First Stage: Features with a correlation of $70\%$ or more were intriguingly grouped into Cluster 1, which indicates a substantial correlation between the observed frequencies.

  -

  Second Stage: Features with a correlation of $80\%$ or more were significantly grouped into Cluster 2, reflecting a strong correlation between the frequencies.

  -

  Third Stage: Finally, features with a correlation of $90\%$ or more were grouped into Cluster 3, highlighting a robust correlation. Each stage was meticulously planned to ensure a rigorous and detailed analysis of data trends by Benford’s Law.

  -

  Fourth Stage: A comparison was made between the number of features extracted by the method based on Pearson’s correlation and other methods based on distance functions. The results show that the correlation technique more effectively selects the ideal features for identifying malicious flows.

• Second phase:

  -

  An ensemble was developed from the p-values to maximize the detection of malicious flows, reducing the number of false positives and improving the evaluation of the model.

5.1. First Stage: Features with a Correlation of $70\%$ or More

All the network flows were then processed, resulting in the graphic shown in Figure 8. Graphical analysis reveals some discrepancies in the digits, particularly digits 2, 4, and 6. It can be seen that digits 2 and 4 occur less frequently than expected, while digit 6 appears more frequently than predicted by the empirical distribution. These discrepancies suggest the presence of malicious flows in the dataset. Pearson’s correlation was calculated to determine whether the dataset adheres to Benford’s Law, resulting in a value of $98.11\%$. This high percentage indicates that the dataset generally follows Benford’s Law. However, the anomalies observed in the graphics indicate flows that do not conform to this law, suggesting the existence of anomalous flows in the data.

Subsequently, the p-values of the distance functions were calculated, as detailed in Section 3, whose main objective in this initial phase of the investigation is the detection of potentially malicious flows.

Table 8. Results of the application of distance functions with Benford’s Law in Cluster 1.

Distance Function	Degree of Significance	TP	TN	FP	FN
MAD	0.05	3745	7495	15,255	2505
	0.01	0	10,000	0	19,000
	0.1	17,143	1726	8274	1857
KS test	0.05	8996	3826	6174	10,004
	0.01	4783	6026	3974	14,217
	0.1	13,504	2522	7478	5496
Kullback-Leibler	0.05	3053	8447	1553	15,947
	0.01	1126	9304	696	17,874
	0.1	3359	7841	2159	15,641

presents the results of these calculations, showing the p-values between the frequency of occurrence of each digit and the empirical frequency predicted by Benford’s Law for each distance function specified.

As shown directly in Table 8, the MAD and KS distance functions proved to be the most effective in detecting malicious flows, with success rates of $90.22\%$ and $68.71\%$, respectively, with a significance level of 0.1. The main difference between these two methods lies in each method. The MAD, a measure of dispersion, indicates how much the data deviate from the central value, usually the median. On the other hand, the KS test, commonly used to compare two independent samples, in our case, compares the frequency of occurrence of the digits with the empirical frequency of Benford’s Law to check whether the samples come from the same distribution.

Regarding sensitivity, the MAD is less affected by extreme outliers due to its direct and simple calculation methodology, as long as these outliers are not dispersed among the digits, as seen in Table 9. The KS test, which compares two distributions, can be more sensitive to the presence of outliers if they are concentrated in a single digit and ultimately requires a deeper understanding of the test statistics. This knowledge is easily manageable in a closed network environment but may be inadequate in real environments.

Table 9 shows that the Mean Absolute Deviation (MAD) provides superior results, followed by the Kolmogorov–Smirnov (KS) test. From the values shown in the table, it can be seen that MAD under-performs in detecting benign flows when the frequencies of occurrence of the numbers follow an almost uniform distribution, resulting in erroneous decisions, such as false positives. However, MAD’s performance improves significantly when detecting genuinely malicious flows. On the other hand, the KS test tends to make better decisions under conditions of almost uniform distribution. However, it fails more often when the frequencies are high in the first digit or when they are randomly dispersed across the digits, which can lead to an increase in false negatives, a potentially more damaging situation than the occurrence of false positives.

The visual representation in Figure 9 clearly illustrates the deviation from Benford’s Law in flow 30. The observed frequencies, which are almost uniformly distributed, lead to an incorrect decision by the Mean Absolute Deviation (MAD). This visual evidence underscores the importance of considering the distribution of occurrence frequencies in anomaly detection.

Although the KL distance function could have been more effective in detecting malicious flows, it proved highly accurate in identifying benign flows. The KL measure evaluates the amount of information lost when trying to approximate a data distribution (in this case, the frequency of occurrence of the digits in each network flow) by another reference distribution (the empirical frequency of Benford’s Law). Because it is sensitive to differences, especially in the tails of the distributions, KL can produce worse p-values when these differences are accentuated. In addition, the centrality of the data in the first two or three digits can adversely affect KL, even if the subsequent frequencies overlap in a typical way. KL’s sensitivity to slight variations in probability density, mainly where the frequency of occurrence is more prevalent, also contributes to its inferior performance in the presence of outliers.

Table 9. Comparing the decisions of the different distance functions and the original data labels.

Digits and Flows	2	30	18,342	18,361
1	0.5789	0.3333	0.2857	0.3429
2	0.2105	0.1389	0.1714	0.2286
3	0	0.1014	0.1143	0.0571
4	0	0.1667	0.1429	0.0286
5	0	0.0278	0.0571	0.1143
6	0.2105	0.0556	0.0286	0
7	0	0.0833	0.0857	0.1143
8	0	0.0278	0.0286	0.1143
9	0	0.0278	0.0857	0
MAD	0	1	1	1
KS	1	0	1	0
KL	1	0	0	0
Original Label	0	0	1	1

Table 9. Comparing the decisions of the different distance functions and the original data labels.

Digits and Flows	2	30	18,342	18,361
1	0.5789	0.3333	0.2857	0.3429
2	0.2105	0.1389	0.1714	0.2286
3	0	0.1014	0.1143	0.0571
4	0	0.1667	0.1429	0.0286
5	0	0.0278	0.0571	0.1143
6	0.2105	0.0556	0.0286	0
7	0	0.0833	0.0857	0.1143
8	0	0.0278	0.0286	0.1143
9	0	0.0278	0.0857	0
MAD	0	1	1	1
KS	1	0	1	0
KL	1	0	0	0
Original Label	0	0	1	1

After analyzing the results, it is possible to evaluate the model’s performance considering metrics such as precision, recall, F1-score, and accuracy, whose values are shown in

Table 10. Results of the model evaluation for cluster 1.

Distance Function	Precision	Recall	F1-Score	Accuracy
MAD ($0.1$)	0.6745	0.9023	0.7719	0.6507
KS test ($0.1$)	0.6436	0.7107	0.6755	0.5526
Kullback–Leibler ($0.05$)	0.6628	0.1607	0.2587	0.3966

, corresponding to the significance levels that obtained the best results. Analyzing Table 10, it can be seen that the Mean Absolute Deviation is the distance function that best fits the model, as evidenced by the F1-Score of $77.19\%$, superior to the performance of the other distance functions.

5.2. Second Stage: Features with a Correlation of $80\%$ or More

In the second stage, only the features with a correlation of $80\%$ or more were selected, reducing the initial number from 41 to 27.

Table 11. Features with a correlation greater than or equal to $80\%$.

Flow Packets/s	Bwd IAT Max	Flow IAT Mean	Packet Length Std
Flow Duration	Fwd IAT Mean	Flow IAT Std	Packet Length Variance
Total Fwd Packets	Fwd IAT Std	Active Std	Down/Up Ratio
Total Backward Packets	Bwd IAT Total	Subflow Fwd Packets	Idle Std
Total Length of Fwd Packets	Bwd IAT Std	Subflow Fwd Bytes	Bwd Packet’s
Total Length of Bwd Packets	Bwd Packet Length Std	Subflow Bwd Packets	act_data_pkt_fwd
Fwd Packet’s	Flow Bytes/s	Subflow Bwd Bytes

shows the new features obtained from a correlation of $80\%$ or more.

The graphical analysis of this phase did not reveal any significant changes compared to the first phase’s graphic, as seen in Figure 10.

The results derived from the three distance functions are detailed in

Table 12. Results of the application of distance functions with Benford’s Law in cluster 2.

Distance Function	Degree of Significance	TP	TN	FP	FN
MAD	0.1	16,389	1788	8212	2611
KS test	0.1	13,504	2522	7478	5496
Kullback–Leibler	0.05	2715	8290	1710	16,285

, where we focus on the results with the best scores. It can be seen that these values are in line with those presented in Table 8. The values obtained by the Mean Absolute Deviation consistently exceed those generated by the Kolmogorov–Smirnov (KS) and Kullback–Leibler (KL) distance functions.

Concerning the model’s performance metrics, including precision, recall, F1-score, and accuracy,

Table 13. Results of the model evaluation for cluster 2.

Distance Function	Precision	Recall	F1-Score	Accuracy
MAD ($0.1$)	0.6662	0.8626	0.7518	0.6268
KS test ($0.1$)	0.6436	0.7107	0.6755	0.5526
Kullback–Leibler ($0.05$)	0.6136	0.1429	0.2318	0.3795

shows the values achieved for the significance levels with the best results.

As shown in Table 13, the Mean Absolute Deviation continues to be the most suitable distance function for the model, demonstrated by an F1-Score of $75.18\%$, which is superior to the performance of the other distance functions. However, there is a slight reduction in the detection of malicious flows, which moderately affects the model’s performance due to the increase in false positives. This is because, with the reduction in the number of features, the frequency of occurrence of the digits tends to increase and become more widely distributed among the remaining digits.

5.3. Third Stage: Features with a Correlation of $90\%$ or More

In the third stage, only features with a correlation of 90 percent or higher were considered, reducing the initial number from 27 to 20. The focus was to investigate whether features with robust correlations improve the detection of malicious flows, given that a correlation above $90\%$ makes it possible to assess the extent of adherence to Benford’s Law more accurately. Similarly to Figure 8 and Figure 10, the graphic generated from the features with almost perfect correlation does not reveal significant differences that confirm full compliance with the frequencies expected by Benford’s Law, although the distances are smaller, as can be seen from Figure 11. This observation suggests that, despite the high correlation, the data may not perfectly follow the predictions of the law, which implies the need for a more detailed analysis to understand the discrepancies observed.

Significant deviations between the frequencies observed and those expected by Benford’s Law can suggest anomalies, intrusions, or even system failures. A near-perfect correlation between observed and expected frequencies is expected to improve the accuracy of predictions, providing a clearer understanding of network activity. Meanwhile, correlations of $70\%$ and $80\%$, although considered strong, may indicate the existence of different probability distributions in the analysis, given that the proximity between the frequencies obtained and those expected does not suggest a clear distinction between abnormal behavior and that considered normal. Many studies have shown that characteristics with a strong correlation with Benford’s Law can indicate data behavior that is more consistent with Benford’s Law and, in turn, more natural. The application of these studies has allowed patterns to be identified, particularly in diverse fields such as genetics, which indicate the presence of irregularities but, in many cases, require further investigation. At this stage, the aim is to understand how the data behave in the face of near-perfect correlations with Benford’s Law and whether such correlations contribute to better efficiency in detecting malicious flows.

Table 14. Features with a correlation greater than or equal to $90\%$.

Flow Duration	Bwd Packets/s
Total Backward Packets	Packet Length Std
Total Length of Fwd Packets	Packet Length Variance
Bwd Packet Length Std	Subflow Fwd Packets
Flow Bytes/s	Subflow Bwd Packets
Flow Packets/s	act_data_pkt_fwd
Flow IAT Mean	Active Std
Flow IAT Std	Idle Std
Fwd IAT Mean	Bwd IAT Std
Fwd IAT Std	Fwd Packets/s

and

Table 15. Results of the application of distance functions with Benford’s Law in cluster 3.

Distance Function	Degree of Significance	TP	TN	FP	FN
MAD	0.1	15,757	1938	8062	3243
KS test	0.1	13,504	2522	7478	5496
Kullback-Leibler	0.05	2735	8197	1803	16,265

summarize the features that showed a correlation of $90\%$ or more and the results obtained by distance functions.

Analyzing Table 15 and comparing with Table 12, we see a modest reduction of less than $3.9\%$ in detecting malicious flows, contrasting with a considerable increase of approximately $20\%$ in cases where malicious flows were wrongly classified as benign. This situation is worrying in a forensic analysis context of detecting anomalies or intrusions in computer networks, suggesting that the high correlation with Benford’s Law may not necessarily translate into better model performance. A plausible explanation for this phenomenon could be the similarity between the frequencies observed in benign and malicious flows, making it difficult for the model to distinguish between them effectively.

Table 16. For example, four flows, two benign and two malicious, are compared, as well as the frequency of each digit’s occurrence. The analysis includes the decision made by the model, which is contrasted with the original classification of each flow to determine the model’s effectiveness in correctly identifying the benign and malicious nature of the flows analyzed.

	Flow	1	2	3	4	5	6	7	8	9	Decision by MAD 0.1	Original Label
Benign	2	0.6667	0.3333	0	0	0	0	0	0	0	0	0
	81	0.5384	0	0.1538	0.0769	0	0.0769	0.1538	0	0	1	0
Malicious	23777	0.6250	0	0.125	0	0	0.25	0	0	0	0	1
	28690	0.5000	0.2500	0	0	0.0833	0	0.1666	0	0	1	1

exemplifies this situation by showing two flows, benign and malicious, respectively, with their observed frequencies compared to those expected by Benford’s Law and the decisions resulting from the model.

When we analyze the distance function of the Mean Absolute Deviation in more detail, we see, as shown in Table 16, that high frequencies of occurrence in the first digit often lead the model to incorrectly classify originally malicious flows as benign. This pattern is worrying and suggests a vulnerability of the model to false negatives, significantly when the frequency of the first digit exceeds $60\%$. This behavior deviates considerably from the frequencies expected by Benford’s Law, increasing the risk of the model generating numerous false positives or false negatives.

This analysis highlights the need for adjustments to the model to improve its accuracy and reliability in detecting threats. Two different approaches were implemented in this context, giving rise to the fourth and fifth stages. The first approach involved analyzing selected features following methodologies documented in the literature [6]. The second approach sought to improve the robustness of the analysis by combining the p-values derived from the distance functions, creating an ensemble of p-values. As recommended in the literature, two statistical techniques were used: the Fisher and Tippett techniques, both recognized for their effectiveness in combining statistical evidence from multiple tests. These approaches aim to identify abnormal patterns in the analyzed data, thereby improving the model’s accuracy in detecting malicious flows.

Regarding the first approach and following the research by Mbona, we found that the author integrated seven features that had not been considered in our study, as seen in

Table 17. Features suggested by Mbona and their correspondence with our research findings.

Flow Duration	Packet Length Mean
Fwd Packet Length Mean	Packet Length Std
Fwd Packet Length Std	Packet Length Variance
Bwd Packet Length Mean	Avg Fwd Segment Size
Flow Bytes/s	Avg Bwd Segment Size
Flow Packets/s	Subflow Fwd Packets
Flow IAT Mean	Subflow Fwd Bytes
Flow IAT Std	Subflow Bwd Packets
Fwd Packets/s	Avg Fwd Segment Size
Max Packet Length	Avg Bwd Segment Size

and

Table 18. Features suggested by Mbona that were not included in our research.

Features	Correlation	Features	Correlation
Bwd Packet Length Min	$24.91\%$	Bwd Avg Packets/Bulk	-
Flow IAT Min	$66.22\%$	Bwd Avg Bulk Rate	-
Average Packet Size	$69.13\%$	Init_Win_bytes_backward	$44.33\%$
Fwd Avg Bytes/Bulk	-

. The exclusion of these features in our study was because they presented either exclusively zeros or ones or because the correlation between the frequency of occurrence of each digit and the frequency expected by Benford’s Law was below the 70 percent threshold established by us. However, to assess the relevance of including these features, we incorporated them, as Mbona suggested. Figure 12 illustrates that, although there is apparent adherence to the expected frequency for digit 1, lower results are observed for digits 2 and 6, where the differences are more marked. There are also more minor deviations for digits 3, 8, and 9. As for the results, analyzing

Table 19. Results achieved using the features identified by Mbona.

Distance Function	Degree of Significance	TP	TN	FP	FN
MAD	0.1	15,686	1905	8095	3314
KS test	0.1	12745	3998	6002	6255
Kullback–Leibler	0.05	3235	7978	2022	15,765

reveals no significant changes compared to previous evaluations, suggesting that the features proposed by Mbona can be optionally omitted from future analyses.

Regarding the evaluation of the proposed model,

Table 20. Results of the model evaluation for the features proposed by Mbona.

Distance Function	Precision	Recall	F1-Score	Accuracy
MAD ($0.1$)	0.6596	0.8256	0.7333	0.6066
KS test ($0.1$)	0.6798	0.6708	0.6753	0.5773
Kullback–Leibler ($0.05$)	0.6154	0.1703	0.2667	0.3867

shows the results obtained with the new features, aligning closely with the initial predictions of our research.

5.4. Fourth Stage and Second Phase: Method Combining the Three Distance Functions, Benford’s Law, and Bayes’ Theorem

The second approach proposed combined the multiple p-values obtained through the distance functions, resulting in an overall p-value. In developing this p-value, two consolidated statistical methodologies were used to aggregate evidence in multiple tests: the Fisher and Tippett methods [46,48]. In addition, Bayes’ Theorem was used as the primary classification mechanism. On the other hand, after comparing the results of the model evaluation in clusters 1, 2, and 3, we chose to generate the ensemble based on the data from cluster 2, which proved to be the most promising. In this context, $35\%$ of the flows analyzed were identified as benign and $65\%$ as malicious. Figure 13 shows the decision tree developed using Bayes’ Theorem, detailing the classification process used.

Figure 13 illustrates the use of Bayes’ Theorem to classify malicious and benign flows. A Prior variable was created, representing the proportion of malicious flows in the dataset. Combining the results of the three distance functions made it possible to calculate a p-value for each flow based on the frequency of the digits originating from the initial p-values. Subsequently, the Fisher and Tippett methods generated a global p-value, allowing us to decide on the nature of each flow by comparing it with standard significance thresholds.

Table 21. Detection of malicious and benign flows using Bayes’ Theorem in conjunction with Fisher’s and Tippett’s methods to generate a global p-value for network flow classification.

	$\mathit{\alpha }$	TP	TN	FP	FN
Fisher method	0.05	8733	5360	4640	10,267
	0.01	4136	7622	2378	14,864
	0.1	12,885	3134	6866	6115
Tippett method	0.05	18,890	204	9796	110
	0.01	2448	9211	789	16,552
	0.1	19,000	0	10,000	0

details the results achieved after implementing this original method.

Table 21 compares the results obtained by applying the Fisher and Tippett methods to detect malicious flows. The Tippett method, which selects the lowest p-values, proved more effective in identifying malicious flows due to its less conservative nature. Table 21 shows that the method achieved high detection rates for malicious flows but a low hit rate for benign flows, with efficiencies of $99.42\%$ and $2.04\%$, respectively. The presence of false positives is relatively high, with a rate of $97.96\%$, in contrast to the presence of false negatives, with a rate of $0.57\%$, at a significance level of $0.05$. This method becomes helpful in scenarios where a single significant test is enough to validate the network flow analysis, resulting in a high detection rate of malicious flows, although with less accuracy in identifying benign flows. On the other hand, Fisher’s method, which adds up the logarithms of the p-values and applies the Chi-squared distribution to calculate an overall p-value, shows greater sensitivity when all the individual p-values are low. Table 21 shows that the method achieved detection rates of $67.81\%$ for malicious flows and $31.34\%$ for benign flows, at a significance level of $0.1$, making it more balanced than the Tippett method. However, there was a significant increase in both the number of false positives and the number of false negatives. This behavior makes it more suitable for situations that require a consistent evaluation of multiple pieces of evidence but can lead to less accurate decisions if the data are not uniformly significant.

In evaluating the model,

Table 22. Model evaluation results were obtained from creating an ensemble using the Fisher and Tippett methods and applied to cluster 3.

Ensemble Method	Precision	Recall	F1-Score	Accuracy
Fisher method ($\alpha =0.1$)	0.6524	0.6782	0.6650	0.5524
Tippett method ($\alpha =0.05$)	0.6585	0.9942	0.7923	0.6584

shows the results achieved by the Fisher and Tippett methods, highlighting the most effective classifications as indicated in Table 21. Analyzing the table, it is clear that Tippett’s method outperforms Fisher’s, achieving an F1 score close to $80\%$ and showing slightly better accuracy. It can, therefore, be concluded that Tippett’s method is more suitable for the problem being analyzed.

6. Conclusions and Future Work

Developing faster and more efficient techniques that consume less energy and computing resources has been vital in supporting forensic teams in detecting anomalies or intrusions in computer networks. Over the last few years, this field has seen significant progress, although with advances in the application of purely statistical techniques to the detriment of the massive use of models based on machine learning. The method we propose, based on Benford’s Law and documented in various studies, particularly in financial auditing and accounting, aims to create a balanced, fast, and efficient model for detecting potentially malicious network flows. This model is based on advanced statistical techniques, including distance functions such as the mean absolute deviation, the Kolmogorov–Smirnov test, and the Kullback–Leibler divergence, which serve as robust measures of dispersion to quantify the magnitude of anomalies detected in the flows of a computer network. In addition, we integrated Bayes’ Theorem with the three distance functions mentioned to develop a model that generates a single global p-value. This model makes it possible to identify discrepancies in the digits, making it easier to conclude the nature of the flows analyzed—whether malicious or benign. The research was conducted using the CIC-IDS2017 public dataset.

The research carried out in this study was structured into five phases, focusing on the correlation of features with the data and the implementation of an ensemble to generate a global p-value, classifying network flows as malicious or benign. In the first phase, we selected features with a correlation of at least $70\%$ with Benford’s Law. The results indicated that the mean absolute deviation was more effective in detecting malicious flows, identifying 17,143 out of 19,000 malicious flows. The Kolmogorov–Smirnov (KS) test also showed high performance, detecting 13,504 malicious flows. In contrast, the Kullback–Leibler (KL) test was less effective at detecting malicious flows but showed high accuracy in identifying benign flows. As discussed in Section 5, these results reflect the frequencies of occurrence of each digit, where higher frequencies in the first digit suggest benign flows and a more even distribution between digits can result in false positives or negatives. This leads to the model performing worse when compared to ML-based models.

In the second phase, we only considered features with a correlation of at least $80\%$. The results obtained by the mean absolute deviation remained higher, although there was a slight reduction in the detection of malicious flows and an increase in false positives and negatives. In the third and fourth phases, we focused on features with a correlation greater than or equal to $90\%$, observing results similar to those of the second phase. These indicate that using features strongly correlated with Benford’s Law can deteriorate the detection of malicious flows, influenced by the proximity or dependence between the features used.

A high false positive rate was observed in many of the proposed scenarios, where the model classified specific benign flows as potentially malicious. A high false positive rate overloads network administrators, generating many alerts that result in unnecessary allocation of resources, such as time and effort, to investigate threat scenarios that are not real. This process can lead to network administrators becoming desensitized to the alerts generated, increasing the risk of overlooking genuine alerts. The model proposed in this study uses a set of adjustable thresholds (significance levels) for detecting malicious flows, making it possible to calibrate the model to reduce the false positive rate without compromising its sensitivity. About false negatives, the rate was low in almost all the scenarios analyzed. False negatives represent a high security risk, since real attacks can go undetected. The combination of distance functions, namely the mean absolute deviation, Kolmogorov–Smirnov test, and Kullback–Leibler divergence, increased the model’s robustness, helping keep the false negative rate low.

Future research should explore the initial identification of features that have little dependence on each other but still show a strong correlation with Benford’s Law. In addition, compared to other studies, the correlation-based method extracted fewer features, producing more effective results when applied to the Benford’s Law-based model.

In the last phase of the study, an ensemble was developed combining the p-values to assess the effectiveness of the Benford’s Law-based model in detecting malicious and benign flows. This ensemble was based on two methods, Fisher and Tippett, with the Tippett method showing the best results. Evaluating the model based on Benford’s Law in conjunction with distance functions, it was possible to achieve an F1-score close to $80\%$ with a recall of $99.42\%$. However, the model’s precision and accuracy were lower than expected, approximately $65\%$, a result influenced by the proximity in the frequencies of occurrence of each digit.

Although this model’s results are lower than those of the usual machine learning (ML) techniques, several factors should be considered, such as the model’s speed and the low consumption of computational resources, which essentially highlight the high detection rates of malicious flows. These aspects underline the model’s significant potential in practical applications where efficiency and speed are crucial, with promising results despite being inferior. One possibility for improving the proposed model could be to integrate it into various existing security systems, such as intrusion detection systems (IDSs) and security information and event management systems (SIEM). Whether integrated into IDS or SIEM, the model can be incorporated into tools like Snort or Splunk via specific plugins or modules. These plugins or modules can monitor and analyze network flows based on Benford’s Law, adding an extra layer of security in detecting potentially malicious flows.

The method proposed in this study detects malicious flows in a network and can be seamlessly integrated into existing security systems, significantly improving threat protection and response capabilities in various scenarios. These scenarios include:

Corporate Networks:

• Detection of Fraudulent Financial Activities: The model will be able to identify possible fraudulent financial activities, detecting fraudulent transactions that do not follow the frequency of occurrence of the digits based on Benford’s Law.
• False Positive Reduction: Adjusting detection thresholds based on digit analysis may reduce the false positive rate, allowing network administrators to focus on real threats.
• Integration with Accounting and ERP Systems: Integrating the model into accounting and ERP (Enterprise Resource Planning) systems will enable real-time and continuous monitoring of financial activities.

Industrial Control Systems:

• Critical Infrastructure Protection: The method will detect malicious activity in critical infrastructures like energy and telecommunications by analyzing SCADA (Supervisory Control and Data Acquisition) data flows.
• Analyzing industrial protocols: The proposed model makes it possible to detect flows resulting from injection attacks by analyzing the traffic obtained from the Modbus and DNP3 (Distributed Network Protocol 3) protocols.

Critical Infrastructures:

• Anomaly Detection in Water and Sanitation Systems: The model could be used to identify possible anomalies in sensors or control systems, guaranteeing the safety and continuity of operations in them.

In future research, we plan to reduce the dependency between the extracted features and introduce two new distance functions: the Chi-squared distance function and the Euclidean distance. In addition, we will explore the model’s applicability to Zipf’s Law to assess the coherence between the results under these two laws in contexts of the forensic analysis of computer networks. Finally, we intend to improve the model by incorporating unsupervised machine learning techniques to reduce high false positive rates.