A Study on Effects of Species with the Adaptive Sex-Ratio on Bio-Community Based on Mechanism Analysis and ODE
Abstract
:1. Introduction
- (1)
- Use mechanism analysis and the relevant ODE models to construct the ODE environmental model to simulate the evolution of the bio-community under one species’ different male–female sex ratios. This model consists of various factors, and the numerical solution actually means the densities of various species;
- (2)
- Given different living environments during one species’ lifecycle, the ODE environmental model is optimized. The relative standard deviation and the phase-track maps are chosen to explore the effects from the perspective of quantitative analysis;
- (3)
- Given different living environments in one species’ lifecycle, the ODE environmental model is optimized. The relative standard deviation and the phase-track map are chosen to explore the effects from the perspective of quantitative analysis;
- (4)
- Finally, putting lamprey in the optimal model, speeds at which equilibrium points in corresponding phase-track maps are reached and the values of the volatility depicted by relative standard deviation can be gained to compare the stability states of the bio-communities in different environments of lifecycle and the corresponding male–female sex-ratios of lamprey. Based on this, the effects can be figured out, and some problems in the relevant bio-communities can obtain some directive options.
2. The Construction of the ODE Environmental Model and Instantiation
2.1. The Conception of the ODE Environmental Model
2.2. The Conception of the Optimal ODE Environmental Model
2.3. The Superiority of Using Lamprey as an Example of Instantiating the Models
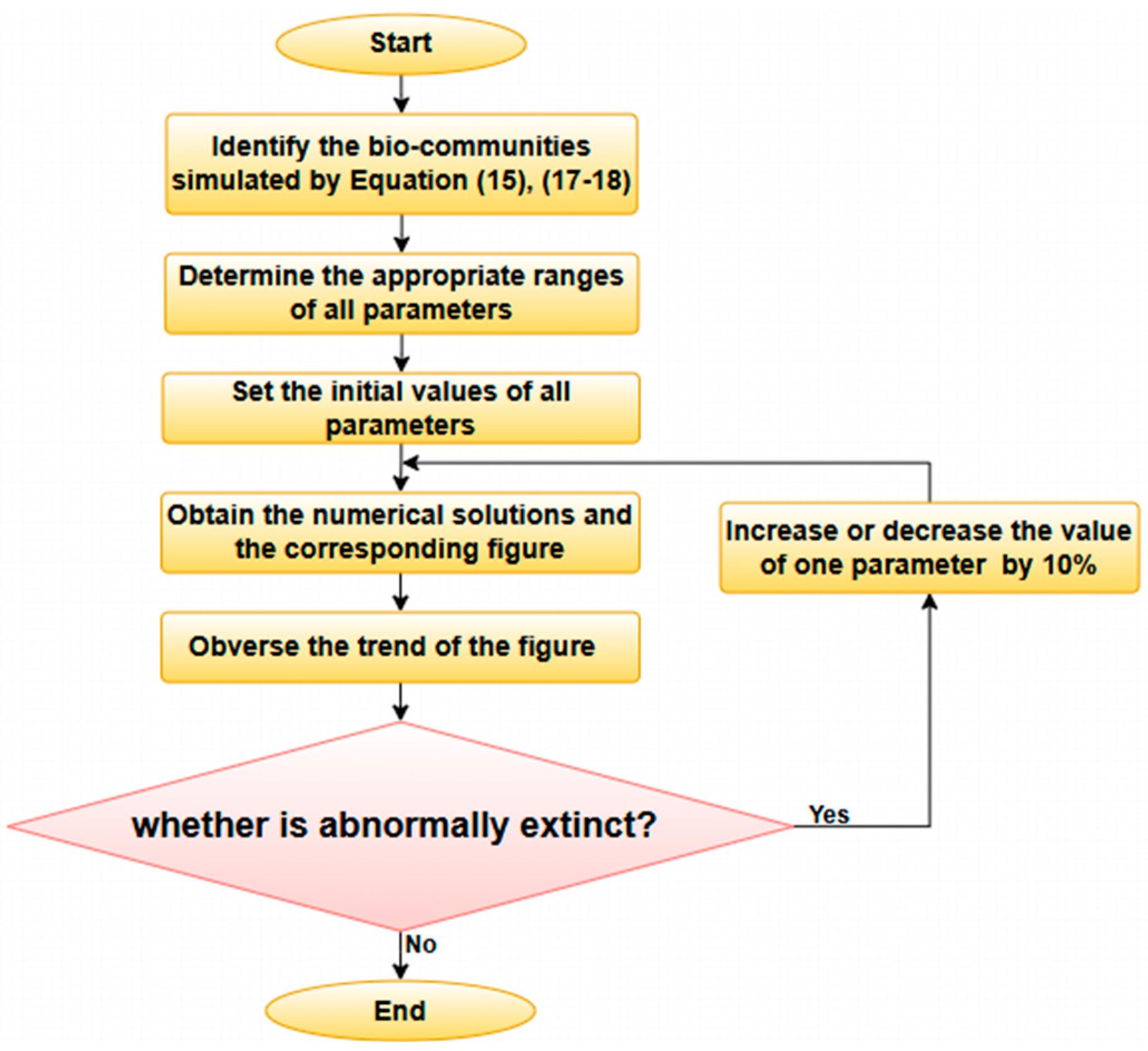
3. Model Validation
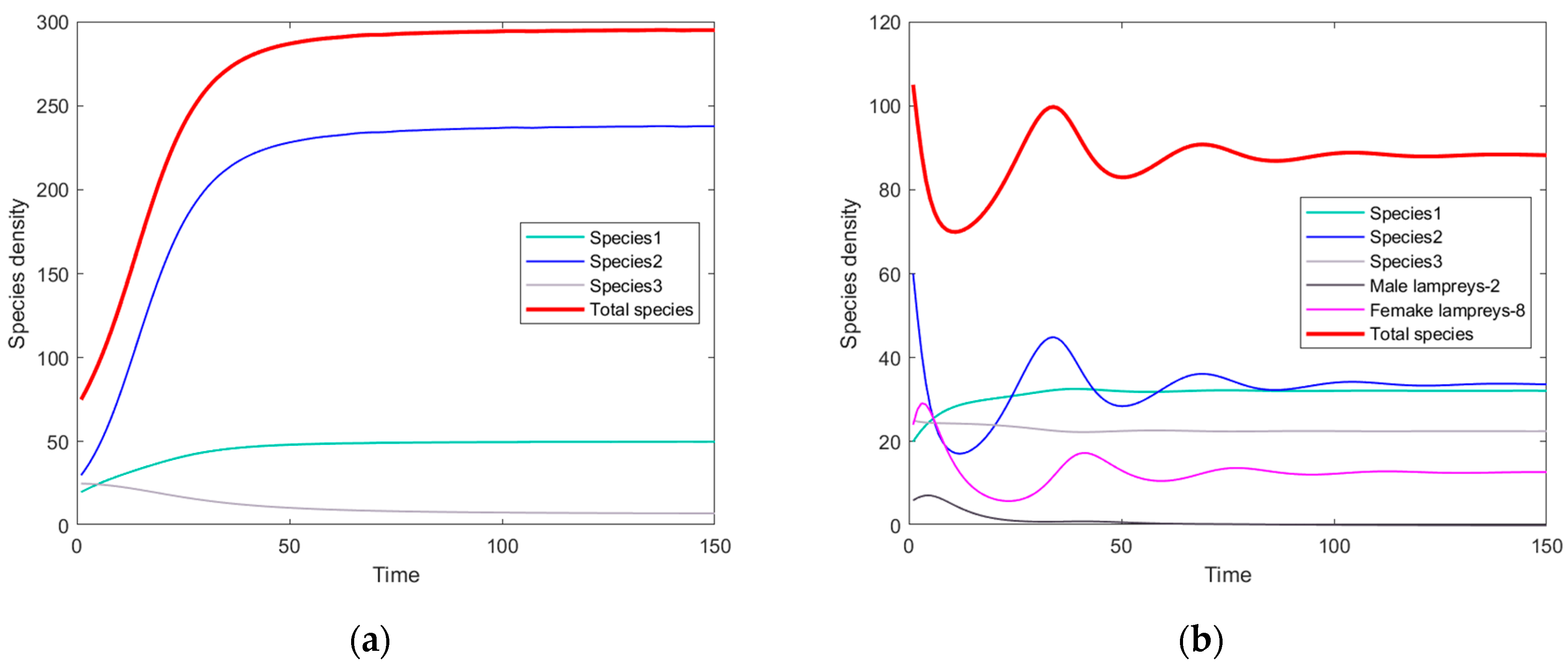
3.1. The Simulation Result of the ODE Environmental Model
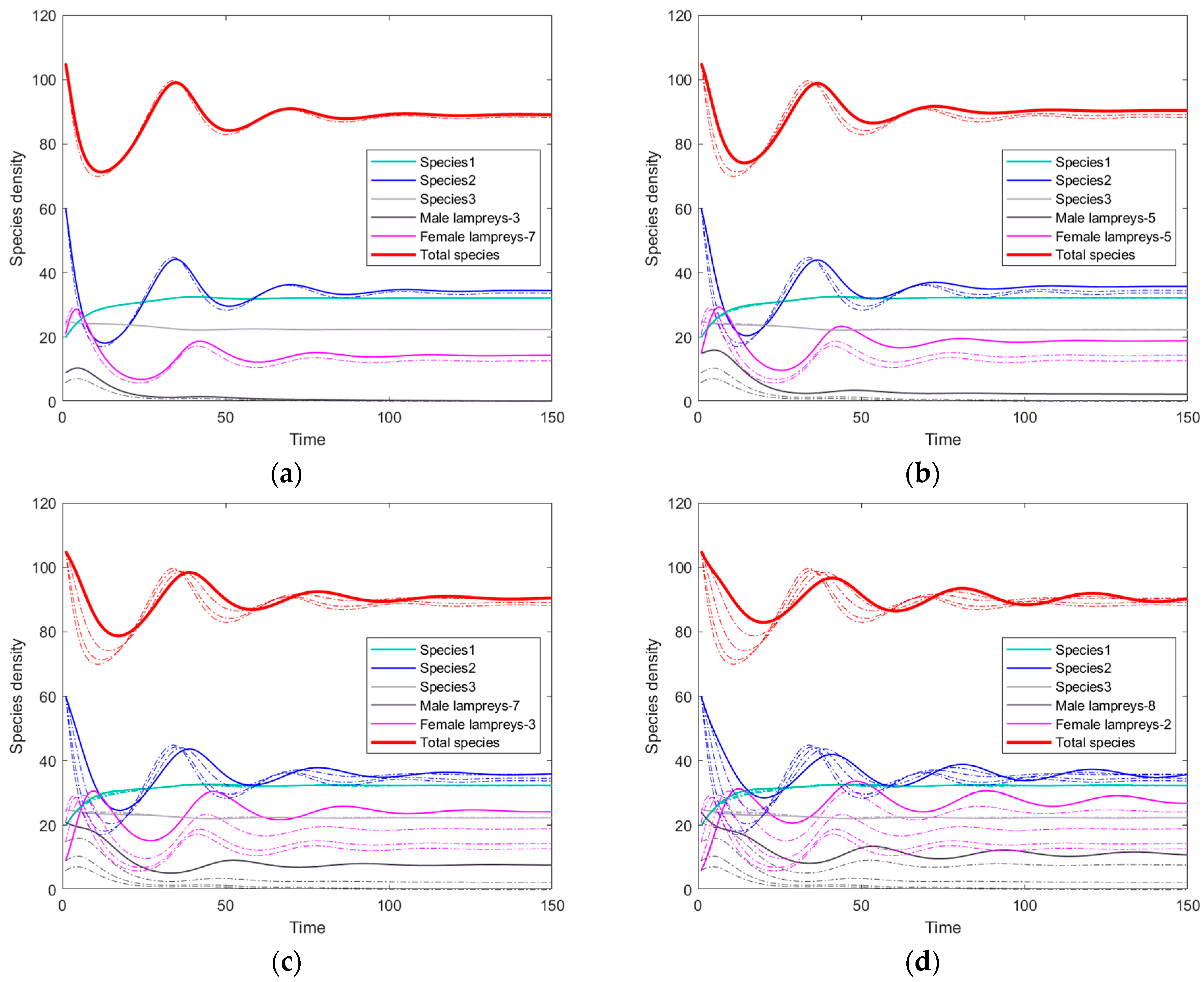
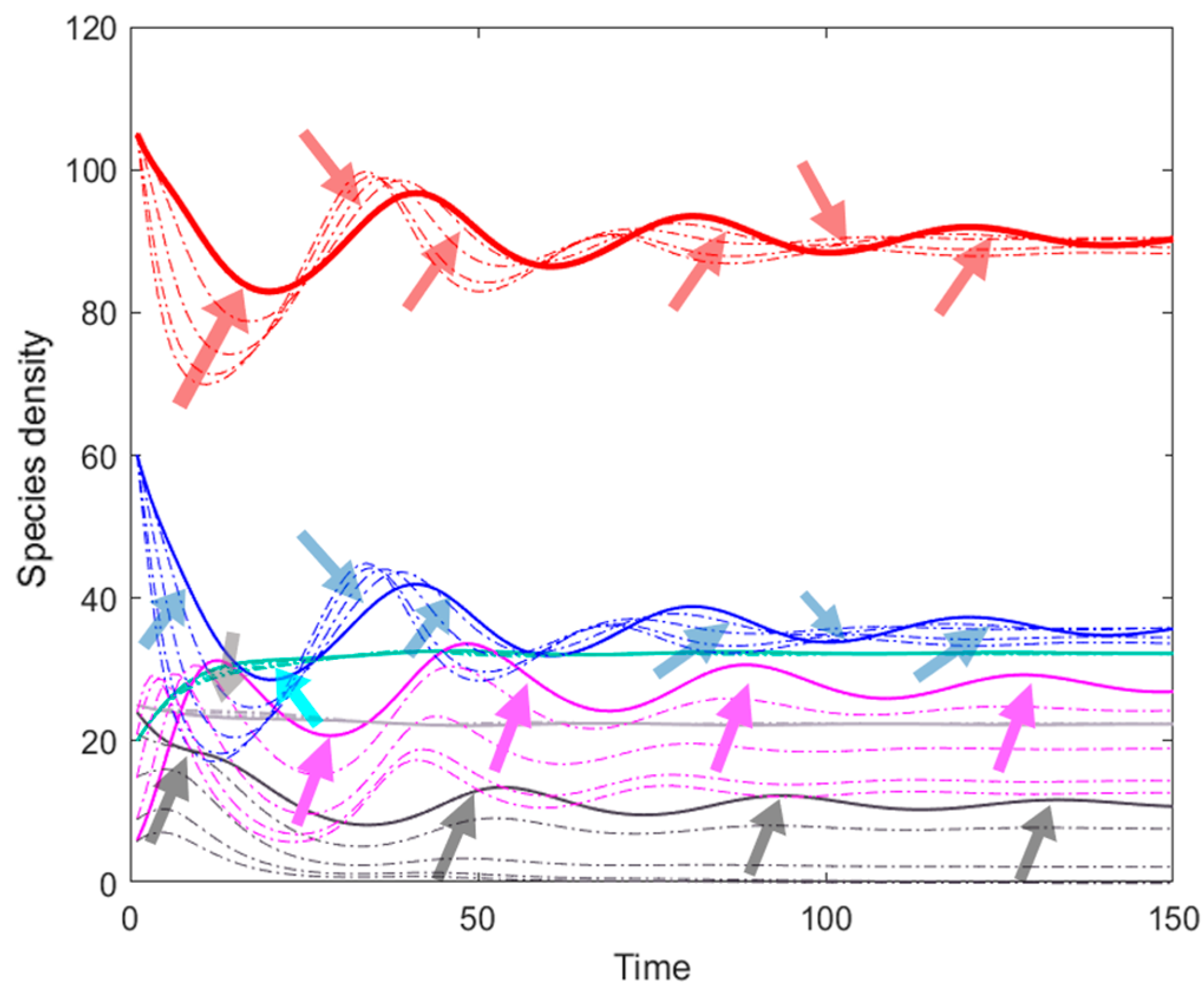
3.2. The Simulation Result of the Optimal ODE Environmental Model
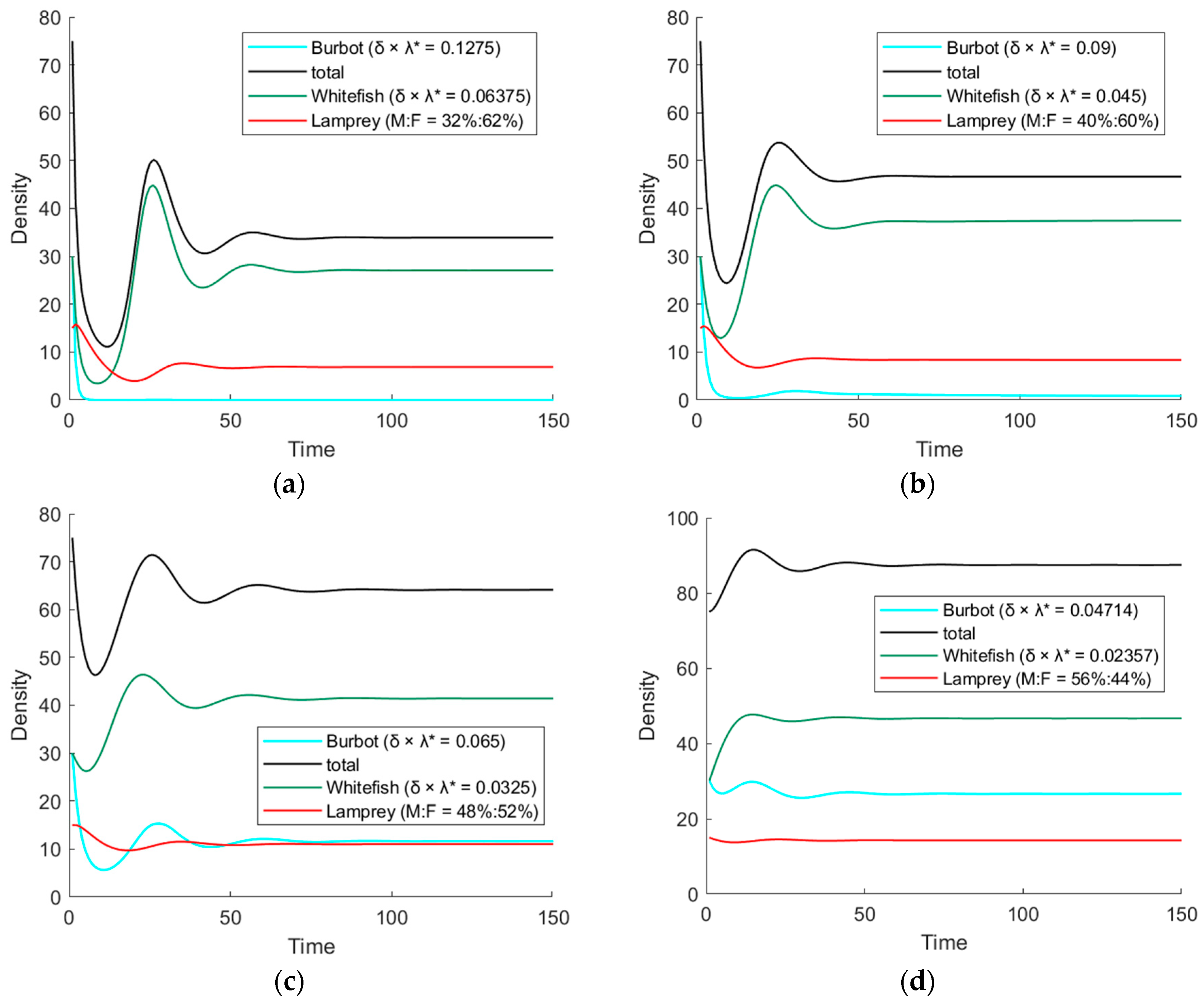
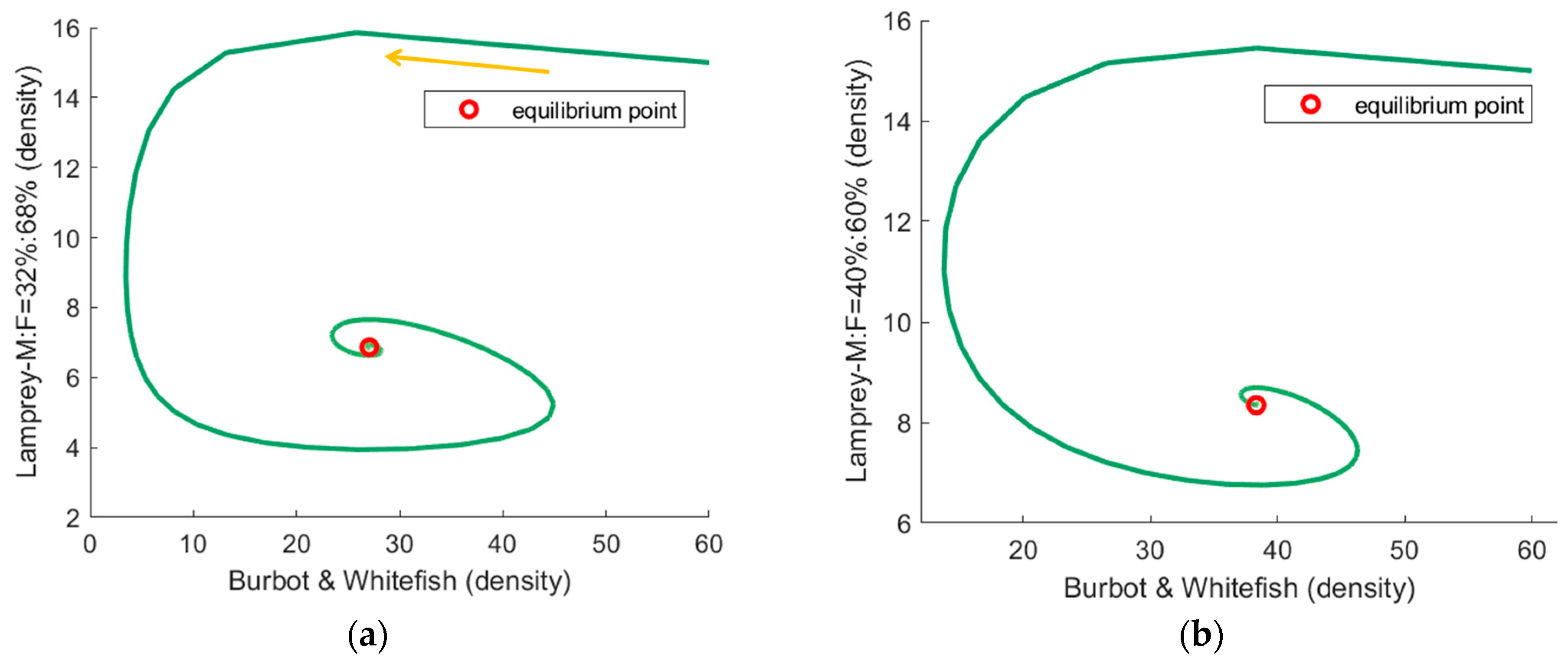
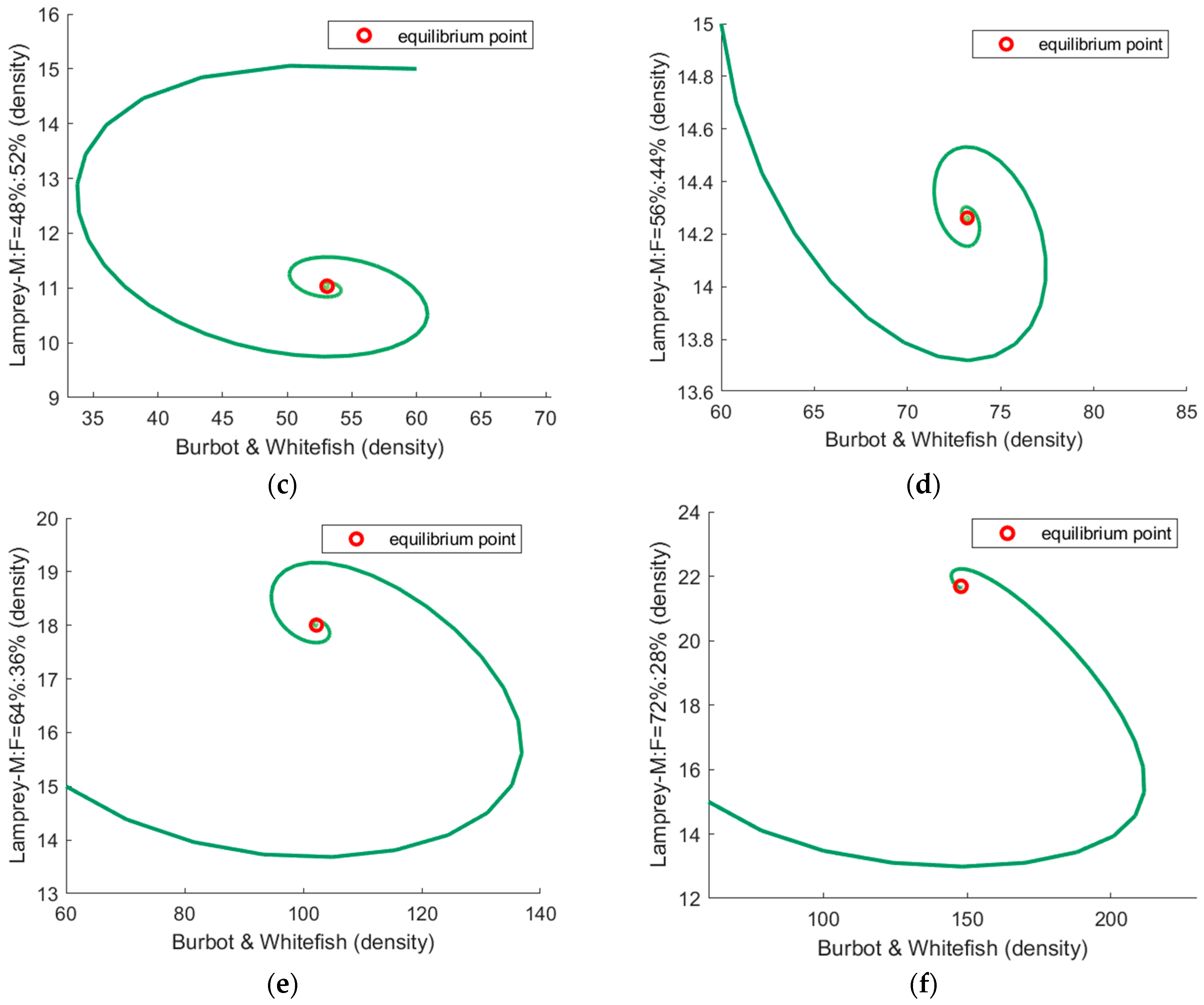
3.2.1. Stocks in Riverine Environments
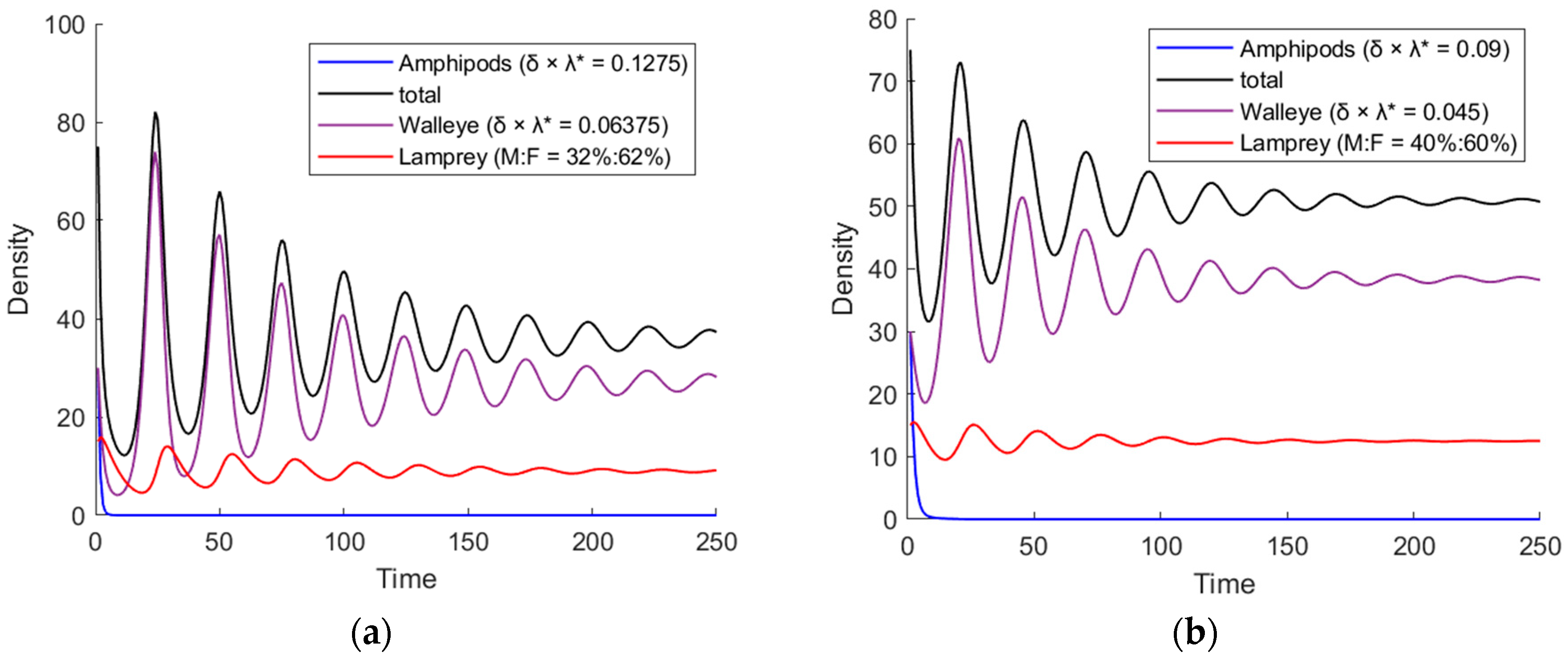
3.2.2. Stocks in Marine Environments
4. Discussion
5. Conclusions and Outlooks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yan, H.; Liang, L.; Chang, Y.; Sun, B.; Su, B. Effects of inheritance and temperature on sex determination and differentiation related genes and sex ratio in fish: A review. J. Dalian Ocean. Univ. 2017, 32, 111–118. [Google Scholar] [CrossRef]
- Yang, B.; Shao, L.; Dai, X.; Liu, Y.-H. Analysis of the Aquaculture Prospects of the Northeast Lamprey. Agro-Tech. Serv. 2017, 34, 114. [Google Scholar] [CrossRef]
- Lu, T.-H.; Yi, X.-R. Stability and Hopf Bifurcation of the Lotka-Volterra Competition Model with Time Delay and Refuge. J. Jilin Norm. Univ. Nat. Sci. Ed. 2024, 45, 50–59. [Google Scholar] [CrossRef]
- Xu, J.; Lou, X.; Tu, Y.; Wan, S.; Mao, R. Intra-specific and Inter-Specific Competition of Arbuscular Mycorrhizal and Ectomycorrhizal Tree Saplings in a Subtropical Phyllostachys edulis Forest. J. Jiangxi Agric. Univ. 2021, 43, 1107–1115. [Google Scholar] [CrossRef]
- Zhang, Q.; Yeerjiang, B.; Wang, J. Gender Differences in Responses to Interspecific Competition among Dioecious Individuals of Rhamnus schneideri var. manshurica. For. Sci. 2023, 59, 33–41. [Google Scholar] [CrossRef]
- Lv, L.; Li, X. Stability and Bifurcation Analysis in a Discrete Predator–Prey System of Leslie Type with Radio-Dependent Simplified Holling Type IV Functional Response. Mathematics 2024, 12, 1803. [Google Scholar] [CrossRef]
- Zhang, S. Dynamical Stability Analysis of Population with Stage Structure. Master’s Thesis, Anqing Normal University, Anqing, China, 2024. [Google Scholar]
- Liu, M.; Liu, J.; Wang, Y.; Yu, X.; Fang, X.; You, L. Improvement of the Stability of Excimer Laser Output Pulse Energy by Beam Combination. Infrared Laser Eng. 2024, 53, 135–143. [Google Scholar] [CrossRef]
- Dang, G. Ecological Consequences of St. Lawrence Seaway Exploitation and the U.S. Response (1954–2008). Master’s Thesis, Shandong Normal University, Jinan, China, 2023. [Google Scholar]
- Zhu, Y.G.; Li, J.; Pang, Y.; Li, Q.W. Lamprey: An important animal model of evolution and disease research. Hereditas 2020, 42, 847–857. [Google Scholar] [CrossRef] [PubMed]
- Zou, P. Example Analysis of Mathematical Modeling in Differential Equations. Sci. Technol. Wind 2024, (05), 43–45. [Google Scholar] [CrossRef]
- Zheng, Y.; Chang, C. Research on associative relationship of concepts based on the Lotka-Volterra Predator-Prey Model. Chin. Med. Libr. Inf. Sci. 2022, 31, 7–13. [Google Scholar]
- Qu, Q.; Wu, W. Stability Characteristics of Multi-Model Precipitation Forecast. Meteorological 2024, 50, 420–433. [Google Scholar] [CrossRef]
- Docker, M.F. Section 1.3.2. In Lampreys: Biology; Conservation and Control; Fish & Fisheries Series 37; Docker, M.F., Ed.; Springer: Dordrecht, The Netherlands, 2015; Volume 1, pp. 22–24. [Google Scholar]
- Bear, R. Principles of Biology; OpenStax CNX: Houston, TX, USA, 2022; p. 75. [Google Scholar]
- Vinoth, S.; Vadivel, R.; Hu, N.-T.; Chen, C.-S.; Gunasekaran, N. Bifurcation Analysis in a Harvested Modified Leslie–Gower Model Incorporated with the Fear Factor and Prey Refuge. Mathematics 2023, 11, 3118. [Google Scholar] [CrossRef]
- Jia, X. Dynamics Analysis of Leslie-Gower Predator-Prey Diffusion Model with Fear Factor. Master’s Thesis, Northwest Normal University, Lanzhou, China, 2024. [Google Scholar]
- Liu, C.; Chen, Y.; Yu, Y.; Wang, Z. Bifurcation and Stability Analysis of a New Fractional-Order Prey–Predator Model with Fear Effects in Toxic Injections. Mathematics 2023, 11, 4367. [Google Scholar] [CrossRef]
- Yang, M. Propagation Dynamics of a Three-Species Predator-Prey Model in a Shifting Environment. Master’s Thesis, Lanzhou University, Lanzhou, China, 2023. [Google Scholar]
- Barman, D.; Upadhyay, R.K. Modelling Predator–Prey Interactions: A Trade-Off between Seasonality and Wind Speed. Mathematics 2023, 11, 4863. [Google Scholar] [CrossRef]
- Lv, X.; Zhang, Y.; Gao, D.; Sun, C.; Li, H. Seasonal Succession of Rotifer Communities in Northern Lake Erhai, Southwest China. J. Lake Sci. 2023, 35, 289–297. [Google Scholar]
- Lv, C. A Predator-Prey Model with Free Boundary in a Climate Change Environment. Master’s Thesis, Southeast University, Nanjing, China, 2022. [Google Scholar]
- Deng, S.; Guo, W.; Wen, W.; Wang, M.G.; Huang, L.P.; Chen, Z.D.; Chen, G.J.; Zhao, S.Y. The Effects of Water Eutrophication and Species Invasion on the Food Web of Xingyun Lake. Chin. Environ. Sci. 2024, 44, 932–943. [Google Scholar]
- Wang, Z. Research on ODE Modeling Method and Application of UHVDC Converter Station. Master’s Thesis, Southeast University, Nanjing, China, 2022. [Google Scholar] [CrossRef]
- Zhao, Q.; Niu, X. Dynamics of a Stochastic Predator–Prey Model with Smith Growth Rate and Cooperative Defense. Mathematics 2024, 12, 1796. [Google Scholar] [CrossRef]
- Bi, Z. Spatial Pattern Behavior Analysis of Marine Organism Population Density. Master’s Thesis, Shandong University, Jinan, China, 2024. [Google Scholar] [CrossRef]
- Liao, X. Stability Analysis of a Volterra Biological Mathematical Model Based on Constant Coefficient. J. Ningxia Norm. Univ. 2022, 43, 30–37. [Google Scholar] [CrossRef]
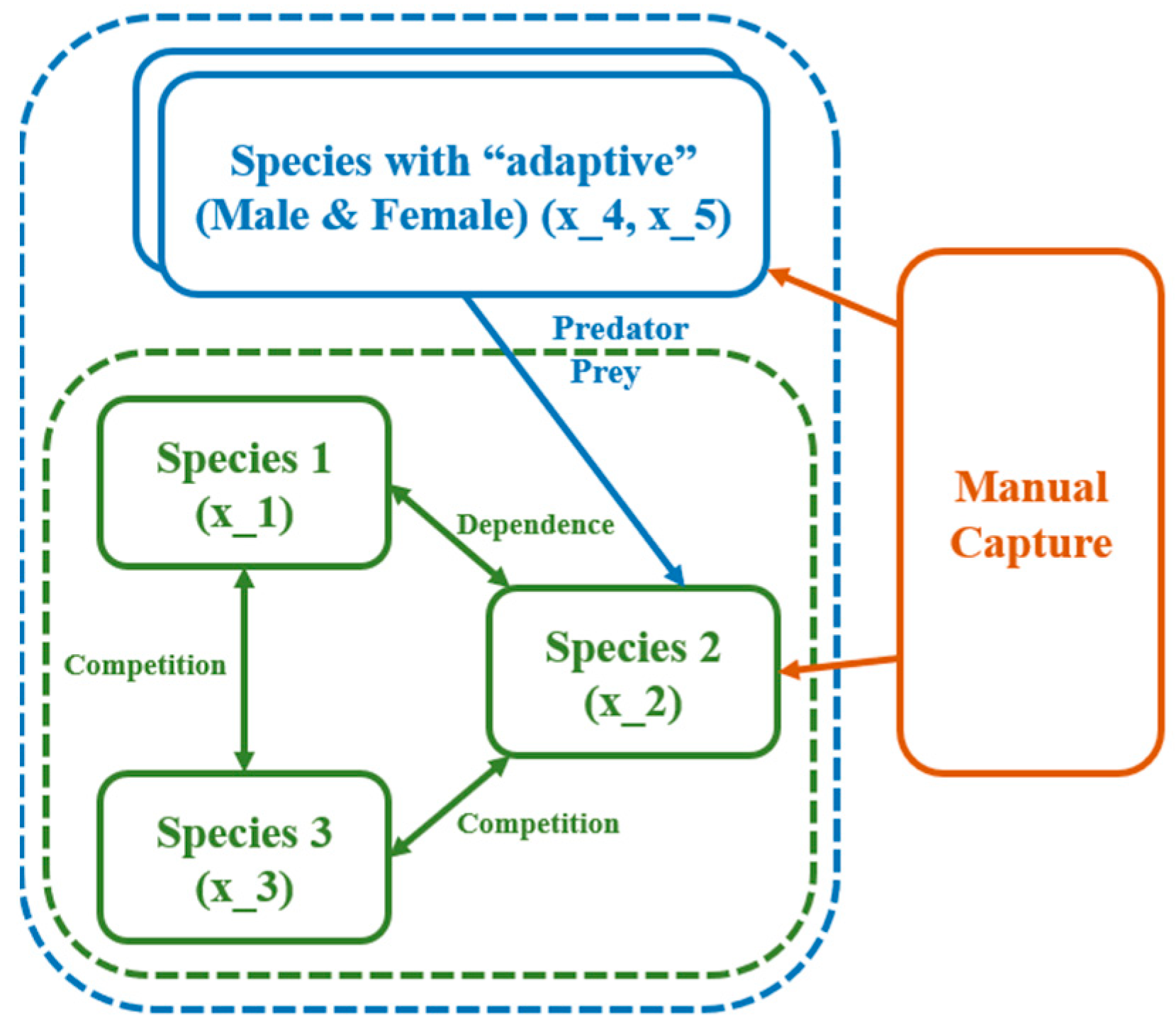
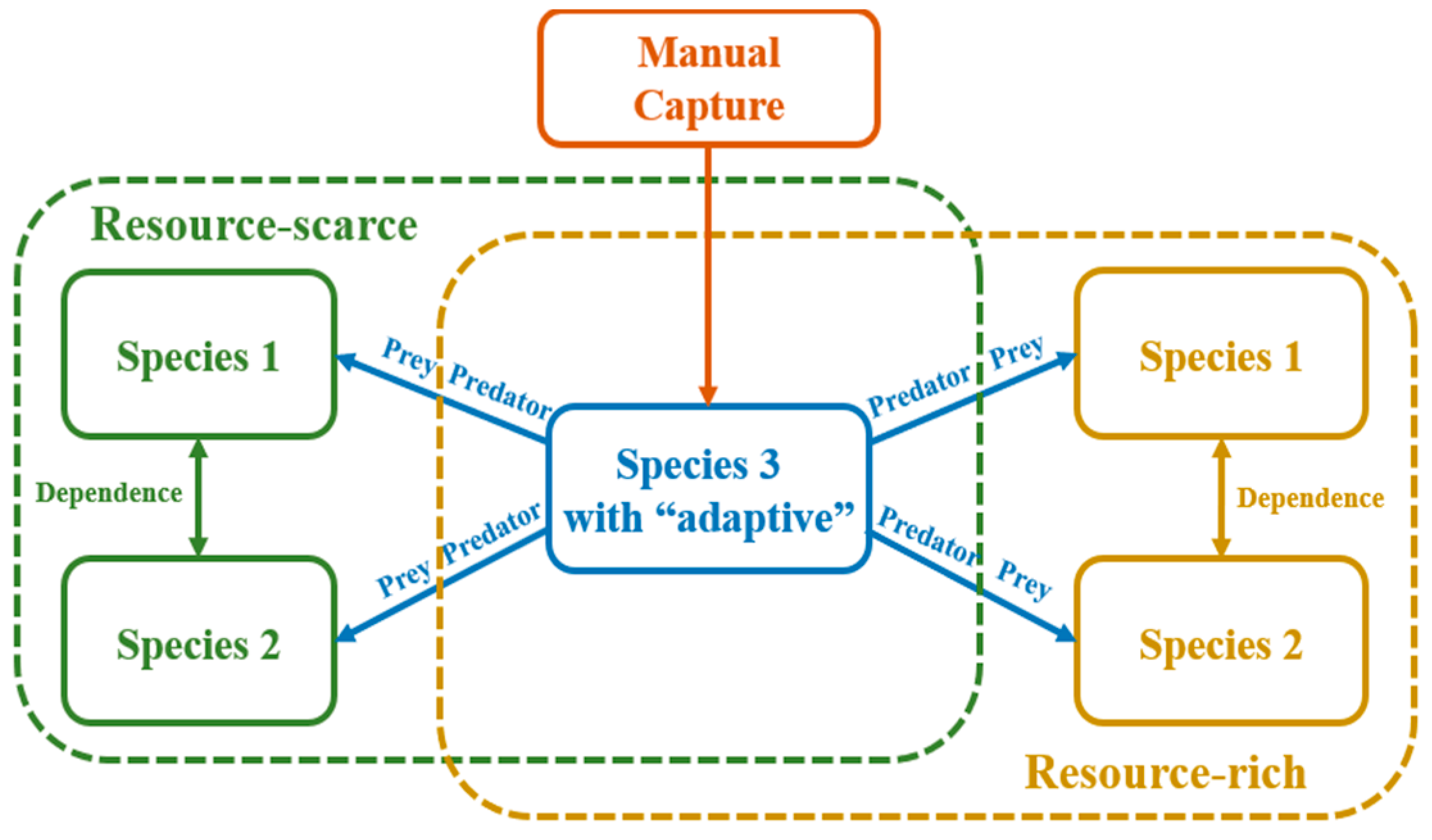
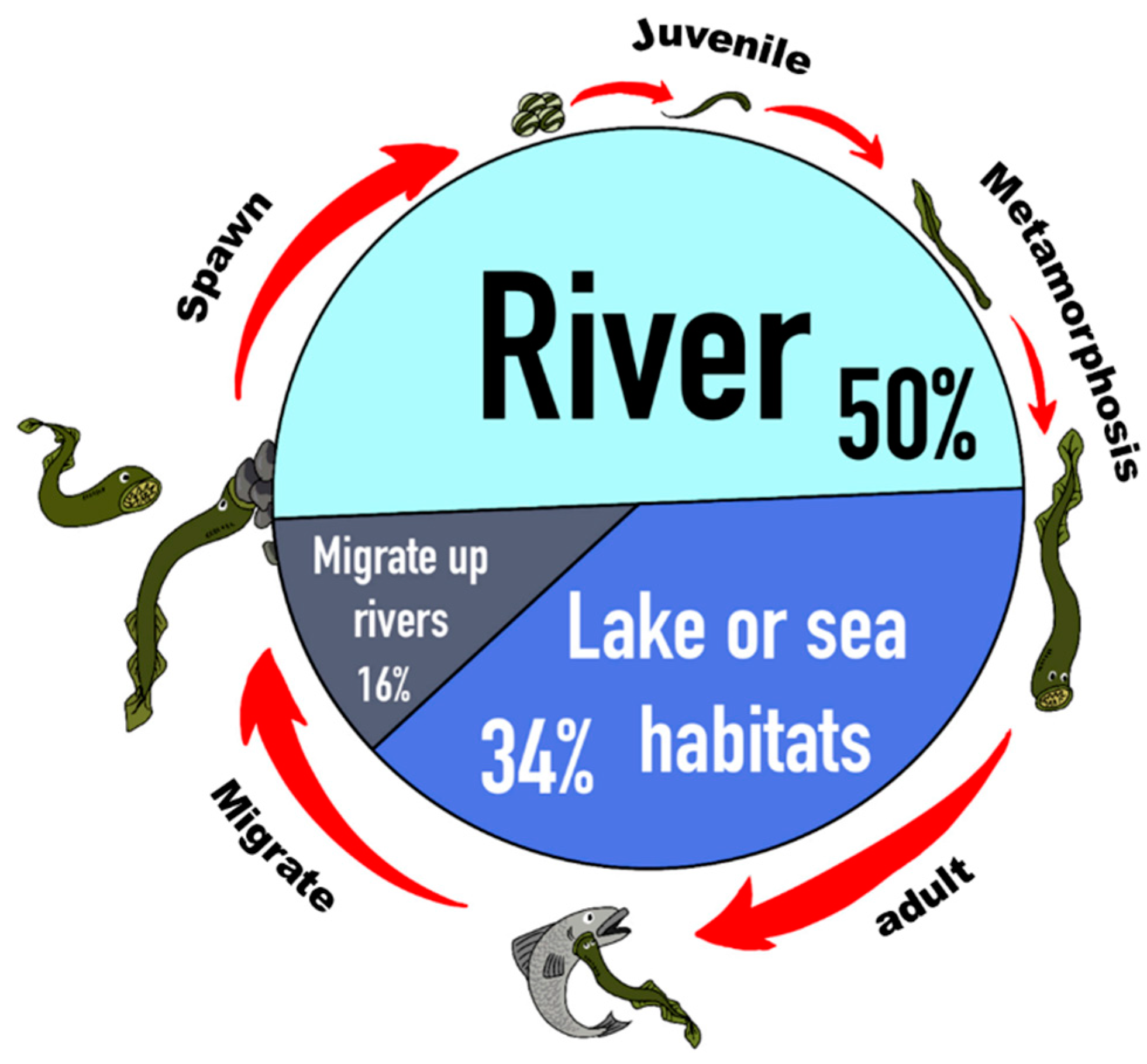
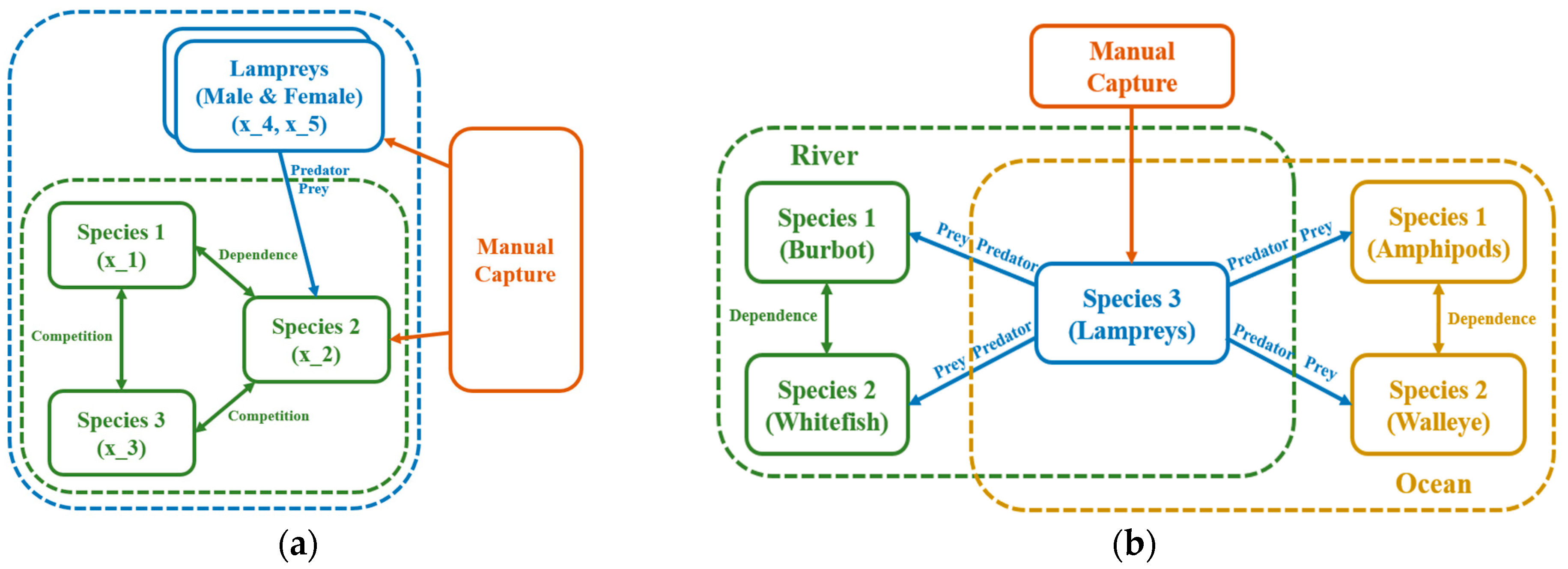

| Notation | Description |
|---|---|
| The species index | |
| The density of species | |
| The environmental carrying capacity of species | |
| The binary variable showing whether it can survive on species ’s own | |
| The intrinsic growth rate (mortality) of species | |
| The binary variable showing the relationship between species and | |
| The relative standard deviation of species | |
| The male–female sex ratio coefficient | |
| The predation coefficient between species and j | |
| The combined predation coefficient between species and j | |
| The multiple of species ’s consumption of food relative to species ’s consumption of food |
| Variable Information | ||||
|---|---|---|---|---|
| Retrieve a value | 1 | −1 | 1 | −1 |
| Hidden meaning | competition | dependence | survive alone | unable to survive alone |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| * | 20 | * | 30 |
| * | 25 | 20 | |
| 60 | 25 | ||
| 0.2 | 0.1 | ||
| 0.15 | 0.2 | ||
| 0.2 | 35 | ||
| 100 | 30 | ||
| 50 | 50 | ||
| 1 | 1 | ||
| 1 | −1 | ||
| −1 | −1 | ||
| 1 | 1 | ||
| −1 | e | 0.015 | |
| 0.2 | 1 | ||
| 0.2 | 0.2 | ||
| 0.2 | 0.2 | ||
| 1 | 1 | ||
| 0.006 | 0.004 | ||
| 0.012 | 0.008 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 30 | 30 | ||
| 15 | 0.7 | ||
| 0.6 | 0.1 | ||
| e | 0.015 | 1 | |
| 1 | 200 | ||
| 100 | * | 1200 | |
| * | 600 | −1 | |
| 0.2 | 0.2 |
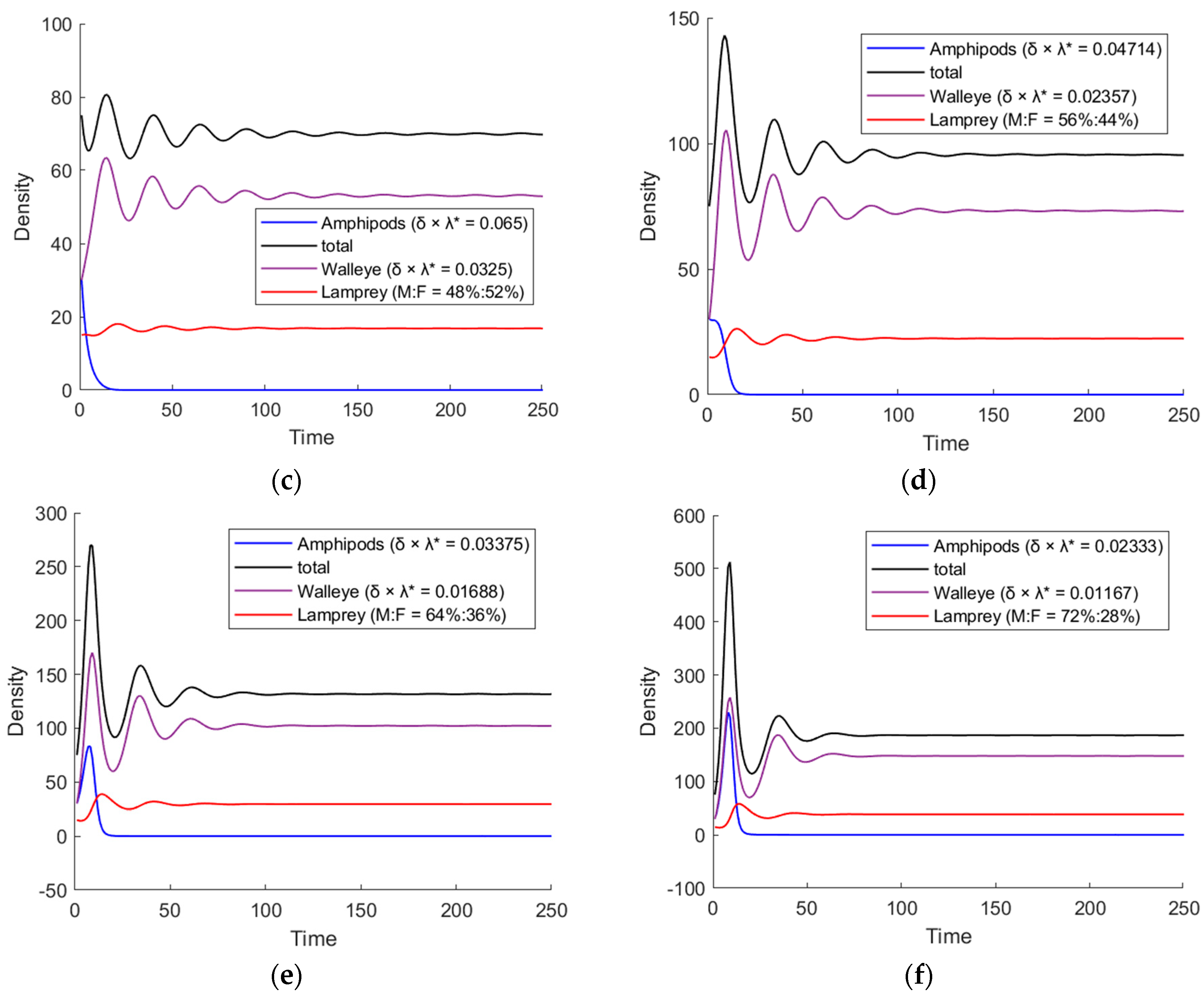
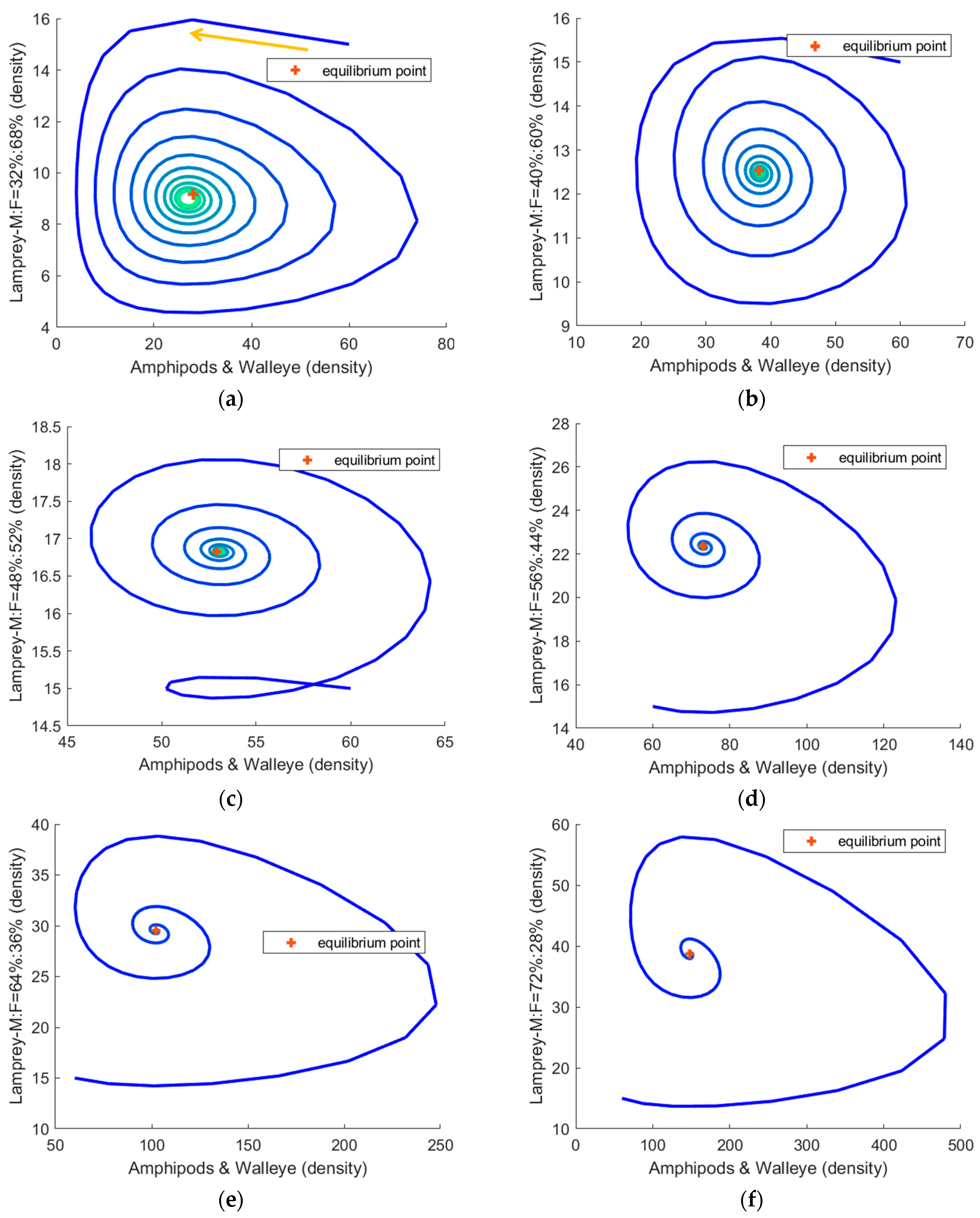
| Male: Female | Steady State Fast or Slow | Equilibrium Point * | Volatility |
|---|---|---|---|
| 32%:68% | Fast | (27.1, 6.9) | 0.239 |
| 40%:60% | Fast | (38.3, 8,3) | 0.134 |
| 48%:52% | Slow | (53.1, 11.0) | 0.073 |
| 56%:44% | Slow | (73.2, 14.3) | 0.025 |
| 64%:36% | Fast | (102.2, 18.0) | 0.073 |
| 72%:28% | Fast | (147.9, 21.7) | 0.101 |
| Male: Female | Steady State Fast or Slow | Equilibrium Point * | Volatility |
|---|---|---|---|
| 32%:68% | slowest | (28.1, 9.2) | 0.319 |
| 40%:60% | slower | (38.2, 12.5) | 0.122 |
| 48%:52% | general | (52.9, 16.8) | 0.034 |
| 56%:44% | general | (73.1, 22.3) | 0.087 |
| 64%:36% | quicker | (102.2, 29.5) | 0.158 |
| 72%:28% | fastest | (147.9, 38.8) | 0.237 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Wan, X.; Hou, J.; Lian, J.; Wang, Y. A Study on Effects of Species with the Adaptive Sex-Ratio on Bio-Community Based on Mechanism Analysis and ODE. Mathematics 2024, 12, 2298. https://doi.org/10.3390/math12142298
Wang H, Wan X, Hou J, Lian J, Wang Y. A Study on Effects of Species with the Adaptive Sex-Ratio on Bio-Community Based on Mechanism Analysis and ODE. Mathematics. 2024; 12(14):2298. https://doi.org/10.3390/math12142298
Chicago/Turabian StyleWang, Haoyu, Xiaoyuan Wan, Junyao Hou, Jing Lian, and Yuzhao Wang. 2024. "A Study on Effects of Species with the Adaptive Sex-Ratio on Bio-Community Based on Mechanism Analysis and ODE" Mathematics 12, no. 14: 2298. https://doi.org/10.3390/math12142298
APA StyleWang, H., Wan, X., Hou, J., Lian, J., & Wang, Y. (2024). A Study on Effects of Species with the Adaptive Sex-Ratio on Bio-Community Based on Mechanism Analysis and ODE. Mathematics, 12(14), 2298. https://doi.org/10.3390/math12142298





