Anti-Disturbance Bumpless Transfer Control for a Switched Systems via a Switched Equivalent-Input-Disturbance Approach
Abstract
:1. Introduction
- Although there exist many works on the ADBT control design problem, such as [10,30,31], the definitions of the ADBT control problem are different. In all these works, the BT performance is described by limiting the jump amplitude at switching instants or the amplitude difference between the actual control law and the auxiliary control signal rather than requiring the controller to operate continuously. In our work, a continuous controller is obtained. Moreover, in these existing works, reliable controller design (as in [30]) and disturbance observer design (as in [10,31]) are always provided to achieve the AD performance. However, a switched EID methodology is introduced in our paper to achieve the AD performance. In fact, rare results are provided on the design of the switched EID estimator for switched systems.
- We extend the EID estimator design issue from its original nonswitched version. The switched EID estimator, which relies on switching signals, indicates that each subsystem possesses its own EID estimator. To reduce the conservativeness that arises from using a common EID estimator for all subsystems, distinct EID estimators are designed for each subsystem.
- Based on the switched EID estimator, through the construction of an additional compensator, a new formulation for the ADBT controller is devised for switched systems. Through an ADT switching methodology, sufficient conditions are derived for the ADBT control of switched systems. A continuous controller and an ADT switching strategy are jointly developed to address the ADBT control design problem for switched systems.
| Notations | Meaning |
| n-dimensional real vector space | |
| 2-norm of x | |
| () | Greatest (least) eigenvalue of the matrix P |
| N | Set of natural numbers |
| LMI | Linear matrix inequality |
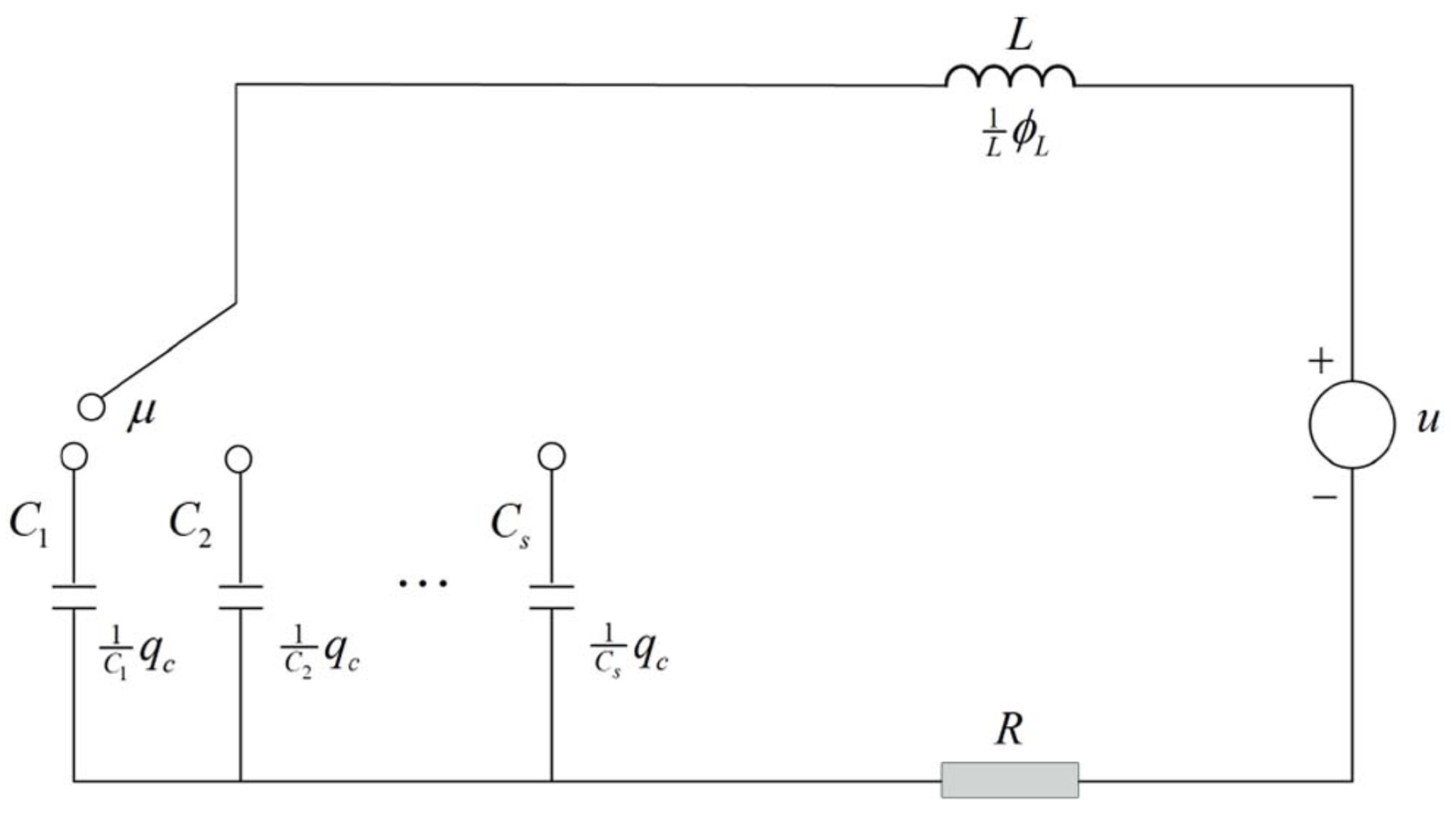
2. Configuration of Switched EID-Based ADBT Control and Problem Formulation
3. Anti-Disturbance Bumpless Transfer Control
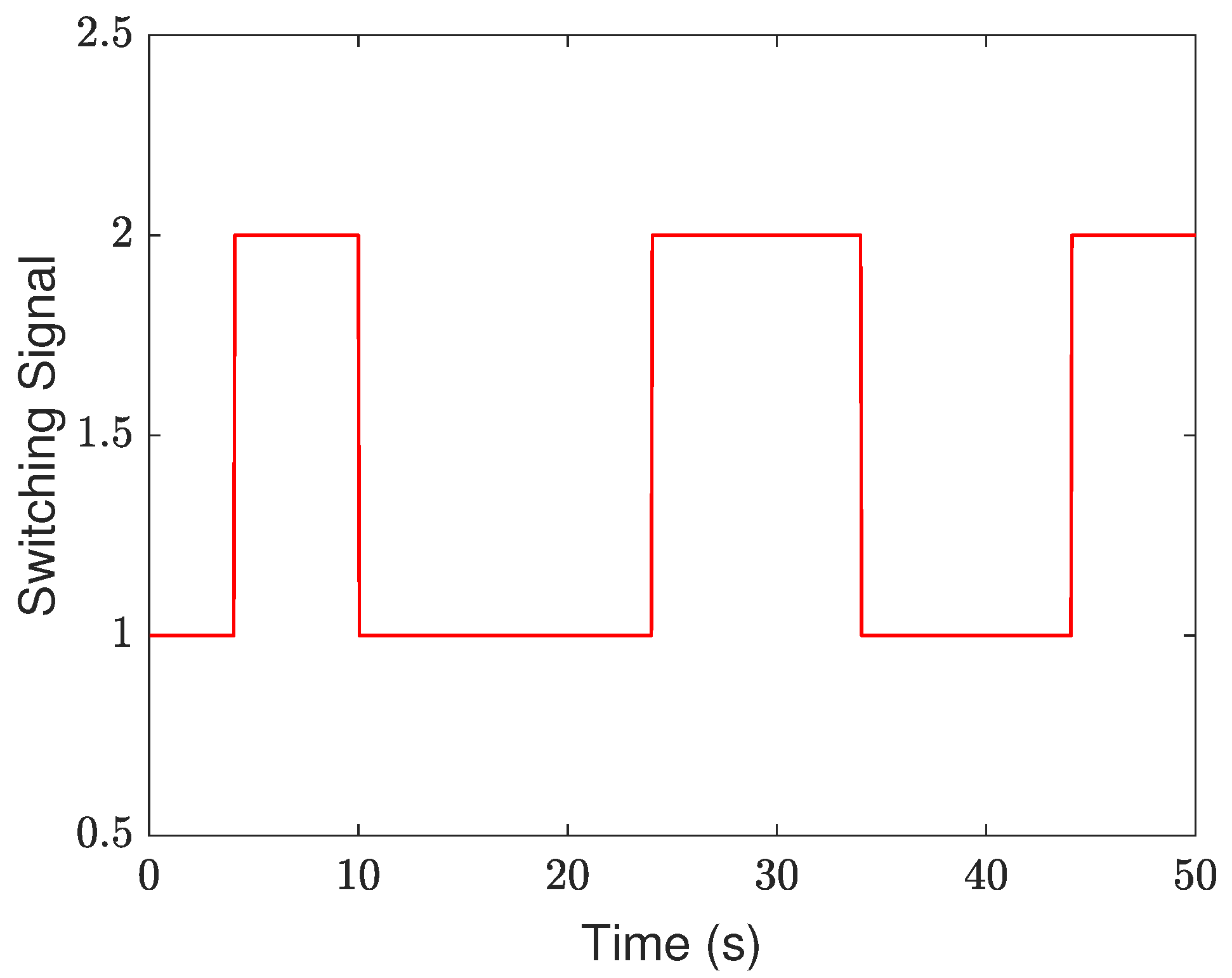
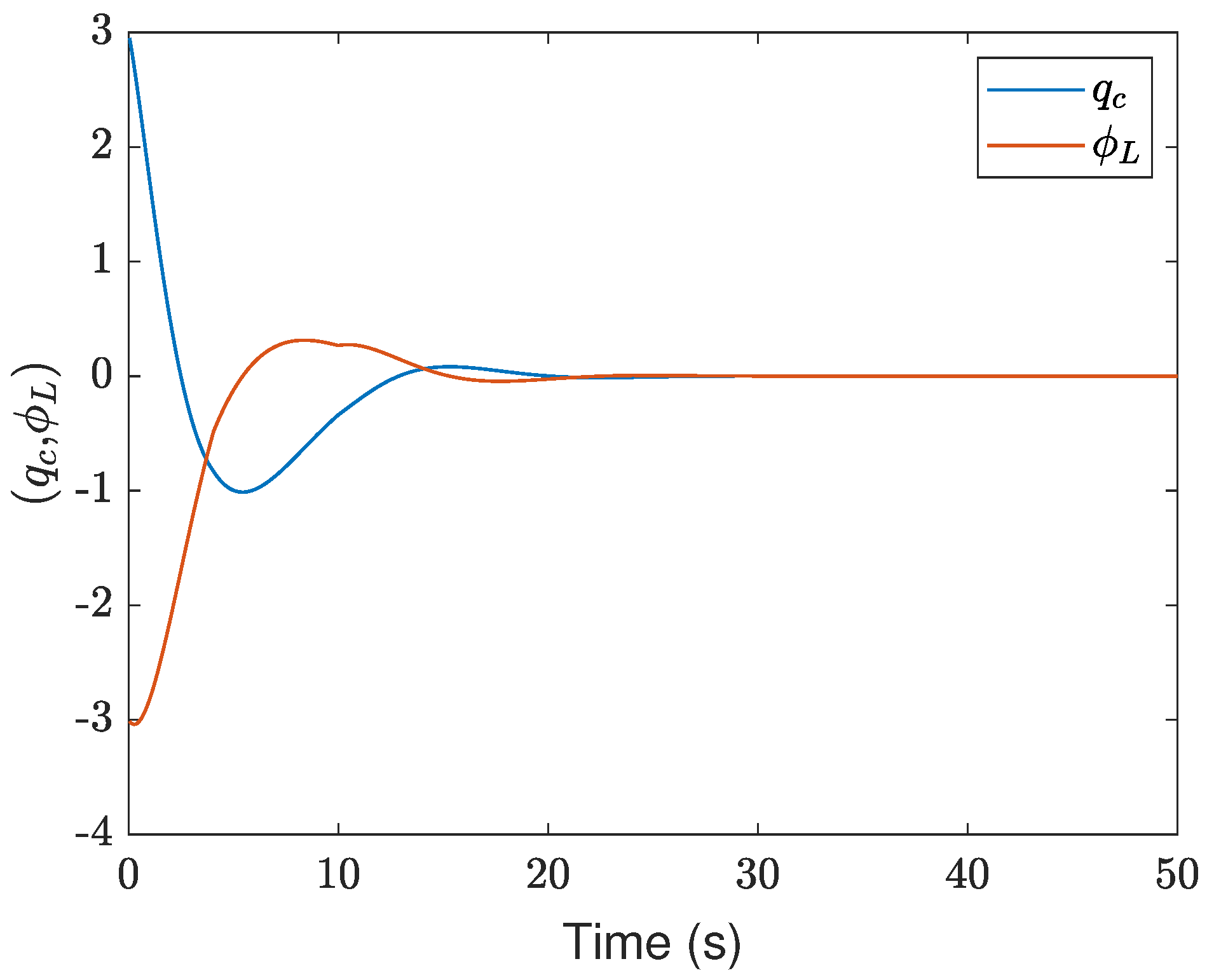
4. Simulation Example
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.; Huang, J.; Li, C. Distributed interval observers with switching topology design for cyber-physical systems. Mathematics 2024, 12, 163. [Google Scholar] [CrossRef]
- Ronanki, D.; Dasari, Y.; Williamson, S.S. Power electronics-based switched supercapacitor bank circuits with enhanced power delivery capability for pulsed power applications. In Proceedings of the 2021 IEEE Applied Power Electronics Conference and Exposition (APEC), Phoenix, AZ, USA, 14–17 June 2021; pp. 2271–2276. [Google Scholar]
- Shi, Y.; Sun, X. Bumpless transfer control for switched linear systems and its application to aero-engines. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 2171–2182. [Google Scholar] [CrossRef]
- Zong, G.; Yang, D.; Lam, J.; Song, X. Fault-tolerant control of switched LPV systems: A bumpless transfer approach. IEEE/ASME Trans. Mechatron. 2021, 27, 1436–1446. [Google Scholar]
- Chen, W.; Yang, J.; Guo, L.; Li, S. Disturbance-observer-based control and related methods—An overview. IEEE Trans. Ind. Electron. 2015, 63, 1083–1095. [Google Scholar] [CrossRef]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Guo, L.; Cao, S. Anti-Disturbance Control for Systems with Multiple Disturbances; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Guo, L.; Cao, S. Anti-disturbance control theory for systems with multiple disturbances: A survey. ISA Trans. 2014, 53, 846–849. [Google Scholar] [CrossRef] [PubMed]
- Yong, K.; Chen, M.; Wu, Q. Anti-disturbance control for nonlinear systems based on interval observer. IEEE Trans. Ind. Electron. 2019, 67, 1261–1269. [Google Scholar] [CrossRef]
- Zhao, Y.; Wu, D.; Xu, C.; Yu, S.; Liu, T.; Yang, D. Adaptive anti-disturbance bumpless transfer control for switched neural network systems with its application to switched circuit model. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 411–420. [Google Scholar] [CrossRef]
- Liu, F.; Chen, M.; Shi, S.; Tao, L. Almost output regulation for turbofan switched systems under multi-source disturbances and time delay. Int. J. Robust Nonlinear Control 2024, 34, 378–396. [Google Scholar] [CrossRef]
- Yang, Y.; Zheng, W.; Liu, B. Adaptive anti-disturbance control for systems with saturating input via dynamic neural network disturbance modeling. IEEE Trans. Cybern. 2020, 52, 5290–5300. [Google Scholar]
- Zhang, S.; Zhang, B.; Li, X.; Wang, Z.; Qian, F. A method of enhancing fast steering mirror’s ability of anti-disturbance based on adaptive robust control. Math. Probl. Eng. 2019, 2019, 2152858. [Google Scholar] [CrossRef]
- Huang, Y.; Xue, W. Active disturbance rejection control: Methodology and theoretical analysis. ISA Trans. 2014, 53, 963–976. [Google Scholar] [CrossRef] [PubMed]
- Feng, H.; Guo, B. Active disturbance rejection control: Old and new results. Annu. Rev. Control 2017, 44, 238–248. [Google Scholar] [CrossRef]
- Du, Y.; Cao, W.; She, J.; Wu, M.; Fang, M.; Kawata, S. Disturbance rejection and robustness of improved equivalent-input-disturbance-based system. IEEE Trans. Cybern. 2021, 52, 8537–8546. [Google Scholar] [CrossRef]
- Yu, P.; Liu, K.Z.; Wu, M.; She, J. Improved Equivalent-Input-Disturbance Approach Based on H∞ Control. IEEE Trans. Ind. Electron. 2019, 67, 8670–8679. [Google Scholar] [CrossRef]
- Mei, Q.; She, J.; Wang, F.; Nakanishi, Y.; Hashimoto, H.; Chugo, D. Disturbance rejection and control system design using 1-inverse-based equivalent-input-disturbance approach. IEEE Trans. Ind. Electron. 2022, 70, 1666–1675. [Google Scholar] [CrossRef]
- Zhang, L.; Xu, K.; Yang, J.; Han, M.; Yuan, S. Transition-dependent bumpless transfer control synthesis of switched linear systems. IEEE Trans. Autom. Control 2022, 68, 1678–1684. [Google Scholar] [CrossRef]
- Wu, T.; Zhu, Y.; Zhang, L.; Shi, P. Bumpless transfer model predictive control for Markov jump linear systems. IEEE Trans. Autom. Control 2023. [Google Scholar] [CrossRef]
- Yang, Y.; Huang, Z.; Zhang, P. Double-observer-based bumpless transfer control of switched positive systems. Mathematics 2024, 12, 1724. [Google Scholar] [CrossRef]
- Li, J.; Zhao, J. Bumpless transfer control for switched linear systems with bump induced event-triggered mechanism. J. Frankl. Inst. 2023, 360, 6081–6098. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Zhao, Y.; Chen, Y.; Li, W. Finite-time event-triggered bumpless transfer control for switched systems. Int. J. Robust Nonlinear Control 2022, 32, 6962–6982. [Google Scholar] [CrossRef]
- Zong, G.; Huang, C.; Yang, D. Bumpless transfer fault detection for switched systems: A state-dependent switching approach. Sci. China Inf. Sci. 2021, 64, 172208. [Google Scholar] [CrossRef]
- Shi, J.; Zhao, J. State bumpless transfer control for a class of switched descriptor systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 3846–3856. [Google Scholar] [CrossRef]
- Zhang, S.; Zhao, J. Dwell-Time-Dependent H∞ Bumpless transfer control for discrete-time switched interval type-2 fuzzy systems. IEEE Trans. Fuzzy Syst. 2021, 30, 2426–2437. [Google Scholar] [CrossRef]
- Wen, S.X.; Shi, Y.; Pan, Z.R.; Sun, X.M. Practical bumpless transfer design for switched linear systems: Application to aeroengines. IEEE Trans. Ind. Inform. 2023, 19, 11910–11919. [Google Scholar] [CrossRef]
- Wu, F.; Wang, D.; Lian, J. Bumpless transfer control for switched systems via a dynamic feedback and a bump-dependent switching law. IEEE Trans. Cybern. 2022, 53, 5372–5379. [Google Scholar] [CrossRef]
- Shi, Y.; Zhao, J.; Sun, X. A bumpless transfer control strategy for switched systems and its application to an aero-engine. IEEE Trans. Ind. Inform. 2020, 17, 52–62. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, J. H∞ reliable bumpless transfer control for switched systems with state and rate constraints. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 3925–3935. [Google Scholar] [CrossRef]
- Yang, D.; Zong, G.; Nguang, S.K.; Zhao, X. Bumpless transfer H∞ anti-disturbance control of switching Markovian LPV systems under the hybrid switching. IEEE Trans. Cybern. 2020, 52, 2833–2845. [Google Scholar] [CrossRef]
- Levine, W.S. The Control Handbook; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Zhai, G.; Hu, B.; Kazunori, Y.; Michel, A. L2 gain analysis of switched systems with average dwell time. Trans. Soc. Instrum. Control Eng. 2000, 36, 937–942. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Liu, Q.; Yu, P. Anti-Disturbance Bumpless Transfer Control for a Switched Systems via a Switched Equivalent-Input-Disturbance Approach. Mathematics 2024, 12, 2307. https://doi.org/10.3390/math12152307
Wu J, Liu Q, Yu P. Anti-Disturbance Bumpless Transfer Control for a Switched Systems via a Switched Equivalent-Input-Disturbance Approach. Mathematics. 2024; 12(15):2307. https://doi.org/10.3390/math12152307
Chicago/Turabian StyleWu, Jiawen, Qian Liu, and Pan Yu. 2024. "Anti-Disturbance Bumpless Transfer Control for a Switched Systems via a Switched Equivalent-Input-Disturbance Approach" Mathematics 12, no. 15: 2307. https://doi.org/10.3390/math12152307




