A Discrete Hamilton–Jacobi Theory for Contact Hamiltonian Dynamics
Abstract
:1. Introduction
2. Fundamentals of Continuous Contact Dynamics
2.1. Contact Manifolds
2.2. Contact Lagrangian Dynamics
2.3. Contact Hamiltonian Dynamics
2.4. A Continuous Geometric Hamilton–Jacobi Theory on Contact Manifolds

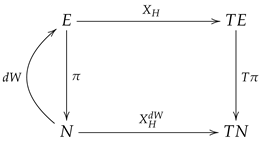
- The vector fields and are γ-related, that is,where is the tangent mapping of the section γ.
- The equationis fulfilled.
3. Discrete Contact Dynamics
3.1. Discrete Contact Lagrangian Dynamics
3.2. Discrete Contact Hamiltonian Dynamics
3.3. Discrete Contact Hamilton–Jacobi Theory
- 1.
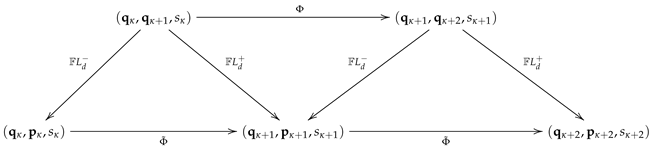
- The old and new coordinates are related by a generating function of the type
- 2.
- The dynamics in the new coordinates is rendered trivial, i.e.,
3.4. A Geometric Discrete Hamilton–Jacobi Theory on Contact Manifolds
- 1.
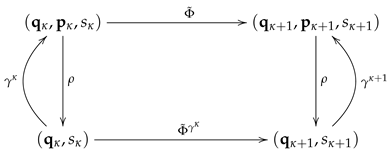
- The flows and commute, i.e.,
- 2.
- S solves the HJ Equation (86).
4. Application
4.1. Free Single Particle Contact Hamiltonian
4.2. Rayleigh Systems
5. Commentaries
- Contact Hamiltonian dynamics do not preserve the Hamiltonian function. There exists an alternative characterization of Hamiltonian dynamics on contact manifolds that preserves the energy, known as evolution dynamics [50,61]. We wish to examine the discretization of evolution dynamics and their HJ formulation.
- For the extended cotangent bundle , the continuous HJ theory for contact Hamiltonian dynamics was presented in [11,58,59]. The authors consider the base manifold as the extended configuration space . In this work, we consider the base manifold to be Q. We wish to write a discrete HJ equation on contact manifolds with base manifold .
- If a Lagrangian is degenerate, then one cannot arrive at explicit Euler–Lagrange equations. In this case, the Legendre transformation is not immediate. Tulczyjew’s triple is a geometric formulation that allows us to also achieve this in singular cases [62]. In a discrete framework, Tulczyjew’s triple was constructed in [63]. This determines a proper geometry for implicit discrete Lagrangian and Hamiltonian dynamics [64]. For the continuous case, a geometric HJ theory has been recently given in [18,65] in the symplectic framework and in [59] in the contact framework. We wish to concentrate on generalizing the discrete HJ theories both for symplectic and contact geometry including the implicit case. On the other hand, Tulczyjew’s triple for contact geometry has been recently constructed in [57]. In the future, we aim at constructing a discrete contact Tulczyjew’s triple.
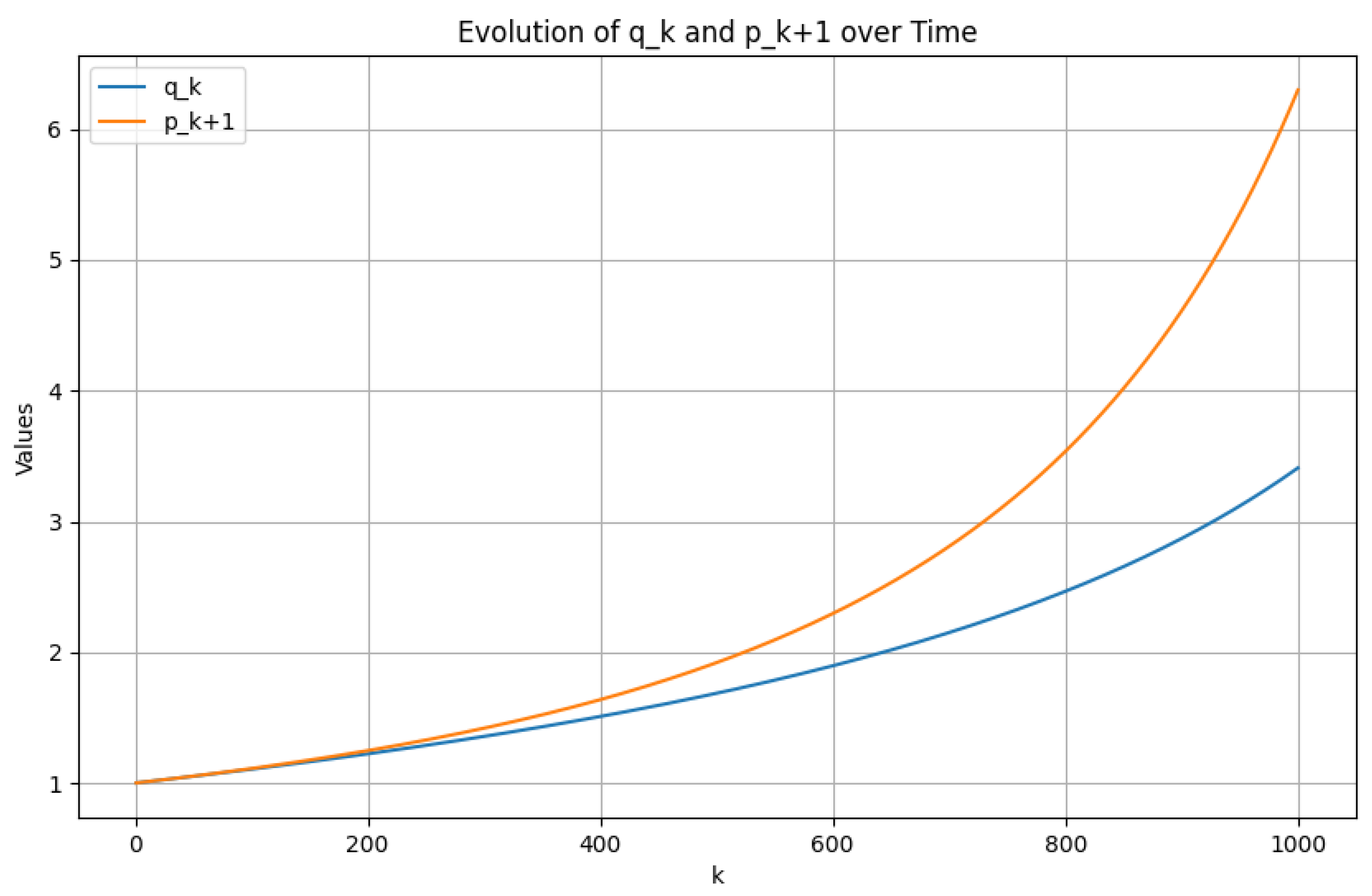
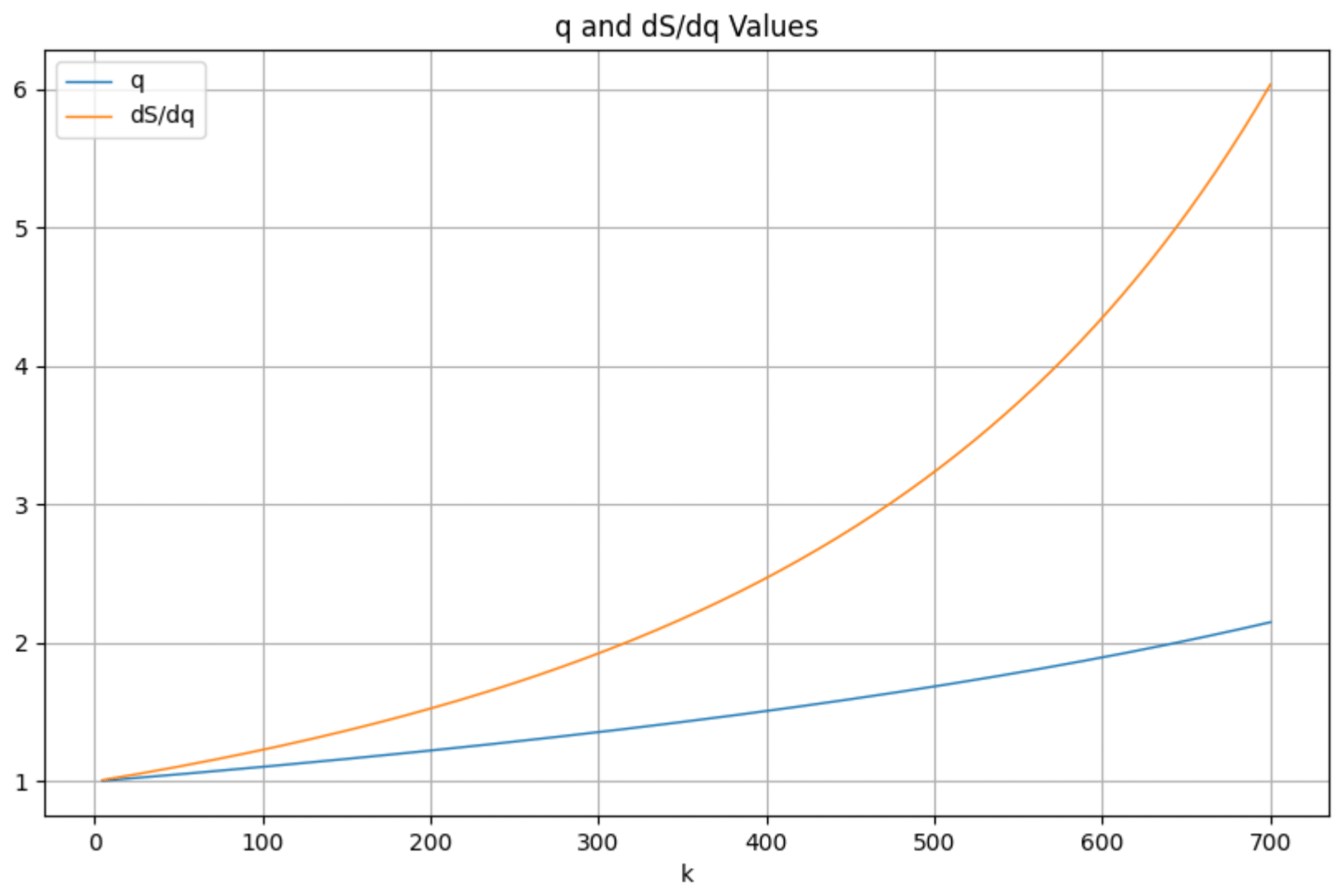
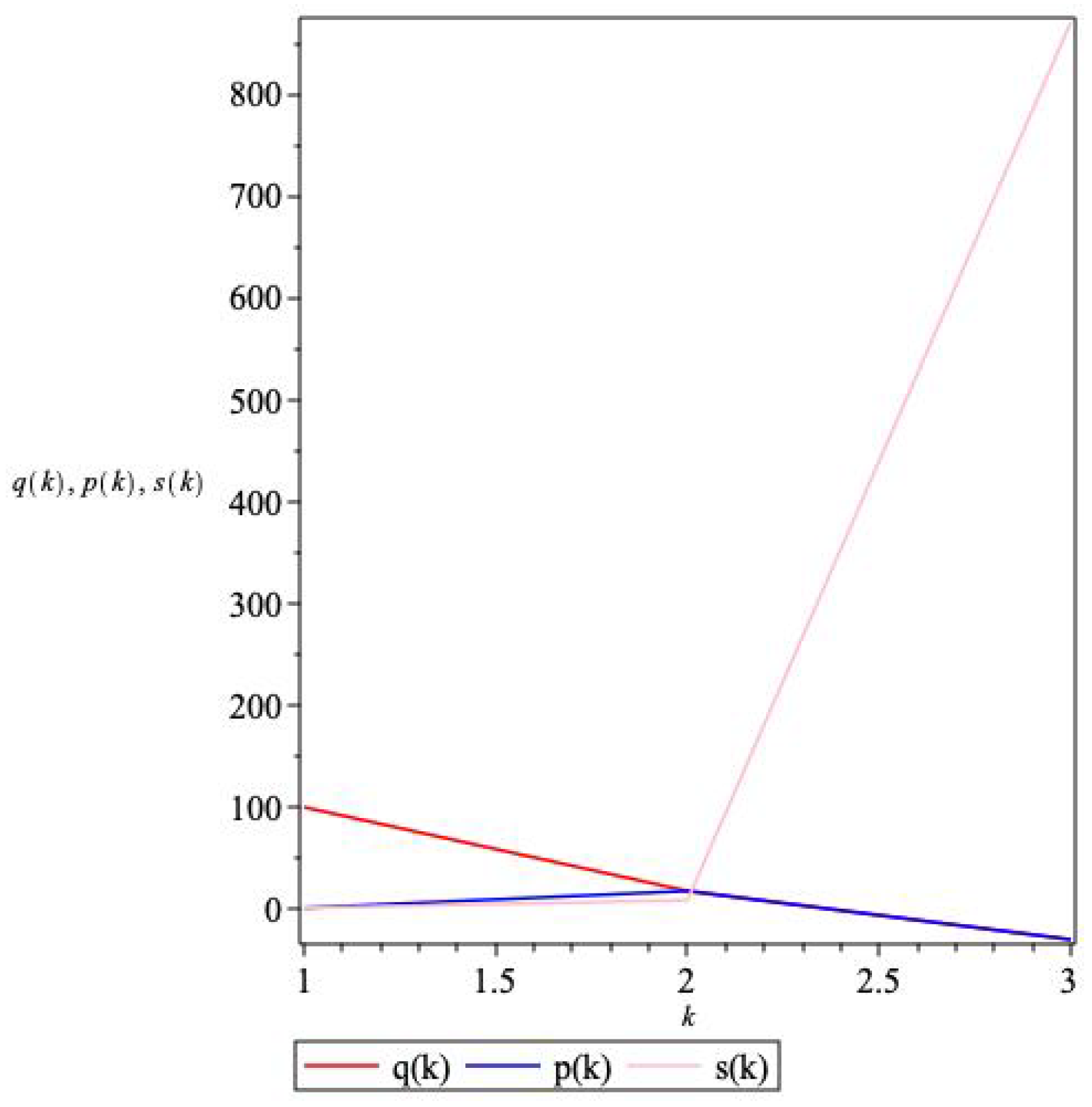
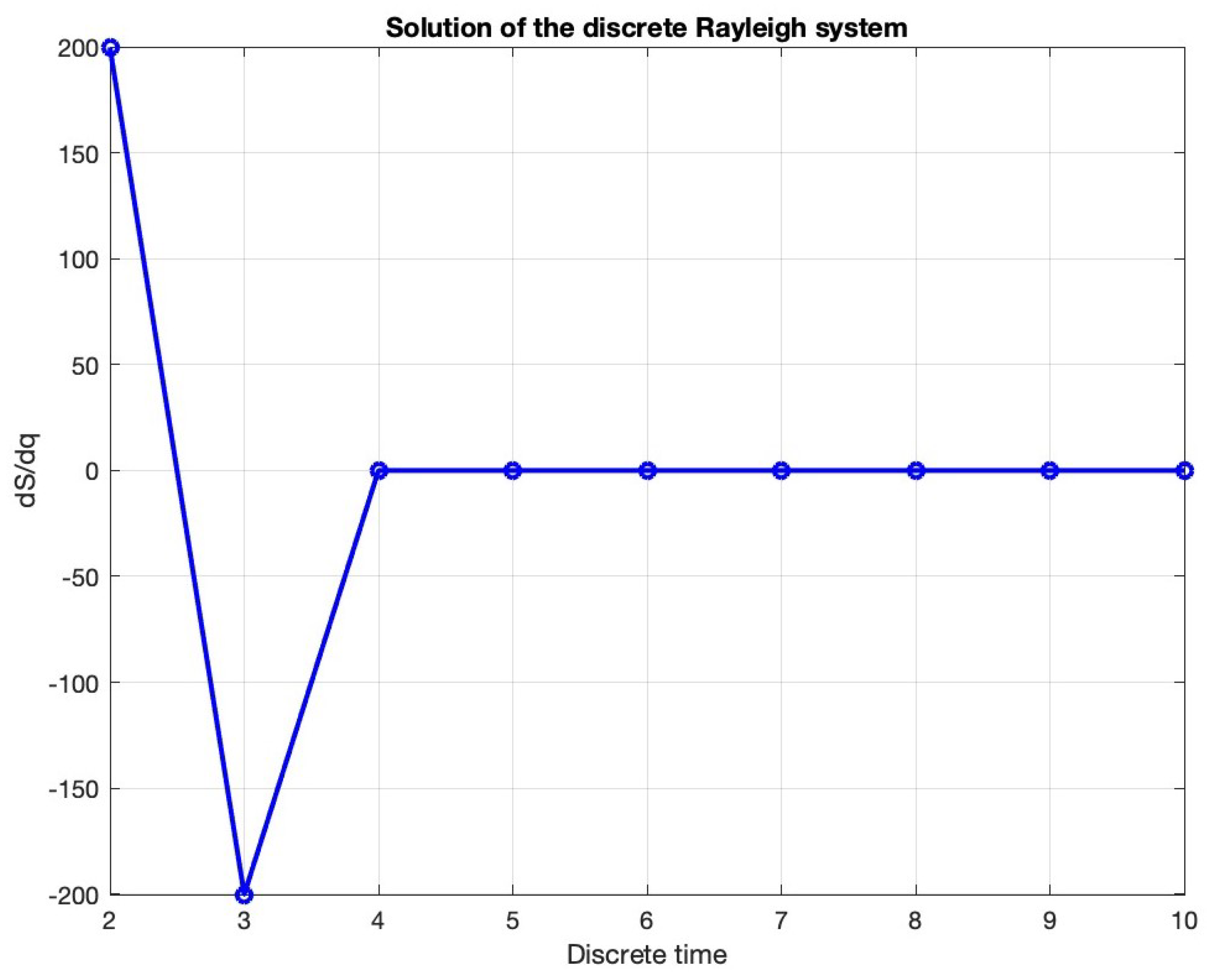
- One could wonder what are the limitations of the discrete contact Hamilton–Jacobi equation. The equation has been exactly derived, so the limitations are up to the numerical integration of choice. For a simple visualization like the one we have displayed, the behavior is fair, given that the Euler method is the simplest method we can choose and the number of iterations is small. One could greatly diminish the error with a different integration procedure.
- In the limit of very big number of steps in the discretization, one can easily depict that one retrieves the continuous contact HJ equation.
- In the future, we would like to explore more intricate examples and implement more sophisticated numerical methods for the integration, since Euler is unstable. As we have mentioned, in modern control systems, controllers operate on discrete-time signals, making the discretization of continuous-time models necessary.
- The discretization of field theories and the formulation of a corresponding HJ theory to study families of discrete Hamiltonian mappings as in [66] and the effects of diffusion.
- Study of integrability properties of discrete solitons as in [67] by developing a discrete field HJ theory.
- To redefine step by step our HJ theory to solve more real-world scenarios. The generalization of an HJ theory to classical mechanics and field theory from a discrete or quantum point of view will bring several potential difficulties. These can arise from both the theoretical aspects of the method and the practical considerations of implementation. Some challenges will be nonlinear effects, chaos and sensitivity, as in [66,67,68].
- To find specific geometric integrators that preserve the contact discrete geometry. In this paper, we have used a very simple Euler method to depict the dynamic of simple discrete contact systems. Nonetheless, the Euler method does not preserve the geometric background of the system, and this is why we need to come up with specific integrators for these systems.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arnold, V.I. Mathematical Methods of Classical Mechanics, 2nd ed.; Vogtmann, K.; Weinstein, A., Translators; Graduate Texts in Mathematics; Springer: New York, NY, USA, 1989; Volume 60, p. xvi+508. [Google Scholar]
- Goldstein, H. Classical Mechanics, 2nd ed.; Addison-Wesley Series in Physics; Addison-Wesley Publishing Co.: Reading, MA, USA, 1980; p. xiv+672. [Google Scholar]
- Abraham, R.; Marsden, J. Foundations of Mechanics; AMS Chelsea Publishing, AMS Chelsea Pub./American Mathematical Society: New York, NY, USA, 2008. [Google Scholar]
- Cariñena, J.F.; Gràcia, X.; Marmo, G.; Martínez, E.; Muñoz Lecanda, M.G.; Román-Roy, N. Geometric Hamilton–Jacobi theory. Int. J. Geom. Methods Mod. Phys. 2006, 3, 1417–1458. [Google Scholar] [CrossRef]
- Abraham, R.; Marsden, J.E. Foundations of mechanics; Benjamin/Cummings Publishing Co., Inc., Advanced Book Program: Reading, MA, USA, 1978; pp. xxii+m–xvi+806. [Google Scholar]
- Cariñena, J.F.; Gràcia, X.; Marmo, G.; Martínez, E.; Muñoz Lecanda, M.G.; Román-Roy, N. Geometric Hamilton-Jacobi theory for nonholonomic dynamical systems. Int. J. Geom. Methods Mod. Phys. 2010, 7, 431–454. [Google Scholar] [CrossRef]
- Cariñena, J.F.; Gràcia, X.; Marmo, G.; Martínez, E.; Muñoz Lecanda, M.C.; Román-Roy, N. Structural aspects of Hamilton-Jacobi theory. Int. J. Geom. Methods Mod. Phys. 2016, 13, 1650017. [Google Scholar] [CrossRef]
- Cariñena, J.F.; Martínez, E.; Marmo, G.; Gràcia, X.; Muñoz Lecanda, M.C. A quantum route to Hamilton-Jacobi equation: Comments and remarks. In Geometry of Jets and Fields; The Institute of Mathematics of the Polish Academy of Sciences: Warsaw, Poland, 2016; Volume 110, pp. 41–56. [Google Scholar]
- de León, M.; Sardón, C. Geometric Hamilton-Jacobi theory on Nambu-Poisson manifolds. J. Math. Phys. 2017, 58, 033508. [Google Scholar] [CrossRef]
- de León, M.; Sardón, C. Cosymplectic and contact structures for time-dependent and dissipative Hamiltonian systems. J. Phys. A 2017, 50, 255205. [Google Scholar] [CrossRef]
- de León, M.; Sardón, C. Geometry of the discrete Hamilton-Jacobi equation: Applications in optimal control. Rep. Math. Phys. 2018, 81, 39–63. [Google Scholar] [CrossRef]
- Iglesias-Ponte, D.; de León, M.; Martín de Diego, D. Towards a Hamilton-Jacobi theory for nonholonomic mechanical systems. J. Phys. A 2008, 41, 015205. [Google Scholar] [CrossRef]
- de León, M.; Sardón, C. A geometric Hamilton-Jacobi theory on a Nambu-Jacobi manifold. Int. J. Geom. Methods Mod. Phys. 2019, 16, 1940007. [Google Scholar] [CrossRef]
- de León, M.; Marrero, J.C.; de Diego, D.M. A geometric Hamilton-Jacobi theory for classical field theories. In Variations, Geometry and Physics; Nova Science Publishers: New York, NY, USA, 2009; pp. 129–140. [Google Scholar]
- Colombo, L.; De Léon, M.; Prieto-Martínez, P.D.; Román-Roy, N. Unified formalism for the generalized kth-order Hamilton-Jacobi problem. Int. J. Geom. Methods Mod. Phys. 2014, 11, 1460037. [Google Scholar] [CrossRef]
- de León, M.; Martín de Diego, D.; Vaquero, M. A Hamilton-Jacobi theory on Poisson manifolds. J. Geom. Mech. 2014, 6, 121–140. [Google Scholar] [CrossRef]
- Esen, O.; de León, M.; Sardón, C.; Zajac, M. Hamilton-Jacobi formalism on locally conformally symplectic manifolds. J. Math. Phys. 2021, 62, 033506. [Google Scholar] [CrossRef]
- Esen, O.; de León, M.; Sardón, C. A Hamilton-Jacobi formalism for higher order implicit Lagrangians. J. Phys. A 2020, 53, 075204. [Google Scholar] [CrossRef]
- Esen, O.; de León, M.; Lainz, M.; Sardón, C.; Zajac, M. Reviewing the Geometric Hamilton-Jacobi Theory concerning Jacobi and Leibniz identities. arXiv 2022, arXiv:2202.06896. [Google Scholar] [CrossRef]
- Román-Roy, N. An overview of the Hamilton–Jacobi theory: The classical and geometrical approaches and some extensions and applications. Mathematics 2021, 9, 85. [Google Scholar] [CrossRef]
- Atkinson, K.; Han, W. Theoretical Numerical Analysis, 3rd ed.; Texts in Applied Mathematics; Springer: Dordrecht, The Netherlands, 2009; Volume 39, p. xvi+625, A functional analysis framework. [Google Scholar]
- Iserles, A. A First Course in the Numerical Analysis of Differential Equations, 2nd ed.; Cambridge Texts in Applied Mathematics, Cambridge University Press: Cambridge, UK, 2009; p. xx+459. [Google Scholar]
- Blanes, S.; Casas, F. A Concise Introduction to Geometric Numerical Integration; Monographs and Research Notes in Mathematics; CRC Press: Boca Raton, FL, USA, 2016; p. xiv+218. [Google Scholar]
- Hairer, E.; Lubich, C.; Wanner, G. Geometric Numerical Integration; Springer Series in Computational Mathematics; Springer: Berlin/Heidelberg, Germany, 2010; Volume 31, p. xviii+644, Structure-preserving algorithms for ordinary differential equations, Reprint of the second (2006) edition. [Google Scholar]
- Candy, J.; Rozmus, W. A symplectic integration algorithm for separable Hamiltonian functions. J. Comput. Phys. 1991, 92, 230–256. [Google Scholar] [CrossRef]
- Yoshida, H. Construction of higher order symplectic integrators. Phys. Lett. A 1990, 150, 262–268. [Google Scholar] [CrossRef]
- Quispel, G.R.W.; McLaren, D.I. A new class of energy-preserving numerical integration methods. J. Phys. A 2008, 41, 045206. [Google Scholar] [CrossRef]
- LaBudde, R.A.; Greenspan, D. Energy and momentum conserving methods of arbitrary order of the numerical integration of equations of motion. I. Motion of a single particle. Numer. Math. 1975, 25, 323–346. [Google Scholar] [CrossRef]
- Bravetti, A.; Cruz, H.; Tapias, D. Contact Hamiltonian mechanics. Ann. Phys. 2017, 376, 17–39. [Google Scholar] [CrossRef]
- de León, M.; Gaset, J.; Lainz, M.; Rivas, X.; Román-Roy, N. Unified Lagrangian-Hamiltonian formalism for contact systems. Fortschr. Phys. 2020, 68, 2000045. [Google Scholar] [CrossRef]
- de León, M.; Lainz Valcázar, M. Contact Hamiltonian systems. J. Math. Phys. 2019, 60, 102902. [Google Scholar] [CrossRef]
- de León, M.; Lainz Valcázar, M. A review on contact Hamiltonian and Lagrangian systems. arXiv 2020, arXiv:2011.05579. [Google Scholar]
- de León, M.; Lainz Valcázar, M. Infinitesimal symmetries in contact Hamiltonian systems. J. Geom. Phys. 2020, 153, 103651. [Google Scholar] [CrossRef]
- Herglotz, G. Berührungstransformationen, Lectures at the University of Göttingen; University of Göttingen: Göttingen, Germany, 1930. [Google Scholar]
- Herglotz, G. Vorlesungen über die Mechanik der Kontinua; Teubner-Archiv zur Mathematik [Teubner Archive on Mathematics]; BSB B. G. Teubner Verlagsgesellschaft: Leipzig, Germany, 1985; Volume 3, p. 251, With a preface by H. Beckert, Edited and with a foreword by Ronald B. Guenther and Hans Schwerdtfeger, With English, French and Russian summaries. [Google Scholar]
- Bravetti, A. Contact Hamiltonian dynamics: The concept and its use. Entropy 2017, 19, 535. [Google Scholar] [CrossRef]
- Bravetti, A. Contact geometry and thermodynamics. Int. J. Geom. Methods Mod. Phys. 2019, 16, 1940003. [Google Scholar] [CrossRef]
- Gaset, J.; Gracia, X.; Munoz-Lecanda, M.C.; Rivas, X.; Román-Roy, N. New contributions to the Hamiltonian and Lagrangian contact formalisms for dissipative mechanical systems and their symmetries. Int. J. Geom. Methods Mod. Phys. 2020, 17, 2050090. [Google Scholar] [CrossRef]
- Goto, S. Contact geometric descriptions of vector fields on dually flat spaces and their applications in electric circuit models and nonequilibrium statistical mechanics. J. Math. Phys. 2016, 57, 102702. [Google Scholar] [CrossRef]
- Grmela, M. Contact geometry of mesoscopic thermodynamics and dynamics. Entropy 2014, 16, 1652–1686. [Google Scholar] [CrossRef]
- Mrugala, R.; Nulton, J.D.; Schön, J.C.; Salamon, P. Contact structure in thermodynamic theory. Rep. Math. Phys. 1991, 29, 109–121. [Google Scholar] [CrossRef]
- Rajeev, S.G. Quantization of contact manifolds and thermodynamics. Ann. Phys. 2008, 323, 768–782. [Google Scholar] [CrossRef]
- Marsden, J.E.; West, M. Discrete mechanics and variational integrators. Acta Numer. 2001, 10, 357–514. [Google Scholar] [CrossRef]
- Guibout, V.M.; Bloch, A.M. Discrete variational principles and Hamilton-Jacobi theory for mechanical systems and optimal control problems. arXiv 2004, arXiv:math/0409296. [Google Scholar]
- Marsden, J.E. Lectures on Mechanics; London Mathematical Society Lecture Note Series; Cambridge University Press: Cambridge, UK, 1992; Volume 174, p. xii+254. [Google Scholar]
- Lall, S.; West, M. Discrete variational Hamiltonian mechanics. J. Phys. A 2006, 39, 5509–5519. [Google Scholar] [CrossRef]
- Budd, C.J.; Piggott, M.D. Geometric integration and its applications. In Handbook of Numerical Analysis, Vol. XI; North-Holland: Amsterdam, The Nederland, 2003; pp. 35–139. [Google Scholar]
- Bravetti, A.; Seri, M.; Vermeeren, M.; Zadra, F. Numerical integration in celestial mechanics: A case for contact geometry. Celest. Mech. Dynam. Astron. 2020, 132, 7. [Google Scholar] [CrossRef]
- Bravetti, A.; Seri, M.; Zadra, F. New directions for contact integrators. In Proceedings of the International Conference on Geometric Science of Information, St. Malo, France, 30 August–1 September 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 209–216. [Google Scholar]
- Simoes, A.A.; de León, M.; Lainz Valcázar, M.; de Diego, D.M. Contact geometry for simple thermodynamical systems with friction. Proc. A. 2020, 476, 20200244. [Google Scholar] [CrossRef]
- Simoes, A.A.; Martín de Diego, D.; Lainz Valcázar, M.; de León, M. On the geometry of discrete contact mechanics. J. Nonlinear Sci. 2021, 31, 53. [Google Scholar] [CrossRef]
- Vermeeren, M.; Bravetti, A.; Seri, M. Contact variational integrators. J. Phys. A 2019, 52, 445206. [Google Scholar] [CrossRef]
- Ohsawa, T.; Bloch, A.M.; Leok, M. Discrete Hamilton-Jacobi theory. SIAM J. Control Optim. 2011, 49, 1829–1856. [Google Scholar] [CrossRef]
- Banyaga, A. The Structure of Classical Diffeomorphism Groups; Mathematics and Its Applications; Kluwer Academic Publishers Group: Dordrecht, The Netherlands, 1997; Volume 400, p. xii+197. [Google Scholar]
- de León, M.; Lainz, M.V. Singular Lagrangians and precontact Hamiltonian systems. Int. J. Geom. Methods Mod. Phys. 2019, 16, 1950158. [Google Scholar] [CrossRef]
- Guenther, R.B.; Schwerdtfeger, H.; Herglotz, G.; Guenther, C.; Gottsch, J. The Herglotz Lectures on Contact Transformations and Hamiltonian Systems; Juliusz Schauder Center for Nonlinear Studies; Nicholas Copernicus University: Toruń, Poland, 1996. [Google Scholar]
- Esen, O.; Lainz Valcázar, M.; de León, M.; Marrero, J.C. Contact dynamics: Legendrian and Lagrangian submanifolds. Mathematics 2021, 9, 2704. [Google Scholar] [CrossRef]
- de León, M.; Lainz, M.; Muñiz-Brea, Á. The Hamilton–Jacobi theory for contact Hamiltonian systems. Mathematics 2021, 9, 1993. [Google Scholar] [CrossRef]
- Esen, O.; Valcázar, M.L.; de León, M.; Sardón, C. Implicit Contact Dynamics and Hamilton-Jacobi Theory. arXiv 2021, arXiv:2109.14921. [Google Scholar] [CrossRef]
- de León, M.; Lainz, M.; López-Gordón, A. Discrete Hamilton–Jacobi theory for systems with external forces. J. Phys. Math. Theor. 2022, 55, 205201. [Google Scholar] [CrossRef]
- Simoes, A.A.; de Diego, D.M.; Valcázar, M.L.; de León, M. The geometry of some thermodynamic systems. In Geometric Structures of Statistical Physics, Information Geometry, and Learning; Springer: Cham, Switzerland, 2021; Volume 361, pp. 247–275. [Google Scholar]
- Tulczyjew, W.M. The Legendre transformation. Ann. Inst. H. Poincaré Sect. A (N.S.) 1977, 27, 101–114. [Google Scholar]
- Leok, M.; Ohsawa, T. Discrete Dirac structures and implicit discrete Lagrangian and Hamiltonian systems. In XVIII International Fall Workshop on Geometry and Physics; American Institute of Physics: Melville, NY, USA, 2010; Volume 1260, pp. 91–102. [Google Scholar]
- Iglesias-Ponte, D.; Marrero, J.C.; Martín de Diego, D.; Padrón, E. Discrete dynamics in implicit form. Discret. Contin. Dyn. Syst. 2013, 33, 1117–1135. [Google Scholar] [CrossRef]
- Esen, O.; de León, M.; Sardón, C. A Hamilton-Jacobi theory for implicit differential systems. J. Math. Phys. 2018, 59, 022902. [Google Scholar] [CrossRef]
- Borin, D.; Livorati, A.L.P.; Leonel, E.D. An investigation of the survival probability for chaotic diffusion in a family of discrete Hamiltonian mappings. Chaos Solitons Fractals 2023, 175, 113965. [Google Scholar] [CrossRef]
- Yuan, C.; Yang, H.; Meng, X.; Tian, Y.; Zhou, Q.; Liu, W. Modulational instability and discrete rogue waves with adjustable positions for a two-component higher-order Ablowitz–Ladik system associated with 4 × 4 Lax pair. Chaos Solitons Fractals 2023, 168, 113180. [Google Scholar] [CrossRef]
- Al-Raeei, M. Applying fractional quantum mechanics to systems with electrical screening effects. Chaos Solitons Fractals 2021, 150, 111209. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esen, O.; Sardón, C.; Zajac, M. A Discrete Hamilton–Jacobi Theory for Contact Hamiltonian Dynamics. Mathematics 2024, 12, 2342. https://doi.org/10.3390/math12152342
Esen O, Sardón C, Zajac M. A Discrete Hamilton–Jacobi Theory for Contact Hamiltonian Dynamics. Mathematics. 2024; 12(15):2342. https://doi.org/10.3390/math12152342
Chicago/Turabian StyleEsen, Oğul, Cristina Sardón, and Marcin Zajac. 2024. "A Discrete Hamilton–Jacobi Theory for Contact Hamiltonian Dynamics" Mathematics 12, no. 15: 2342. https://doi.org/10.3390/math12152342
APA StyleEsen, O., Sardón, C., & Zajac, M. (2024). A Discrete Hamilton–Jacobi Theory for Contact Hamiltonian Dynamics. Mathematics, 12(15), 2342. https://doi.org/10.3390/math12152342






