Research on Stability and Bifurcation for Two-Dimensional Two-Parameter Squared Discrete Dynamical Systems
Abstract
:1. Introduction
2. Existence and Stability of Fixed Points
2.1. Existence of Fixed Points
2.2. Stability at the Fixed Point
- (1)
- When :
- (2)
- When :
- (3)
- When :
2.3. Stability at the Nonzero Fixed Point
- (1)
- When :
- (2)
- When :
- (3)
- When :
3. Bifurcation Analysis
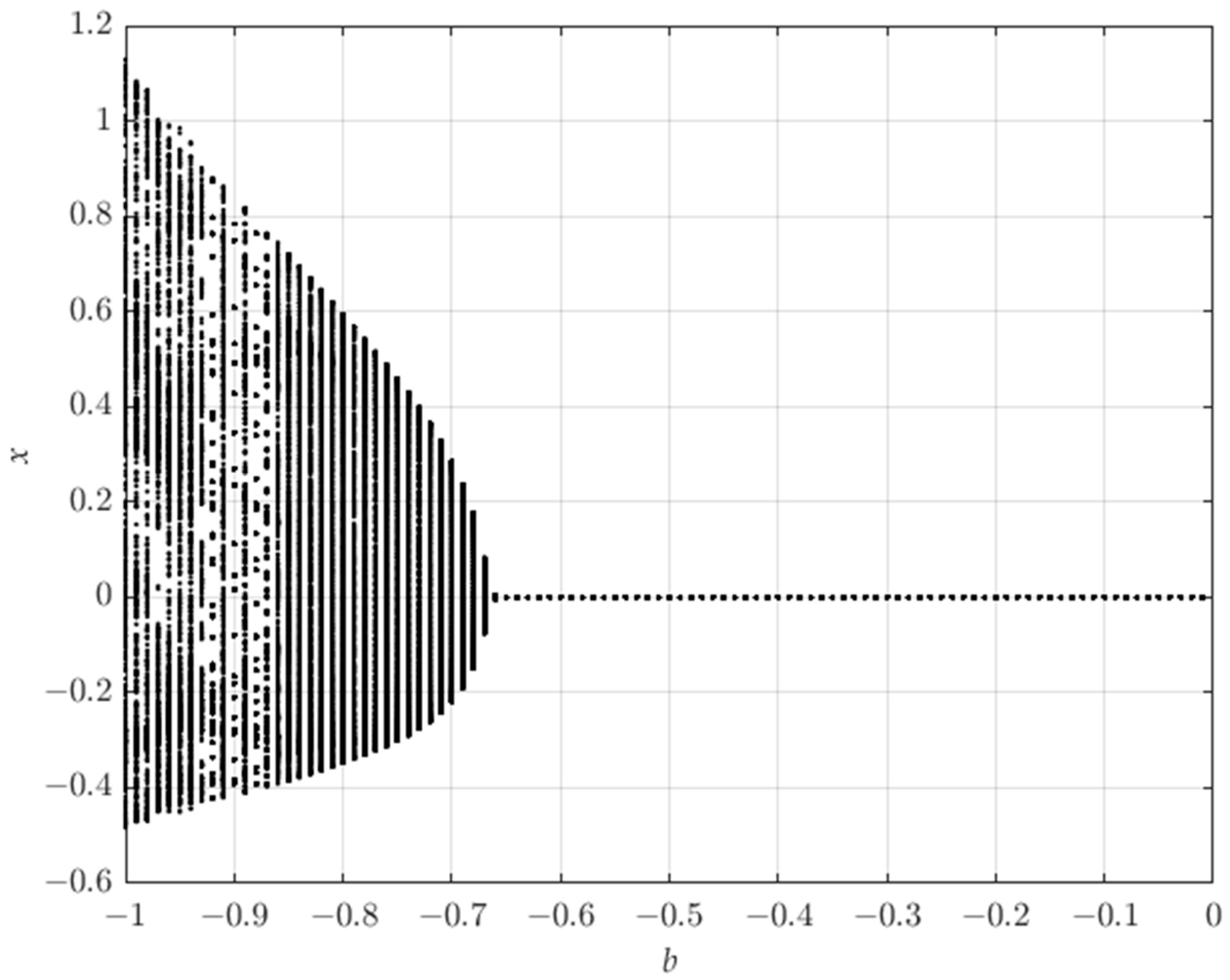
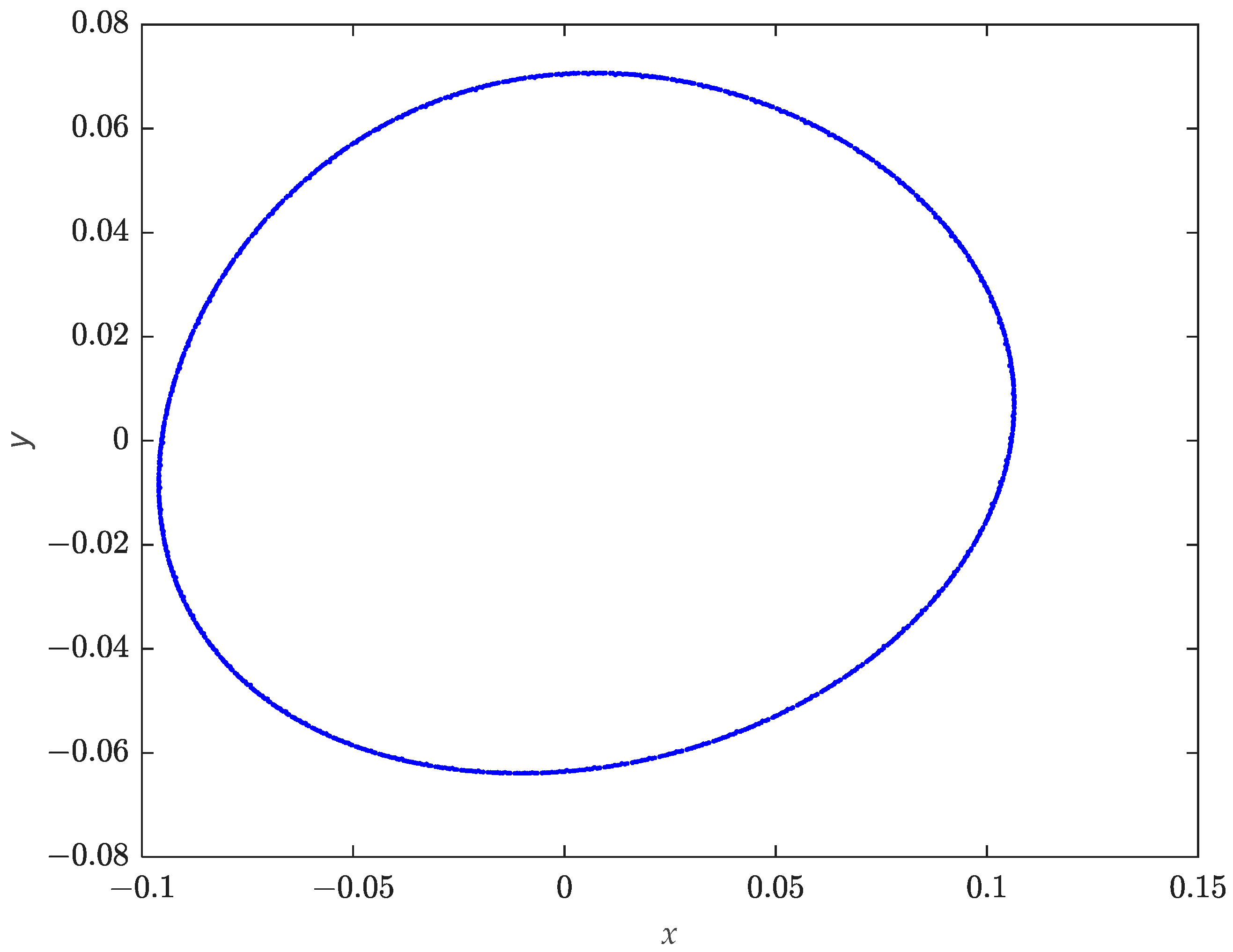
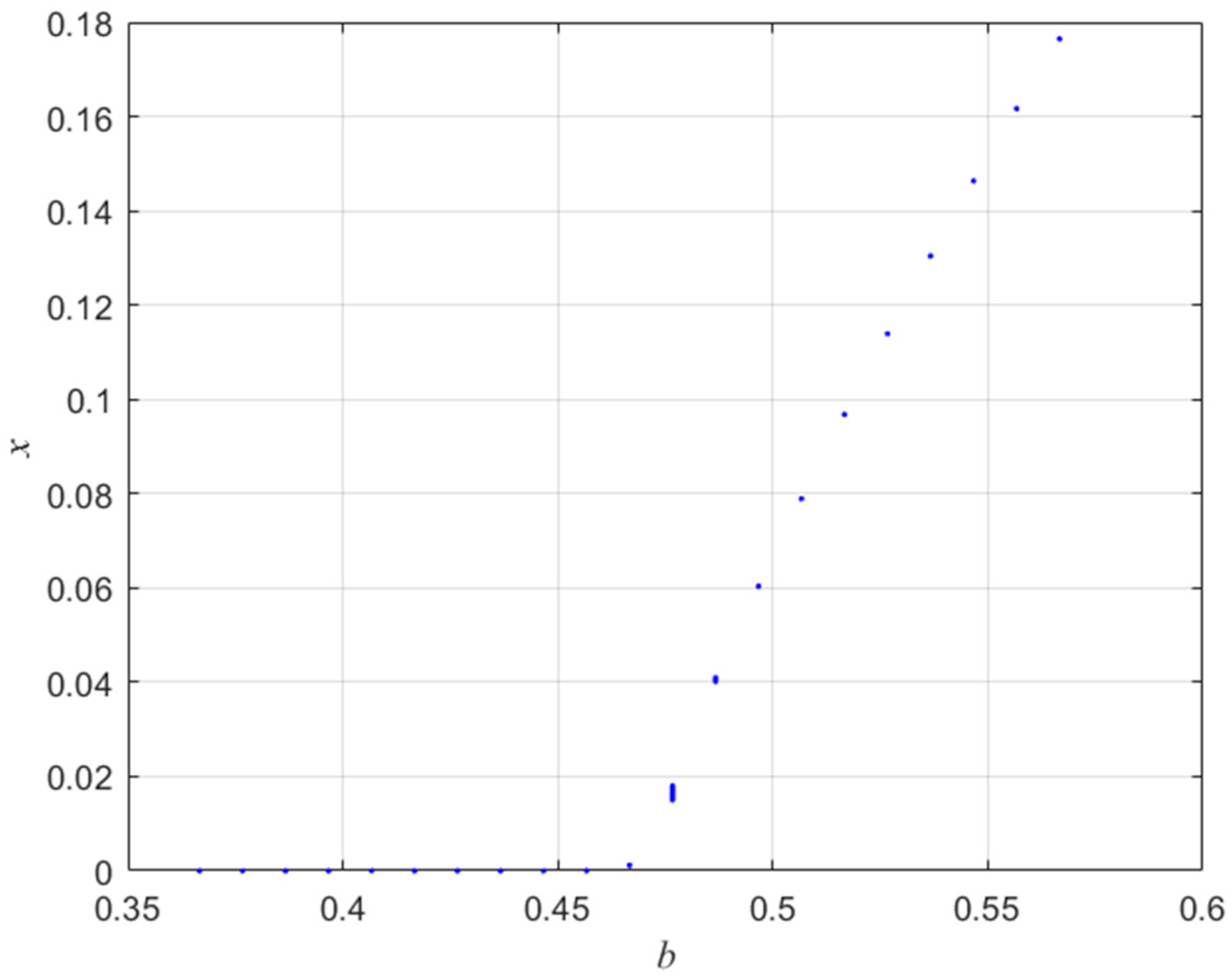
4. Numerical Analysis
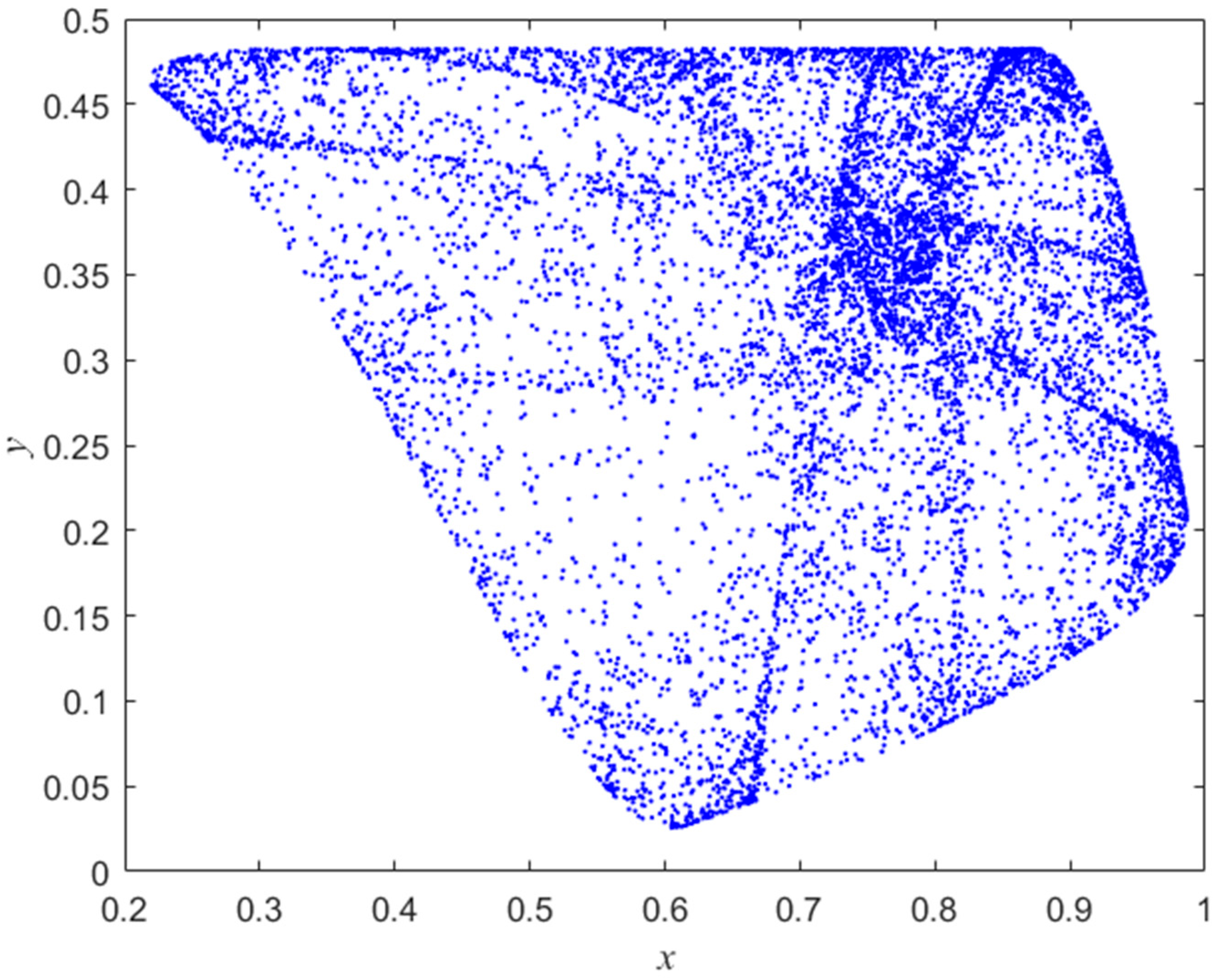
4.1. Numerical Simulations on the Existence of Bifurcations in the Proposed System (1)
4.2. Numerical Simulations of Image Encryption with the Proposed Bifurcation System (1)
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Strogatz, S. Sync: The Emerging Science of Spontaneous Order; Hyperion: New York, NY, USA, 2003. [Google Scholar]
- Udwadia, F.E.; Raju, N. Dynamics of coupled nonlinear maps and its application to ecological modeling. Appl. Math. Comput. 1997, 82, 137–179. [Google Scholar] [CrossRef]
- Zengru, D.; Sanglier, M. A two-dimensional logistic model for the interaction of demand and supply and its bifurcations. Chao Solitons Fractals 1996, 7, 2259–2266. [Google Scholar] [CrossRef]
- Barrat, A.; Barthelemy, M.; Vespignani, A. Dynamical Processes on Complex Networks; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Jike, W.; Kefu, H. Bifurcation Problems and Numerical Methods for Them; Beijing Institute of Technology Press: Beijing, China, 2019. [Google Scholar]
- May, R.M. Simple mathematical models with very complicated dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef] [PubMed]
- Whitley, D. Discrete dynamical systems in dimensions one and two. Bull. Lond. Math. Soc. 1983, 15, 177–217. [Google Scholar] [CrossRef]
- Pareek, N.K.; Patidar, V.; Sud, K.K. Image encryption using chaotic logistic map. Image Vis. Comput. 2006, 24, 926–934. [Google Scholar] [CrossRef]
- Li, S.; Ding, W.; Yin, B. A novel delay linear coupling logistics map model for color image encryption. Entropy 2018, 20, 463. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Alzabut, J.; Kumari, S. Dynamical properties of a novel one dimensional chaotic map. Math. Biosci. Eng. 2022, 19, 2489–2505. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Yang, S.; Ye, R. Efficient symmetric image encryption by using a novel 2D chaotic system. IET Image Process. 2020, 14, 1157–1163. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; He, Y.; Wang, X.Y. Spatiotemporal chaos in mixed linear–nonlinear two-dimensional coupled logistic map lattice. Phys. A Stat. Mech. Its Appl. 2018, 490, 148–160. [Google Scholar] [CrossRef]
- Wiggins, S. Introduction to Applied Nonlinear Dynamical Systems and Chaos; Springer Science + Business Media: New York, NY, USA, 1990; Volume 9. [Google Scholar]
- Benedicks, M.; Carleson, L. The dynamics of the Hénon map. Ann. Math. 1991, 133, 73–169. [Google Scholar] [CrossRef]
- Peng, Y.; Sun, K.; He, S. A discrete memristor model and its application in Hénon map. Chaos Solitons Fractals 2020, 137, 109873. [Google Scholar] [CrossRef]
- Gao, X. A color image encryption algorithm based on an improved Hénon map. Phys. Scr. 2021, 96, 065203. [Google Scholar] [CrossRef]
- Ran, J. Discrete chaos in a novel two-dimensional fractional chaotic map. Adv. Differ. Equ. 2018, 2018, 294. [Google Scholar] [CrossRef]
- Soula, Y.; Jahanshahi, H.; Al-Barakati, A.A.; Moroz, I. Dynamics and Global Bifurcations in Two Symmetrically Coupled Noninvertible Maps. Mathematics 2023, 11, 1517. [Google Scholar] [CrossRef]
- Elsadany, A.A.; Yousef, A.M.; Elsonbaty, A. Further analytical bifurcation analysis and applications of coupled logistic maps. Appl. Math. Comput. 2018, 338, 314–336. [Google Scholar] [CrossRef]
- Gao, Y. Complex dynamics in a two-dimensional noninvertible map. Chaos Solut. Fractals 2009, 39, 1798–1810. [Google Scholar] [CrossRef]
- Meng, J.D.; Bao, B.C.; Xu, Q. Dynamics of two-dimensional parabolic discrete mapping. J. Phys. 2011, 60, 010504. [Google Scholar]
- Chowdhury, R.A.; Chowdhury, K. Bifurcations in a coupled logistic map. Int. J. Theor. Phys. 1991, 30, 97–106. [Google Scholar] [CrossRef]
- Kaneko, K. From globally coupled maps to complex-systems biology. Chaos Interdiscip. J. Nonlinear Sci. 2015, 25, 097608. [Google Scholar] [CrossRef] [PubMed]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Applied Mathematical Sciences; Springer Science + Business Media: New York, NY, USA, 1983; Volume 42, pp. 162–165. [Google Scholar]
- Koepf, W. Efficient computation of truncated power series: Direct approach versus newton’s method. Util. Math. 2010, 83, 37. [Google Scholar]
- Guariglia, E. Fractional calculus, zeta functions and Shannon entropy. Open Math. 2021, 19, 87–100. [Google Scholar] [CrossRef]
- Ripon, S.M. Generalization of a class of logarithmic integrals. Integral Transform. Spec. Funct. 2015, 26, 229–245. [Google Scholar] [CrossRef]
- Li, B.; He, Q. Bifurcation analysis of a two-dimensional discrete Hindmarsh-Rose type model. Adv. Differ. Equ. 2019, 2019, 124. [Google Scholar] [CrossRef]

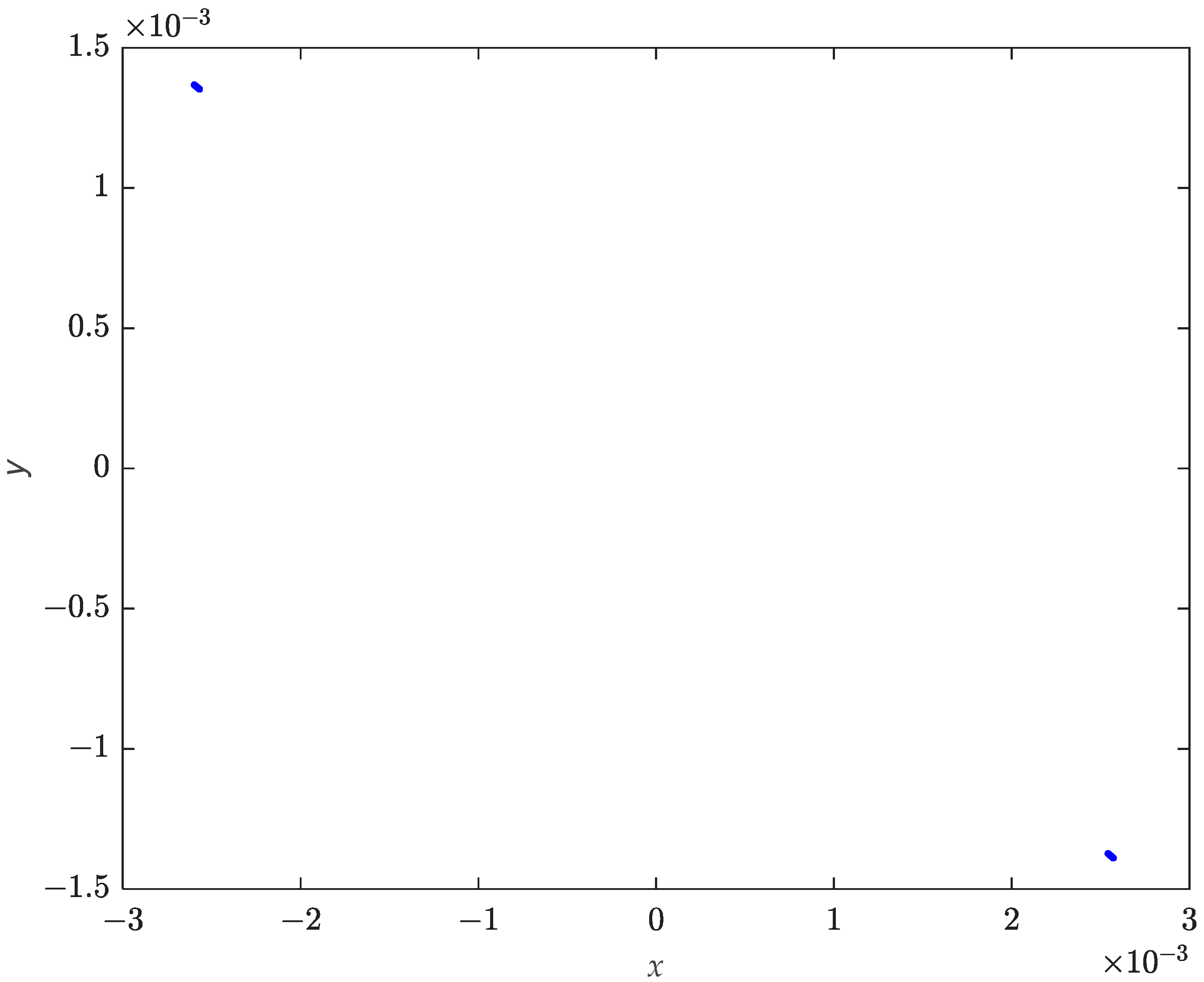

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Zhong, X. Research on Stability and Bifurcation for Two-Dimensional Two-Parameter Squared Discrete Dynamical Systems. Mathematics 2024, 12, 2423. https://doi.org/10.3390/math12152423
Liu L, Zhong X. Research on Stability and Bifurcation for Two-Dimensional Two-Parameter Squared Discrete Dynamical Systems. Mathematics. 2024; 12(15):2423. https://doi.org/10.3390/math12152423
Chicago/Turabian StyleLiu, Limei, and Xitong Zhong. 2024. "Research on Stability and Bifurcation for Two-Dimensional Two-Parameter Squared Discrete Dynamical Systems" Mathematics 12, no. 15: 2423. https://doi.org/10.3390/math12152423




