Pricing Decisions in Dual-Channel Supply Chains Considering the Offline Channel Preference and Service Level
Abstract
:1. Introduction
2. Literature Review
2.1. Research on E-Commerce Sales in the Supply Chain
2.2. The Impact of Consumer’s Preference on the Pricing of a Dual-Channel Supply Chain
2.3. The Impact of Service Level on the Pricing of a Two-Channel Supply Chain
| Author(s) | Supply Chain Structure | Pricing Policies | Service Level | Channel Preference | Green Preference | Service Preference | Price Preference |
|---|---|---|---|---|---|---|---|
| Zhang et al. [1] | One manufacturer, two retailers | √ | √ | √ | |||
| Ke & Liu [3] | Multiple manufacturers, two retailers | √ | √ | √ | |||
| Zong et al. [5] | One manufacturer, two retailers | √ | √ | ||||
| Ji et al. [12] | One manufacturer, two retailers | √ | √ | ||||
| Ali et al. [26] | One manufacturer, two retailers | √ | √ | √ | √ | ||
| Ma & Hong [26] | One manufacturer, two retailers | √ | √ | √ | |||
| This study | One manufacturer, two retailers | √ | √ | √ | √ |
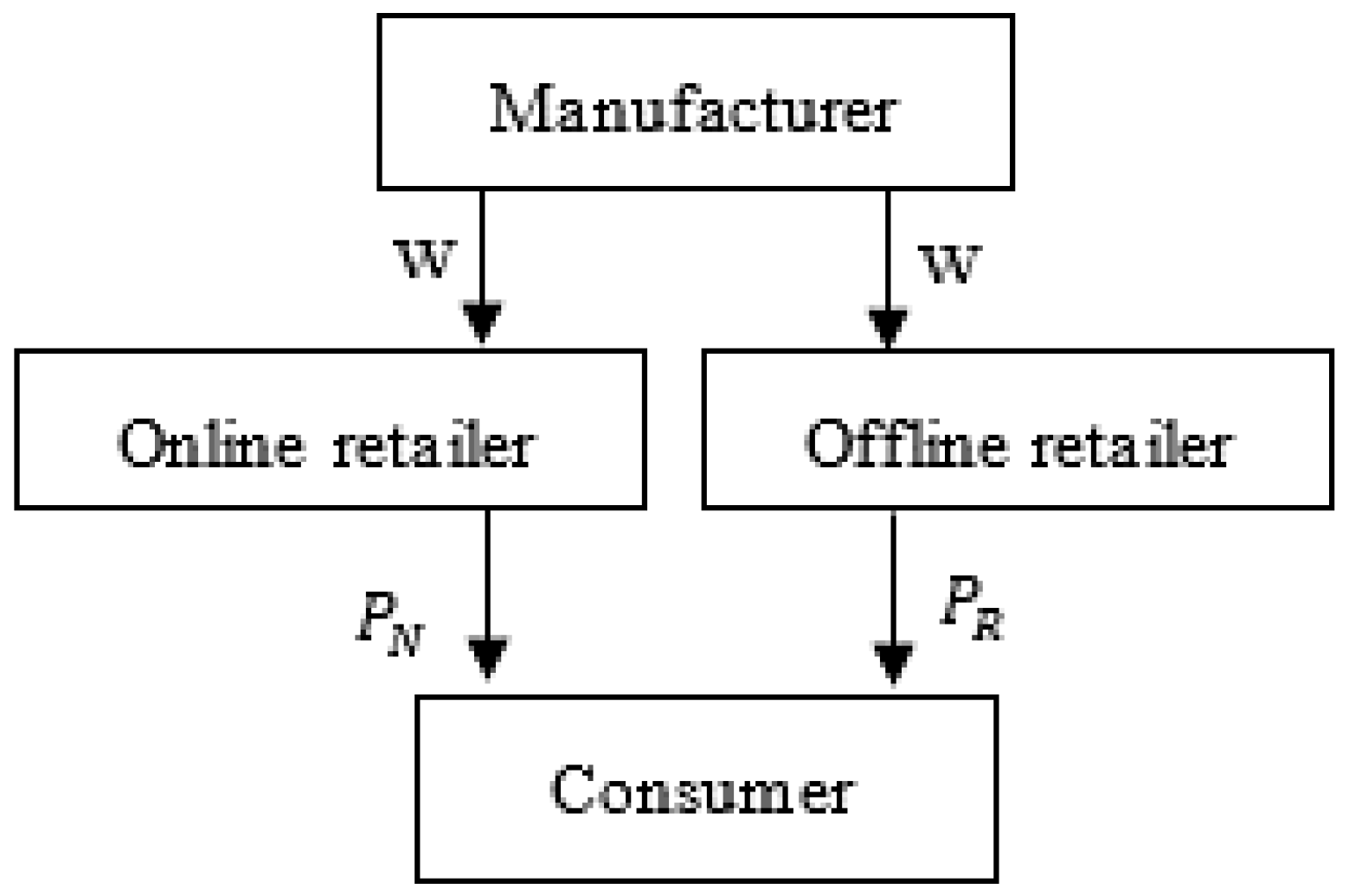
3. The Stackleberg Game Model
3.1. Notations
3.2. Model Formulation
4. Model Analysis
4.1. Centralized Decision-Making
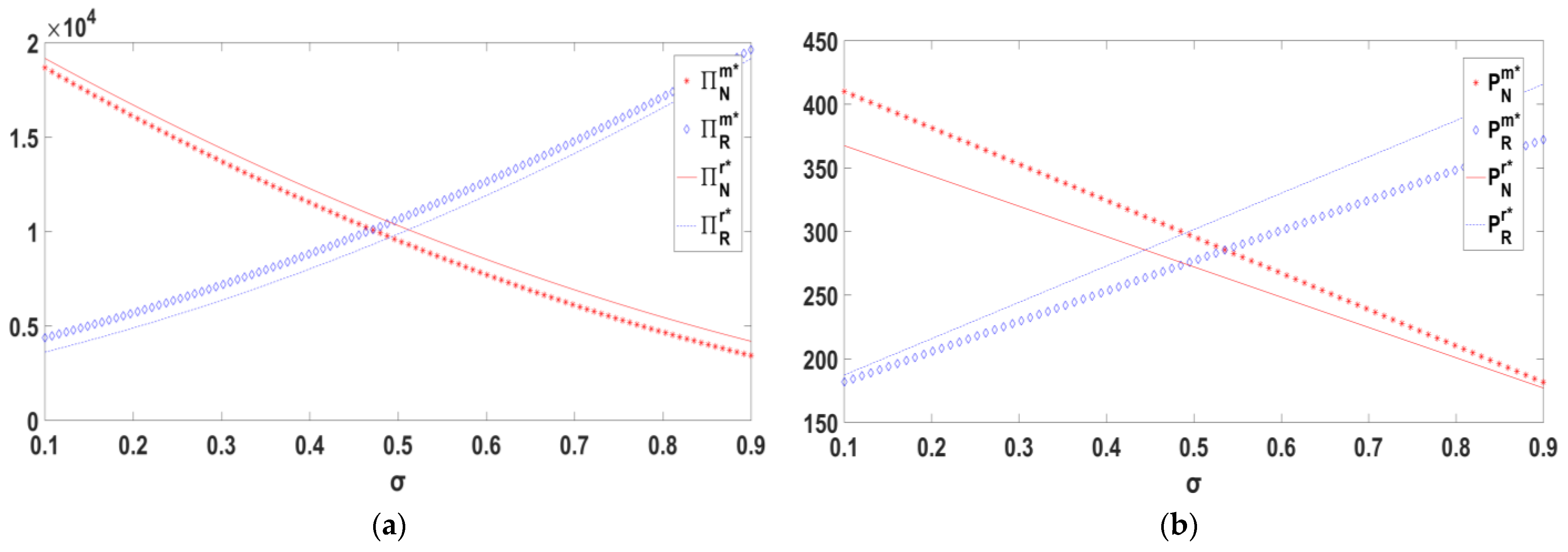
4.2. Decentralized Decision-Making with the Online Retailer Dominant
4.3. Decentralized Decision-Making with the Offline Retailer Dominant
- When , we have . Moreover, when , we have . When , we have .
- When , we have . Moreover, when , we have . When , we have .
- When, we have . Moreover, when , we have . When , we have .
- When , we have . Moreover, when , we have . When , we have .
- When , we have . Moreover, when , we have . When , we have .
- When , we have . Moreover, when , we have . When , we have .
- When, we have . Moreover, when , we have . When , we have .
- When , we have . Moreover, when , we have . When , we have .
5. Numerical Experiments
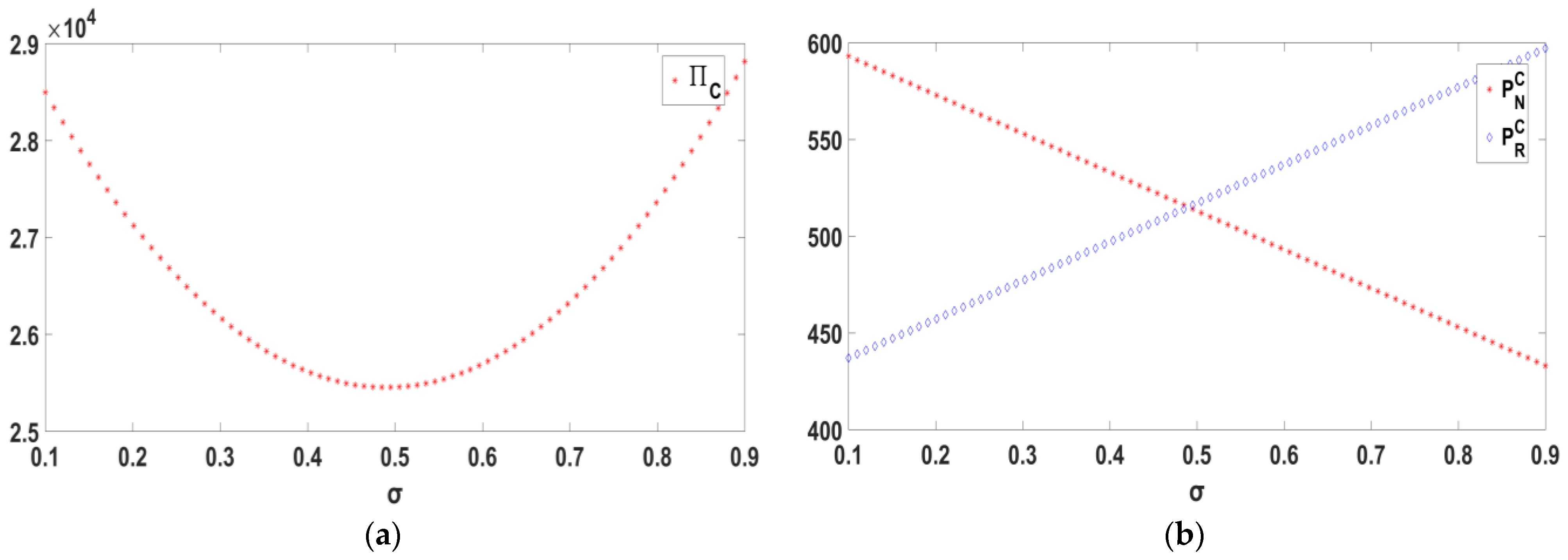
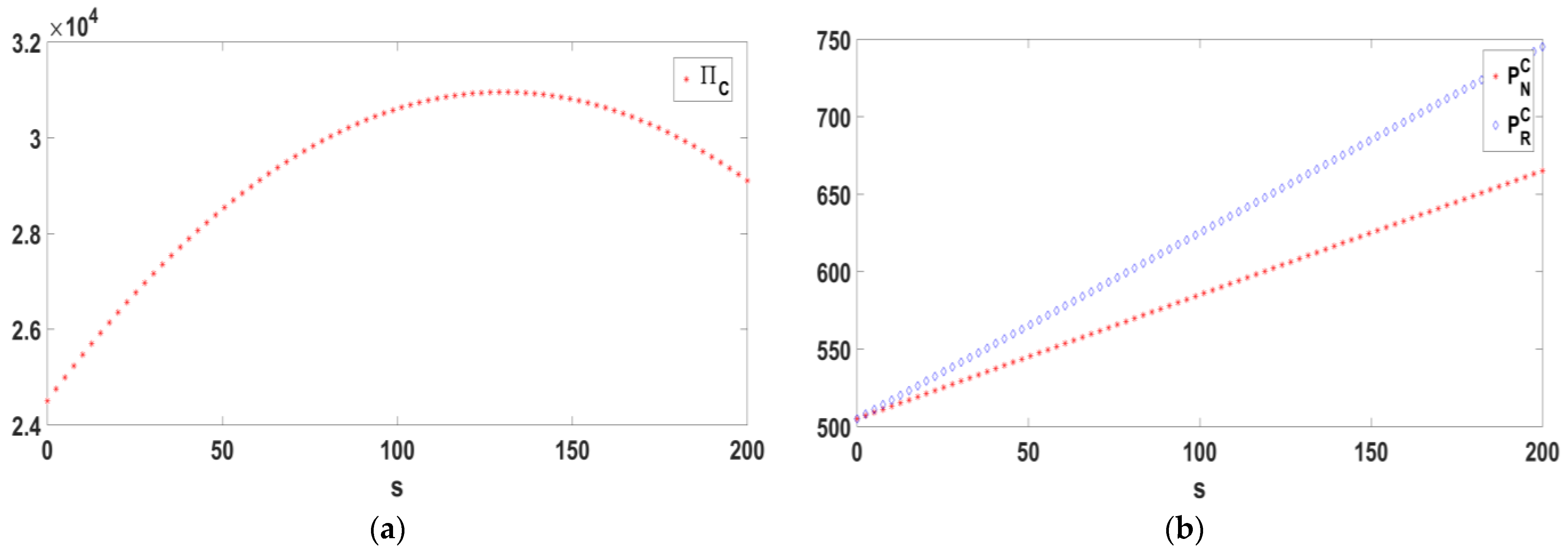
5.1. Centralized Decision-Making
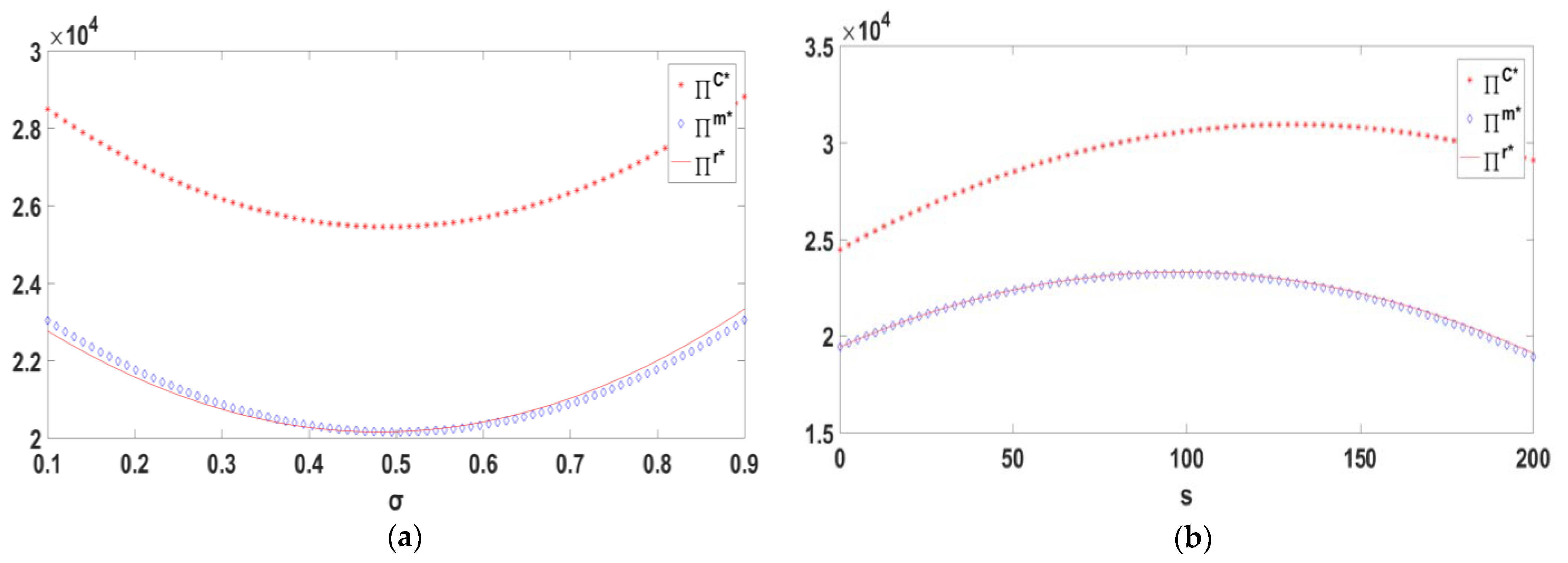
5.2. Decentralized Decision-Making
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Proof of Theorem 1
Appendix A.2. Proof of Corollary 1
Appendix A.3. Proof of Corollary 2
Appendix A.4. Proof of Theorem 2
Appendix A.5. Proof of Corollary 3
Appendix A.6. Proof of Corollary 4
Appendix A.7. Proof of Corollary 5
Appendix A.8. Proof of Corollary 6
References
- Zhang, G.; Dai, G.; Sun, H.; Zhang, G.; Yang, Z. Equilibrium in supply chain network with competition and service level between channels considering consumers’ channel preference. J. Retail. Consum. Serv. 2020, 57, 102199. [Google Scholar] [CrossRef]
- Sharma, A.; Sharma, A.; Kaur, H. Comparative analysis between online and offline shopping approach and behavior of consumers. J. Comput. Theor. Nanosci. 2020, 17, 4965–4970. [Google Scholar] [CrossRef]
- Wang, Z.; Kim, Y. How marketing factors influence online browsing and sales: Evidence from China’s e-commerce market. J. Appl. Bus. Res. 2018, 34, 253–264. [Google Scholar] [CrossRef]
- Ke, H.; Liu, J. Dual-channel supply chain competition with channel preference and sales effort under uncertain environment. Ambient. Intell Hum. Comput. 2017, 8, 781–795. [Google Scholar] [CrossRef]
- Zong, S.; Shen, C. Decision-making and coordination in an e-commerce supply chain under channel selection. OPSEARCH 2022, 60, 326–369. [Google Scholar] [CrossRef]
- Pan, X.; Shankar, B.; Ratchford, B. Price competition between pure play versus bricks and clicks e-tailers: Analytical model and empirical analysis. Adv. Appl. Microecon. 2002, 52, 29–61. [Google Scholar]
- Cattani, W.; Gilland Heese, S. Boiling frogs: Pricing strategies for a manufacturer adding an internet channel. Prod. Oper. Manag. 2006, 15, 40–56. [Google Scholar] [CrossRef]
- Huang, W.; Swaminathan, J.M. Introduction of a second channel: Implications for pricing and profits. Eur. J. Oper. Res. 2009, 19, 258–279. [Google Scholar] [CrossRef]
- Abhishek, V.; Jerath, K.; Zhang, Z.J. Agency selling or reselling? Channel structures in electronic retailing. Manag. Sci. 2016, 62, 2259–2280. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, D.; Cheng, T.; Zhou, R. Decision and coordination of E-commerce closed-loop supply chains with fairness concern. Transp. Res. Part E Logist. Transp. Rev. 2023, 173, 103092. [Google Scholar] [CrossRef]
- Siqin, T.; Yang, L.; Chung, S.; Wen, X. Cross-channel influences in mobile-app-website e-commerce supply chains: When to weaken the influence? Transp. Res. Part E Logist. Transp. Rev. 2023, 182, 103408. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, J.; Li, F.; Xu, Y.; Zhao, J.; Su, J. Risk aversion of B2C cross-border e-commerce supply chain. Sustainability 2022, 14, 8088. [Google Scholar] [CrossRef]
- Ji, J.; Zhang, Z.; Yang, L. Carbon emission reduction decisions in the retail-/dual-channel supply chain with consumers’ preference. J. Clean. Prod. 2017, 141, 852–867. [Google Scholar] [CrossRef]
- Xin, C.; Zhou, Y.; Zhu, X.; Li, L.; Chen, X. Optimal decisions for carbon emission reduction through technological innovation in a hybrid-channel supply chain with consumers’ channel preference. Discret. Dyn. Nat. Soc. 2019, 1–24. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, J.; Xu, B. Designing buy-online-and-pick-up-in-store (bops) contract of dual-channel low-carbon supply chain considering consumers’ low-carbon preference. Math. Probl. Eng. 2020, 1–15. [Google Scholar] [CrossRef]
- Moutaz, K.; Sungjune, P.; George, C. Channel selection and pricing in the presence of retail-captive consumers. Int. J. Prod. Econ. 2010, 125, 84–95. [Google Scholar]
- Xu, S.; Tang, H.; Lin, Z.; Lu, J. Pricing and sales-effort analysis of dual-channel supply chain with channel preference, cross-channel return and free-riding behavior based on revenue-sharing contract. Int. J. Prod. Econ. 2022, 249, 108506. [Google Scholar] [CrossRef]
- Xu, Y.; Tian, Y.; Pang, C.; Tang, H. Manufacturer vs. Retailer: A comparative analysis of different government subsidy strategies in a dual-channel supply chain considering green quality and channel preferences. Mathematics 2024, 12, 1433. [Google Scholar] [CrossRef]
- Wang, R.; Wang, S.; Yan, S. Pricing and coordination strategies of dual channels considering consumers’ channel preferences. Sustainability 2021, 13, 11191. [Google Scholar] [CrossRef]
- Liu, C.; Lee, C.; Linda, L. Pricing strategy in a dual-channel supply chain with overconfident consumers. Comput. Ind. Eng. 2022, 172, 108515. [Google Scholar] [CrossRef]
- Tsay, A.; Agrawal, N. Channel dynamics under price and service competition. Manuf. Serv. Oper. Manag. 2000, 2, 372–391. [Google Scholar] [CrossRef]
- Cao, B.; Zhang, Q.; Cao, M. Optimizing hybrid-channel supply chains with promotional effort and differential product quality: A game-theoretic analysis. Mathematics 2022, 10, 1798. [Google Scholar] [CrossRef]
- Chen, X.; Wang, J.; Xu, P.; Walker, T.; Yang, G. Emission reduction and channel decisions in a two-echelon supply chain considering service spillovers. Mathematics 2023, 11, 4423. [Google Scholar] [CrossRef]
- Dan, B.; Xu, G.; Liu, C. Pricing policies in a dual-channel supply chain with retail services. Int. J. Prod. Econ. 2012, 139, 312–320. [Google Scholar] [CrossRef]
- He, Q.; Shi, T.; Wang, P. Mathematical modeling of pricing and service in the dual channel supply chain considering underservice. Mathematics 2022, 10, 1002. [Google Scholar] [CrossRef]
- Ma, J.; Hong, Y. Dynamic game analysis on pricing and service strategy in a retailer-led supply chain with risk attitudes and free-ride effect. Kybernetes 2022, 51, 1199–1230. [Google Scholar] [CrossRef]
- Ali, S.M.; Rahman, M.H.; Tumpa, T.J. Examining price and service competition among retailer in a supply chain under potential demand disruption. J. Retail. Consum. Serv. 2018, 40, 40–47. [Google Scholar] [CrossRef]
- Wang, S.; Liu, L.; Wen, J.; Wang, G. Product pricing and green decision-making considering consumers’ multiple preference under chain-to-chain competition. Kybernetes 2024, 53, 152–187. [Google Scholar] [CrossRef]
- Meng, Q.; Li, M.; Liu, W.; Li, Z.; Zhang, J. Pricing policies of dual-channel green supply chain: Considering government subsidies and consumers’ dual preferences. Sustain. Prod. Consum. 2021, 26, 1021–1030. [Google Scholar] [CrossRef]
- Wen, X.; Cheng, H.; Cai, J.; Lu, C. Government subside policies and effect analysis in green supply chain. Chin. J. Manag. 2018, 15, 625–632. [Google Scholar]
- Ghosh, D.; Shah, J. A comparative analysis of greening policies across supply chain structures. Int. J. Prod. Econ. 2012, 135, 568–583. [Google Scholar] [CrossRef]
- Xin, B.; Zhang, L.; Xie, L. Pricing decision of a dual-channel supply chain with different payment, corporate social responsibility and service level. RAIRO Oper. Res. 2021, 56, 49–75. [Google Scholar] [CrossRef]
- Kevin, W.; Chhajed, D.; James, D. Direct marketing, indirect profits: A strategic analysis of dual-channel supply-chain design. Manag. Sci. 2003, 49, 1–20. [Google Scholar]
- Peng, H.; Pang, T.; Cong, J. Coordination contracts for a supply chain with yield uncertainty and low-carbon preference. J. Clean. Prod. 2018, 205, 291–302. [Google Scholar] [CrossRef]

| Model Parameters | |
| Cost of commodities | |
| Total potential demand for commodities in the market | |
| Cost of offline retailer services | |
| Coefficient of elasticity of demand for offline service level impact | |
| Service level efficiency | |
| Sensitivity coefficient of consumers to the price of channel demand | |
| Elasticity of the impact of price changes in other channels on consumer demand | |
| Decision Variables | |
| Demand for online and offline channels | |
| Product prices for online and offline channels | |
| Profit from online and offline channels | |
| Total profit of the dual-channel supply chain | |
| Willingness to buy from offline channels | |
| Offline channel service level | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Wu, M. Pricing Decisions in Dual-Channel Supply Chains Considering the Offline Channel Preference and Service Level. Mathematics 2024, 12, 2468. https://doi.org/10.3390/math12162468
Chen Y, Wu M. Pricing Decisions in Dual-Channel Supply Chains Considering the Offline Channel Preference and Service Level. Mathematics. 2024; 12(16):2468. https://doi.org/10.3390/math12162468
Chicago/Turabian StyleChen, Yanting, and Mengling Wu. 2024. "Pricing Decisions in Dual-Channel Supply Chains Considering the Offline Channel Preference and Service Level" Mathematics 12, no. 16: 2468. https://doi.org/10.3390/math12162468
APA StyleChen, Y., & Wu, M. (2024). Pricing Decisions in Dual-Channel Supply Chains Considering the Offline Channel Preference and Service Level. Mathematics, 12(16), 2468. https://doi.org/10.3390/math12162468





