Validation of a Multi-Strain HIV Within-Host Model with AIDS Clinical Studies
Abstract
1. Introduction
2. Model Formulation
3. Identifiability Analysis
Structural Identifiability Analysis
- Globally identifiable: Let p and be two distinct parameter vectors. The model (2) is said to be structurally globally (uniquely) identifiable if
- Locally identifiable: The model (2) is said to be locally structurally locally identifiable if for any p within an open neighborhood of in the parameter space,
4. Parameter Estimation and Data
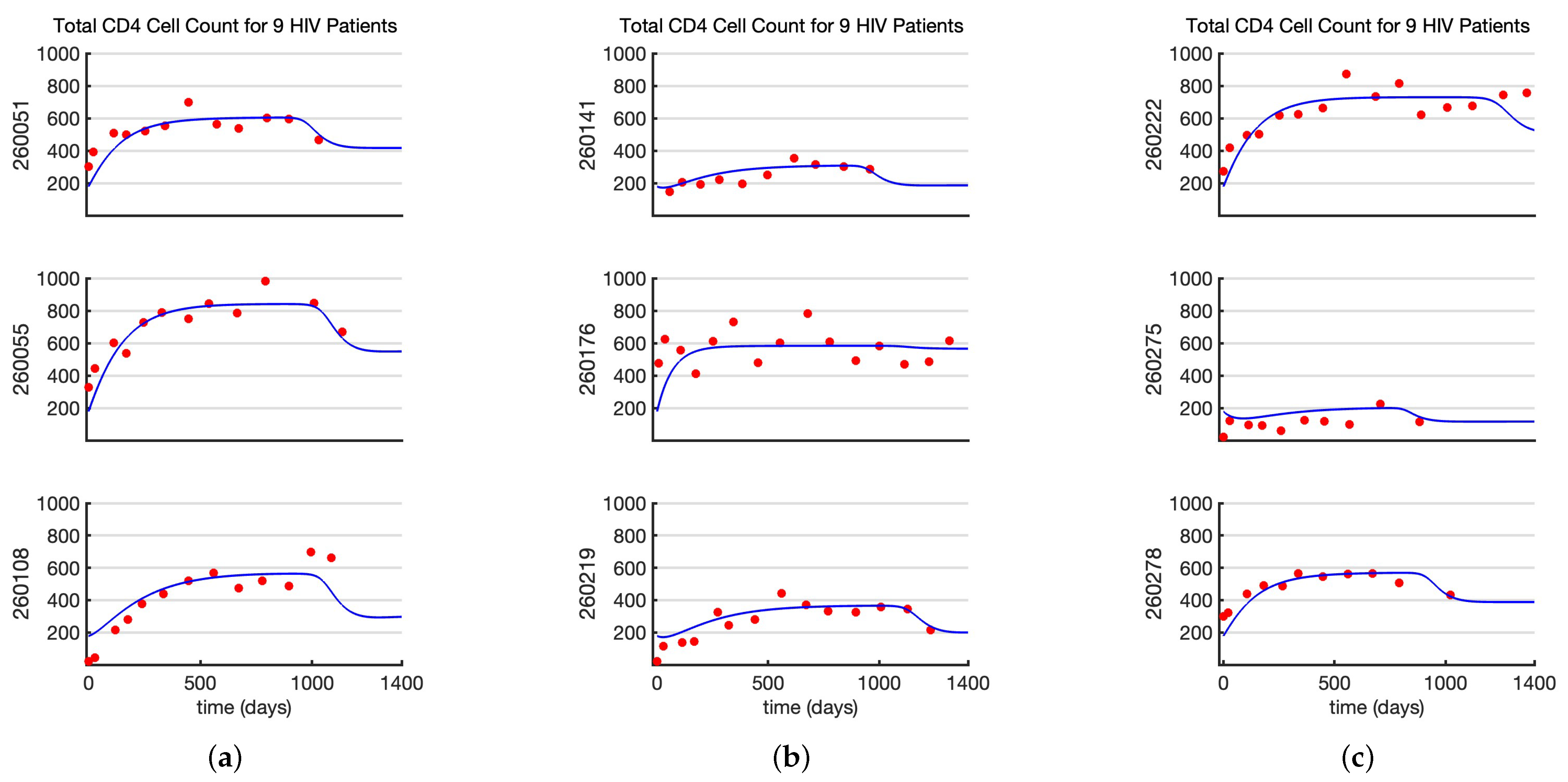
4.1. Estimating Model Parameters from AIDS Clinical Trial Data Set with Nine Patients
- Estimating Model Parameters From Data Set 1: Since we had data from 9 HIV infected individuals from the AIDS clinical data set [35], to estimate the parameters of the within-host model (1), we used the nonlinear mixed effect modeling approach. The nonlinear mixed effect model is definedwhere is the model prediction of total CD4+ T-cell counts at time of the ith individual, and is the CD4+ T-cell count of the ith individual at time . Similarly, is the model prediction of the total viral load on log scale at time of the ith individual, and is the log scale viral load data of the ith individuals at time . The terms and represent the statistical error models. In most cases, , which corresponds to the constant (or additive) error model, and when , it is called the relative (proportional) error model. We assume that the total CD4+ T-cell count follows an additive error model, while the viral load data follow a relative error model. The is the parameter vector for the ith individual. The random effect is then defined aswhere is the fixed population parameter, and is the random effect. The individual parameters follow a normal distribution whose mean is the fixed population parameter , and the standard deviation is .
Practical Identifiability Analysis
4.2. Estimating Model Parameters from Published Data with Single HIV Patient
- Data Set 2: Our structural identifiability analysis shows that measuring sensitive and resistant viral loads separately can uniquely determine the parameters of the within-host model (1). However, we failed to find any AIDS clinical trials in the Stanford HIV Drug Resistance Database [34] that assessed both resistant and sensitive viruses individually. On the other hand, we did find a clinical trial with data published in [3] where the resistant and sensitive virus were measured separately. We used the published data in [3] where HIV-infected individuals were prescribed with the non-nucleoside reverse transcriptase (NNRT) inhibitor Nevirapine (NVP), and their response to the medication was assessed at specific time points: 0, 14, 28, 56, and 140 days after initiating therapy. During these evaluations, the total CD4+ T-cell count per µL was measured, along with the presence of HIV strains (per µL plasma) that are sensitive or resistant to NVP [3].
- Estimating Model Parameters from Data Set 2: To estimate the within-host model (1) parameters, we fit the predicted total CD4+ cell count and drug-resistant and drug-sensitive viral loads to the published data in [3]. Simply put, we minimized the Euclidean distances between the model predictions and the data. Specifically, we minimized the following objective function with constraints to estimate the model parameters.where and are the lower and upper bounds for the parameters p, respectively. We assume known initial conditions. The initial conditions are determined by the data at the initiation of the treatment. As before, we set , cells per µL, and RNA copies per µL. The total CD4+ cell count at is 116 cells per µL; therefore, we set , and the total viral load at is 130 viral RNA copies per µL, that is, . Because the drug-sensitive virus decreases significantly during the first 14 days of the therapy and the drug-resistant virus emerges after 14 days, we assume that the drug-resistant parameters are time-dependent. Moreover, we suppose that the parameters , , and u vary with time. They are specifically described as the step functions listed below.
4.3. Structural Identifiability Analysis of Within-Host Model with Time-Dependent Parameters
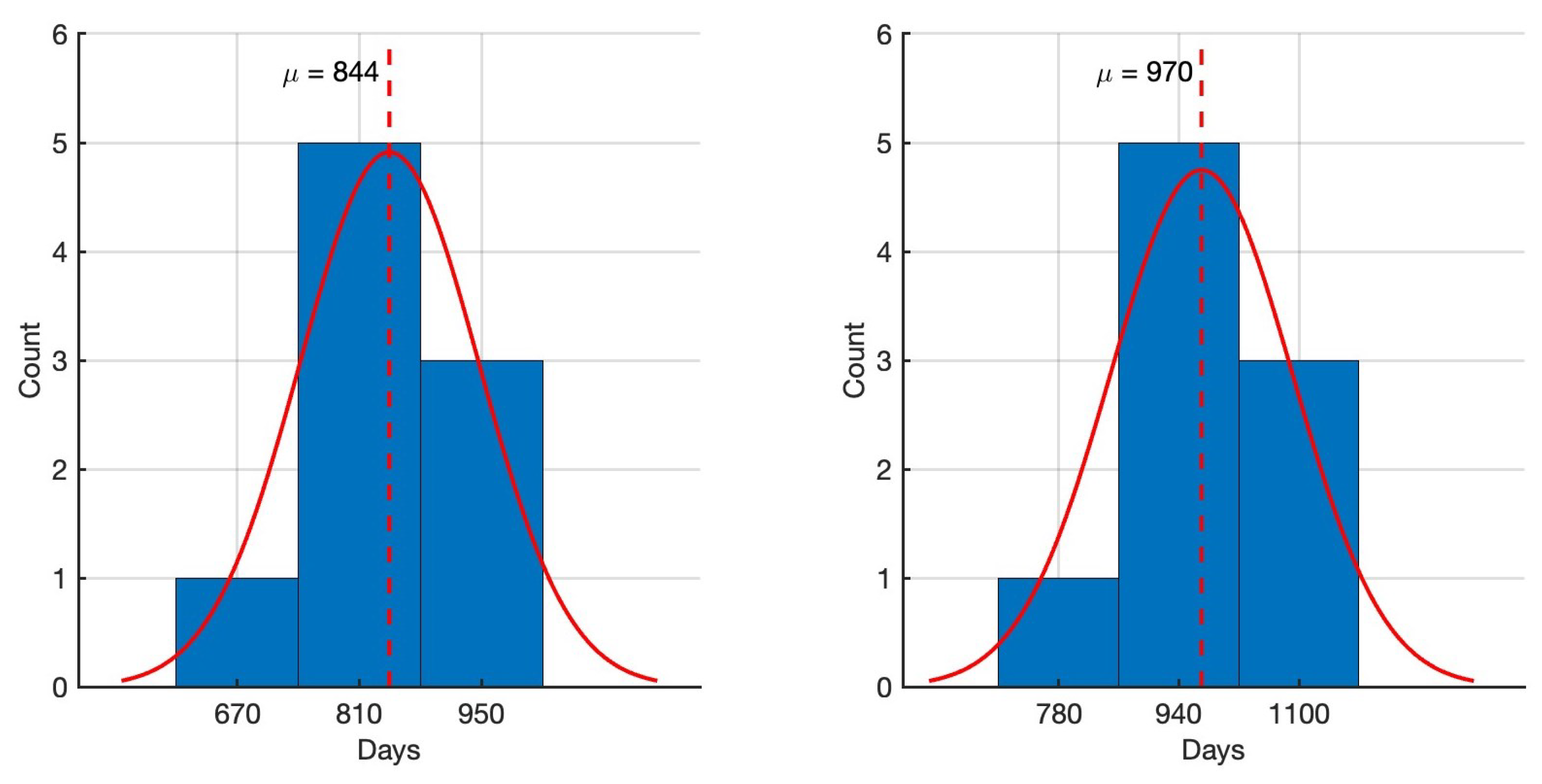
4.4. Practical Identifiability Analysis of Within-Host Model Parameters from Data Set 2
- i.
- If , then parameter p is (strongly) practically identifiable;
- ii.
- If , then parameter p is weakly practically identifiable;
- iii.
- If , then parameter p is not practically identifiable.
5. Discussion
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Data Set 1

References
- HIV.gov. A Timeline of HIV and AIDS. Available online: https://www.hiv.gov/hiv-basics/overview/history/hiv-and-aids-timeline/ (accessed on 12 June 2024).
- Larder, B.A.; Kemp, S.D. Multiple mutations in HIV-1 reverse transcriptase confer high-level resistance to zidovudine (AZT). Science 1989, 246, 1155–1158. [Google Scholar]
- Nowak, M.A.; Bonhoeffer, S.; Shaw, G.M.; May, R.M. Anti-viral drug treatment: Dynamics of resistance in free virus and infected cell populations. J. Theor. Biol. 1997, 184, 203–217. [Google Scholar] [CrossRef]
- Larder, B.A.; Kemp, S.D.; Harrigan, P.R. Potential mechanism for sustained antiretroviral efficacy of AZT-3TC combination therapy. Science 1995, 269, 696–699. [Google Scholar] [PubMed]
- National HIV Curriculum. Evaluation and Management of Virologic Failure. Available online: https://www.hiv.uw.edu/go/antiretroviral-therapy/evaluation-management-virologic-failure/core-concept/all (accessed on 1 June 2024).
- Rocheleau, G.; Brumme, C.J.; Shoveller, J.; Lima, V.D.; Harrigan, P.R. Longitudinal trends of HIV drug resistance in a large Canadian cohort, 1996–2016. Clin. Microbiol. Infect. 2018, 24, 185–191. [Google Scholar]
- Ngina, P.; Mbogo, R.W.; Luboobi, L.S. HIV drug resistance: Insights from mathematical modelling. Appl. Math. Model. 2019, 75, 141–161. [Google Scholar] [CrossRef]
- Nowak, M.A.; May, R.M. Virus Dynamics: Mathematical Principles of Immunology and Virology; Oxford University Press: Oxford, UK, 2000; pp. xii+237. [Google Scholar]
- Rong, L.; Feng, Z.; Perelson, A.S. Emergence of HIV-1 Drug Resistance during Antiretroviral Treatment. Bull. Math. Biol. 2007, 69, 2027–2060. [Google Scholar] [CrossRef] [PubMed]
- Rong, L.; Gilchrist, M.A.; Feng, Z.; Perelson, A.S. Modeling within-host HIV-1 dynamics and the evolution of drug resistance: Trade-offs between viral enzyme function and drug susceptibility. J. Theor. Biol. 2007, 247, 804–818. [Google Scholar]
- Rosenbloom, D.I.; Hill, A.L.; Rabi, S.A.; Siliciano, R.F.; Nowak, M.A. Antiretroviral dynamics determines HIV evolution and predicts therapy outcome. Nat. Med. 2012, 18, 1378–1385. [Google Scholar]
- Hill, A.L.; Rosenbloom, D.I.S.; Nowak, M.A.; Siliciano, R.F. Insight into treatment of HIV infection from viral dynamics models. Immunol. Rev. 2018, 285, 9–25. [Google Scholar] [PubMed]
- De Leenheer, P.; Pilyugin, S.S. Multistrain virus dynamics with mutations: A global analysis. Math Med Biol. 2008, 25, 285–322. [Google Scholar]
- Browne, C.J.; Smith, H.L. Dynamics of virus and immune response in multi-epitope network. J. Math. Biol. 2018, 77, 1833–1870. [Google Scholar]
- Dorratoltaj, N.; Nikin-Beers, R.; Ciupe, S.M.; Eubank, S.G.; Abbas, K.M. Multi-scale immunoepidemiological modeling of within-host and between-host HIV dynamics: Systematic review of mathematical models. PeerJ 2017, 5, e3877. [Google Scholar]
- Perelson, A.S.; Ribeiro, R.M. Modeling the within-host dynamics of HIV infection. BMC Biol. 2013, 11, 96. [Google Scholar]
- Eisenberg, M.C.; Robertson, S.L.; Tien, J.H. Identifiability and estimation of multiple transmission pathways in cholera and waterborne disease. J. Theor. Biol. 2013, 324, 84–102. [Google Scholar] [CrossRef] [PubMed]
- Tuncer, N.; Marctheva, M.; LaBarre, B.; Payoute, S. Structural and Practical Identifiability Analysis of Zika Epidemiological Models. Bull. Math. Biol. 2018, 80, 2209–2241. [Google Scholar] [CrossRef] [PubMed]
- Tuncer, N.; Gulbudak, H.; Cannataro, V.L.; Martcheva, M. Structural and practical identifiability issues of immuno-epidemiological vector-host models with application to Rift Valley Fever. Bull. Math. Biol. 2016, 78, 1796–1827. [Google Scholar]
- Miao, H.; Xia, X.; Perelson, A.S.; Wu, H. On Identifiability of Nonlinear ODE Models and Applications in Viral Dynamics. SIAM Rev. 2011, 53, 3–39. [Google Scholar] [CrossRef]
- Monolix, version 2019R2; Lixoft SAS: Antony, France, 2019.
- Pohjanpalo, H. System identifiability based on the power series expansion of the solution. Math. Biosci. 1978, 41, 21–33. [Google Scholar] [CrossRef]
- Vajda, S.; Godfrey, K.R.; Rabitz, H. Similarity transformation approach to identifiability analysis of nonlinear compartmental models. Math. Biosci. 1989, 93, 217–248. [Google Scholar] [CrossRef]
- Walter, E.; Lecourtier, Y. Global approaches to identifiability testing for linear and nonlinear state space models. Math. Comput. Simul. 1982, 24, 472–482. [Google Scholar]
- Ljung, L.; Glad, T. On global identifiability for arbitrary model parametrizations. Automatica 1994, 30, 265–276. [Google Scholar] [CrossRef]
- Bellu, G.; Saccomani, M.; Audoly, S.; D’Angio, L. DAISY: A new software tool to test global identifiability of biological and physiological systems. Comput. Methods Programs Biomed. 2007, 88, 52–61. [Google Scholar]
- Raue, A.; Kreutz, C.; Maiwald, T.; Bachmann, J.; Schilling, M.; Klingmüller, U.; Timmer, J. Structural and practical identifiability analysis of partially observed dynamical models by exploiting the profile likelihood. Bioinformatics 2009, 25, 1923–1929. [Google Scholar]
- Heitzman-Breen, N.; Liyanage, Y.R.; Duggal, N.; Tuncer, N.; Ciupe, S.M. The Effect of Model Structure and Data Availability on Usutu Virus Dynamics at Three Biological Scales. R. Soc. Open Sci. 2024, 11, 231146. [Google Scholar] [CrossRef]
- Tuncer, N.; Martcheva, M. Determining reliable parameter estimates for within-host and within-vector models of Zika virus. J. Biol. Dyn. 2021, 15, 430–454. [Google Scholar]
- Tuncer, N.; Le, T.T. Structural and practical identifiability analysis of outbreak models. Math. Biosci. 2018, 299, 1–18. [Google Scholar] [PubMed]
- Miao, H.; Dykes, C.; Demeter, L.M.; Cavenaugh, J.; Park, S.Y.; Perelson, A.S.; Wu, H. Modeling and estimation of kinetic parameters and replicative fitness of HIV-1 from flow-cytometry-based growth competition experiments. Bull. Math. Biol. 2008, 70, 1749–1771. [Google Scholar] [PubMed]
- Kao, Y.H.; Eisenberg, M.C. Practical unidentifiability of a simple vector-borne disease model: Implications for parameter estimation and intervention assessment. Epidemics 2018, 25, 89–100. [Google Scholar] [CrossRef] [PubMed]
- Gupta, C.; Tuncer, N.; Martcheva, M. Immuno-epidemiological co-affection model of HIV infection and opioid addiction. Math. Biosci. Eng. 2022, 19, 3636–3672. [Google Scholar] [CrossRef]
- Rhee, S.Y.; Gonzales, M.; Kantor, R.; Betts, B.; Ravela, J.; Shafer, R.W. Human immunodeficiency virus reverse transcriptase and protease sequence database. Nucleic Acids Res. 2003, 31, 298–303. [Google Scholar] [CrossRef]
- Lennox, J.L.; Landovitz, R.J.; Ribaudo, H.J.; Ofotokun, I.; Na, L.H.; Godfrey, C.; Kuritzkes, D.R.; Sagar, M.; Brown, T.T.; Cohn, S.E.; et al. Efficacy and tolerability of 3 nonnucleoside reverse transcriptase inhibitor-sparing antiretroviral regimens for treatment-naive volunteers infected with HIV-1: A randomized, controlled equivalence trial. Ann. Intern. Med. 2014, 161, 461–471. [Google Scholar] [CrossRef] [PubMed]
- Sreejithkumar, V.; Ghods, K.; Bandara, T.; Martcheva, M.; Tuncr, N. Modeling the interplay between albumin-globulin metabolism and HIV infection. Math. Biosci. Eng. 2023, 20, 19527–19552. [Google Scholar] [PubMed]
- Martcheva, M. An evolutionary model of influenza A with drift and shift. J. Biol. Dyn. 2012, 6, 299–332. [Google Scholar] [PubMed]
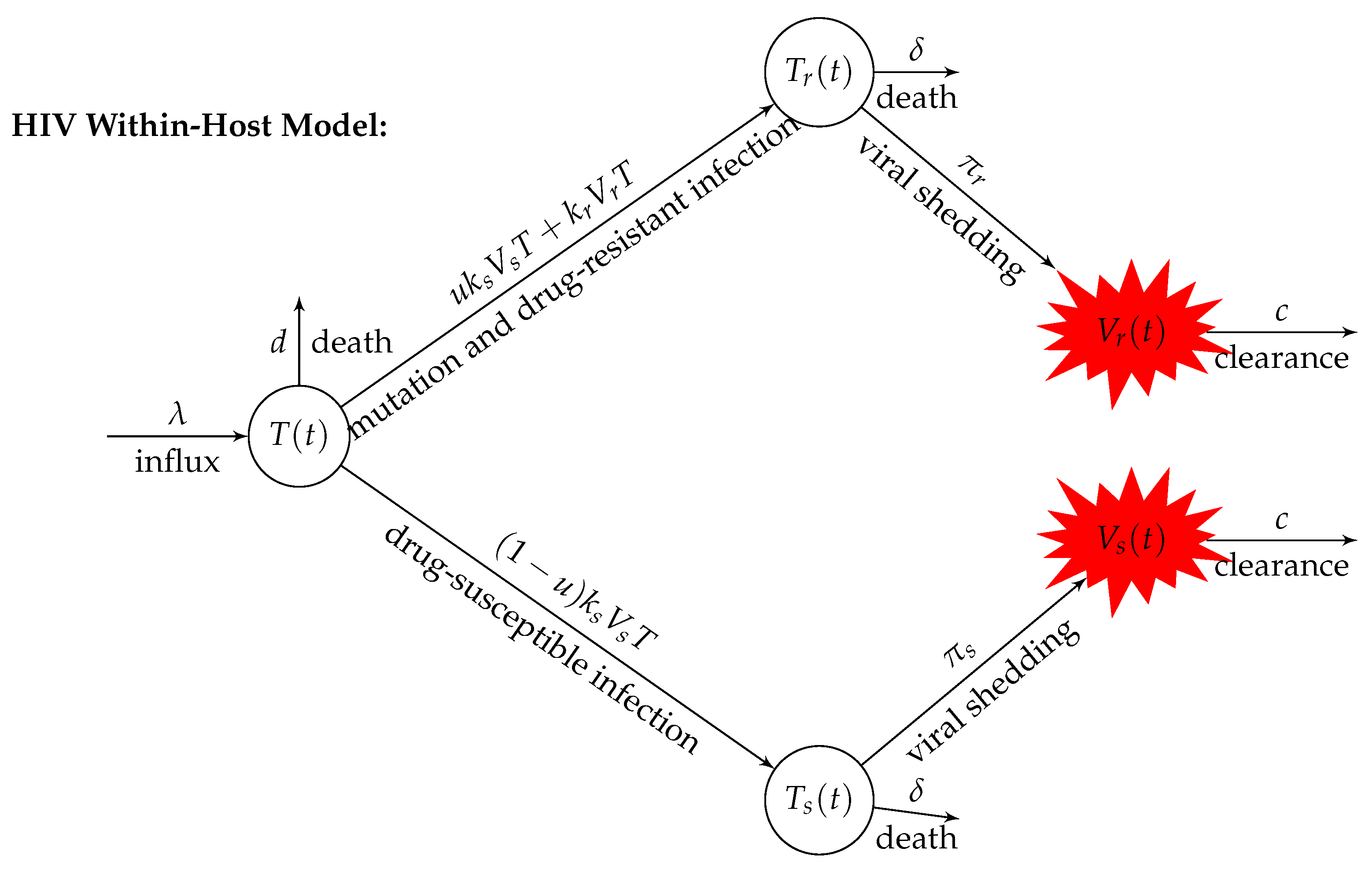




| Parameter | Definition | Units |
|---|---|---|
| Recruitment rate of uninfected target cells | ||
| Infection rate of target cells by drug-sensitive virus | ||
| Infection rate of target cells by drug-resistant virus | ||
| u | Mutation rate from sensitive strain to resistant strain | |
| Burst size of drug-resistant strain | ||
| Burst size of drug-sensitive strain | ||
| c | Clearance rate of free virus | |
| Death rate of infected cells | ||
| State Variable | Definition | Units |
| T | Population of Target (CD4+) Cells | per µL |
| Population of Infected Target (CD4+) Cells with Drug-Resistant Virus | per µL | |
| Population of Infected Target (CD4+) Cells with Drug-Susceptible Virus | per µL | |
| Drug-Resistant Viral Load | ||
| Drug-Susceptible Viral Load |
| Patient ID | d | c | u | |||||
|---|---|---|---|---|---|---|---|---|
| 260108 | 3.1432 | 0.0052 | 1.7003 × 10−5 | 2.0280 × 10−5 | 14.2923 | 2.6698 | 0.0151 | 2.2205 × 10−16 |
| 260176 | 8.5243 | 0.0146 | 1.7020 × 10−5 | 2.0086 × 10−5 | 13.9616 | 3.0708 | 0.0153 | 2.2205 × 10−16 |
| 260141 | 2.2569 | 0.0070 | 1.7086 × 10−5 | 2.2728 × 10−5 | 14.8627 | 1.5793 | 0.0153 | 2.2205 × 10−16 |
| 260051 | 5.3588 | 0.0086 | 1.7076 × 10−5 | 2.2009 × 10−5 | 14.3102 | 3.1006 | 0.0152 | 2.2205 × 10−16 |
| 260055 | 6.7139 | 0.0077 | 1.7129 × 10−5 | 2.0807 × 10−5 | 13.5409 | 4.1148 | 0.0153 | 2.2205 × 10−16 |
| 260275 | 1.4573 | 0.0069 | 1.7190 × 10−5 | 2.4921 × 10−5 | 16.3691 | 1.0295 | 0.0155 | 2.2205 × 10−16 |
| 260219 | 2.1811 | 0.0057 | 1.7189 × 10−5 | 2.0317 × 10−5 | 13.8618 | 1.7939 | 0.0154 | 2.2205 × 10−16 |
| 260222 | 6.2164 | 0.0082 | 1.7144 × 10−5 | 1.9117 × 10−5 | 12.9615 | 3.5886 | 0.0152 | 2.2205 × 10−16 |
| 260278 | 5.0414 | 0.0086 | 1.7000 × 10−5 | 2.2101 × 10−5 | 14.7130 | 2.8675 | 0.0153 | 2.2205 × 10−16 |
| 3.86 | 0.0075 | 0.000017 | 0.000022 | 14.12 | 2.42 | 0.015 | 2.2205 × 10−16 | |
| 0.6 | 0.36 | 0.025 | 0.11 | 0.11 | 0.42 | 0.031 | 3.58 |
| Parameter | [lb,ub] | Estimated Value | Units |
|---|---|---|---|
| µL−1 | |||
| d | |||
| µL | |||
| µL | |||
| u | |||
| c | |||
| Parameter | ARE with | ARE with | ARE with | ARE with |
|---|---|---|---|---|
| 0.26 | 0.97 | 1.92 | 4.26 | |
| d | 2.85 | 13.46 | 21.27 | 31.31 |
| 1.69 | 7.12 | 14.52 | 33. 28 | |
| 1.29 | 6.62 | 13.18 | 22.35 | |
| u | 5.95 | 38.26 | 108.38 | 211.75 |
| 0.6 | 2.6 | 4.45 | 8.12 | |
| 1.52 | 6.68 | 13.2 | 26.43 | |
| c | 0.24 | 1 | 2.34 | 5.62 |
| 0.74 | 3.17 | 6.44 | 13.32 |
| Parameter | ARE with | ARE with | ARE with | ARE with |
|---|---|---|---|---|
| 0.01 | 0.1 | 0.23 | 0.56 | |
| d | 0.2 | 1.54 | 3.69 | 8.06 |
| 0.08 | 0.53 | 1.25 | 2. 99 | |
| 0.08 | 0.52 | 1.07 | 2.39 | |
| u | 0.53 | 4.24 | 9.26 | 21.01 |
| 0.02 | 0.21 | 0.52 | 1.27 | |
| 0.06 | 0.44 | 1.07 | 2.49 | |
| c | 0.01 | 0.09 | 0.2 | 0.46 |
| 0.06 | 0.33 | 0.71 | 1.49 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tuncer, N.; Ghods, K.; Sreejithkumar, V.; Garbowit, A.; Zagha, M.; Martcheva, M. Validation of a Multi-Strain HIV Within-Host Model with AIDS Clinical Studies. Mathematics 2024, 12, 2583. https://doi.org/10.3390/math12162583
Tuncer N, Ghods K, Sreejithkumar V, Garbowit A, Zagha M, Martcheva M. Validation of a Multi-Strain HIV Within-Host Model with AIDS Clinical Studies. Mathematics. 2024; 12(16):2583. https://doi.org/10.3390/math12162583
Chicago/Turabian StyleTuncer, Necibe, Kia Ghods, Vivek Sreejithkumar, Adin Garbowit, Mark Zagha, and Maia Martcheva. 2024. "Validation of a Multi-Strain HIV Within-Host Model with AIDS Clinical Studies" Mathematics 12, no. 16: 2583. https://doi.org/10.3390/math12162583
APA StyleTuncer, N., Ghods, K., Sreejithkumar, V., Garbowit, A., Zagha, M., & Martcheva, M. (2024). Validation of a Multi-Strain HIV Within-Host Model with AIDS Clinical Studies. Mathematics, 12(16), 2583. https://doi.org/10.3390/math12162583







