Singularity, Observability, and Independence: Unveiling Lorenz’s Cryptographic Potential
Abstract
1. Introduction
2. Theoretical Background
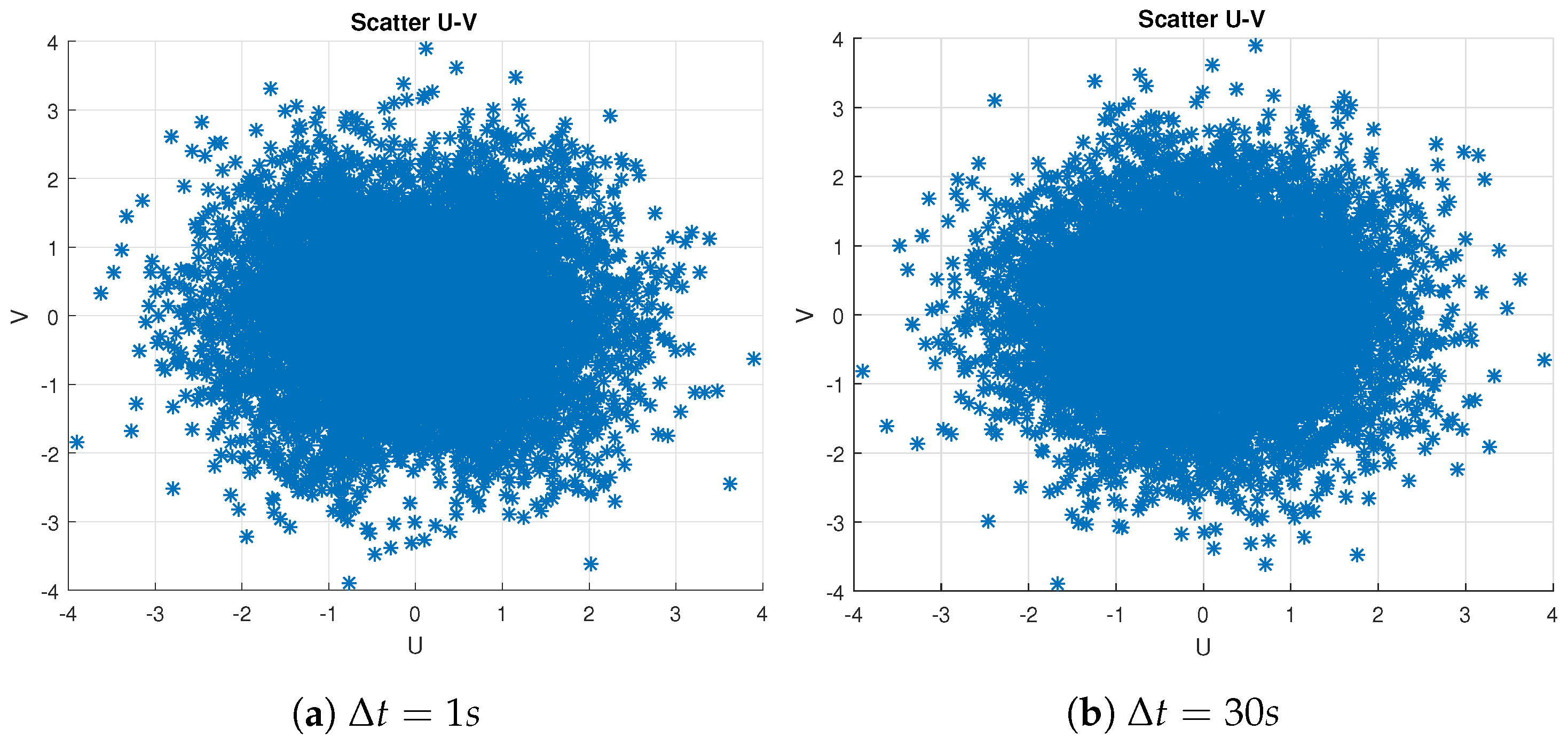
- —null hypothesis: The datasets (U and V) conform to the bivariate normal distribution described in (3), indicating that U and V (and hence X and Y) are statistically independent.
- —alternative hypothesis: The datasets (U and V) do not adhere to the bivariate normal distribution described in (3), suggesting that U and V (and hence X and Y) are not statistically independent.
3. Experimental Results
3.1. Observability
- Write the fluency matrix by replacing each (non)constant element of the Jacobian matrix with () 1, and zero otherwise.The Jacobian for the Lorenz system is calculated considering the equations from (1) and their partial derivatives with respect to the state variables (for the Lorenz system, the state variables are represented by x, y, and z). The result is shown in (4), which is the Jacobian of the Lorenz system.The fluency matrix is presented in (5):
- The next step is to choose a state variable to reconstruct the dynamics of the Lorenz system. One should also define the column array , with 1 on the ith position and 0 elsewhere: for x for y and for z.
- Matrix is an auxiliary variable required in the algorithm, calculated by multiplying each line from the fluency matrix (5) with the corresponding element from array and replacing element with a ·.for x; for y; for z.
- Next, variable will be used to count the number of linear elements from and is storing the number of non-linear elements from , for each state variable .
- Going further, the · elements from matrices are replaced with their corresponding element from the fluency matrix, and the resulting matrix is transposed:→ for x→ for y→ for z
- Arrays are computed by summing the elements of the lines of the previously defined matrices (1 and are considered as 1):for x for y and for z.
- One of the final steps of the procedure used to calculate the observability coefficients for the Lorenz system consists in calculating the matrices. They are created by replacing any non-zero element from with a · and the zero elements with the corresponding terms from the fluency matrix multiplied by the corresponding element from arrayfor x, for y and, for z
- Similarly to , the quantities will count the number of linear elements from and the number of non-linear elements from , for each state variable.
- The observability coefficient for each state variable, , is computed based on the below formulas:where for .The observability coefficients for the Lorenz system are as follows:
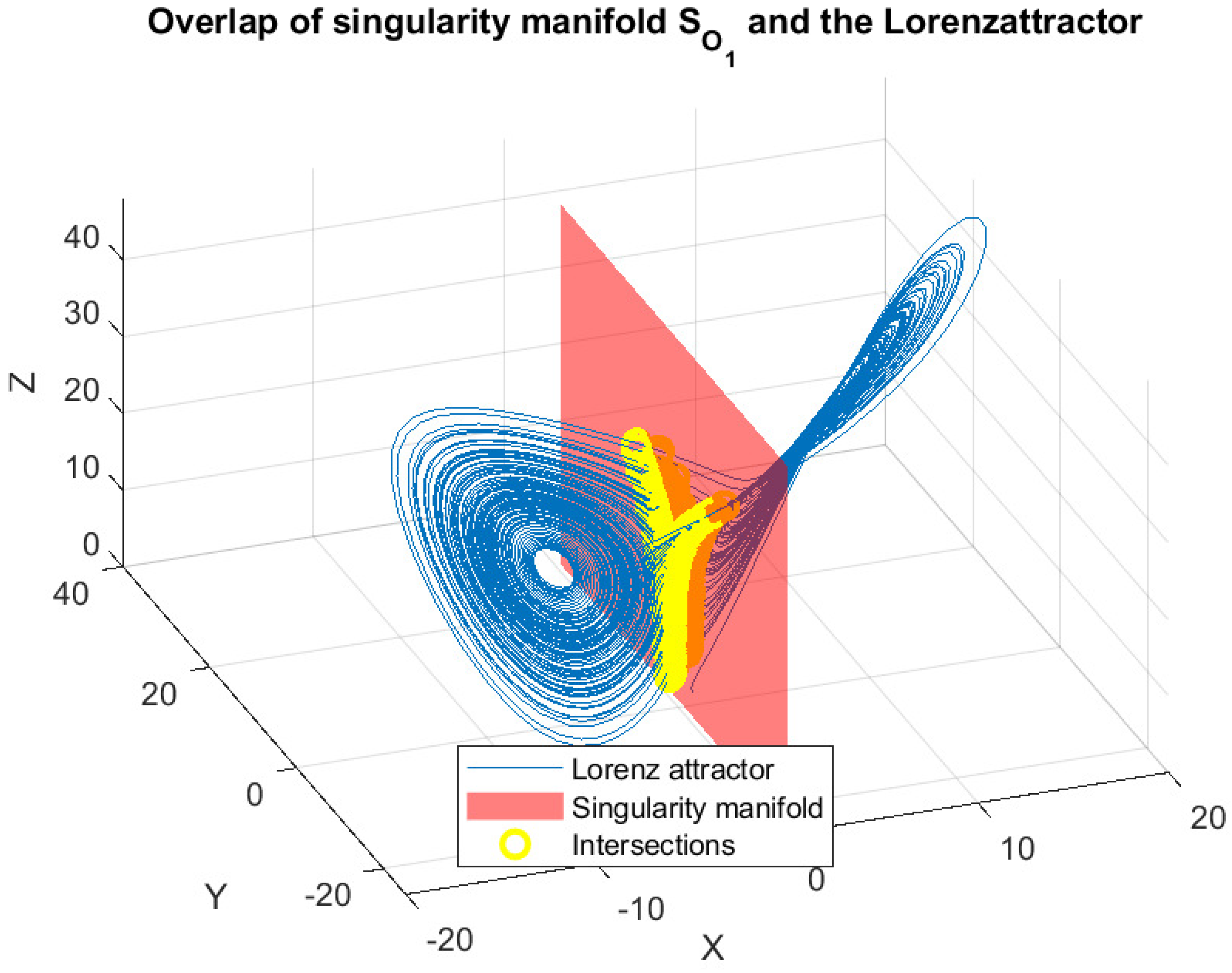
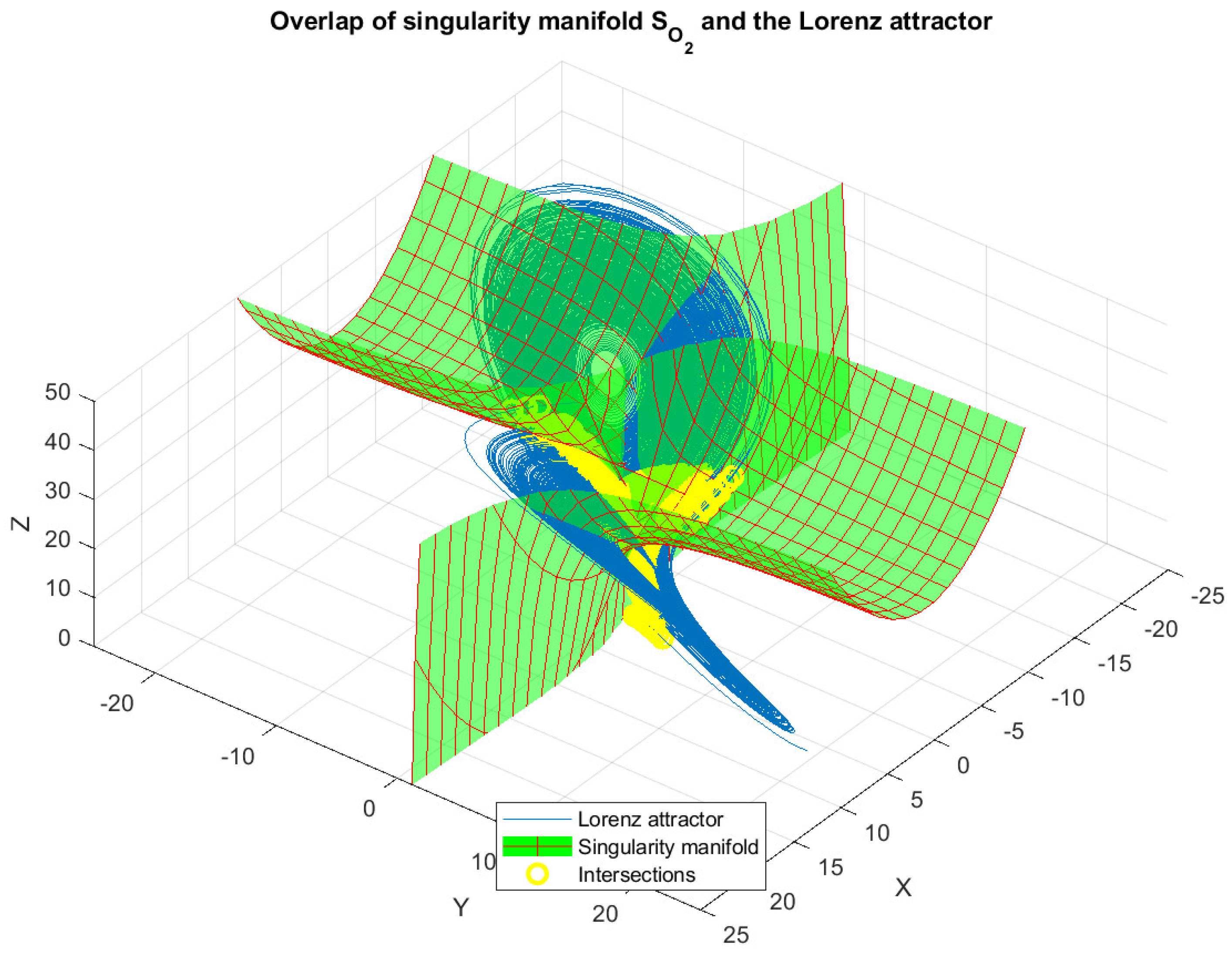
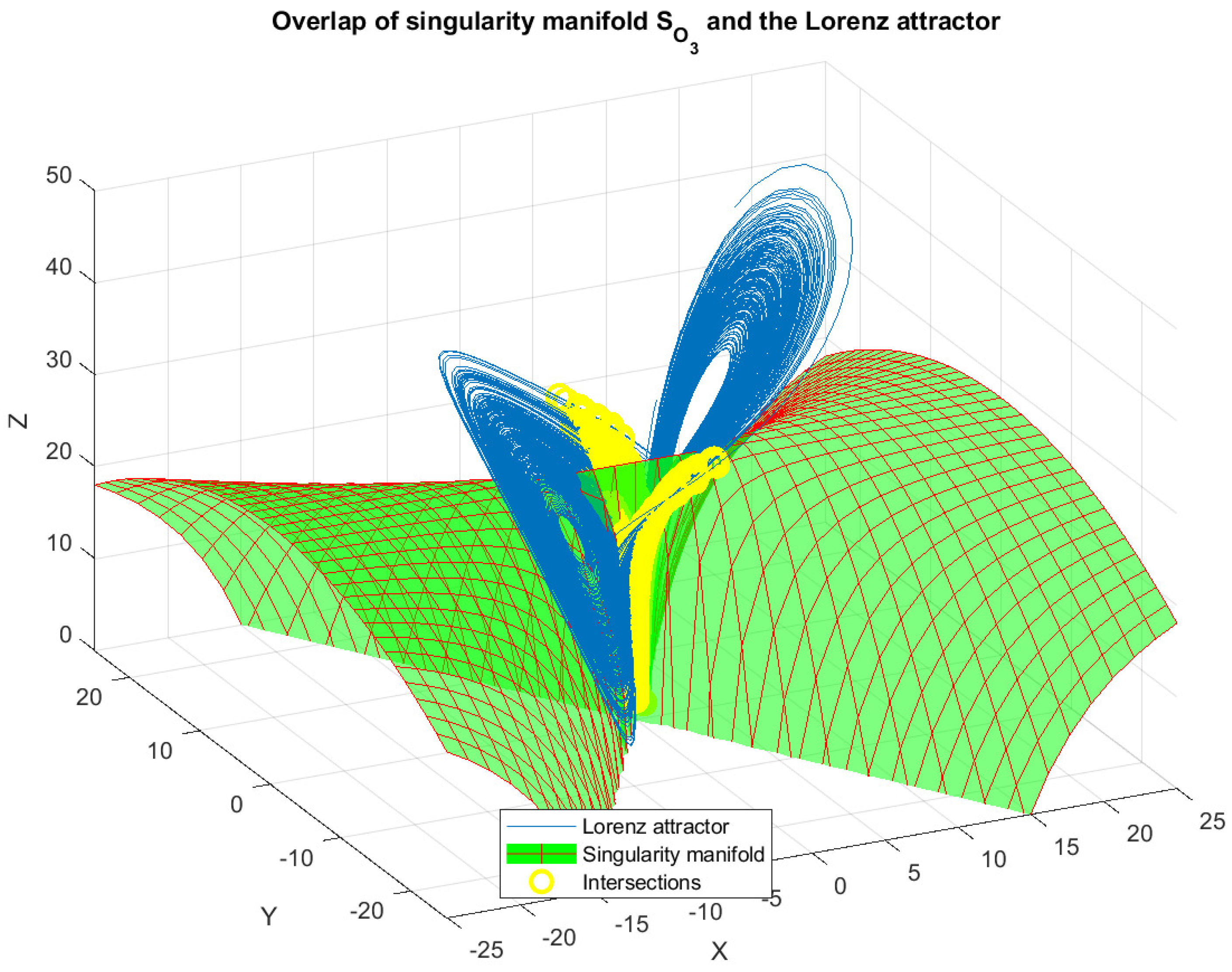
3.2. Singularity
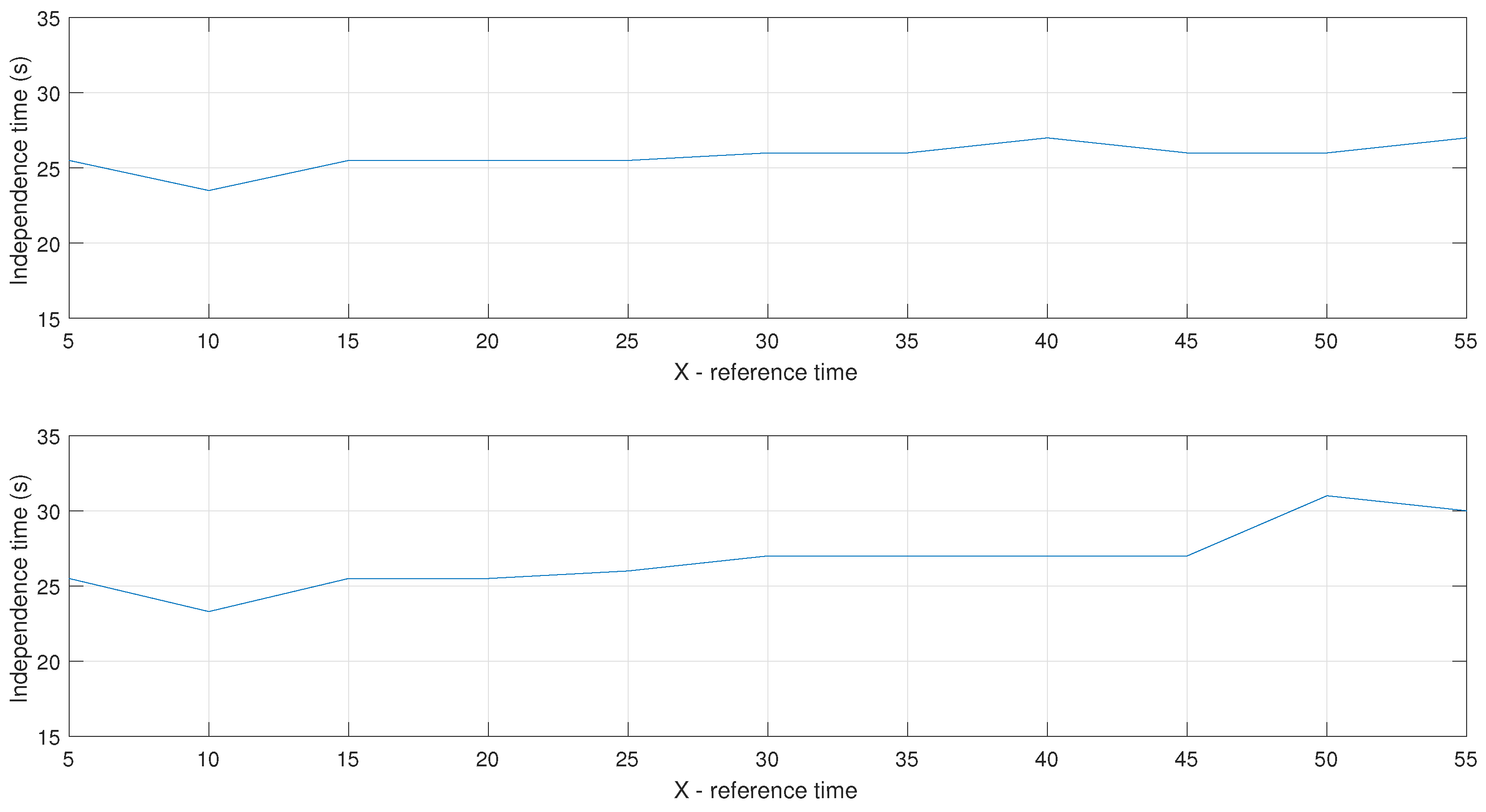
3.3. Statistical Independence
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liao, T.-L.; Chen, H.-C.; Peng, C.-Y.; Hou, Y.-Y. Chaos-Based Secure Communications in Biomedical Information Application. Electronics 2021, 10, 359. [Google Scholar] [CrossRef]
- Taleby Ahvanooey, M.; Li, Q.; Hou, J.; Rajput, A.R.; Chen, Y. Modern Text Hiding, Text Steganalysis, and Applications: A Comparative Analysis. Entropy 2019, 21, 355. [Google Scholar] [CrossRef] [PubMed]
- Shukla, P.K.; Khare, A.; Rizvi, M.A.; Stalin, S.; Kumar, S. Applied Cryptography Using Chaos Function for Fast Digital Logic-Based Systems in Ubiquitous Computing. Entropy 2015, 17, 1387–1410. [Google Scholar] [CrossRef]
- Knežević, M.; Tomović, S.; Mihaljević, M.J. Man-In-The-Middle Attack against Certain Authentication Protocols Revisited: Insights into the Approach and Performances Re-Evaluation. Electronics 2020, 9, 1296. [Google Scholar] [CrossRef]
- Hamida, E.B.; Noura, H.; Znaidi, W. Security of Cooperative Intelligent Transport Systems: Standards, Threats Analysis and Cryptographic Countermeasures. Electronics 2015, 4, 380–423. [Google Scholar] [CrossRef]
- Maurer, U.; Rüedlinger, A.; Tackmann, B. Confidentiality and Integrity: A Constructive Perspective. In Theory of Cryptography Conference; Springer: Berlin/Heidelberg, Germany, 2012; pp. 209–229. [Google Scholar]
- Vijayakumar, M.D.; Natiq, H.; Leutcho, G.D.; Rajagopal, K.; Jafari, S.; Hussain, I. Hidden and Self-Excited Collective Dynamics of a New Multistable Hyper-Jerk System with Unique Equilibrium. Int. J. Bifurc. Chaos 2022, 32, 2250063. [Google Scholar] [CrossRef]
- Perez-Padron, J.; Posadas-Castillo, C.; Paz-Perez, J.; Zambrano-Serrano, E.; Platas-Garza, M.A. Fpga realization and Lyapunov–Krasovskii analysis for a master-slave synchronization scheme involving chaotic systems and time-delay neural networks. Math. Probl. Eng. 2021, 2021, 2604874. [Google Scholar] [CrossRef]
- Jones, A.; Smith, B. Recent Advances in Chaotic Systems for Cryptography. J. Cryptogr. Res. 2023, 12, 45–60. [Google Scholar]
- Li, C.; Zhang, D. Hyperchaotic Systems and Their Applications in Secure Communications. Int. J. Inf. Secur. 2024, 18, 123–134. [Google Scholar]
- Wang, L.; Zhou, Y. Fractional-Order Chaotic Systems: A Comprehensive Review. IEEE Trans. Circuits Syst. 2023, 70, 1002–1014. [Google Scholar]
- Lee, M.; Kim, S. Optimizing Chaotic Maps for High-Performance Image Encryption. J. Appl. Math. 2024, 30, 15–28. [Google Scholar]
- Patel, R.; Kumar, N. Advances in Cryptographic Algorithms Based on Chaotic Systems. Cryptogr. Commun. 2023, 15, 500–515. [Google Scholar]
- Toktas, F.; Erkan, U.; Yetgin, Z. Cross-Channel Color Image Encryption via 2D Hyperchaotic Hybrid Map and Optimization Test Functions. Expert Syst. Appl. 2024, 249, 123583. [Google Scholar] [CrossRef]
- Kocak, O.; Erkan, U.; Toktas, A.; Gao, S. PSO-Based Image Encryption Scheme Using Modular Integrated Logistic Exponential Map. Expert Syst. Appl. 2024, 237 Pt A, 121452. [Google Scholar] [CrossRef]
- Feng, W.; Wang, Q.; Liu, H.; Ren, Y.; Zhang, J.; Zhang, S.; Qian, K.; Wen, H. Exploiting Newly Designed Fractional-Order 3D Lorenz Chaotic System and 2D Discrete Polynomial Hyper-Chaotic Map for High-Performance Multi-Image Encryption. Fractal Fract. 2023, 7, 887. [Google Scholar] [CrossRef]
- Feng, W.; Zhao, X.; Zhang, J.; Qin, Z.; Zhang, J.; He, Y. Image Encryption Algorithm Based on Plane-Level Image Filtering and Discrete Logarithmic Transform. Mathematics 2022, 10, 2751. [Google Scholar] [CrossRef]
- Martínez, V.G.; Hernández-Álvarez, L.; Encinas, L.H. Analysis of the Cryptographic Tools for Blockchain and Bitcoin. Mathematics 2020, 8, 131. [Google Scholar] [CrossRef]
- Wang, L.; Cheng, H. Pseudo-Random Number Generator Based on Logistic Chaotic System. Entropy 2019, 21, 960. [Google Scholar] [CrossRef]
- Dinu, A.; Frunzete, M. Singularity, Observability and Statistical Independence in the Context of Chaotic Systems. Mathematics 2023, 11, 305. [Google Scholar] [CrossRef]
- Letellier, C.; Aguirre, L.A. Interplay between synchronization, observability, and dynamics. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2010, 82 Pt 2, 016204. [Google Scholar] [CrossRef]
- Frunzete, M.; Barbot, J.P.; Letellier, C. Influence of the singular manifold of nonobservable states in reconstructing chaotic attractors. Phys. Rev. E 2012, 86, 026205. [Google Scholar] [CrossRef] [PubMed]
- Frunzete, M.; Luca, A.; Vlad, A.; Barbot, J.P. Observability and singularity in the context of rössler map. Univ. Politeh. Buchar. Sci. Bull. Ser. Appl. Math. Phys. 2012, 74, 83–92. [Google Scholar]
- Frunzete, M. Quality Evaluation for Reconstructing Chaotic Attractors. Mathematics 2022, 10, 4229. [Google Scholar] [CrossRef]
- Badea, B.; Vlad, A. Revealing statistical independence of two experimental data sets. In An Improvement on Spearman’s Algorithm, Lectures Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3980 (ICCSA 2006), pp. 1166–1176. ISSN 0302-9743. [Google Scholar]
- Vaduva, A.; Vlad, A.; Badea, B. Evaluating the performance of a test-method for statistical independence decision in the context of chaotic signals. In Proceedings of the 2016 International Conference on Communications (COMM), Bucharest, Romania, 9–11 June 2016; pp. 417–422. [Google Scholar] [CrossRef]
- Dinu, A.; Frunzete, M. The Lorenz chaotic system, statistical independence and sampling frequency. In Proceedings of the 2021 International Symposium on Signals, Circuits and Systems (ISSCS), Iasi, Romania, 15–16 July 202; pp. 1–4. [CrossRef]
- Goodson, R.; Klein, R. A definition and some results for distributed system observability. IEEE Trans. Autom. Control 1970, 15, 165–174. [Google Scholar] [CrossRef]
- Hermann, R.; Krener, A. Nonlinear controllability and observability. IEEE Trans. Autom. Control 1977, 22, 728–740. [Google Scholar] [CrossRef]
- Diop, R.S.; Fliess, M. Nonlinear observability, identifiability, and persistent trajectories. In Proceedings of the 30th IEEE Conference on Decision and Control, Brighton, UK, 11–13 December 1991; pp. 714–719. [Google Scholar]
- Frunzete, M.; Cucu, H. Observability coefficient for 2D dynamical systems. In Proceedings of the 2017 Signal Processing: Algorithms, Architectures, Arrangements, and Applications (SPA), Poznan, Poland, 20–22 September 2017; pp. 292–295. [Google Scholar] [CrossRef]
- Walpole, R.E.; Myers, R.H. Probability and Statistics for Engineers and Scientists, 4th ed.; MacMillan Publishing: New York, NY, USA, 1989. [Google Scholar]
- Dinu, A.; Vlad, A. The compound tent map and the connection between Gray codes and the initial condition recovery. UPB Sci. Bull. Ser. A Appl. Math. Phys 2014, 76, 17–28. Available online: https://www.scientificbulletin.upb.ro/rev_docs_arhiva/full72a_882955.pdf (accessed on 20 July 2024).

| Chaotic System | Observability Coefficient | Observability Coefficient | Observability Coefficient |
|---|---|---|---|
| Clifford (discrete) | 0.54 | 0.54 | Not Applicable (NA) |
| Ikeda (discrete) | 0.17 | 0.17 | NA |
| Tinkerbell (discrete) | 0.44 | 0.88 | NA |
| Lorenz (continuous) | 0.88 | 0.27 | 0.32 |
| Chaotic System | Overlap Attractor and | Overlap Attractor and | Overlap Attractor and |
|---|---|---|---|
| Clifford (discrete) | 12.26% | 22.02 | NA% |
| Ikeda (discrete) | 0% | 0.41 | NA% |
| Tinkerbell (discrete) | 2.84% | 4.83 | NA% |
| Lorenz (continuous) | 11.84% | 3.04 | 3.50% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dinu, A. Singularity, Observability, and Independence: Unveiling Lorenz’s Cryptographic Potential. Mathematics 2024, 12, 2798. https://doi.org/10.3390/math12182798
Dinu A. Singularity, Observability, and Independence: Unveiling Lorenz’s Cryptographic Potential. Mathematics. 2024; 12(18):2798. https://doi.org/10.3390/math12182798
Chicago/Turabian StyleDinu, Alexandru. 2024. "Singularity, Observability, and Independence: Unveiling Lorenz’s Cryptographic Potential" Mathematics 12, no. 18: 2798. https://doi.org/10.3390/math12182798
APA StyleDinu, A. (2024). Singularity, Observability, and Independence: Unveiling Lorenz’s Cryptographic Potential. Mathematics, 12(18), 2798. https://doi.org/10.3390/math12182798





