Abstract
There are several common procedures used to numerically integrate second-order ordinary differential equations. The most common one is to reduce the equation’s order by duplicating the number of variables. This allows one to take advantage of the family of Runge–Kutta methods or the Adams family of multi-step methods. Another approach is the use of methods that have been developed to directly integrate an ordinary differential equation without increasing the number of variables. An important drawback when using Runge–Kutta methods is that when one tries to apply them to differential algebraic equations, they require a reduction in the index, leading to a need for stabilization methods to remove the drift. In this paper, a new family of methods for the direct integration of second-order ordinary differential equations is presented. These methods can be considered as a generalization of the central differences method. The methods are classified according to the number of derivatives they take into account (degree). They include some parameters that can be chosen to configure the equation’s behavior. Some sets of parameters were studied, and some examples belonging to structural dynamics and multibody dynamics are presented. An example of the application of the method to a differential algebraic equation is also included.
Keywords:
ordinary differential equations; differential algebraic equations; multibody dynamics; structural dynamics MSC:
65L05
1. Introduction
The topic of this paper is the numerical integration of second-order ordinary differential equations (ODEs) in the following form:
with the following set of initial conditions:
These equations arise in several fields of engineering [1]. Among them, in the field of mechanical engineering, there are two important problems that are described by these kinds of equations: structural dynamics and multibody dynamics [2,3,4]. Oddly enough, the usual way to deal with these equations in structural dynamics is completely different to that used in multibody dynamics. In structural dynamics, the equilibrium equation is usually solved by means of methods that directly integrate the second-order differential equation [5]. These methods are often classified among explicit and implicit methods, but this classification does not exactly comply to the rigorous explicit and implicit classification used in methods for first-order ODEs. In structural dynamics, explicit methods are those that formulate the equilibrium in to obtain the solution in [2,5]. This is due to the fact that these methods were initially developed for structural linear dynamics and, thus, methods that lead to implicit equations in the general case become explicit due to the particular conditions of the problem. Implicit methods usually employed in structural mechanics include the Newmark method [6], the HHT method [7] and the Wilson-ө method [8]. The most typical explicit method employed in structural dynamics is the central differences method [5], which is the core of commercial software such as ANSYS® LS-DYNA®. In the case of multibody dynamics, the usual approach has, for a long time, been the reduction in the order of the differential equation so that any method suitable for first-order differential equations can be used [3,4,9]. Usually, these come in the form of Runge–Kutta integrators. More recently, the use of structural methods has gained considerable relevance in the field, mainly using implicit methods [10,11,12,13], although there are some explicit implementations [14,15]. The main advantage of structural methods over Runge–Kutta (RK) methods is that structural methods only need one evaluation of the function per time step, while RK methods usually require more than one [16]. This advantage is also present in the Adams family of methods, but in these methods, an increase in convergence is obtained by increasing the number of previous steps involved in the resolution of the current step. This hampers the stability behavior of the method. Additionally, the use of RK methods in DAEs is usually performed by reducing the DAE index and, thus, the introduction of a stabilization technique to avoid the drift is required [3,17,18]. This stabilization method might also limit the time step because it can introduce additional stability issues [19]. This has probably been the key reason for this recent interest, because methods such as central differences do not require a reduction in the DAE index (see ref. [20]).
It is also important to mention that there are other alternatives applicable to conservative systems. Among them, one can find the Störmer–Verlet methods, including Velocity–Verlet (ref. [21,22,23]). Also, in the same conditions, one can find the Leapfrog integration method (ref. [24]), the Yoshida method (ref. [25]) and the Beeman method (ref. [26]).
The separate development of structural integrators and Runge–Kutta integrators has led to different philosophies. Since structural methods, as mentioned, have typically been developed for a particular problem, they have been developed with an application in mind. In contrast, Runge–Kutta methods have been developed with a generic approach in mind. As a consequence, for example, different approaches to analyzing stability have been used. In the case of structural dynamics, the stability analysis is focused on obtaining the maximum time step that can be used in the process [6]. In order to achieve this, the analysis takes advantage of the particularities of the problem. In the case of Runge–Kutta methods, there are several types of stability that are considered, allowing one to study the method regardless of the particular physical phenomenon that is described by the equation that needs to be integrated (see ref. [27]). This is of a broader scope, but it may be less practical.
Among the structural methods, the use of the second-order central differences method is of broad use in structural dynamics [28,29]. This is due to the high nonlinearity of the problem and the small time steps required to properly handle events such as contacts. In these methods, higher-order convergence is not usually a priority, and the second-order central differences method presents second-order convergence. In any case, a method with similar characteristics along with higher-order convergence would be of interest.
In this paper, the central differences method is extended in order to reach a configurable method (in a similar way to the Newmark or HHT methods). Furthermore, more complex (here named higher-degree) versions of the method are proposed and discussed. In order to show the behavior of the newly devised methods, some examples are also presented. The initial steps in this work were developed in the framework of the Ph. D. thesis of Dr. Haritz Uriarte [30]. The preliminary ideas behind the method presented here are presented in [31].
The organization of this paper is as follows. First, a brief summary of the classical central differences method is presented, including some important considerations regarding its classification. Afterwards, some hints for reducing the cancellation error are presented. These hints allow one to devise a generalization of the central differences method, which will be discussed. The behavior of this generalization is explained afterwards. A further generalization that can be used to improve the convergence is then introduced along with its performance. Some examples of the resolution of ODEs and DAEs are presented. Finally, some conclusions are drawn, and future works will be addressed.
2. The Central Differences Method for Structural Dynamics
Although this paper deals with equations in the more general form defined by the set of Equations (1) and (2), the central differences method was tailored to solve second-order ODEs in the following particular form:
with the set of initial conditions exposed in Equation (2).
In this equation, , and are the mass, damping and stiffness matrices of a structural or multibody dynamic problem. is the applied external force, and determines the position of the Degrees of Freedom (DoF) of the problem.
Initially, the central differences method was developed with linear systems in mind, but currently, one can find implementations where , and can be functions of , and (see [5,14], for examples). In these conditions, the most general situation can be considered, where , and . A consideration like this will be made here. In cases where presents degeneracy, two possibilities can arise. If this degeneracy comes about because of redundancy in the equations and the number of equations is equal to the number of variables, the system lacks a single solution. This is out of the scope of this document. In the other case, the problem should be reformulated as a DAE. In cases of near degeneracy, again, two cases can arise. The first one is related to a considerable difference in the natural frequencies of the system, and this is a stability-related issue. The second one might be due to a problem of scale, which will not be addressed in this document.
The original formulation of the method uses the following equations:
and
with being the step size used in the integration. By substituting this into Equation (3), it is easy to reach the following:
This expression is applied step by step in order to reach, at each step , the value of for the next one, . Obviously, in the first step, one does not know the value of , but, instead, the value is known. Taking into account Equations (3)–(5) for this situation, one can reach the following:
There are also alternatives to this method for variable time steps. For simplicity, in this document, only fixed-step approaches are considered.
This method is quite useful for structural dynamics. It features extremely low costs and predictable stability. It is useful not only for linear problems but also for non-linear ones; this, however, might lead to an iterative scheme if any of the matrices or the force vector depend on the velocity. This is due to the fact that Equation (6) is implicit only if no dependence on appears in its right-hand side. Therefore, the method can behave as explicit or implicit. This is the reason why the term “conditionally explicit” will be used for methods showing this behavior in this document. The method is usually classified as explicit in the structural analysis field. This can be misleading. The reason behind this classification is probably the fact that, for structural linear and nonlinear dynamics where no solid–rigid gyroscopic effects are considered, the matrices , and and the vector do not depend on and, thus, the resultant problem behaves like an explicit one. However, this is an inconvenience, because the method itself can also be applied in cases where a dependence on exists [14]. In those cases, the method behaves as an implicit one. However, even in that case, the fact that there is dependence on but not on has some advantages, because a dependence on is not as common as a dependence on . For example, does not depend on . Thus, strictly speaking, the method is implicit, but due to the usual field of application, it does not seem quite incorrect to classify it as explicit.
In structural linear dynamics, , and do not usually depend on , and the method behaves as an explicit one. In structural nonlinear dynamics, they depend on , and in 3D multibody dynamics, also depends on . In this latter case, the method behaves as an implicit one.
As formulated in Equations (6) and (7), the method delivers the vector of the variables without the need to store derivatives. This is quite convenient for structural dynamics, where the vector of the variables is composed of nodal displacements, which, in turn, are used to obtain strains and stresses. However, this might be a problem if one wants to generalize the method to other problems, such as multibody dynamics. In this field, velocities and accelerations are of concern, and, therefore, the use of Equations (4) and (5) is necessary after the integration process. This is a major inconvenience, because these equations lead to heavy cancellation problems, which might limit the maximum achievable precision. For example, let us consider Equation (4). If the time step is reduced, the integration method will increase its precision, but the numerical difference among and will diminish. Thus, the number of significant digits in its difference will be reduced and, therefore, the number of valid digits obtained in Equation (4) will be reduced. Thus, although the integration quality will improve, the obtained velocity values will degrade. In any case, if a high degree of precision is not needed, one can successfully use the scheme defined in the above equations [14,15].
Another issue is that this formulation, as demonstrated, is only suitable for equations of a second order in the form of Equation (3). Although one could write any second-order ODE in this form by using the Taylor expansion, this requires additional work.
3. A Reformulation of the Central Differences Method to Avoid Cancellation
As demonstrated before, the problem of cancellation appears because of the use of Equations (4) or (5). This is an inconvenience, for example, in multibody dynamics, because depends on the velocity, and the use of Equation (4) might lead to a considerable loss of precision due to cancellation. On the other hand, this is not usually a concern in structural dynamics.
In order to avoid cancellation problems, one can reformulate the problem so that the result in each iteration is obtained in accelerations. The reformulation of the method can be obtained by a simple manipulation of Equations (4) and (5) and by storing in each iteration, at least, both and ( is not needed).
By adding Equation (4) multiplied by and Equation (5) multiplied by , one reaches the following:
Which is obviously an expression of the truncated Taylor series for the displacement in :
If the same is carried out whilst eliminating , one reaches the expression of the truncated Taylor series in :
This means that, in fact, the use of the central differences approach is equivalent to using Equations (9) and (10).
From Equation (9), but formulated for the previous step, the following can be obtained:
And, combining Equation (11) with (10) gives:
Finally, introducing Equation (11) in (9) gives:
The use of Equations (9) and (12) leads to a central differences implementation but without cancellation problems. This is similar to using a single-step method, but in common single-step methods, one obtains , and from , and . In this approach, instead, in each step, one obtains , and from , and .
Rigorously speaking, it could be stated that this is a two-step method, because it uses values taken in two time instants ( and ) to obtain results in and . It is also interesting to mention that the central differences method also has some resemblance to an implicit Adams scheme but including derivatives along with the variable itself.
Influence of the Cancellation Problem
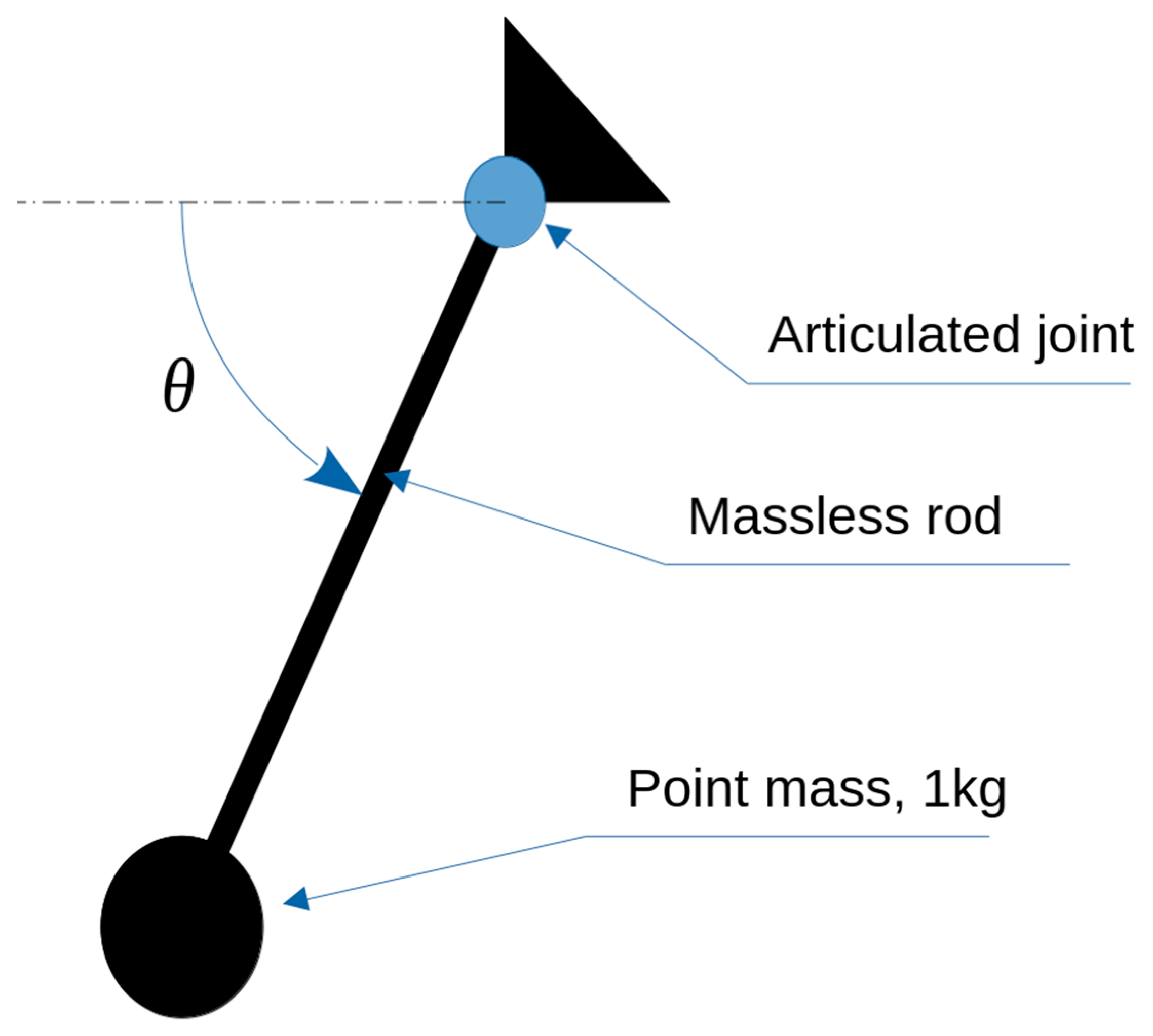
It looks interesting at this point to show the influence of using Equations (9) and (12) (reformulated central differences) instead of Equations (4) and (5). In order to achieve this, the example of the simple planar pendulum described in the IFTOMM Multibody Benchmark will be used. In this example, one is required to solve the free oscillations of a simple pendulum composed of a massless rod of a length of 1 m and with a point mass of 1 kg at its end.
The system moves under the effects of gravity. In this example, the problem is solved by using a single-parameter modelization, as shown in Figure 1. The resolution was implemented in C by the authors, as were all the problems presented in this document. This leads to a single-DOF ODE. The differential equation to be solved is as follows:
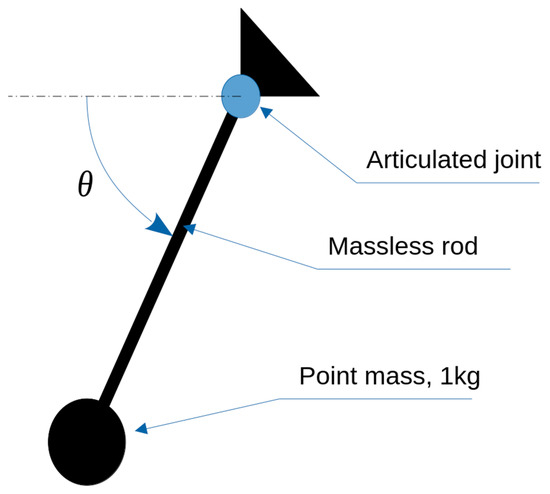
Figure 1.
A simple planar pendulum.
The beauty of the problem lies on the fact that the forces are conservative and, thus, energy conservation is a good measurement of the error. The proposal on the IFTOMM Multibody Benchmark is to simulate 10 s while keeping the energy drift below J. In this case, instead, the aim is to see the maximum precision that can be obtained from both approaches. In Table 1, the maximum energy drift obtained using the classical approach and the reformulated one can be seen. As shown, for large time steps, the error coincides, but as the time step is reduced, the error in the classical central differences formulation is increased when compared to the reformulated version. In this problem, this error only manifests itself in the computation of the velocities and acceleration due to the heavy cancellation in Equations (4) and (5). But, in the general case, it can also introduce errors in the displacements if the differential equation depends on the velocity. It is interesting to see that below a particular time step, the reformulated version also reduces its precision too, but this reduction does not seem to increase as fast as in the case of the classical approach. Obviously, in both cases, the computational cost is about the same.

Table 1.
Energy drift (error) obtained in the simple planar pendulum.
4. A Generalization of the Central Differences Method
Although the resolution of the cancellation problem is a justification in itself for the reformulation of the problem, it also leads to an interesting idea. Taking a look at Equations (9) and (12), one can modify them so that an alternative method can be devised. Let us consider the following:
and
The use of the configurable parameters and in Equations (15) and (16) are similar to those employed in the Newmark method. These parameters allow one to modify the convergence and stability characteristics of the algorithm. One could argue that Equation (15) lacks coherence, because it should weight and , but that would lead to a couple of drawbacks. First, one would need , which, in the approach considered here, is obtained in the following time step. Second, it would not be possible to take advantage of the parameters to modify the order of the error in each time step. On the other hand, one can reach the following:
and
Thus, the error committed in Equation (15) is, at most, .
4.1. Convergence Analysis
The third-degree method has a first- or second-order convergence.
To demonstrate this, the convergence analysis of the method is performed here. We will resort to a single variable. The order of the convergence is obtained as the lowest error order in the variable and its first derivative minus one. If one considers the known values of one time step as exact and denotes the approximated values in the form of , one arrives at the following equations for each time step:
One can write:
So:
On the other hand, the precise expression for the first derivative is:
Subtracting from Equation (21) gives the following:
By substituting Equation (25) into Equation (23), it is easy to find out that has an error of . In these terms:
Taking into account the following:
One reaches:
Thus, the error order in the derivative of the function is 3 if or 2 in the other case. Resorting now to Equation (19), the precise expression is:
Subtracting from Equation (20) and taking into account the fact that the error in is of a higher order:
One can write:
This leads to:
The error order in the variable is 4 if:
And it is 3 in the other case. Taking this into account, the order of the convergence is determined by the derivative of the variable, because it will be always equal or lower than that of the variable. Thus, the convergence of the third-order algorithm is 2 if and 1 in the other case.
If is chosen, one can eliminate the third-order error by using . Is this modification useful? If one considers the usual definition of the error order for second-order ODEs, as shown in [1], the order of the method is equal to the lower order that appears in the variable and its first derivative. In these terms, increasing the error order of the variable by using will not change the overall order. But, can affect the stability.
4.2. Stability Analysis
In order to study the stability, one can formulate the equations in the following form:
Here, the typical stability analysis performed for structural dynamics is posed, so the aim is to obtain the required for the integration to be stable. In order to simplify the problem, null damping is considered. This is quite common in structural dynamics because structural damping is always positive, and situations where a negative damping appears (self-excited vibrations) are usually to be avoided, so they are not usually integrated. Furthermore, they lead to an exponential growth of the vibrations. It is also considered a scalar problem (the case of vectorial problems can be always reduced to a set of scalar problems and, thus, the results are easily applicable). Thus, equations in the form of:
are considered.
In the case of structural dynamics, it is easy to see that:
with being the dynamic stiffness of the system and its mass. This means that is the natural frequency of the system. Note that this approach is general, and one could just substitute by to apply the analysis to any second-order differential equation. Note that, in the general case, and, thus, the stability limit might vary along the integration process. Under these conditions, one can reach the following:
In order for the method to be stable, the spectral radius of matrix A must be lower than one. The characteristic polynomial of A is as follows:
By introducing , one obtains the stability limits. For and , it is easy to find that . This is predictable, because these parameters lead to the reformulated central differences approach. The set of parameters and require for the method to be stable. As will be shown later, an interesting phenomenon appears with and . In this case, .
In order to generalize the results to systems of differential equations, one can obtain the natural frequencies of the system and use the largest , , to obtain the limit. One can also use techniques to obtain a bound on the largest to approximate this limit, as is usually performed in finite-element analysis when applying the central differences method or the conditionally stable Newmark configurations.
4.3. Behavior of the Method
In order to check the method’s performance, a couple of simple examples will be shown. The first example is the simple pendulum demonstrated before, while the second is devised to verify the stability behavior. Three parameter sets will be considered. All of them share , while was chosen to take values of 1 (reformulated central differences method), (theoretical best) and 2. behaves obviously like the reformulated central differences method shown before (Table 2).

Table 2.
Error (energy drift) for various configurations of the modified central differences approach.
The results come with a surprise. The use of delivers a moderate improvement, as expected, but the use of leads to an unexpected and considerable improvement in the results. However, the order of the convergence does not seem to change. The use of values for that are different to does not lead to improvements in precision or stability at the cost of the other.
Another interesting phenomenon is that the saturation of the floating-point precision behaves the same in all methods. This means that for quite small values of , the floating-point precision is unable to lead to better results. This is not quite unexpected, because there is no reason for this phenomenon to depend on the configuration parameters.
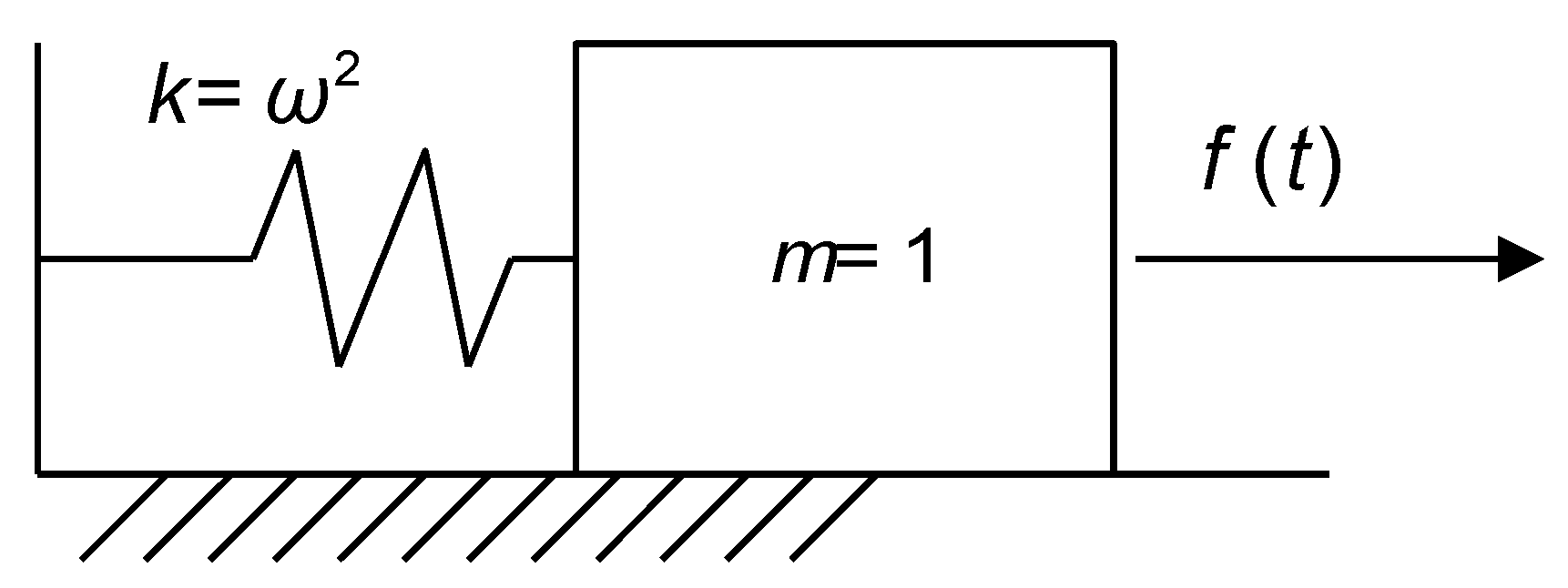
The next example is a simple one-degree-of-freedom (DOF) vibration model. The reason behind the use of this problem is the fact that the system can easily be tuned so that the natural frequency and, thus, the stiffness of the problem are different. Furthermore, it is a classical problem in linear structural dynamics, and as such it covers a different scope from that of the pendulum example (more related to multibody dynamics) while keeping its simplicity (Figure 2).
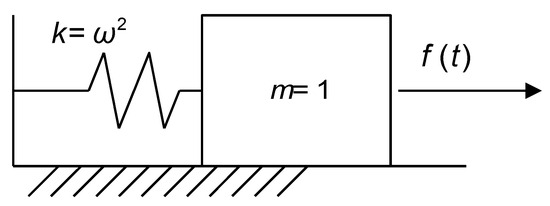
Figure 2.
A simple single-DOF vibration system.
The idea is that if is harmonic with a very low frequency when compared to , one could numerically solve the particular solution of the response with a noticeable , but this will compromise the stability. In the example, the following is used:
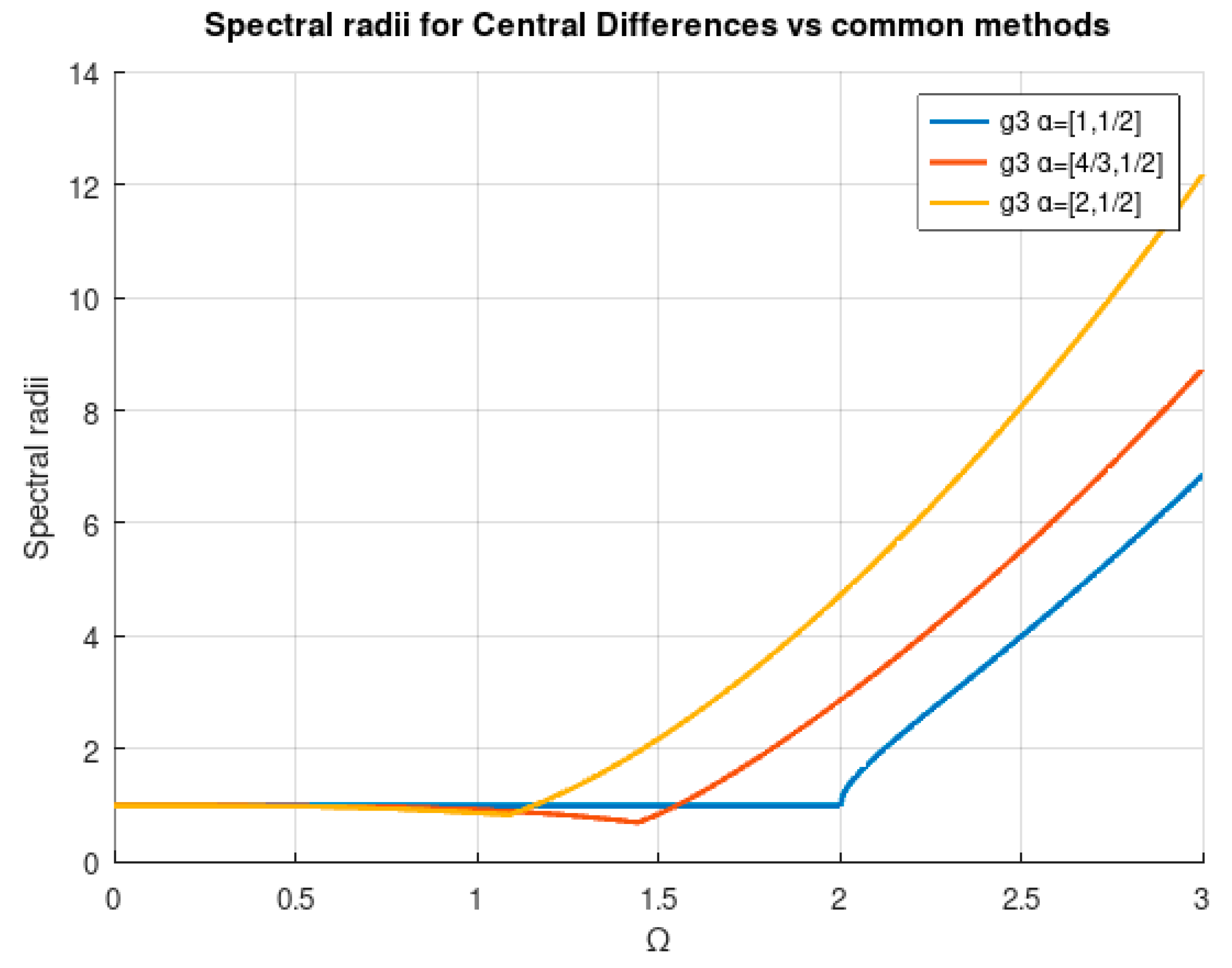
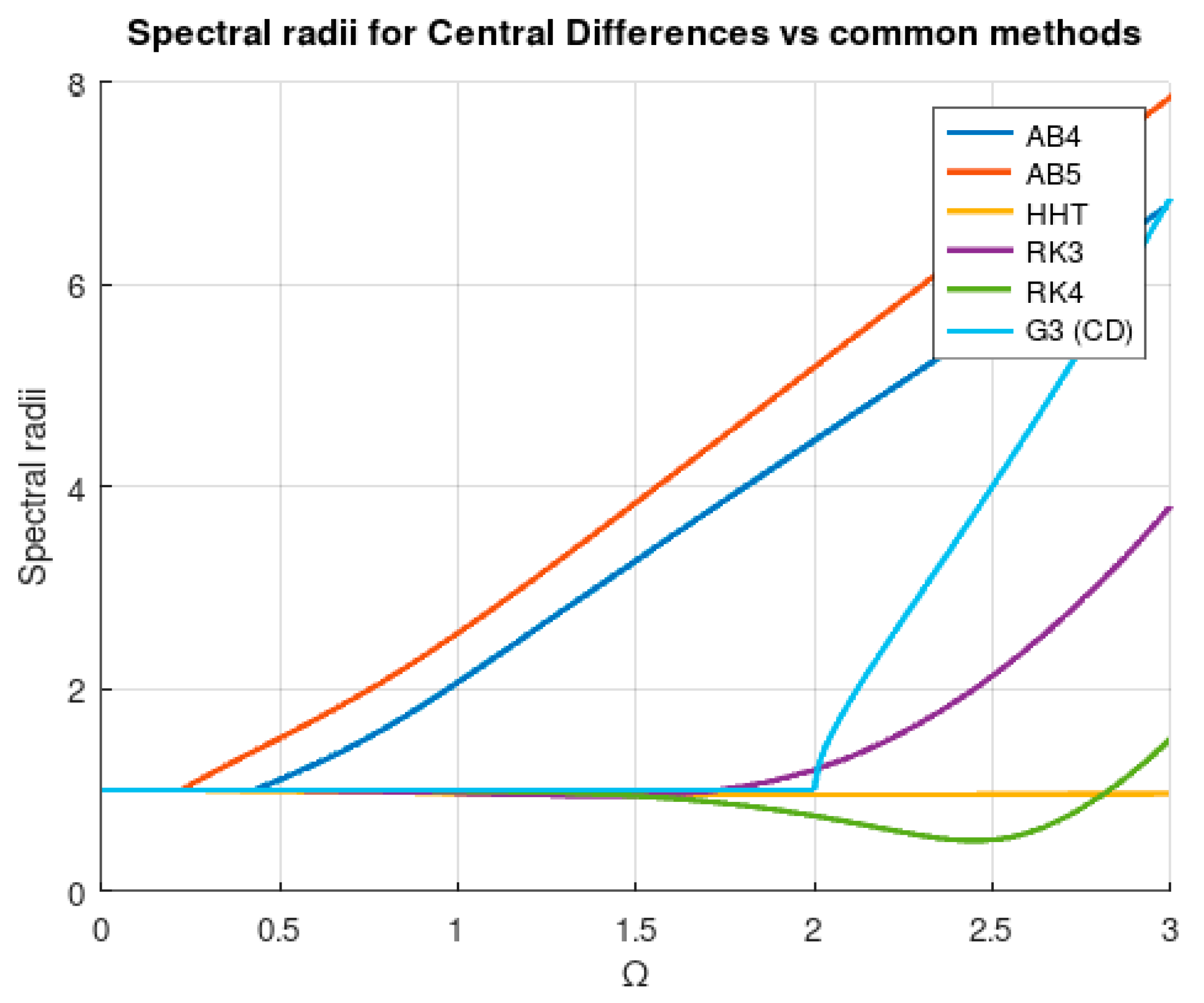
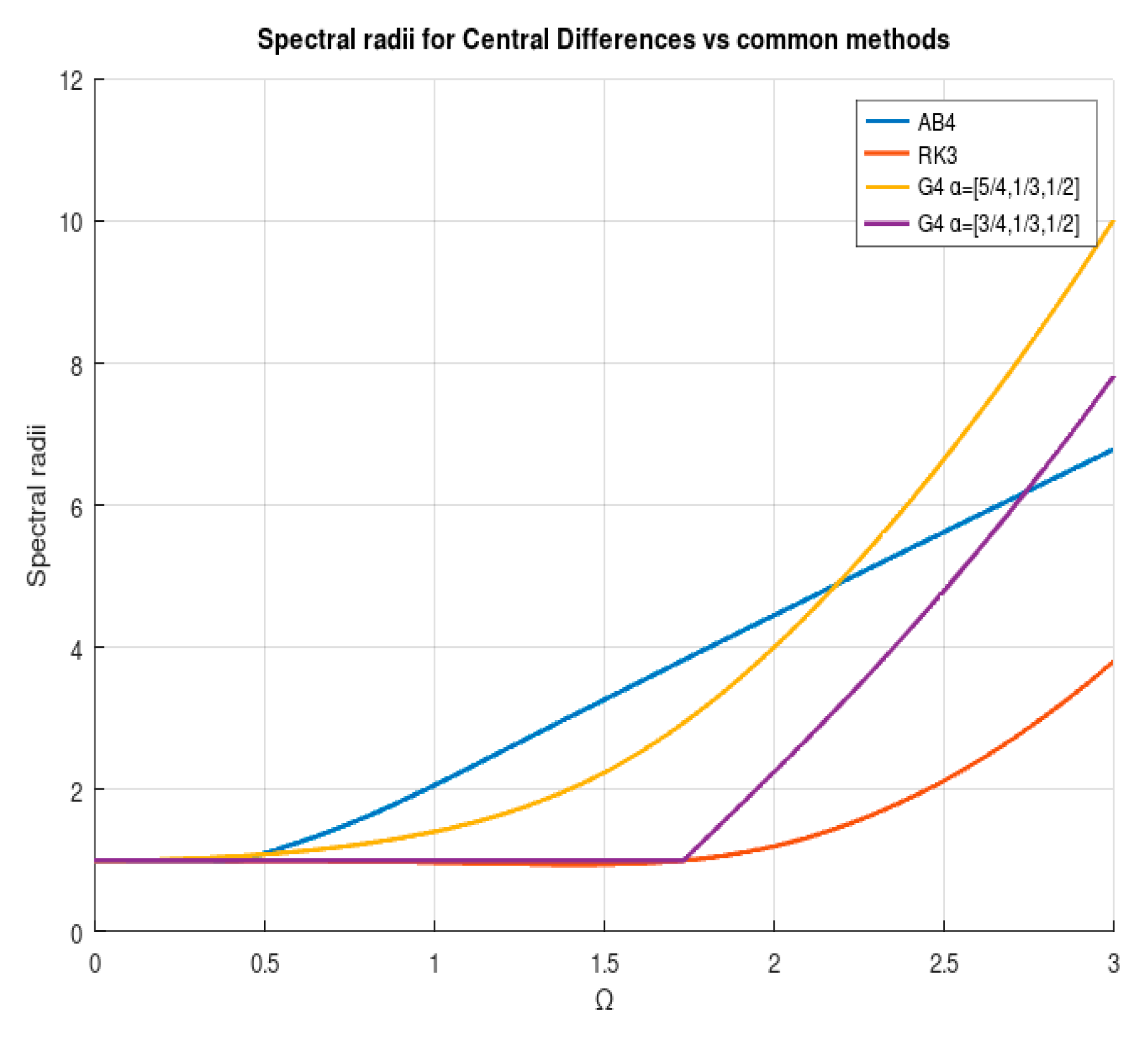
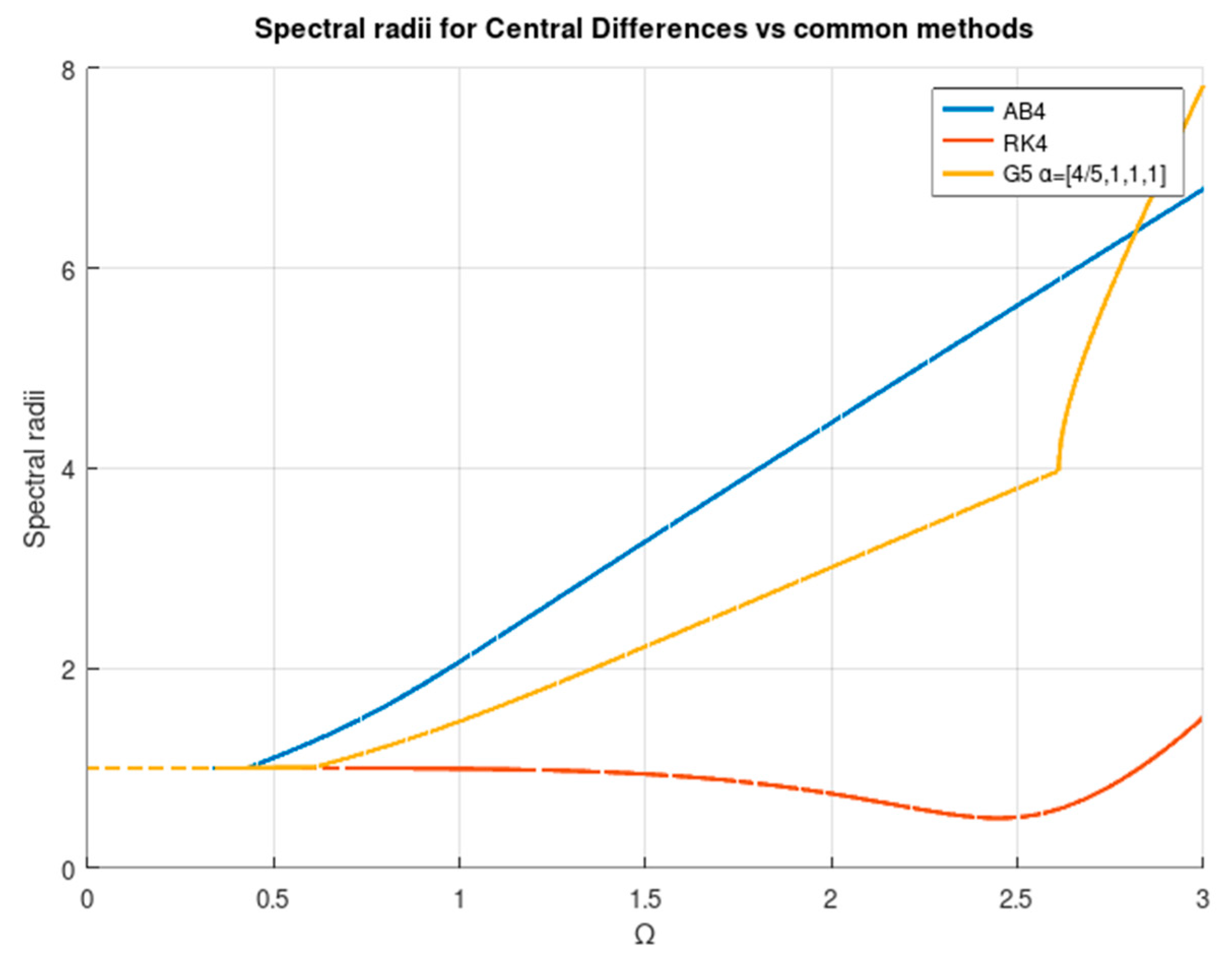
The considered frequencies are and . In order for the transitory to be as low as possible, the initial values are and . Taking into account the force frequency, a good value of to solve the problem could be computed in the form of in order to obtain 10 result points for each load cycle. Nevertheless, limitations come in the form of stability. In Table 3, one can find the theoretical limits for the stability. In Figure 3, one can see the spectral radius of the stability matrix for the indicated parameter sets. The algorithm is stable provided that the spectral radius is equal to or lower than one. In terms of stability, the central differences method is better than the other presented configurations. In Figure 4, the spectral radius for different typical methods is shown, including the central differences method. As one can see, being unconditionally stable, HHT is obviously the best in terms of stability. Rk4 behaves quite well but at the cost of more evaluations of the error function.

Table 3.
Stability limit for different configuration parameters.
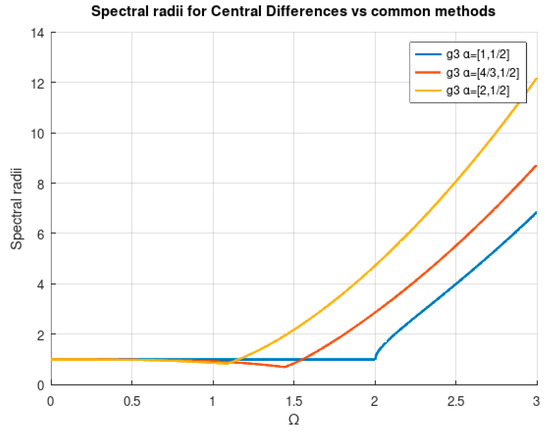
Figure 3.
Spectral radius of three configurations of the third-degree method vs. .
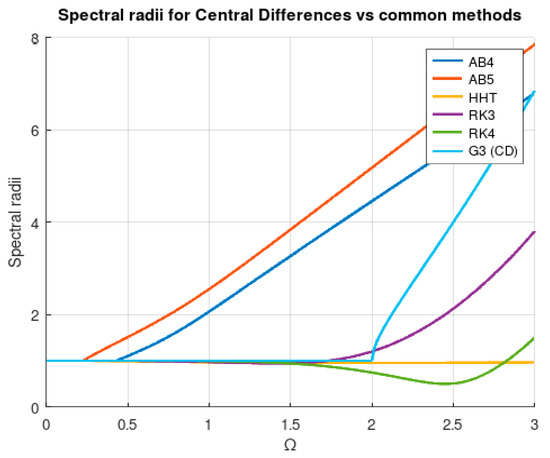
Figure 4.
Spectral radius of various methods vs. . AB4: Adams–Bashforth, fourth-order; AB5: Adams–Bashforth, fifth-order; HHT method, third-order RK; fourth-order RK; and the third-degree method in the central differences configuration (G3 (CD)).
Thus, the problem was tested with all of these parameters for values of the time step of 2.1, 2, 1.54 and 1.15. This allows one to check if the theoretical stability values match the results.
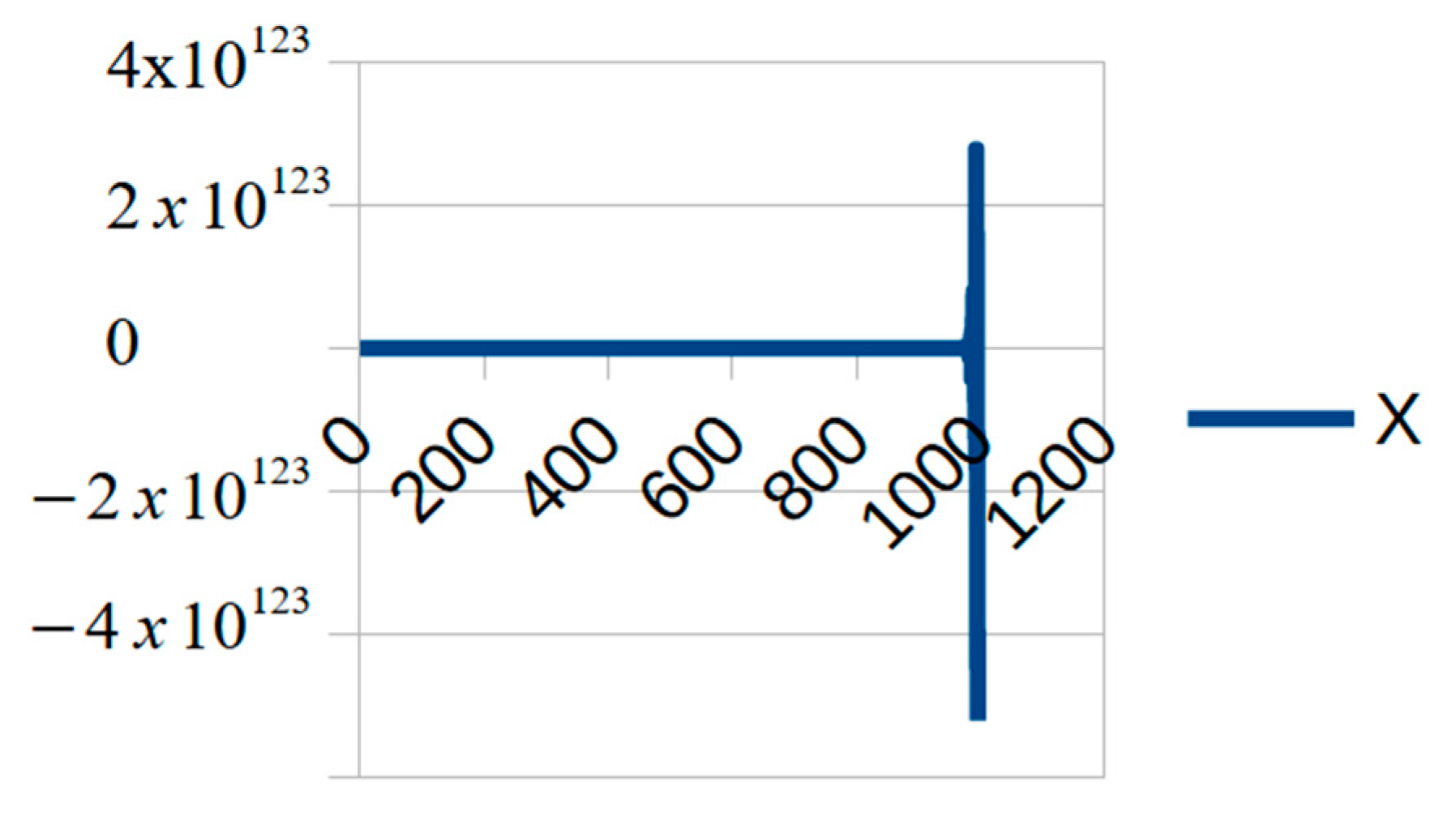
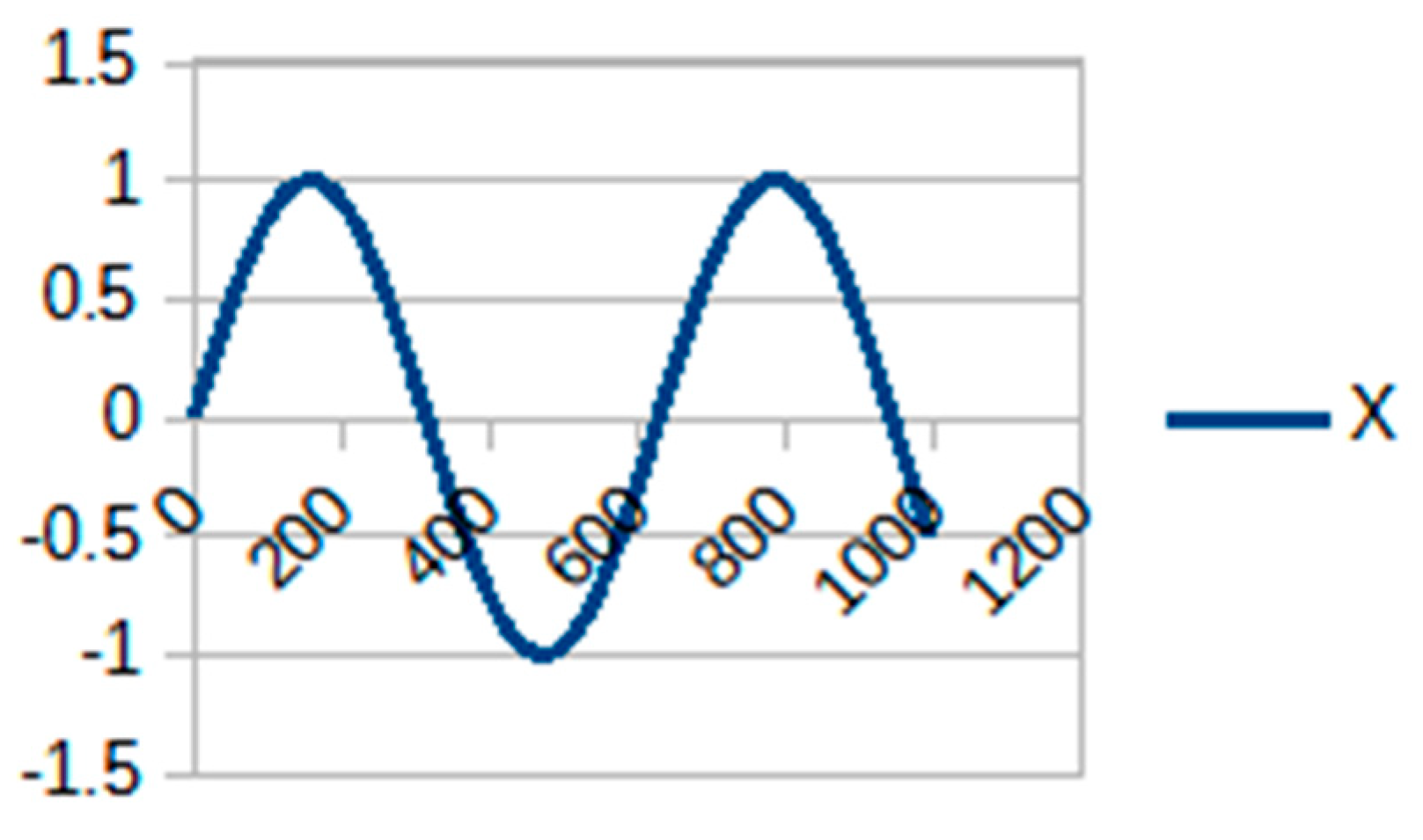
As expected, the use of led to instability in all of the cases. The use of led to stable results only in the case of and (see Figure 5 and Figure 6). The use of higher values of led to a behavior similar to that shown in Figure 6. A step size of allowed for the use of but was still unstable for . As predicted, all the cases were stable with , with similar results. This is a clear case of stability-limited problem, where an implicit and unconditionally stable method would have been a better choice.
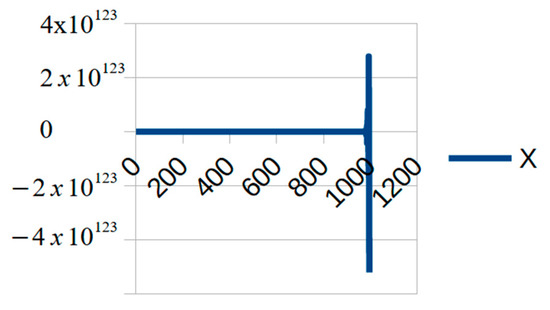
Figure 5.
Unstable result (, and ).
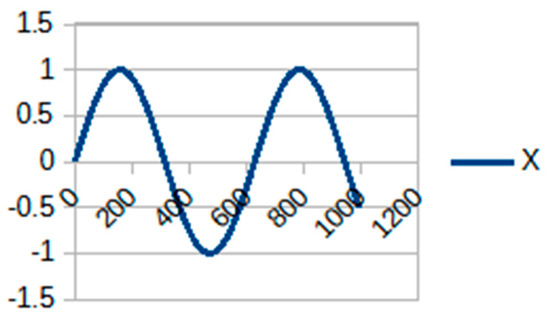
Figure 6.
Stable result (, and ).
5. Higher-Degree Methods
An explanation of the term higher-degree method is due here. In this paper, the term degree is related to the number of derivatives (including the variable itself) taken into account in the integration process. Thus, the methods derived from Equations (19)–(21) would be named third-degree methods. A similar approach was presented in reference [32]. In that case, it was applied to an explicit method.
One can guess that it is possible to generalize the ideas stated before to devise an even-higher-order method. In order to achieve this, one can formulate the following equations:
and
This would conform a fourth-degree method. One could also use an equation in the following form:
This would remove the need for Equation (42), but this has some drawbacks. First, one has either to analytically or numerically derive Equation (43). If this is carried out numerically, this is equivalent to Equation (42) with . Second, one cannot take advantage of to reduce the error or improve the stability.
5.1. Convergence of the Fourth-Degree Method
The fourth-degree method presents a second- or third-order convergence.
In order to analyze the convergence, one can assume that the previous results are obtained without error:
The precise equation for accelerations is as follows:
By subtracting Equations (47) and (49) and assuming that the error in is negligible (this can be demonstrated in a similar manner to that of the third-degree method), the following can be obtained:
One can state:
Thus:
And:
If one is to eliminate the first-order error in this equation, a value of should be used, but this is of little interest. As for the velocity equations, the precise expression is:
By subtracting Equation (53) from Equation (45):
One can write:
Leading to:
By incorporating Equation (53), the following can be obtained:
This demonstrates that the local error in is, at most, of the order . If one is to cancel the error of order , is needed.
The final issue is in the values of the function. One can write:
And thus:
By introducing:
One reaches:
And:
Using Equation (53) gives:
And introducing Equation (58), the final expression is:
Thus, the fourth-order method is either second-order (if ) or third-order.
5.2. Stability of the Fourth-Degree Method
Let us now focus on the stability of the method. An equation in the form Equation (65) is needed:
If one rearranges Equations (40)–(43), the following can be obtained:
The problem when using , and is that the system is always unstable, no matter how small is. Oddly enough, with these parameters, the spectral radius tends asymptotically to 1 as decreases. This means that for small values of and if the total time of the integration is not large, these parameters will lead to acceptable results. Unfortunately, extreme care should be taken in this case. A good choice for the parameters seems to be , and . In these conditions, one can obtain stable behavior provided that , with quite good results. Surprisingly enough, as one increases , the results and stability improve, reaching a maximum at . In this case, . This is nearly as good as the central differences method in terms of stability but with an improved order of convergence. Unfortunately, higher values of lead to instability, provided that and . In Table 4, one can see the results provided by these parameter sets in the simple pendulum problem. Since jerk was required in the initial step, it was introduced as .

Table 4.
Results obtained with the fourth-degree method.
The results obtained using are impressive. It more than doubled the number of significant digits when compared to the classical central differences approach. As stated before, these results come with a considerable handicap: the method is unstable, as one can see in Figure 7. On the other hand, the results obtained with are of considerable interest. While it has similar stability limits, it outperformed the classical central differences approach by a considerable margin, and it also outperformed the best parameter set obtained in the second-degree formulation. In Figure 7, one can see that the stability region is similar (slightly better) than that of the third-order Runge–Kutta method, which exhibited the same convergence but required three evaluations of the error function per step.
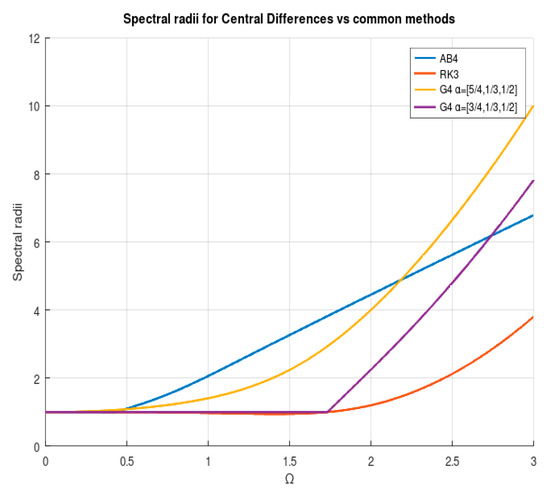
Figure 7.
Spectral radius of stability matrix vs. for the fourth-degree method in two configurations. Also included are the spectral radii of the fourth-order Adams–Bashforth and third-order Runge–Kutta methods.
An interesting phenomenon can be seen for very small time steps. In these cases, the error starts to grow in the same way as happened in the original central differences formulation. This happens because when using (41)–(43) to obtain , one reaches:
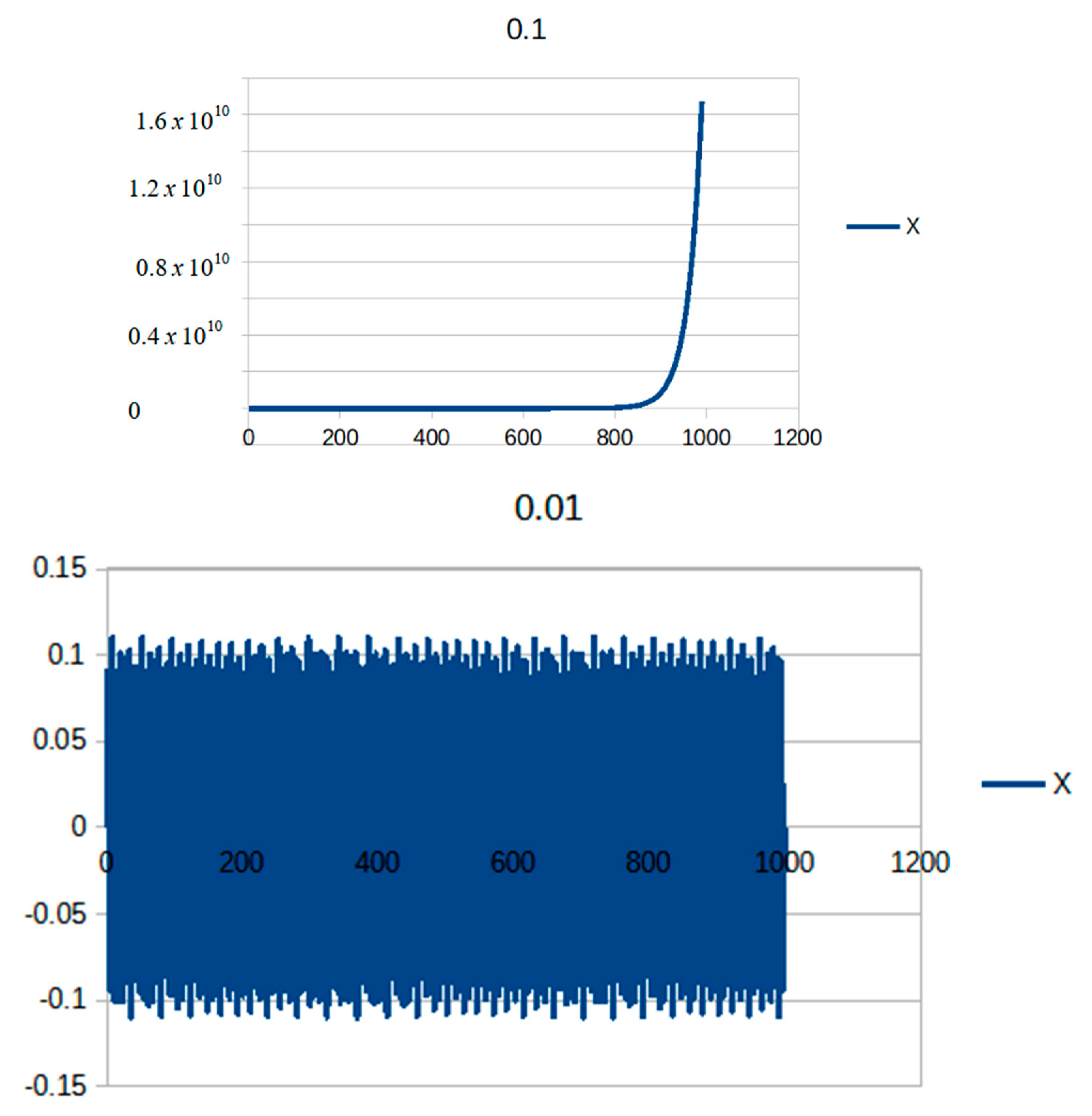
This leads to cancellation for small time steps. It is also interesting to show the behavior of the method with . As stated before, the method is unstable, because the spectral radius is larger than one no matter the value of used, but it also decreases as decreases. In order to check how it translates to real-life problems, a one-DOF model similar to that used to check the stability of the second-degree methods was devised. In this case, the parameters and were used. The total integration time was 1000 s (Figure 8).
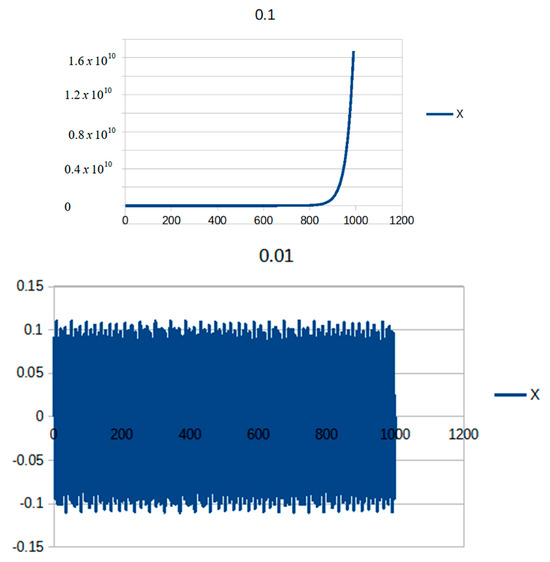
Figure 8.
Results for the one-DOF model with and time steps of 0.1 (top) and 0.01 (bottom).
Surprisingly enough, the integrator was capable of performing 1000 s of integration with a time step of 0.01 with no signs of instability. It was checked whether instability was noticeable at about 5000 s of integration. A time step of 0.001 showed instability at about 50,000 s of integration. In Table 5, one can see the values of the spectral radii and the integration times, where the instability is clearly visible. Obviously, the latter were approximated and should not be used as a reference for the total integration time without further analysis, because they might considerably change from problem to problem.

Table 5.
Some experimental results using .
The question arises quickly as to whether it is possible to introduce a small perturbation to the parameters so that one can stabilize the method. The answer is yes. One can find that when using , the spectral radii are kept (at least numerically) equal to or below 1 for values of . Furthermore, the use of along with leads to the same situation for values of . The problem is that these modifications, although they might look quite small, come at the cost of precision, and they render the method with a precision similar to that of or even worse.
5.3. Fifth-Degree Method
One can be tempted to employ Equations (68)–(72) to arrive to fifth-degree methods by using the following:
and
The matrix that determines the stability in this case, for a non-damped system, is:
In this case, it is more difficult to obtain parameters that allow for stability. It is easy to guess that the optimal case to reduce the error as much as possible is that where , , and . Unfortunately, this configuration is unstable. The use of the parameters and leads to a conditionally stable method.
In Figure 9, one can see that the stability area of the method is quite reduced when compared to RK4, but one has to take into account the number of evaluations of the equation to integrate when using RK4. The stability condition for this set is, approximately . This is a quite competitive situation for this method, as it allows for third-order convergence along with a very small penalty in stability when compared to the central differences method. When this method is applied to the simple pendulum problem, it leads to the results presented in Table 6.
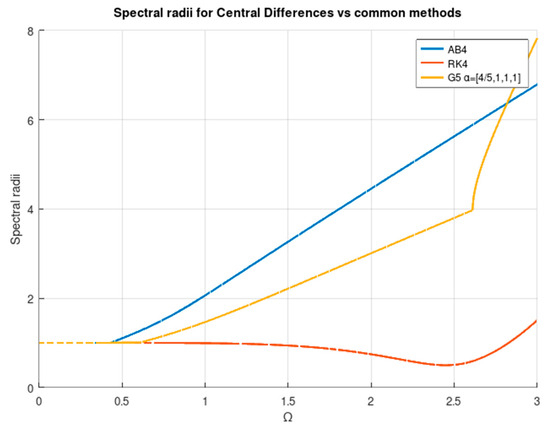
Figure 9.
Spectral radius of stability matrix vs. for the fifth-degree method with parameters and .

Table 6.
Results for the fifth-degree method with and .
One can see how the method delivers similar results to that of the unstable configuration of the fourth-degree method with best third-order convergence, but this time, the method is conditionally stable. It is also noticeable how cancellation problems lead to the decrease in precision for time steps lower than 2 × 10−4, where the error reaches 4.32751 × 10−13, in a similar way to what happened in the other methods.
It is interesting to compare these results to those in the IFTOMM multibody benchmark. In this benchmark, the best result posted (posted by Francisco González) was programmed in C++ using the trapezoidal rule and run in an Intel Core-i7-4790 K@4.00 GHz, which should exhibit similar performance to the one used in all of the tests presented here (AMD Ryzen 2600 @3.4 GHz). In this case, the total execution time was 0.0254, with an accuracy of 0.917 × 10−5. In the algorithm presented here, an accuracy of 6.71 × 10−11 was reached in 4 × 10−4 s. This is reasonable due to the fact that the trapezoidal rule is of a second-order accuracy. There is also another result in the benchmark of interest. Using Simbody, Luca Tagliapietra posted an accuracy of 4 × 10−11 with a total time of 0.637 s. Here, an error of 1.97 × 10−11 was obtained in 0.004 s.
6. Spinning Top Example
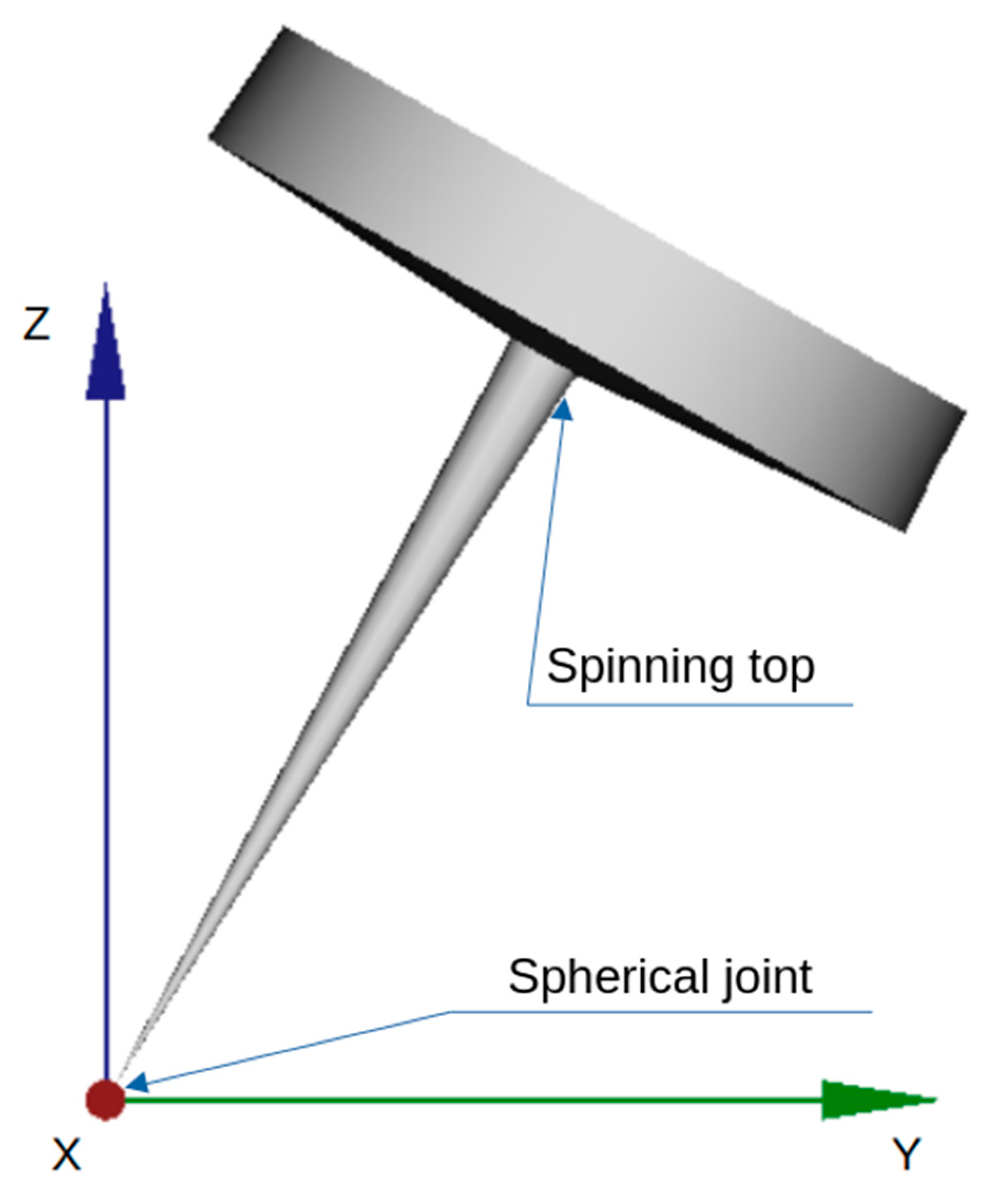
As stated before, the second-order central differences method and the method presented here are conditionally explicit. This means that they are explicit provided that the equation to be integrated can be represented in the form of Equation (77). In any case, it is interesting to obtain an insight into the performance of the method on problems in the more general form of Equation (1). The considered problem is a spinning top (Figure 10). The problem is modelized in Euler angles (ZXZ), and it is built on minimal coordinates, so the problem is reduced to an ODE.
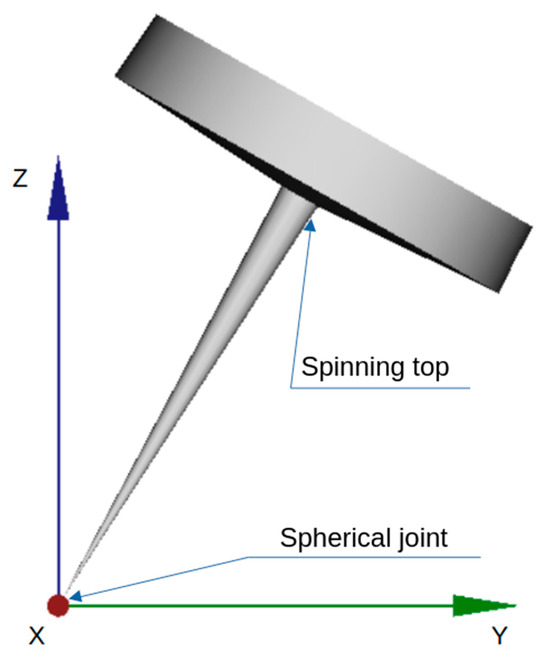
Figure 10.
Spinning top.
In the example, the spinning top is rotating about its axis with a speed of , and the angle with respect to the z axis is . The moments of inertia on the principal axes measured in the origin of the global coordinate system are Kgm2 and Kgm2. The total mass of the spinning top is Kg. The distance from the base of the spinning top to its center of gravity is , and gravity is set to .
The total simulation time is 10 s. The EDO to be solved is, thus, the Euler equation:
where is the angular velocity vector, is the Euler angle’s vector, is the rotation matrix, is the diagonal tensor of inertia, is the angular acceleration of the spinning top when and is the moment vector introduced by the gravitational force. It holds that:
where is the vector of the position of the center of gravity of the spinning top in the local frame of reference, which is: .
In order to solve the problem with the method presented here, one needs to iteratively approach Equation (75). This is the main disadvantage of these methods when dealing with problems in the form of Equation (1) instead of Equation (79). The linearized form of Equation (75) can be written in the following form:
with:
The problem was solved using the fifth-degree method presented here. The computer’s CPU was an AMD Ryzen 2600. The clock speed was fixed at 3.4 GHz. For all the considered time steps, the times were averaged on 10 runs. Error was measured as the maximum fluctuation of the total mechanical energy in the simulation. The employed parameters were , , and . The results are as shown in Table 7.

Table 7.
Spinning top results.
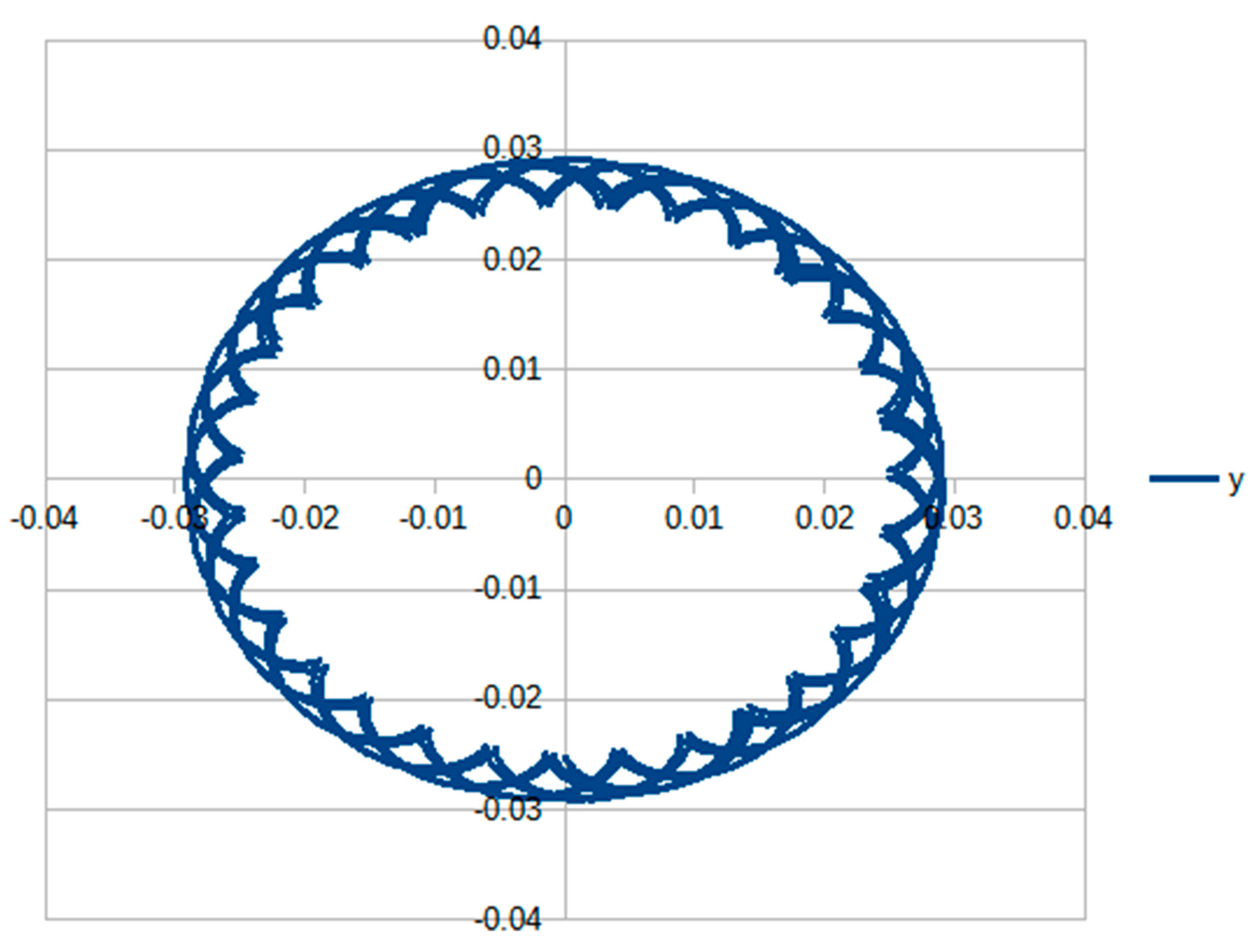
As presented before, this is an example that is ill-suited for the method presented here. But, in any case, it handled the problem in a quite reasonably manner. As can be seen in the results (Table 7), the maximum precision was limited to about 1 × 10−13. If one plots the trajectory of the center of gravity of the spinning top as obtained by the algorithm, the results are as one would expect (see Figure 11). The gyroscopic effect is what keeps the spinning top from falling down.
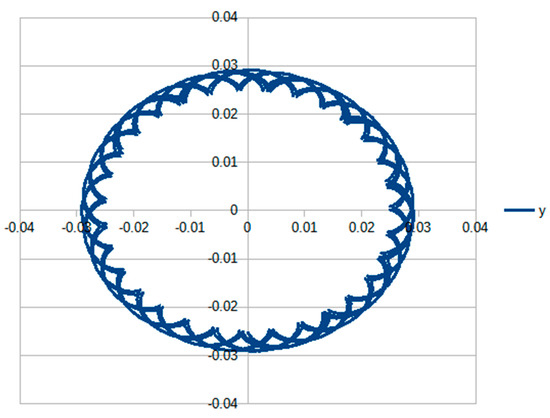
Figure 11.
Spinning top trajectory as seen from above.
7. Comparison with Runge–Kutta Methods
When speaking about ODEs, Runge–Kutta methods are among the most simple and versatile of the methods that one can find. The main disadvantage of Runge–Kutta methods is the fact that when they are applied to differential algebraic equations (DAEs), they require a reduction in the index of the DAE to be applied [17]. This leads to the drift phenomenon, which has to be dealt with using stabilization methods such as the Baumgarte [18] or projection methods [33], which are not exempt from issues [19]. One can also resort to the use of coordinate partitioning methods [3,34,35] or, whenever possible, the reformulation of the problem so that it can lead to an ODE (the use of minimal coordinate formulations [36]). Unfortunately, the last two alternatives are not exempt from problems.
On the other hand, the use of conditionally explicit methods such as the central differences method has shown that their application to DAEs does not incur additional stability issues apart from those that also appear in ODEs [10,14,15]. The methods proposed here are based on similar premises to those present in the central differences method and, thus, should present similar behavior. This is one advantage that they might present.
In order to carry out a comparison, the spinning top problem was programmed using a third-order Runge–Kutta method. The third-order method was selected to keep the same theoretical order of the integrator. One must take into account that the Runge–Kutta approach is explicit, while the conditionally explicit method is, in this case, implicit. The obtained results, using the same computer and under the same conditions used for the conditionally explicit method, are presented in Table 8.

Table 8.
Results for the spinning top problem using an RK3 method.
The first thing that leads to a surprise is that the time results for the method presented here were quite competitive for the smaller time steps. This was due to the fact that for the smaller time steps, the conditionally explicit method has to perform a small number of iterations. As for the precision, the conditionally explicit method showed a slightly better convergence, apparently at the cost of an earlier precision limitation. Taking into account that the conditionally explicit method is implicit for this case, the results were quite competitive, but one should make no mistake, in that the explicit method requires derivatives, which were analytically obtained for this case. This requires some additional work that the explicit RK3 method does not need. This is a disadvantage that does not appear when dealing with ODEs where the conditionally explicit method behaves as an explicit one. In any case, one can see that the conditionally explicit method did not lag a lot behind the Runge–Kutta approach. One also has to take into account the fact that these methods require several evaluations of the error function per step, which severely increases the cost. The method presented here also might require more than one resolution of the system of equations, but only when the equation to integrate depends on .
8. Application to DAEs
Probably the most interesting potential use of the algorithm lies in its application to DAEs. This is because, as happens when using the central differences method, the method needs no index reduction, thus avoiding the drift without any correction. In order to apply the method to DAEs, Equation (13) can be used, so one can introduce restrictions in terms of the variable but expressed in accelerations. This will lead to a vector verifying the coordinate restrictions. For example, let us consider a restriction in the following form:
which is a restriction in terms of displacements. By introducing Equation (13) into Equation (79), one expresses this equation in terms of but enforcing Equation (79).
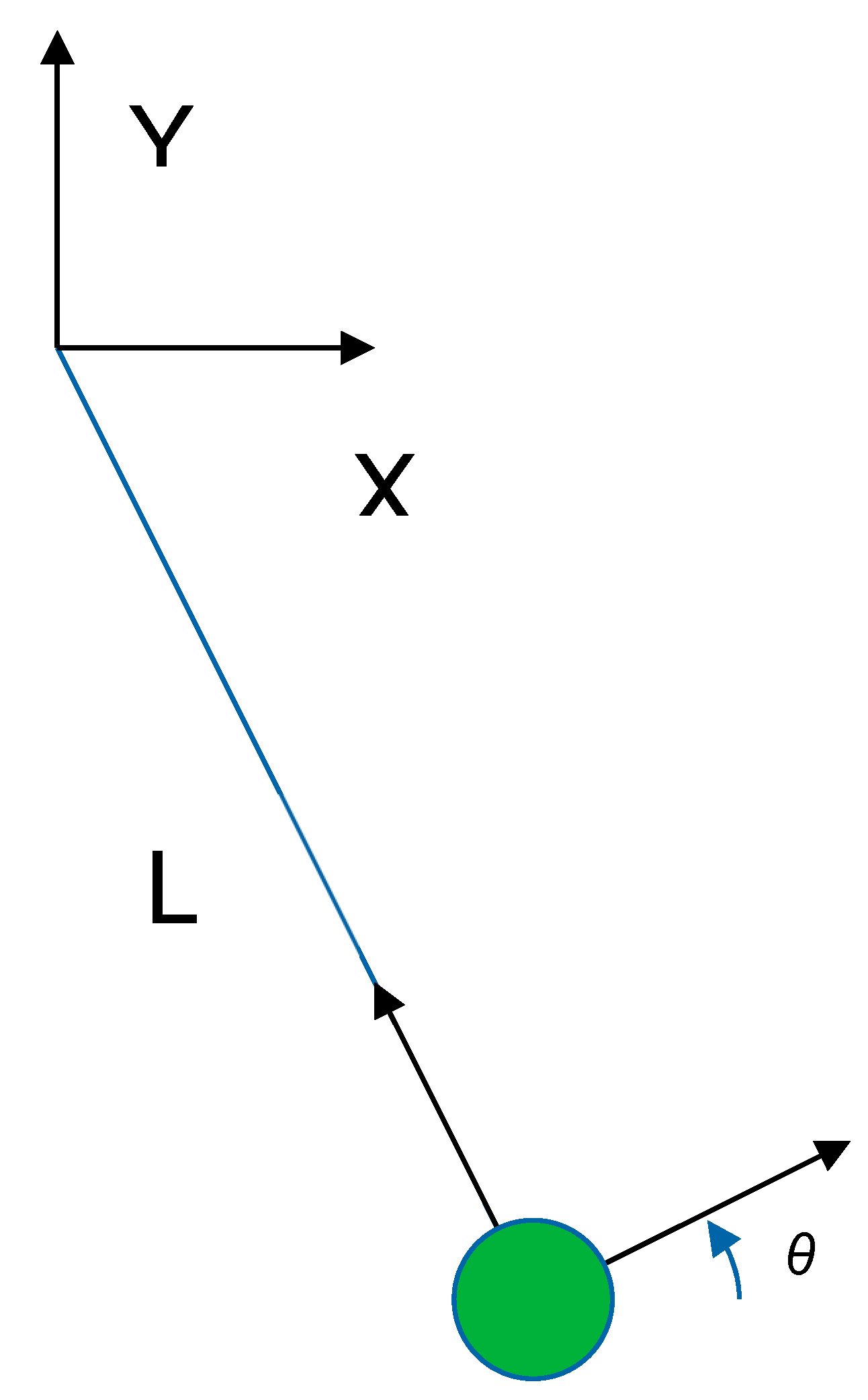
In order to compare both methods, the same pendulum problem stated before is solved in this section, but, in this case, the equilibrium equations are formulated in the center of gravity of the pendulum, which means that the R joint will require two restrictions. The coordinate system is presented in Figure 12. The pendulum starts from a horizontal position, i.e., , and it is let free. Thus, this is a problem with energy conservation.
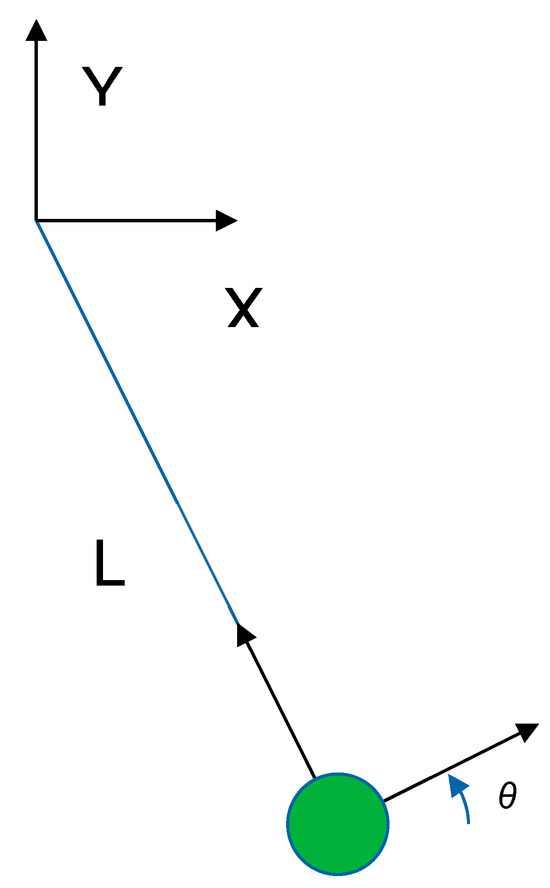
Figure 12.
Coordinate system for the DAE resolution of the pendulum problem.
The system of equations to be solved is, thus, composed of:
The reduction in the index of this DAE system (required for the RK3 method) leads to:
If one solves the system without stabilization, one obtains the results presented in Table 9.

Table 9.
Results for the DAE pendulum using an RK3 method without drift stabilization.
Here, the drift was measured as the assembly error; this is the squared length of the truss as defined by the pendulum coordinates minus the squared original length .
In order to remove the drift, a simple coordinate projection method was implemented. The results are indicated in Table 10.

Table 10.
Results for the DAE pendulum using an RK3 method with stabilization (projection).
In order to solve the problem using one of the methods formulated here, a linearization of the restrictions is needed. One can write the following for the equilibrium equation:
And the linearized restrictions are:
with being the current approximation of . Now, one can use Equations (69)–(73) to write and in the following form:
and
This allows one to write the following:
and
Grouping the equations gives:
One could also take advantage of the fact that Equation (88) does not change along the iterative process of solving the step. This would allow for the use of a fundamental basis of the null space of the system to considerably reduce the computational cost. But, for the shake of simplicity, the whole system was solved in each iteration.
The iterative resolution of Equation (90) allows one to solve , which, in turn, allows one to obtain the position and its derivatives. It is important to not introduce the convergence criteria using because its contribution can be so small that very small error values should be used. The use of the variation in to measure the error is recommended. With all of these in mind, one can reach the results shown in Table 11. All the parameters were set to 1.

Table 11.
Results for the DAE pendulum using a fifth-degree conditionally explicit method.
The results for the method presented here were quite good. It obtained similar results to the stabilized RK3 method in terms of the coordinate drift but with much better error results and by using less than half of the time. The RK3 results, in time, could have been improved by using a symmetric matrix approach, but this would have as much halved the computational times. On the other hand, as stated before, one could also reduce the computational cost of the method presented here by a considerable amount. Finally, the problem size should benefit the conditionally explicit method because of the reduction in the number of error function evaluations.
9. Conclusions and Future Work
A new family of conditionally explicit integrators for second-order ODEs order were introduced in this paper. This has led to configurable methods, which might allow for existing code to obtain additional convergence in some cases with little effort.
A fourth-degree configurable method was proposed. A couple of parameter sets for this method were considered. One of them led to great convergence but with compromised stability. The other set increased the convergence when compared to the third-degree conditionally explicit methods with a quite moderate reduction in the range of stability.
Finally, a fifth-degree method was presented, along with a set of parameters that allow for a conditionally stable integration of third-order convergence, leading to only about half the time step limit required for the central differences method.
The method presented here is of special interest for the case of differential algebraic equation systems. It requires no drift stabilization, and it shows good performance. This is an interesting practical advantage.
Taking into account that the method can be considered a generalization of the central differences method, it might allow one to reuse code developed with the central differences approach to improve on convergence with a moderate cost.
In order to check the behavior of the methods, some simple examples were presented. These belong both to the structural dynamics and the multibody dynamics fields, thus allowing one to obtain an idea of the performance of the methods in different circumstances.
In future work, a deeper analysis of different parameter sets should be performed. The study of even-higher-degree methods is also of interest. Obviously, the application of these methods to different areas should be studied, along with more complex problems in multibody dynamics and structural dynamics. Finally, a global convergence analysis for the higher-degree methods is of interest.
Author Contributions
All authors have contributed to all of the tasks required to develop this work in similar proportions. All authors have read and agreed to the published version of the manuscript.
Funding
The authors would like to thank to the Basque Government for its funding to the research group, recognized under section IT1542-22. The authors also specially thank the grant PID2021-124677NB-I00 funded by MCIN/AEI/10.13039/501100011033 and by “ERDF A way of making Europe”.
Data Availability Statement
The datasets generated and/or analyzed during the current study are available from the corresponding author at a reasonable request.
Acknowledgments
We want to thank the anonymous reviewers who helped us a lot in improving this work.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Hairer, E.; Nørsett, S.P.; Wanner, G. Solving Ordinary Differential Equations I. Nonstiff Problems (Springer Series in Computational Mathematics, Vol. 8). In Mathematics and Computers in Simulation; Springer: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Avilés, R. Métodos de Análisis Para Diseño Mecánico: Diseño Mecánico, Análisis Estático, Elementos Finitos En Estática, Elementos Finitos En Dinámica, Análisis de Fatiga; Escuela Superior de Ingenieros: Bilbao, Spain, 2003; ISBN 84-95809-09-5. [Google Scholar]
- García de Jalon, J.; Bayo, E. Kinematic and Dynamic Simulation of Multibody Systemas; Springer: New York, NY, USA, 1994; ISBN 978-1-4612-7601-2. [Google Scholar]
- Bauchau, O.A. Flexible Multibody Dynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010; Volume 176, ISBN 94-007-0335-X. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Fox, D. The Finite Element Method for Solid and Structural Mechanics, 7th ed.; Elsevier: Amsterdam, The Netherlands, 2013; pp. 1–624. [Google Scholar] [CrossRef]
- Newmark, N.M. A Method of Computation for Structural Dynamics. J. Eng. Mech. Div. 1959, 85, 67–94. [Google Scholar] [CrossRef]
- Hilber, H.M.; Hughes, T.J.R.; Taylor, R.L. Improved Numerical Dissipation for Time Integration Algorithms in Structural Dynamics. Earthq. Eng. Struct. Dyn. 1977, 5, 283–292. [Google Scholar] [CrossRef]
- Wilson, E.L. A Computer Program for the Dynamic Stress Analysis of Underground Structures. Struct. Eng. Mech. Mater. 1968. [Google Scholar]
- Shabana, A.A. Dynamics of Multibody Systems; Cambridge University Press: Cambridge, UK, 2013; ISBN 978-1-107-33721-3. [Google Scholar]
- Fernández de Bustos, I.; Uriarte, H.; Urkullu, G.; García-Marina, V. A Non-Damped Stabilization Algorithm for Multibody Dynamics. Meccanica 2022, 57, 371–399. [Google Scholar] [CrossRef]
- Gavrea, B.; Negrut, D.; Potra, F.A. The Newmark Integration Method for Simulation of Multibody Systems: Analytical Considerations. In Proceedings of the ASME 2005 International Mechanical Engineering Congress and Exposition, Orlando, FL, USA, 5–11 November 2005. [Google Scholar]
- Negrut, D.; Rampalli, R.; Ottarsson, G.; Sajdak, A. On an Implementation of the Hilber-Hughes-Taylor Method in the Context of Index 3 Differential-Algebraic Equations of Multibody Dynamics (DETC2005-85096). J. Comput. Nonlinear Dyn. 2007, 2, 73–85. [Google Scholar] [CrossRef]
- Dopico, D.; Lugris, U.; Gonzalez, M.; Cuadrado, J. IRK vs Structural Integrators for Real-Time Applications in MBS. J. Mech. Sci. Technol. 2005, 19, 388–394. [Google Scholar] [CrossRef]
- Urkullu, G.; de Bustos, I.F.; García-Marina, V.; Uriarte, H. Direct Integration of the Equations of Multibody Dynamics Using Central Differences and Linearization. Mech. Mach. Theory 2019, 133, 432–458. [Google Scholar] [CrossRef]
- Urkullu, G.; Fernández-de-Bustos, I.; Olabarrieta, A.; Ansola, R. Estudio de La Eficiencia Del Método de Integración Directa Mediante Diferencias Centrales (DIMCD). DYNA-Ing. Ind. 2021, 96, 512. [Google Scholar]
- Kovalnogov, V.N.; Fedorov, R.V.; Karpukhina, T.V.; Simos, T.E.; Tsitouras, C. Runge–Kutta Embedded Methods of Orders 8(7) for Use in Quadruple Precision Computations. Mathematics 2022, 10, 3247. [Google Scholar] [CrossRef]
- Petzold, L. Differential/Algebraic Equations Are Not ODE’ s. SIAM J. Sci. Stat. Comput. 1982, 3, 367–384. [Google Scholar] [CrossRef]
- Baumgarte, J. Stabilization of Constraints and Integrals of Motion in Dynamical Systems. Comput. Methods Appl. Mech. Eng. 1972, 1, 1–16. [Google Scholar] [CrossRef]
- Flores, P.; Pereira, R.; Machado, M.; Seabra, E. Investigation on the Baumgarte Stabilization Method for Dynamic Analysis of Constrained Multibody Systems. In Proceedings of the EUCOMES 2008—The 2nd European Conference on Mechanism Science, Cassino, Italy, 17–20 September 2008; pp. 305–312. [Google Scholar] [CrossRef]
- Fernández de Bustos, I.; Urkullu, G.; García Marina, V.; Ansola, R. Optimization of Planar Mechanisms by Using a Minimum Distance Function. Mech. Mach. Theory 2019, 138, 149–168. [Google Scholar] [CrossRef]
- Verlet, L. Computer “Experiments” on Classical Fluids. I. Thermodynamical Properties of Lennard−Jones Molecules. Phys. Rev. 1967, 159, 98–103. [Google Scholar] [CrossRef]
- Hairer, E.; Lubich, C.; Wanner, G. Geometric Numerical Integration Illustrated by the Störmer/Verlet Method. Acta Numer. 2003, 12, 399–450. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, T.W.; Flannery, B.P. Numerical Recipes: The Art of Scientific Computing; Cambridge University Press: New York, NY, USA, 2007; ISBN 978-0-521-88068-8. [Google Scholar]
- Birdsall, C.K.; Langdon, A.B. Plasma Physics via Computer Simulation; CRC Press: Boca Raton, FL, USA, 1991; ISBN 978-1-315-27504-8. [Google Scholar]
- Yoshida, H. Construction of Higher Order Symplectic Integrators. Phys. Lett. 1990, 150, 262–268. [Google Scholar] [CrossRef]
- Beeman, D. Some Multistep Methods for Use in Molecular Dynamics Calculations. J. Comput. Phys. 1976, 20, 130–139. [Google Scholar] [CrossRef]
- Hairer, E.; Wanner, G. Solving Ordinary Differential Equations II; Springer Series in Computational Mathematics; Springer: Berlin/Heidelberg, Germany, 1991; Volume 14, ISBN 978-3-662-09949-0. [Google Scholar]
- Park, K.C.; Underwood, P.G. A Variable-Step Central Difference Method for Structural Dynamics Analysis-Part I. Theoretical Aspects: Park, K C and Underwood, P G Comput. Methods and Appl. Mechan. Engng Vol 22 No 2 (May 1980) pp 241–258. Comput.-Aided Des. 1981, 13, 51. [Google Scholar] [CrossRef]
- Kim, W. Higher-Order Explicit Time Integration Methods for Numerical Analyses of Structural Dynamics. Lat. Am. J. Solids Struct. 2019, 16, e201. [Google Scholar] [CrossRef]
- Uriarte, H. Integration of the Equations of Multibody Dynamics Using Structural Methods. Ph.D. Thesis, University of the Basque Country, Bilbao, Spain, 2023. [Google Scholar]
- Fernández de Bustos, I.; Uriarte, H.; Coria, I.; Urkullu, G. A New Approach to Formulate Structural Methods for Multibody Dynamics. In Proceedings of the ECCOMAS Thematic Conference on Multibody Dynamics, Lisbon, Portugal, 24–28 July 2023. [Google Scholar]
- Urkullu, G.; de Bustos, I.F.; Coria, I.; Uriarte, H. Explicit Higher-Order Integrator for Multibody Dynamics. In Advances in Mechanism and Machine Science; Okada, M., Ed.; Springer Nature: Cham, Switzerland, 2024; pp. 593–604. [Google Scholar]
- Eich, E. Convergence Results for a Coordinate Projection Method Applied to Mechanical Systems with Algebraic Constraints. SIAM J. Numer. Anal. 1993, 30, 1467–1482. [Google Scholar] [CrossRef]
- Haug, E.J. Computer Aided Kinematics and Dynamics of Mechanical Systems; Allyn and Bacon Boston: Boston, MA, USA, 1989; Volume 1. [Google Scholar]
- Wehage, R.A.; Haug, E.J. Generalized Coordinate Partitioning for Dimension Reduction in Analysis of Constrained Dynamic Systems. J. Mech. Des. 1982, 104, 247–255. [Google Scholar] [CrossRef]
- Hiller, M.; Kecskeméthy, A. Dynamics of Multibody Systems with Minimal Coordinates. In Computer-Aided Analysis of Rigid and Flexible Mechanical Systems; Springer: Dordrecht, The Netherlands, 1994; pp. 61–100. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).