Multi-Task Forecasting of the Realized Volatilities of Agricultural Commodity Prices
Abstract
1. Introduction
2. Data
3. Methods
3.1. Forecasting Models
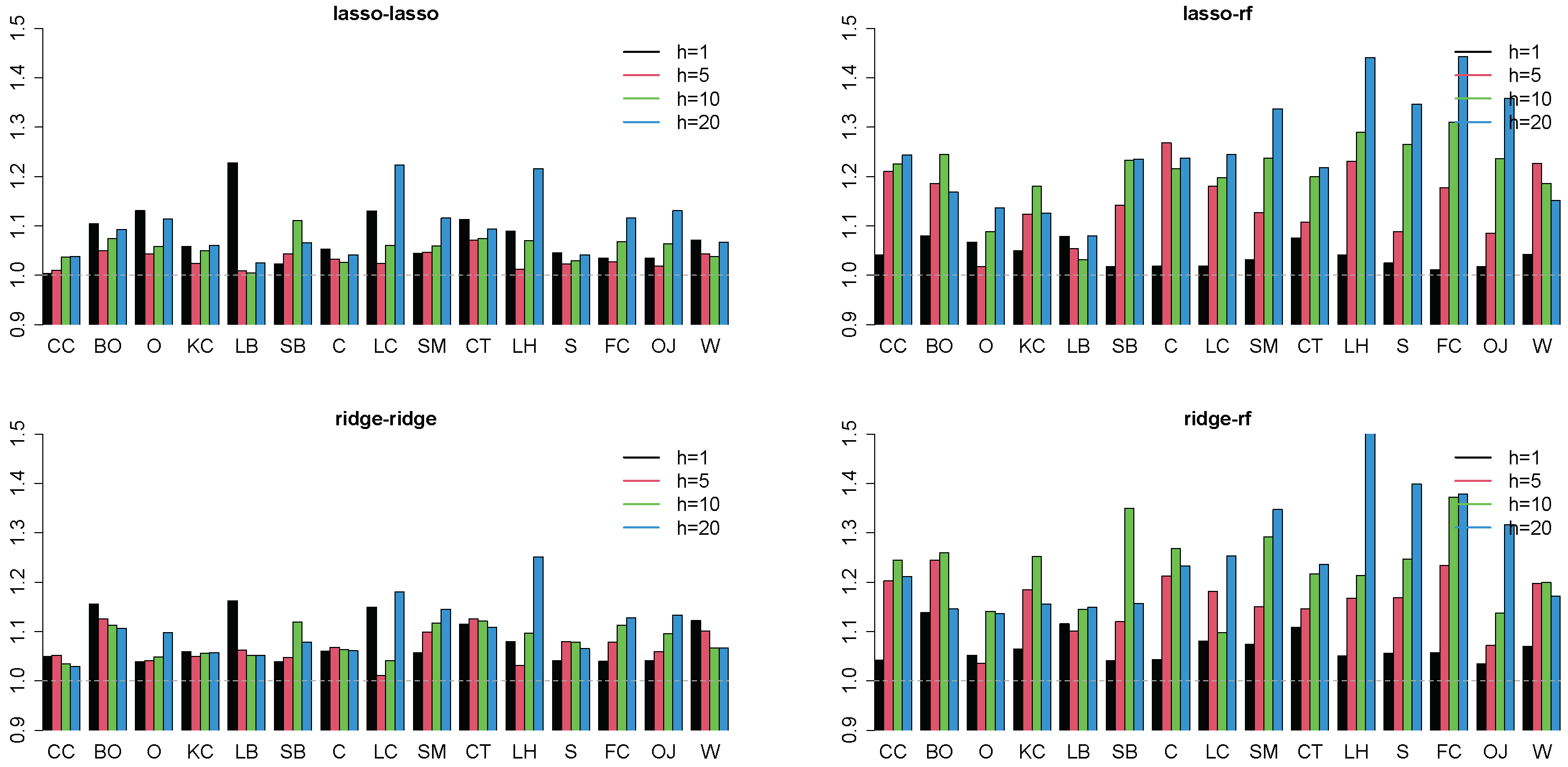
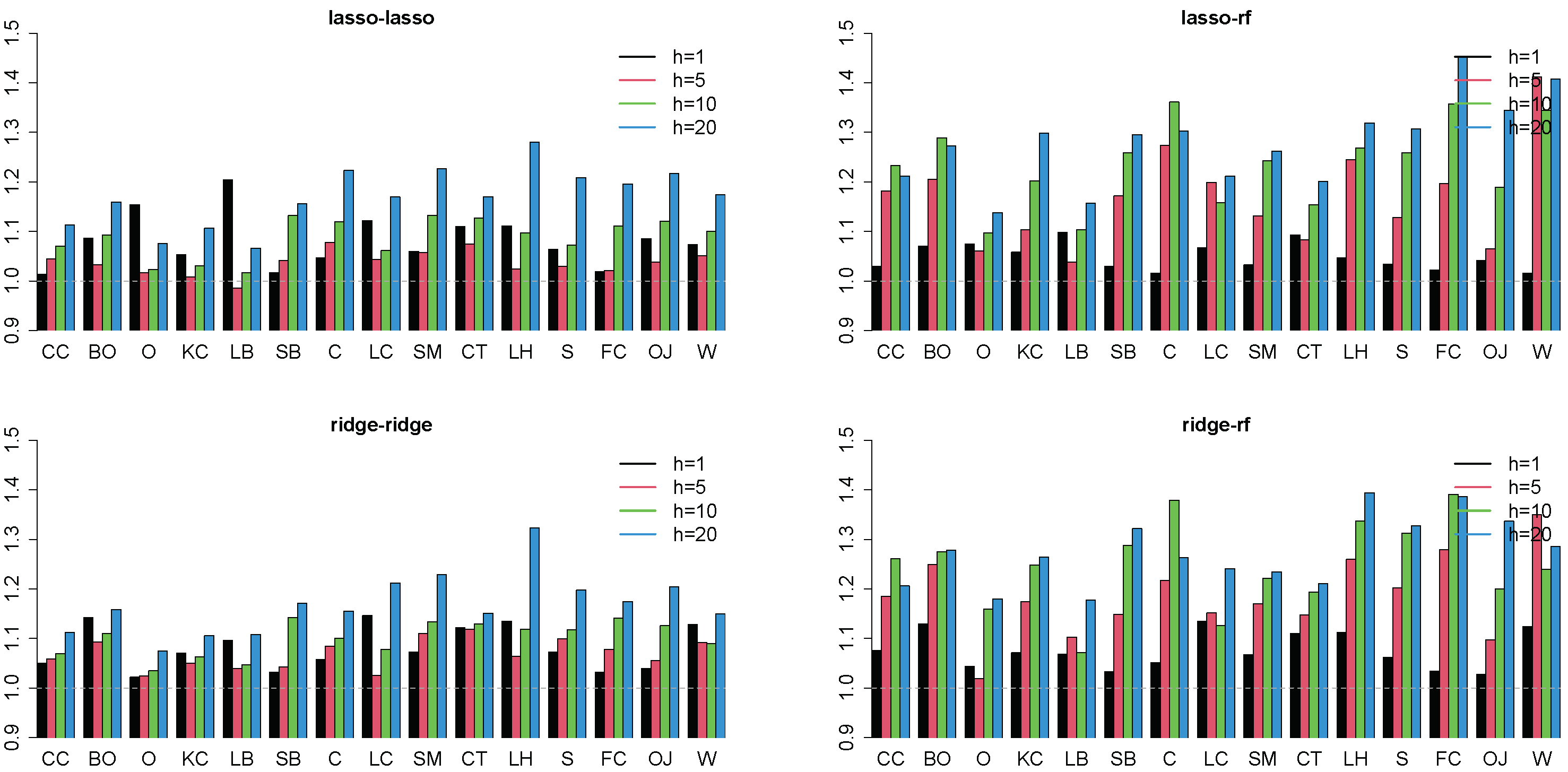
3.2. Stacking Algorithms
4. Empirical Results
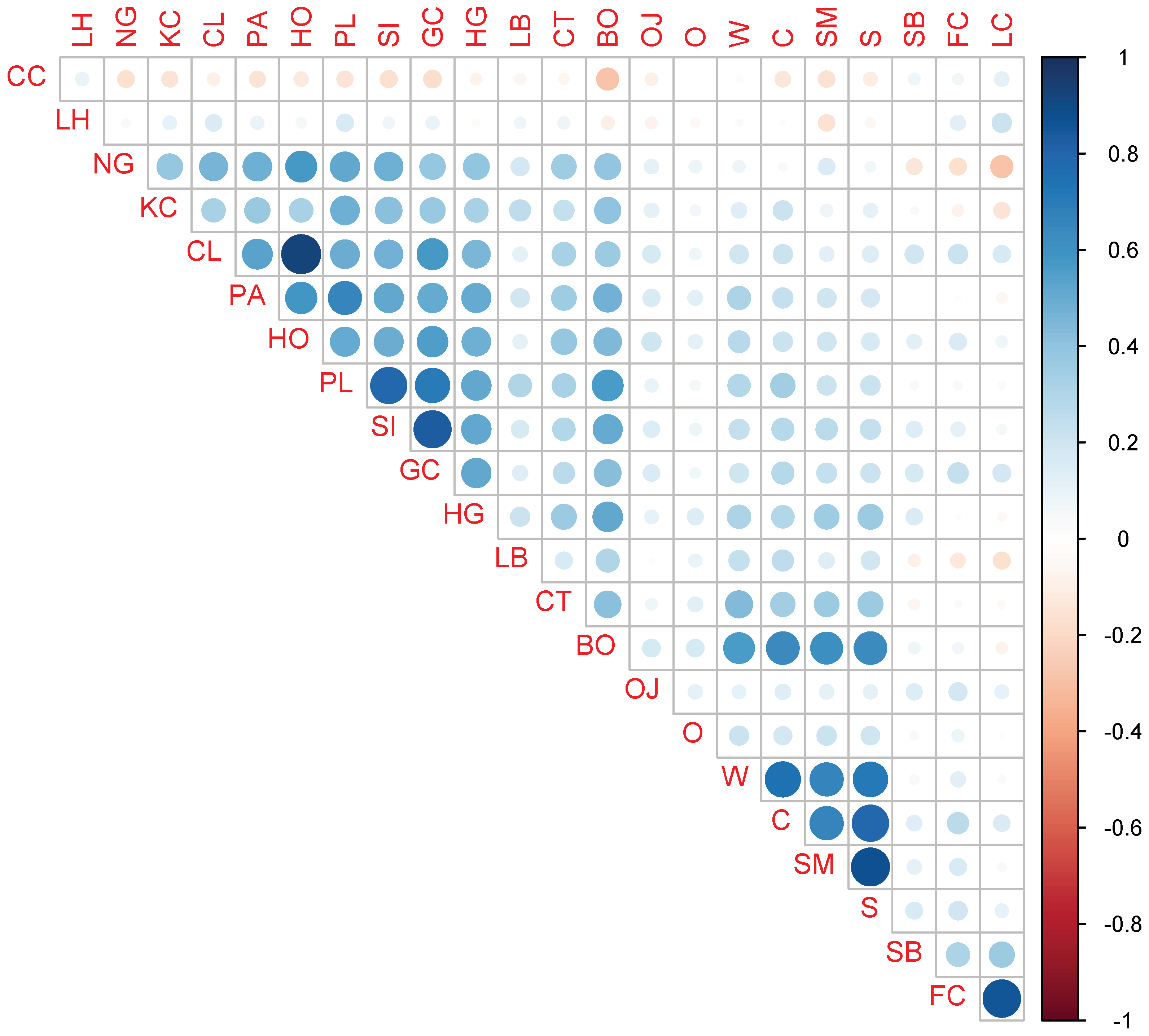
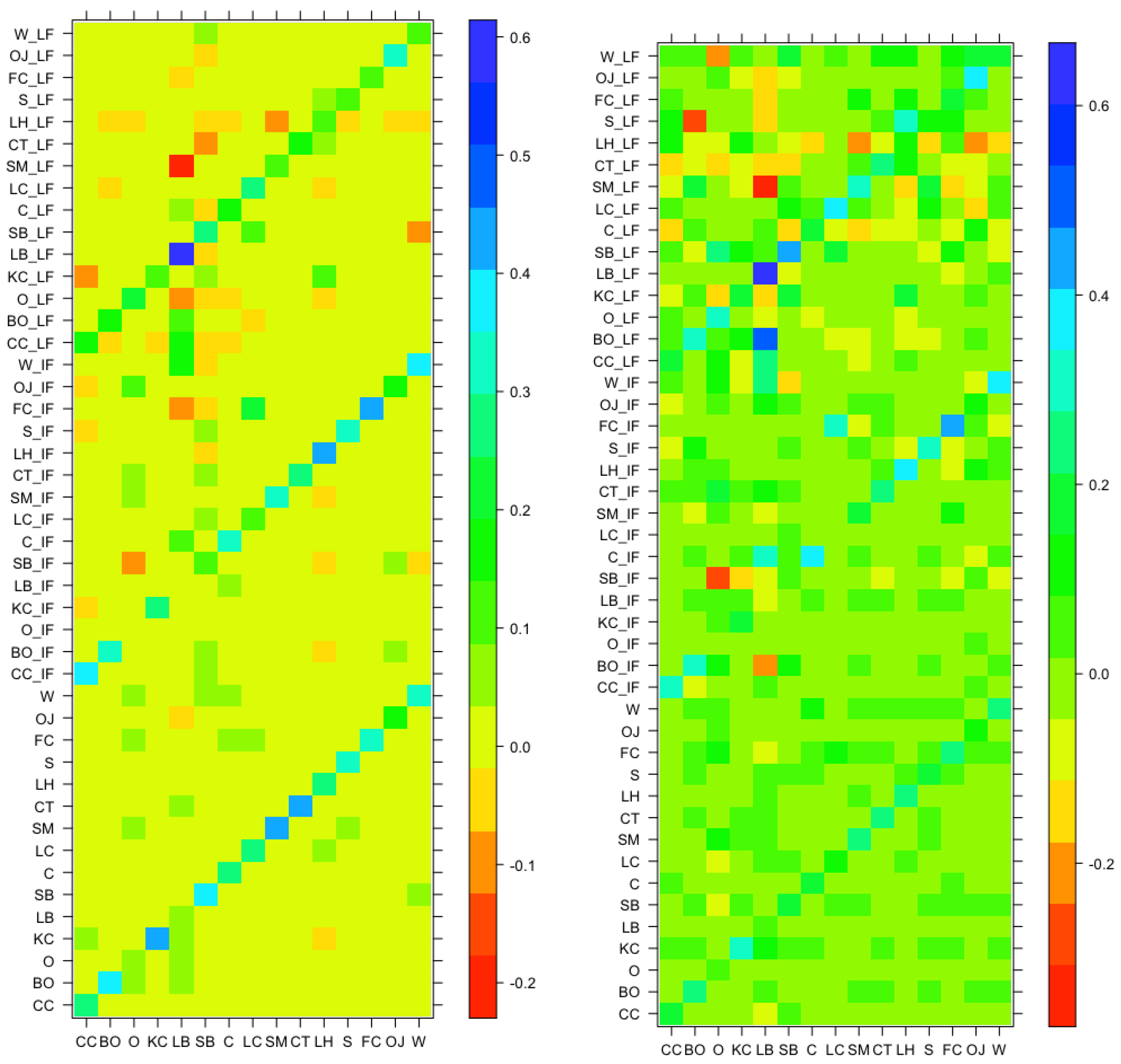
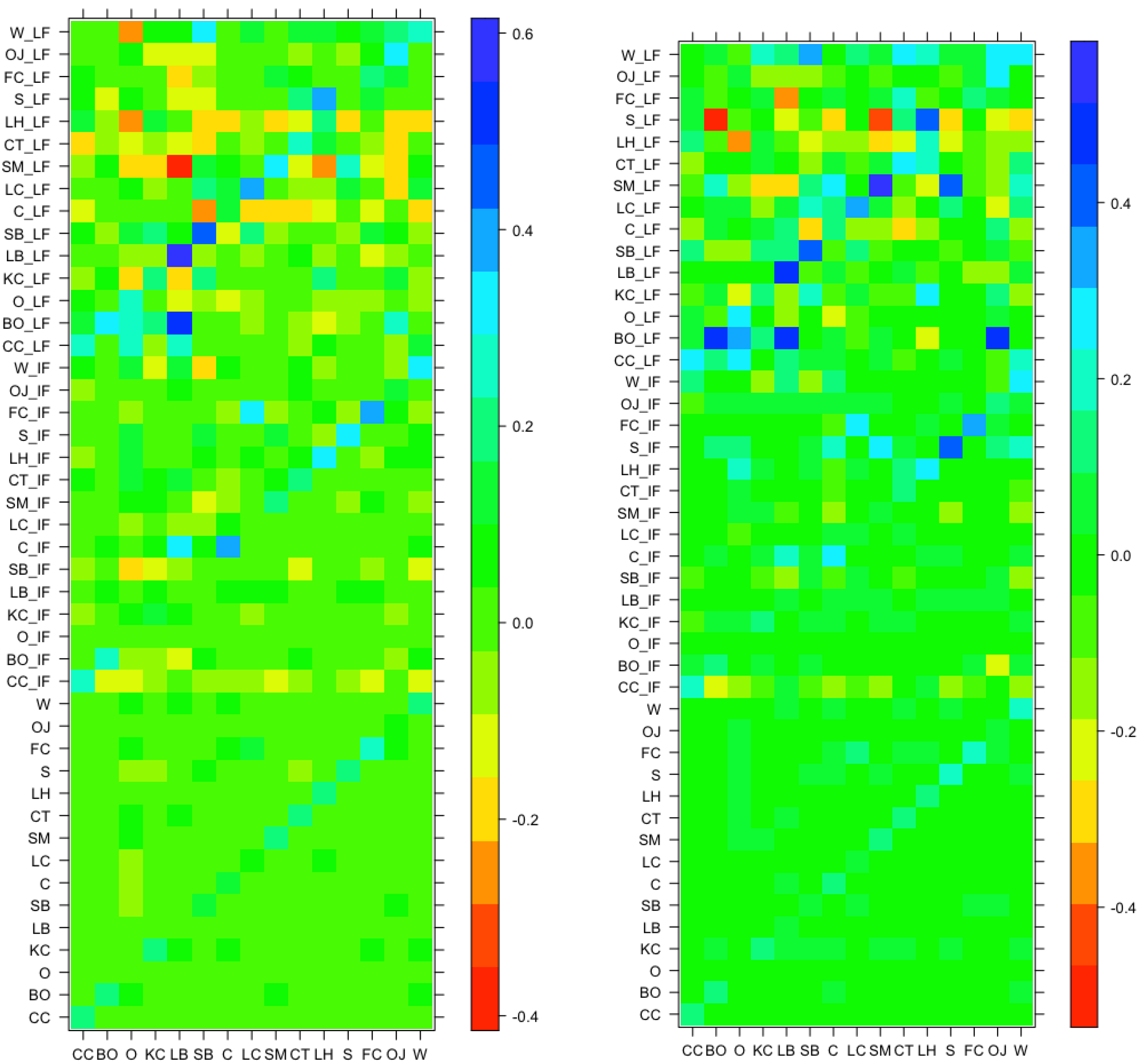
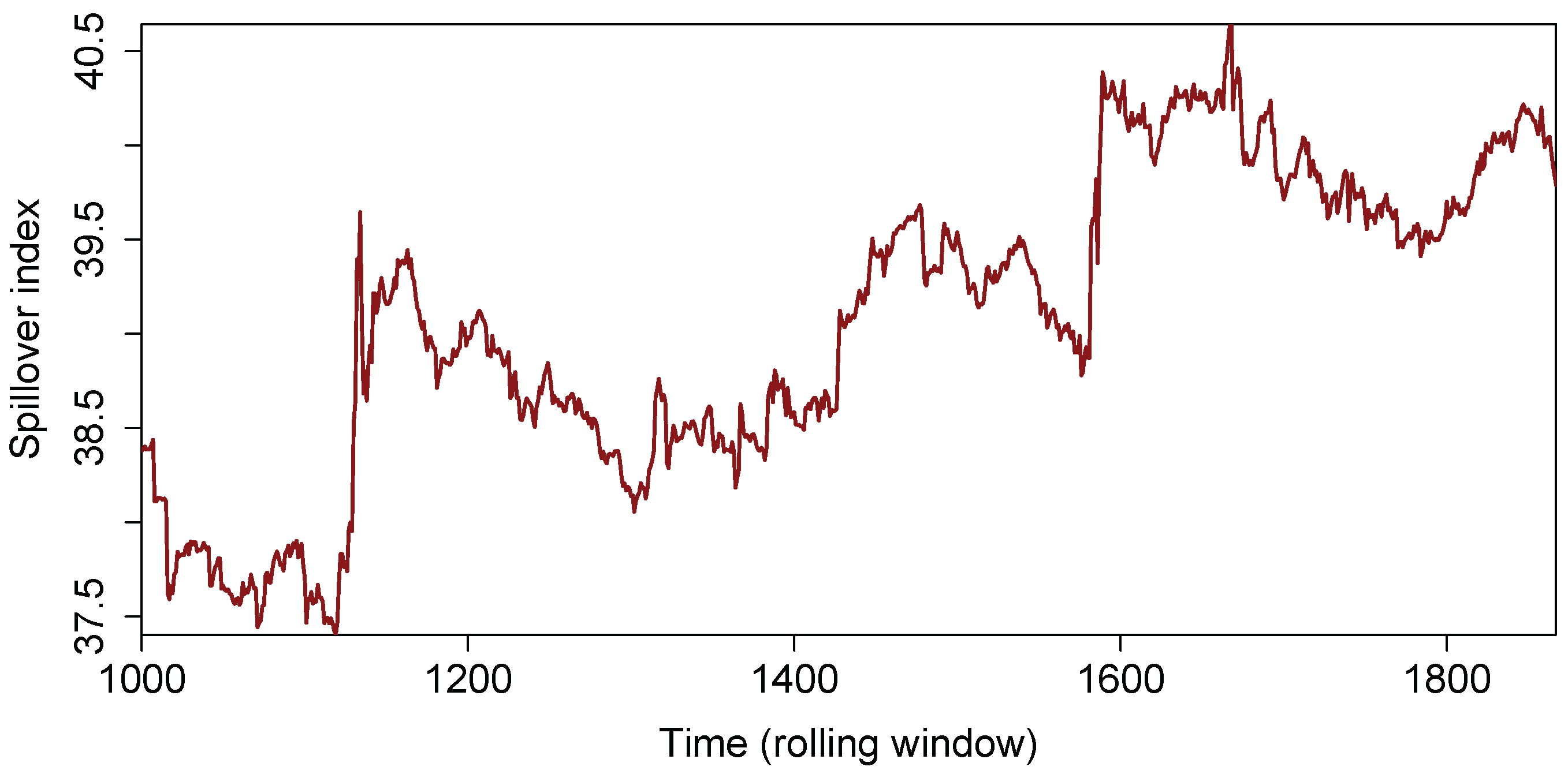
4.1. Full-Sample Results
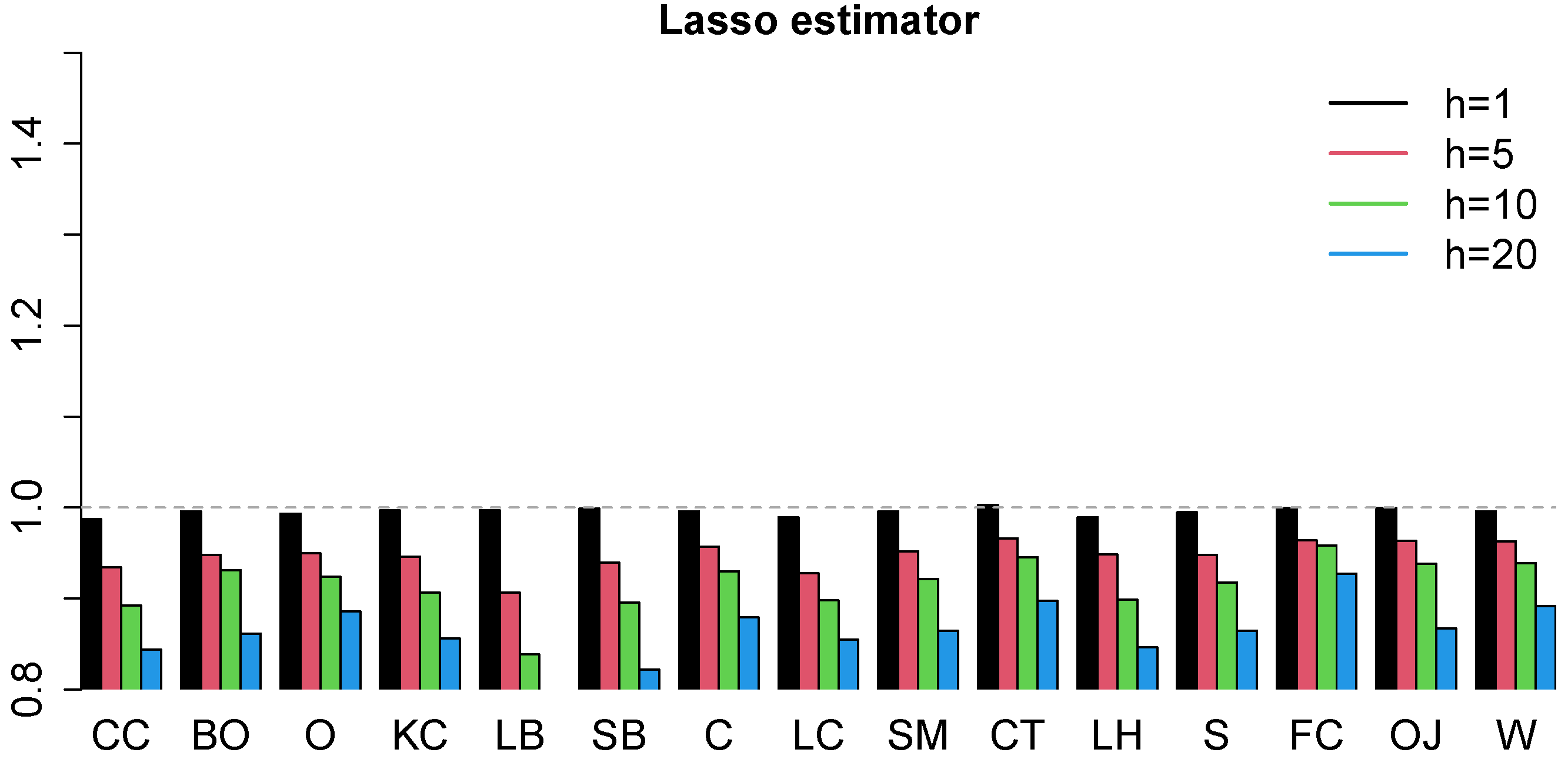
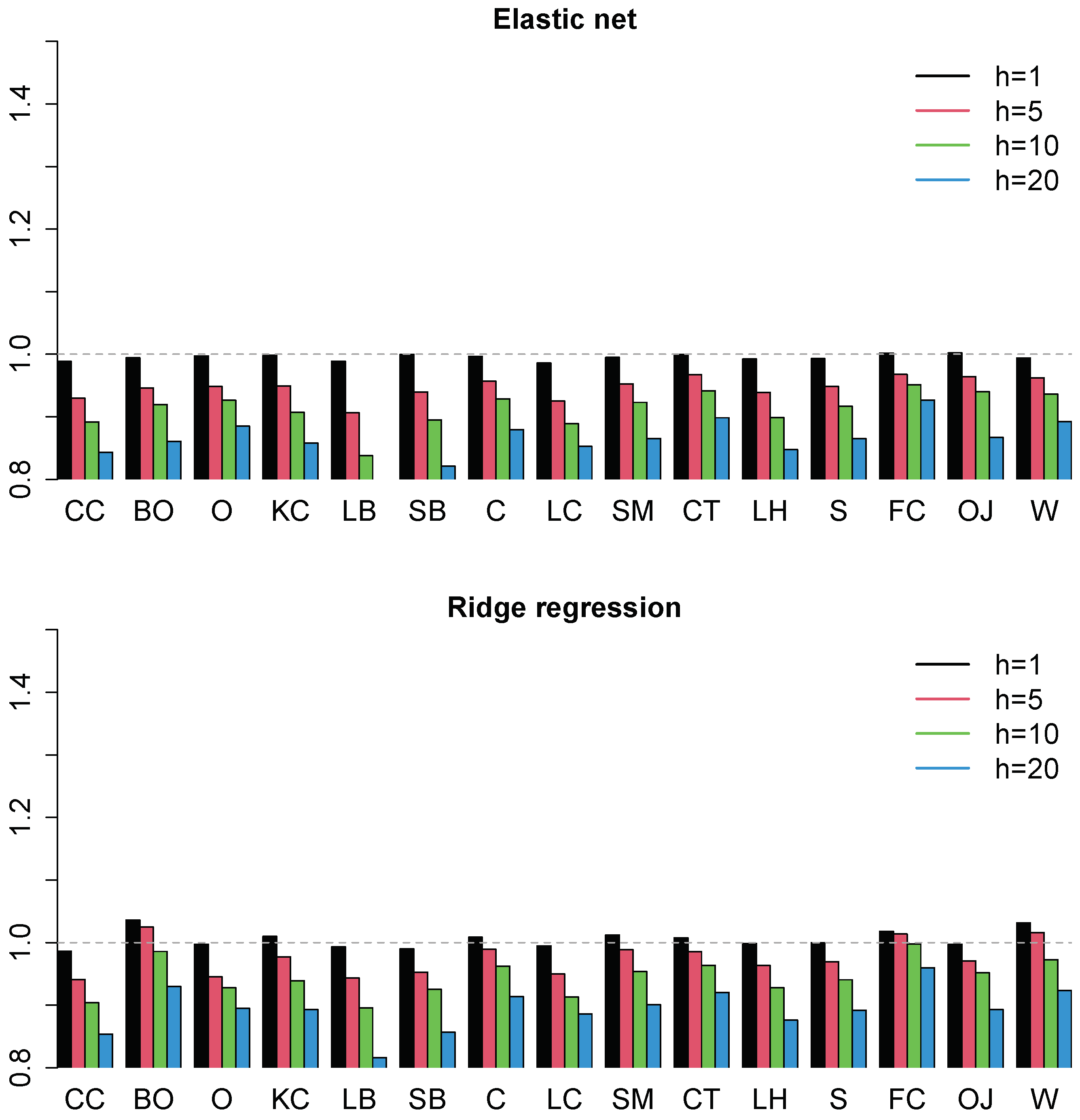
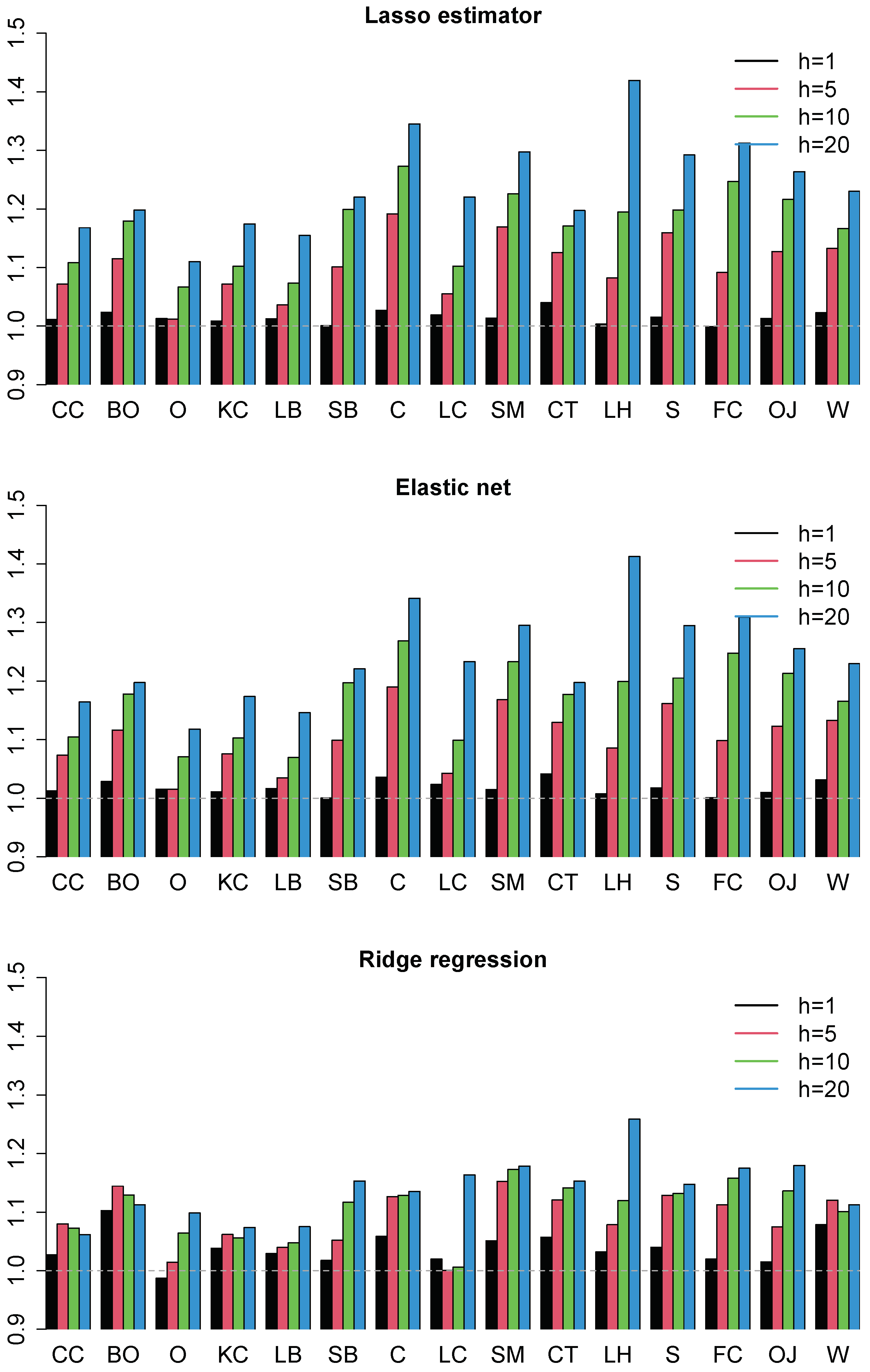
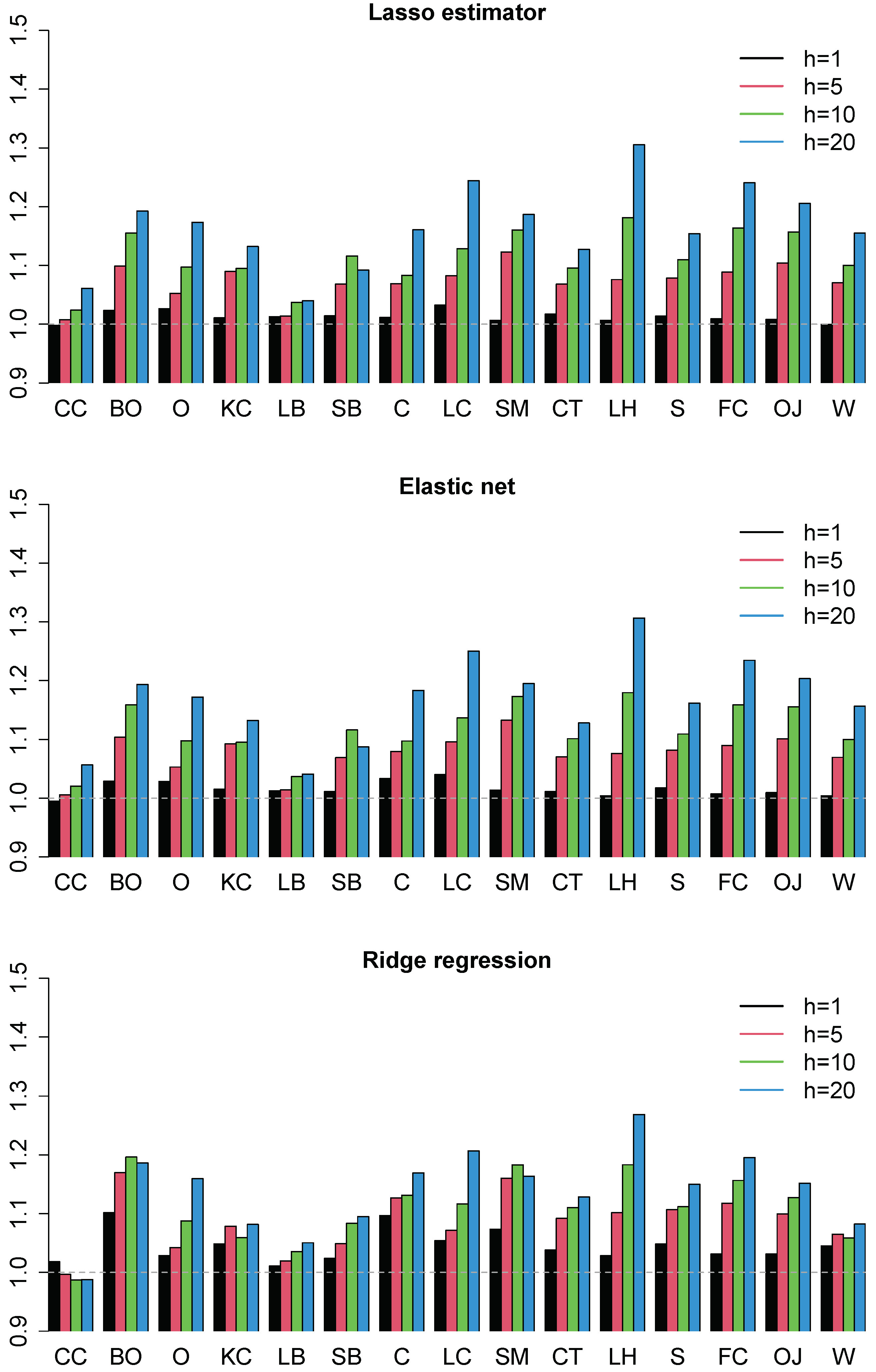
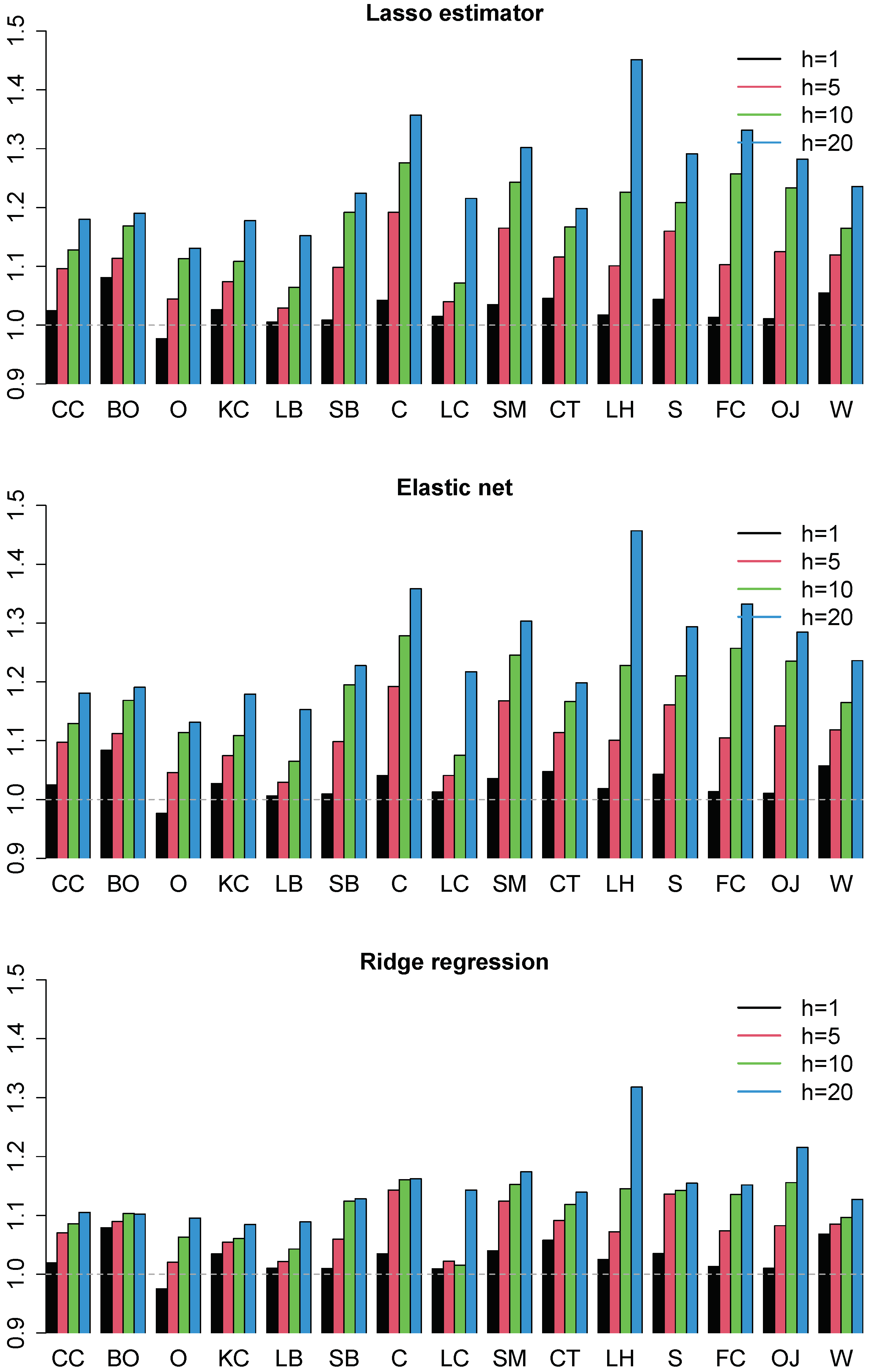
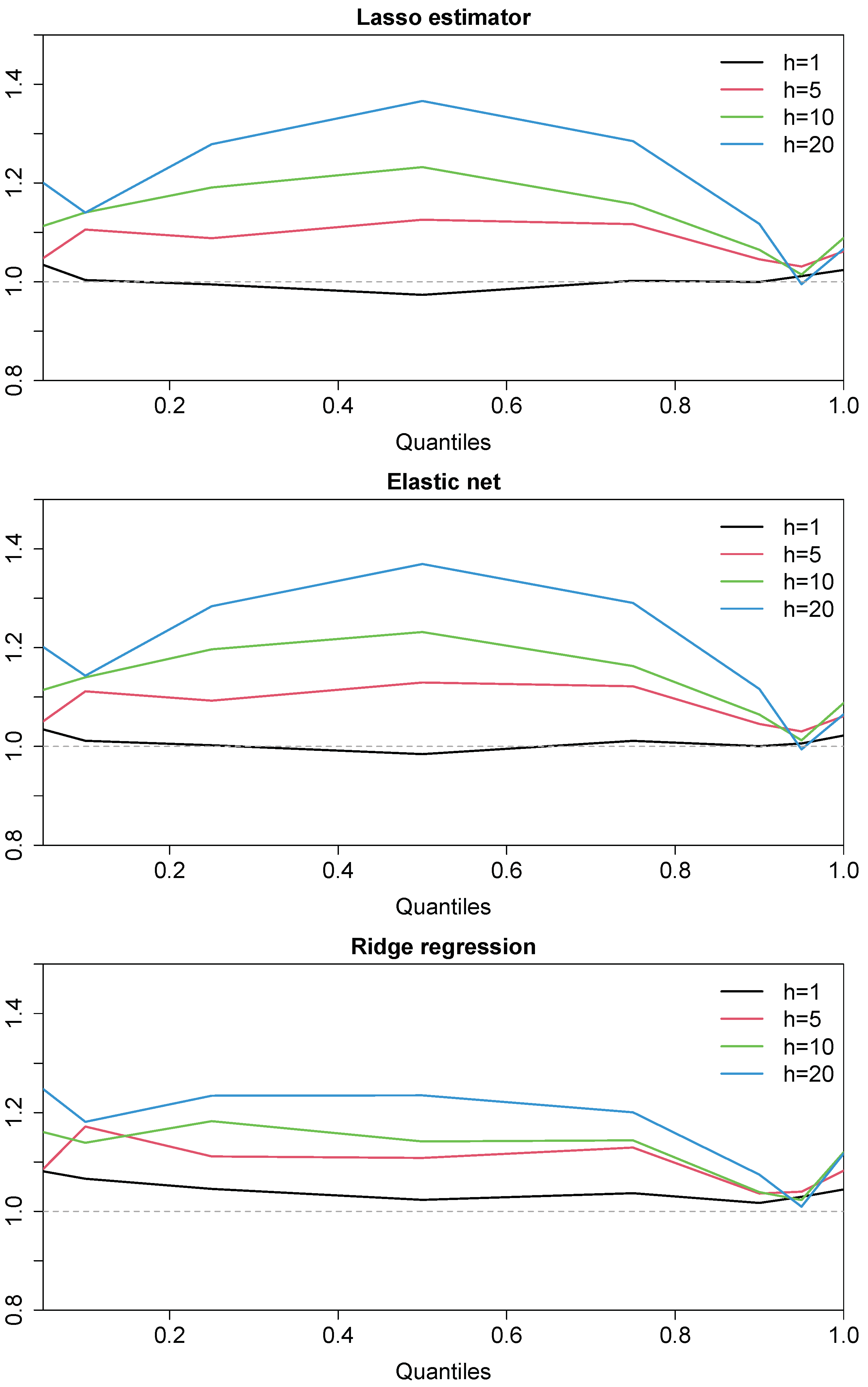
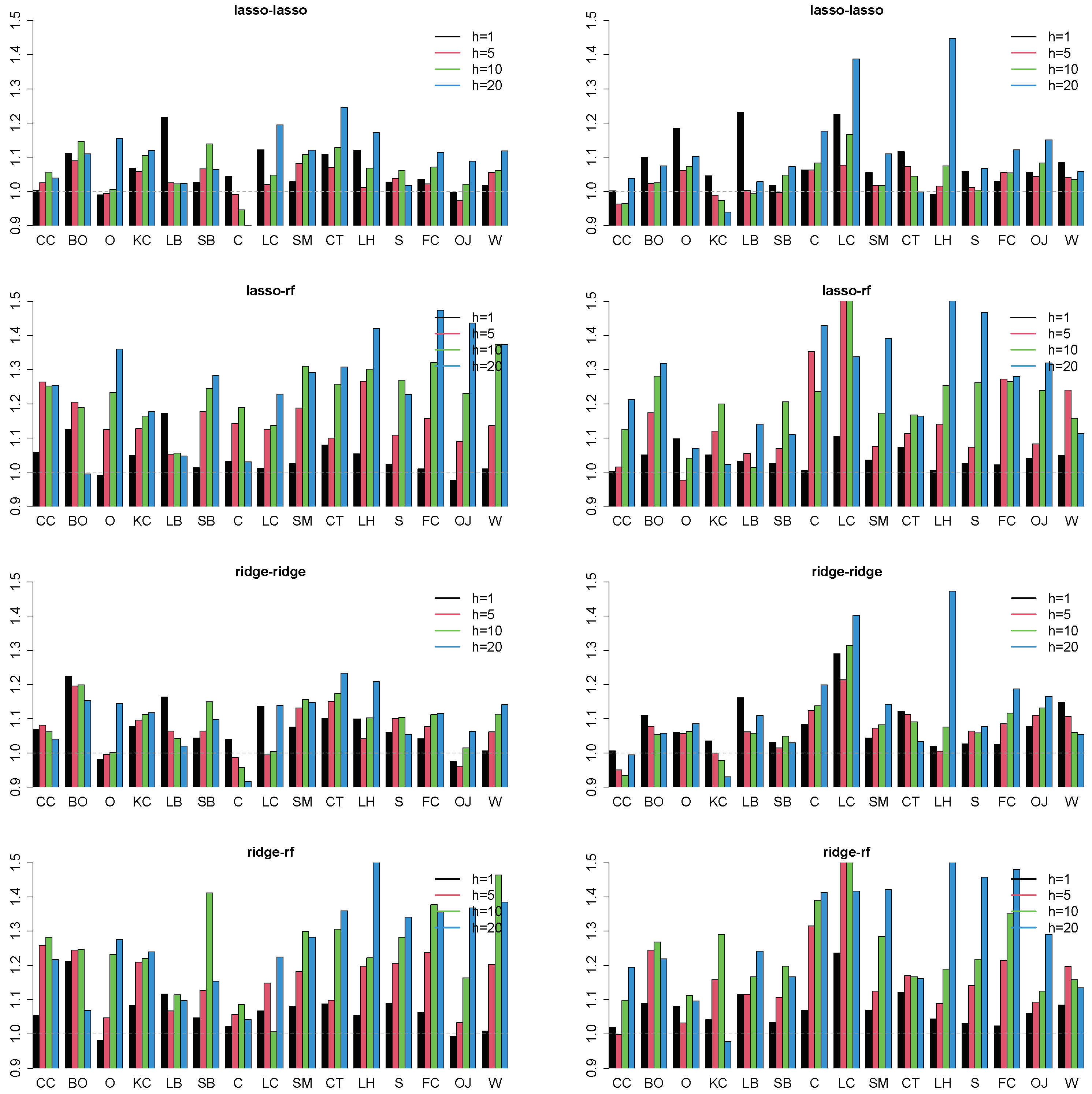
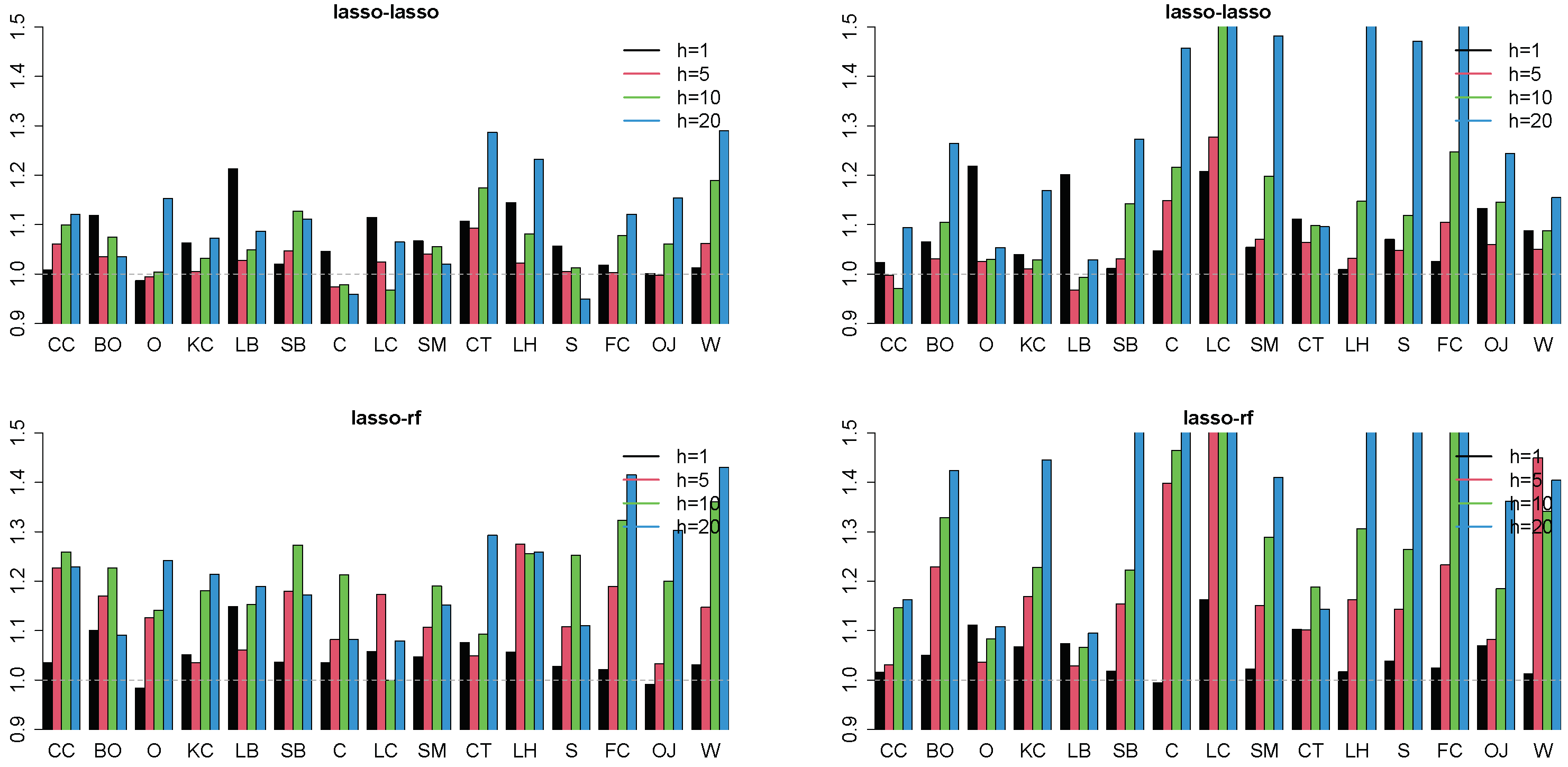
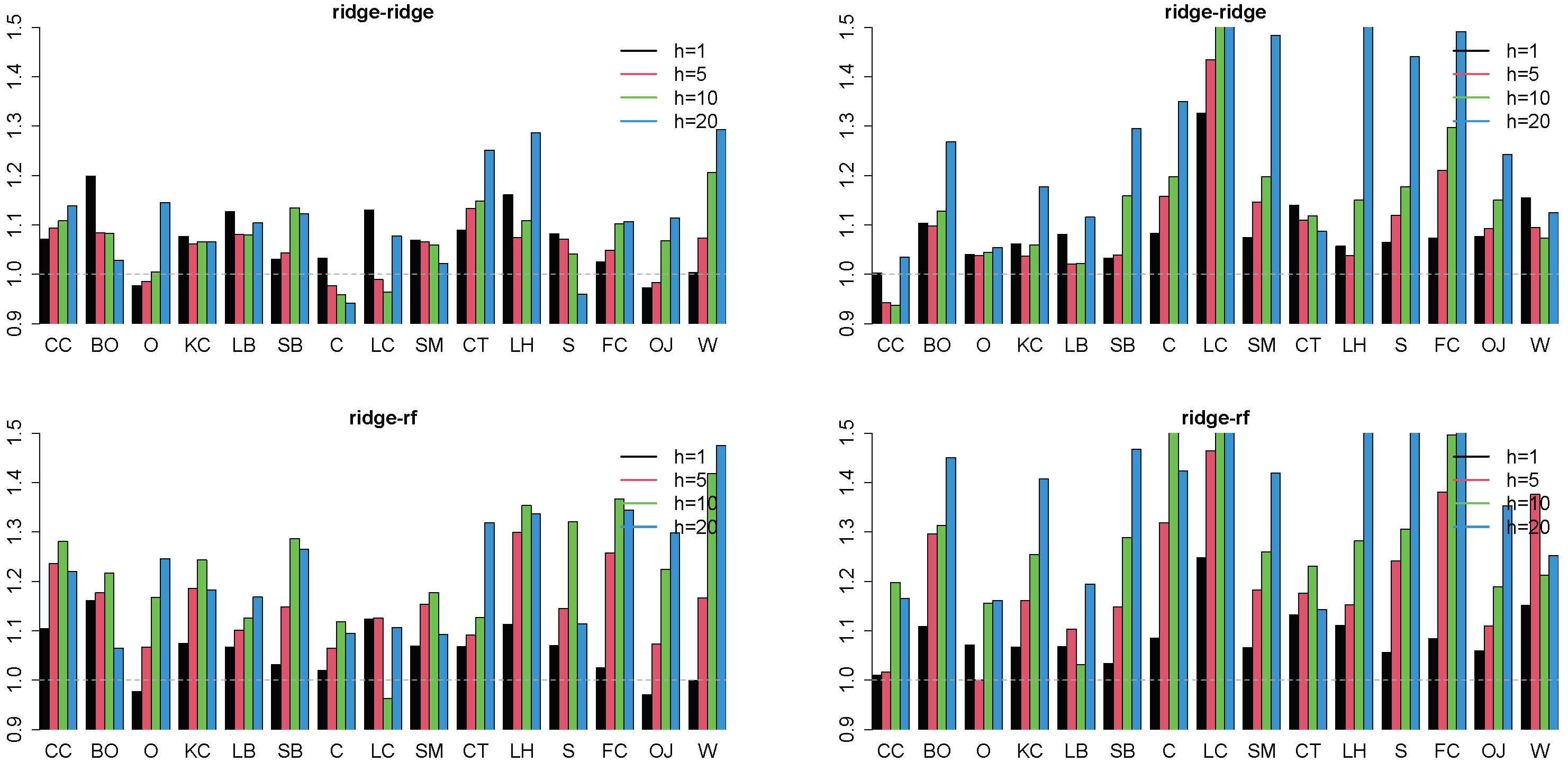
4.2. Forecasting Results
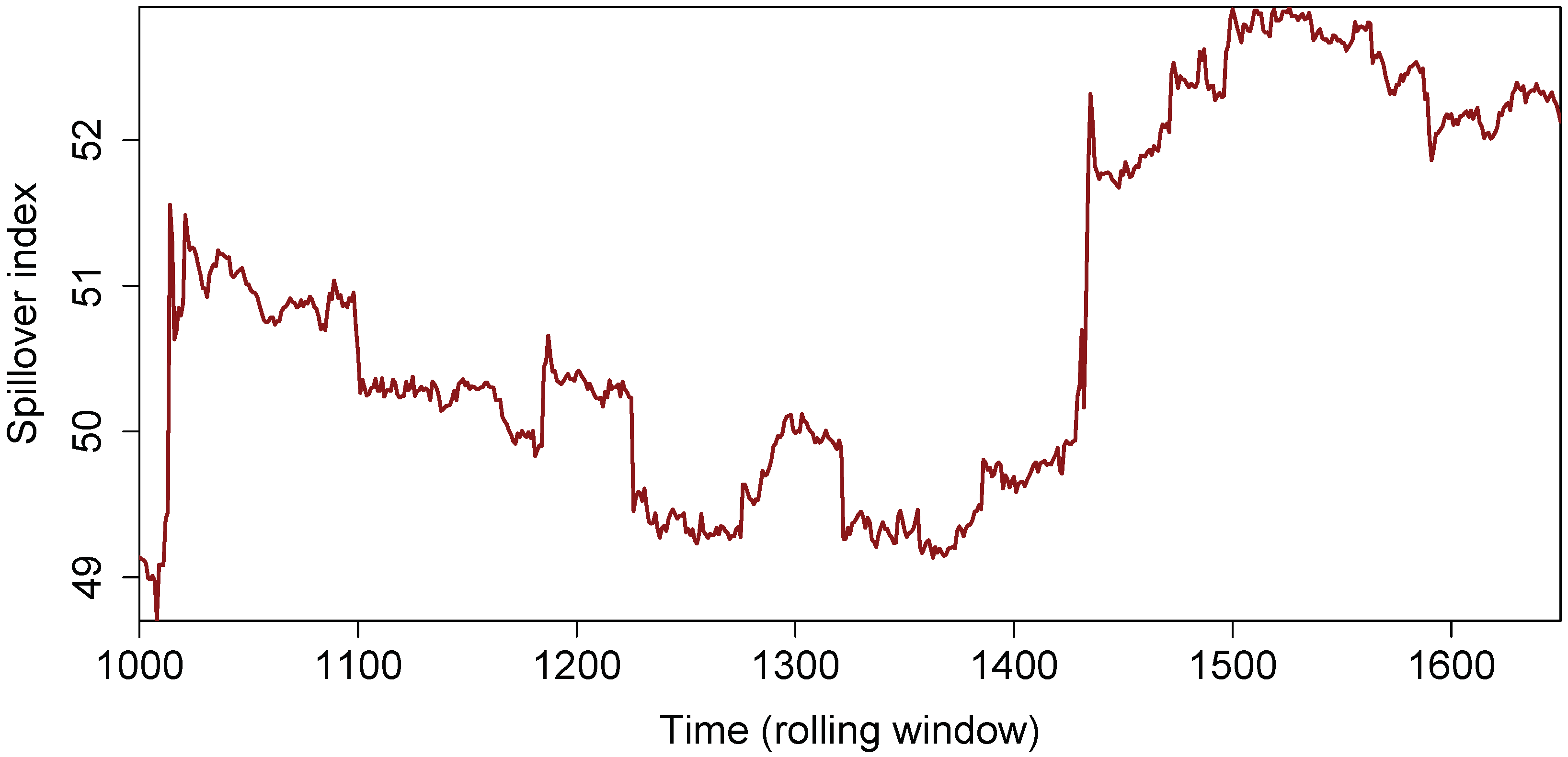
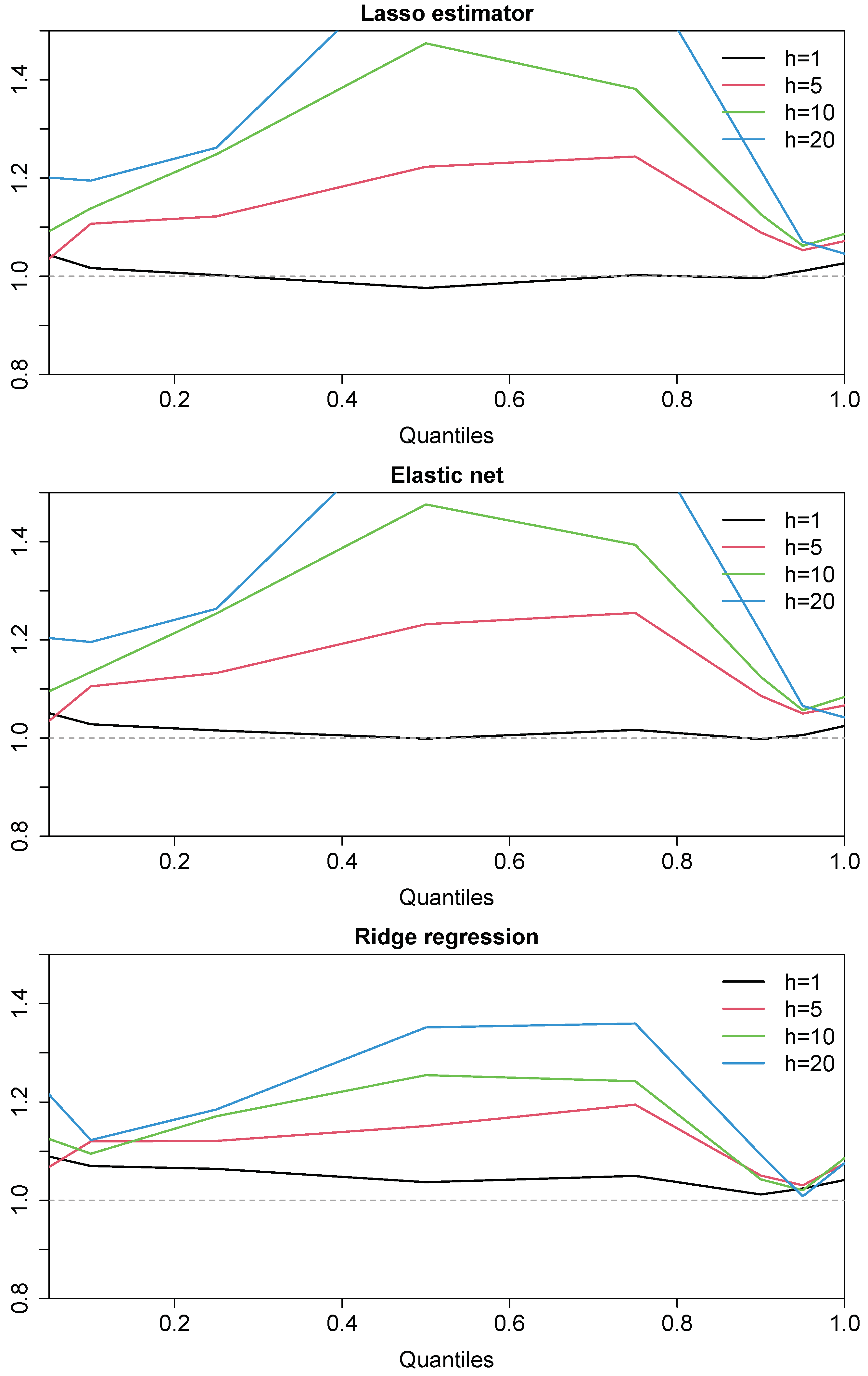
4.3. Robustness Checks
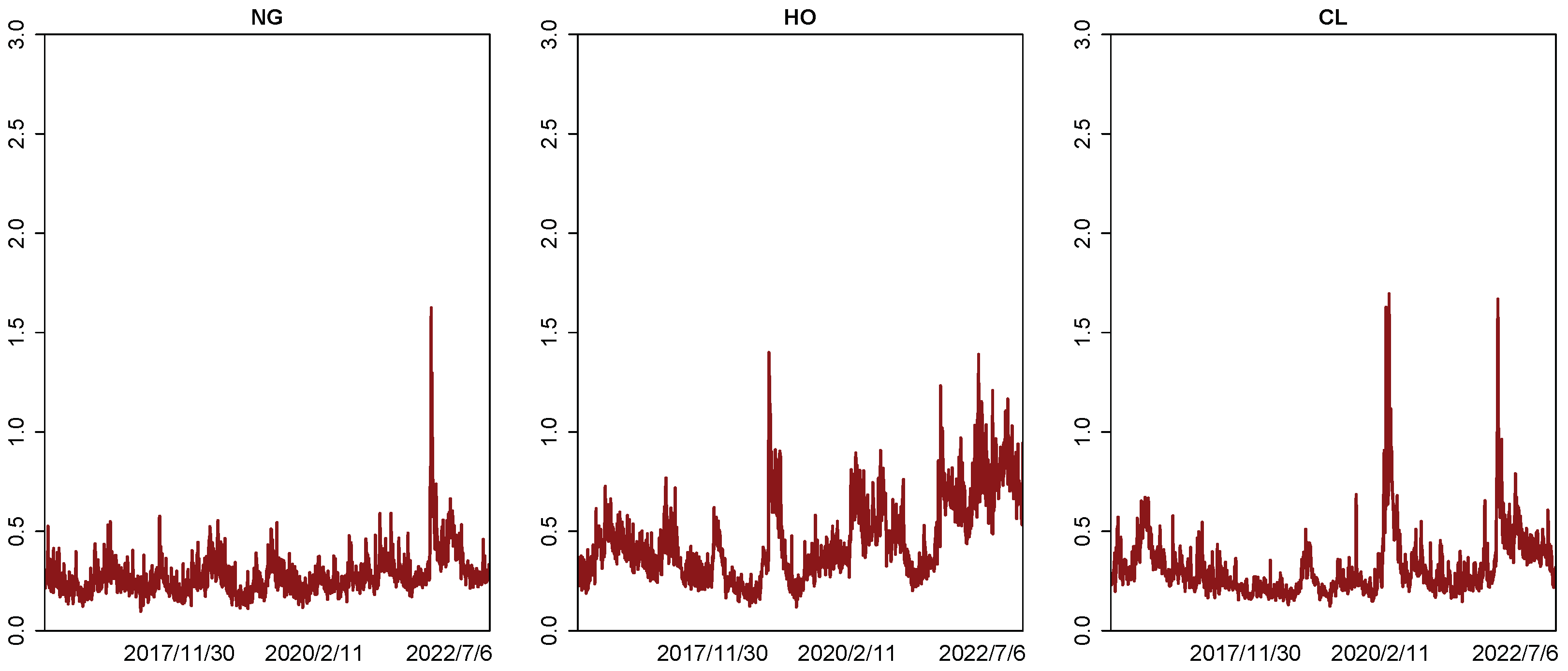
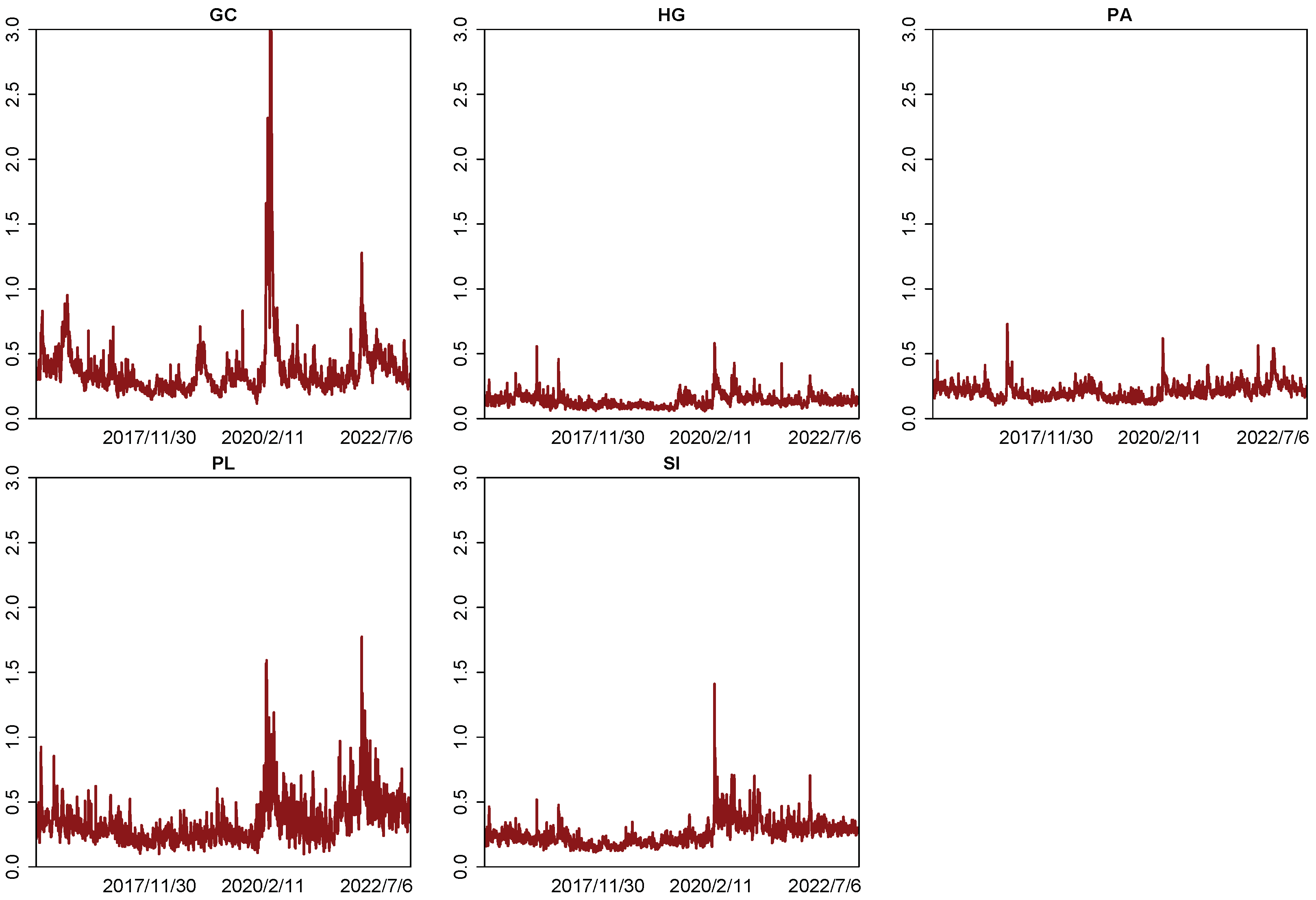
4.4. Extension to Energy Commodities and Precious Metals
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
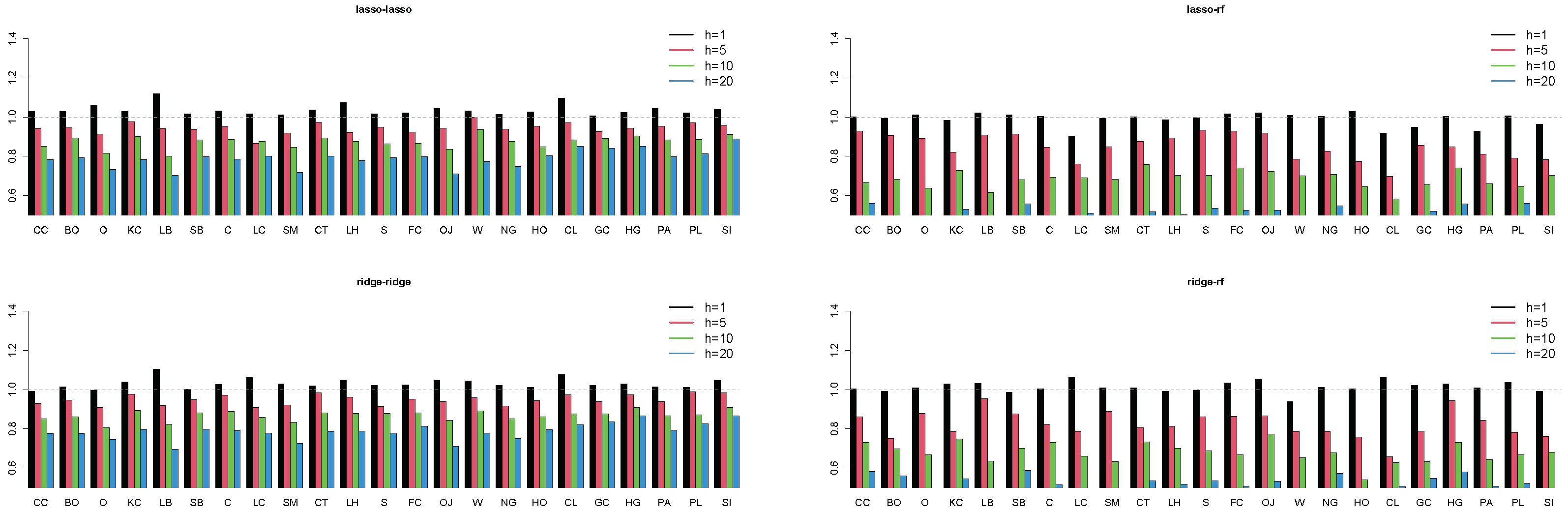
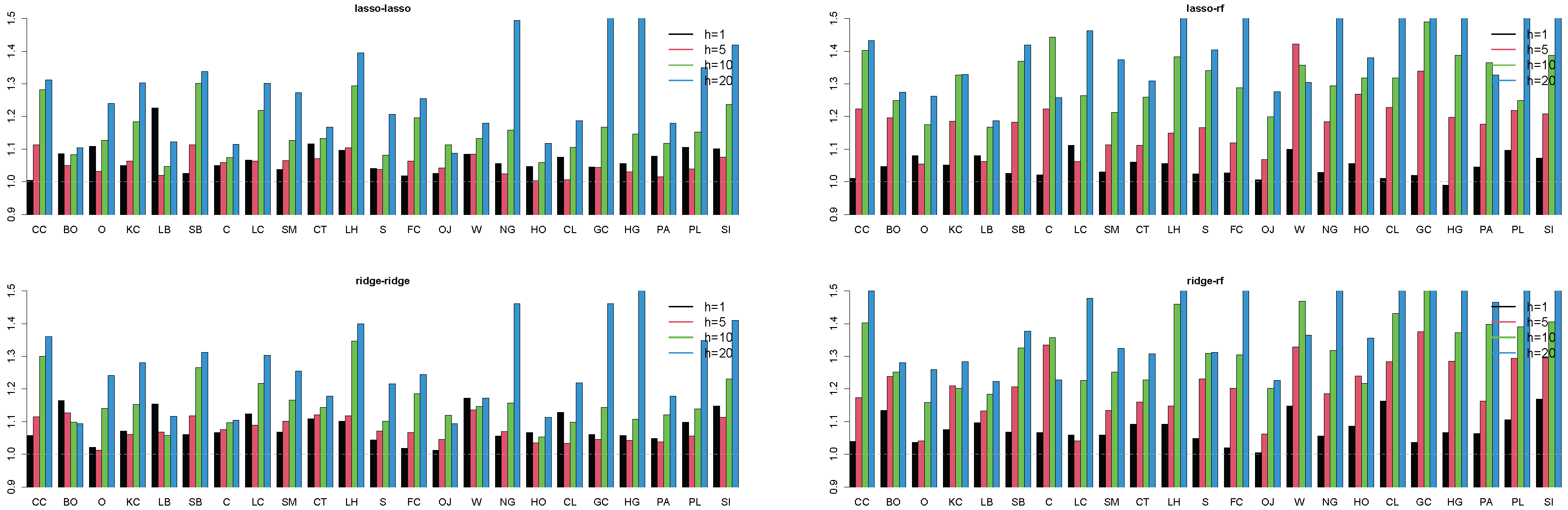
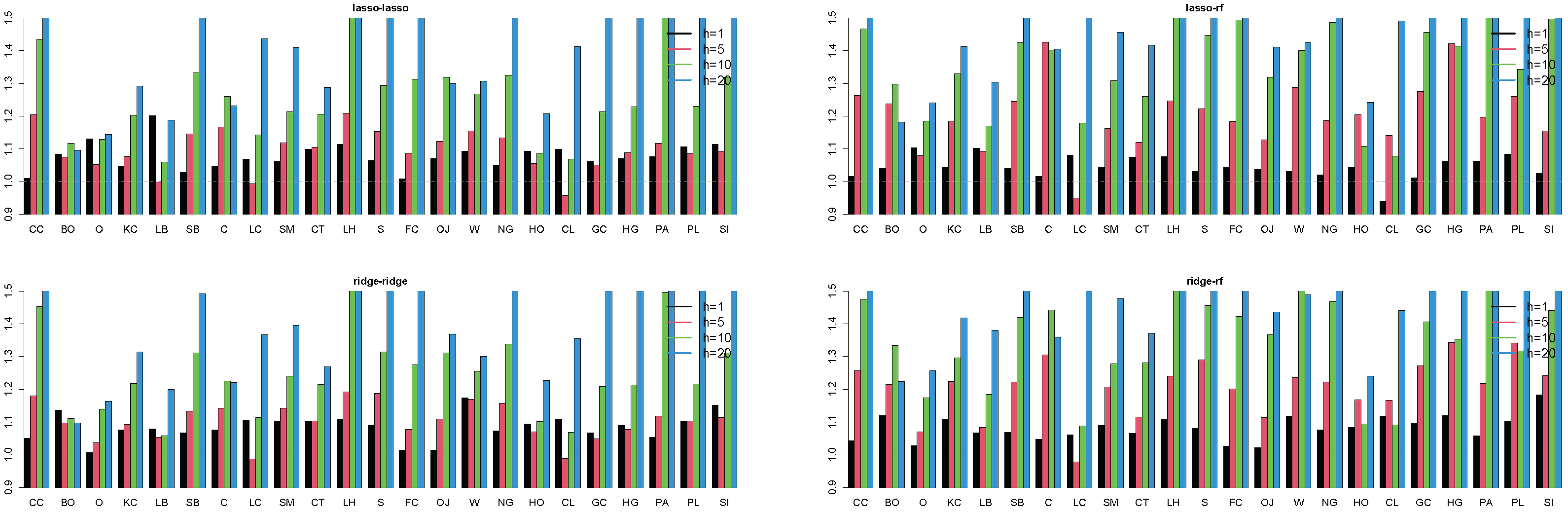
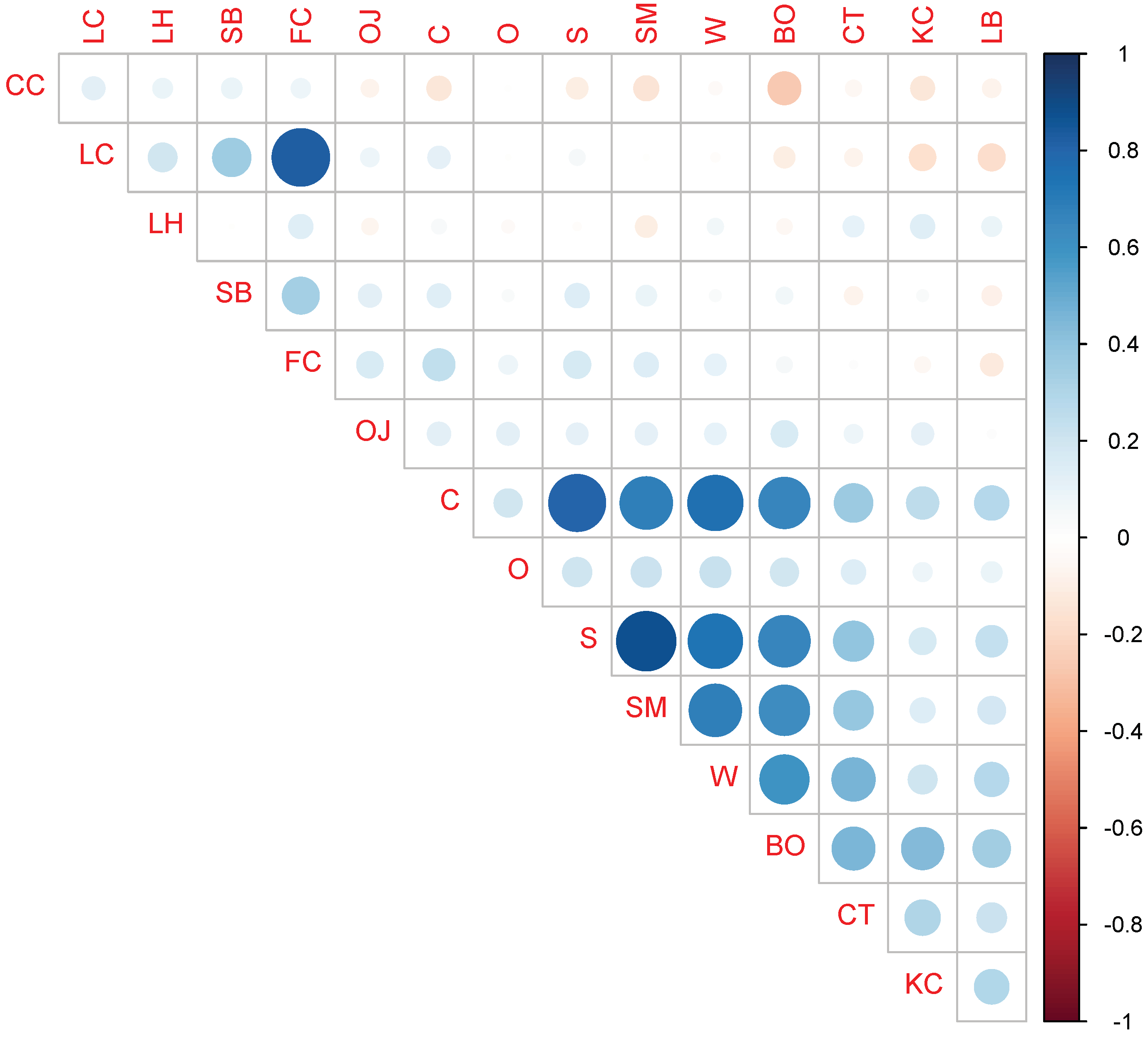
References
- Trujillo-Barrera, A.; Mallory, M.; Garcia, P. Volatility spillovers in U.S. crude oil, ethanol, and corn futures markets. J. Agric. Resour. Econ. 2012, 37, 247–262. [Google Scholar]
- Beckmann, J.; Czudaj, R. Volatility transmission in agricultural futures markets. Econ. Model. 2014, 36, 541–546. [Google Scholar] [CrossRef]
- Gardebroek, C.; Hernandez, M.; Robles, M. Market interdependence and volatility transmission among major crops. Agric. Econ. 2016, 47, 141–155. [Google Scholar] [CrossRef]
- Bonato, M. Realized correlations, betas and volatility spillover in the agricultural commodity market: What has changed? J. Int. Financ. Mark. Inst. Money 2019, 62, 184–202. [Google Scholar] [CrossRef]
- Luo, J.; Chen, L. Multivariate realized volatility forecasts of agricultural commodity futures. J. Futures Mark. 2019, 39, 1565–1586. [Google Scholar] [CrossRef]
- Cagli, E.C.; Mandaci, P.E.; Taskin, D. The volatility connectedness between agricultural commodity and agri businesses: Evidence from time-varying extended joint approach. Financ. Res. Lett. 2023, 52, 103555. [Google Scholar] [CrossRef]
- Luo, J.; Marfatia, H.A.; Ji, Q.; Klein, T. Co-volatility and asymmetric transmission of risks between the global oil and China’s futures markets. Energy Econ. 2023, 117, 106466. [Google Scholar] [CrossRef]
- Marfatia, H.A.; Luo, J.; Ji, Q. Forecasting the volatility of agricultural commodity futures: The role of co-volatility and oil volatility. J. Forecast. 2022, 41, 383–404. [Google Scholar] [CrossRef]
- Kyriazi, F.; Thomakos, D.D.; Guerard, J.B. Adaptive learning forecasting, with applications in forecasting agricultural prices. Int. J. Forecast. 2019, 35, 1356–1369. [Google Scholar] [CrossRef]
- Karali, B.; Irwin, S.H.; Isengildina-Massa, O. Supply fundamentals and grain futures price movements. Am. J. Agric. Econ. 2020, 102, 548–568. [Google Scholar] [CrossRef]
- Kwas, M.; Paccagnini, A.; Rubaszek, M. Common factors and the dynamics of cereal prices. A forecasting perspective. J. Commod. Mark. 2022, 28, 100240. [Google Scholar] [CrossRef]
- Andersen, T.G.; Bollerslev, T. Answering the skeptics: Yes, standard volatility models do provide accurate forecasts. Int. Econ. Rev. 1998, 39, 885–905. [Google Scholar] [CrossRef]
- McAleer, M.; Medeiros, M.C. Realized volatility: A review. Econ. Rev. 2008, 27, 10–45. [Google Scholar] [CrossRef]
- Chatziantoniou, I.; Degiannakis, S.; Filis, G.; Lloyd, T. Oil price volatility is effective in predicting food price volatility. Or is it? Energy J. 2021, 42, 25–48. [Google Scholar] [CrossRef]
- Degiannakis, S.; Filis, G.; Klein, T.; Walther, T. Forecasting realized volatility of agricultural commodities. Int. J. Forecast. 2022, 38, 74–96. [Google Scholar] [CrossRef]
- Luo, J.; Klein, T.; Ji, Q.; Hou, C. Forecasting realized volatility of agricultural commodity futures with infinite hidden Markov HAR models. Int. J. Forecast. 2022, 38, 51–73. [Google Scholar] [CrossRef]
- Corsi, F. A simple approximate long-memory model of realized volatility. J. Financ. Econ. 2009, 7, 174–196. [Google Scholar] [CrossRef]
- Bonato, M.; Cepni, O.; Gupta, R.; Pierdzioch, C. El Niño, La Niñna, and forecastability of the realized variance of agricultural commodity prices: Evidence from a machine learning approach. J. Forecast. 2022, 42, 785–801. [Google Scholar] [CrossRef]
- Bonato, M.; Cepni, O.; Gupta, R.; Pierdzioch, C. Forecasting the realized volatility of agricultural commodity prices: Does sentiment matter? J. Forecast. 2024, 43, 2088–2125. [Google Scholar] [CrossRef]
- Bonato, M.; Cepni, O.; Gupta, R.; Pierdzioch, C. Financial stress and realized volatility: The case of agricultural commodities. Res. Int. Bus. Financ. 2024, 71, 102442. [Google Scholar] [CrossRef]
- Gil-Alana, L.A.; Cunado, J.; de Gracia, F.P. Persistence, long memory, and unit roots in commodity prices. Can. J. Agric. Econ. 2012, 60, 451–468. [Google Scholar] [CrossRef]
- Živkov, D.; Njegić, J.; Pexcxanac, M. Multiscale interdependence between the major agricultural commodities. Agric. Econ. 2019, 65, 82–92. [Google Scholar] [CrossRef]
- Živkov, D.; Duraškovič, J.; Gajixcx-Glamoxcxlija, M. Multiscale downside risk interdependence between the major agricultural commodities. Agribusiness 2022, 38, 990–1011. [Google Scholar] [CrossRef]
- Müller, U.A.; Dacorogna, M.M.; Davé, R.D.; Olsen, R.B.; Pictet, O.V. Volatilities of different time resolutions—Analyzing the dynamics of market components. J. Empir. Financ. 1997, 4, 213–239. [Google Scholar] [CrossRef]
- Bubák, V.; Kočenda, E.; Žikeš, F. Volatility transmission in emerging European foreign exchange markets. J. Bank. Financ. 2011, 35, 2829–2841. [Google Scholar] [CrossRef]
- De Nicola, F.; De Pace, H. Co-movement of major energy, agricultural, and food commodity price returns: A time-series assessment. Energy Econ. 2016, 57, 28–41. [Google Scholar] [CrossRef]
- Luo, J.; Chen, L. Modeling and forecasting the multivariate realized volatility of financial markets with time-varying sparsity. Emerg. Mark. Financ. Trade 2020, 56, 392–408. [Google Scholar] [CrossRef]
- Luo, J.; Chen, L. Realized volatility forecast with the Bayesian random compressed multivariate HAR model. Int. J. Forecast. 2020, 36, 781–799. [Google Scholar] [CrossRef]
- Asai, M.; McAleer, M. The impact of jumps and leverage in forecasting co-volatility. Econ. Rev. 2017, 36, 638–650. [Google Scholar] [CrossRef]
- Čech, F.; Baruník, J. On the modelling and forecasting of multivariate realized volatility: Generalized Heterogeneous Autoregressive (GHAR) Model. J. Forecast. 2017, 36, 181–206. [Google Scholar] [CrossRef]
- Asai, M.; Gupta, R.; McAleer, M. The Impact of jumps and leverage in forecasting the co-Volatility of oil and gold futures. Energies 2019, 12, 3379. [Google Scholar] [CrossRef]
- Asai, M.; Gupta, R.; McAleer, M. Forecasting volatility and co-volatility of crude oil and gold futures: Effects of leverage, jumps, spillovers, and geopolitical risks. Int. J. Forecast. 2020, 36, 933–948. [Google Scholar] [CrossRef]
- Zhao, A.B.; Cheng, T. Stock return prediction: Stacking a variety of models. J. Empir. Financ. 2022, 67, 288–317. [Google Scholar] [CrossRef]
- Tian, F.; Yang, K.; Chen, L. Realized volatility forecasting of agricultural commodity futures using long memory and regime switching. J. Forecast. 2017, 36, 421–430. [Google Scholar] [CrossRef]
- Tian, F.; Yang, K.; Chen, L. Realized volatility forecasting of agricultural commodity futures using the HAR model with time-varying sparsity. Int. J. Forecast. 2017, 33, 132–152. [Google Scholar] [CrossRef]
- Yang, K.; Tian, F.; Chen, L.; Li, S. Realized volatility forecast of agricultural futures using the HAR models with bagging and combination approaches. Int. Rev. Econ. Financ. 2017, 49, 276–291. [Google Scholar] [CrossRef]
- Shiba, S.; Aye, G.C.; Gupta, R.; Goswami, S. Forecastability of agricultural commodity futures realised volatility with daily infectious disease-related uncertainty. J. Risk Financ. Manag. 2022, 15, 525. [Google Scholar] [CrossRef]
- Gupta, R.; Pierdzioch, C. Climate risk and the volatility of agricultural commodity price fluctuations: A prediction experiment. In Behavioral Finance and Asset Prices: The Influence of Investor’s Emotions; Bourghelle, D., Grandin, P., Jawadi, F., Rozin, P., Eds.; Contributions to Finance and Accounting; Springer: Cham, Switzerland; New York, NY, USA, 2023; pp. 23–44. [Google Scholar]
- Luo, J.; Zhang, Q. Air pollution, weather factors, and realized volatility forecasts of agricultural commodity futures. J. Futures Mark. 2024, 44, 151–217. [Google Scholar] [CrossRef]
- Bahloul, W.; Balcilar, M.; Cunado, J.; Gupta, R. The role of economic and financial uncertainties in predicting commodity futures returns and volatility: Evidence from a nonparametric causality-in-quantiles test. J. Multinatl. Financ. Manag. 2018, 45, 52–71. [Google Scholar] [CrossRef]
- Aït-Youcef, C. How index investment impacts commodities: A story about the financialization of agricultural commodities. Econ. Model. 2019, 80, 23–33. [Google Scholar] [CrossRef]
- Ji, Q.; Bahloul, W.; Geng, J.-B.; Gupta, R. Trading behaviour connectedness across commodity markets: Evidence from the hedgers’ sentiment perspective. Res. Int. Bus. Financ. 2020, 52, 101114. [Google Scholar] [CrossRef]
- Poon, S.-H.; Granger, C.W.J. Forecasting volatility in financial markets: A review. J. Econ. Lit. 2003, 41, 478–539. [Google Scholar] [CrossRef]
- Rapach, D.E.; Wohar, M.E.; Strauss, J. Forecasting stock return volatility in the presence of structural breaks. In Forecasting in the Presence of Structural Breaks and Model Uncertainty; Frontiers of Economics and Globalization; Rapach, D.E., Wohar, M.E., Eds.; Emerald: Bingley, UK, 2018; pp. 381–416. [Google Scholar]
- FAO. Price Volatility in Agricultural Markets: Evidence, Impact on Food Security and Policy Responses. 2010. Available online: http://www.fao.org/docrep/013/am053e/am053e00.pdf (accessed on 1 March 2024).
- FAO. Price Volatility in Food and Agricultural Markets: Policy Responses. 2011. Available online: http://www.fao.org/fileadmin/templates/est/Volatility/Interagency_Report_to_the_G20_on_Food_Price_Volatility.pdf (accessed on 1 March 2024).
- Ordu, B.M.; Oran, A.; Soytas, U. Is food financialized? Yes, but only when liquidity is abundant. J. Bank. Financ. 2018, 95, 82–96. [Google Scholar] [CrossRef]
- Greb, F.; Prakash, A. Has price volatility changed? In Food Outlook; Food and Agriculture Organization of the United Nations: Rome, Italy, 2015. [Google Scholar]
- Greb, F.; Prakash, A. Assessing volatility patterns in food crops. In FAO Commodity and Trade Policy Research Working Paper Series; FAO: Rome, Italy, 2017; Available online: http://www.fao.org/3/a-i7066e.pdf (accessed on 1 March 2024).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023; Available online: https://www.R-project.org/ (accessed on 4 May 2024).
- Rauschenberger, A.; Glaab, E. Predicting correlated outcomes from molecular data. Bioinformatics 2021, 37, 3889–3895. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. Journal of the Royal Statistical. Soc. Ser. B Stat. Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Xing, L.; Lesperance, M.L.; Zhang, X. Simultaneous prediction of multiple outcomes using revised stacking algorithms. Bioinformatics 2020, 36, 65–72. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and Regression Trees; Wadsworth: Belmont, CA, USA, 1984. [Google Scholar]
- Friedman, J.; Tibshirani, R.; Hastie, T. Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Diebold, F.X.; Yilmaz, K. Measuring financial asset return and volatility spillovers, with application to global equity markets. Econ. J. 2009, 119, 158–171. [Google Scholar] [CrossRef]
- Diebold, F.X.; Yilmaz, K. Better to give than to receive: Predictive directional measurement of volatility spillovers. Int. J. Forecast. 2012, 28, 57–66. [Google Scholar] [CrossRef]
- Urbina, J. Spillover: Spillover/Connectedness Index Based on VAR Modelling. R Package Version 0.1.0.3. 2023. Available online: https://CRAN.R-project.org/package=Spillover (accessed on 6 June 2024).
- Dai, Z.; Zhang, X.; Liang, C. Efficient predictability of oil price: The role of VIX-based panic index shadow line difference. Energy Econ. 2024, 129, 107234. [Google Scholar] [CrossRef]
- Liang, C.; Wang, L.; Duon, D. More attention and better volatility forecast accuracy: How does war attention affect stock volatility predictability? J. Econ. Behav. Org. 2024, 218, 1–9. [Google Scholar] [CrossRef]
- Nazlioglu, S.; Erdem, C.; Soytas, U. Volatility spillover between oil and agricultural commodity markets. Energy Econ. 2013, 36, 658–665. [Google Scholar] [CrossRef]
- Kang, S.H.; McIver, R.; Yoon, S.M. Dynamic spillover effects among crude oil, precious metal, and agricultural commodity futures markets. Energy Econ. 2017, 62, 19–32. [Google Scholar] [CrossRef]
- Mensi, W.; Tiwari, A.K.; Bouri, E.; Roubaud, D.; Al-Yahyaee, K.H. The dependence structure across oil, wheat, and corn: A wavelet-based copula approach using implied volatility indexes. Energy Econ. 2017, 66, 122–139. [Google Scholar] [CrossRef]
- Ji, Q.; Bouri, E.; Roubaud, D.; Shahzad, S.J.H. Risk spillover between energy and agricultural commodity markets: A dependence-switching CoVaR-copula model. Energy Econ. 2018, 75, 14–27. [Google Scholar] [CrossRef]
- Luo, J.; Ji, Q. High-frequency volatility connectedness between the US crude oil market and China’s agricultural commodity markets. Energy Econ. 2018, 76, 424–438. [Google Scholar] [CrossRef]
- Chang, C.L.; Liu, C.P.; McAleer, M. Volatility spillovers for spot, futures, and ETF prices in agriculture and energy. Energy Econ. 2019, 81, 779–792. [Google Scholar] [CrossRef]
- Lu, Y.; Yang, L.; Liu, L. Volatility spillovers between crude oil and agricultural commodity markets since the financial crisis. Sustainability 2019, 11, 396. [Google Scholar] [CrossRef]
- Dahl, R.E.; Oglend, A.; Yahya, M. Dynamics of volatility spillover in commodity markets: Linking crude oil to agriculture. J. Commod. Mark. 2020, 20, 100–111. [Google Scholar] [CrossRef]
- Luo, J.; Zhang, Q. Risk contagions between global oil markets and China’s agricultural commodity markets under structural breaks. Appl. Econ. 2020, 53, 1–22. [Google Scholar] [CrossRef]
- Yip, P.S.; Brooks, R.; Do, H.X.; Nguyen, D.K. Dynamic volatility spillover effects between oil and agricultural products. Int. Rev. Financ. Anal. 2020, 69, 101465. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gupta, R.; Pierdzioch, C. Multi-Task Forecasting of the Realized Volatilities of Agricultural Commodity Prices. Mathematics 2024, 12, 2952. https://doi.org/10.3390/math12182952
Gupta R, Pierdzioch C. Multi-Task Forecasting of the Realized Volatilities of Agricultural Commodity Prices. Mathematics. 2024; 12(18):2952. https://doi.org/10.3390/math12182952
Chicago/Turabian StyleGupta, Rangan, and Christian Pierdzioch. 2024. "Multi-Task Forecasting of the Realized Volatilities of Agricultural Commodity Prices" Mathematics 12, no. 18: 2952. https://doi.org/10.3390/math12182952
APA StyleGupta, R., & Pierdzioch, C. (2024). Multi-Task Forecasting of the Realized Volatilities of Agricultural Commodity Prices. Mathematics, 12(18), 2952. https://doi.org/10.3390/math12182952






