A Fixed-Time Event-Triggered Consensus of a Class of Multi-Agent Systems with Disturbed and Non-Linear Dynamics

Abstract

This paper investigates the problem of fixed-time event-triggered consensus control for a class of multi-agent systems with disturbed and non-linear dynamics. A fixed-time consensus protocol based on an event-triggered strategy is proposed, which can ensure a fixed-time event-triggered consensus, reduce energy consumption, and decrease the frequency of controller updates. The control protocol can also be applied to the case when the systems are free of disturbances; it solves the problem of high convergence time of the systems and reduces energy consumption of the systems. Sufficient conditions are proposed for the multi-agent systems with disturbed and non-linear dynamics to achieve the fixed-time event-triggered consensus by using algebraic graph theory, inequalities, fixed-time stability theory, and Lyapunov stability theory. Finally, simulation results show that the proposed control protocol has the advantages of both event-triggered and fixed-time convergence; compared to previous work, the convergence time of the new control protocol is greatly reduced (about 1.5 s) and the update times are also greatly reduced (less than 50 times), which is consistent with the theoretical results.

1. Introduction

Consensus is a relatively important issue in the collaborative control [1,2,3,4] of multi-agent systems. The convergence rate is an important performance metric for evaluating the proposed consensus protocols [5]. The convergence rate was shown to be influenced by the algebraic connectivity, which is the second smallest eigenvalue of the Laplacian matrix. In [6], researchers can improve the convergence rate to linear protocols, but only asymptotically. In practice, it is sometimes necessary for multi-agent systems to achieve consensus in finite time [7,8,9]. However, the finite-time consensus has a major drawback in that the convergence time of the systems still depends on the initial conditions of the multi-agent systems. Therefore, it is difficult to provide a strict estimate of the convergence time. Furthermore, the issue of how to decrease the loss of energy of the agents is also a noted research topic. Therefore, the aim of this paper is to research this problem; specifically, it will be based on fixed-time convergence and event-triggered mechanisms to propose a new strategy: a fixed-time event-triggered consensus control protocol.

Fixed-time stability [10] refers to a state where the convergence time of a closed-loop system is independent of the initial conditions. A fixed-time averaging consensus algorithm was discussed for multi-agent systems with integrator dynamics in an undirected topology [11]; then, conclusions on finite-time and fixed-time stability analysis of non-linear systems were presented by using an implicit Lyapunov function approach [12]. Then, the robust fixed-time consensus problem for multi-agent systems with non-linear dynamics and uncertain disturbances was studied [13]. Researchers investigated the fixed-time consensus problem for a class of heterogeneous non-linear multi-agent systems and proposed a new control protocol to achieve the fixed-time consensus problem for leaderless and leader-following systems by using fixed-time control theory and graph theory [14]. In [15], the fixed-time leader-following consensus problem for higher-order non-linear multi-agent systems was studied. Based on a fixed-time distributed observer and a dynamic gain control method, a dynamic controller was proposed to achieve fixed-time tracking consensus. In [16], a non-singular sliding-mode control law was designed based on fixed-time synchronization stability, thus solving the fixed-time synchronization consensus problem. Researchers studied the fixed-time consensus tracking problem of second-order multi-agent systems under a directed interaction topology, designed a sliding surface, and established a non-singular terminal sliding-mode consensus protocol to achieve fixed-time convergence of the tracking error to the origin [17]. In [18], an ideal fixed-time stable virtual control protocol was derived by adding power integrator techniques, radial basis function neural network approximation, and adaptive methods; it solved the problems of unknown control direction and external disturbances of the system. In [19], the fixed-time control of a second-order perturbed non-linear multi-agent system was studied. A new non-singular terminal sliding-mode control protocol was proposed to achieve the fixed-time convergence of the system, and an explicit estimation of the settling time was given. It is worth noting that the loss of energy of the agents is not considered in the above-mentioned studies on the fixed-time consensus of multi-agent systems. Additionally, the event-triggered control problem is closely related to the measurement feedback control problem. An event-triggered control system is a sampled-data system in which the sampling time instants are determined by events generated by the real-time system state. By taking advantage of the inter-sample behavior, event-triggered sampling may realize improved control performance over periodic sampling. It also has the advantages of saving communication bandwidth, improving system response speed, reducing control cost, improving system robustness, and applying to complex systems [9,20,21,22,23,24]. Therefore, it is important to combine the event-triggered mechanism with multi-agent systems with fixed-time consensus to reduce the energy consumption and the frequency of controller updates. Additionally, researchers studied the fixed-time event-triggered consensus problem of uncertain non-linear multi-agent systems [20], proposed two fixed-time event-triggered consensus controllers, and obtained sufficient conditions for the fixed-time convergence of the system. Ref. [21] studied the problem of achieving fixed-time average consensus for a class of multi-agent systems under switching topology and intermittent communication based on the event-based control strategy, and obtained sufficient conditions for the system to achieve fixed-time average consensus. Ref. [22] proposed a new fixed-time event-triggered control protocol based on a dynamic compensator approach to obtain a sufficient condition for the fixed-time consensus of linear multi-agent systems. An event-triggered consensus protocol was proposed in [23]; it obtained sufficient conditions for convergence of event-triggered attitude consensus for multi-agent systems. In [24], researchers studied the fixed-time event-triggered consensus of a class of non-linear multi-agent systems with switching topologies and gave an upper bound on the fixed-time convergence time of the system and sufficient conditions for the convergence of the system.

It should be noted that the previous works have made significant contributions to the field of multi-agent consensus control, but some issues have not been considered. In [13], a non-linear multi-agent system control protocol was proposed in first-order multi-agent systems with disturbed and non-linear dynamics, but when the agents are internally powered by their own power supply or battery, the bandwidth is easily limited and the loss of communication resources occurs, which have not been considered. In addition, researchers studied the fixed-time event-triggered consensus problem for a class of non-linear multi-agent systems. Ref. [24] proposed a control algorithm that considers its influence by uncertain non-linear terms, but the disturbance of the systems was not considered; the algorithm provided a high prediction of the upper bound on the convergence time. Motivated by the previous works, in this paper, a fixed-time event-triggered consensus control protocol is proposed, which can achieve fixed-time event-triggered consensus for multi-agent systems with disturbed and non-linear dynamics. The control protocol is also suitable for the case when the systems are free of disturbances. Compared with the previous works, the results shown in this paper have the following features: Firstly, this protocol reduces power consumption. Secondly, compared to [24], this paper can provide a more accurate upper bound estimation of convergence time and save more resources. Finally, the multi-agent systems with external disturbances are considered. Results about the fixed-time event-triggered consensus for multi-agent systems with disturbed and non-linear dynamics are available.

This paper is organized as follows: Preparation and problem formulation are presented in Section 2. In Section 3, a fixed-time event-triggered consensus control protocol is proposed and consensus analyses are reviewed. In Section 4, some simulation examples are provided to illustrate the effectiveness of the fixed-time event-triggered consensus protocol. Conclusions are drawn in Section 5.

2. Preparation and Problem Description

In this section, firstly, the knowledge of the graph theory will be introduced. Secondly, some lemmas used in this paper will be introduced. Finally, the problem formulation will be presented.

A.

the basic graph theory

Let $G(V,E,A)$ be an undirected graph G of order N. The $V=\left\{1,2,\cdots ,N\right\}$ indicates that the graph has N nodes and $E\subseteq V\times V$ is the set of edges. An edge $(i,j)\in E$ indicates that note j can exchange information state from note $i$ and note $i$ can also exchange information from note $j$. In this paper, agents are considered nodes. Agent $i$ and $j$ can communicate with each other. $A=[a_{ij}]\in R^{n\times n}$ is an N order matrix when edge $(i,j)\in E$, $a_{ij}>0$; otherwise, $a_{ij}=0$, $A$ is known as an adjacency matrix. The degree matrix is defined as $D=diag\left\{d_1,\cdots ,d_N\right\}$, $d_i={\displaystyle {\sum }_{j=1,j\ne i}^N{a}_{ij}}$. The Laplacian matrix of graph $G$ is defined by $L=D-A$.

B.

Some lemmas

Lemma 1

([13]). The graph $G$ is undirected and connected, and the following three conclusions hold:

(1) 

0 is an eigenvalue of the matrix $L$ and the corresponding eigenvector is $1_n$, $L{1}_n=0$.

(2) 

The Laplace matrix is positive semidefinite, and all the eigenvalues of the matrix satisfy the following relation:

$$0\le {\lambda }_2\le \cdots \le {\lambda }_n,1^{T}x=0 \mathrm{then} x^{T}Lx\ge {\lambda }_2{x}^{T}x.$$

Algebraic connectivity of the graph $G$; the second smallest eigenvalue of the Laplace matrix is ${\lambda }_2$.

(3) 

For any $x={(x_1,x_2,\cdots ,x_N)}^T\in R^N$, $x^{T}Lx=\frac{1}{2}{\displaystyle {\sum }_{i=1}^N{\displaystyle {\sum }_{j=1}^N{a}_{ij}{(x_j-x_i)}^2}}$.

Lemma 2

([11]). If there is a continuous radial unbounded function $V(x(t))$: $R_n\to R^{+}\cup \left\{0\right\}$ such that $x=0\iff V(x)=0$

$x$ satisfies the inequality

$$\dot{V}(t)\le -a{V}^p(x(t))-b{V}^q(x(t))$$

(1)

for $a,b>0,p\in (0,1),q>1$. $p=1-\frac{1}{2\gamma },q=1+\frac{1}{2\gamma }$, $\gamma >1$. then, the fixed-time stable can be achieved and the settling time $T$ satisfies the following conditions: where, $\gamma$

$$T(x)\le T_{\max }=\frac{\pi \gamma }{\sqrt{ab}},\forall x_0\in R^n$$

(2)

Lemma 3

([13]). Let $x_1,x_2,\cdots ,x_N\ge 0$,$0<p\le 1$ and $q>1$. Then

$${\displaystyle {\sum }_{i=1}^N{x}_i^p}\ge ({\displaystyle {\sum }_{i=1}^N{x}_i{)}^p}, {\displaystyle {\sum }_{i=1}^N{x}_i^q\ge N^{1-q}({\displaystyle {\sum }_{i=1}^N{x}_i{)}^q}}$$

(3)

C.

the problem formulation

The multi-agent systems consist of $N$ agents and the dynamics model of the agents can be described by the following differential equation:

$${\dot{x}}_i(t)=u_i(t)+f(x_i(t),t)+d_i(x_i(t),t)$$

(4)

where $i=1,2,\cdots ,N$, $u_i(t)\in R^N$ is the control input of the multi-agent systems, $x_i(t)\in R^N$ is the state of agent, $f(x_i(t),t)$ is a non-linear function, and $d_i(x_i(t),t)$ are disturbances. In this paper, before moving on, the following assumptions are made:

Assumption 1.

$f(x_i(t),t)$ is a non-linear function; there exists a positive constant $k$, $0<p<1$ and $q>1$, $p<\eta <q$, $p,q$ and $q$ are the ratios of positive odd numbers, such that

$$|f(x_i(t),t)-f(x_j(t),t)|\le k|x_i(t)-x_j(t){|}^{\eta }$$

(5)

For example, a non-linear function $f\left(x\left(t\right)\right)=\frac{1}{2}\left|x\left(t\right)+1\right|+sin\left(t\right)$, and $x_i\left(t\right)$ is the state of agent $i$, $x_j\left(t\right)$ is the state of agent $j$, so $\left|f\left(x_i\left(t\right)\right)-f\left(x_j\left(t\right)\right)\right|=\left|\frac{1}{2}\left|x_i\left(t\right)+1\right|-\frac{1}{2}\left|x_j\left(t\right)+1\right|\right|\le \frac{1}{2}\left|x_i\left(t\right)-x_j\left(t\right)\right|$, $k=\frac{1}{2}$, $ƞ=1$.

Assumption 2.

The disturbances $d_i(x_i(t),t)$ are bounded by

$$|d_i(x_i(t),t)|\le d$$

(6)

where the number $d$ is assumed to be given, and $i=1,2,\cdots ,N$.

• For example, a disturbances function $d\left(x\left(t\right),t\right)=sin\left(x\left(t\right)cos\left(x\left(t\right)\right)\right)$, then for the state of agent $i$, $d\left(x_i\left(t\right),t\right)=sin\left(x_i\left(t\right)cos\left(x_i\left(t\right)\right)\right)\le 1$ as well as $d=1$.

Definition 1.

With a given control protocol, the fixed-time consensus of the multi-agent systems (4) is that there exists a fixed-time $T$ such that $\underset{t\to T}{\lim }|x_i(t)-x_j(t)|=0$ and when $t\ge T$, $x_i(t)=x_j(t)(i,j=1,2,\cdots ,N)$, if for any initial value $x_i(0)$, there is a positive constant $T_{\max }$, such that $T\le T_{\max }$, multi-agent systems will be said to achieve fixed-time consensus.

3. Fixed-Time Event-Triggered Consensus Protocol

In this section, the main results of the fixed-time event-triggered consensus of the system (4) are investigated.

Consider the following control protocol:

$$\begin{gathered} u_i(t)=-k_1{\displaystyle {\sum }_{j=1}^N{a}_{ij}{(x_i(t_k^i)-x_j(t_k^i))}^p} \\ -k_2{\displaystyle {\sum }_{j=1}^N{a}_{ij}{(x_i(t_k^i)-x_j(t_k^i))}^q} \\ -k_3{\displaystyle {\sum }_{j=1}^N{a}_{ij}{(x_i(t_k^i)-x_j(t_k^i))}^{\eta }} \\ -k_4{\displaystyle {\sum }_{j=1}^N{a}_{ij}sign(x_i(t_k^i)-x_j(t_k^i))} \end{gathered}$$

(7)

where $k_1,k_2,k_3,k_4>0,0<p<1,q>1,p<\eta <q$. $p,\eta$ and $q$ are the ratios of positive odd numbers. $t_k^i$ is the kth event-triggered instants of the agent $i$. Additionally, parameters k1, k2, k3, and k4 affect the consistency of different orders, respectively, and the interaction reaches the consistency of fixed time.

Define a measurement error; the event-triggered function is related to this measurement error.

$$\begin{gathered} e_i(t)=k_1{\displaystyle {\sum }_{j=1}^N{a}_{ij}{(x_i(t_k^i)-x_j(t_k^i))}^p}+k_2{\displaystyle {\sum }_{j=1}^N{a}_{ij}{(x_i(t_k^i)-x_j(t_k^i))}^q} \\ +k_3{\displaystyle {\sum }_{j=1}^N{a}_{ij}{(x_i(t_k^i)-x_j(t_k^i))}^{\eta }}+k_4{\displaystyle {\sum }_{j=1}^N{a}_{ij}sign(x_i(t_k^i)-x_j(t_k^i))} \\ -k_1{\displaystyle {\sum }_{j=1}^N{a}_{ij}{(x_i(t)-x_j(t))}^p}-k_2{\displaystyle {\sum }_{j=1}^N{a}_{ij}{(x_i(t)-x_j(t))}^q} \\ -k_3{\displaystyle {\sum }_{j=1}^N{a}_{ij}{(x_i(t)-x_j(t))}^{\eta }}-k_4{\displaystyle {\sum }_{j=1}^N{a}_{ij}sign(x_i(t)-x_j(t))} \end{gathered}$$

(8)

The following event-triggered function is constructed based on the measurement error:

$$\begin{gathered} \phi (t)=|e_i(t)|-m{k}_1{{\displaystyle {\sum }_{j=1}^N{a}_{ij}|x_i(t)-x_j(t)|}}^p-m{k}_2{{\displaystyle {\sum }_{j=1}^N{a}_{ij}|x_i(t)-x_j(t)|}}^q \\ -m{k}_3{{\displaystyle {\sum }_{j=1}^N{a}_{ij}|x_i(t)-x_j(t)|}}^{\eta }-m{k}_{4}N \end{gathered}$$

(9)

where $0<m<1$, $k_1,k_2,k_3,k_4>0,0<p<1,q>1$.

The event-triggered conditions are as follows:

$$t_{k+1}^i=\inf \left\{t>t_k^i|\phi (t)\ge 0\right\}$$

(10)

Based on trigger conditions, at the next trigger moment, each agent will be updated within its trigger period and will send the updated state information to its neighbors.

Theorem 1.

Under all assumptions above, the multi-agent systems, composed of the controlled plant (4) and the control protocol (7), satisfy the event-triggered condition (10); the multi-agent systems can achieve fixed-time consensus, if the following inequalities hold:

$$\sqrt{2}mN{\lambda }_N{(L_{2/p})}^{\frac{p}{2}}\le N^{1-p}{\lambda }_N{(L_{2/p+1})}^{\frac{p+1}{2}}$$

(11)

$$\sqrt{2}mN{\lambda }_N{(L_{2/q})}^{\frac{q}{2}}\le {\lambda }_N{(L_{2/q+1})}^{\frac{q+1}{2}}$$

(12)

$$k{2}^{\frac{\eta +1}{2}}\le 2^{\eta }{k}_3{\lambda }_2{(L_{2/\eta +1})}^{\frac{\eta +1}{2}}$$

(13)

$$\sqrt{2}{N}^{\frac{1}{2}}(m{k}_{4}N+d)\le k_4{\lambda }_2{(L_2)}^{\frac{1}{2}}$$

(14)

where $L_{2/p}$ denotes the Laplacian matrix of a graph, where the value of each element is $a_{ij}^{2/p}$; $L_{\frac{2}{p+1}}$ denotes the Laplacian matrix of a graph, where the value of each element is $a_{ij}^{\frac{2}{p+1}}$; $L_{\frac{2}{q+1}}$ denotes the Laplacian matrix of a graph, where the value of each element is $a_{ij}^{\frac{2}{q+1}}$; and $L_{\frac{2}{ƞ+1}}$ denotes the Laplacian matrix of a graph, where the value of each element is $a_{ij}^{\frac{2}{ƞ+1}}$.

The systems (4) can achieve fixed-time consensus under the control protocol (7), and the system convergence time satisfies:

$$T\le T_{\max }=\frac{\pi \gamma }{\sqrt{\overline{\alpha }\overline{\beta }}}$$

(15)

where the parameters $\overline{\alpha }$, $\overline{\beta }$ are as follows:

$$\overline{\alpha }=k_1{2}^p{N}^{1-p}{\lambda }_N{(L_{2/p+1})}^{\frac{p+1}{2}}-k_1{2}^p\sqrt{2}mN{\lambda }_N{(L_{2/p})}^{\frac{p}{2}}$$

(16)

$$\overline{\beta }=2^q{k}_2{\lambda }_N{(L_{2/q+1})}^{\frac{q+1}{2}}-\sqrt{2}{2}^q{k}_{2}mN{\lambda }_N{(L_{2/q})}^{\frac{q}{2}}.$$

(17)

Proof. 

Introducing $\overline{x}(t)$, let $\overline{x}(t)=\frac{1}{N}{\displaystyle {\sum }_{j=1}^N{x}_j(t)}$ define the state error as follows:

$${\epsilon }_i(t)=x_i(t)-\overline{x}(t)$$

(18)

Consider the Lyapunov function as

$$V(t)=\frac{1}{2}{\displaystyle {\sum }_{i=1}^N{\epsilon }_i^2}(t)$$

(19)

Differentiating,

$$\begin{gathered} \dot{V}(t)={\displaystyle {\sum }_{i=1}^N{\epsilon }_i(t)(u_i(t)+f(x_i(t),t)+d_i}(x_i(t),t)-\overline{\dot{x}}(t)) \\ ={\displaystyle {\sum }_{j=1}^N{\epsilon }_i}(t)(-e_i(t)-k_1{\displaystyle {\sum }_{j=1}^N{a}_{ij}{(x_i(t)-x_j(t))}^p}-k_2{\displaystyle {\sum }_{j=1}^N{a}_{ij}{(x_i(t)-x_j(t))}^q} \\ -k_3{\displaystyle {\sum }_{j=1}^N{a}_{ij}{(x_i(t)-x_j(t))}^{\eta }}-k_4{\displaystyle {\sum }_{j=1}^N{a}_{ij}sign(x_i(t)-x_j(t))}+d_i(x_i(t),t)) \\ +{\displaystyle {\sum }_{i=1}^N{\epsilon }_i(t)(f(x_i(t),t)}-\overline{\dot{x}}(t)) \end{gathered}$$

(20)

According to the state error and the inequalities, one obtains

$$\begin{gathered} \dot{V}(t)\le {\displaystyle {\sum }_{i=1}^N{\epsilon }_i(t)(f(x_i(t),t)-f}(\overline{x}(t),t)+f(\overline{x}(t),t) \\ -\frac{1}{N}{\displaystyle {\sum }_{j=1}^{N}f(x_j(t),t)-\frac{1}{N}}{\displaystyle {\sum }_{j=1}^N{d}_j(x_j(t),t))} \\ +{\displaystyle {\sum }_{i=1}^N|}{\epsilon }_i(t)|(|e_i(t)|+d) \\ -k_1{\displaystyle {\sum }_{i=1}^N{\epsilon }_i(t)({\displaystyle {\sum }_{j=1}^N{a}_{ij}({\epsilon }_i(t)-}}{\epsilon }_j(t){)}^p) \\ -k_2{\displaystyle {\sum }_{i=1}^N{\epsilon }_i(t)({\displaystyle {\sum }_{j=1}^N{a}_{ij}({\epsilon }_i(t)-}}{\epsilon }_j(t){)}^q) \\ -k_3{\displaystyle {\sum }_{i=1}^N{\epsilon }_i(t)({\displaystyle {\sum }_{j=1}^N{a}_{ij}({\epsilon }_i(t)-}}{\epsilon }_j(t){)}^{\eta })-k_4{\displaystyle {\sum }_{i=1}^N{\epsilon }_i(t)({\displaystyle {\sum }_{j=1}^N{a}_{ij}sign({\epsilon }_i(t)-}}{\epsilon }_j(t))) \\ \le {\displaystyle {\sum }_{i=1}^N{\epsilon }_i(t)(f(x_i(t),t)-f}(\overline{x}(t),t)+f(\overline{x}(t),t) \\ -\frac{1}{N}{\displaystyle {\sum }_{j=1}^{N}f(x_j(t),t)-\frac{1}{N}}{\displaystyle {\sum }_{j=1}^N{d}_j(x_j(t),t))}+{\displaystyle {\sum }_{i=1}^N|}{\epsilon }_i(t)|(|e_i(t)|+d) \\ -\frac{k_1}{2}{\displaystyle {\sum }_{i=1}^N{\displaystyle {\sum }_{j=1}^N{a}_{ij}(}}{\epsilon }_i(t)-{\epsilon }_j(t)){({\epsilon }_i(t)-{\epsilon }_j(t))}^p \\ -\frac{k_2}{2}{\displaystyle {\sum }_{i=1}^N{\displaystyle {\sum }_{j=1}^N{a}_{ij}(}}{\epsilon }_i(t)-{\epsilon }_j(t)){({\epsilon }_i(t)-{\epsilon }_j(t))}^q \\ -\frac{k_3}{2}{\displaystyle {\sum }_{i=1}^N{\displaystyle {\sum }_{j=1}^N{a}_{ij}(}}{\epsilon }_i(t)-{\epsilon }_j(t)){({\epsilon }_i(t)-{\epsilon }_j(t))}^{\eta } \\ -\frac{k_4}{2}{\displaystyle {\sum }_{i=1}^N{\displaystyle {\sum }_{j=1}^N{a}_{ij}(}}{\epsilon }_i(t)-{\epsilon }_j(t))sign({\epsilon }_i(t)-{\epsilon }_j(t)) \end{gathered}$$

(21)

Since ${\displaystyle {\sum }_{i=1}^N{\epsilon }_i(t)=0}$, one has $({\displaystyle {\sum }_{i=1}^N{\epsilon }_i(t)})(f(\overline{x}(t),t)-\frac{1}{N}{{\displaystyle {\sum }_{j=1}^{N}f(x}}_j(t),t))=0$ and $({\displaystyle {\sum }_{i=1}^N{\epsilon }_i(t)})(\frac{1}{N}{\displaystyle {\sum }_{j=1}^N{d}_j(x_j(t),t))=0}$ and

$${\sum }_{i=1}^N{\sum }_{j=1}^N{a}_{ij}\left({ϵ}_i\left(t\right)-{ϵ}_j\left(t\right)\right)sign\left({ϵ}_i\left(t\right)-{ϵ}_j\left(t\right)\right)={\sum }_{i=1}^N{\sum }_{j=1}^N{a}_{ij}\left|{ϵ}_i\left(t\right)-{ϵ}_j\left(t\right)\right|$$

(22)

Substituting Assumption 1 with Assumption 2, and substituting the event-triggered conditions, one has

$$\begin{gathered} \dot{V}(t)\le k{\displaystyle {\sum }_{i=1}^N|{\epsilon }_i(t){|}^2+(m{k}_{4}N}+d)N^{\frac{1}{2}}({\displaystyle {\sum }_{i=1}^N|{\epsilon }_i(t){|}^2{)}^{\frac{1}{2}}} \\ +m{k}_{1}N({\displaystyle {\sum }_{i=1}^N|{\epsilon }_i(t){|}^2{)}^{\frac{1}{2}}}{({\displaystyle {\sum }_{i=1}^N{\displaystyle {\sum }_{j=1}^N{a_{ij}}^{\frac{2}{p}}|}}{\epsilon }_i(t)-{\epsilon }_j(t){|}^2)}^{\frac{p}{2}} \\ +m{k}_{2}N({\displaystyle {\sum }_{i=1}^N|{\epsilon }_i(t){|}^2{)}^{\frac{1}{2}}}{({\displaystyle {\sum }_{i=1}^N{\displaystyle {\sum }_{j=1}^N{a_{ij}}^{\frac{2}{q}}|}}{\epsilon }_i(t)-{\epsilon }_j(t){|}^2)}^{\frac{q}{2}} \\ +m{k}_{3}N({\displaystyle {\sum }_{i=1}^N|{\epsilon }_i(t){|}^2{)}^{\frac{1}{2}}}{({\displaystyle {\sum }_{i=1}^N{\displaystyle {\sum }_{j=1}^N{a_{ij}}^{\frac{2}{\eta }}|}}{\epsilon }_i(t)-{\epsilon }_j(t){|}^2)}^{\frac{\eta }{2}} \\ -\frac{k_1}{2}{N}^{1-p}{({\displaystyle {\sum }_{i=1}^N{\displaystyle {\sum }_{j=1}^N{a_{ij}}^{\frac{2}{p+1}}|}}{\epsilon }_i(t)-{\epsilon }_j(t){|}^2)}^{\frac{p+1}{2}}-\frac{k_2}{2}{({\displaystyle {\sum }_{i=1}^N{\displaystyle {\sum }_{j=1}^N{a_{ij}}^{\frac{2}{q+1}}|}}{\epsilon }_i(t)-{\epsilon }_j(t){|}^2)}^{\frac{q+1}{2}} \\ -\frac{k_3}{2}{({\displaystyle {\sum }_{i=1}^N{\displaystyle {\sum }_{j=1}^N{a_{ij}}^{\frac{2}{\eta +1}}|}}{\epsilon }_i(t)-{\epsilon }_j(t){|}^2)}^{\frac{\eta +1}{2}}-\frac{k_4}{2}{({\displaystyle {\sum }_{i=1}^N{\displaystyle {\sum }_{j=1}^N{a_{ij}}^2|}}{\epsilon }_i(t)-{\epsilon }_j(t){|}^2)}^{\frac{1}{2}} \end{gathered}$$

(23)

Invoking Lemma 1, the following inequalities can be obtained:

$${\displaystyle {\sum }_{i=1}^N{\displaystyle {\sum }_{j=1}^N{a_{ij}}^{\frac{2}{p}}|}}{\epsilon }_i(t)-{\epsilon }_j(t){|}^2=2{\epsilon }^T{L}_{2/p}\epsilon \ge 4{\lambda }_2(L_{2/p})V(t)$$

$${\displaystyle {\sum }_{i=1}^N{\displaystyle {\sum }_{j=1}^N{a_{ij}}^{\frac{2}{p}}|}}{\epsilon }_i(t)-{\epsilon }_j(t){|}^2=2{\epsilon }^T{L}_{2/q}\epsilon \ge 4{\lambda }_2(L_{2/q})V(t)$$

$${\displaystyle {\sum }_{i=1}^N{\displaystyle {\sum }_{j=1}^N{a_{ij}}^{\frac{2}{\eta }}|}}{\epsilon }_i(t)-{\epsilon }_j(t){|}^2=2{\epsilon }^T{L}_{2/\eta }\epsilon \ge 4{\lambda }_2(L_{2/\eta })V(t)$$

$${\displaystyle {\sum }_{i=1}^N{\displaystyle {\sum }_{j=1}^N{a_{ij}}^{\frac{2}{p+1}}|}}{\epsilon }_i(t)-{\epsilon }_j(t){|}^2=2{\epsilon }^T{L}_{2/p+1}\epsilon \ge 4{\lambda }_2(L_{2/p+1})V(t)$$

$${\displaystyle {\sum }_{i=1}^N{\displaystyle {\sum }_{j=1}^N{a_{ij}}^{\frac{2}{q+1}}|}}{\epsilon }_i(t)-{\epsilon }_j(t){|}^2=2{\epsilon }^T{L}_{2/q+1}\epsilon \ge 4{\lambda }_2(L_{2/q+1})V(t)$$

where $L_{2/p}$, $L_{2/q}$, $L_{2/\eta }$, $L_{2/p+1}$, and $L_{2/q+1}$ are the Laplacian matrices of the weighted graphs $G(A^{[2/p]})$, $G(A^{[2/q]})$, $G(A^{[2/\eta ]})$, $G(A^{[2/p+1]})$, and $G(A^{[2/q+1]})$, respectively.

By Lemma 2, the following inequality can be obtained:

$$\begin{gathered} \dot{V}(t)\le -(k_1{N}^{1-p}{\lambda }_N{(L_{2/p+1})}^{\frac{p+1}{2}}-k_1\sqrt{2}mN{\lambda }_N{(L_{2/p})}^{\frac{p}{2}})2^p{V}^{\frac{p+1}{2}}(t) \\ -(k_2{\lambda }_N{(L_{2/q+1})}^{\frac{q+1}{2}}-\sqrt{2}{k}_{2}mN{\lambda }_N{(L_{2/q})}^{\frac{q}{2}})2^q{V}^{\frac{q+1}{2}}(t) \\ +(k{2}^{\frac{\eta +1}{2}}-2^{\eta }{k}_3{\lambda }_2{(L_{2/\eta +1})}^{\frac{\eta +1}{2}})V^{\frac{\eta +1}{2}}(t) \\ +(\sqrt{2}{N}^{\frac{1}{2}}(m{k}_{4}N+d)-k_4{\lambda }_2{(L_2)}^{\frac{1}{2}})V^{\frac{1}{2}}(t) \end{gathered}$$

(24)

By Inequalities (13) and (14)

$$\dot{V}(t)\le -\overline{\alpha }{V}^{\frac{p+1}{2}}(t)-\overline{\beta }{V}^{\frac{q+1}{2}}(t)$$

(25)

When $p=1+\frac{1}{\gamma },q=1-\frac{1}{\gamma },\gamma >1$, one has

$$\dot{V}(t)\le -\overline{\alpha }{V}^{1-\frac{1}{2\gamma }}(t)-\overline{\beta }{V}^{1+\frac{1}{2\gamma }}(t)$$

(26)

According to Lemma 2, the systems’ convergence time satisfies:

$$T\le T_{\max }=\frac{\pi \gamma }{\sqrt{\overline{\alpha }\overline{\beta }}}$$

(27)

Here are the parameters $\overline{\alpha }$, $\overline{\beta }$ as follows:

$$\overline{\alpha }=k_1{N}^{1-p}{2}^p{\lambda }_N{(L_{2/p+1})}^{\frac{p+1}{2}}-k_1\sqrt{2}{2}^{p}mN{\lambda }_N{(L_{2/p})}^{\frac{p}{2}}$$

$$\overline{\beta }=k_2{2}^q{\lambda }_N{(L_{2/q+1})}^{\frac{q+1}{2}}-\sqrt{2}{2}^q{k}_{2}mN{\lambda }_N{(L_{2/q})}^{\frac{q}{2}}$$

where ${\lambda }_N(L_{2/p+1})$, ${\lambda }_N(L_{2/p})$, ${\lambda }_N(L_{2/q+1})$, and ${\lambda }_N(L_{2/q})$ are the biggest eigenvalues of the Laplacian matrices $L_{2/p+1}$, $L_{2/p}$, $L_{2/q+1}$, and $L_{2/q}$ in the connected undirected graphs $G(A^{[2/p+1]})$, $G(A^{[2/p]})$, $G(A^{[2/q+1]})$, and $G(A^{[2/p]})$. The multi-agent systems can achieve fixed-time consensus.

Under the control protocol (7), the inter-event interval is lower bounded; this can be proven in the following theorem: □

Theorem 2.

Considering the multi-agent systems (4) with disturbed and non-linear dynamics, for any initial condition, the inter-event interval is lower bounded by the strictly positive.

Proof. 

The presence of a functional term in the measurement error is non-differentiable, and the next proof process involves the derivation of the measurement error, which is now generally treated in two ways in the literature—either by approximating the symbolic function with a saturation function, which requires a segmented discussion, or by replacing the symbolic function with a hyperbolic tangent function. The second approach will be used in this part of the proof. The measurement error can be written as

$$\begin{gathered} e_i(t)=k_1{\displaystyle {\sum }_{j=1}^N{a}_{ij}{(x_i(t_k^i)-x_j(t_k^i))}^p}+k_2{\displaystyle {\sum }_{j=1}^N{a}_{ij}{(x_i(t_k^i)-x_j(t_k^i))}^q} \\ +k_3{\displaystyle {\sum }_{j=1}^N{a}_{ij}{(x_i(t_k^i)-x_j(t_k^i))}^{\eta }}+k_4{\displaystyle {\sum }_{j=1}^N{a}_{ij}\tanh (n(x_i(t_k^i)-x_j(t_k^i)))} \\ -k_1{\displaystyle {\sum }_{j=1}^N{a}_{ij}{(x_i(t)-x_j(t))}^p}-k_2{\displaystyle {\sum }_{j=1}^N{a}_{ij}{(x_i(t)-x_j(t))}^q} \\ -k_3{\displaystyle {\sum }_{j=1}^N{a}_{ij}{(x_i(t)-x_j(t))}^{\eta }}-k_4{\displaystyle {\sum }_{j=1}^N{a}_{ij}\tanh (n(x_i(t)-x_j(t)))} \end{gathered}$$

(28)

For $\tanh (n(x_i(t)-x_j(t))$, $n\gg 1$, one has

$$\begin{gathered} |{\dot{e}}_i(t)|\le |{\displaystyle {\sum }_{j=1}^N{a}_{ij}{(k_{1}p(x_i(t)-x_j(t)))}^{p-1}+k_2}q{(x_i(t)-x_j(t))}^{q-1}+k_3\eta {(x_i(t)-x_j(t))}^{\eta -1}+k_{4}n(1-{\tanh }^2(n(x_i(t)-x_j(t)))) \\ \ast (u_i(t)+f(x_i(t),t)+d_i(x_i(t),t)-u_j(t)+f(x_j(t),t)+d_j(x_j(t),t))| \end{gathered}$$

(29)

Substitute Assumptions 1 and 2

$$\begin{gathered} |{\dot{e}}_i(t)|\le |{\displaystyle {\sum }_{j=1}^N{a}_{ij}{(k_{1}p(x_i(t)-x_j(t)))}^{p-1}+k_2}q{(x_i(t)-x_j(t))}^{q-1} \\ +k_3\eta {(x_i(t)-x_j(t))}^{\eta -1}+k_{4}n)\ast (|u_i(t)-u_j(t)|+k|x_i(t)-x_j(t){|}^{\eta }+2d) \end{gathered}$$

(30)

Substituting the state error and deflating:

$$\begin{gathered} |{\dot{e}}_i(t)|\le k_{1}pk{\displaystyle {\sum }_{j=1}^N{a}_{ij}|{\epsilon }_i(t)-}{\epsilon }_j(t){|}^{p+\eta -1}+k_{2}qk{\displaystyle {\sum }_{j=1}^N{a}_{ij}|{\epsilon }_i(t)-}{\epsilon }_j(t){|}^{q+\eta -1} \\ +k_3\eta k{\displaystyle {\sum }_{j=1}^N{a}_{ij}|{\epsilon }_i(t)-}{\epsilon }_j(t){|}^{2\eta -1}+k_{4}nk{\displaystyle {\sum }_{j=1}^N{a}_{ij}|{\epsilon }_i(t)-}{\epsilon }_j(t){|}^{\eta } \\ +{\displaystyle {\sum }_{j=1}^N{a}_{ij}(k_{1}p|{\epsilon }_i(t)-}{\epsilon }_j(t){|}^{p-1}+k_{2}q|{\epsilon }_i(t)-{\epsilon }_j(t){|}^{q-1} \\ +k_3\eta |{\epsilon }_i(t)-{\epsilon }_j(t){|}^{\eta -1})\ast (|u_i(t)-u_j(t)|+2d) \end{gathered}$$

(31)

According to Lemma 1,

$$\begin{gathered} |{\dot{e}}_i(t)|\le k_{1}pk{(4{\lambda }_N(L_{2/p+\eta -1})V(0))}^{\frac{p+\eta -1}{2}}+k_{2}qk{(4{\lambda }_N(L_{2/q+\eta -1})V(0))}^{\frac{q+\eta -1}{2}} \\ +k_3\eta k{(4{\lambda }_N(L_{2/2\eta -1})V(0))}^{\frac{2\eta -1}{2}}+k{k}_{4}n{(4{\lambda }_N(L_{2/\eta })V(0))}^{\frac{\eta }{2}} \\ +[k_{1}p{(4{\lambda }_N(L_{2/p-1})V(0))}^{\frac{p-1}{2}}+k_{2}q{(4{\lambda }_N(L_{2/p-1})V(0))}^{\frac{q-1}{2}} \\ +k_3\eta k{(4{\lambda }_N(L_{2/\eta -1})V(0))}^{\frac{\eta -1}{2}}]\ast (N|u_i(t_k^i)|+|{\displaystyle {\sum }_{j=1}^N{u}_j(t_{\overline{k}}^j})+2d) \end{gathered}$$

(32)

The Equation (32) can be written as the sum of two functions on $t_k^i$, $t_{\overline{k}}^j$.

$$|{\dot{e}}_i(t)|\le l_1(t_k^i)+l_2(t_{\overline{k}}^j)$$

(33)

It is also clear from the event-triggering mechanism that the following equation holds:

$$e_i(t_k^i)=0$$

(34)

By the integral inequalities, one has

$$\begin{gathered} |e_i(t)|\le {\displaystyle {\int }_{t_k^i}^t|{\dot{e}}_i(t)|du\le }{\displaystyle {\int }_{t_k^i}^t(l_1(t_k^i)+l_2(t_{\overline{k}}^j))du} \\ |e_i(t_{k+1}^i)|\le {\displaystyle {\int }_{t_k^i}^{t_{k+1}^i}(l_1(t_k^i)+l_2(t_{\overline{k}}^j))du\le }{\displaystyle {\int }_{t_k^i}^{t_{k+1}^i}(l_1^{*}+l_2^{*})du} \end{gathered}$$

(35)

where $l_1^{*}=\max \left\{l_1(t_0^i),l_2(t_1^i),\cdots \right\},l_2^{*}=\max \left\{l_1(t_0^j),l_2(t_1^j),\cdots \right\}$.

The inter-event interval is

$$t_{k+1}^i-t_k^i\ge \frac{m{k}_4}{l_1^{*}+l_2^{*}}>0$$

(36)

The multi-agent systems under the control protocol (7) have a positive lower bound on the event-triggered interval. □

4. Numerical Examples

In this section, numerical simulation examples and comparative experiments are used to verify the effectiveness of the proposed solution. It is assumed that the multi-agent systems consist of five agents with the following dynamics models described by

$${\dot{x}}_i(t)=u_i(t)+f(x_i(t),t)+d_i(x_i(t),t)$$

(37)

The control input for the multi-agent systems is (7).

$$\begin{gathered} u_i(t)=-k_1{\displaystyle {\sum }_{j=1}^N{a}_{ij}{(x_i(t_k^i)-x_j(t_k^i))}^p}-k_2{\displaystyle {\sum }_{j=1}^N{a}_{ij}{(x_i(t_k^i)-x_j(t_k^i))}^q} \\ -k_3{\displaystyle {\sum }_{j=1}^N{a}_{ij}{(x_i(t_k^i)-x_j(t_k^i))}^{\eta }}-k_4{\displaystyle {\sum }_{j=1}^N{a}_{ij}sign(x_i(t_k^i)-x_j(t_k^i))} \end{gathered}$$

The interaction topology is represented by the following undirected graph shown in Figure 1. Furthermore, suppose the five agents in Figure 1 represent five smart car robots or aircraft. The collaboration between them is shown in the figure.

From the graph, we can obtain the adjacency matrix and the Laplacian matrix:

$$A=\left[\begin{array}{ccccc}0& 1& 0& 0& 1\\ 1& 0& 1& 0& 1\\ 0& 1& 0& 1& 0\\ 0& 0& 1& 0& 1\\ 1& 1& 0& 1& 0\end{array}\right]$$

$$L=D-A=\left[\begin{array}{ccccc}2& -1& 0& 0& -1\\ -1& 3& -1& 0& -1\\ 0& -1& 2& -1& 0\\ 0& 0& -1& 2& -1\\ -1& -1& 0& -1& 3\end{array}\right]$$

Let $f(x_i(t),t)=0.3x_i(t)+0.5\cos (t),$ $d_i(x_i(t),t)=$$0.5\cos (x_i(t))$, choose the initial conditions of the multi-agent systems. Additionally, the goal of setting two different initial states is to verify that the control protocol presented in this article is not affected by the initial state.

$$x_1(0)={[-4,-1,0,1,3]}^T$$

$$x_2(0)={[-400,-100,0,100,300]}^T$$

The Laplacian matrix $L$ satisfy Lemma 1 and the second smallest eigenvalue ${\lambda }_2=2$. When the system is in a small initial condition, the values of the parameters of the fixed-time control protocol are $\eta =1, p=0.6, q=1.4$, $k_1=0.5,$$k_2=0.6, k_3=1.5, k_4=1.5. m=0.3, \gamma =2.5$ which satisfy the conditions. The simulation results for the proposed non-linear control protocol are shown in Figure 2.

The parameters are substituted into the expression for estimating the upper bound on the convergence time of the system; the time to converge $T$ satisfies that $T\le T_{\max }=2.12 s$ when the system is in a big initial condition The simulation results for the proposed non-linear control protocol are shown in Figure 3.

A comparison of Figure 2 with Figure 3 shows that the convergence time of the system is not affected by the initial state of the intelligence in the system under the action of the control protocol proposed in this paper.

It is assumed that the multi-agent systems consist of five agents with the following dynamics models described by

$${\dot{x}}_i(t)=u_i(t)+f(x_i(t),t)$$

(38)

where $i=1,2,\cdots ,N$, $d_i(x_i(t),t)=0$; the interaction topology is represented by the following undirected graph shown in Figure 1. In [24], consider the following control protocol:

$$\begin{gathered} u_i(t)=-k_1({\displaystyle {\sum }_{j=1}^N{a}_{ij}(x_i(t_k^i)-x_j(t_k^i)){)}^p}-k_2({\displaystyle {\sum }_{j=1}^N{a}_{ij}(x_i(t_k^i)-x_j(t_k^i)){)}^q} \\ -k_3({\displaystyle {\sum }_{j=1}^N{a}_{ij}(x_i(t_k^i)-x_j(t_k^i)))} \end{gathered}$$

(39)

Let $f(x_i(t),t)=0.3x_i(t)+0.5\cos (t),$ and the values of the parameters of the fixed-time control protocol be $p=0.5, q=1.5$, $k_1=0.5,$ $k_2=0.6, k_3=1.5$,

$$T\le T_{1\max }=\frac{1}{k_1{2}^{\frac{p-1}{2}}{{\lambda }_2}^{\frac{p+1}{2}}(1-p)}+\frac{1}{k_3{2}^{\frac{q-1}{2}}{{\lambda }_2}^{\frac{q+1}{2}}{N}^{\frac{1-q}{2}}(q-1)}$$

(40)

The theoretical estimates $T\le T_{1\max }=7.04 s$ and the simulation results for the proposed non-linear control protocol are shown in Figure 4. Control inputs of the agents are shown in Figure 5.

The simulation results for the proposed non-linear control protocol (7) are presented in Figure 5. The values of the parameters of the fixed-time control protocol are $p=0.5, q=1.5,$ $k_1=0.5, k_2=0.6$, and $k_3=1.5$; from the analysis of Theorem 1, the time to converge $T$ satisfies that

$$T\le T_{\max }=\frac{\pi \gamma }{\sqrt{\overline{\alpha }\overline{\beta }}}$$

(41)

The theoretical estimates $T\le T_{1\max }=1.52 s$ and the simulation results for the proposed non-linear control protocol are shown in Figure 6. Control inputs of the agents are shown in Figure 7.

A comparison of Figure 5 with Figure 7 shows that the event-triggered fixed-time consensus protocol (7), where the controller updates only at its event time, updates in Figure 7. Figure 5, where the controller achieves synchronous updates, has a higher number of controller updates compared to Figure 7. Figure 8 shows the event-triggered interval of the five agents in the systems under the control protocol proposed in this paper. The agents are triggered at their respective event times to update the control inputs under this scheme to reduce the resource consumption of the system and the number of updates to the system controller. The event-trigger interval under protocol (37) is shown in Figure 9.

Comparing Figure 8 with Figure 9 shows that the event-triggered fixed-time consensus control protocol (7) can reduce the frequency of system controller updates and save the system’s energy.

Figure 5, Figure 7, Figure 8 and Figure 9 show that the event-triggered protocol reduces updates, and a numerical analysis of how significant this reduction is shown in

Table 1. A summary table comparing the number of updates.

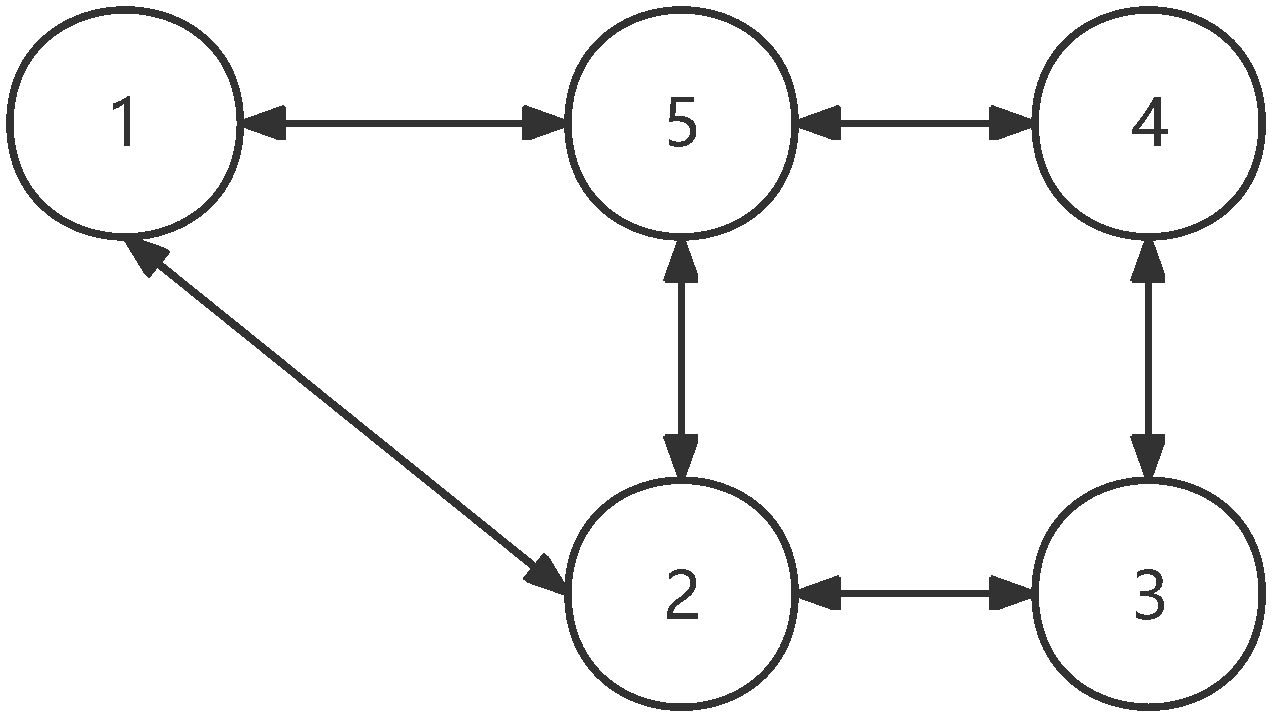
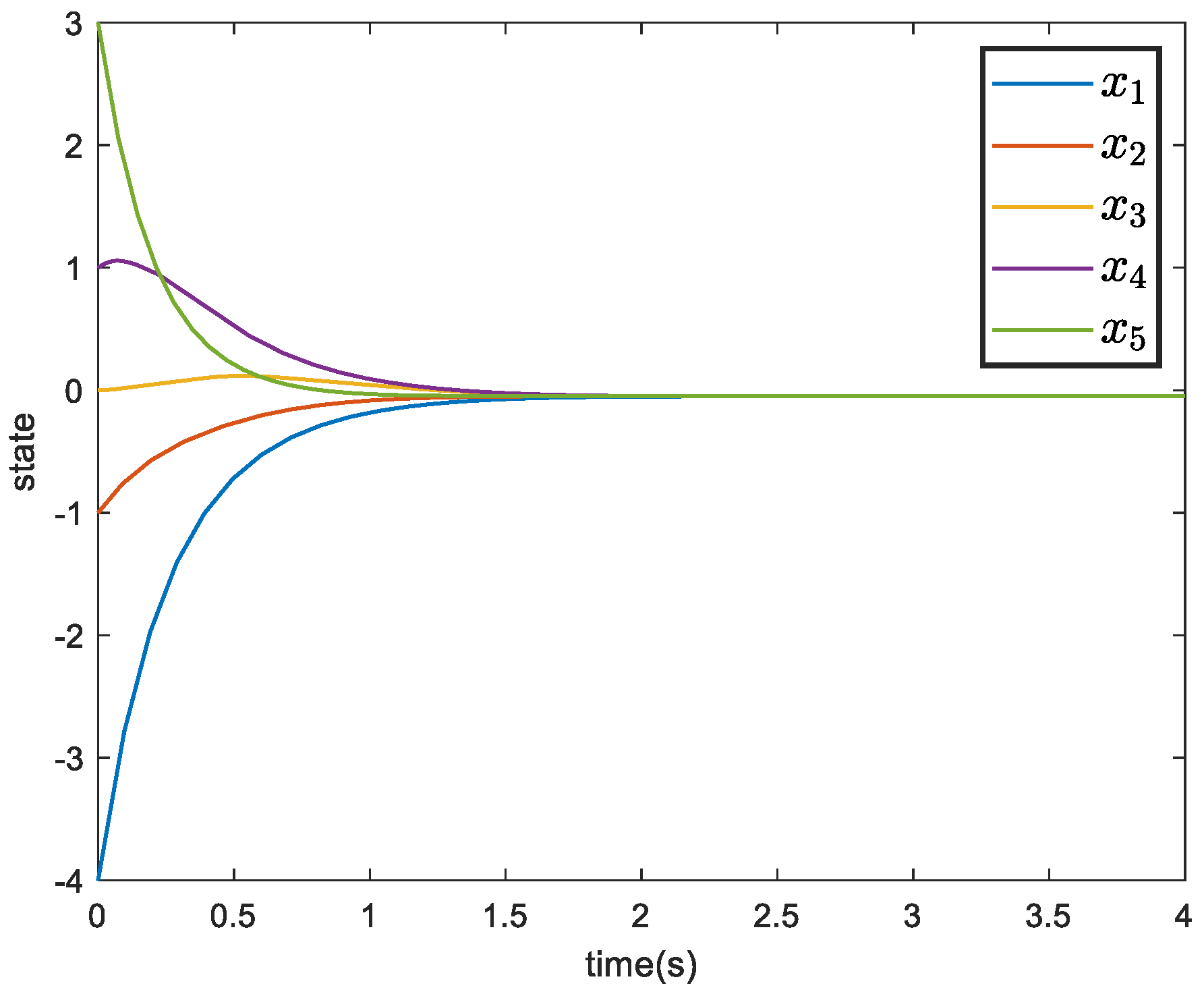
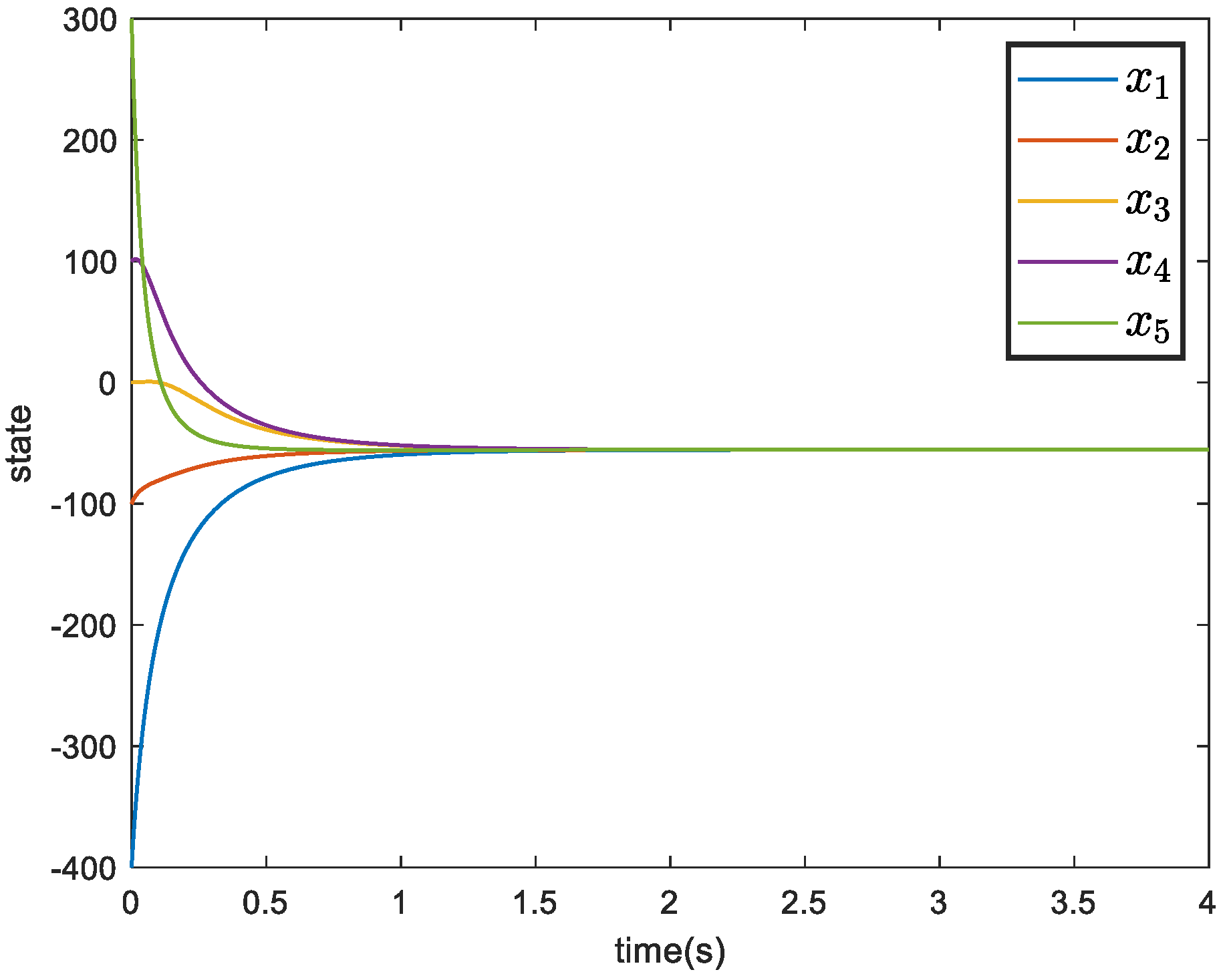
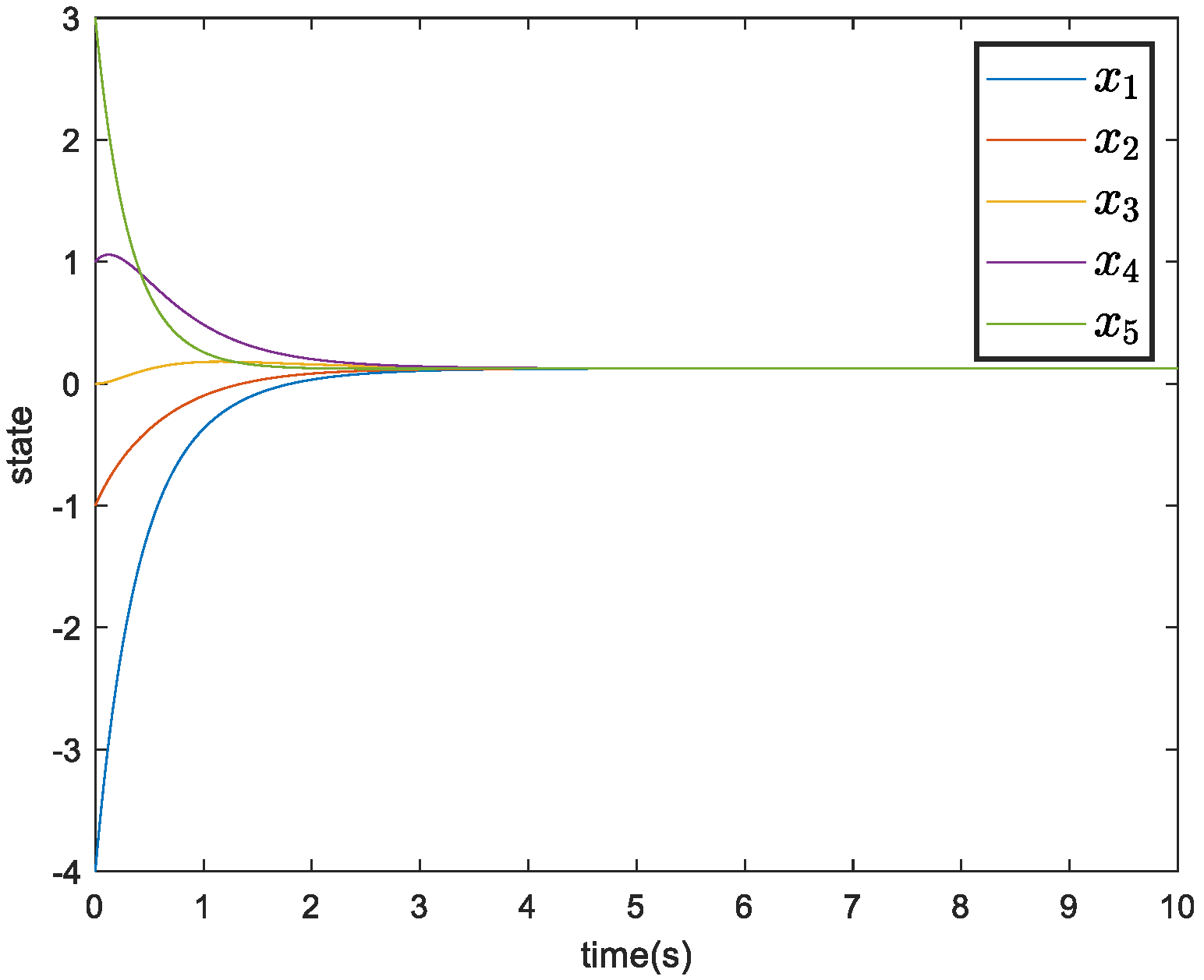
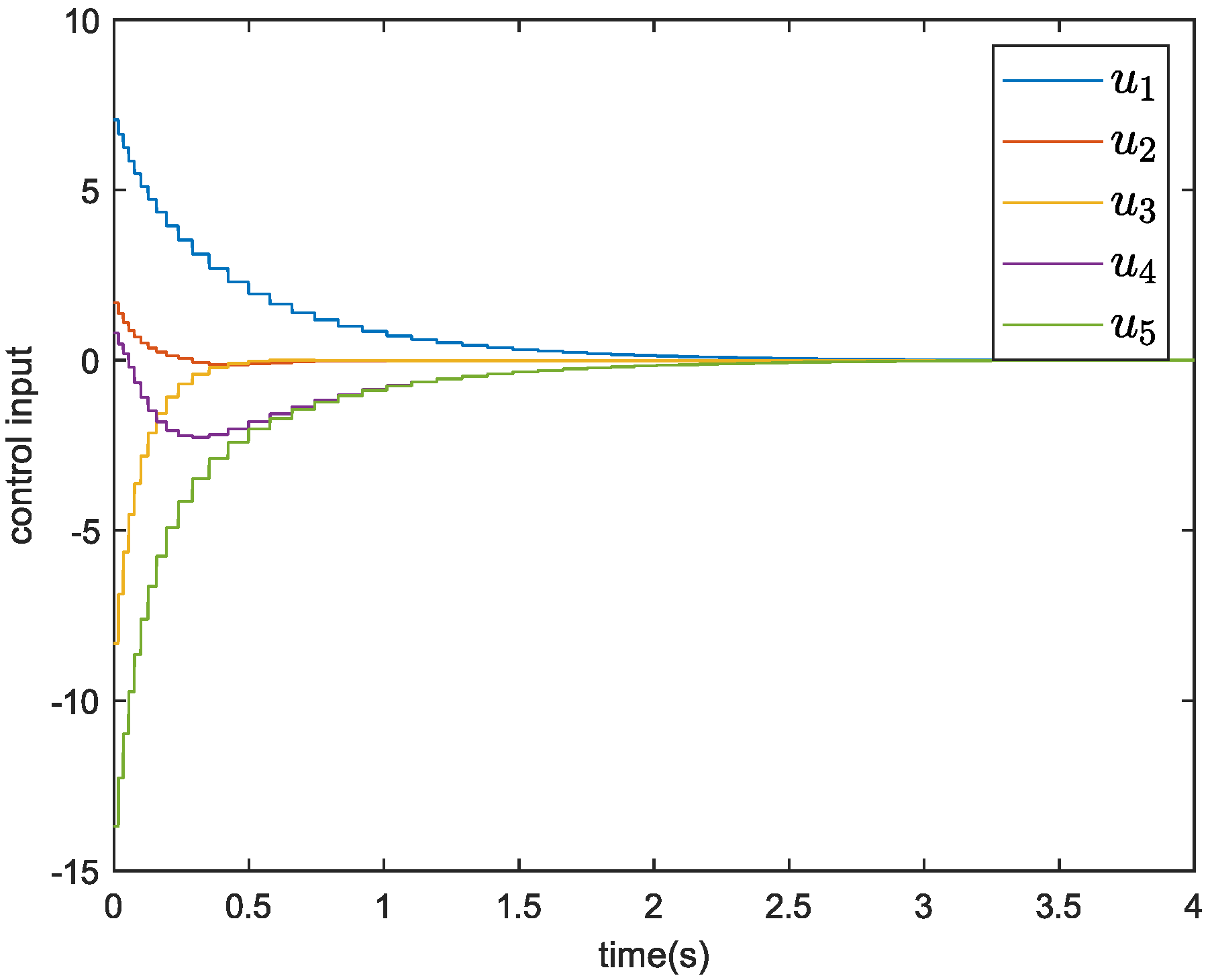
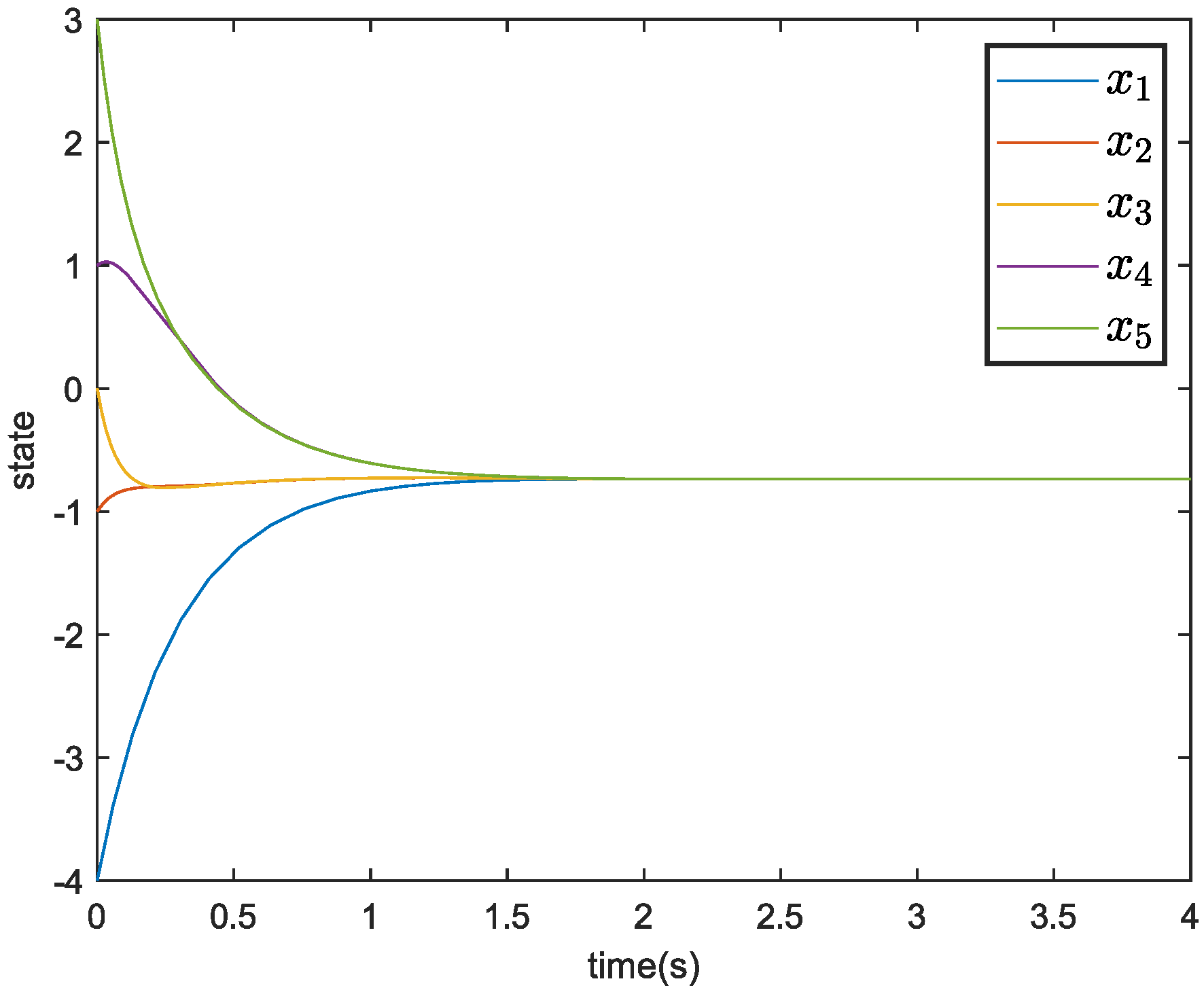
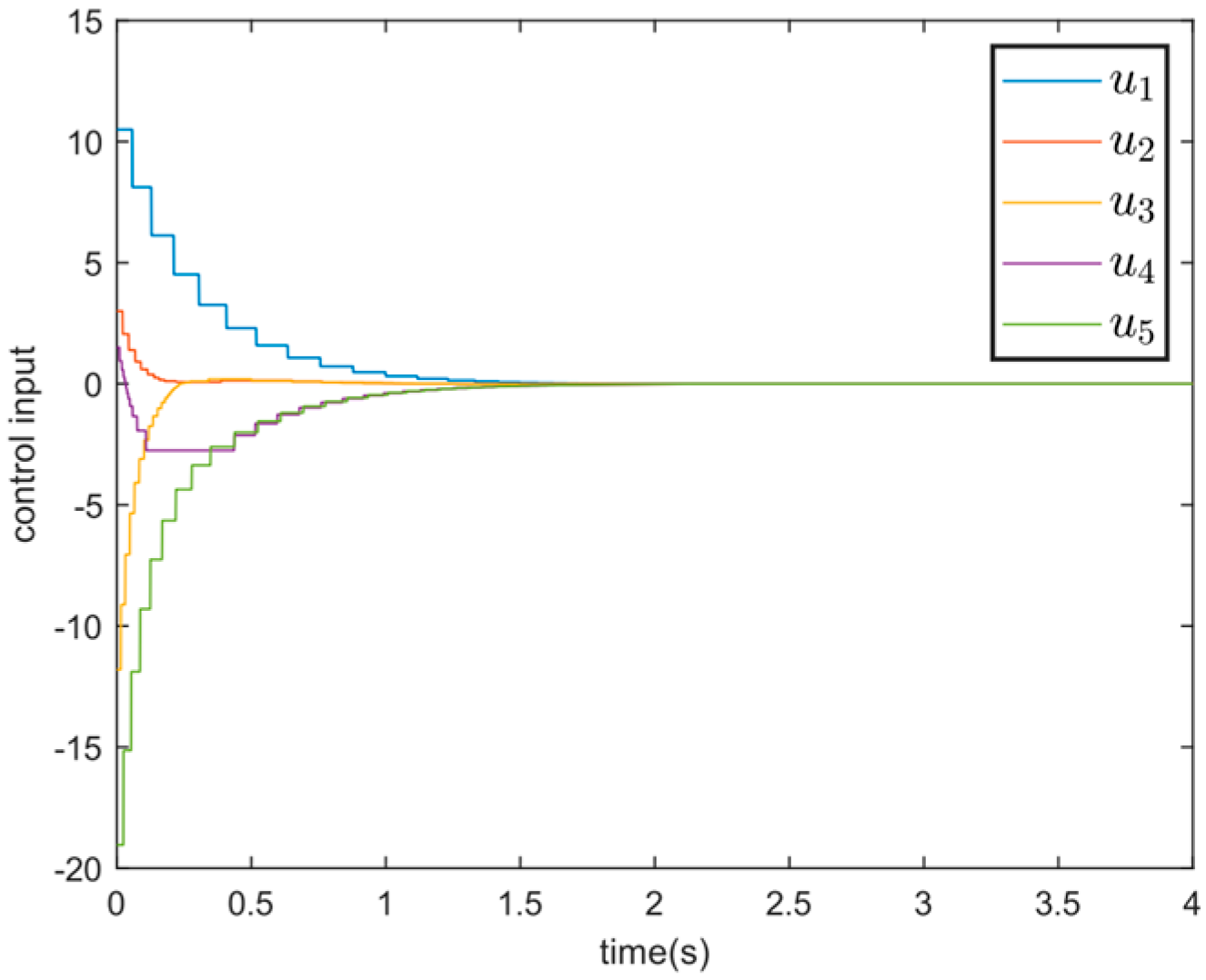
	Theoretical Convergence Time	Simulation Convergence Time
Figure 5—under control protocol (39)	$\le$7.04 s	$\approx$3.30 s
Figure 7—under control protocol (7)	$\le$1.52 s	$\approx$1.53 s
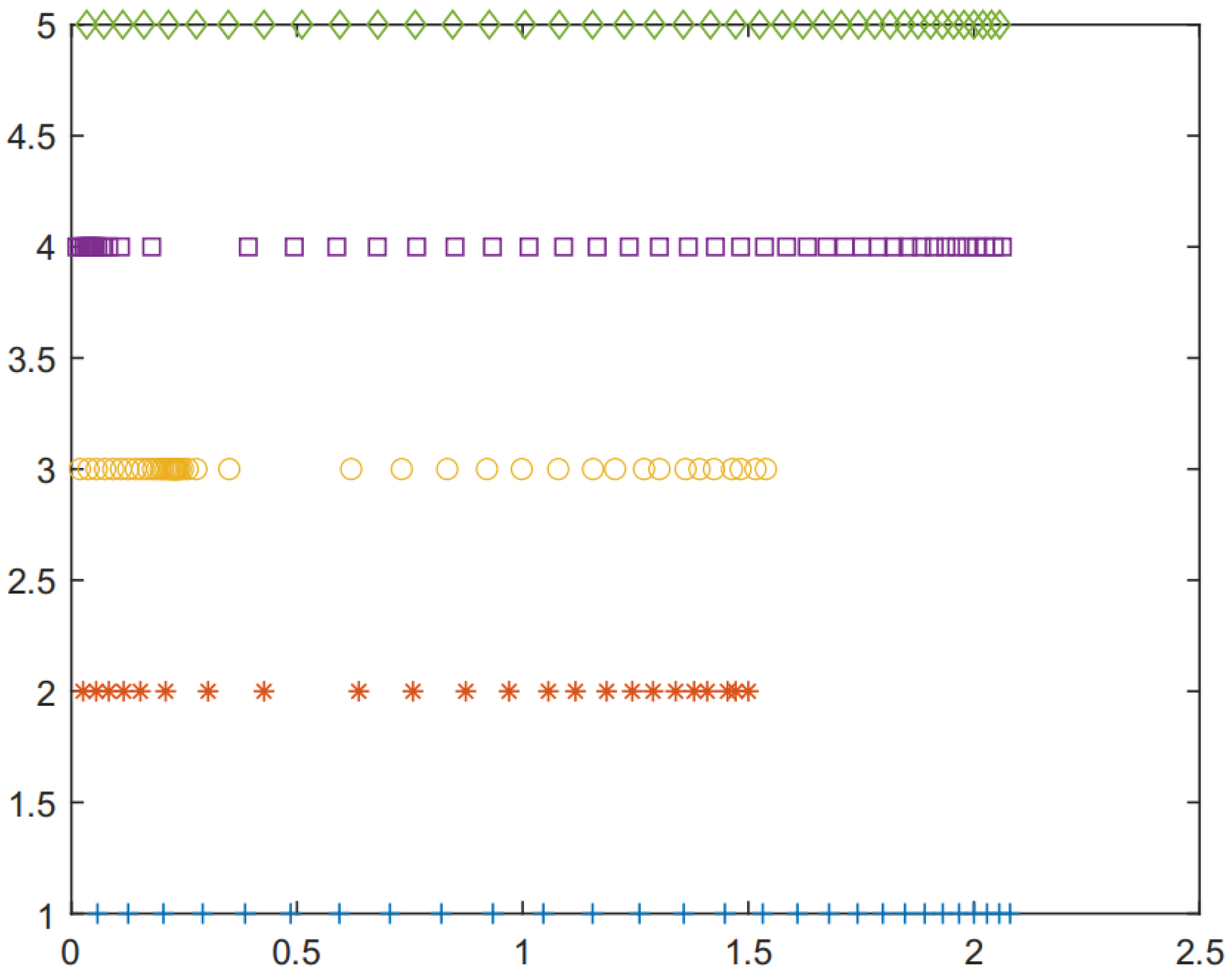
	Agent	the number of updates
Figure 8—under control protocol (7)	Agent 1	28
	Agent 2	23
	Agent 3	34
	Agent 4	51
	Agent 5	39
Figure 9—under control protocol (39)	Agent 1	number of iterations $\gg$ 51
	Agent 2	number of iterations $\gg$ 51
	Agent 3	number of iterations $\gg$ 51
	Agent 4	number of iterations $\gg$ 51
	Agent 5	number of iterations $\gg$ 51

. In short, from the results outlined above, we can determine that the simulation results show that the proposed control protocol has the advantages of both event-triggered and fixed-time convergence, the convergence time of the new control protocol is greatly reduced (about 1.5 s), and the update times are also greatly reduced (less than 50 times), which is consistent with the theoretical results.

5. Conclusions

For disturbed and non-linear dynamics, in this paper, the main contribution is the proposal of a fixed-time event-triggered consensus method protocol that can shorten the time to reach conformance and reduce the update times of the control protocol. Compared with the consensus protocol in Equation (39), the proposed protocol in this paper can reduce the frequency of system controller updates and obtain a more accurate estimate of the upper bound of the convergence time. Finally, examples are presented to show the effectiveness of the control protocol. It has a fast convergence time and does not need to control updates frequently. Therefore, this has potential applications in UAV formation, smart car collaboration, and factory smart robot collaboration. Furthermore, many existing AI models adopt progressive convergence and non-event triggering, so if the consistency control strategy of fixed-time event triggering can be applied to existing AI models, replacing the progressive convergence and non-event-triggering strategies would greatly improve AI performance.

However, this paper does not consider the problem of transmission delay between sensor nodes, the network attacks on nodes, or the problem of limited transmission. The transmission delay will cause the information interaction between each node and the neighbor node to be inappropriately timed. Failure to interact with real-time information can result in poor consistency performance. These questions are also the focus of follow-up research.