Performance Analysis for Predictive Voltage Stability Monitoring Using Enhanced Adaptive Neuro-Fuzzy Expert System
Abstract
1. Introduction
Review of Machine Learning Applications for Voltage Stability Analysis
2. Models and Methods
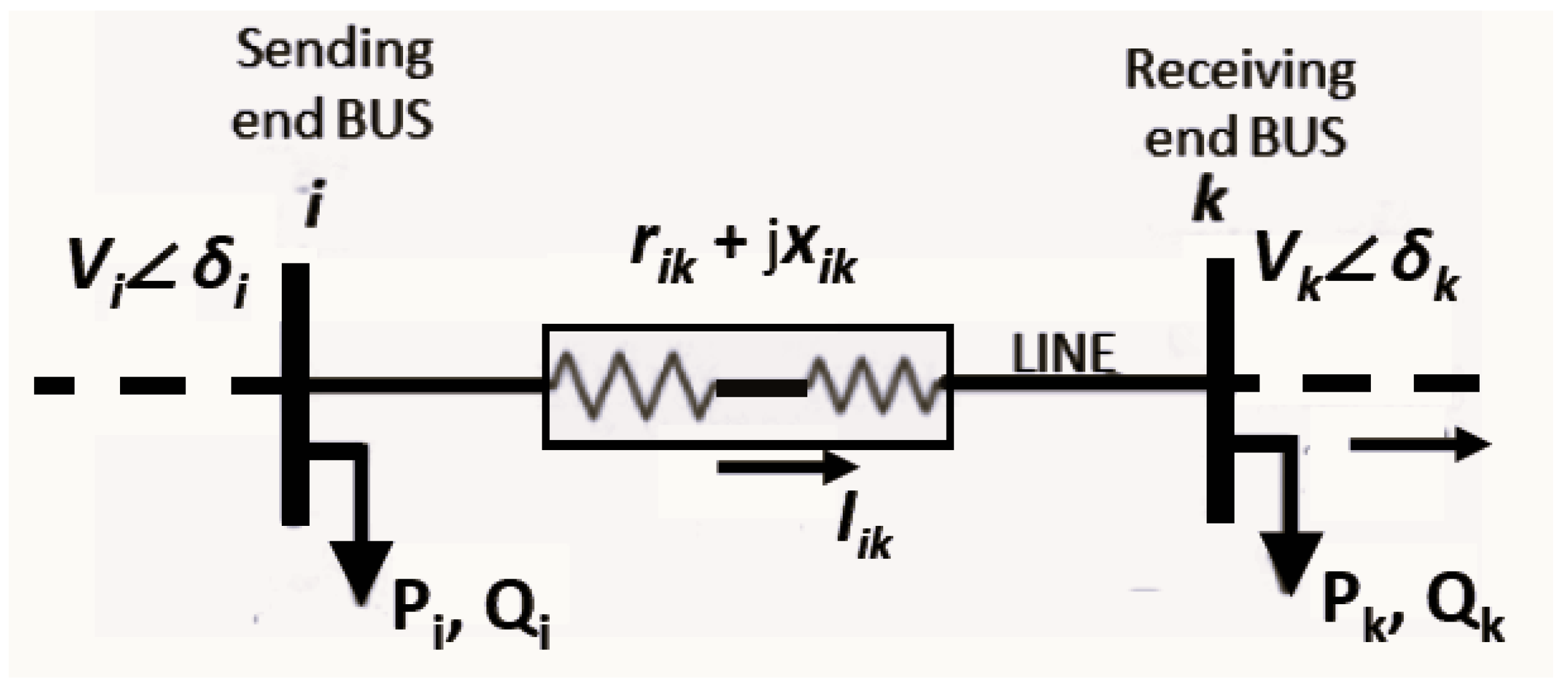
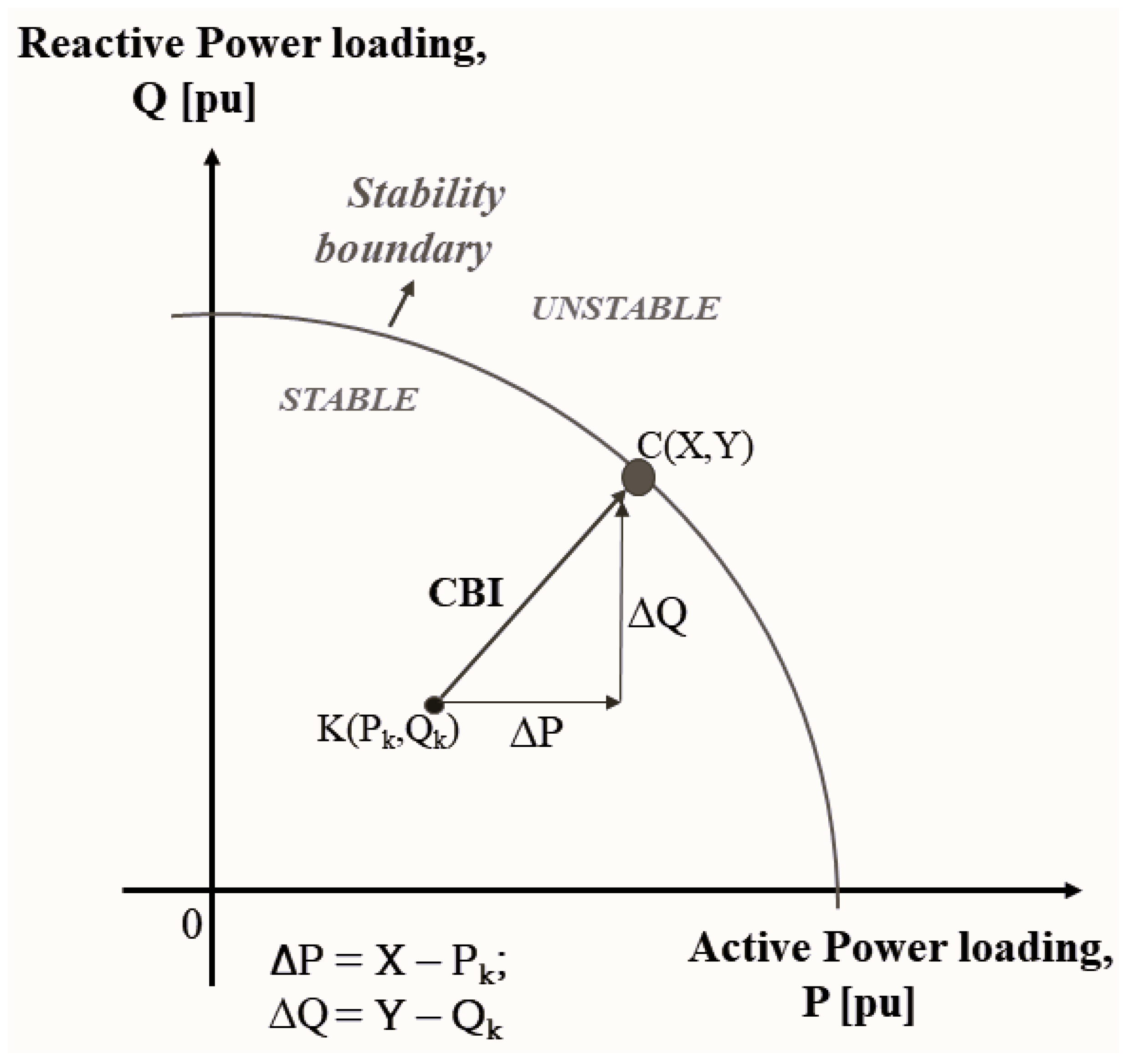
2.1. Derivation of Voltage Stability Indices
2.2. Implementing ANFIS for Voltage Stability Monitoring
- Layer 1—In the fuzzification layer, square adaptive nodes have fuzzy membership functions represented by specific inference rules:
- Layer 2 —The multiplication/product layer processes fuzzification layer input values based on membership function strength and the pre-specified product rule. This layer’s fixed and non-adaptive nodes multiply input values to determine each node’s output (fuzzy rule firing strength):
- Layer 3—This layer normalizes the projected firing strengths from rule 2 by comparing each rule’s firing strength to all the rules’ overall firing strengths. The nodes are fixed and non-adaptive, and the k-th rule’s normalized firing strength is as follows:
- Layer 4—the adaptive nodes in this layer decode the normalized firing strengths from layer three based on layer two’s inference rules. Finding the product of the normalized firing strengths yields a first-order polynomial function that shows the model’s output as a result of the third layer’s k-th rule and based on the consequent parameters, as described:
- Layer 5—The last layer has one non-adaptive summation node. This node sums the output values from layer 4 to obtain the final output, and all fuzzy categorizations of results are then converted to concrete/interpretable values.
2.2.1. Data Preparation
2.2.2. Performance Metrics
- Percentage Relative Root Mean Square Error (): Comparing quantities of different ranges, units, and magnitudes is more objective using the relative root mean square error (RRMSE). RRMSE is calculated by dividing RMSE with the average value of the measured data, i.e., the estimated VSI values from load flow analysis [48]. Thus, the percentage RRMSE is calculated as follows:The benefit of using for validating model accuracy is the standardized scale of performance interpretations as specified: ’Excellent’ when ≤ 10%, ’Good’ if 10% ≤ ≤ 20%, ’Fair’ if 20% ≤ ≤ 30%, and ’Poor’ if ≥ 30%.
- Mean Percentage Absolute Error (): This is also known as the mean absolute percentage error or the mean absolute percentage deviation. It is one of the primary, simple, yet objective measures for prediction accuracy in the cross-correlated data system. Performance accuracy is measured as a percent of the actual value for easy understanding [49]. For effective model performance, the value of this metric should be close to zero percent.
- Coefficient of correlation (R): The strength of the relationship between the input variables and the expected output is often measured using the correlation coefficients. The standard coefficient of correlation metric is Pearson’s correlation, R, used for linear regression analysis. A value of R sufficiently close to 1.0 shows that the selected input information significantly influences the values of the desired output.
3. Simulation
3.1. Conditions and Assumptions
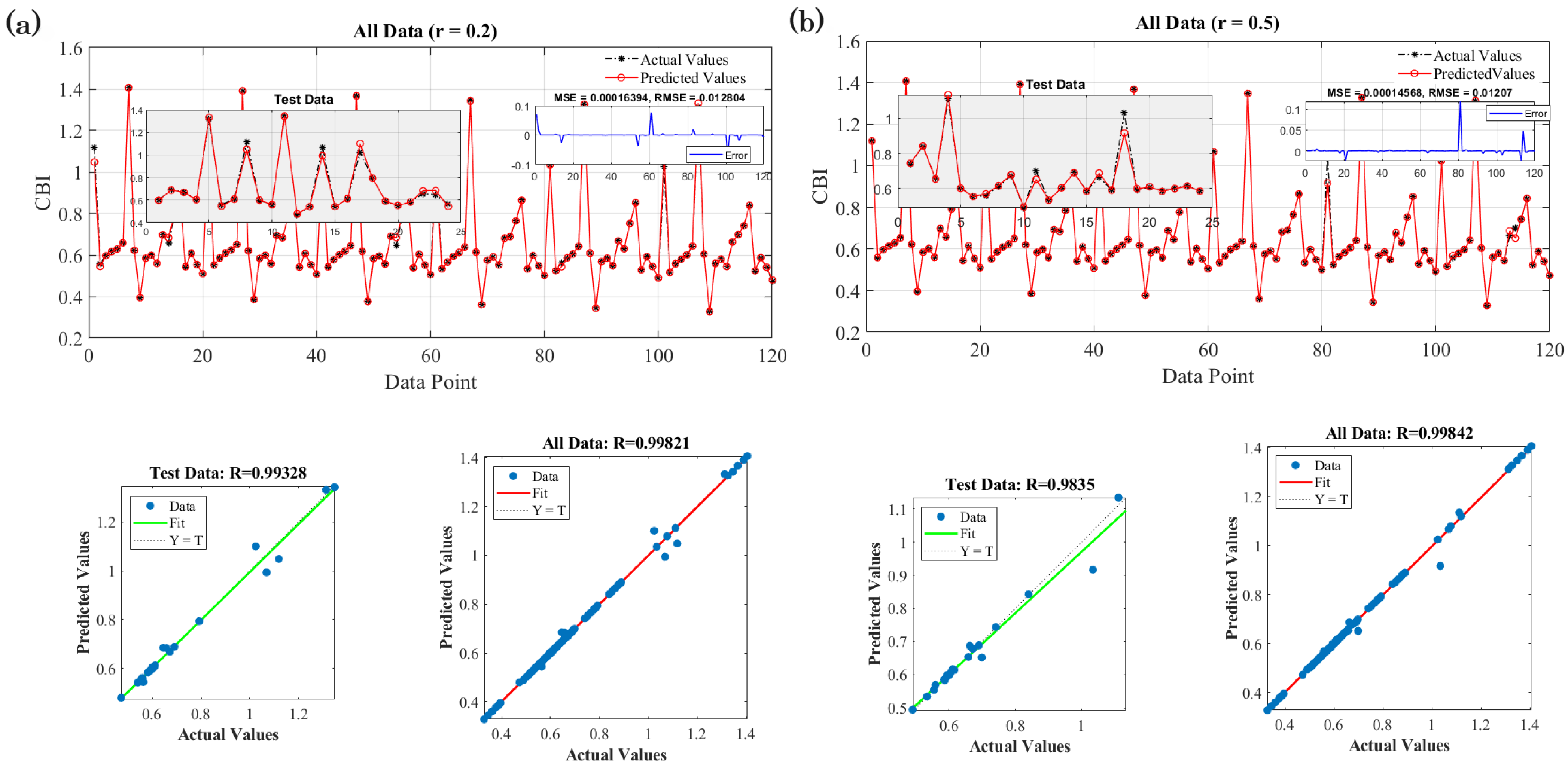
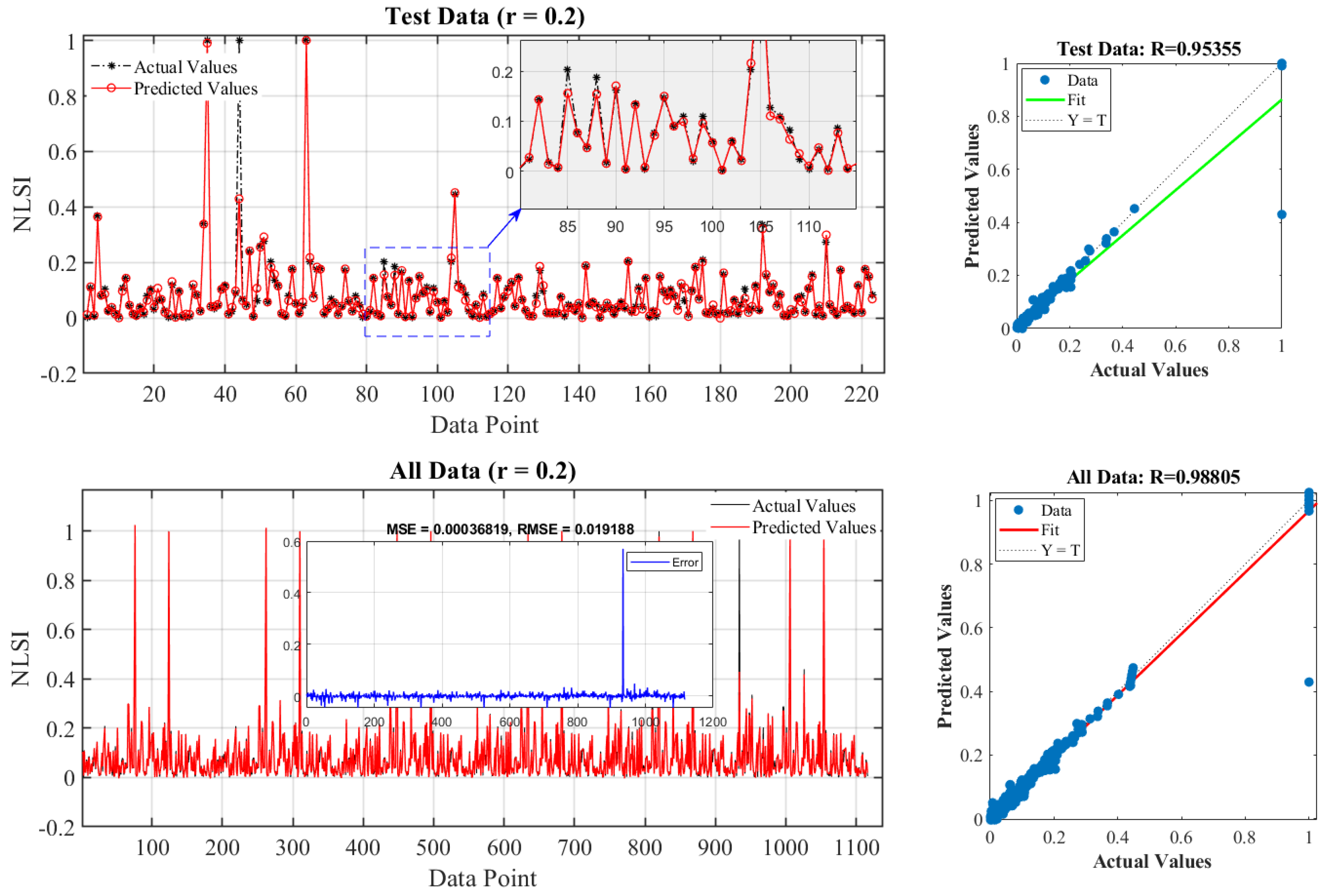
3.2. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Krishnamurthy, S.; Mohlwini, E.X. Voltage stability index method for optimal placement of capacitor banks in a radial network using real-time digital simulator. In Proceedings of the 2016 International Conference on the Domestic Use of Energy (DUE), Cape Town, South Africa, 30–31 March 2016; pp. 1–8. [Google Scholar]
- Adewuyi, O.B.; Howlader, H.O.R.; Olaniyi, I.O.; Konneh, D.A.; Senjyu, T. Comparative analysis of a new VSC-optimal power flow formulation for power system security planning. Int. Trans. Electr. Energy Syst. 2020, 30, e12250. [Google Scholar] [CrossRef]
- Kumar, R.; Mittal, A.; Sharma, N.; Duggal, I.V.; Kumar, A. PV and QV curve analysis using series and shunt compensation. In Proceedings of the 2020 IEEE 9th Power India International Conference (PIICON), Sonepat, India, 28 February–1 March 2020; pp. 1–6. [Google Scholar]
- Danish, M.S.S.; Senjyu, T.; Danish, S.M.S.; Sabory, N.R.; Mandal, P. A recap of voltage stability indices in the past three decades. Energies 2019, 12, 1544. [Google Scholar] [CrossRef]
- Furukakoi, M.; Adewuyi, O.B.; Danish, M.S.S.; Howlader, A.M.; Senjyu, T.; Funabashi, T. Critical Boundary Index (CBI) based on active and reactive power deviations. Int. J. Electr. Power Energy Syst. 2018, 100, 50–57. [Google Scholar] [CrossRef]
- Sarker, I.H. Ai-based modeling: Techniques, applications and research issues towards automation, intelligent and smart systems. SN Comput. Sci. 2022, 3, 158. [Google Scholar] [CrossRef] [PubMed]
- Suliman, S.I.; Rahman, T.K.A. Artificial immune system based machine learning for voltage stability prediction in power system. In Proceedings of the 2010 4th International Power Engineering and Optimization Conference (PEOCO), Shah Alam, Malaysia, 23–24 June 2010; pp. 53–58. [Google Scholar] [CrossRef]
- El-Keib, A.; Ma, X. Application of artificial neural networks in voltage stability assessment. IEEE Trans. Power Syst. 1995, 10, 1890–1896. [Google Scholar] [CrossRef]
- Sharma, A.K.; Saxena, A.; Soni, B.P.; Gupta, V. Voltage stability assessment using artificial neural network. In Proceedings of the 2018 IEEMA Engineer Infinite Conference (eTechNxT), New Delhi, India, 13–14 March 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Rahi, O.; Yadav, A.K.; Malik, H.; Azeem, A.; Kr, B. Power system voltage stability assessment through artificial neural network. Procedia Eng. 2012, 30, 53–60. [Google Scholar] [CrossRef]
- Popović, D.; Kukolj, D.; Kulić, F. Monitoring and assessment of voltage stability margins using artificial neural networks with a reduced input set. IEEE Proc. Gener. Transm. Distrib. 1998, 145, 355–362. [Google Scholar] [CrossRef]
- Goh, H.; Chua, Q.; Lee, S.; Kok, B.; Goh, K.; Teo, K. Evaluation for voltage stability indices in power system using artificial neural network. Procedia Eng. 2015, 118, 1127–1136. [Google Scholar] [CrossRef]
- Nakawiro, W.; Erlich, I. Online voltage stability monitoring using artificial neural network. In Proceedings of the 2008 Third International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, Nanjing, China, 6–9 April 2008; pp. 941–947. [Google Scholar]
- Ashraf, S.M.; Gupta, A.; Choudhary, D.K.; Chakrabarti, S. Voltage stability monitoring of power systems using reduced network and artificial neural network. Int. J. Electr. Power Energy Syst. 2017, 87, 43–51. [Google Scholar] [CrossRef]
- Jayasankar, V.; Kamaraj, N.; Vanaja, N. Estimation of voltage stability index for power system employing artificial neural network technique and TCSC placement. Neurocomputing 2010, 73, 3005–3011. [Google Scholar] [CrossRef]
- Bahmanyar, A.; Karami, A. Power system voltage stability monitoring using artificial neural networks with a reduced set of inputs. Int. J. Electr. Power Energy Syst. 2014, 58, 246–256. [Google Scholar] [CrossRef]
- Singh, P.; Parida, S.; Chauhan, B.; Choudhary, N. Online Voltage Stability Assessment Using Artificial Neural Network considering Voltage stability indices. In Proceedings of the 2020 21st National Power Systems Conference (NPSC), Gandhinagar, India, 17–19 December 2020; pp. 1–5. [Google Scholar]
- Ibrahim, A.M.; El-Amary, N.H. Particle Swarm Optimization trained recurrent neural network for voltage instability prediction. J. Electr. Syst. Inf. Technol. 2018, 5, 216–228. [Google Scholar] [CrossRef]
- Rao, A.N.; Vijayapriya, P. A robust neural network model for monitoring online voltage stability. Int. J. Comput. Appl. 2019, 44, 1103–1112. [Google Scholar] [CrossRef]
- Adhikari, A.; Naetiladdanon, S.; Sagswang, A.; Gurung, S. Comparison of Voltage Stability Assessment using Different Machine Learning Algorithms. In Proceedings of the 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), Wuhan, China, 30 October–1 November 2020; pp. 2023–2026. [Google Scholar]
- Ashfaq, M. A Tribute to Father of Fuzzy Set Theory and Fuzzy Logic (Dr. Lotfi A. Zadeh). J. Swarm. Intel. Evol. Comput. 2018, 7, 2. [Google Scholar]
- Mendel, J.M. Type-2 fuzzy sets as well as computing with words. IEEE Comput. Intell. Mag. 2019, 14, 82–95. [Google Scholar] [CrossRef]
- Jang, J.S. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Rashed, B.M.; Popescu, N. Medical Image-Based Diagnosis Using a Hybrid Adaptive Neuro-Fuzzy Inferences System (ANFIS) Optimized by GA with a Deep Network Model for Features Extraction. Mathematics 2024, 12, 633. [Google Scholar] [CrossRef]
- Ljepava, N.; Jovanović, A.; Aleksić, A. Industrial Application of the ANFIS Algorithm—Customer Satisfaction Assessment in the Dairy Industry. Mathematics 2023, 11, 4221. [Google Scholar] [CrossRef]
- Bardhan, A.; Singh, R.K.; Ghani, S.; Konstantakatos, G.; Asteris, P.G. Modelling soil compaction parameters using an enhanced hybrid intelligence paradigm of ANFIS and improved grey wolf optimiser. Mathematics 2023, 11, 3064. [Google Scholar] [CrossRef]
- Nayak, N.; Das, S.R.; Panigrahi, T.K.; Das, H.; Nayak, S.R.; Singh, K.K.; Askar, S.; Abouhawwash, M. Overshoot Reduction Using Adaptive Neuro-Fuzzy Inference System for an Autonomous Underwater Vehicle. Mathematics 2023, 11, 1868. [Google Scholar] [CrossRef]
- Ramadan, A.; Kamel, S.; Hamdan, I.; Agwa, A.M. A novel intelligent ANFIS for the dynamic model of photovoltaic systems. Mathematics 2022, 10, 1286. [Google Scholar] [CrossRef]
- Modi, P.; Singh, S.P.; Sharma, J. Fuzzy neural network based voltage stability evaluation of power systems with SVC. Appl. Soft Comput. 2008, 8, 657–665. [Google Scholar] [CrossRef]
- Wu, H.; Dong, P.; Liu, M. Distribution network reconfiguration for loss reduction and voltage stability with random fuzzy uncertainties of renewable energy generation and load. IEEE Trans. Ind. Inform. 2018, 16, 5655–5666. [Google Scholar] [CrossRef]
- Rezaie, H.; Kazemi-Rahbar, M.H. Enhancing voltage stability and LVRT capability of a wind-integrated power system using a fuzzy-based SVC. Eng. Sci. Technol. Int. J. 2019, 22, 827–839. [Google Scholar] [CrossRef]
- Ghaghishpour, A.; Koochaki, A. An intelligent method for online voltage stability margin assessment using optimized ANFIS and associated rules technique. ISA Trans. 2020, 102, 91–104. [Google Scholar] [CrossRef]
- Amroune, M.; Musirin, I.; Bouktir, T.; Othman, M.M. The amalgamation of SVR and ANFIS models with synchronized phasor measurements for on-line voltage stability assessment. Energies 2017, 10, 1693. [Google Scholar] [CrossRef]
- Adewuyi, O.B.; Adeagbo, A.P.; Adebayo, I.G.; Howlader, H.O.R.; Sun, Y. Modified analytical approach for PV-DGs integration into a radial distribution network considering loss sensitivity and voltage stability. Energies 2021, 14, 7775. [Google Scholar] [CrossRef]
- Mohamed, A.; Jasmon, G.; Yusoff, S. A static voltage collapse indicator using line stability factors. J. Ind. Technol. 1989, 7, 73–85. [Google Scholar]
- Moghavvemi, M.; Omar, F. Technique for contingency monitoring and voltage collapse prediction. IEEE Proc. Gener. Transm. Distrib. 1998, 145, 634–640. [Google Scholar] [CrossRef]
- Musirin, I.; Rahman, T.A. Novel fast voltage stability index (FVSI) for voltage stability analysis in power transmission system. In Proceedings of the Student Conference on Research and Development, Shah Alam, Malaysia, 17 July 2002; pp. 265–268. [Google Scholar]
- Kanimozhi, R.; Selvi, K. A novel line stability index for voltage stability analysis and contingency ranking in power system using fuzzy based load flow. J. Electr. Eng. Technol. 2013, 8, 694–703. [Google Scholar] [CrossRef]
- Mokred, S.; Wang, Y.; Chen, T. Modern voltage stability index for prediction of voltage collapse and estimation of maximum load-ability for weak buses and critical lines identification. Int. J. Electr. Power Energy Syst. 2023, 145, 108596. [Google Scholar] [CrossRef]
- Yazdanpanah-Goharrizi, A.; Asghari, R. A novel line stability index (NLSI) for voltage stability assessment of power systems. In Proceedings of the 7th WSEAS International Conference on Power Systems, Beijing, China, 15–17 September 2007; pp. 164–167. [Google Scholar]
- Adedeji, P.A.; Akinlabi, S.A.; Madushele, N.; Olatunji, O.O. Hybrid neurofuzzy investigation of short-term variability of wind resource in site suitability analysis: A case study in South Africa. Neural Comput. Appl. 2021, 33, 13049–13074. [Google Scholar] [CrossRef]
- Singh, R.; Kainthola, A.; Singh, T. Estimation of elastic constant of rocks using an ANFIS approach. Appl. Soft Comput. 2012, 12, 40–45. [Google Scholar] [CrossRef]
- Adedeji, P.A.; Akinlabi, S.; Madushele, N.; Olatunji, O.O. Wind turbine power output very short-term forecast: A comparative study of data clustering techniques in a PSO-ANFIS model. J. Clean. Prod. 2020, 254, 120135. [Google Scholar] [CrossRef]
- Benmouiza, K.; Cheknane, A. Clustered ANFIS network using fuzzy c-means, subtractive clustering, and grid partitioning for hourly solar radiation forecasting. Theor. Appl. Climatol. 2019, 137, 31–43. [Google Scholar] [CrossRef]
- Adeleke, O.; Akinlabi, S.A.; Jen, T.C.; Dunmade, I. Prediction of municipal solid waste generation: An investigation of the effect of clustering techniques and parameters on ANFIS model performance. Environ. Technol. 2022, 43, 1634–1647. [Google Scholar] [CrossRef]
- Sarkar, J.; Prottoy, Z.H.; Bari, M.T.; Al Faruque, M.A. Comparison of ANFIS and ANN modeling for predicting the water absorption behavior of polyurethane treated polyester fabric. Heliyon 2021, 7, e08000. [Google Scholar] [CrossRef]
- Adewuyi, O.B.; Krishnarmurthy, S. Performance Assessment of Steady-State Voltage Stability Indices for Parameter Validation Using ANFIS. In Proceedings of the 2023 10th International Conference on Power and Energy Systems Engineering (CPESE), Nagoya, Japan, 8–10 September 2023; pp. 129–134. [Google Scholar]
- Despotovic, M.; Nedic, V.; Despotovic, D.; Cvetanovic, S. Evaluation of empirical models for predicting monthly mean horizontal diffuse solar radiation. Renew. Sustain. Energy Rev. 2016, 56, 246–260. [Google Scholar] [CrossRef]
- Chou, J.S.; Ngo, N.T.; Chong, W.K. The use of artificial intelligence combiners for modeling steel pitting risk and corrosion rate. Eng. Appl. Artif. Intell. 2017, 65, 471–483. [Google Scholar] [CrossRef]
- Pena, I.; Martinez-Anido, C.B.; Hodge, B.M. An extended IEEE 118-bus test system with high renewable penetration. IEEE Trans. Power Syst. 2017, 33, 281–289. [Google Scholar] [CrossRef]



| Load Levels | Input Data | Output Data | |||||
|---|---|---|---|---|---|---|---|
| VSI | |||||||
| Base | ⋮× | ||||||
| Base + ( × Base) | |||||||
| Base + 2 ( × Base) | |||||||
| Base + 3 ( × Base) | |||||||
| Base + 4 ( × Base) | |||||||
| Base + 5 ( × Base) | |||||||
| Data size | (6 ) by 7 | ||||||
| Test Systems | ||||
|---|---|---|---|---|
| IEEE 14 | 20 | 120 | 102 | 18 |
| IEEE 118 | 186 | 1116 | 949 | 167 |
| Parameter | Value |
|---|---|
| Primary step size | 0.01 |
| Decline rate of step size | 0.90 |
| Increment rate of step size | 1.10 |
| Cluster radius, r | 0.2, 0.5 (IEEE 14); 0.2 (IEEE 118) |
| Epochs | 200 (IEEE 14); 1500 (IEEE 118) |
| Run | NLSI | CBI | ||
|---|---|---|---|---|
| Test | All | Test | All | |
| 1 | 0.71725 | 0.85194 | 0.99847 | 0.99936 |
| 2 | 0.48290 | 0.69972 | 0.99849 | 0.99964 |
| 3 | 0.03234 | 0.81707 | 0.99685 | 0.99910 |
| 4 | −0.06015 | 0.92002 | 0.86164 | 0.99190 |
| 5 | −0.44144 | 0.83160 | 0.99769 | 0.99945 |
| 6 | 0.14935 | 0.83190 | 0.99918 | 0.99967 |
| 7 | −0.19599 | 0.75219 | 0.99214 | 0.99638 |
| 8 | 0.51961 | 0.85642 | 0.99328 | 0.99821 |
| r | VSI | IEEE 14 | IEEE 118 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | RRMSEp (%) | MAPE (%) | R | RMSE | RRMSEp (%) | MAPE (%) | R | ||
| 0.2 | NLSI | 0.03051 | 25.029 | 3.150 | 0.8564 | 0.01919 | 22.286 | 31.255 | 0.9881 |
| CBI | 0.01280 | 1.930 | 0.361 | 0.9982 | 0.00692 | 1.248 | 1.749 | 0.9980 | |
| 0.5 | NLSI | 0.05208 | 42.724 | 8.746 | 0.7702 | ||||
| CBI | 0.01207 | 1.819 | 0.306 | 0.9984 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adewuyi, O.B.; Krishnamurthy, S. Performance Analysis for Predictive Voltage Stability Monitoring Using Enhanced Adaptive Neuro-Fuzzy Expert System. Mathematics 2024, 12, 3008. https://doi.org/10.3390/math12193008
Adewuyi OB, Krishnamurthy S. Performance Analysis for Predictive Voltage Stability Monitoring Using Enhanced Adaptive Neuro-Fuzzy Expert System. Mathematics. 2024; 12(19):3008. https://doi.org/10.3390/math12193008
Chicago/Turabian StyleAdewuyi, Oludamilare Bode, and Senthil Krishnamurthy. 2024. "Performance Analysis for Predictive Voltage Stability Monitoring Using Enhanced Adaptive Neuro-Fuzzy Expert System" Mathematics 12, no. 19: 3008. https://doi.org/10.3390/math12193008
APA StyleAdewuyi, O. B., & Krishnamurthy, S. (2024). Performance Analysis for Predictive Voltage Stability Monitoring Using Enhanced Adaptive Neuro-Fuzzy Expert System. Mathematics, 12(19), 3008. https://doi.org/10.3390/math12193008







