Finite-Time Asynchronous H∞ Control for Non-Homogeneous Hidden Semi-Markov Jump Systems
Abstract
:1. Introduction
2. Materials and Methods
3. Results
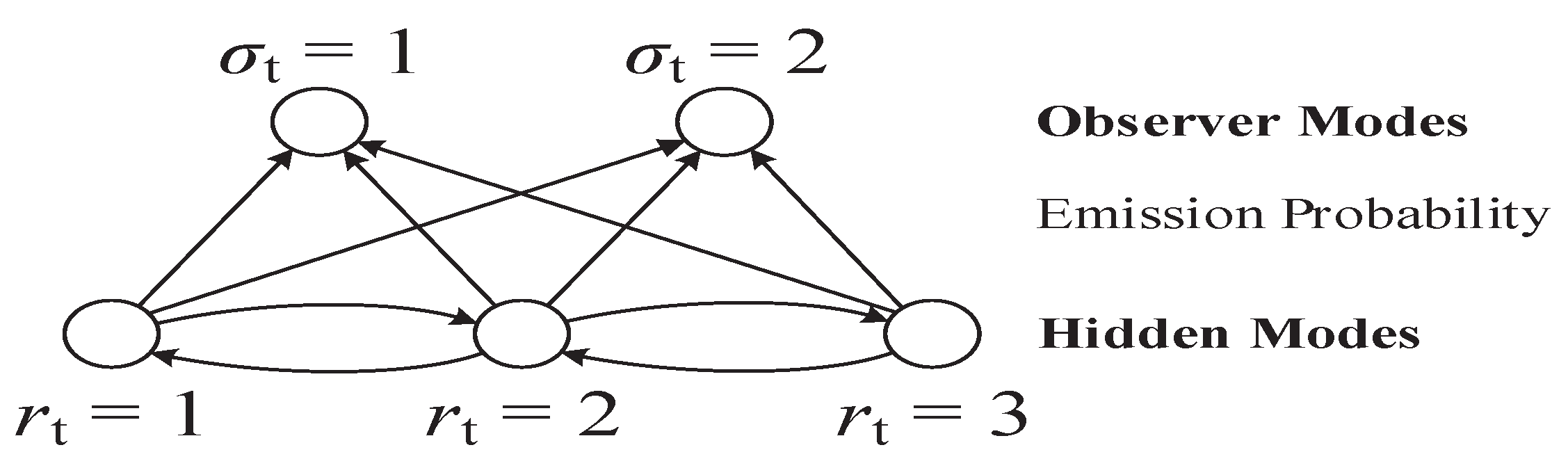
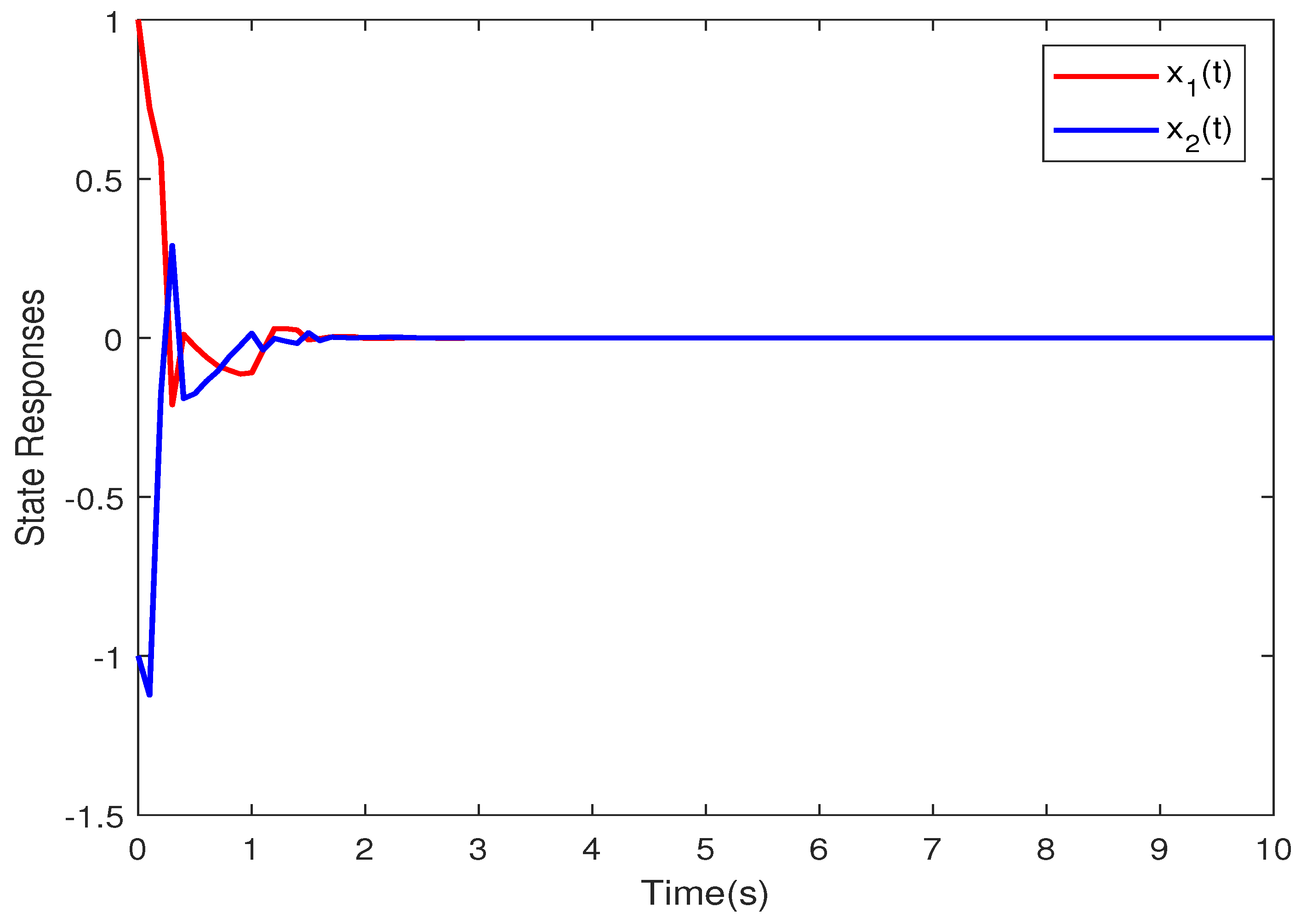
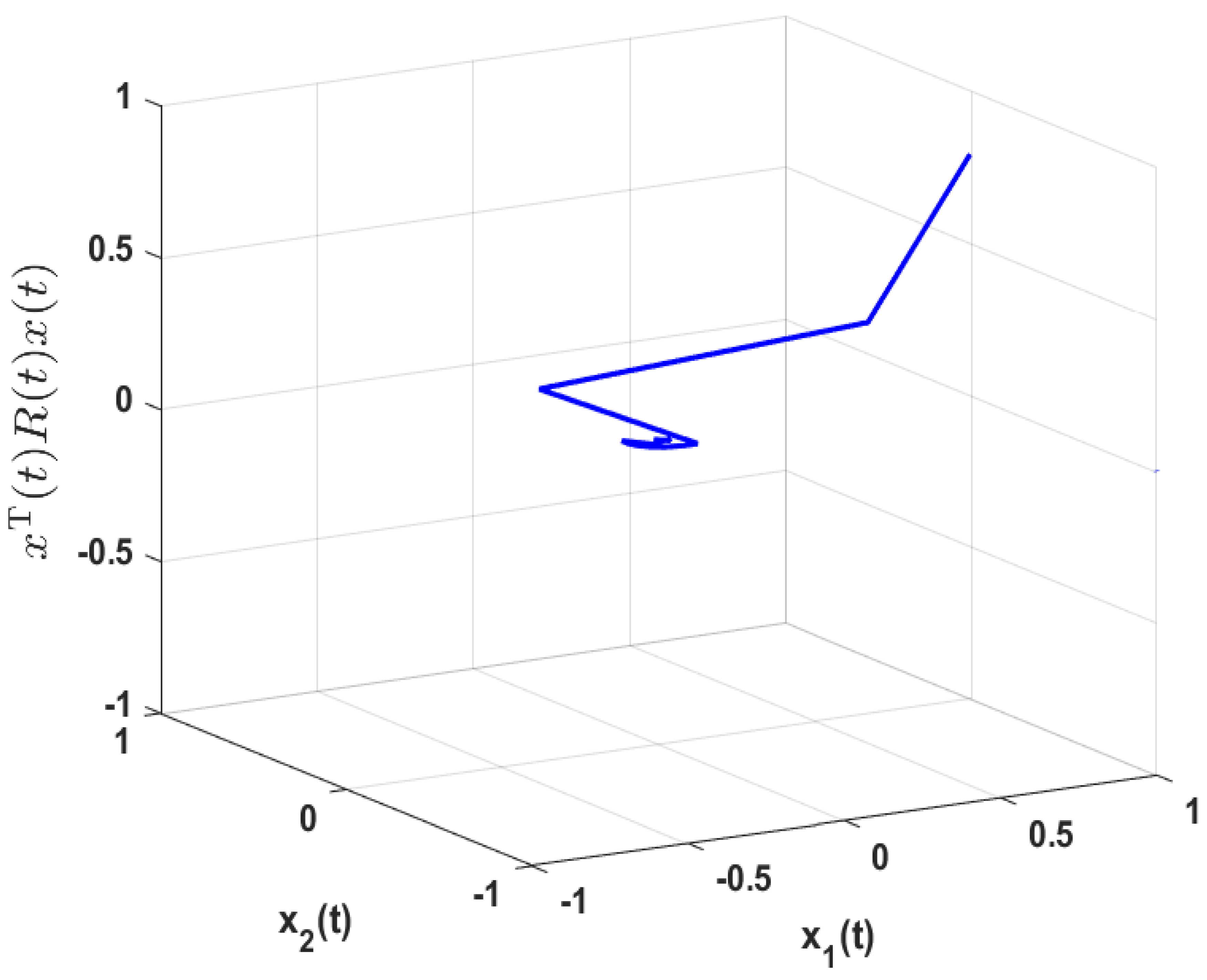
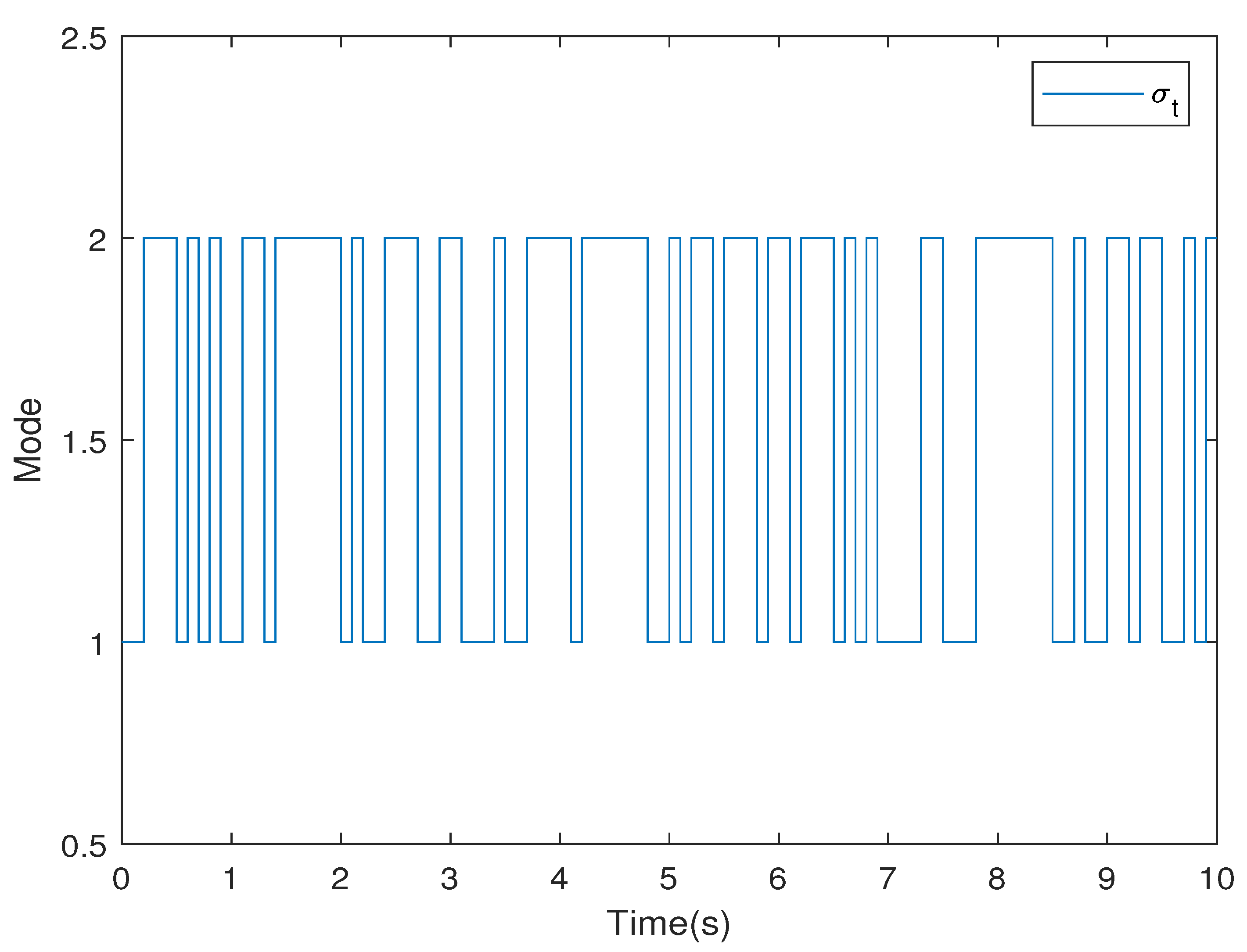
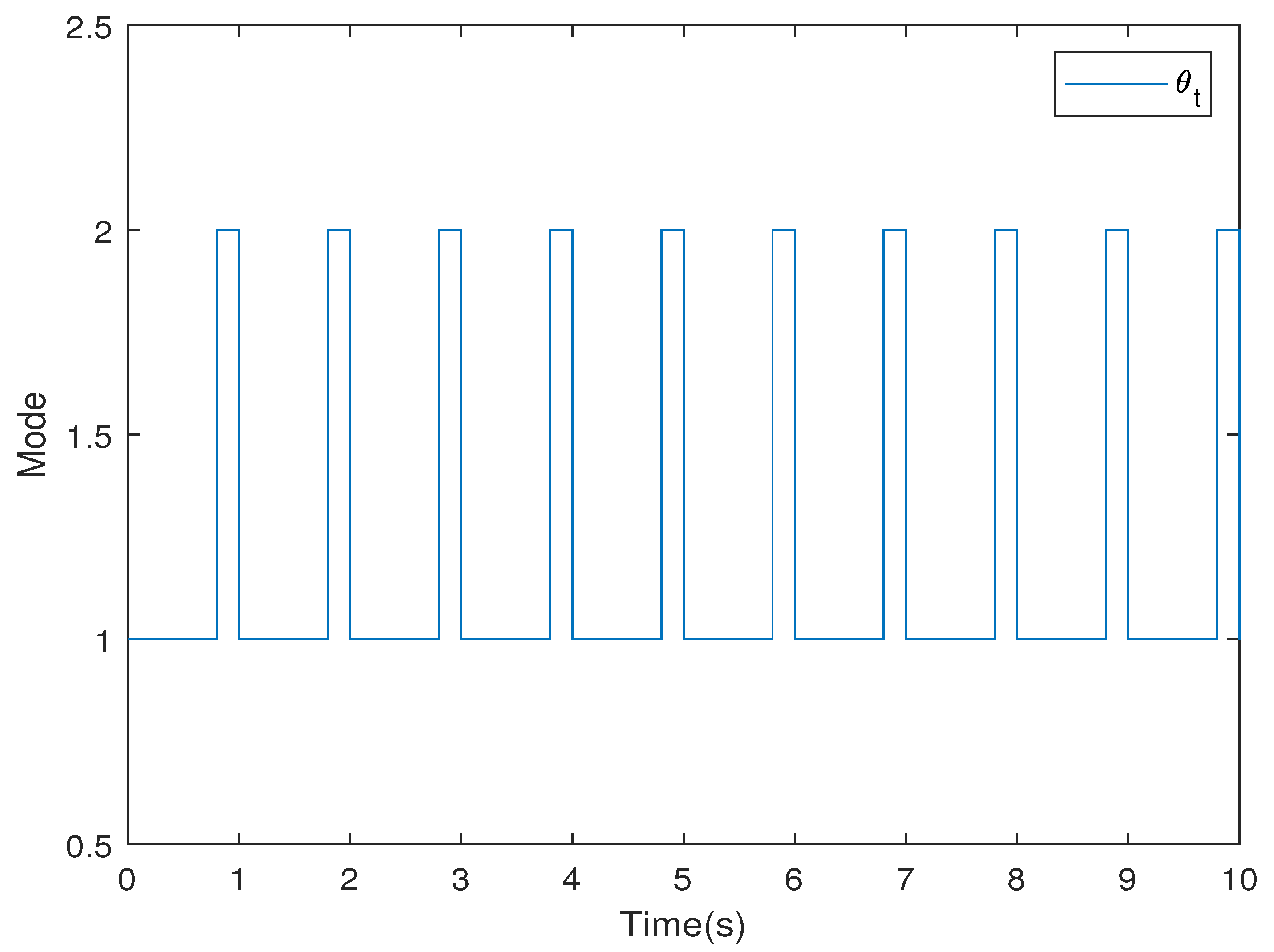
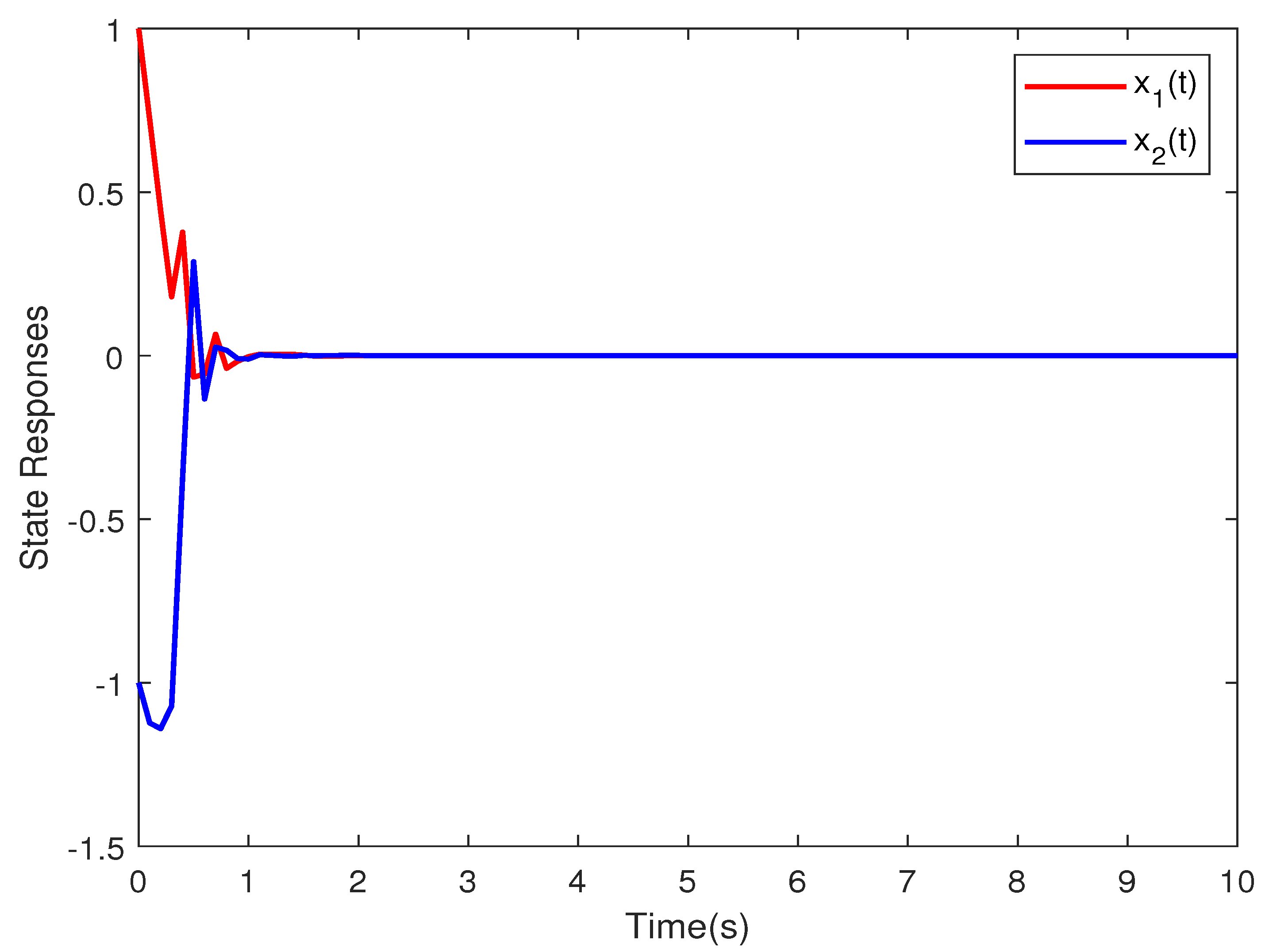
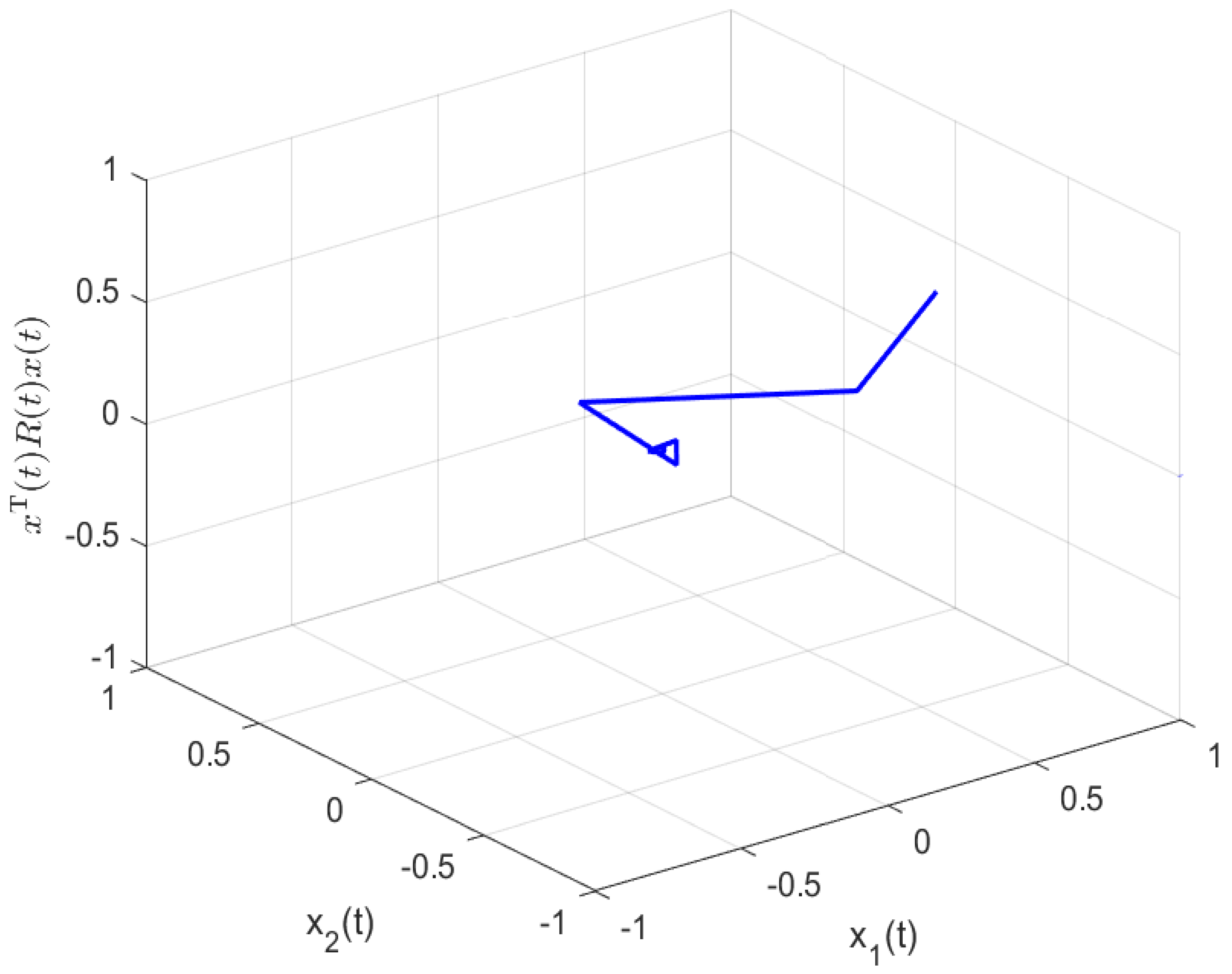
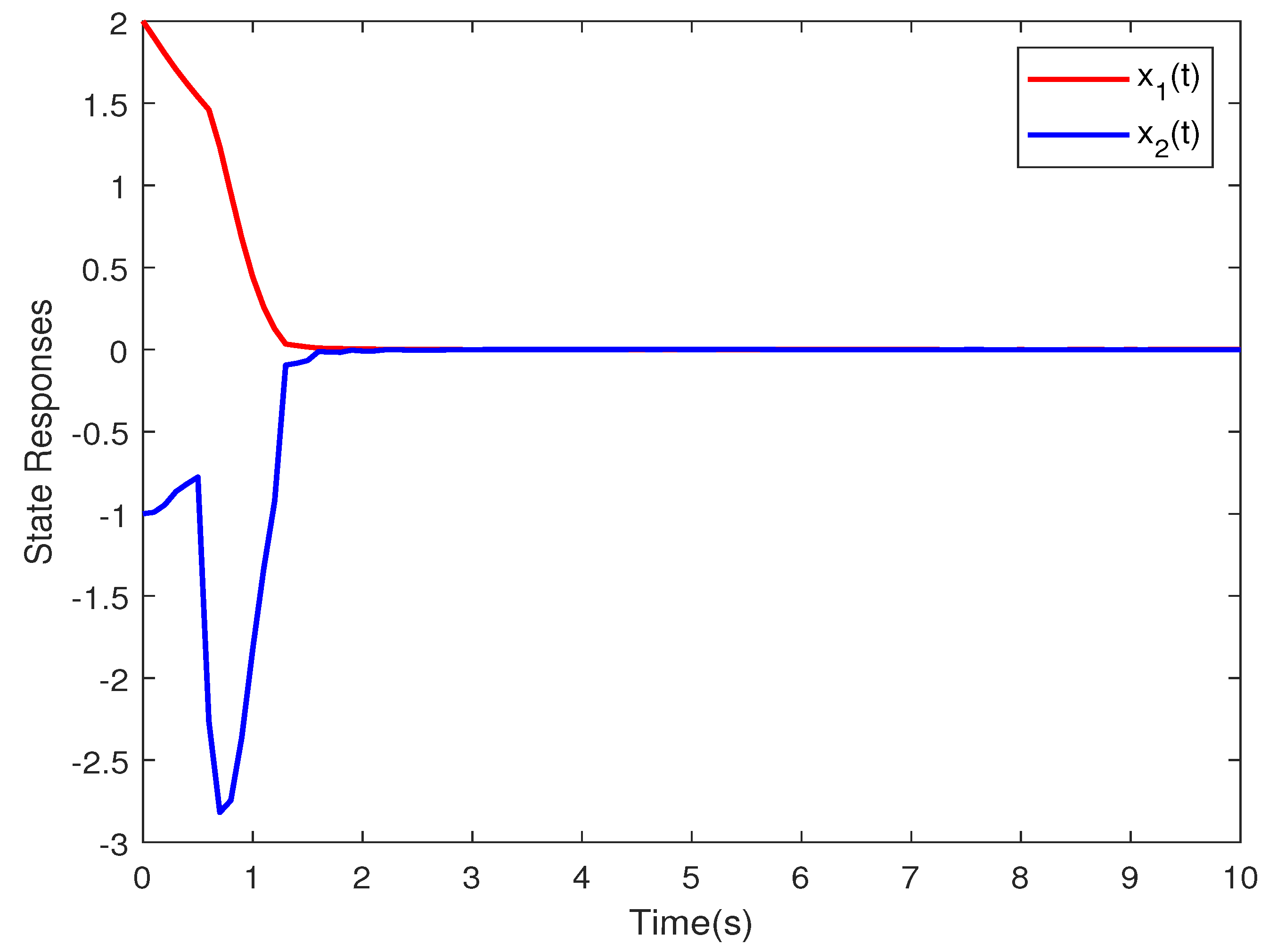
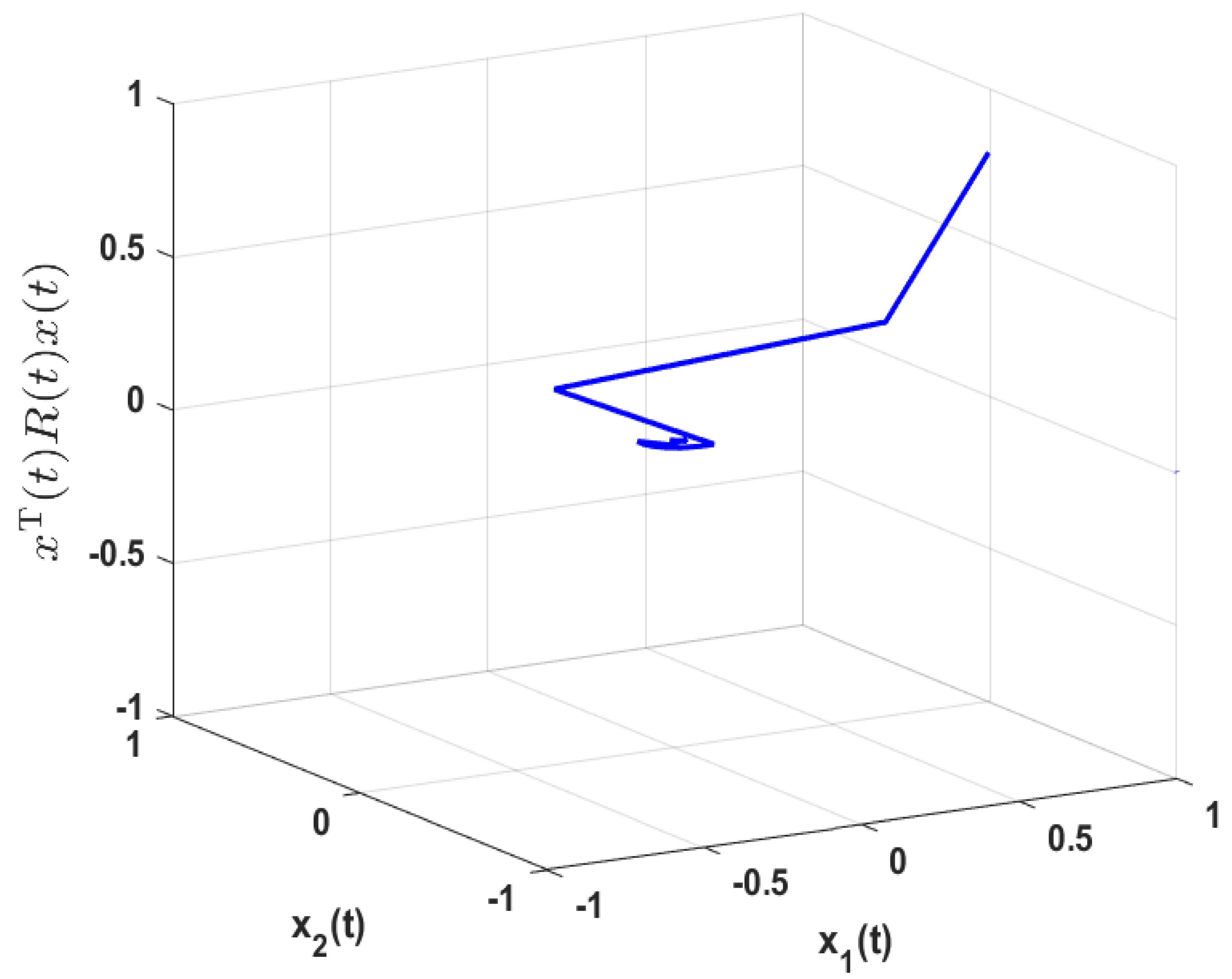
4. Illustrative Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, Z.; Shi, P.; Shu, Z.; Su, H.; Lu, R. Passivity-Based Asynchronous Control for Markov Jump Systems. IEEE Trans. Autom. Control 2017, 62, 2020–2025. [Google Scholar] [CrossRef]
- Wang, Y.; Zhuang, G.; Chen, X.; Wang, Z.; Chen, F. Dynamic event-based finite-time mixed H∞ and passive asynchronous filtering for T-S fuzzy singular Markov jump systems with general transition rates. Nonlinear Anal.-Hybrid Syst. 2020, 36, 100874. [Google Scholar] [CrossRef]
- Cheng, J.; Wu, Y.; Yan, H.; Wu, Z.; Shi, K. Protocol-based filtering for fuzzy Markov affine systems with switching chain. Automatica 2022, 141, 110321. [Google Scholar] [CrossRef]
- Wang, H.; Luan, X.; Stojanovic, V.; Liu, F. Self-triggered finite-time control for discrete-time Markov jump systems. Inf. Sci. 2023, 634, 101–121. [Google Scholar]
- Shen, H.; Hu, X.; Wang, J.; Cao, J.; Qian, W. Non-Fragile H∞ Synchronization for Markov Jump Singularly Perturbed Coupled Neural Networks Subject to Double-Layer Switching Regulation. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 2682–2692. [Google Scholar] [CrossRef]
- Li, F.; Wu, L.; Shi, P.; Lim, C. State estimation and sliding mode control for semi-Markovian jump systems with mismatched uncertainties. Automatica 2015, 51, 385–393. [Google Scholar] [CrossRef]
- Shen, H.; Park, J.; Wu, Z.; Zhang, Z. Finite-time H∞ synchronization for complex networks with semi-Markov jump topology. Commun. Nonlinear Sci. Numer. Simul. 2015, 24, 40–51. [Google Scholar] [CrossRef]
- Wang, B.; Zhu, Q. Stability analysis of semi-Markov switched stochastic systems. Automatica 2018, 94, 72–80. [Google Scholar] [CrossRef]
- Wang, J.; Hu, X.; Wei, Y.; Wang, Z. Sampled-data synchronization of semi-Markov jump complex dynamical networks subject to generalized dissipativity property. Appl. Math. Comput. 2019, 346, 853–864. [Google Scholar] [CrossRef]
- Zhang, L.; Lam, H.; Liang, Y.S.H. Fault Detection for Fuzzy Semi-Markov Jump Systems Based on Interval Type-2 Fuzzy Approach. IEEE Trans. Fuzzy Syst. 2020, 28, 2375–2388. [Google Scholar] [CrossRef]
- Yang, J.; Zhu, Y.; Zhang, L.; Duan, G. Smooth control with flexible duration for semi-Markov jump linear systems. Automatica 2024, 164, 111612. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, X.; Zhang, R. Finite-time H∞ control for continuous-time non-homogeneous semi-Markov jump systems. In Proceedings of the 2023 IEEE 11th International Conference on Information, Communication and Networks, Xi’an, China, 17–20 August 2023. [Google Scholar]
- Kim, S. Stochastic stability and stabilization conditions of semi-Markovian jump systems with mode transition-dependent sojourn-time distributions. Inf. Sci. 2017, 385–386, 314–324. [Google Scholar] [CrossRef]
- Nguyen, K.; Kim, S. Observer-based control design of semi-Markovian jump systems with uncertain probability intensities and mode-transition-dependent sojourn-time distribution. Appl. Math. Comput. 2020, 372, 124968. [Google Scholar] [CrossRef]
- Cheng, J.; Xie, L.; Park, J.; Yan, H. Protocol-Based Output-Feedback Control for Semi-Markov Jump Systems. IEEE Trans. Autom. Control 2022, 67, 4346–4353. [Google Scholar] [CrossRef]
- Wang, D.; Wu, F.; Lian, J.; Li, S. Observer-Based Asynchronous Control for Stochastic Nonhomogeneous Semi-Markov Jump Systems. IEEE Trans. Autom. Control 2024, 69, 2559–2566. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, Y.; Li, H.; Liang, H.; Wang, J. Event-triggered fault detection for nonlinear semi-Markov jump systems based on double asynchronous filtering approach. Automatica 2022, 138, 110144. [Google Scholar] [CrossRef]
- Men, Y.; Sun, J. Asynchronous Control of 2-D Semi-Markov Jump Systems Under Actuator Saturation. IEEE Trans. Circuits Syst. II-Express Briefs 2023, 70, 4118–4122. [Google Scholar] [CrossRef]
- Li, R.; Qi, W.; Park, J.; Cheng, J.; Shi, K. Sliding mode control for discrete interval type-2 fuzzy semi-Markov jump models with delay in controller mode switching. Fuzzy Sets Syst. 2024, 483, 108915. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, H.; Zhang, X. Stability and H∞ performance of human-in-the-loop control systems through hidden semi-Markov human behavior modeling. Appl. Math. Model. 2023, 116, 799–815. [Google Scholar] [CrossRef]
- Cai, B.; Zhang, L.; Shi, Y. Control Synthesis of Hidden Semi-Markov Uncertain Fuzzy Systems via Observations of Hidden Modes. IEEE Trans. Cybern. 2020, 50, 3709–3718. [Google Scholar] [CrossRef]
- Men, Y.; Sun, J. H∞ control of singularly perturbed systems using deficient hidden semi-Markov model. Nonlinear Anal.-Hybrid Syst. 2024, 52, 101453. [Google Scholar] [CrossRef]
- Wu, E.; Zhu, L.; Li, G.; Li, H. Nonparametric Hierarchical Hidden Semi-Markov Model for Brain Fatigue Behavior Detection of Pilots during Flight. IEEE Trans. Intell. Transp. Syst. 2022, 23, 5245–5256. [Google Scholar] [CrossRef]
- Li, F.; Zheng, W.; Xu, S. Stabilization of Discrete-Time Hidden Semi-Markov Jump Singularly Perturbed Systems with Partially Known Emission Probabilities. IEEE Trans. Autom. Control 2022, 67, 4234–4240. [Google Scholar] [CrossRef]
- Zhang, L.; Cai, B.; Tan, T. Stabilization of non-homogeneous hidden semi-Markov Jump systems with limited sojourn-time information. Automatica 2020, 117, 108963. [Google Scholar] [CrossRef]
- Shen, H.; Zhang, Z.; Li, F.; Yan, H. Non-Fragile H∞ Control for Piecewise Homogeneous Hidden Semi-Markov Lur’e Systems. IEEE Trans. Circuits Syst. II-Express Briefs 2024, 71, 306–310. [Google Scholar] [CrossRef]
- He, S.; Song, J.; Liu, F. Robust Finite-Time Bounded Controller Design of Time-Delay Conic Nonlinear Systems Using Sliding Mode Control Strategy. IEEE Trans. Syst. Man Cybern. 2018, 48, 1863–1873. [Google Scholar] [CrossRef]
- Qi, W.; Zong, G.; Ahn, C. Input-Output Finite-Time Asynchronous SMC for Nonlinear Semi-Markov Switching Systems with Application. IEEE Trans. Syst. Man Cybern. 2022, 52, 5344–5353. [Google Scholar] [CrossRef]
- Xia, Z.; He, S. Finite-time asynchronous H∞ fault-tolerant control for nonlinear hidden markov jump systems with actuator and sensor faults. Appl. Math. Comput. 2022, 428, 127212. [Google Scholar] [CrossRef]
- Wang, J.; Ru, T.; Xia, J. Finite-time synchronization for complex dynamic networks with semi-Markov switching topologies: An H∞ event-triggered control scheme. Appl. Math. Comput. 2019, 356, 235–251. [Google Scholar] [CrossRef]
- Zhong, S.; Zhang, W.; Li, K. Finite-time stability and asynchronous resilient control for Itô stochastic semi-Markovian jump systems. J. Frankl. Inst. 2022, 359, 1531–1557. [Google Scholar] [CrossRef]

| Notations | Meanings |
|---|---|
| n-dimensional Euclidean space | |
| Euclidean norm | |
| U is a positive-definite symmetric matrix | |
| the transpose of U | |
| the inverse of U | |
| , | maximum and minimum eigenvalues of U |
| U + | |
| the mathematical expectation | |
| ∗ | the elision for symmetry matrix |
| 1,2, … | |
| 1,2, … | |
| 1,2, …N |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Zhang, X.; Shao, Y.; Shi, K. Finite-Time Asynchronous H∞ Control for Non-Homogeneous Hidden Semi-Markov Jump Systems. Mathematics 2024, 12, 3036. https://doi.org/10.3390/math12193036
Wang Q, Zhang X, Shao Y, Shi K. Finite-Time Asynchronous H∞ Control for Non-Homogeneous Hidden Semi-Markov Jump Systems. Mathematics. 2024; 12(19):3036. https://doi.org/10.3390/math12193036
Chicago/Turabian StyleWang, Qian, Xiaojun Zhang, Yu Shao, and Kaibo Shi. 2024. "Finite-Time Asynchronous H∞ Control for Non-Homogeneous Hidden Semi-Markov Jump Systems" Mathematics 12, no. 19: 3036. https://doi.org/10.3390/math12193036







