Inequalities for Basic Special Functions Using Hölder Inequality

Abstract

Let $p,q\ge 1$ be two real numbers such that ${\displaystyle \frac{1}{p}}+{\displaystyle \frac{1}{q}}=1$, and let $a,b\in \mathbb{R}$ be two parameters defined on the domain of a function, for example, f. Based on the well known Hölder inequality, we propose a generic inequality of the form $\left|f({\displaystyle \frac{a}{p}}+{\displaystyle \frac{b}{q}})\right|\le \left|f\left(a\right){|}^{{\displaystyle \frac{1}{p}}}\right|f\left(b\right){|}^{{\displaystyle \frac{1}{q}}},$ and show that many basic special functions, such as the gamma and polygamma functions, Riemann zeta function, beta function and Gauss and confluent hypergeometric functions, satisfy this type of inequality. In this sense, we also present some particular inequalities for the Gauss and confluent hypergeometric functions to confirm the main obtained inequalities.

1. Introduction

Mathematical inequalities, which strengthen the connection of mathematical sciences with applied sciences such as physics, engineering, numerical analysis and statistics, have been widely used in many fields, such as convex analysis, convex programming, approximation theory, special functions, fractional analysis and quantum analysis, and have also brought new orientations to these fields. One of these inequalities is the well-known Hölder inequality, which plays a significant role in different branches of mathematical sciences [1,2].

Let $L_w^p[\alpha ,\beta ]$ denote a weighted space of p-power integrable functions with the standard norm

$${∥f∥}_{w,p}={\left({\int }_{\alpha }^{\beta }w\left(t\right){\left|f\left(t\right)\right|}^{p}dt\right)}^{{\displaystyle \frac{1}{p}}},$$

where $w\left(t\right)$ is a positive function on the interval $[\alpha ,\beta ]$, and let $L_j^p\left(A^{*}\right)$ denote a weighted discrete space of p-power functions with the norm

$${∥f∥}_{w,p}={\left(\sum _{t\in A^{*}}j\left(t\right){\left|f\left(t\right)\right|}^p\right)}^{{\displaystyle \frac{1}{p}}},$$

where $j\left(t\right)$ is a positive jump function on the counter set $A^{*}$.

Throughout this paper, we assume that $p,q\in [1,\infty )$ are two real numbers such that ${\displaystyle \frac{1}{p}}+{\displaystyle \frac{1}{q}}=1$. For two given functions $f,g$ in a linear normed space, the weighted Hölder inequality [3]

$${∥fg∥}_{w,1}\le {∥f∥}_{w,p}{∥g∥}_{w,q},$$

can be indicated in a continuous space as

$$\begin{array}{cc}\hfill \left|{\int }_{\alpha }^{\beta }w\left(t\right)f\left(t\right)g\left(t\right)dt\right|& \le {\int }_{\alpha }^{\beta }w\left(t\right)\left|f\left(t\right)\right|\left|g\left(t\right)\right|dt\hfill \\ \hfill & \le {\left({\int }_{\alpha }^{\beta }w\left(t\right){\left|f\left(t\right)\right|}^{p}dt\right)}^{{\displaystyle \frac{1}{p}}}{\left({\int }_{\alpha }^{\beta }w\left(t\right){\left|g\left(t\right)\right|}^{q}dt\right)}^{{\displaystyle \frac{1}{q}}},\hfill \end{array}$$

(1)

and in a discrete space as

$$\left|\sum _{t\in A^{*}}j\left(t\right)f\left(t\right)g\left(t\right)\right|\le \sum _{t\in A^{*}}j\left(t\right)\left|f\left(t\right)\right|\left|g\left(t\right)\right|\le {\left(\sum _{t\in A^{*}}j\left(t\right){\left|f\left(t\right)\right|}^p\right)}^{{\displaystyle \frac{1}{p}}}{\left(\sum _{t\in A^{*}}j\left(t\right){\left|g\left(t\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}.$$

(2)

If $w\left(t\right)=j\left(t\right)=1$ and also

$$f\left(t\right)=g_1^{{\displaystyle \frac{1+r_1}{2}}}\left(t\right)g_2^{{\displaystyle \frac{1+r_2}{2}}}\left(t\right)\dots g_m^{{\displaystyle \frac{1+r_m}{2}}}\left(t\right)\mathrm{and}g\left(t\right)=g_1^{{\displaystyle \frac{1-r_1}{2}}}\left(t\right)g_2^{{\displaystyle \frac{1-r_2}{2}}}\left(t\right)\dots g_m^{{\displaystyle \frac{1-r_m}{2}}}\left(t\right),$$

(3)

where ${\left\{r_i\right\}}_{i=1}^m$ are free parameters, inequalities (1) and (2), respectively, change to

$$\begin{array}{c}\left|{\int }_{\alpha }^{\beta }{g}_1\left(t\right)g_2\left(t\right)\dots g_m\left(t\right)dt\right|\le {\int }_{\alpha }^{\beta }\left|g_1\left(t\right)\right|\left|g_2\left(t\right)\right|\dots \left|g_m\left(t\right)\right|dt\hfill \\ \le {\left({\int }_{\alpha }^{\beta }{\left|g_1^{{\displaystyle \frac{1+r_1}{2}}}\left(t\right)\right|}^p{\left|g_2^{{\displaystyle \frac{1+r_2}{2}}}\left(t\right)\right|}^p\dots {\left|g_m^{{\displaystyle \frac{1+r_m}{2}}}\left(t\right)\right|}^{p}dt\right)}^{{\displaystyle \frac{1}{p}}}\\ \hfill \times {\left({\int }_{\alpha }^{\beta }{\left|g_1^{{\displaystyle \frac{1-r_1}{2}}}\left(t\right)\right|}^q{\left|g_2^{{\displaystyle \frac{1-r_2}{2}}}\left(t\right)\right|}^q\dots {\left|g_m^{{\displaystyle \frac{1-r_m}{2}}}\left(t\right)\right|}^{q}dt\right)}^{{\displaystyle \frac{1}{q}}},\end{array}$$

(4)

and

$$\begin{array}{c}\left|\sum _{t\in A^{*}}{g}_1\left(t\right)g_2\left(t\right)\dots g_m\left(t\right)\right|\le \sum _{t\in A^{*}}\left|g_1\left(t\right)\right|\left|g_2\left(t\right)\right|\dots \left|g_m\left(t\right)\right|\hfill \\ \le {\left(\sum _{t\in A^{*}}{\left|g_1^{{\displaystyle \frac{1+r_1}{2}}}\left(t\right)\right|}^p{\left|g_2^{{\displaystyle \frac{1+r_2}{2}}}\left(t\right)\right|}^p\dots {\left|g_m^{{\displaystyle \frac{1+r_m}{2}}}\left(t\right)\right|}^p\right)}^{{\displaystyle \frac{1}{p}}}\\ \hfill \times {\left(\sum _{t\in A^{*}}{\left|g_1^{{\displaystyle \frac{1-r_1}{2}}}\left(t\right)\right|}^q{\left|g_2^{{\displaystyle \frac{1-r_2}{2}}}\left(t\right)\right|}^q\dots {\left|g_m^{{\displaystyle \frac{1-r_m}{2}}}\left(t\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}.\end{array}$$

(5)

In this paper, we apply inequalities (4) and (5) to obtain new types of inequalities for many basic special functions. First, by noting (5), we derive an inequality for the Riemann zeta function with infinite series representation. Then, in Section 2.2 and Section 2.3, we respectively obtain new inequalities for gamma and polygamma functions with integral representations. Finally, in Section 2.4, Section 2.5 and Section 2.6, we introduce new types of inequality for some multi-argument functions such as the beta, Gauss and confluent hypergeometric functions. In this sense, some particular inequalities are given for the first time for very important Gauss and confluent hypergeometric series.

2. Results

In 2012, we proposed a generic inequality of the form [4]

$$f^2\left(x\right)\le k\left(x\right)f\left(ax+b\right)f\left((2-a)x-b\right),$$

(6)

where $a,b$ are real parameters and $k\left(x\right)$ is a specific function, and then applied it to some special functions. Recently, in [5], we modified inequality (6) to

$$f^2\left(x\right)\le f\left(s\right)f\left(2x-s\right),$$

(7)

whose generalization is in the form

$$f^2(x_1,x_2,\dots ,x_n)\le f(s_1,s_2,\dots ,s_n)f\left(2x_1-s_1,2x_2-s_2,\dots ,2x_n-s_n\right).$$

If in (7), $2x-s=b$ and $s=a$, it clearly changes to

$$f^2\left({\displaystyle \frac{a+b}{2}}\right)\le f\left(a\right)f\left(b\right).$$

(8)

Noting Hölder inequality (4) and (5), an extension of inequality (7) can be proposed as follows:

$$\left|f\left(x\right)\right|\le \left|f\left(s\right){|}^{{\displaystyle \frac{1}{p}}}\right|f\left((x-{\displaystyle \frac{s}{p}})q\right){|}^{{\displaystyle \frac{1}{q}}},$$

(9)

whose generalization is as follows:

$$|f(x_1,x_2,\dots ,x_n)|\le |f(s_1,s_2,\dots ,s_n){|}^{{\displaystyle \frac{1}{p}}}|f\left((x_1-{\displaystyle \frac{s_1}{p}})q,(x_2-{\displaystyle \frac{s_2}{p}})q,\dots ,(x_n-{\displaystyle \frac{s_n}{p}})q\right){|}^{{\displaystyle \frac{1}{q}}}.$$

(10)

Noting (8), the equivalent forms of (9) and (10) are, respectively,

$$\left|f\left({\displaystyle \frac{a}{p}}+{\displaystyle \frac{b}{q}}\right)\right|\le \left|f\left(a\right){|}^{{\displaystyle \frac{1}{p}}}\right|f\left(b\right){|}^{{\displaystyle \frac{1}{q}}},$$

(11)

and

$$\left|f\left({\displaystyle \frac{a_1}{p}}+{\displaystyle \frac{b_1}{q}},{\displaystyle \frac{a_2}{p}}+{\displaystyle \frac{b_2}{q}},\dots ,{\displaystyle \frac{a_n}{p}}+{\displaystyle \frac{b_n}{q}}\right)\right|\le \left|f(a_1,a_2,\dots ,a_n){|}^{{\displaystyle \frac{1}{p}}}\right|f(b_1,b_2,\dots ,b_n){|}^{{\displaystyle \frac{1}{q}}},$$

(12)

in which $p,q\ge 1$ and ${\displaystyle \frac{1}{p}}+{\displaystyle \frac{1}{q}}=1$ as before.

In this section, we show that many basic special functions would satisfy inequalities of types (9) and (10), and/or their equivalent forms (11) and (12).

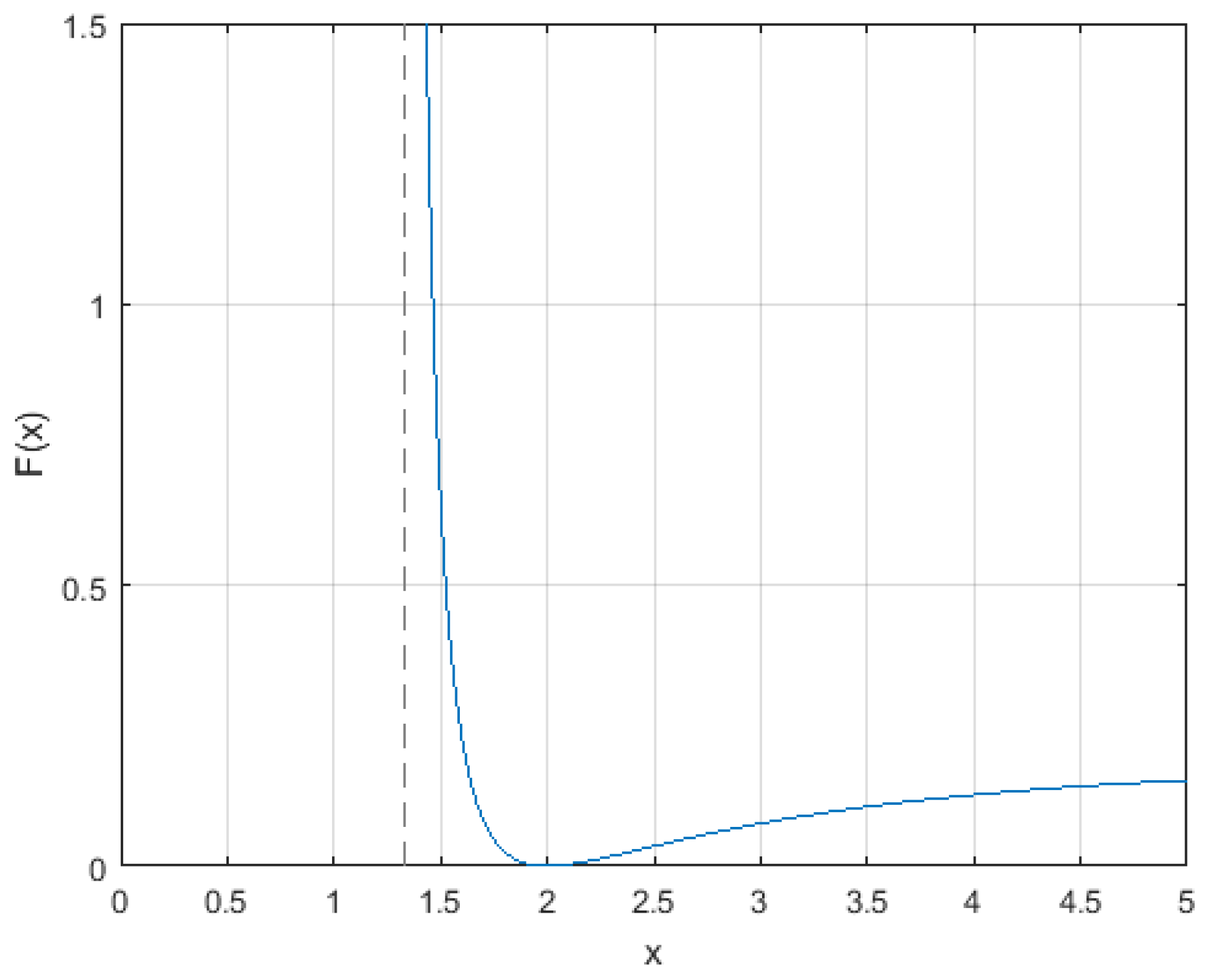
2.1. An Inequality for the Riemann Zeta Function

For $x>1$, the Riemann zeta function [6] is defined by

$$\zeta \left(x\right)=\sum _{n=1}^{\infty }{\displaystyle \frac{1}{n^x}}.$$

By substituting $g_1\left(x\right)={\displaystyle \frac{1}{n^x}}=\left|g_1\left(x\right)\right|$ into (5) for $r_1={\displaystyle \frac{2s}{px}}-1$, one obtains

$$\sum _{n=1}^{\infty }{\displaystyle \frac{1}{n^x}}\le {\left(\sum _{n=1}^{\infty }{\displaystyle \frac{1}{n^s}}\right)}^{{\displaystyle \frac{1}{p}}}{\left(\sum _{n=1}^{\infty }{\displaystyle \frac{1}{n^{(x-\frac{s}{p})q}}}\right)}^{{\displaystyle \frac{1}{q}}},$$

which means

$$\zeta \left(x\right)\le {\zeta }^{{\displaystyle \frac{1}{p}}}\left(s\right){\zeta }^{{\displaystyle \frac{1}{q}}}\left((x-{\displaystyle \frac{s}{p}})q\right),$$

(13)

provided that $1<s<(x-{\displaystyle \frac{1}{q}})p$.

Clearly, inequality (13) is equivalent to

$$\zeta \left({\displaystyle \frac{a}{p}}+{\displaystyle \frac{b}{q}}\right)\le {\zeta }^{{\displaystyle \frac{1}{p}}}\left(a\right){\zeta }^{{\displaystyle \frac{1}{q}}}\left(b\right)(a,b>1).$$

For example, for $p=3$ and $q={\displaystyle \frac{3}{2}}$, inequality (13) reads as

$$\zeta \left(x\right)\le {\zeta }^{{\displaystyle \frac{1}{3}}}\left(s\right){\zeta }^{{\displaystyle \frac{2}{3}}}\left({\displaystyle \frac{3x-s}{2}}\right)(1<s<3x-2).$$

(14)

In order to graphically illustrate the correctness of inequality (14), we can first define the two-variable function

$$F_1(x,s)={\zeta }^{{\displaystyle \frac{1}{3}}}\left(s\right){\zeta }^{{\displaystyle \frac{2}{3}}}\left({\displaystyle \frac{3x-s}{2}}\right)-\zeta \left(x\right),$$

and show that its plot is always positive on the domain $D_1=\left\{(x,s)\right|1<s<3x-2\}$. For instance, replacing $s=2$ shows that the univariate function

$$F_1(x,2)=\sqrt[3]{{\displaystyle \frac{{\pi }^2}{6}}}{\zeta }^{{\displaystyle \frac{2}{3}}}\left({\displaystyle \frac{3}{2}}x-1\right)-\zeta \left(x\right),$$

is always positive on the real interval $({\displaystyle \frac{4}{3}},\infty )$ according to Figure 1.

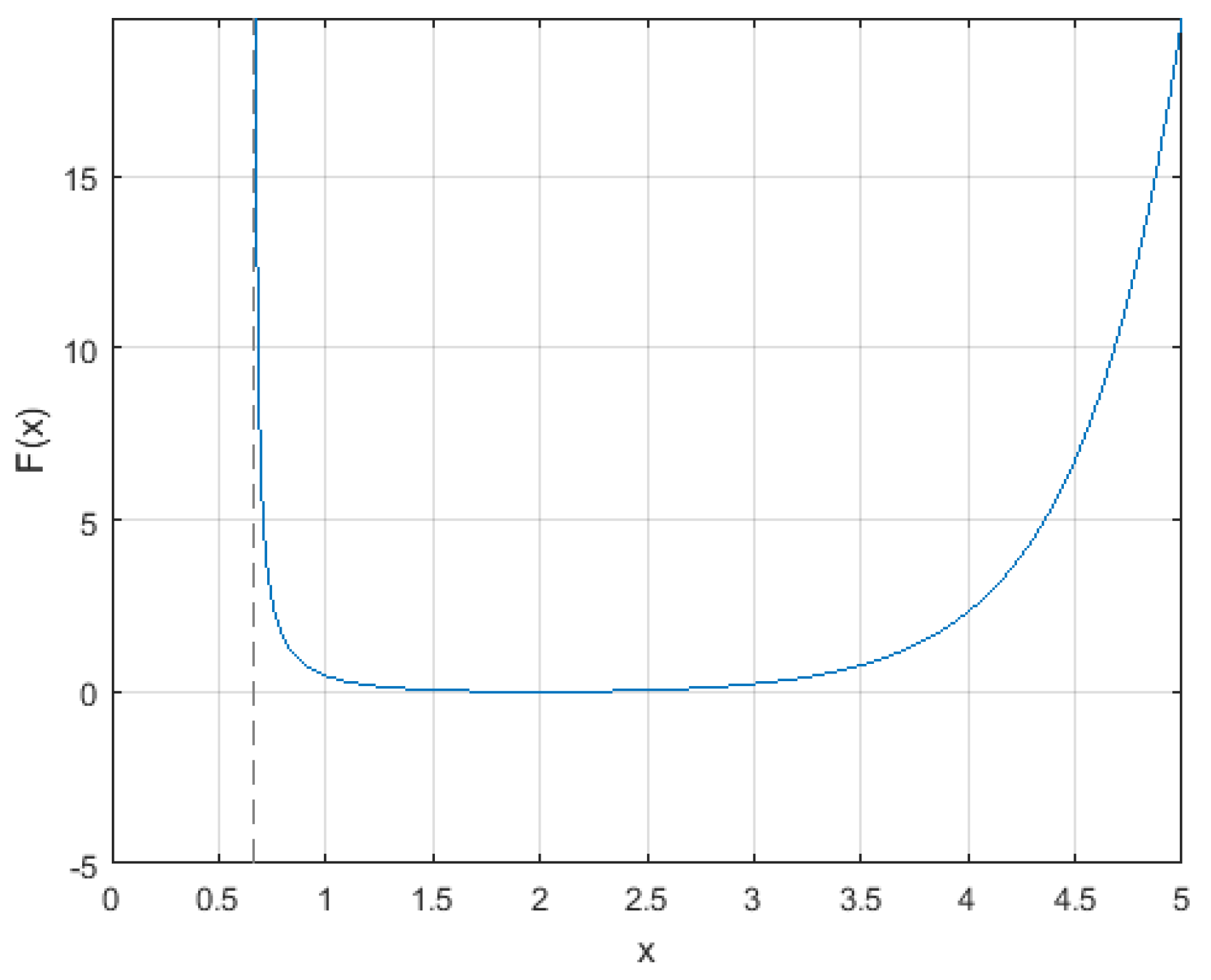
2.2. An Inequality of Type (9) or (11) for the Gamma Function

As the integral representation of the gamma function is

$$\Gamma \left(x\right)={\int }_0^{\infty }{t}^{x-1}{e}^{-t}dt(x>0).$$

For $t\ge 0$, if we replace

$$\begin{array}{cc}\hfill & g_1\left(t\right)=t^x=|g_1\left(t\right)|,g_2\left(t\right)=t^{-1}=|g_2\left(t\right)|,g_3\left(t\right)=e^{-t}=\left|g_3\left(t\right)\right|,\hfill \\ \hfill & r_1={\displaystyle \frac{2s}{px}}-1,r_2=r_3={\displaystyle \frac{2}{p}}-1,\hfill \end{array}$$

and $[\alpha ,\beta ]=[0,\infty )$ in (4), then

$${\int }_0^{\infty }{t}^{x-1}{e}^{-t}dt\le {\left({\int }_0^{\infty }{t}^{s-1}{e}^{-t}dt\right)}^{{\displaystyle \frac{1}{p}}}{\left({\int }_0^{\infty }{t}^{(x-{\displaystyle \frac{s}{p}})q-1}{e}^{-t}dt\right)}^{{\displaystyle \frac{1}{q}}},$$

leading to

$$\Gamma \left(x\right)\le {\Gamma }^{{\displaystyle \frac{1}{p}}}\left(s\right){\Gamma }^{{\displaystyle \frac{1}{q}}}\left((x-{\displaystyle \frac{s}{p}})q\right)(0<s<px),$$

(15)

which is equivalent to

$$\Gamma \left({\displaystyle \frac{a}{p}}+{\displaystyle \frac{b}{q}}\right)\le {\Gamma }^{{\displaystyle \frac{1}{p}}}\left(a\right){\Gamma }^{{\displaystyle \frac{1}{q}}}\left(b\right)(a,b>0).$$

For example, replacing $p=3$ and $q={\displaystyle \frac{3}{2}}$ in (15) gives

$$\Gamma \left(x\right)\le {\Gamma }^{{\displaystyle \frac{1}{3}}}\left(s\right){\Gamma }^{{\displaystyle \frac{2}{3}}}\left({\displaystyle \frac{3x-s}{2}}\right)(0<s<3x).$$

(16)

Similar to the previous example, in order to graphically illustrate the correctness of inequality (16), one can define the two-variable function

$$F_2(x,s)={\Gamma }^{{\displaystyle \frac{1}{3}}}\left(s\right){\Gamma }^{{\displaystyle \frac{2}{3}}}\left({\displaystyle \frac{3x-s}{2}}\right)-\Gamma \left(x\right),$$

and show that its plot is always positive on the triangular domain $D_2=\left\{(x,s)\right|0<s<3x\}$.

As a very particular sample, for $s=2$, Figure 2 shows the positivity of

$$F_2(x,2)={\Gamma }^{{\displaystyle \frac{2}{3}}}\left({\displaystyle \frac{3}{2}}x-1\right)-\Gamma \left(x\right),$$

on the real interval $({\displaystyle \frac{2}{3}},\infty )$.

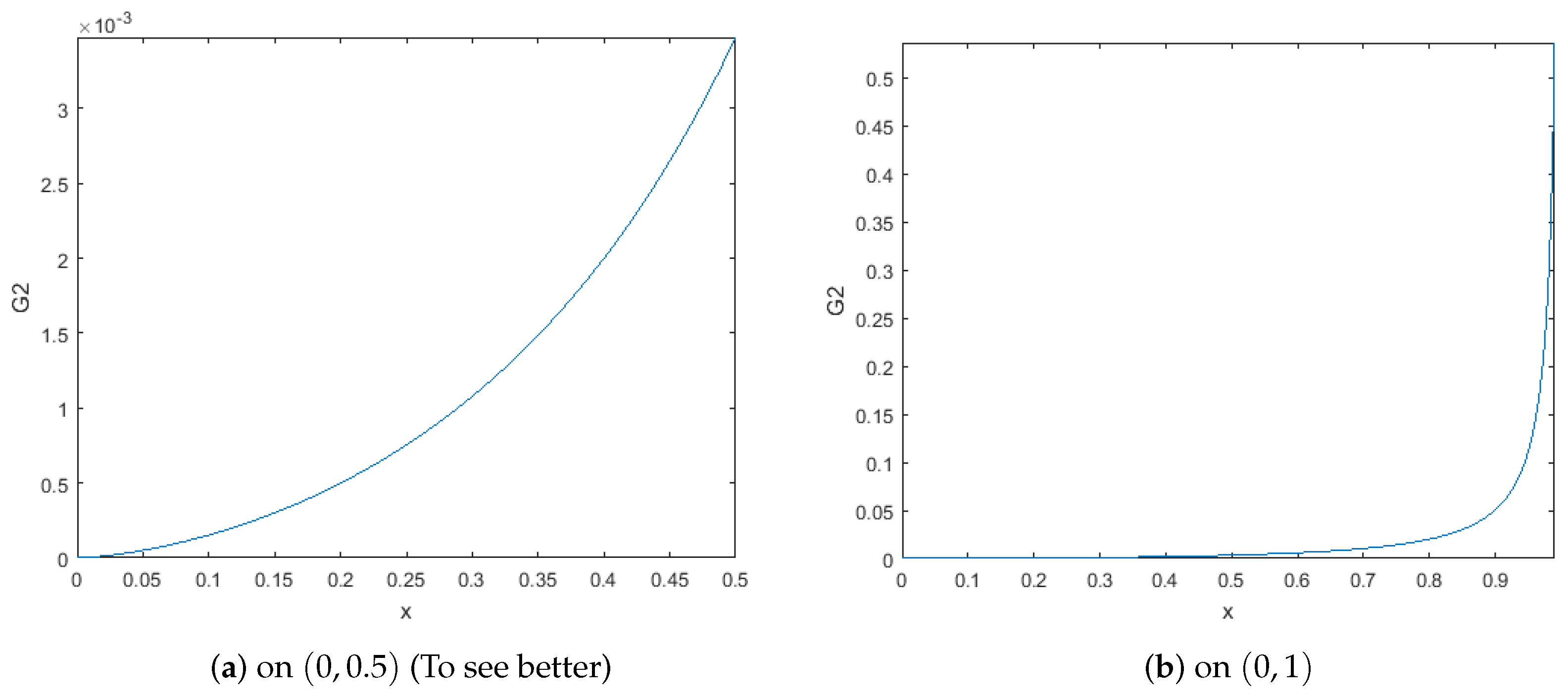
2.3. An Inequality for the Polygamma Function

The polygamma function ${\Psi }_n\left(x\right)={\displaystyle \frac{d^n\Psi \left(x\right)}{d{x}^n}}$, known as the n-th derivative of the Psi function

$$\Psi \left(x\right)={\displaystyle \frac{{\Gamma }^{\prime }\left(x\right)}{\Gamma \left(x\right)}}(x>0),$$

has an integral representation [6] of the form

$${\Psi }_n\left(x\right)={(-1)}^{n+1}{\int }_0^{\infty }{\displaystyle \frac{t^n}{1-e^{-t}}}{e}^{-xt}dt(n\in \mathbb{N},x>0).$$

For $t\ge 0$, if

$$g_1\left(t\right)={\displaystyle \frac{t^n}{1-e^{-t}}}=|g_1\left(t\right)|,g_2\left(t\right)=e^{-xt}=\left|g_2\left(t\right)\right|,r_1={\displaystyle \frac{2}{p}}-1,r_2={\displaystyle \frac{2s}{px}}-1,$$

and $[\alpha ,\beta ]=[0,\infty )$ are replaced in (4), then the inequality

$${\int }_0^{\infty }{\displaystyle \frac{t^n}{1-e^{-t}}}{e}^{-xt}dt\le {\left({\int }_0^{\infty }{\displaystyle \frac{t^n}{1-e^{-t}}}{e}^{-st}dt\right)}^{{\displaystyle \frac{1}{p}}}{\left({\int }_0^{\infty }{\displaystyle \frac{t^n}{1-e^{-t}}}{e}^{-(x-{\displaystyle \frac{s}{p}})qt}dt\right)}^{{\displaystyle \frac{1}{q}}},$$

yields

$${(-1)}^{n+1}{\Psi }_n\left(x\right)\le {(-1)}^{n+1}{\left({\Psi }_n\left(s\right)\right)}^{{\displaystyle \frac{1}{p}}}{\left({\Psi }_n\left((x-{\displaystyle \frac{s}{p}})q\right)\right)}^{{\displaystyle \frac{1}{q}}}(0<s<px),$$

(17)

which is equivalent to

$${(-1)}^{n+1}{\Psi }_n\left({\displaystyle \frac{a}{p}}+{\displaystyle \frac{b}{q}}\right)\le {(-1)}^{n+1}{\left({\Psi }_n\left(a\right)\right)}^{{\displaystyle \frac{1}{p}}}{\left({\Psi }_n\left(b\right)\right)}^{{\displaystyle \frac{1}{q}}}(a,b>0).$$

As we have observed up to now, inequalities (15), (17) and (13) are all of type (9).

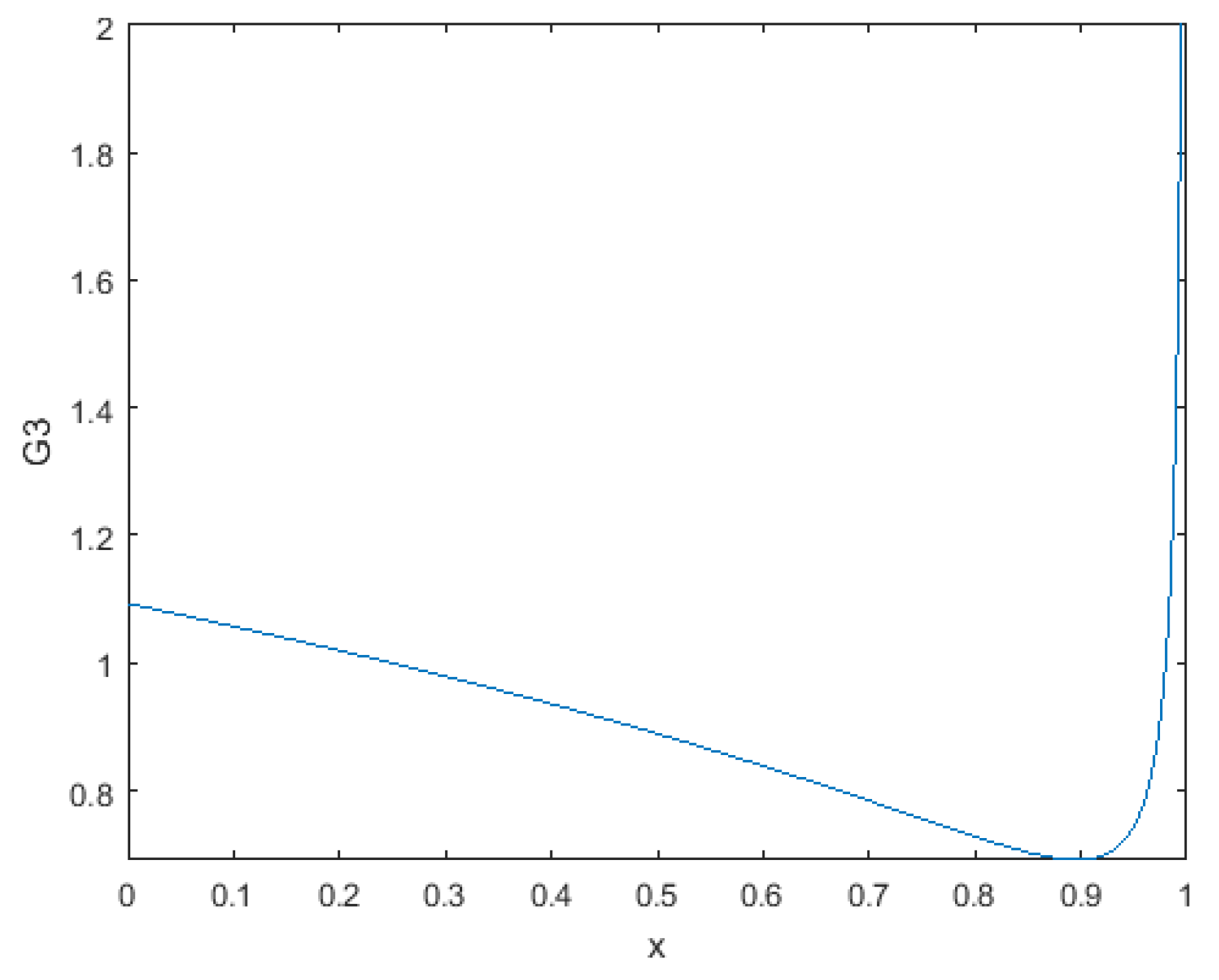
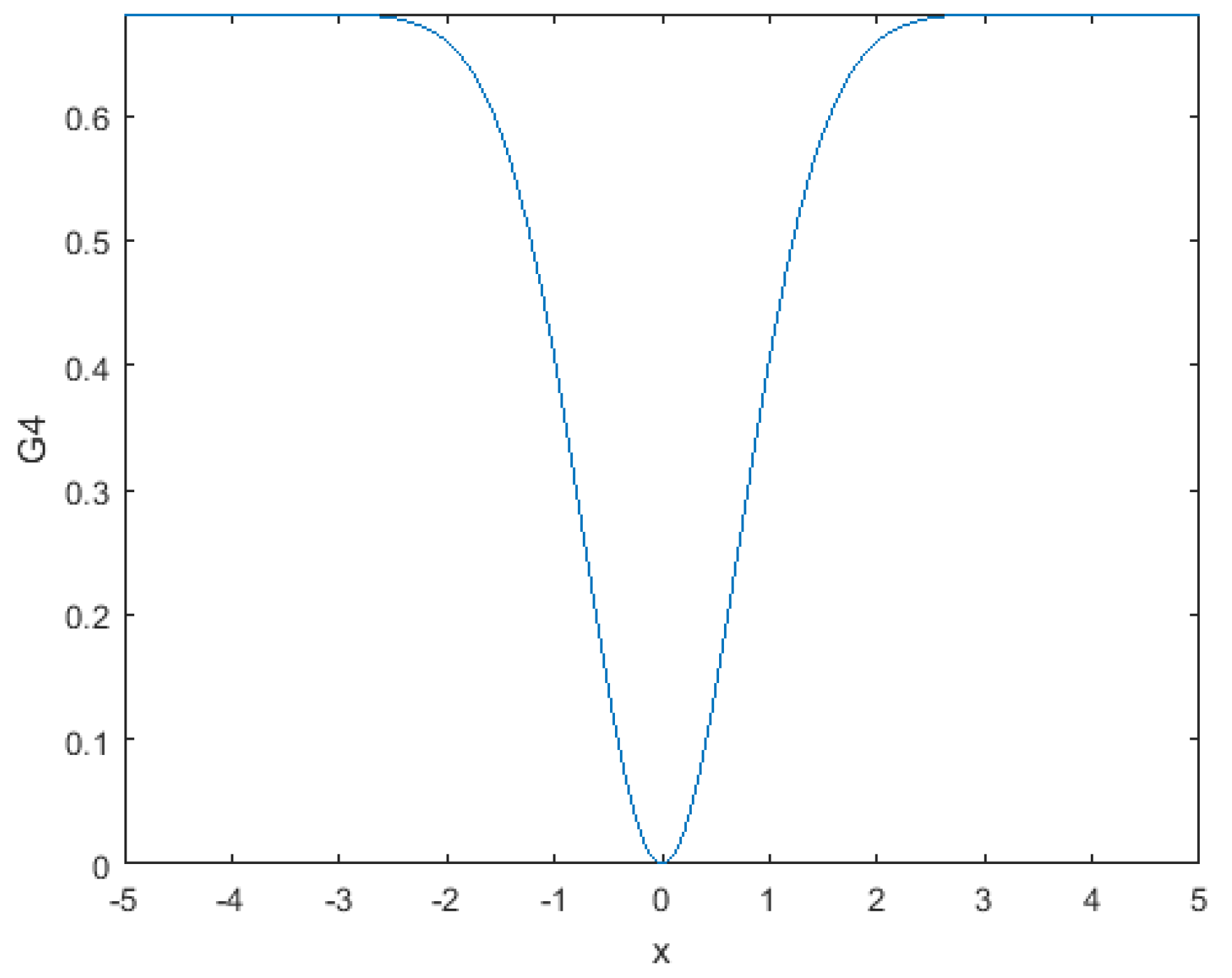
2.4. An Inequality of Type (10) or (12) for the Beta Function

By considering the integral representation of the beta function

$$\mathbf{B}(x_1,x_2)={\int }_0^1{t}^{x_1-1}{(1-t)}^{x_2-1}dt={\displaystyle \frac{\Gamma \left(x_1\right)\Gamma \left(x_2\right)}{\Gamma (x_1+x_2)}}(x_1,x_2>0),$$

and replacing

$$\begin{array}{cc}\hfill & g_1\left(t\right)=t^{x_1}=|g_1\left(t\right)|,g_2\left(t\right)=t^{-1}=|g_2\left(t\right)|,g_3\left(t\right)={(1-t)}^{x_2}=\left|g_3\left(t\right)\right|,\hfill \\ \hfill & g_4\left(t\right)={(1-t)}^{-1}=\left|g_4\left(t\right)\right|,\hfill \end{array}$$

and

$$r_1={\displaystyle \frac{2s_1}{p{x}_1}}-1,r_2={\displaystyle \frac{2}{p}}-1,r_3={\displaystyle \frac{2s_2}{p{x}_2}}-1,r_4={\displaystyle \frac{2}{p}}-1,$$

in (4), the following inequality

$${\int }_0^1{t}^{x_1-1}{(1-t)}^{x_2-1}dt\le {\left({\int }_0^1{t}^{s_1-1}{(1-t)}^{s_2-1}dt\right)}^{{\displaystyle \frac{1}{p}}}{\left({\int }_0^1{t}^{(x_1-{\displaystyle \frac{s_1}{p}})q-1}{(1-t)}^{(x_2-{\displaystyle \frac{s_2}{p}})q-1}dt\right)}^{{\displaystyle \frac{1}{q}}},$$

is derived which is equivalent to

$$\mathbf{B}(x_1,x_2)\le {\mathbf{B}}^{{\displaystyle \frac{1}{p}}}\left(s_1,s_2\right){\mathbf{B}}^{{\displaystyle \frac{1}{q}}}\left((x_1-{\displaystyle \frac{s_1}{p}})q,(x_2-{\displaystyle \frac{s_2}{p}})q\right),$$

(18)

provided that $0<s_1<p{x}_1$ and $0<s_2<p{x}_2$.

Another shape of (18) is as follows:

$$\mathbf{B}\left({\displaystyle \frac{a_1}{p}}+{\displaystyle \frac{b_1}{q}},{\displaystyle \frac{a_2}{p}}+{\displaystyle \frac{b_2}{q}}\right)\le {\mathbf{B}}^{{\displaystyle \frac{1}{p}}}(a_1,a_2){\mathbf{B}}^{{\displaystyle \frac{1}{q}}}(b_1,b_2)(a_1,a_2,b_1,b_2>0).$$

2.5. An Inequality for the Gauss Hypergeometric Function

The hypergeometric series

$${}_{2}F_1\left(\left.\begin{array}{c}\begin{array}{cc}a,& b\end{array}\\ c\end{array}\right|x\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{{\left(a\right)}_k{\left(b\right)}_k}{{\left(c\right)}_k}}{\displaystyle \frac{x^k}{k!}},$$

(19)

is convergent for all $x\in [-1,1]$ (where $c\ne 0,-1,-2,\dots$ and ${\left(a\right)}_k=a(a+1)\dots (a+k-1)$) whose integral representation is denoted by

$${}_{2}F_1\left(\left.\begin{array}{c}\begin{array}{cc}a,& b\end{array}\\ c\end{array}\right|x\right)={\displaystyle \frac{\Gamma \left(c\right)}{\Gamma \left(a\right)\Gamma (c-a)}}{\int }_0^1{t}^{a-1}{(1-t)}^{c-a-1}{(1-xt)}^{-b}dt,(c>a>0).$$

(20)

The importance of the Gauss hypergeometric function is that many special functions can directly be represented in terms of it, e.g., see [7]. Hence, finding an inequality for this important function will cause us to automatically find an inequality for many applied functions.

In order to apply (20) for deriving a straightforward inequality of type (10) for the Gauss hypergeometric function (19), we first substitute

$$\begin{array}{cc}\hfill & g_1\left(t\right)=t^{a-2}=|g_1\left(t\right)|,g_2\left(t\right)=t=|g_2\left(t\right)|,g_3\left(t\right)={(1-t)}^{c-a-2}=\left|g_3\left(t\right)\right|,\hfill \\ \hfill & g_4\left(t\right)=1-t=|g_4\left(t\right)|,g_5\left(t\right)={(1-xt)}^{-b-1}=\left|g_5\left(t\right)\right|,\hfill \\ \hfill & g_6\left(t\right)=1-xt=\left|g_6\left(t\right)\right|,\hfill \\ \hfill & r_1={\displaystyle \frac{2}{p}}-1,r_2={\displaystyle \frac{2}{p}}(A-a+1)-1,r_3={\displaystyle \frac{2}{p}}-1,\hfill \\ \hfill & r_4={\displaystyle \frac{2}{p}}(C-A-c+a+1)-1,r_5={\displaystyle \frac{2}{q}}-1,r_6=-{\displaystyle \frac{2B}{p}}+{\displaystyle \frac{2(b+1)}{q}}-1,\hfill \end{array}$$

into (4) to obtain

$$\begin{array}{c}{\int }_0^1{t}^{a-1}{(1-t)}^{c-a-1}{(1-xt)}^{-b}dt\le {\left({\int }_0^1{t}^{A-1}{(1-t)}^{C-A-1}{(1-xt)}^{-B}dt\right)}^{{\displaystyle \frac{1}{p}}}\hfill \\ \hfill \times {\left({\int }_0^1{t}^{a-(A-a){\displaystyle \frac{q}{p}}-1}{(1-t)}^{c-a-1-(C-A-c+a){\displaystyle \frac{q}{p}}}{(1-xt)}^{(B-b){\displaystyle \frac{q}{p}}-b}dt\right)}^{{\displaystyle \frac{1}{q}}},\end{array}$$

which is equivalent to

$$\begin{array}{c}\mathbf{B}(a,c-a){}_{2}F_1\left(\left.\begin{array}{c}\begin{array}{cc}a,& b\end{array}\\ c\end{array}\right|x\right)\le {\mathbf{B}}^{{\displaystyle \frac{1}{p}}}(A,C-A){}_{2}F_1^{\frac{1}{p}}\left(\left.\begin{array}{c}\begin{array}{cc}A,& B\end{array}\\ C\end{array}\right|x\right)\hfill \\ \hfill \times {\mathbf{B}}^{{\displaystyle \frac{1}{q}}}\left(a-(A-a){\displaystyle \frac{q}{p}},c-a-(C-A-c+a){\displaystyle \frac{q}{p}}\right){}_{2}F_1^{\frac{1}{q}}\left(\left.\begin{array}{c}\begin{array}{cc}a-(A-a){\displaystyle \frac{q}{p}},& b-(B-b){\displaystyle \frac{q}{p}}\end{array}\\ c-(C-c){\displaystyle \frac{q}{p}}\end{array}\right|x\right),\end{array}$$

and can be simplified as

$$\begin{array}{cc}\hfill {}_{2}F_1\left(\left.\begin{array}{c}\begin{array}{cc}a,& b\end{array}\\ c\end{array}\right|x\right)& \le {\displaystyle \frac{{\mathbf{B}}^{\frac{1}{p}}(A,C-A){\mathbf{B}}^{\frac{1}{q}}\left((a-\frac{A}{p})q,(c-a-\frac{C-A}{p})q\right)}{\mathbf{B}(a,c-a)}}\hfill \\ \hfill & \times {}_{2}F_1^{\frac{1}{p}}\left(\left.\begin{array}{c}\begin{array}{cc}A,& B\end{array}\\ C\end{array}\right|x\right){}_{2}F_1^{\frac{1}{q}}\left(\left.\begin{array}{c}\begin{array}{cc}(a-{\displaystyle \frac{A}{p}})q,& (b-{\displaystyle \frac{B}{p}})q\end{array}\\ (c-{\displaystyle \frac{C}{p}})q\end{array}\right|x\right),\hfill \end{array}$$

(21)

where $0<a<c$, $0<A<C$ and $0<ap-A<cp-C$.

Note that the equality is achieved in (21) when $A=a$, $B=b$ and $C=c$.

Finally, if $(a-{\displaystyle \frac{A}{p}})q=A^{*}$, $(b-{\displaystyle \frac{B}{p}})q=B^{*}$ and $(c-{\displaystyle \frac{C}{p}})q=C^{*}$, (21) changes to the standard form

$$\begin{array}{cc}\hfill {}_{2}F_1\left(\left.\begin{array}{c}\begin{array}{cc}{\displaystyle \frac{A}{p}}+{\displaystyle \frac{A^{*}}{q}},& {\displaystyle \frac{B}{p}}+{\displaystyle \frac{B^{*}}{q}}\end{array}\\ {\displaystyle \frac{C}{p}}+{\displaystyle \frac{C^{*}}{q}}\end{array}\right|x\right)& \le {\displaystyle \frac{{\mathbf{B}}^{\frac{1}{p}}(A,C-A){\mathbf{B}}^{\frac{1}{q}}(A^{*},C^{*}-A^{*})}{\mathbf{B}\left(\frac{A}{p}+\frac{A^{*}}{q},\frac{C-A}{p}+\frac{C^{*}-A^{*}}{q}\right)}}\hfill \\ \hfill & \times {}_{2}F_1^{\frac{1}{p}}\left(\left.\begin{array}{c}\begin{array}{cc}A,& B\end{array}\\ C\end{array}\right|x\right){}_{2}F_1^{\frac{1}{q}}\left(\left.\begin{array}{c}\begin{array}{cc}{A}^{*},& B^{*}\end{array}\\ C^{*}\end{array}\right|x\right),\hfill \end{array}$$

(22)

which is the most general inequality for Gauss hypergeometric series in the literature as far as we know.

Interesting cases in (22) are when the parameters p and q take special values. For instance, for $p=3$ and $q={\displaystyle \frac{3}{2}}$, (22) changes to

$$\begin{array}{cc}\hfill {{}_{2}F_1}^3\left(\left.\begin{array}{c}\begin{array}{cc}{\displaystyle \frac{A+2A^{*}}{3}},& {\displaystyle \frac{B+2B^{*}}{3}}\end{array}\\ {\displaystyle \frac{C+2C^{*}}{3}}\end{array}\right|x\right)& \le {\displaystyle \frac{\mathbf{B}(A,C-A){\mathbf{B}}^2(A^{*},C^{*}-A^{*})}{{\mathbf{B}}^3\left(\frac{A+2A^{*}}{3},\frac{C-A+2(C^{*}-A^{*})}{3}\right)}}\hfill \\ \hfill & \times {}_{2}F_1\left(\left.\begin{array}{c}\begin{array}{cc}A,& B\end{array}\\ C\end{array}\right|x\right){}_{2}F_1^2\left(\left.\begin{array}{c}\begin{array}{cc}{A}^{*},& B^{*}\end{array}\\ C^{*}\end{array}\right|x\right).\hfill \end{array}$$

(23)

Also, for the standard case $p=q=2$, we have

$$\begin{array}{cc}\hfill {{}_{2}F_1}^2\left(\left.\begin{array}{c}\begin{array}{cc}{\displaystyle \frac{A+A^{*}}{2}},& {\displaystyle \frac{B+B^{*}}{2}}\end{array}\\ {\displaystyle \frac{C+C^{*}}{2}}\end{array}\right|x\right)& \le {\displaystyle \frac{\mathbf{B}(A,C-A)\mathbf{B}(A^{*},C^{*}-A^{*})}{{\mathbf{B}}^2\left(\frac{A+A^{*}}{2},\frac{C-A+C^{*}-A^{*}}{2}\right)}}\hfill \\ \hfill & \times {}_{2}F_1\left(\left.\begin{array}{c}\begin{array}{cc}A,& B\end{array}\\ C\end{array}\right|x\right){}_{2}F_1\left(\left.\begin{array}{c}\begin{array}{cc}{A}^{*},& B^{*}\end{array}\\ C^{*}\end{array}\right|x\right).\hfill \end{array}$$

(24)

This is a good point to consider some particular cases of inequality (23).

Example 1.

Noting (23), the inequality

$${{}_{2}F_1}^3\left(\left.\begin{array}{c}\begin{array}{cc}{\displaystyle \frac{7}{12}},& {\displaystyle \frac{13}{12}}\end{array}\\ {\displaystyle \frac{3}{2}}\end{array}\right|x\right)\le {\displaystyle \frac{\mathbf{B}(\frac{1}{4},\frac{5}{4}){\mathbf{B}}^2(\frac{3}{4},\frac{3}{4})}{{\mathbf{B}}^3(\frac{7}{12},\frac{11}{12})}}{}_{2}F_1\left(\left.\begin{array}{c}\begin{array}{cc}{\displaystyle \frac{1}{4}},& {\displaystyle \frac{3}{4}}\end{array}\\ {\displaystyle \frac{3}{2}}\end{array}\right|x\right){}_{2}F_1^2\left(\left.\begin{array}{c}\begin{array}{cc}{\displaystyle \frac{3}{4}},& {\displaystyle \frac{5}{4}}\end{array}\\ {\displaystyle \frac{3}{2}}\end{array}\right|x\right),$$

is equivalent to

$$\begin{array}{c}x(1-x)\sqrt{x}{\left({(1-\sqrt{x})}^{-{\displaystyle \frac{1}{6}}}-{(1+\sqrt{x})}^{-{\displaystyle \frac{1}{6}}}\right)}^3\hfill \\ \hfill \le {\displaystyle \frac{{\left(\Gamma \left(\frac{1}{4}\right)\right)}^4}{3^{\frac{9}{4}}2\sqrt{2}{\pi }^2}}{sin}^3\left({\displaystyle \frac{1}{2}}arcsin\sqrt{x}\right)={\displaystyle \frac{{\left(\Gamma \left(\frac{1}{4}\right)\right)}^4}{8\times 3^{\frac{9}{4}}{\pi }^2}}{\left(1-\sqrt{1-x}\right)}^{{\displaystyle \frac{3}{2}}},\end{array}$$

according to the following identities derived from the site [8]:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{{(1-\sqrt{x})}^{1-2\alpha }-{(\sqrt{x}+1)}^{1-2\alpha }}{2(2\alpha -1)\sqrt{x}}}={}_{2}F_1\left(\left.\begin{array}{c}\begin{array}{cc}\alpha ,& \alpha +{\displaystyle \frac{1}{2}}\end{array}\\ {\displaystyle \frac{3}{2}}\end{array}\right|x\right),\hfill \\ \hfill & {\displaystyle \frac{1}{(2\alpha -1)\sqrt{x}}}sin\left((2\alpha -1)arcsin\sqrt{x}\right)={}_{2}F_1\left(\left.\begin{array}{c}\begin{array}{cc}\alpha ,& 1-\alpha \end{array}\\ {\displaystyle \frac{3}{2}}\end{array}\right|x\right),\hfill \end{array}$$

and

$${\displaystyle \frac{1}{2(\alpha -1)\sqrt{x(1-x)}}}sin\left(2(\alpha -1)arcsin\sqrt{x}\right)={}_{2}F_1\left(\left.\begin{array}{c}\begin{array}{cc}\alpha ,& 2-\alpha \end{array}\\ {\displaystyle \frac{3}{2}}\end{array}\right|x\right).$$

In this regard, Figure 3 shows the positivity of the function

$$G_1\left(x\right)={\displaystyle \frac{{\left(\Gamma \left(\frac{1}{4}\right)\right)}^4}{8\times 3^{\frac{9}{4}}{\pi }^2}}{\left(1-\sqrt{1-x}\right)}^{{\displaystyle \frac{3}{2}}}-x(1-x)\sqrt{x}{\left({(1-\sqrt{x})}^{-{\displaystyle \frac{1}{6}}}-{(1+\sqrt{x})}^{-{\displaystyle \frac{1}{6}}}\right)}^3,$$

graphically on the interval $(0,1)$.

Example 2.

Referring to (23),

$${{}_{2}F_1}^3\left(\left.\begin{array}{c}\begin{array}{cc}{\displaystyle \frac{5}{12}},& {\displaystyle \frac{11}{12}}\end{array}\\ {\displaystyle \frac{3}{2}}\end{array}\right|x\right)\le {\displaystyle \frac{\mathit{B}(\frac{3}{4},\frac{3}{4}){\mathit{B}}^2(\frac{1}{4},\frac{5}{4})}{{\mathit{B}}^3(\frac{5}{12},\frac{13}{12})}}{}_{2}F_1\left(\left.\begin{array}{c}\begin{array}{cc}{\displaystyle \frac{3}{4}},& {\displaystyle \frac{5}{4}}\end{array}\\ {\displaystyle \frac{3}{2}}\end{array}\right|x\right){}_{2}F_1^2\left(\left.\begin{array}{c}\begin{array}{cc}{\displaystyle \frac{1}{4}},& {\displaystyle \frac{3}{4}}\end{array}\\ {\displaystyle \frac{3}{2}}\end{array}\right|x\right),$$

is equivalent to

$${sinh}^3\left({\displaystyle \frac{1}{6}}{tanh}^{-1}\sqrt{x}\right)\le {\displaystyle \frac{{\pi }^2}{3^{\frac{3}{4}}{\left(\Gamma \left(\frac{1}{4}\right)\right)}^4}}x\sqrt{x}{(1-x)}^{-{\displaystyle \frac{3}{4}}}{(\sqrt{1-x}+1)}^{-{\displaystyle \frac{3}{2}}},$$

as we have [8]

$$\begin{array}{cc}\hfill & {\displaystyle \frac{6{(1-x)}^{\frac{1}{12}}}{\sqrt{x}}}sinh\left({\displaystyle \frac{1}{6}}{tanh}^{-1}\sqrt{x}\right)={}_{2}F_1\left(\left.\begin{array}{c}\begin{array}{cc}{\displaystyle \frac{5}{12}},& {\displaystyle \frac{11}{12}}\end{array}\\ {\displaystyle \frac{3}{2}}\end{array}\right|x\right),\hfill \\ \hfill & {\displaystyle \frac{\sqrt{2}{\left(\sqrt{1-x}+1\right)}^{-\frac{1}{2}}}{\sqrt{1-x}}}={}_{2}F_1\left(\left.\begin{array}{c}\begin{array}{cc}{\displaystyle \frac{3}{4}},& {\displaystyle \frac{5}{4}}\end{array}\\ {\displaystyle \frac{3}{2}}\end{array}\right|x\right),\hfill \end{array}$$

and

$$\sqrt{2}{\left(\sqrt{1-x}+1\right)}^{-{\displaystyle \frac{1}{2}}}={}_{2}F_1\left(\left.\begin{array}{c}\begin{array}{cc}{\displaystyle \frac{1}{4}},& {\displaystyle \frac{3}{4}}\end{array}\\ {\displaystyle \frac{3}{2}}\end{array}\right|x\right).$$

In this sense, Figure 4 shows the positivity of the function

$$G_2\left(x\right)={\displaystyle \frac{{\pi }^2}{3^{\frac{3}{4}}{\left(\Gamma \left(\frac{1}{4}\right)\right)}^4}}x\sqrt{x}{(1-x)}^{-{\displaystyle \frac{3}{4}}}{(\sqrt{1-x}+1)}^{-{\displaystyle \frac{3}{2}}}-{sinh}^3\left({\displaystyle \frac{1}{6}}{tanh}^{-1}\sqrt{x}\right),$$

graphically on the interval $(0,1)$.

Example 3.

According to (23), one obtains

$${{}_{2}F_1}^3\left(\left.\begin{array}{c}\begin{array}{cc}{\displaystyle \frac{1}{12}},& {\displaystyle \frac{7}{21}}\end{array}\\ {\displaystyle \frac{1}{2}}\end{array}\right|x\right)\le {\displaystyle \frac{\mathit{B}(\frac{1}{6},\frac{1}{3}){\mathit{B}}^2(\frac{1}{24},\frac{11}{24})}{{\mathit{B}}^3(\frac{1}{12},\frac{5}{12})}}{}_{2}F_1\left(\left.\begin{array}{c}\begin{array}{cc}{\displaystyle \frac{1}{6}},& -{\displaystyle \frac{1}{6}}\end{array}\\ {\displaystyle \frac{1}{2}}\end{array}\right|x\right){}_{2}F_1^2\left(\left.\begin{array}{c}\begin{array}{cc}{\displaystyle \frac{1}{24}},& {\displaystyle \frac{23}{24}}\end{array}\\ {\displaystyle \frac{1}{2}}\end{array}\right|x\right),$$

which is equivalent to

$$\begin{array}{c}{cosh}^3\left({\displaystyle \frac{1}{6}}{tanh}^{-1}\sqrt{x}\right)\hfill \\ \hfill \le {\displaystyle \frac{(\sqrt{2}-1)(\sqrt{3}-\sqrt{2}){\pi }^{\frac{3}{2}}{\left(\Gamma \left(\frac{1}{24}\right)\right)}^4\Gamma \left(\frac{1}{3}\right)}{6\times 2^{\frac{2}{3}}{\left(\Gamma \left(\frac{1}{4}\right)\right)}^8}}{(1-x)}^{-{\displaystyle \frac{3}{4}}}cos\left({\displaystyle \frac{1}{3}}arcsin\sqrt{x}\right){cos}^2\left({\displaystyle \frac{11}{12}}arcsin\sqrt{x}\right),\end{array}$$

as we have [8]

$$\begin{array}{cc}\hfill & {(1-x)}^{-\alpha }cosh\left(2\alpha {tanh}^{-1}\sqrt{x}\right)={}_{2}F_1\left(\left.\begin{array}{c}\begin{array}{cc}\alpha ,& \alpha +{\displaystyle \frac{1}{2}}\end{array}\\ {\displaystyle \frac{1}{2}}\end{array}\right|x\right),\hfill \\ \hfill & cos\left(2\alpha arcsin\sqrt{x}\right)={}_{2}F_1\left(\left.\begin{array}{c}\begin{array}{cc}\alpha ,& -\alpha \end{array}\\ {\displaystyle \frac{1}{2}}\end{array}\right|x\right),\hfill \end{array}$$

and

$${\displaystyle \frac{1}{\sqrt{1-x}}}cos\left((2\alpha -1)arcsin\sqrt{x}\right)={}_{2}F_1\left(\left.\begin{array}{c}\begin{array}{cc}\alpha ,& 1-\alpha \end{array}\\ {\displaystyle \frac{1}{2}}\end{array}\right|x\right).$$

In this sense, Figure 5 shows the positivity of the function

$$\begin{array}{cc}\hfill & G_3\left(x\right)=\hfill \\ \hfill & {\displaystyle \frac{(\sqrt{2}-1)(\sqrt{3}-\sqrt{2}){\pi }^{\frac{3}{2}}{\left(\Gamma \left(\frac{1}{24}\right)\right)}^4\Gamma \left(\frac{1}{3}\right)}{6\times 2^{\frac{2}{3}}{\left(\Gamma \left(\frac{1}{4}\right)\right)}^8}}{(1-x)}^{-{\displaystyle \frac{3}{4}}}cos\left({\displaystyle \frac{1}{3}}arcsin\sqrt{x}\right){cos}^2\left({\displaystyle \frac{11}{12}}arcsin\sqrt{x}\right)\hfill \\ \hfill & -{cosh}^3\left({\displaystyle \frac{1}{6}}{tanh}^{-1}\sqrt{x}\right),\hfill \end{array}$$

graphically on the interval $(0,1)$.

Example 4.

Since

$${\displaystyle \frac{arctanx}{x}}={}_{2}F_1\left(\left.\begin{array}{c}\begin{array}{cc}{\displaystyle \frac{1}{2}},& 1\end{array}\\ {\displaystyle \frac{3}{2}}\end{array}\right|-x^2\right),$$

(25)

and

$${\displaystyle \frac{1}{x}}ln(x+\sqrt{1+x^2})={}_{2}F_1\left(\left.\begin{array}{c}\begin{array}{cc}{\displaystyle \frac{1}{2}},& {\displaystyle \frac{1}{2}}\end{array}\\ {\displaystyle \frac{3}{2}}\end{array}\right|-x^2\right),$$

(26)

replacing them with $p=q=2$ in (24) eventually yields

$${\left(arctanx\right)}^2\le {\displaystyle \frac{xln(x+\sqrt{1+x^2})}{\sqrt{1+x^2}}},(x\in \mathbb{R}).$$

(27)

The inequality (27) has recently attracted the attention of some authors [9,10,11,12].

Now, replacing (25) and (26) in the main inequality (22) gives

$$x{}_{2}F_1\left(\left.\begin{array}{c}\begin{array}{cc}{\displaystyle \frac{1}{2}},& 1-{\displaystyle \frac{1}{2q}}\end{array}\\ {\displaystyle \frac{3}{2}}\end{array}\right|-x^2\right)\le {(arctanx)}^{{\displaystyle \frac{1}{p}}}{\left(ln(x+\sqrt{1+x^2})\right)}^{{\displaystyle \frac{1}{q}}},x\in [0,1].$$

(28)

2.6. An Inequality for the Confluent Hypergeometric Function

The hypergeometric series

$${}_{2}F_1\left(\left.\begin{array}{c}a\\ c\end{array}\right|x\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{{\left(a\right)}_k}{{\left(c\right)}_k}}{\displaystyle \frac{x^k}{k!}},$$

(29)

is convergent for any $x\in \mathbb{R}$ (where $c\ne 0,-1,-2,\dots$), whose integral representation is denoted by

$${}_{1}F_1\left(\left.\begin{array}{c}a\\ c\end{array}\right|x\right)={\displaystyle \frac{\Gamma \left(c\right)}{\Gamma \left(a\right)\Gamma (c-a)}}{\int }_0^1{t}^{a-1}{(1-t)}^{c-a-1}{e}^{xt}dt,(c>a>0).$$

(30)

In order to apply (30) for deriving a straightforward inequality of type (10) for the confluent hypergeometric function (29), we first substitute

$$\begin{array}{cc}\hfill & g_1\left(t\right)=t^{a-2}=|g_1\left(t\right)|,g_2\left(t\right)=t=|g_2\left(t\right)|,g_3\left(t\right)={(1-t)}^{c-a-2}=\left|g_3\left(t\right)\right|,\hfill \\ \hfill & g_4\left(t\right)=1-t=|g_4\left(t\right)|,g_5\left(t\right)=e^{xt}=\left|g_5\left(t\right)\right|,\hfill \\ \hfill & r_1=r_3={\displaystyle \frac{2}{p}}-1,r_2={\displaystyle \frac{2}{p}}(A-a+1)-1,r_4={\displaystyle \frac{2}{p}}(C-A-c+a+1)-1,r_5={\displaystyle \frac{2s}{qx}}-1,\hfill \end{array}$$

into (4) to obtain

$$\begin{array}{cc}\hfill \mathbf{B}(a,c-a){}_{1}F_1\left(\left.\begin{array}{c}a\\ c\end{array}\right|x\right)& \le {\left({\int }_0^1{t}^{A-1}{(1-t)}^{C-A-1}{e}^{{\displaystyle \frac{sp}{q}}t}dt\right)}^{{\displaystyle \frac{1}{p}}}\hfill \\ \hfill & \times {\left({\int }_0^1{t}^{(a-{\displaystyle \frac{A}{p}})q-1}{(1-t)}^{(c-a-{\displaystyle \frac{C-A}{p}})q-1}{e}^{(xq-s)t}dt\right)}^{{\displaystyle \frac{1}{q}}},\hfill \end{array}$$

which is equivalent to

$$\begin{array}{cc}\hfill {}_{1}F_1\left(\left.\begin{array}{c}a\\ c\end{array}\right|x\right)& \le {\displaystyle \frac{{\mathbf{B}}^{\frac{1}{p}}(A,C-A){\mathbf{B}}^{\frac{1}{q}}\left((a-\frac{A}{p})q,(c-a-\frac{C-A}{p})q\right)}{\mathbf{B}(a,c-a)}}\hfill \\ \hfill & \times {{}_{1}F_1}^{{\displaystyle \frac{1}{p}}}\left(\left.\begin{array}{c}A\\ C\end{array}\right|{\displaystyle \frac{sp}{q}}\right){{}_{1}F_1}^{{\displaystyle \frac{1}{q}}}\left(\left.\begin{array}{c}(a-{\displaystyle \frac{A}{p}})q\\ (c-{\displaystyle \frac{C}{p}})q\end{array}\right|xq-s\right),\hfill \end{array}$$

(31)

where $0<a<c$, $0<A<C$ and $0<ap-A<cp-C$.

Also, if $(a-{\displaystyle \frac{A}{p}})q=A^{*}$ and $(c-{\displaystyle \frac{C}{p}})q=C^{*}$, (31) changes to the standard form

$$\begin{array}{c}{}_{1}F_1\left(\left.\begin{array}{c}{\displaystyle \frac{A}{p}}+{\displaystyle \frac{A^{*}}{q}}\\ {\displaystyle \frac{C}{p}}+{\displaystyle \frac{C^{*}}{q}}\end{array}\right|x\right)\le {\displaystyle \frac{{\mathbf{B}}^{\frac{1}{p}}(A,C-A){\mathbf{B}}^{\frac{1}{q}}(A^{*},C^{*}-A^{*})}{\mathbf{B}\left(\frac{A}{p}+\frac{A^{*}}{q},\frac{C-A}{p}+\frac{C^{*}-A^{*}}{q}\right)}}\hfill \\ \hfill \times {{}_{1}F_1}^{{\displaystyle \frac{1}{p}}}\left(\left.\begin{array}{c}A\\ C\end{array}\right|{\displaystyle \frac{sp}{q}}\right){{}_{1}F_1}^{{\displaystyle \frac{1}{q}}}\left(\left.\begin{array}{c}{A}^{*}\\ C^{*}\end{array}\right|xq-s\right).\end{array}$$

(32)

Finally if s is considered to be $s=(q-1)x$, (32) is written as

$${}_{1}F_1\left(\left.\begin{array}{c}{\displaystyle \frac{A}{p}}+{\displaystyle \frac{A^{*}}{q}}\\ {\displaystyle \frac{C}{p}}+{\displaystyle \frac{C^{*}}{q}}\end{array}\right|x\right)\le {\displaystyle \frac{{\mathbf{B}}^{\frac{1}{p}}(A,C-A){\mathbf{B}}^{\frac{1}{q}}(A^{*},C^{*}-A^{*})}{\mathbf{B}\left(\frac{A}{p}+\frac{A^{*}}{q},\frac{C-A}{p}+\frac{C^{*}-A^{*}}{q}\right)}}{{}_{1}F_1}^{{\displaystyle \frac{1}{p}}}\left(\left.\begin{array}{c}A\\ C\end{array}\right|x\right){{}_{1}F_1}^{{\displaystyle \frac{1}{q}}}\left(\left.\begin{array}{c}{A}^{*}\\ C^{*}\end{array}\right|x\right).$$

(33)

As before, interesting cases in (33) are when the parameters p and q take special values. For instance, if $p=3$ and $q={\displaystyle \frac{3}{2}}$, then (33) changes to

$${}_{2}F_1^3\left(\left.\begin{array}{c}{\displaystyle \frac{A+2A^{*}}{3}}\\ {\displaystyle \frac{C+2C^{*}}{3}}\end{array}\right|x\right)\le {\displaystyle \frac{\mathbf{B}(A,C-A){\mathbf{B}}^2(A^{*},C^{*}-A^{*})}{{\mathbf{B}}^3\left(\frac{A+2A^{*}}{3},\frac{C-A+2(C^{*}-A^{*})}{3}\right)}}{}_{1}F_1\left(\left.\begin{array}{c}A\\ C\end{array}\right|x\right){{}_{1}F_1}^2\left(\left.\begin{array}{c}{A}^{*}\\ C^{*}\end{array}\right|x\right).$$

(34)

It is now possible to consider many particular cases for inequality (34).

Example 5.

Noting that [8]

$$\begin{array}{cc}\hfill & (\alpha -1)x^{1-\alpha }{e}^x\left(\Gamma (\alpha -1)-\Gamma (\alpha -1,x)\right)={}_{1}F_1\left(\left.\begin{array}{c}1\\ \alpha \end{array}\right|x\right),\hfill \\ \hfill & \alpha {(-x)}^{-\alpha }\left(\Gamma \left(\alpha \right)-\Gamma (\alpha ,-x)\right)={}_{1}F_1\left(\left.\begin{array}{c}\alpha \\ \alpha +1\end{array}\right|x\right),\hfill \end{array}$$

and

$${\displaystyle \frac{2+2e^x(x-1)}{x^2}}={}_{1}F_1\left(\left.\begin{array}{c}2\\ 3\end{array}\right|x\right),$$

in which $\Gamma (s,x)$ denotes the upper incomplete gamma function

$$\Gamma (s,x)={\int }_x^{\infty }{t}^{s-1}{e}^{-t}dt,$$

according to the inequality

$${}_{1}F_1^3\left(\left.\begin{array}{c}1\\ 2\end{array}\right|-x^2\right)\le {\displaystyle \frac{\mathbf{B}(2,1){\mathbf{B}}^2(\frac{1}{2},1)}{{\mathbf{B}}^3(1,1)}}{}_{1}F_1\left(\left.\begin{array}{c}2\\ 3\end{array}\right|-x^2\right){{}_{1}F_1}^2\left(\left.\begin{array}{c}{\displaystyle \frac{1}{2}}\\ {\displaystyle \frac{3}{2}}\end{array}\right|-x^2\right),$$

we obtain

$$-x^{-6}{e}^{-3x^2}{(1-e^{x^2})}^3\le {\displaystyle \frac{1-e^{-x^2}(1+x^2)}{x^6}}{\left(\sqrt{\pi }-\sqrt{\pi }\mathrm{erfc}\left(x\right)\right)}^2,$$

which is equivalent to

$${\displaystyle \frac{1}{\pi }}{\displaystyle \frac{{(e^{-x^2}-1)}^3}{e^{-x^2}(1+x^2)-1}}\le {\left(\mathrm{erf}\left(x\right)\right)}^2.$$

Note that $\mathrm{erf}\left(x\right)$ indicates the error function as follows:

$$\mathrm{erf}\left(x\right)={\displaystyle \frac{2}{\sqrt{\pi }}}{\int }_0^x{e}^{-t^2}dt.$$

In this sense, Figure 6 shows the positivity of the function

$$G_4\left(x\right)={\left(\mathrm{erf}\left(x\right)\right)}^2-{\displaystyle \frac{1}{\pi }}{\displaystyle \frac{{(e^{-x^2}-1)}^3}{e^{-x^2}(1+x^2)-1}},$$

graphically on the real axis $\mathbb{R}$.

3. Conclusions

In this work, based on the well-known Hölder inequality, we introduced a generic inequality for continuous functions and showed that many basic special functions, such as the gamma and polygamma functions, Riemann zeta function, beta function and Gauss and confluent hypergeometric functions satisfy this type of inequality. We also obtained some particular inequalities for the Gauss and confluent hypergeometric functions to confirm our main obtained inequalities.