Dynamic Analysis and Approximate Solution of Transient Stability Targeting Fault Process in Power Systems
Abstract
:1. Introduction
- (1)
- Polynomial Model. Based on observing the sinusoidal coupling characteristics of power grid swing equations, we employ Taylor expansion formulas to expand them into a series of homogeneous polynomials. This results in a generalized matrix description of power system swing equations in perturbation form, thus forming a polynomial mathematical model for power system transient stability.
- (2)
- Approximate Solution Method. During grid faults, we simplify the swing equations into a forced oscillation model and, considering the influence of faults, provide approximate solutions to power system swing equations during fault periods. After fault clearance, by introducing dual-timescale variables, we transform the nonlinear swing equations into a series of linear partial differential equations, obtaining analytical perturbation solutions to post-fault grid equations.
- (3)
- Application and Analysis. Theoretical analysis of approximate solutions demonstrates the rigorous mathematical foundation inherent in power system transient stability. Each solution component embodies distinct motion patterns. Furthermore, based on the structural composition of approximate solutions, we elucidate the morphological characteristics of grid stability motion. Through application to various scenarios, we explore the monotonicity patterns of power system rotor angle swing amplitudes with the fault-clearing time following major disturbances like three-phase short circuits. Finally, through simulations, we further confirm the effectiveness of theoretical analysis.
2. The Polynomial Mathematical Description of Power Systems
2.1. The Polynomial Model of Power Systems Based on Taylor Expansion
2.2. Polynomial Description and Approximate Solution of Power Systems during Fault Process
3. Analytical Method for Power System Transient Stability Equations after Fault Clearance
3.1. The Structural Properties of Block Decoupling for Power System Transient Stability
3.2. Approximate Transient Stability Solution of Power Systems after Fault Clearance
4. Case Study
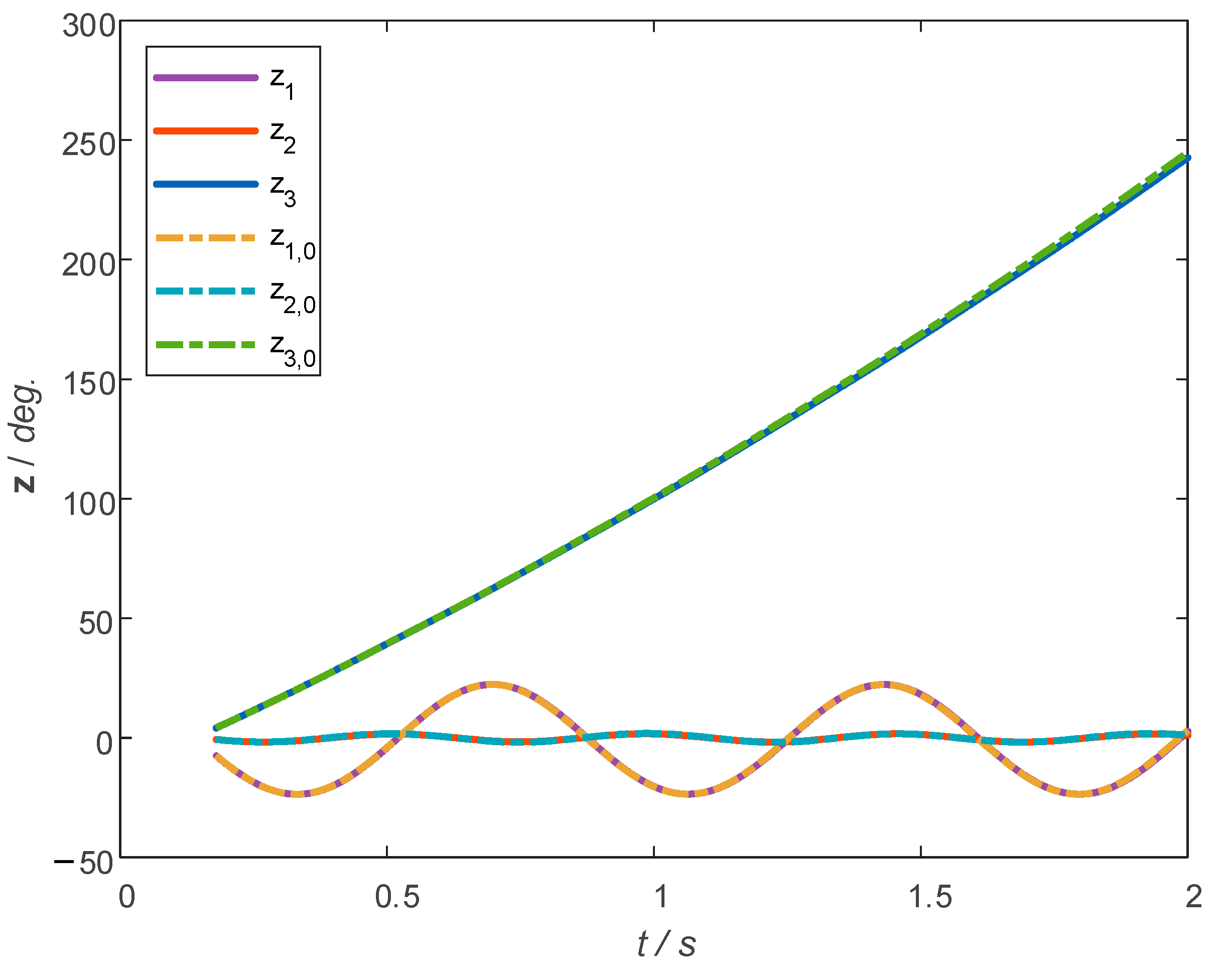
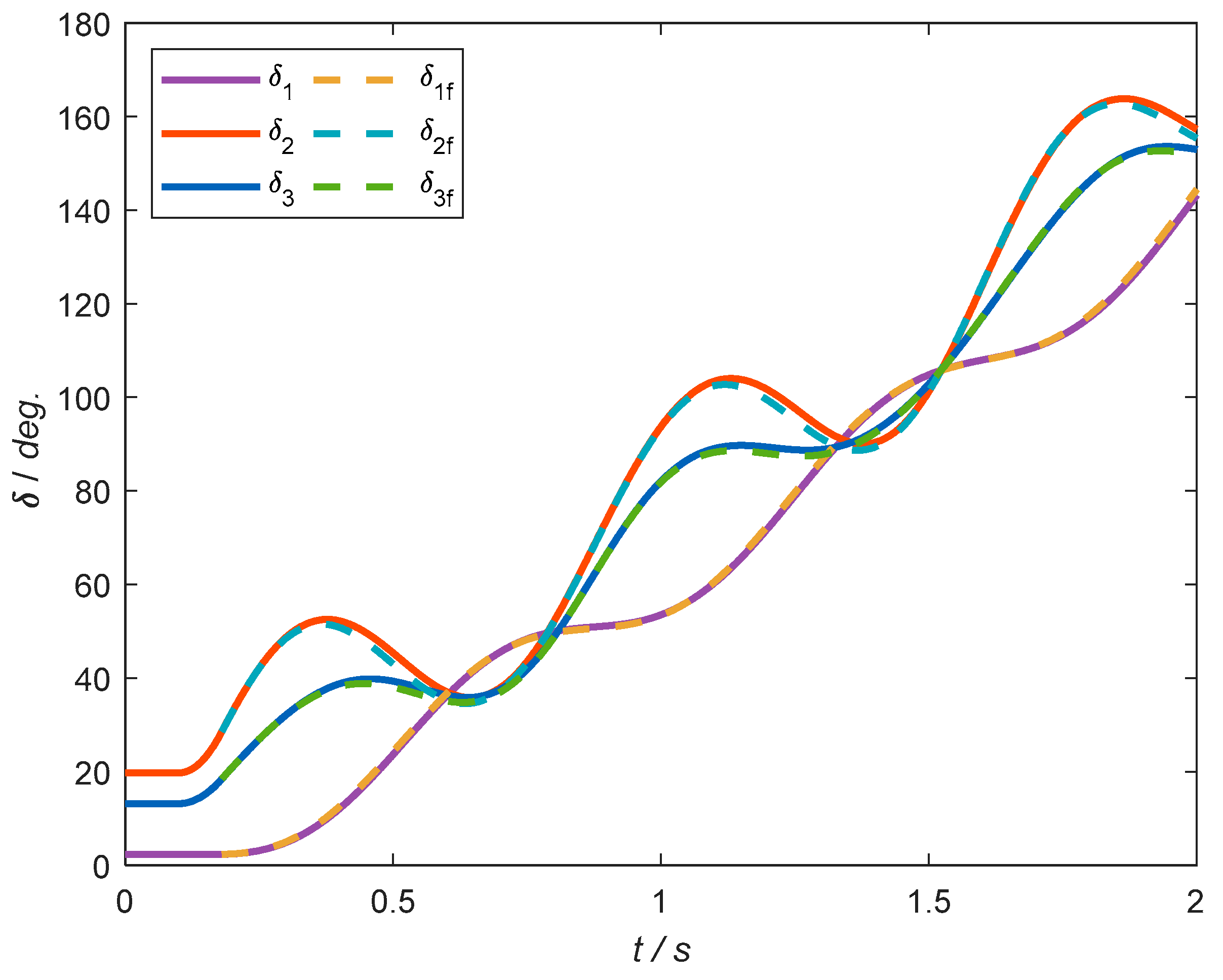
4.1. IEEE Three-Machine Nine-Bus Power System
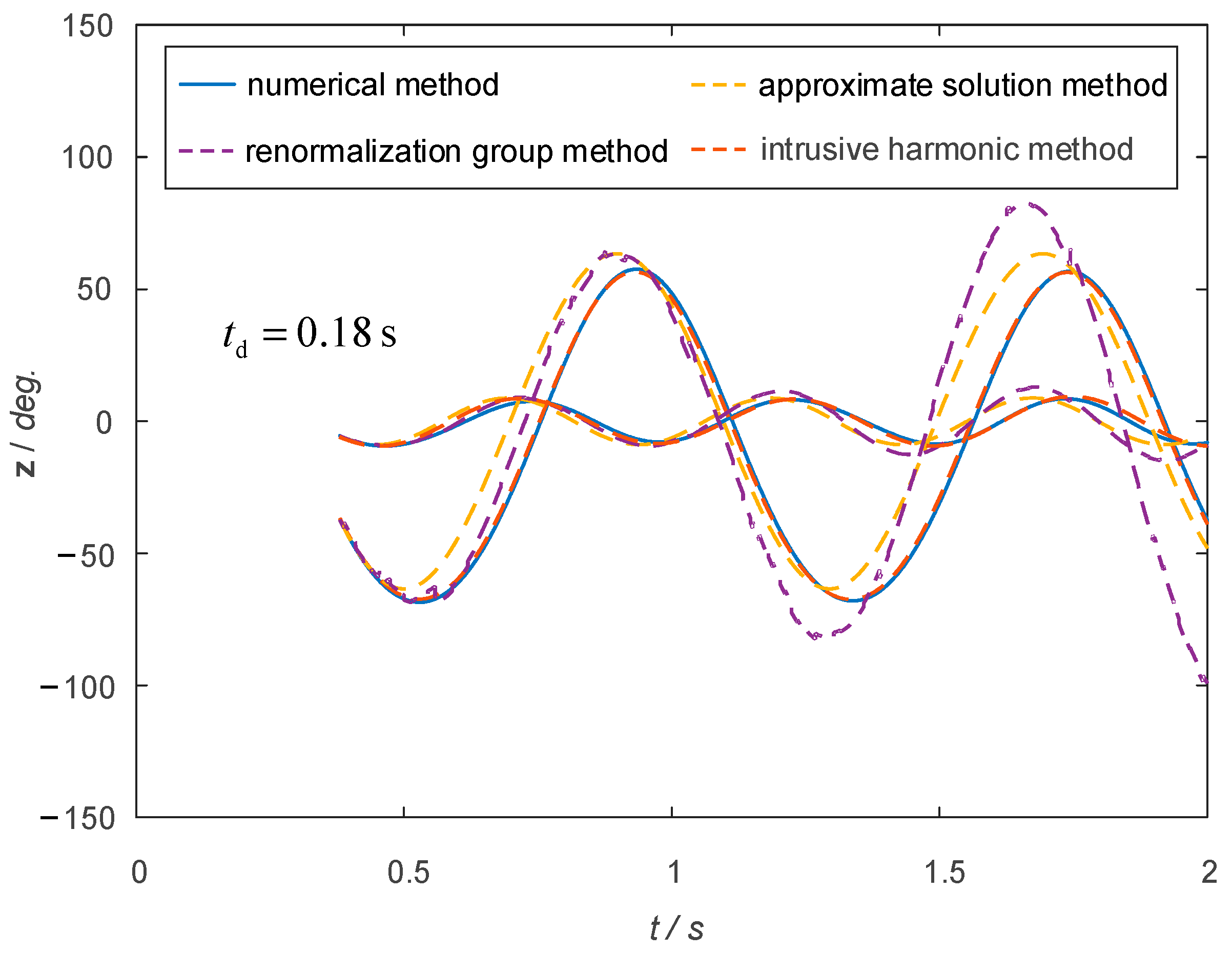
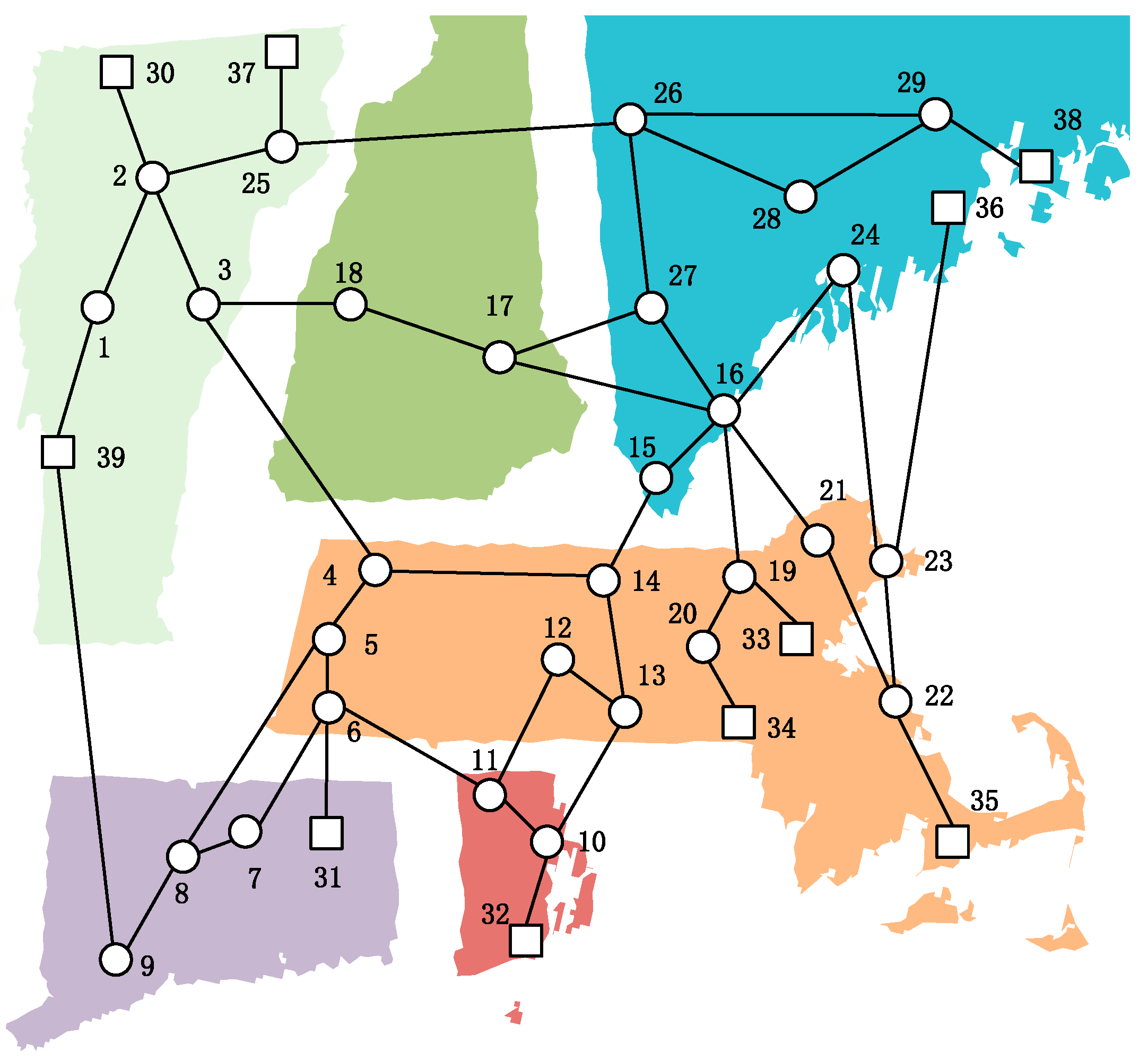
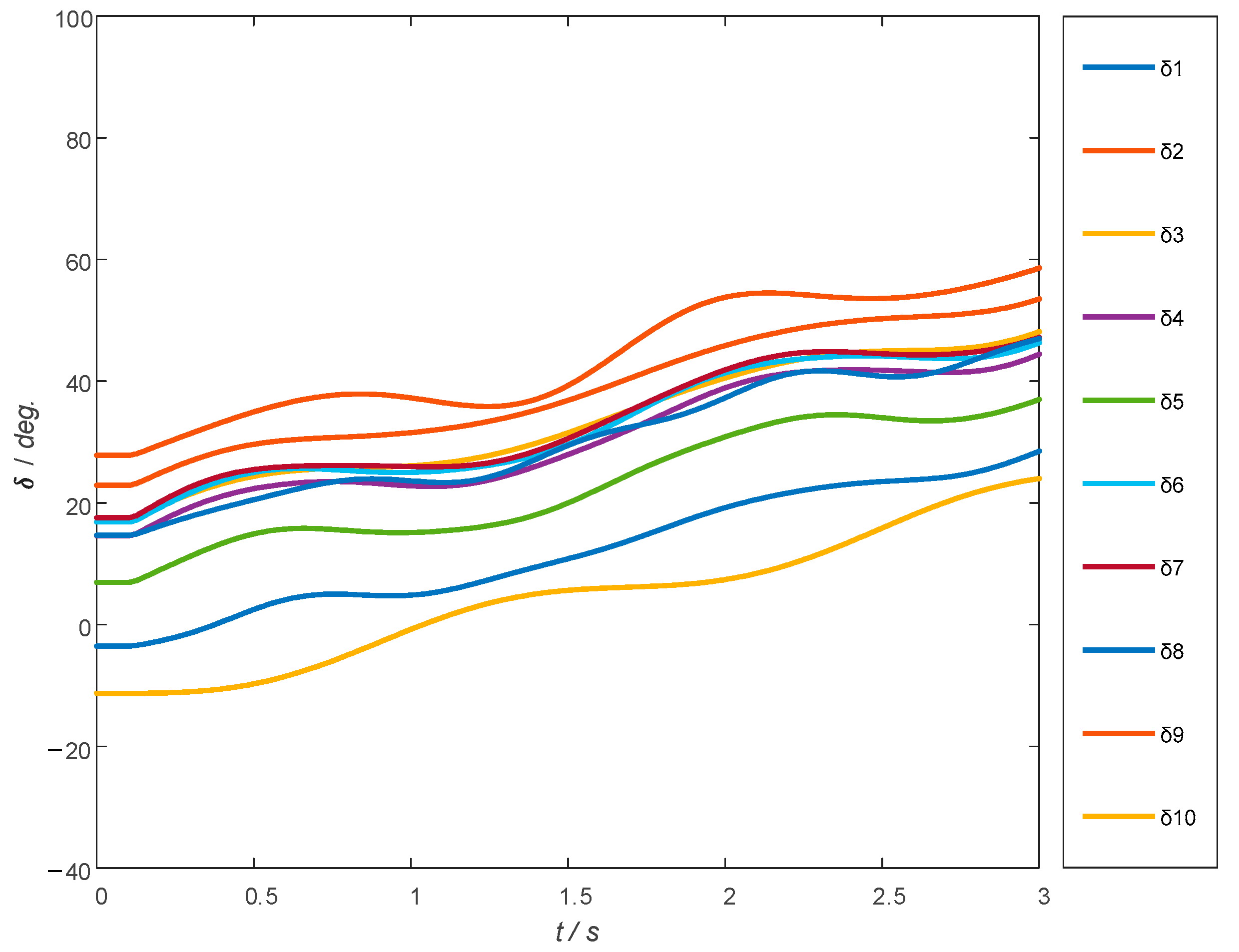
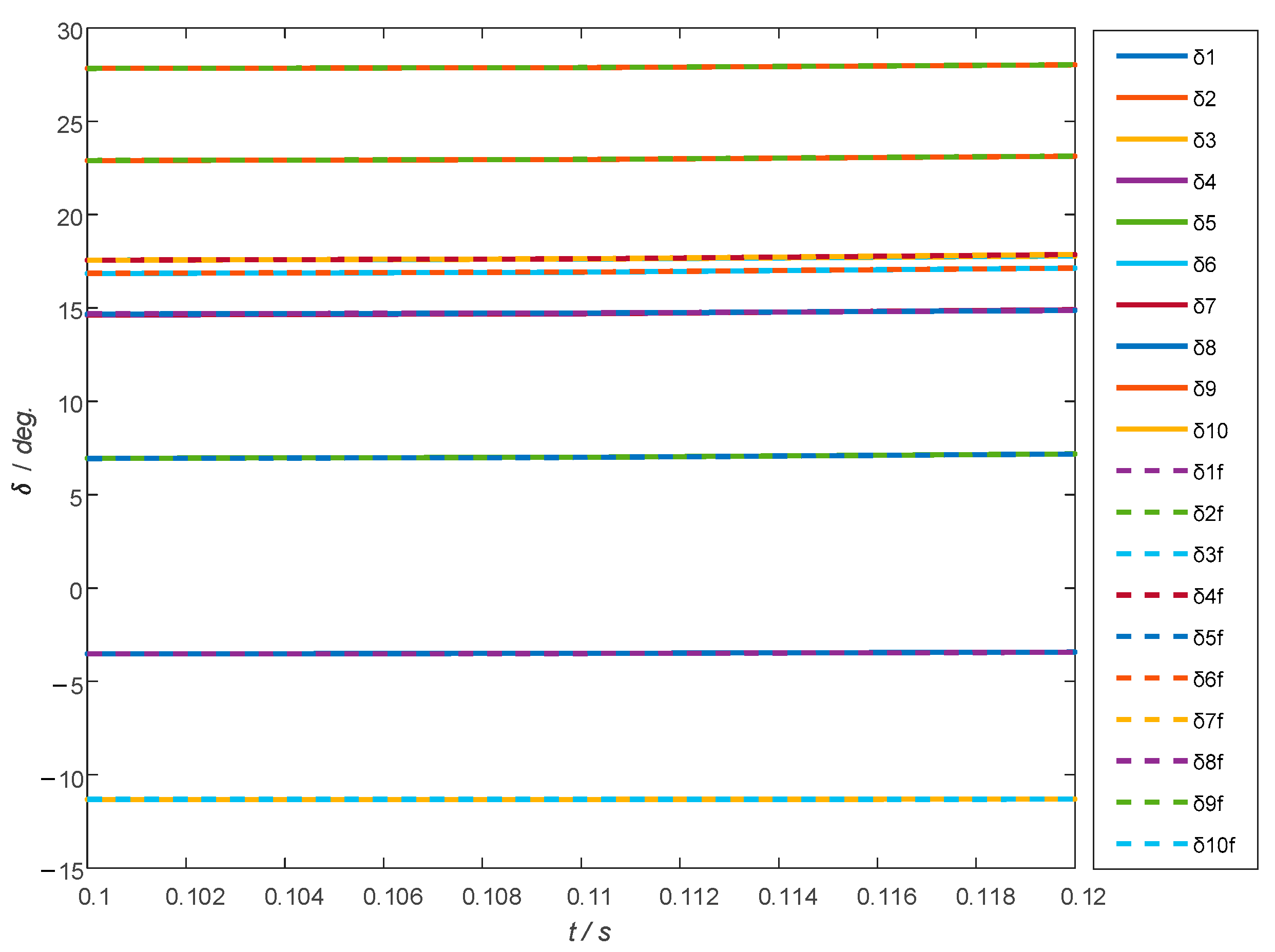
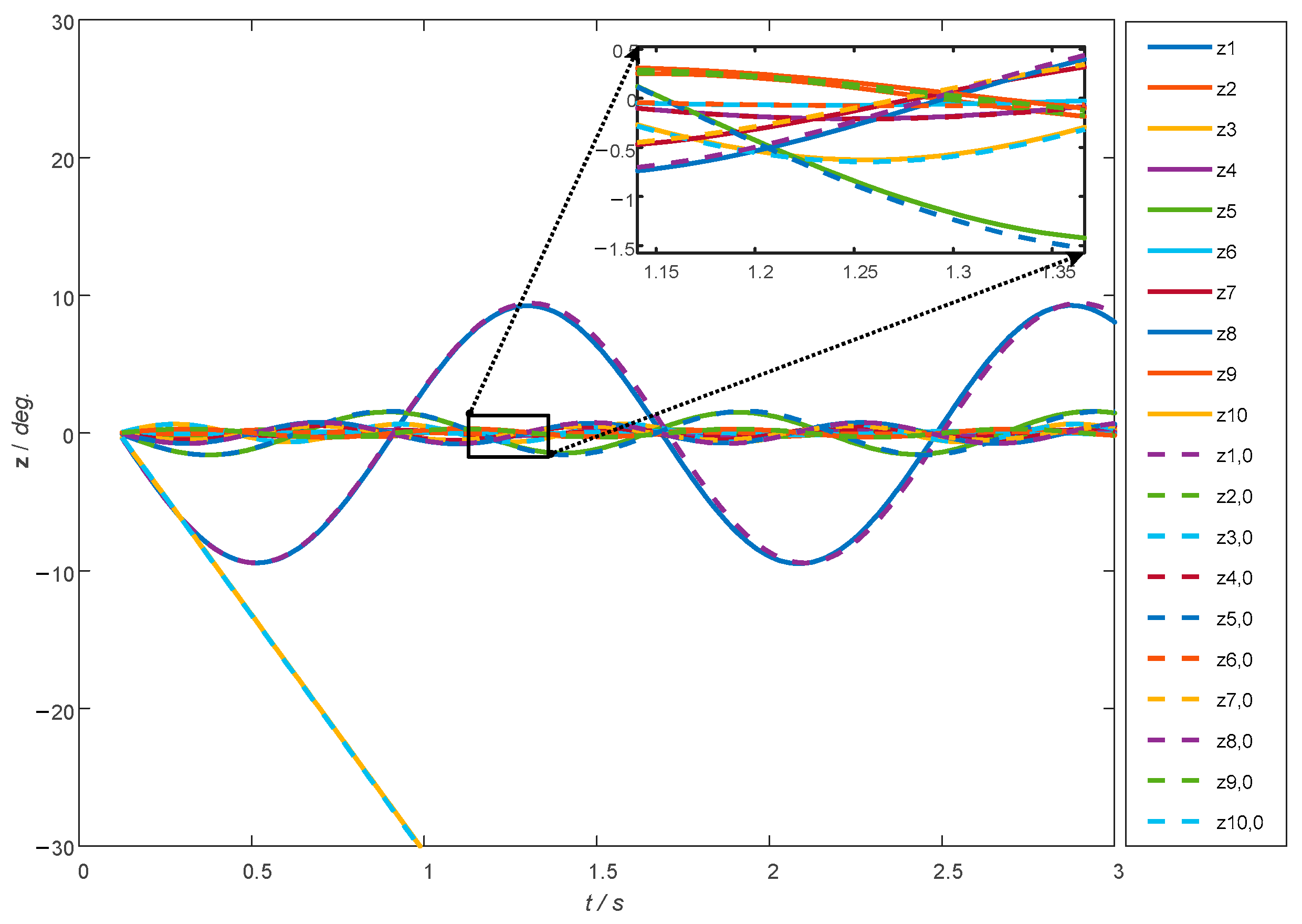
4.2. IEEE 10-Machine 39-Bus Power System
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mochamad, R.F.; Preece, R. Assessing the impact of VSC-HVDC on the interdependency of power system dynamic performance in uncertain mixed AC/DC systems. IEEE Trans. Power Syst. 2019, 35, 63–74. [Google Scholar] [CrossRef]
- Machowski, J.; Lubosny, Z.; Bialek, J.W. Power System Dynamics: Stability and Control; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Ma, R.; Zhang, Y.; Yang, Z. Synchronization stability of power-grid-tied converters. Chaos 2023, 33, 032102. [Google Scholar] [CrossRef] [PubMed]
- Touzé, C.; Vizzaccaro, A.; Thomas, O. Model order reduction methods for geometrically nonlinear structures: A review of nonlinear techniques. Nonlinear Dyn. 2021, 105, 1141–1190. [Google Scholar] [CrossRef]
- Saha, S.; Vittal, V.; Kliemann, W. Local approximation of stability boundary of a power system using the real normal form of vector fields. In Proceedings of the 1995 IEEE International Symposium on Circuits and Systems (ISCAS), Seattle, WA, USA, 30 April–3 May 1995; Volume 3, pp. 2330–2333. [Google Scholar]
- Saha, S.; Fouad, A.A.; Kliemann, W.H. Stability boundary approximation of a power system using the real normal form of vector fields. IEEE Trans. Power Syst. 1997, 12, 797–802. [Google Scholar] [CrossRef]
- Eftekharnejad, S.; Vittal, V.; Heydt, G.T. Impact of increased penetration of photovoltaic generation on power systems. IEEE Trans. Power Syst. 2012, 28, 893–901. [Google Scholar] [CrossRef]
- Hatziargyriou, N.; Milanovic, J.; Rahmann, C. Definition and classification of power system stability–revisited & extended. IEEE Trans. Power Syst. 2020, 36, 3271–3281. [Google Scholar]
- Qi, R. Investigation and Visualization of the Stability Boundary for Stressed Power Systems; Iowa State University: Ames, IA, USA, 1999. [Google Scholar]
- Jiang, L.; Wu, Q.H.; Wang, J. Robust observer-based nonlinear control of multimachine power systems. IEE Proc. Gener. Transm. Distrib. 2001, 148, 623–631. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, B.; Li, M. Study on Electrical Power System Stability Boundary. Proc. CSEE 2002, 22, 73–78. [Google Scholar]
- Cheng, D.; Hu, X.; Shen, T. Analysis and Design of Nonlinear Control Systems; Science Press: Alexandria, NSW, Australia, 2010. [Google Scholar]
- Xue, A.C.; Mei, S.W. Critical clearing time estimation of power system based on quadratic approximation of stability region. Autom. Electr. Power Syst. 2005, 29, 19–24. [Google Scholar]
- Liu, F.; Wei, W.; Mei, S.W. On expansion of estimated stability region: Theory, methodology, and application to power systems. Sci. China Technol. Sci. 2011, 54, 1394–1406. [Google Scholar] [CrossRef]
- Qiu, Q.; Ma, R.; Kurths, J. Swing equation in power systems: Approximate analytical solution and bifurcation curve estimate. Chaos 2020, 30, 013113. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Sun, K. Solving power system differential algebraic equations using differential transformation. IEEE Trans. Power Syst. 2019, 35, 2289–2299. [Google Scholar] [CrossRef]
- Gurrala, G.; Joseph, F.C. Application of Homotopy Methods in Power Systems Simulations. In Power System Simulation Using Semi-Analytical Methods; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2023; pp. 197–238. [Google Scholar] [CrossRef]
- Zhang, W.; Hu, H.L.; Qian, Y.H. A refined asymptotic perturbation method for nonlinear dynamical systems. Arch. Appl. Mech. 2014, 84, 591–606. [Google Scholar] [CrossRef]
- Wang, F.; Bajaj, A.K. On the Formal Equivalence of Normal Form Theory and the Method of Multiple Time Scales. J. Comput. Nonlinear Dyn. 2009, 4, 021005. [Google Scholar] [CrossRef]
- Rega, G. Nonlinear dynamics in mechanics and engineering: 40 years of developments and Ali H. Nayfeh’s legacy. Nonlinear Dyn. 2020, 99, 11–34. [Google Scholar] [CrossRef]
- Krutii, Y.; Vasiliev, A. Development of the Analytical Method of the General Mathieu Equation Solution. East.-Eur. J. Enterp. Technol. 2018, 4, 19–26. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Starosta, R.; Sypniewska-Kamińska, G. Asymptotic analysis of resonances in nonlinear vibrations of the 3-dof pendulum. Differ. Equ. Dyn. Syst. 2013, 21, 123–140. [Google Scholar] [CrossRef]
- Sigamani, V.; Miller, J.J.H.; Narasimhan, R. Differential Equations and Numerical Analysis; Springer: New Delhi, India, 2015. [Google Scholar]
- Zhang, Q.; Gan, D. A Gronwall Inequality Based Approach to Transient Stability Assessment for Power Grids. arXiv 2023, arXiv:2311.02231. [Google Scholar]
- Luongo, A.; Zulli, D. Dynamic analysis of externally excited NES-controlled systems via a mixed Multiple Scale/Harmonic Balance algorithm. Nonlinear Dyn. 2012, 70, 2049–2061. [Google Scholar] [CrossRef]
- Vittal, V.; McCalley, J.D.; Anderson, P.M. Power System Control and Stability; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Fouad, A.A.; Vittal, V. Power System Transient Stability Analysis Using the Transient Energy Function Method; Prentice Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]






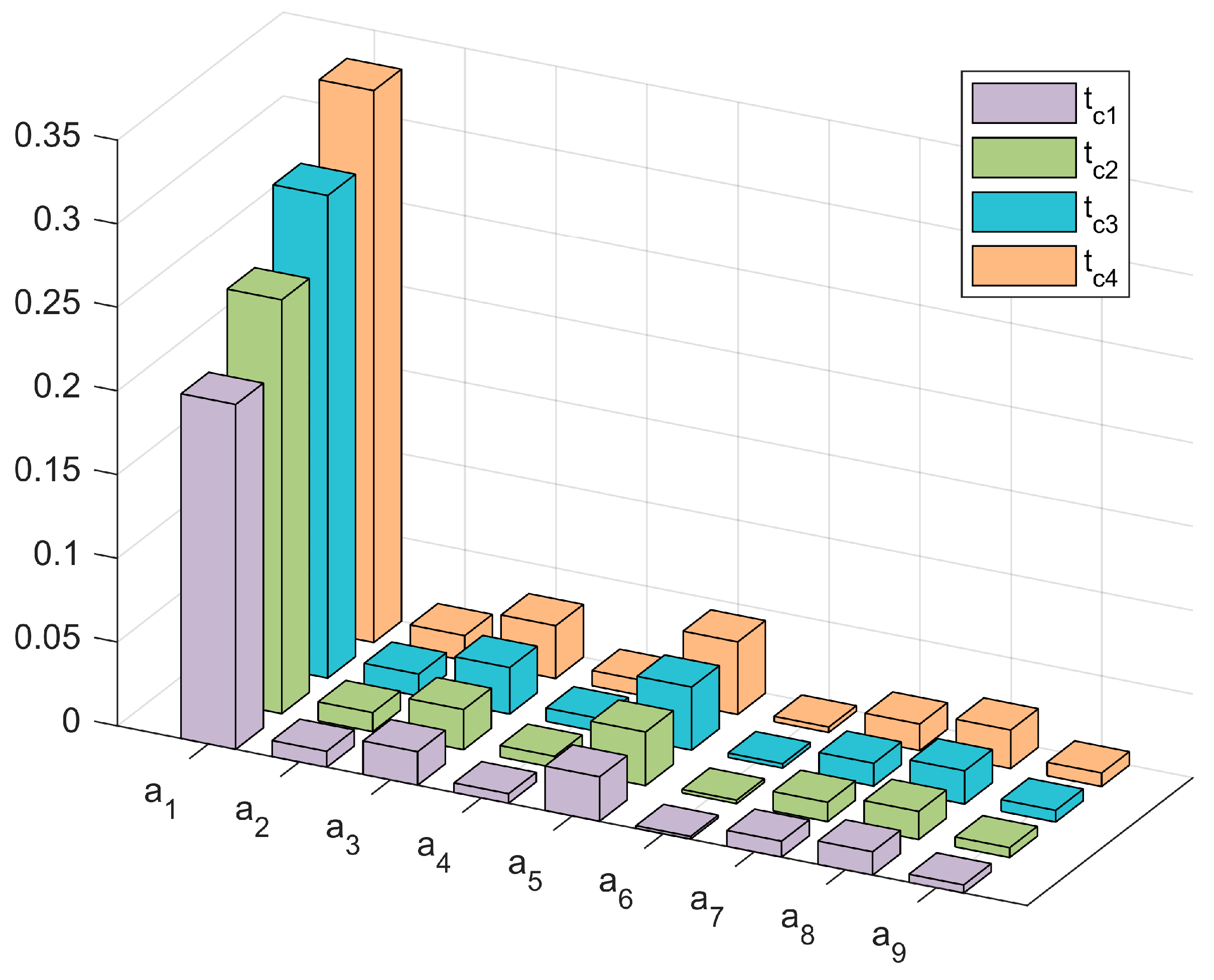
| Generator | D | X’d | Xq | |
|---|---|---|---|---|
| G1 | 23.64 | 0 | 0.0608 | 0.0969 |
| G2 | 6.40 | 0 | 0.1198 | 0.8645 |
| G3 | 3.01 | 0 | 0.1813 | 1.2578 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Li, J. Dynamic Analysis and Approximate Solution of Transient Stability Targeting Fault Process in Power Systems. Mathematics 2024, 12, 3065. https://doi.org/10.3390/math12193065
Wu H, Li J. Dynamic Analysis and Approximate Solution of Transient Stability Targeting Fault Process in Power Systems. Mathematics. 2024; 12(19):3065. https://doi.org/10.3390/math12193065
Chicago/Turabian StyleWu, Hao, and Jing Li. 2024. "Dynamic Analysis and Approximate Solution of Transient Stability Targeting Fault Process in Power Systems" Mathematics 12, no. 19: 3065. https://doi.org/10.3390/math12193065
APA StyleWu, H., & Li, J. (2024). Dynamic Analysis and Approximate Solution of Transient Stability Targeting Fault Process in Power Systems. Mathematics, 12(19), 3065. https://doi.org/10.3390/math12193065





