Mathematical and Statistical Analysis of Fused Filament Fabrication Parameters for Thermoplastic Polyurethane Parts via Response Surface Methodology
Abstract
:1. Introduction
2. Materials and Experiments
2.1. Design of Experiments (DOE)
2.2. Material and Part Fabrication
2.3. Characterization Methods
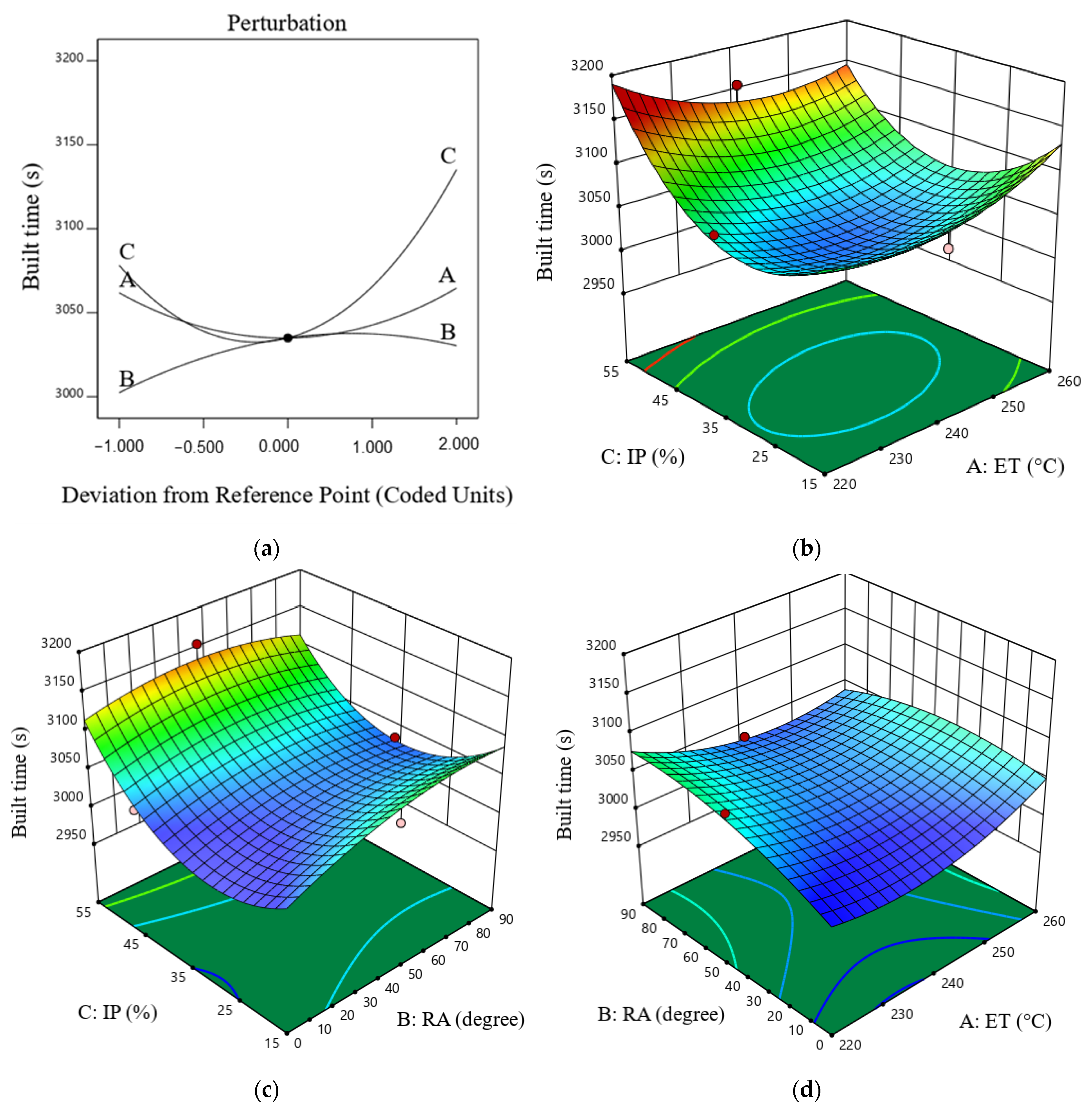
3. Results and Discussion
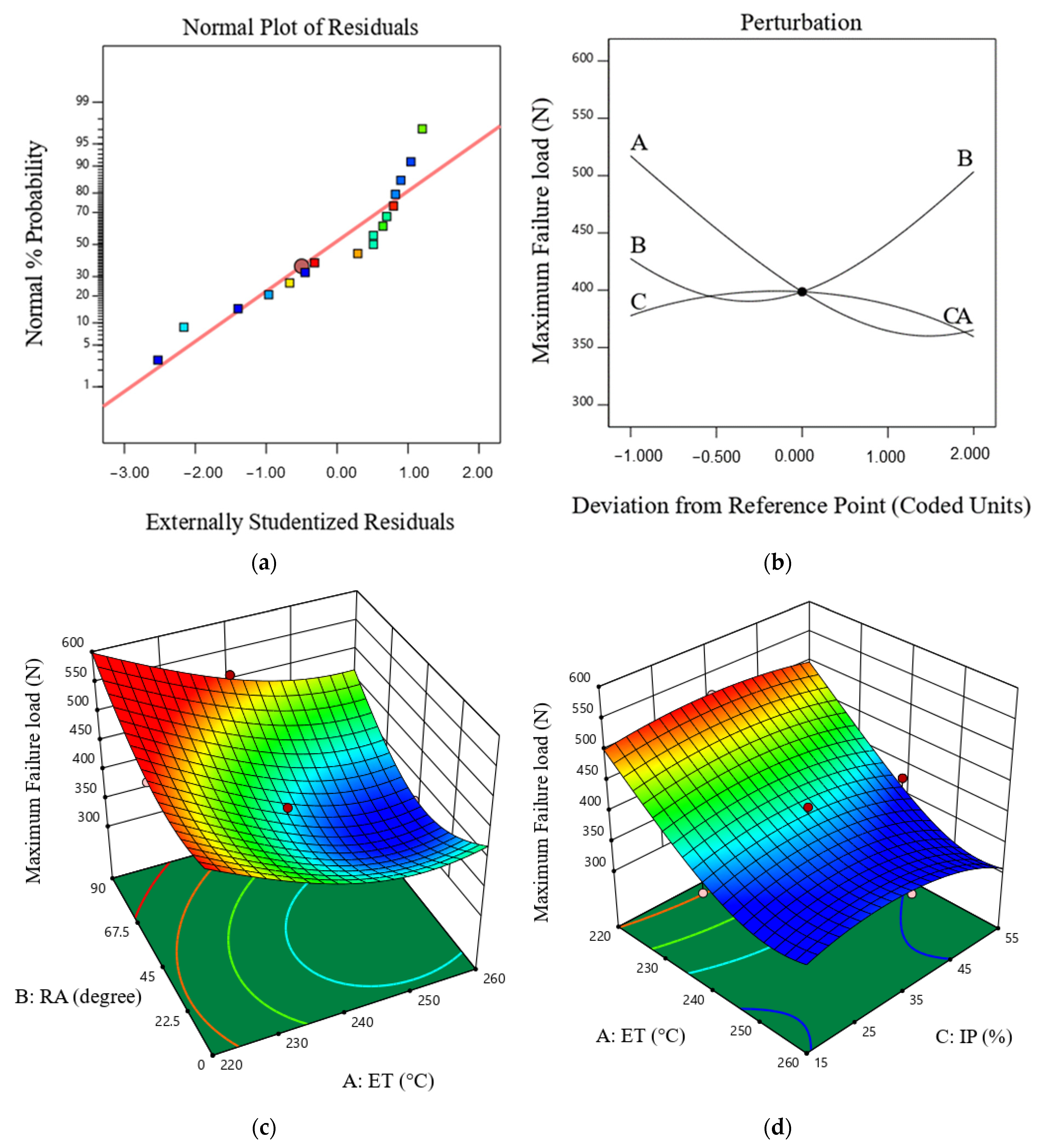
3.1. Maximum Failure Load Model
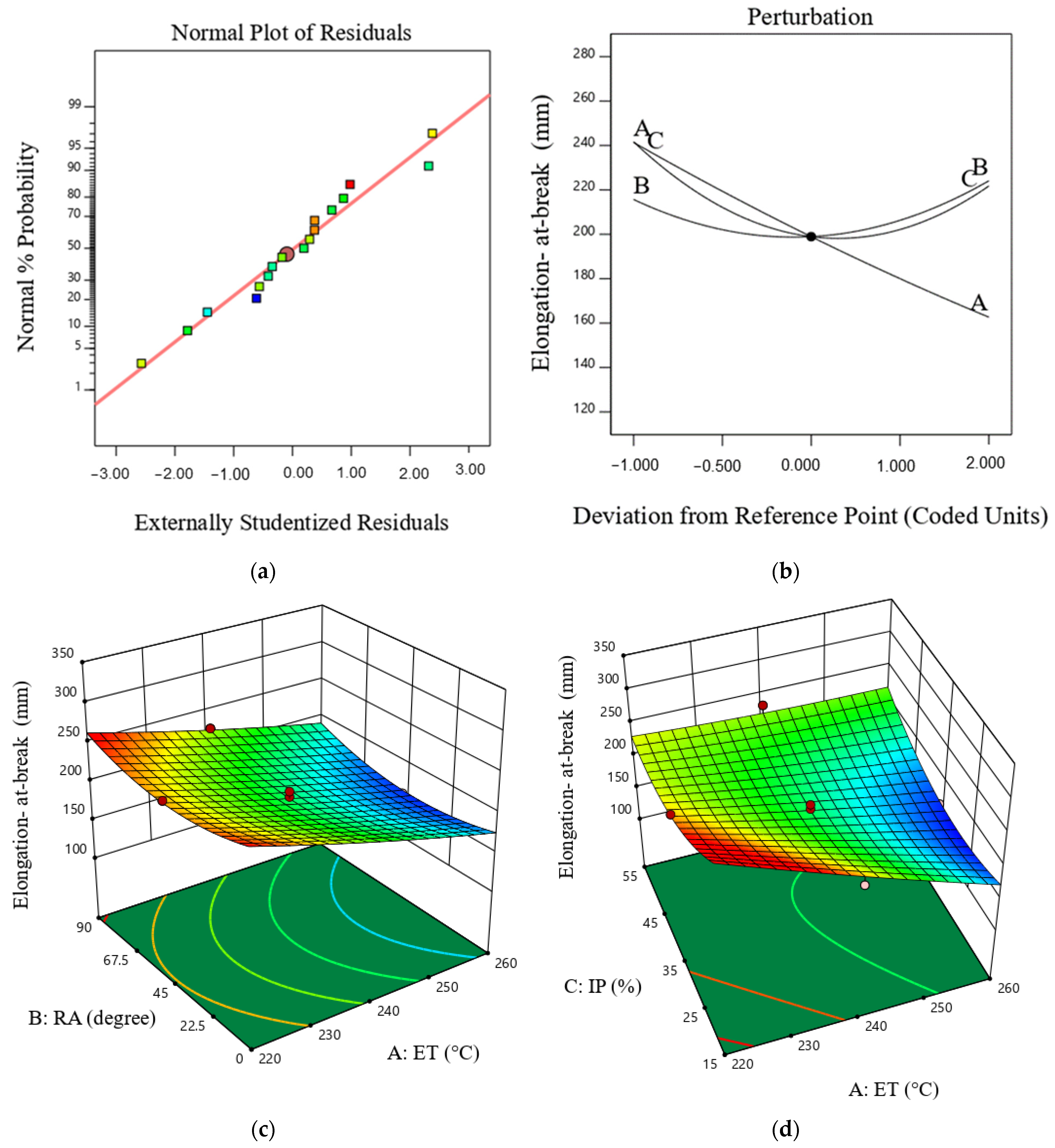
3.2. Elongation at Break Model
3.3. Part Weight Model
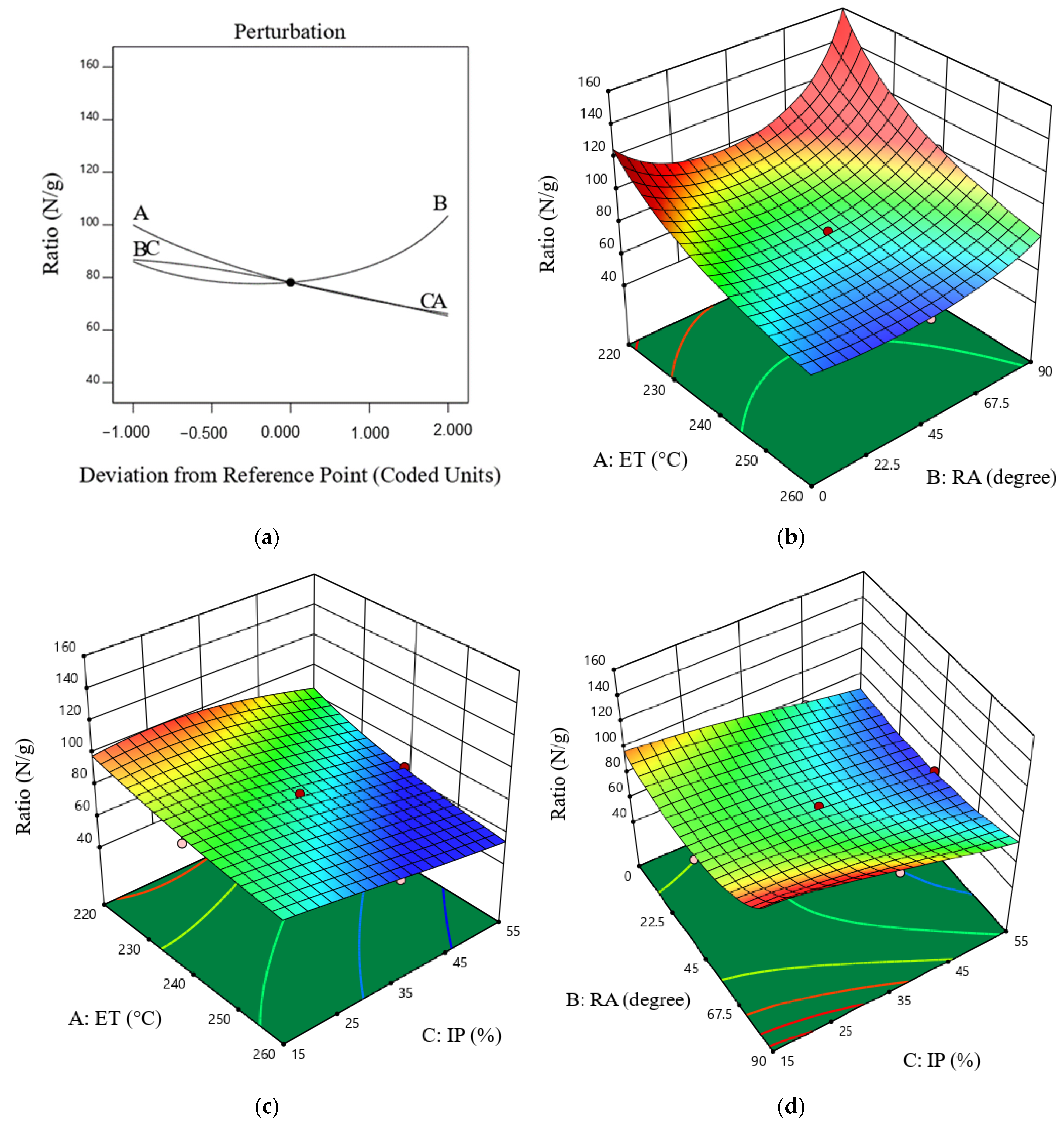
3.4. Ratio of the Maximum Failure Load to Part Weight Model
3.5. Build Time Model
4. Multi-Response Optimization
5. Conclusions
- (1)
- Among the input factors in the FFF process, extruder temperature is the most significant, exerting an inverse effect on mechanical properties (elongation at break and maximum failure load).
- (2)
- The TPU part printed with a raster angle of 45 degrees, an infill percentage of 35%, and an extruder temperature of 220 °C achieved the highest maximum failure load of 515 N.
- (3)
- Increasing the infill percentage increases the weight and build time of TPU parts. Additionally, the raster angle does not affect the part weight and build time. By comparing samples 3 and 4, it is determined that at a constant extruder temperature and raster angle, increasing the infill percentage from 15% to 50% resulted in a 30.8% increase in the part weight.
- (4)
- Within the range of the factors studied in this study, with a decrease in ET and IP, the ratio of the maximum failure load to part weight of the TPU parts increases.
- (5)
- It was found that an ET of 220 °C, an RA of 0°, and an IP of 15% are the optimal combination of input variables for achieving the highest maximum failure load of 511 N, maximum elongation at break of 321 mm, ratio of 124 N/g, build time of 3015 s, and minimum part weight of 4.40 g of the 3D-printed TPU. The value of the desirability obtained is 0.988.
6. Future Research
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mehrabi, O.; Hossein Seyedkashi, S.M.; Moradi, M. Effect of the Laser Power on the Geometrical Features of 316L Stainless Steel Additively Manufactured by Direct Laser Metal Deposition (DLMD). Lasers Eng. 2023, 56, 127. [Google Scholar]
- Mehrabi, O.; Seyedkashi, S.M.H.; Moradi, M. Experimental study of SS316L, Inconel 625, and SS316L-IN625 functionally graded material produced by direct laser metal deposition process. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2024, 238, 8139–8150. [Google Scholar] [CrossRef]
- Cusator, A.; Key, N.L. Development of a Novel Transonic Fan Casing Making Use of Rapid Prototyping and Additive Manufacturing. Appl. Sci. 2024, 14, 8400. [Google Scholar] [CrossRef]
- Wang, J.; Fu, A.; Liu, B.; Chen, Y.; Cao, Y.; Zhou, H.; Wang, B.; Li, X.; Li, J.; Fang, Q.; et al. Weakening the mechanical property anisotropy of additively manufactured medium entropy alloy by controlling the cellular structure. Addit. Manuf. 2024, 89, 104303. [Google Scholar] [CrossRef]
- Cao, Y.; Chen, C.; Xu, S.; Zhao, R.; Guo, K.; Hu, T.; Liao, H.; Wang, J.; Ren, Z. Machine learning assisted prediction and optimization of mechanical properties for laser powder bed fusion of Ti6Al4V alloy. Addit. Manuf. 2024, 91, 104341. [Google Scholar] [CrossRef]
- Lalegani Dezaki, M.; Mohd Ariffin, M.K.A.; Hatami, S. An overview of fused deposition modelling (FDM): Research, development and process optimisation. Rapid Prototyp. J. 2021, 27, 562–582. [Google Scholar] [CrossRef]
- Karthick, N.; Soundararajan, R.; Arul, R.; Prasanth, J.A. Evolution of Tribological Performance of Polypropylene with Carbon Fibre Composites Fabricated Through FDM Technology by Varying Infill Density. J. Inst. Eng. Ser. D 2024, 105, 961–968. [Google Scholar] [CrossRef]
- Karimi, A.; Rahmatabadi, D.; Baghani, M. Various FDM Mechanisms Used in the Fabrication of Continuous-Fiber Reinforced Composites: A Review. Polymers 2024, 16, 831. [Google Scholar] [CrossRef]
- Jiang, Y.; Liu, L.; Yan, J.; Wu, Z. Room-to-low temperature thermo-mechanical behavior and corresponding constitutive model of liquid oxygen compatible epoxy composites. Compos. Sci. Technol. 2024, 245, 110357. [Google Scholar] [CrossRef]
- Nathaphan, S.; Trutassanawin, W. Effects of process parameters on compressive property of FDM with ABS. Rapid Prototyp. J. 2021, 27, 905–917. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, K.; Li, Y.; Chen, F. Mechanical characterization of biocompatible PEEK by FDM. J. Manuf. Process. 2020, 56, 28–42. [Google Scholar] [CrossRef]
- Mohamed, O.A.; Masood, S.H.; Bhowmik, J.L.; Nikzad, M.; Azadmanjiri, J. Effect of Process Parameters on Dynamic Mechanical Performance of FDM PC/ABS Printed Parts Through Design of Experiment. J. Mater. Eng. Perform. 2016, 25, 2922–2935. [Google Scholar] [CrossRef]
- Alarifi, I.M. Mechanical properties and numerical simulation of FDM 3D printed PETG/carbon composite unit structures. J. Mater. Res. Technol. 2023, 23, 656–669. [Google Scholar] [CrossRef]
- Shin, E.J.; Jung, Y.S.; Choi, H.Y.; Lee, S. Synthesis and fabrication of biobased thermoplastic polyurethane filament for FDM 3D printing. J. Appl. Polym. Sci. 2022, 139, e52959. [Google Scholar] [CrossRef]
- Ng, N.Y.Z.; Abdul Haq, R.H.; Marwah, O.M.F.; Ho, F.H.; Adzila, S. Optimization of polyvinyl alcohol (PVA) support parameters for fused deposition modelling (FDM) by using design of experiments (DOE). Mater. Today Proc. 2022, 57, 1226–1234. [Google Scholar] [CrossRef]
- Srivastava, S.; Saritha, D.; Sujithra, R. Effect of fill pattern on flexural performance of FDM printed PLA. Mater. Manuf. Process. 2024, 39, 787–796. [Google Scholar] [CrossRef]
- Moradi, M.; Mehrabi, O.; Rasoul, F.A.; Mattie, A.A.; Schaber, F.; Khandan, R. Enhancing 3D Printing Copper-PLA Composite Fabrication via Fused Deposition Modeling through Statistical Process Parameter Study. Micromachines 2024, 15, 1082. [Google Scholar] [CrossRef]
- Fernández-Cervantes, I.; Morales, M.A.; Agustín-Serrano, R.; Cardenas-García, M.; Pérez-Luna, P.V.; Arroyo-Reyes, B.L.; Maldonado-García, A. Polylactic acid/sodium alginate/hydroxyapatite composite scaffolds with trabecular tissue morphology designed by a bone remodeling model using 3D printing. J. Mater. Sci. 2019, 54, 9478–9496. [Google Scholar] [CrossRef]
- ISO/ASTM 52900; 2021 Additive Manufacturing—General Principles—Fundamentals and Vocabulary. ISO: Geneva, Switzerland, 2021.
- Kam, M.; İpekçi, A.; Şengül, Ö. Investigation of the effect of FDM process parameters on mechanical properties of 3D printed PA12 samples using Taguchi method. J. Thermoplast. Compos. Mater. 2021, 36, 307–325. [Google Scholar] [CrossRef]
- Birosz, M.T.; Ledenyák, D.; Andó, M. Effect of FDM infill patterns on mechanical properties. Polym. Test. 2022, 113, 107654. [Google Scholar] [CrossRef]
- Wang, S.; Ma, Y.; Deng, Z.; Zhang, S.; Cai, J. Effects of fused deposition modeling process parameters on tensile, dynamic mechanical properties of 3D printed polylactic acid materials. Polym. Test. 2020, 86, 106483. [Google Scholar] [CrossRef]
- He, Y.; Shen, M.; Wang, Q.; Wang, T.; Pei, X. Effects of FDM parameters and annealing on the mechanical and tribological properties of PEEK. Compos. Struct. 2023, 313, 116901. [Google Scholar] [CrossRef]
- Murali, A.; Vakkattil, M.A.; Parameswaran, R. Investigating the Effect of Processing Parameters on Mechanical Behavior of 3D Fused Deposition Modeling Printed Polylactic Acid. J. Mater. Eng. Perform. 2023, 32, 1089–1102. [Google Scholar] [CrossRef]
- Wang, P.; Zou, B.; Ding, S.; Li, L.; Huang, C. Effects of FDM-3D printing parameters on mechanical properties and microstructure of CF/PEEK and GF/PEEK. Chin. J. Aeronaut. 2021, 34, 236–246. [Google Scholar] [CrossRef]
- Yin, S.; Du, Y.; Liang, X.; Xie, Y.; Xie, D.; Mei, Y. Surface coating of biomass-modified black phosphorus enhances flame retardancy of rigid polyurethane foam and its synergistic mechanism. Appl. Surf. Sci. 2023, 637, 157961. [Google Scholar] [CrossRef]
- Chen, Y.; Sun, S.; Zhang, T.; Zhou, X.; Li, S. Effects of post-weld heat treatment on the microstructure and mechanical properties of laser-welded NiTi/304SS joint with Ni filler. Mater. Sci. Eng. A 2020, 771, 138545. [Google Scholar] [CrossRef]
- Li, J.; Wang, Z.; Zhang, S.; Lin, Y.; Jiang, L.; Tan, J. Task incremental learning-driven Digital-Twin predictive modeling for customized metal forming product manufacturing process. Robot. Comput.-Integr. Manuf. 2024, 85, 102647. [Google Scholar] [CrossRef]
- Afshari, H.; Taher, F.; Alavi, S.A.; Afshari, M.; Samadi, M.R.; Allahyari, F. Studying the effects of FDM process parameters on the mechanical properties of parts produced from PLA using response surface methodology. Colloid Polym. Sci. 2024, 302, 955–970. [Google Scholar] [CrossRef]
- Johar, M.; Rosli, A.A.; Shuib, R.K.; Abdul Hamid, Z.A.; Abdullah, M.K.; Ku Ishak, K.M.; Rusli, A. Dimensional stability of poly(lactic acid) (PLA) parts fabricated using fused deposition modelling (FDM). Prog. Rubber Plast. Recycl. Technol. 2024, 40, 14777606241262882. [Google Scholar] [CrossRef]
- Sahoo, S.; Sutar, H.; Senapati, P.; Shankar Mohanto, B.; Ranjan Dhal, P.; Kumar Baral, S. Experimental investigation and optimization of the FDM process using PLA. Mater. Today Proc. 2023, 74, 843–847. [Google Scholar] [CrossRef]
- Ambade, V.; Rajurkar, S.; Awari, G.; Yelamasetti, B.; Shelare, S. Influence of FDM process parameters on tensile strength of parts printed by PLA material. Int. J. Interact. Des. Manuf. (IJIDeM) 2023, 17, 1–12. [Google Scholar] [CrossRef]
- Kutnjak-Mravlinčić, S.; Godec, D.; Pilipović, A.; Sutlović, A. Optimization of the FDM Processing Parameters on the Compressive Properties of ABS Objects for the Production of High-Heeled Shoes. J. Manuf. Mater. Process. 2024, 8, 106. [Google Scholar] [CrossRef]
- Kechagias, J.D. 3D printing parametric optimization using the power of Taguchi design: An expository paradigm. Mater. Manuf. Process. 2024, 39, 797–803. [Google Scholar] [CrossRef]
- Farid, M.I.; Wu, W.; Li, G.; Zheng, A.; Zhao, Y. Superior tensile properties of FDM 3D-printed TPU/E-TPU layered structure. J. Mater. Res. 2024, 39, 2051–2066. [Google Scholar] [CrossRef]
- M’Bengue, M.-S.; Mesnard, T.; Chai, F.; Maton, M.; Gaucher, V.; Tabary, N.; García-Fernandez, M.-J.; Sobocinski, J.; Martel, B.; Blanchemain, N. Evaluation of a Medical Grade Thermoplastic Polyurethane for the Manufacture of an Implantable Medical Device: The Impact of FDM 3D-Printing and Gamma Sterilization. Pharmaceutics 2023, 15, 456. [Google Scholar] [CrossRef] [PubMed]
- Soltanmohammadi, K.; Rahmatabadi, D.; Aberoumand, M.; Soleyman, E.; Ghasemi, I.; Baniassadi, M.; Abrinia, K.; Bodaghi, M.; Baghani, M. Effects of TPU on the mechanical properties, fracture toughness, morphology, and thermal analysis of 3D-printed ABS-TPU blends by FDM. J. Vinyl Addit. Technol. 2024, 30, 958–968. [Google Scholar] [CrossRef]
- Rahmatabadi, D.; Soltanmohammadi, K.; Pahlavani, M.; Aberoumand, M.; Soleyman, E.; Ghasemi, I.; Baniassadi, M.; Abrinia, K.; Bodaghi, M.; Baghani, M. Shape memory performance assessment of FDM 3D printed PLA-TPU composites by Box-Behnken response surface methodology. Int. J. Adv. Manuf. Technol. 2023, 127, 935–950. [Google Scholar] [CrossRef]
- Ursini, C.; Collini, L. FDM Layering Deposition Effects on Mechanical Response of TPU Lattice Structures. Materials 2021, 14, 5645. [Google Scholar] [CrossRef]
- Hasdiansah, H.; Yaqin, R.I.; Pristiansyah, P.; Umar, M.L.; Priyambodo, B.H. FDM-3D printing parameter optimization using taguchi approach on surface roughness of thermoplastic polyurethane parts. Int. J. Interact. Des. Manuf. (IJIDeM) 2023, 17, 3011–3024. [Google Scholar] [CrossRef]
- Dixit, N.; Jain, P.K. Properties evaluation of chemically treated TPU parts printed through FFF. Int. J. Adv. Manuf. Technol. 2023, 126, 131–143. [Google Scholar] [CrossRef]
- Zolfaghari, A.; Purrouhani, M.R.; Zolfagharian, A. A response surface methodology study on 4D printing for layered PLA/TPU structures. Prog. Addit. Manuf. 2024, 9, 1–12. [Google Scholar] [CrossRef]
- Pradhan, M.K. Estimating the effect of process parameters on MRR, TWR and radial overcut of EDMed AISI D2 tool steel by RSM and GRA coupled with PCA. Int. J. Adv. Manuf. Technol. 2013, 68, 591–605. [Google Scholar] [CrossRef]
- Hashmi, K.H.; Zakria, G.; Raza, M.B.; Khalil, S. Optimization of process parameters for high speed machining of Ti-6Al-4V using response surface methodology. Int. J. Adv. Manuf. Technol. 2016, 85, 1847–1856. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, K.; Zhang, H.; Tian, X.; Jiang, Q.; Murugadoss, V.; Hou, H. Dislocation motion in plastic deformation of nano polycrystalline metal materials: A phase field crystal method study. Adv. Compos. Hybrid Mater. 2022, 5, 2546–2556. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, T.; Zhang, S.; Sun, C.; Li, J.; Tan, J. Bo-LSTM based cross-sectional profile sequence progressive prediction method for metal tube rotate draw bending. Adv. Eng. Inform. 2023, 58, 102152. [Google Scholar] [CrossRef]
- Li, M. Evaluation of the effect of process parameters on the cut quality in fiber laser cutting of duplex stainless steel using response surface method (RSM). Infrared Phys. Technol. 2021, 118, 103896. [Google Scholar] [CrossRef]
- Selvam, R.; Vignesh, M.; Pugazhenthi, R.; Anbuchezhiyan, G.; Satyanarayana Gupta, M. Effect of process parameter on wire cut EDM using RSM method. Int. J. Interact. Des. Manuf. (IJIDeM) 2024, 18, 2957–2968. [Google Scholar] [CrossRef]
- Tian, X.; Zhao, Y.; Gu, T.; Guo, Y.; Xu, F.; Hou, H. Cooperative effect of strength and ductility processed by thermomechanical treatment for Cu–Al–Ni alloy. Mater. Sci. Eng. A 2022, 849, 143485. [Google Scholar] [CrossRef]
- Cen, Q.; Xing, Z.; Wang, Q.; Li, L.; Wang, Z.; Wu, Z.; Liu, L. Molding simulation of airfoil foam sandwich structure and interference optimization of foam-core. Chin. J. Aeronaut. 2024, 37, 325–338. [Google Scholar] [CrossRef]
- ASTM 638; Standard Test Method for Tensile Properties of Plastics. ASTM International: West Conshohocken, PA, USA, 2014.
- Guessasma, S.; Belhabib, S.; Nouri, H. Thermal cycling, microstructure and tensile performance of PLA-PHA polymer printed using fused deposition modelling technique. Rapid Prototyp. J. 2020, 26, 122–133. [Google Scholar] [CrossRef]
- NurFarrahain, N.A.; Yew, H.W.; Nik, N.N.G. A systematic review of fused deposition modeling process parameters. Soft Sci. 2022, 2, 11. [Google Scholar]
- Syrlybayev, D.; Zharylkassyn, B.; Seisekulova, A.; Akhmetov, M.; Perveen, A.; Talamona, D. Optimisation of Strength Properties of FDM Printed Parts—A Critical Review. Polymers 2021, 13, 1587. [Google Scholar] [CrossRef] [PubMed]
- Dwivedi, A.; Khurana, M.K.; Bala, Y.G. Effect of parameters on quality of IN718 parts using laser additive manufacturing. Mater. Sci. Technol. 2024, 40, 633–648. [Google Scholar] [CrossRef]
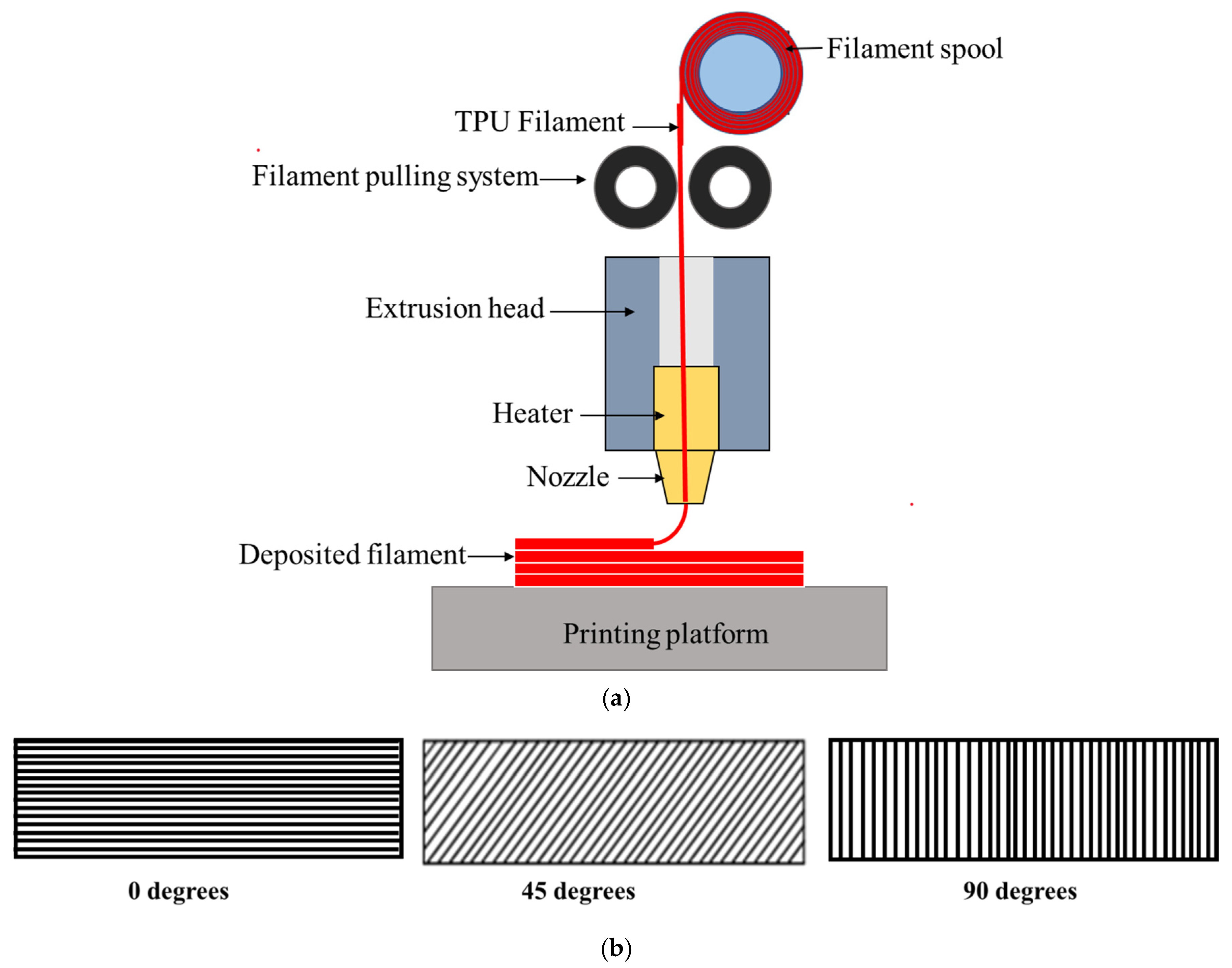

| Variable | Notation | Unit | −2 | −1 | 0 | +1 | +2 |
|---|---|---|---|---|---|---|---|
| Extruder temperature | ET | °C | 220 | 230 | 240 | 250 | 260 |
| Raster angle | RA | degree | 0 | 22.5 | 45 | 67.5 | 90 |
| Infill percentage | IP | % | 15 | 25 | 35 | 45 | 55 |
| Experiment No. | Input Variables | Output Variables | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Coded Values | Actual Values | Maximum Failure Load [N] | Elongation at Break [mm] | Part Weight [g] | Ratio of the MFL to PW [N/g] | Build Time [s] | |||||
| ET [°C] | RA [°] | IP [%] | ET [°C] | RA [°] | IP [%] | ||||||
| 1 | −1 | 1 | −1 | 230 | 67.5 | 25 | 490 | 258.00 | 4.795 | 102.19 | 3060 |
| 2 | 2 | 0 | 0 | 260 | 45 | 35 | 360 | 158.33 | 5.49 | 65.5738 | 3055 |
| 3 | 0 | 0 | 0 | 240 | 45 | 35 | 410 | 201.06 | 5.11 | 80.2348 | 3034 |
| 4 | 0 | 0 | 0 | 240 | 45 | 35 | 360 | 185.33 | 5.04 | 71.4286 | 3034 |
| 5 | 0 | 0 | −2 | 240 | 45 | 15 | 360 | 228.84 | 4.35 | 82.7586 | 3060 |
| 6 | 0 | 0 | 2 | 240 | 45 | 55 | 375 | 251.80 | 5.69 | 65.9051 | 3155 |
| 7 | 1 | −1 | 1 | 250 | 22.5 | 45 | 370 | 193.86 | 5.59 | 66.1896 | 3060 |
| 8 | 1 | −1 | −1 | 250 | 22.5 | 25 | 380 | 211.76 | 4.87 | 78.0287 | 3060 |
| 9 | −1 | −1 | 1 | 230 | 22.5 | 45 | 445 | 220.56 | 5.42 | 82.1033 | 3060 |
| 10 | −1 | −1 | −1 | 230 | 22.5 | 25 | 455 | 243.51 | 4.70 | 96.8085 | 3020 |
| 11 | 1 | 1 | −1 | 250 | 67.5 | 25 | 415 | 202.16 | 4.78 | 86.8201 | 3060 |
| 12 | 0 | 0 | 0 | 240 | 45 | 35 | 410 | 207.88 | 5.10 | 80.3922 | 3034 |
| 13 | 0 | 2 | 0 | 240 | 90 | 35 | 510 | 226.16 | 5.02 | 101.594 | 3034 |
| 14 | 1 | 1 | 1 | 250 | 67.5 | 45 | 385 | 193.11 | 5.64 | 68.2624 | 3060 |
| 15 | −2 | 0 | 0 | 220 | 45 | 35 | 515 | 244.09 | 5.33 | 96.6229 | 3070 |
| 16 | 0 | −2 | 0 | 240 | 0 | 45 | 395 | 222.73 | 5.21 | 75.8157 | 3034 |
| 17 | −1 | 1 | 1 | 230 | 67.5 | 45 | 480 | 205.3 | 5.52 | 86.9565 | 3060 |
| Property | Test Method | Value |
|---|---|---|
| Tensile Strength | ASTM D638 | 40 MPa |
| Elongation at Break | ASTM D638 | 500% |
| Flexural Strength | ASTM D790 | 30 MPa |
| Impact Strength | ASTM D256 | 100 kJ/m2 |
| Shore Hardness (A) | ASTM D2240 | 90 A |
| Density | ASTM D792 | 1.2 g/cm3 |
| Tear Strength | ASTM D624 | 80 kN/m |
| Source | Sum of Squares (SS) | Degrees of Freedom (DF) | Mean Square (MS) | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 1.435 × 1016 | 9 | 1.594 × 1015 | 13.47 | 0.0012 | Significant |
| A—Extruder temperature | 7.937 × 1015 | 1 | 7.937 × 1015 | 67.06 | <0.0001 | Significant |
| B—Raster angle | 2.137 × 1015 | 1 | 2.137 × 1015 | 18.06 | 0.0038 | Significant |
| C—Infill percentage | 5.506 × 1013 | 1 | 5.506 × 1013 | 0.4652 | 0.5171 | |
| AB | 6.560 × 1013 | 1 | 6.560 × 1013 | 0.5543 | 0.4808 | |
| AC | 3.772 × 1012 | 1 | 3.772 × 1012 | 0.0319 | 0.8634 | |
| BC | 1.041 × 1013 | 1 | 1.041 × 1013 | 0.0879 | 0.7754 | |
| A2 | 1.098 × 1015 | 1 | 1.098 × 1015 | 9.27 | 0.0187 | Significant |
| B2 | 1.757 × 1015 | 1 | 1.757 × 1015 | 14.84 | 0.0063 | Significant |
| C2 | 2.061 × 1014 | 1 | 2.061 × 1014 | 1.74 | 0.2285 | |
| Residual | 8.285 × 1014 | 7 | 1.184 × 1014 | |||
| Lack of Fit | 4.980 × 1014 | 5 | 9.960 × 1013 | 0.6027 | 0.7199 | |
| Pure Error | 3.305 × 1014 | 2 | 1.652 × 1014 | |||
| Cor Total | 1.518 × 1016 | 16 | ||||
| R2 = 0.9454 | Adjusted R2 = 0.8752 | |||||
| Source | SS | DF | MS | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 15,087.17 | 9 | 1676.35 | 6.98 | 0.0089 | Significant |
| A—Extruder temperature | 10,240.96 | 1 | 10,240.96 | 42.67 | 0.0003 | Significant |
| B—Raster angle | 103.78 | 1 | 103.78 | 0.4324 | 0.5318 | |
| C—Infill percentage | 674.63 | 1 | 674.63 | 2.81 | 0.1375 | |
| AB | 9.28 | 1 | 9.28 | 0.0387 | 0.8497 | |
| AC | 886.94 | 1 | 886.94 | 3.70 | 0.0960 | |
| BC | 215.40 | 1 | 215.40 | 0.8974 | 0.3750 | |
| A2 | 21.22 | 1 | 21.22 | 0.0884 | 0.7749 | |
| B2 | 830.90 | 1 | 830.90 | 3.46 | 0.1051 | |
| C2 | 2171.36 | 1 | 2171.36 | 9.05 | 0.0197 | Significant |
| Residual | 1680.21 | 7 | 240.03 | |||
| Lack of Fit | 1238.91 | 5 | 247.78 | 1.12 | 0.5331 | |
| Pure Error | 441.29 | 2 | 220.65 | |||
| Cor Total | 16,767.38 | 16 | ||||
| R2 = 0.8998 | Adjusted R2 = 0.7710 | |||||
| Source | SS | DF | MS | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 0.0016 | 9 | 0.0002 | 113.98 | <0.0001 | Significant |
| A—Extruder temperature | 0.0000 | 1 | 0.0000 | 12.84 | 0.0089 | Significant |
| B—Raster angle | 3.432 × 10−6 | 1 | 3.432 × 10−6 | 2.20 | 0.1819 | |
| C—Infill percentage | 0.0014 | 1 | 0.0014 | 906.28 | <0.0001 | Significant |
| AB | 5.685 × 10−6 | 1 | 5.685 × 10−6 | 3.64 | 0.0981 | |
| AC | 2.491 × 10−7 | 1 | 2.491 × 10−7 | 0.1594 | 0.7016 | |
| BC | 2.677 × 10−6 | 1 | 2.677 × 10−6 | 1.71 | 0.2318 | |
| A2 | 0.0001 | 1 | 0.0001 | 49.08 | 0.0002 | Significant |
| B2 | 7.950 × 10−6 | 1 | 7.950 × 10−6 | 5.09 | 0.0587 | |
| C2 | 0.0000 | 1 | 0.0000 | 17.02 | 0.0044 | Significant |
| Residual | 0.0000 | 7 | 1.562 × 10−6 | |||
| Lack of Fit | 8.978 × 10−6 | 5 | 1.796 × 10−6 | 1.84 | 0.3891 | |
| Pure Error | 1.956 × 10−6 | 2 | 9.782 × 10−7 | |||
| Cor Total | 0.0016 | 16 | ||||
| R2 = 0.9932 | Adjusted R2 = 0.9845 | |||||
| Source | SS | DF | MS | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 8.366 × 10−8 | 9 | 9.296 × 10−9 | 14.50 | 0.0010 | Significant |
| A—Extruder temperature | 4.058 × 10−8 | 1 | 4.058 × 10−8 | 63.28 | <0.0001 | Significant |
| B—Raster angle | 3.946 × 10−9 | 1 | 3.946 × 10−9 | 6.15 | 0.0422 | Significant |
| C—Infill percentage | 2.549 × 10−8 | 1 | 2.549 × 10−8 | 39.75 | 0.0004 | Significant |
| AB | 9.811 × 10−11 | 1 | 9.811 × 10−11 | 0.1530 | 0.7073 | |
| AC | 1.347 × 10−9 | 1 | 1.347 × 10−9 | 2.10 | 0.1906 | |
| BC | 1.088 × 10−12 | 1 | 1.088 × 10−12 | 0.0017 | 0.9683 | |
| A2 | 5.596 × 10−13 | 1 | 5.596 × 10−13 | 0.0009 | 0.9773 | |
| B2 | 7.079 × 10−9 | 1 | 7.079 × 10−9 | 11.04 | 0.0127 | |
| C2 | 1.119 × 10−9 | 1 | 1.119 × 10−9 | 1.74 | 0.2281 | |
| Residual | 4.489 × 10−9 | 7 | 6.413 × 10−10 | |||
| Lack of Fit | 1.697 × 10−9 | 5 | 3.394 × 10−10 | 0.2431 | 0.9121 | |
| Pure Error | 2.792 × 10−9 | 2 | 1.396 × 10−9 | |||
| Cor Total | 8.815 × 10−8 | 16 | ||||
| R2 = 0.9491 | Adjusted R2 = 0.8836 | |||||
| Source | SS | DF | MS | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 1.302 × 10−23 | 9 | 1.446 × 10−24 | 4.76 | 0.0258 | Significant |
| A—Extruder temperature | 9.124 × 10−27 | 1 | 9.124 × 10−27 | 0.0301 | 0.8673 | |
| B—Raster angle | 9.083 × 10−25 | 1 | 9.083 × 10−25 | 2.99 | 0.1273 | |
| C—Infill percentage | 3.430 × 10−24 | 1 | 3.430 × 10−24 | 11.30 | 0.0121 | Significant |
| AB | 2.468 × 10−25 | 1 | 2.468 × 10−25 | 0.8131 | 0.3972 | |
| AC | 2.468 × 10−25 | 1 | 2.468 × 10−25 | 0.8131 | 0.3972 | |
| BC | 1.597 × 10−25 | 1 | 1.597 × 10−25 | 0.5261 | 0.4918 | |
| A2 | 1.164 × 10−24 | 1 | 1.164 × 10−24 | 3.83 | 0.0911 | |
| B2 | 5.105 × 10−25 | 1 | 5.105 × 10−25 | 1.68 | 0.2358 | |
| C2 | 7.030 × 10−24 | 1 | 7.030 × 10−24 | 23.16 | 0.0019 | Significant |
| Residual | 2.125 × 10−24 | 7 | 3.036 × 10−25 | |||
| Lack of Fit | 2.125 × 10−24 | 5 | 4.250 × 10−25 | |||
| Pure Error | 0.0000 | 2 | 0.0000 | |||
| Cor Total | 1.514 × 10−23 | 16 | ||||
| R2 = 0.8596 | Adjusted R2 = 0.6792 | |||||
| Parameter or Response | Range/Goal | Lower Limit | Upper Limit | Importance | |
|---|---|---|---|---|---|
| Extruder temperature (°C) | Within range | 260 | 220 | - | |
| Raster angle (degrees) | Within range | 90 | 0 | - | |
| Infill percentage (%) | Within range | 55 | 15 | - | |
| Criteria Set 1 | Maximum failure load (N) | Maximize | 515 | 360 | 3 |
| Elongation at break (mm) | Maximize | 258 | 158.33 | 3 | |
| Part weight (g) | Minimize | 5.69 | 4.35 | 3 | |
| Ratio of the MFL to PW (N/g) | Maximize | 102.19 | 65.5738 | 3 | |
| Build time (s) | Minimize | 3155 | 3020 | 3 | |
| Criteria Set 2 | Maximum failure load (N) | Maximize | 515 | 360 | 5 |
| Elongation at break (mm) | Maximize | 258 | 158.33 | 5 | |
| Part weight (g) | Minimize | 5.69 | 4.35 | 2 | |
| Ratio of the MFL to PW (N/g) | Maximize | 102.19 | 65.5738 | 5 | |
| Build time (s) | Minimize | 3155 | 3020 | 2 | |
| Criteria Set 3 | Maximum failure load (N) | Maximize | 515 | 360 | 3 |
| Elongation at break (mm) | Maximize | 258 | 158.33 | 3 | |
| Part weight (g) | Minimize | 5.69 | 4.35 | 5 | |
| Ratio of the MFL to PW (N/g) | Maximize | 102.19 | 65.5738 | 3 | |
| Build time (s) | Minimize | 3155 | 3020 | 5 |
| Solution | Extruder Temperature (ET) | Raster Angle (RA) | Infill Percentage (IP) | Maximum Failure Load (MFL) | Elongation at Break (E) | Part Weight (PW) | Ratio of the MFL to PW (Ratio) | Build Time (BT) | Composite Desirability (D) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 220.000 | 0.000 | 15.000 | 511.436 | 321.086 | 4.400 | 124.625 | 3015.783 | 0.988 |
| 2 | 220.000 | 0.000 | 15.003 | 511.438 | 321.071 | 4.400 | 124.627 | 3015.772 | 0.990 |
| 3 | 220.000 | 0.000 | 15.000 | 511.435 | 321.087 | 4.400 | 124.624 | 3015.784 | 0.986 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rajhi, W.; Ali, A.B.M.; Jasim, D.J.; Mehrabi, O.; Ben Said, L.; Moradi, M. Mathematical and Statistical Analysis of Fused Filament Fabrication Parameters for Thermoplastic Polyurethane Parts via Response Surface Methodology. Mathematics 2024, 12, 3146. https://doi.org/10.3390/math12193146
Rajhi W, Ali ABM, Jasim DJ, Mehrabi O, Ben Said L, Moradi M. Mathematical and Statistical Analysis of Fused Filament Fabrication Parameters for Thermoplastic Polyurethane Parts via Response Surface Methodology. Mathematics. 2024; 12(19):3146. https://doi.org/10.3390/math12193146
Chicago/Turabian StyleRajhi, Wajdi, Ali B. M. Ali, Dheyaa J. Jasim, Omid Mehrabi, Lotfi Ben Said, and Mahmoud Moradi. 2024. "Mathematical and Statistical Analysis of Fused Filament Fabrication Parameters for Thermoplastic Polyurethane Parts via Response Surface Methodology" Mathematics 12, no. 19: 3146. https://doi.org/10.3390/math12193146
APA StyleRajhi, W., Ali, A. B. M., Jasim, D. J., Mehrabi, O., Ben Said, L., & Moradi, M. (2024). Mathematical and Statistical Analysis of Fused Filament Fabrication Parameters for Thermoplastic Polyurethane Parts via Response Surface Methodology. Mathematics, 12(19), 3146. https://doi.org/10.3390/math12193146









