Mathematical Formulation and Numerical Simulation of the Mechanical Behavior of Ceramic/Metal (TiB/Ti) FG Sheets Subjected to Spherical Indenter
Abstract
1. Introduction
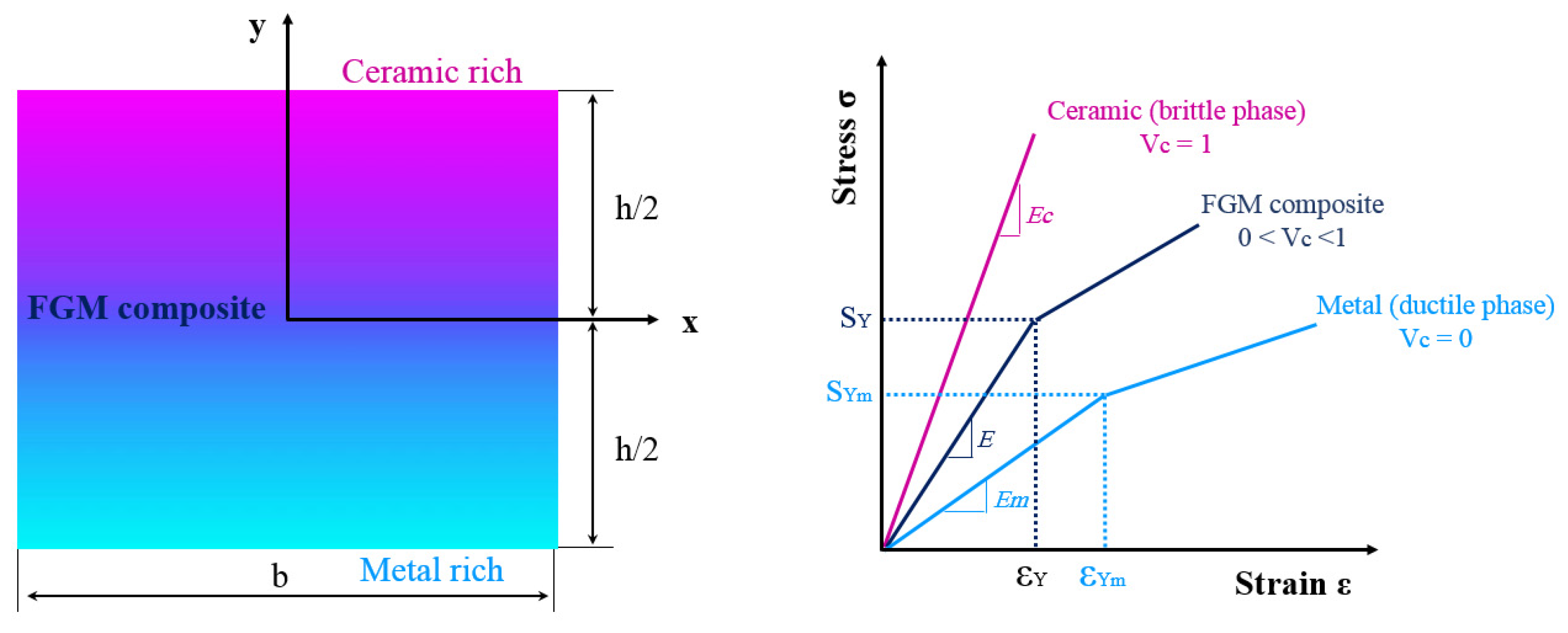
2. Constitutive Model for Elastoplastic FGM
2.1. Effective Elastic Properties of FGM
- : The ceramic volume fraction;
- : The metal volume fraction;
- H: Thickness of the structure;
- k: The power-law index which describes the continuous gradation of material properties through the thickness of the FGM plate.
2.2. Elastoplastic Stress–Strain Relation
2.3. Effective Elastoplastic Properties of the FGM
- : The metal yield strength;
- : Metal strength coefficient;
- : Metal strain-hardening exponent;
- : The cumulated plastic strain.
- : The effective yield strength;
- : The effective strength coefficient;
- n: The effective strain hardening parameter of the studied ceramic/metal FGM.
2.4. Numerical Integration Scheme
2.5. Closed-Form Tangent Operator
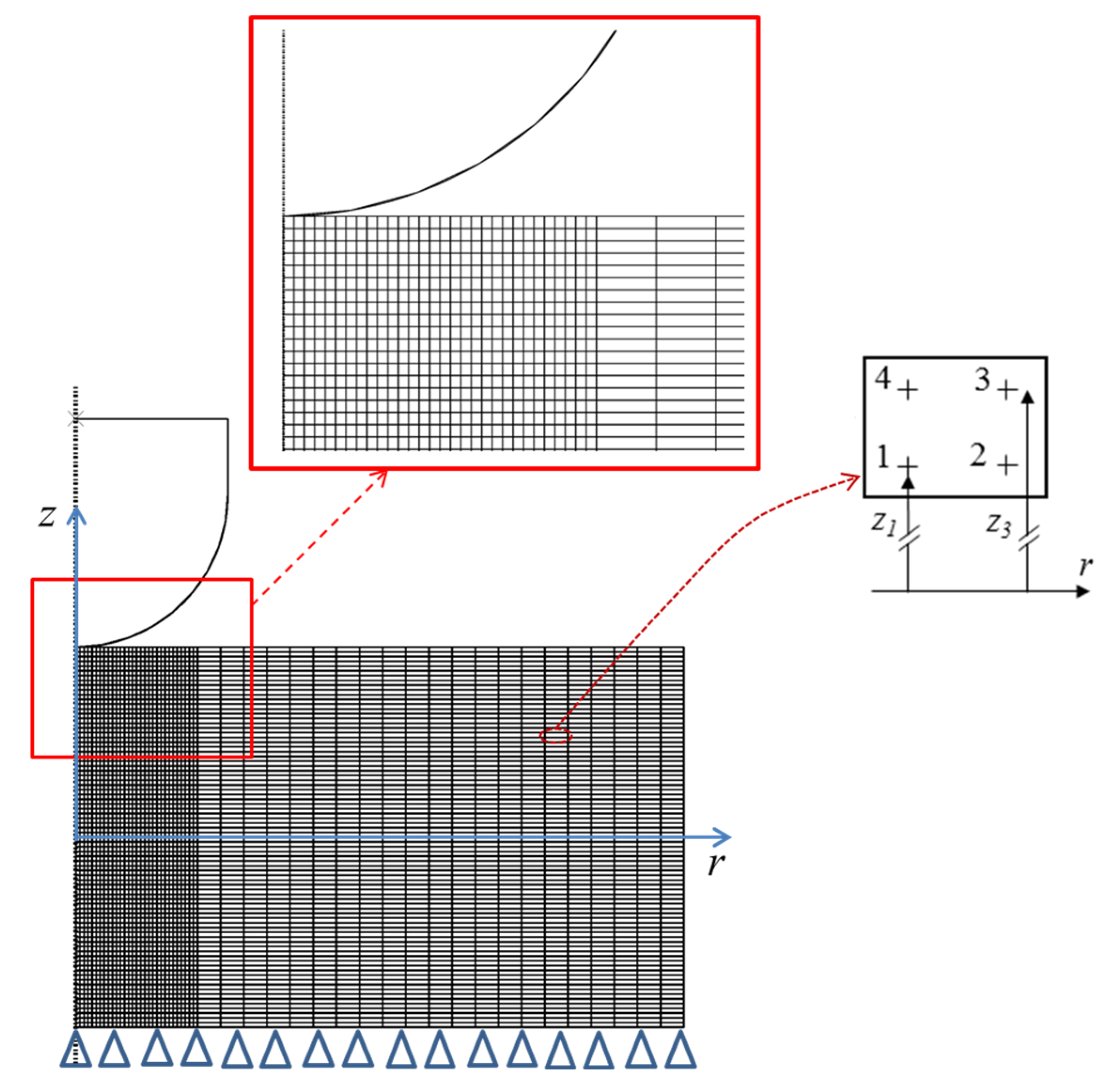
3. Numerical Approach and Model Validation
3.1. Finite Element Model
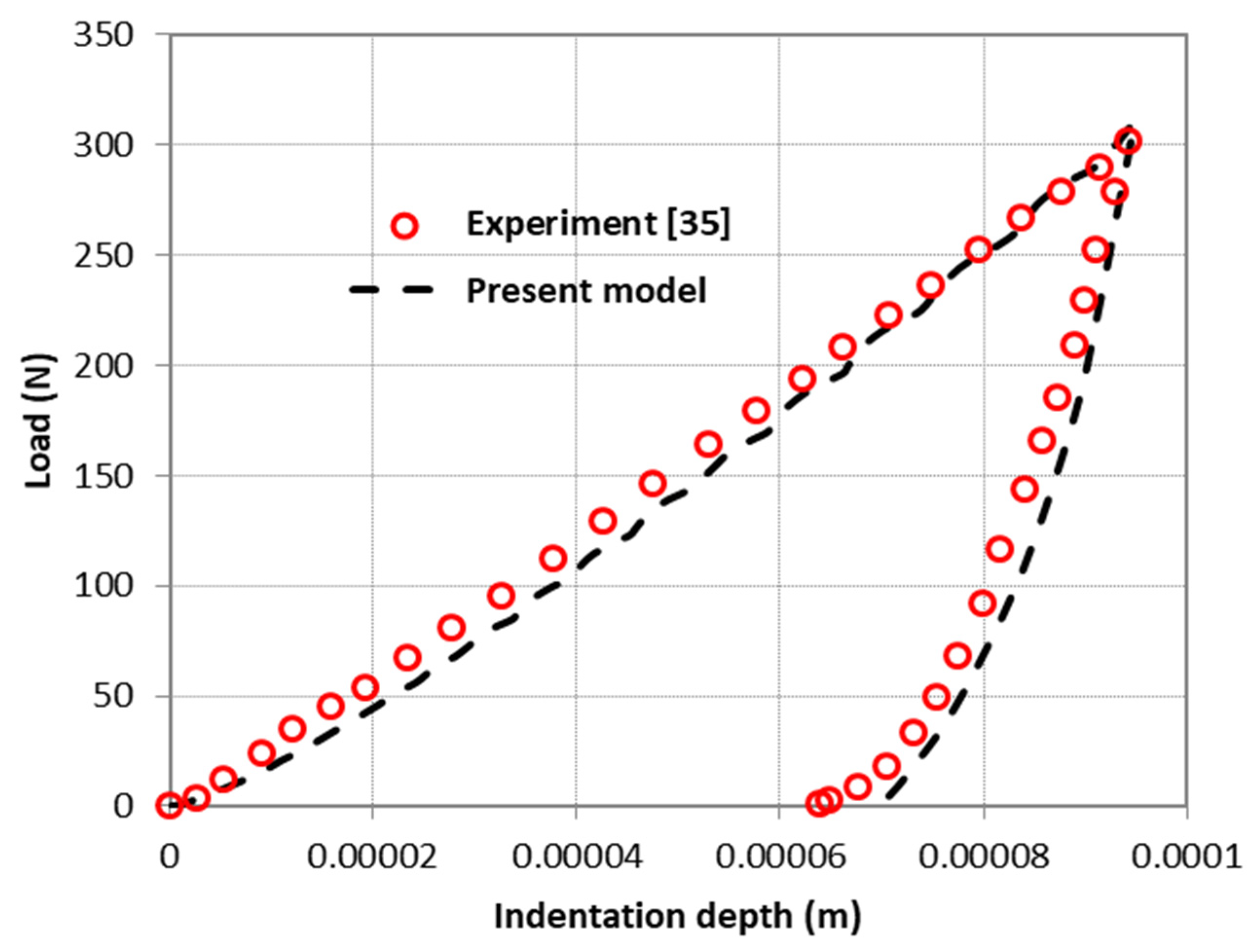
3.2. Model validation
4. Numerical Results and Discussions
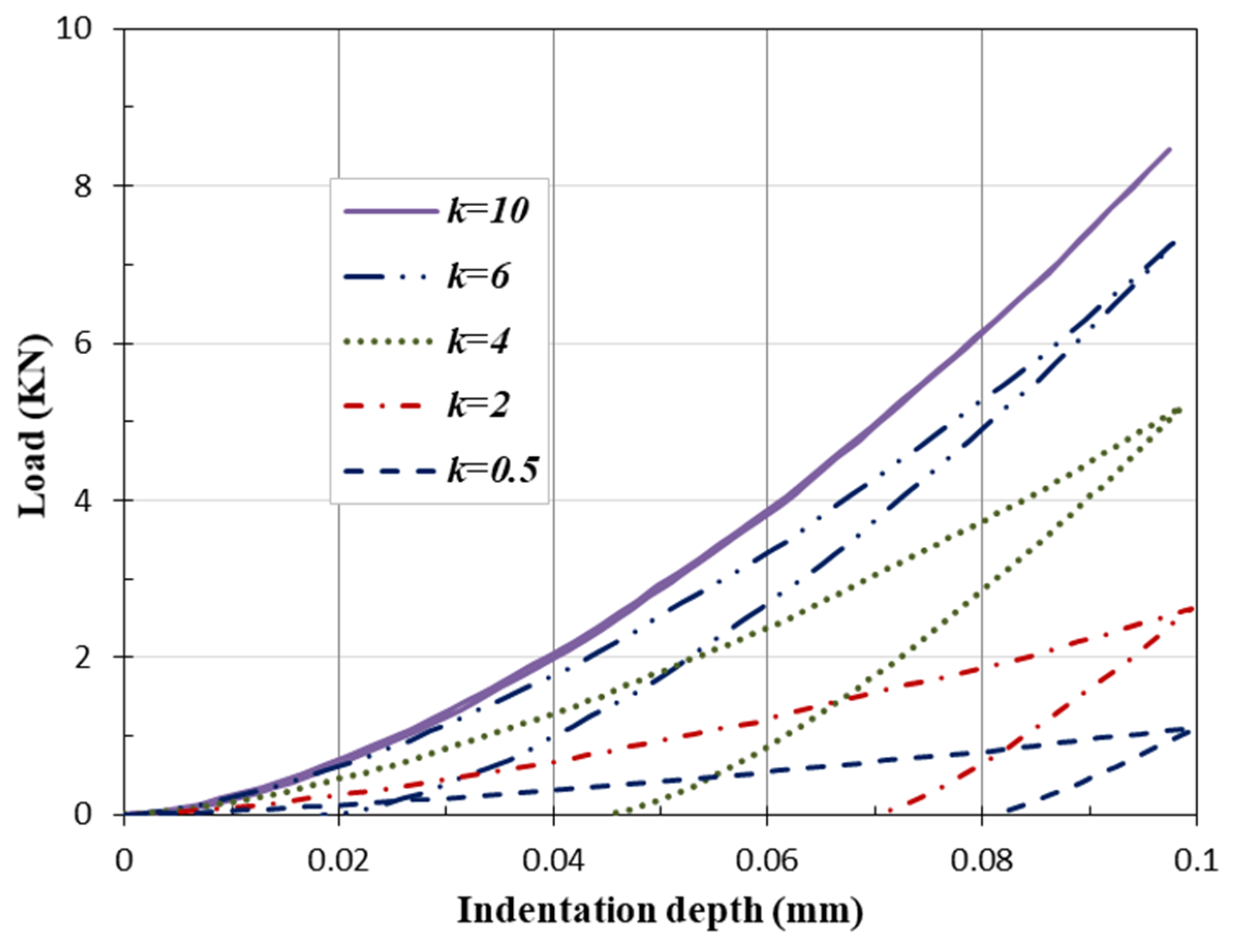
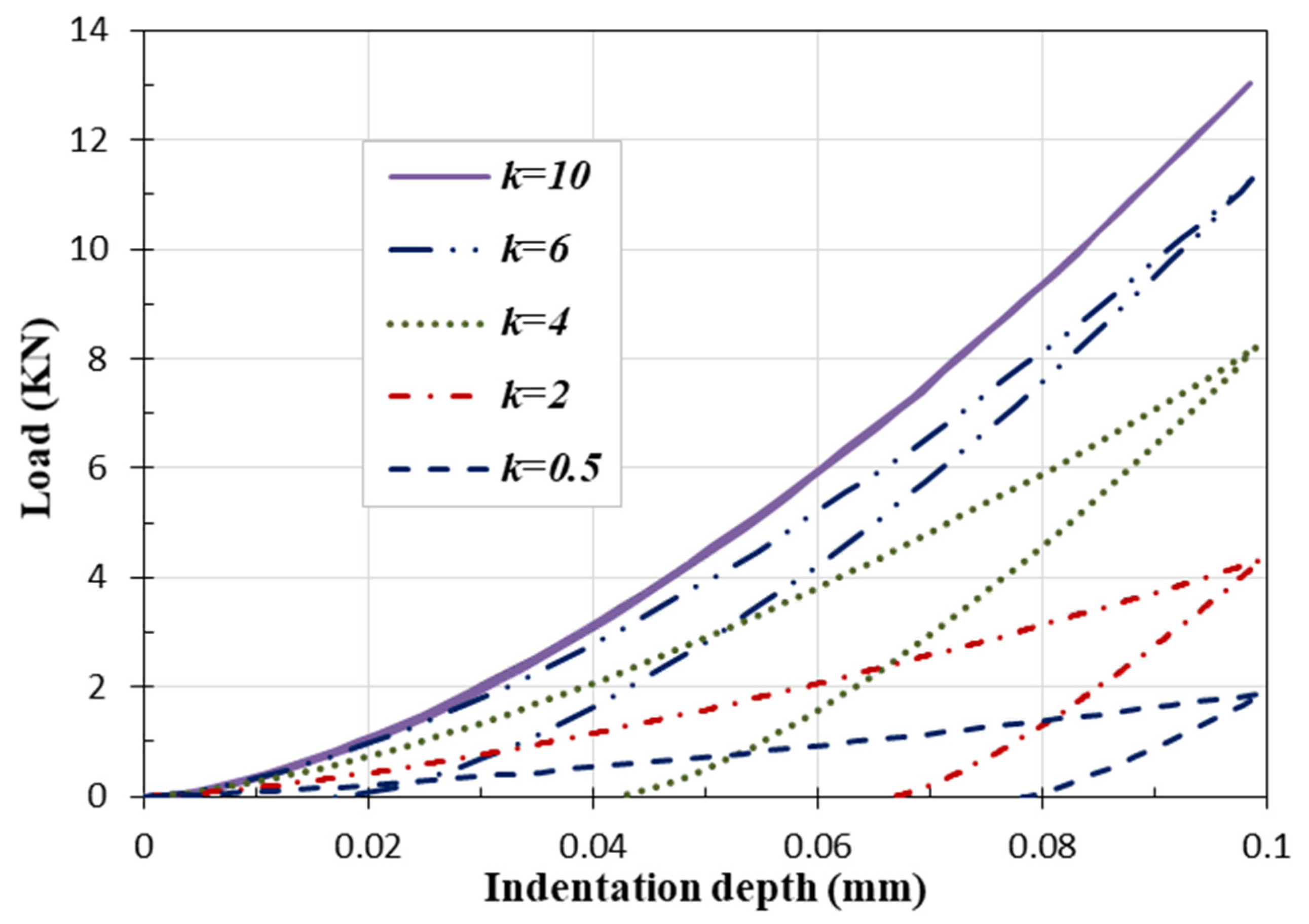
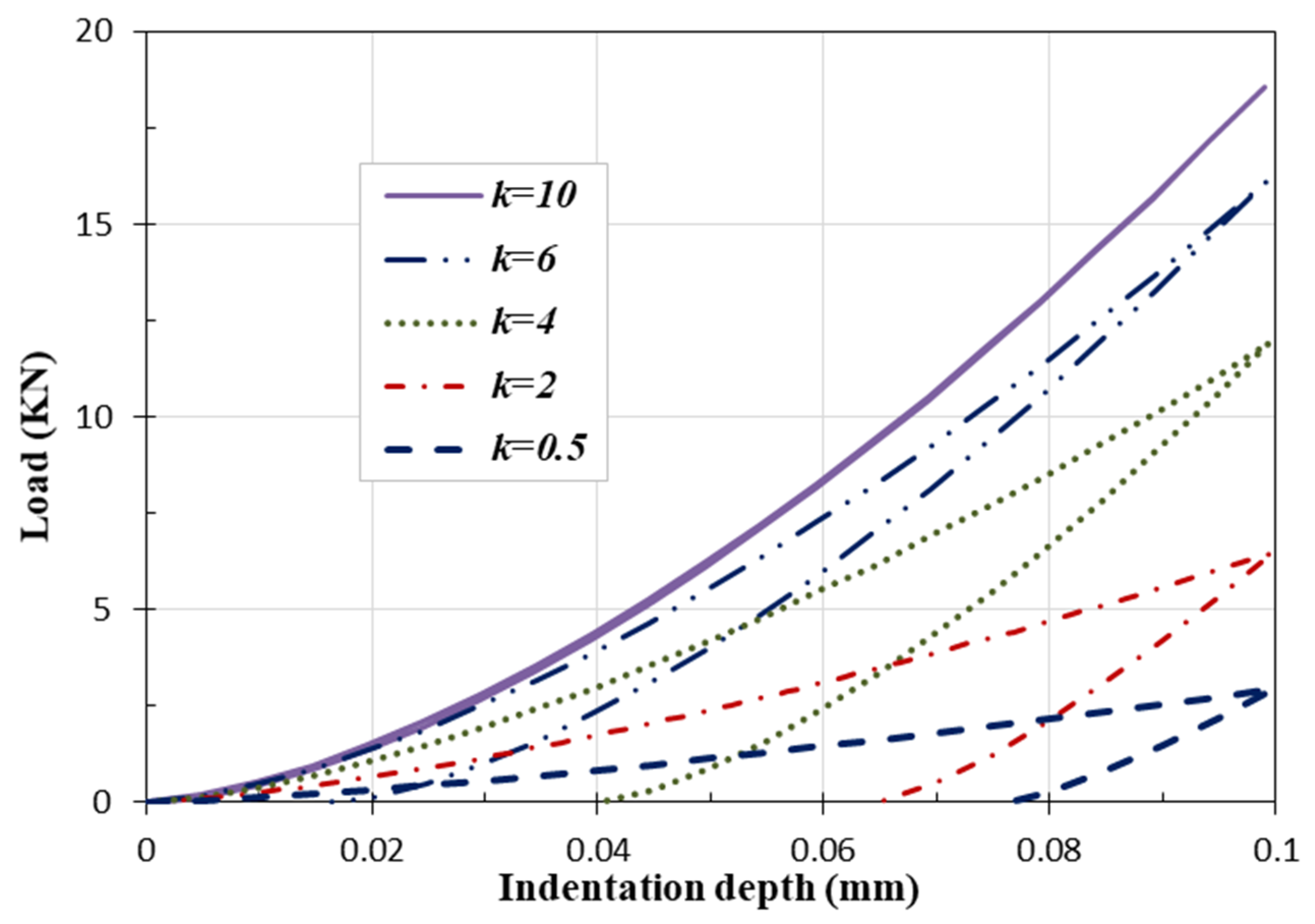
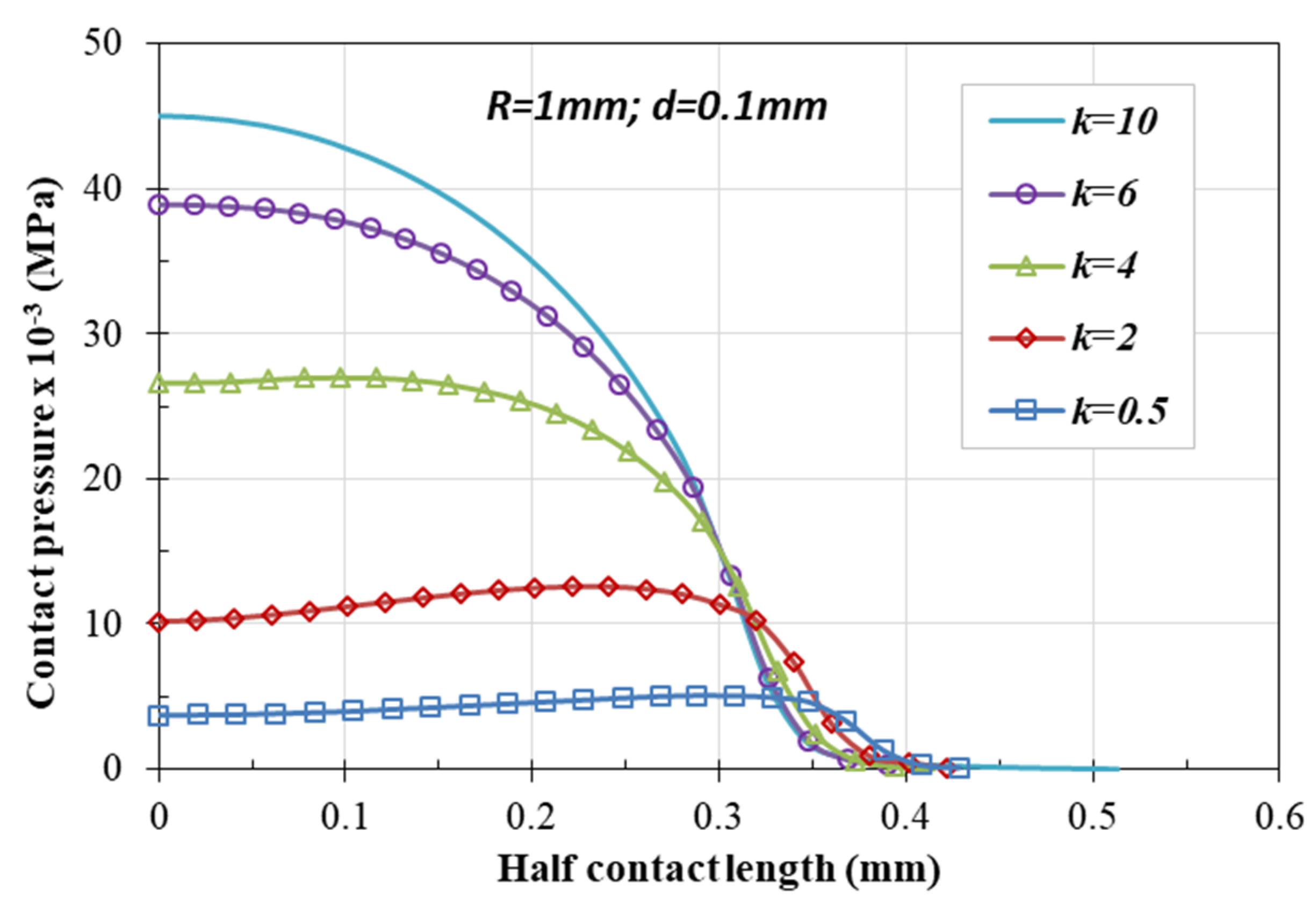
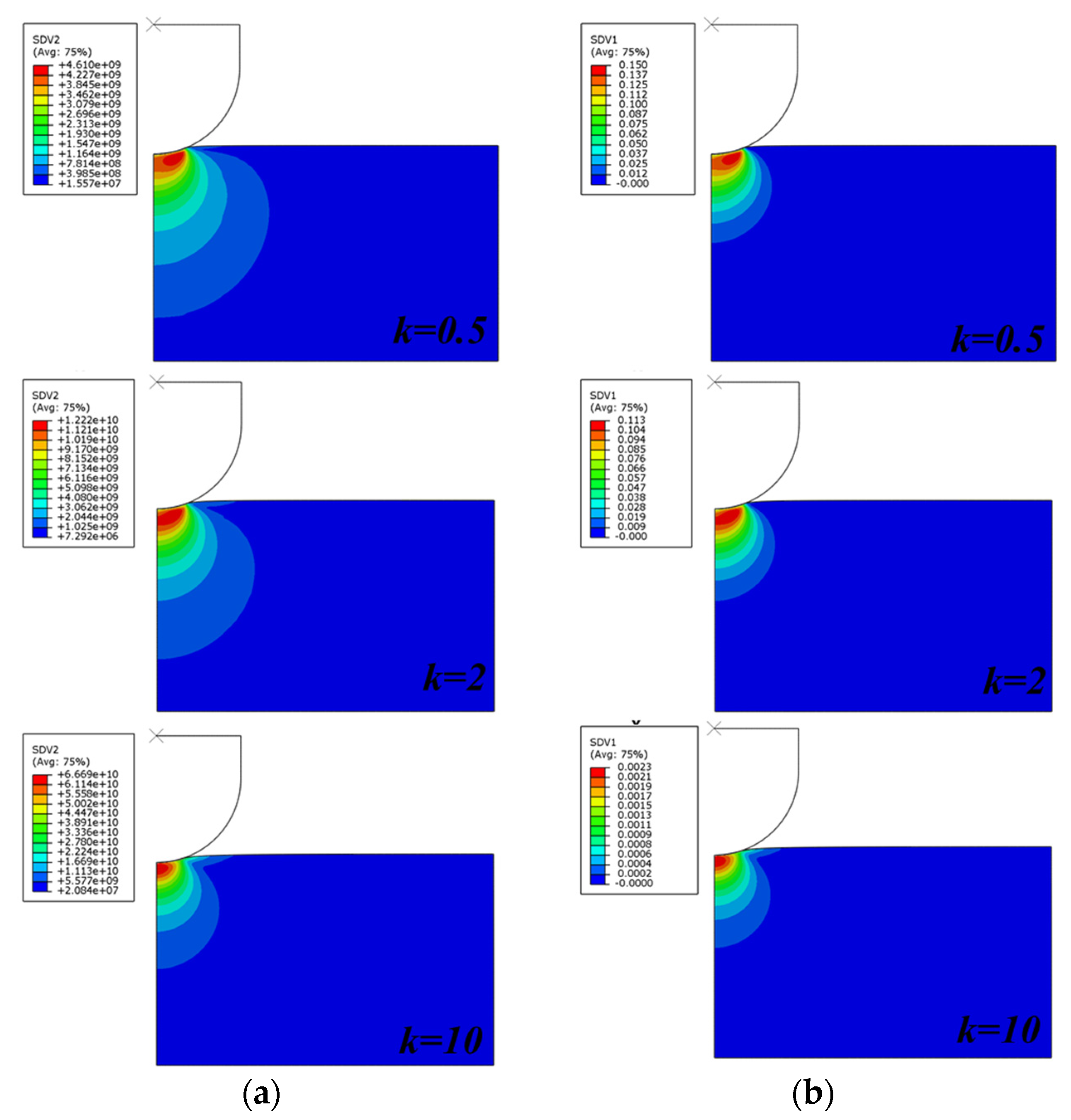
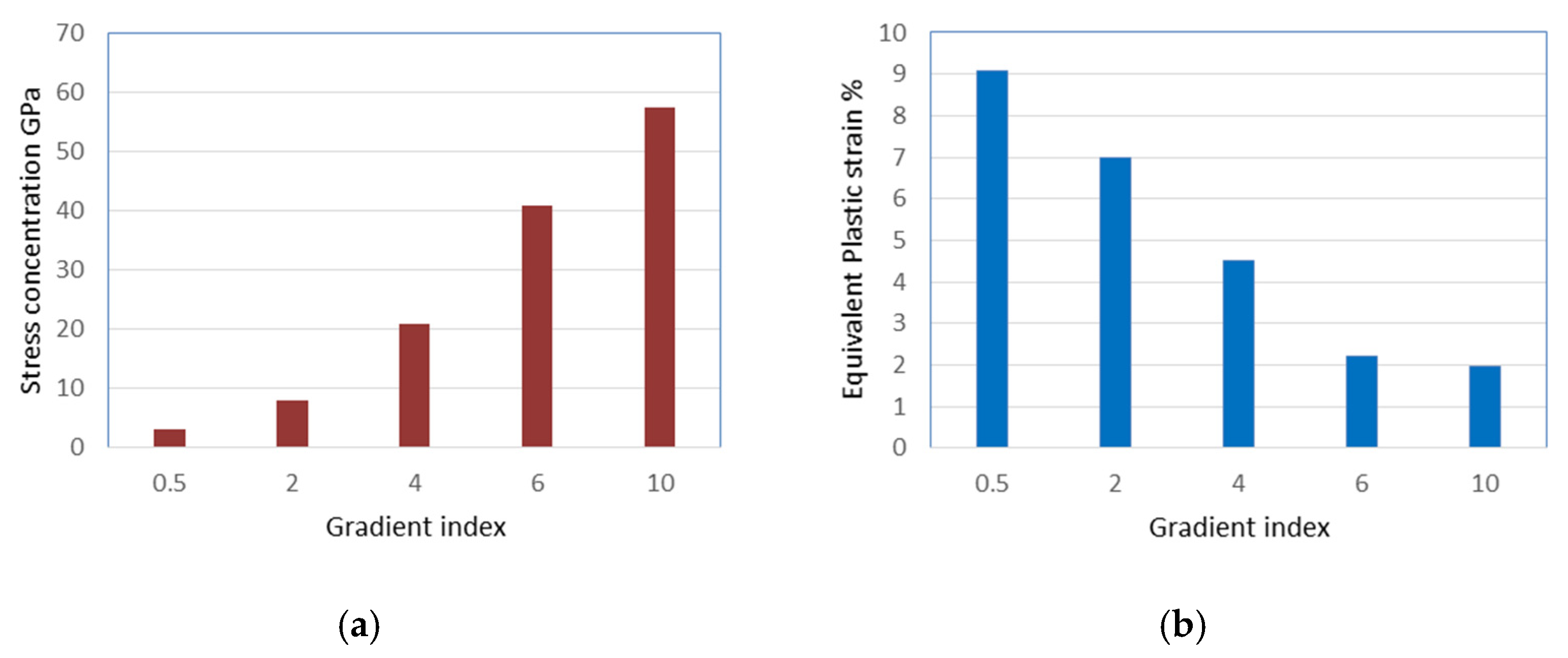
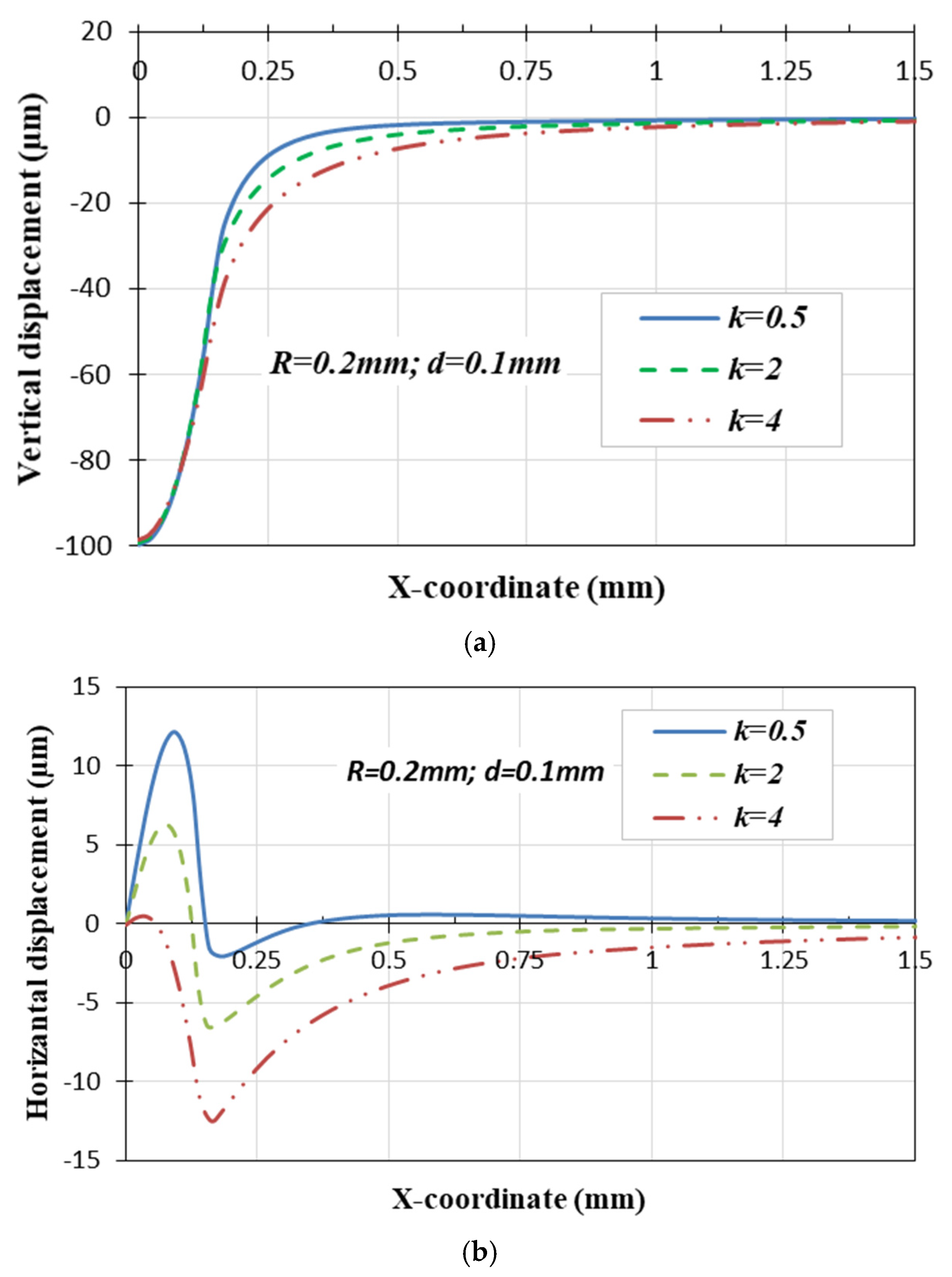
4.1. The Gradient Index Effect
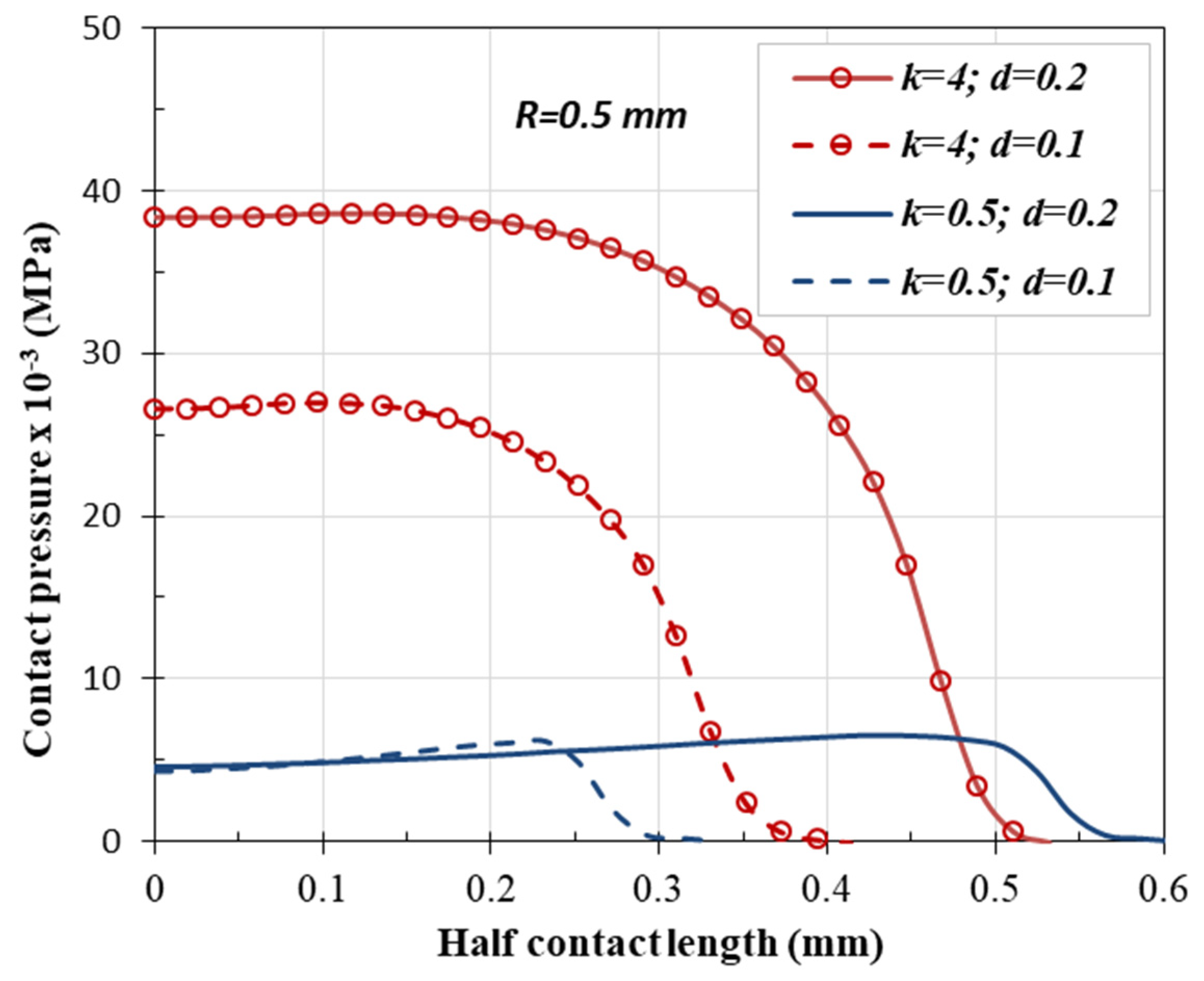
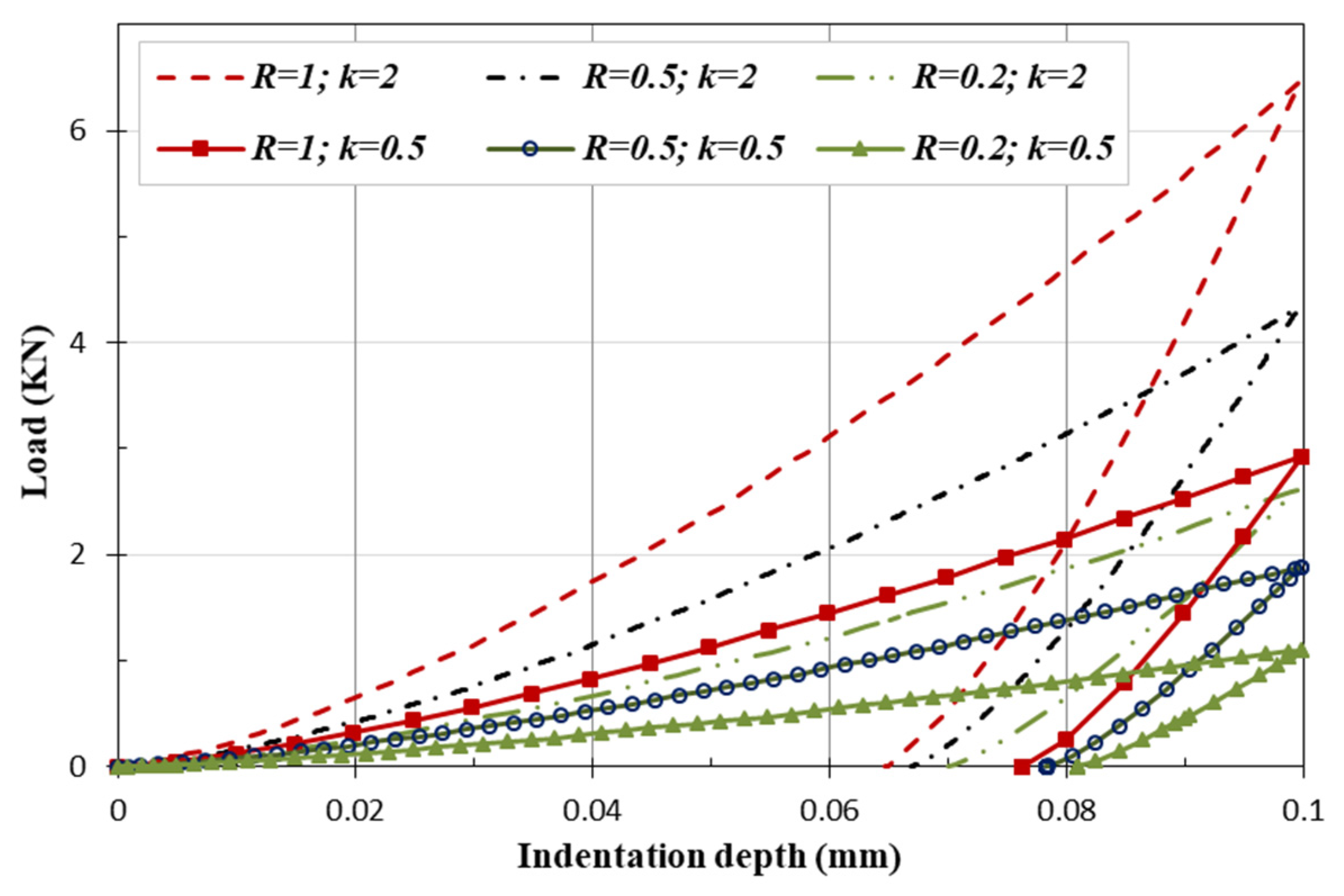
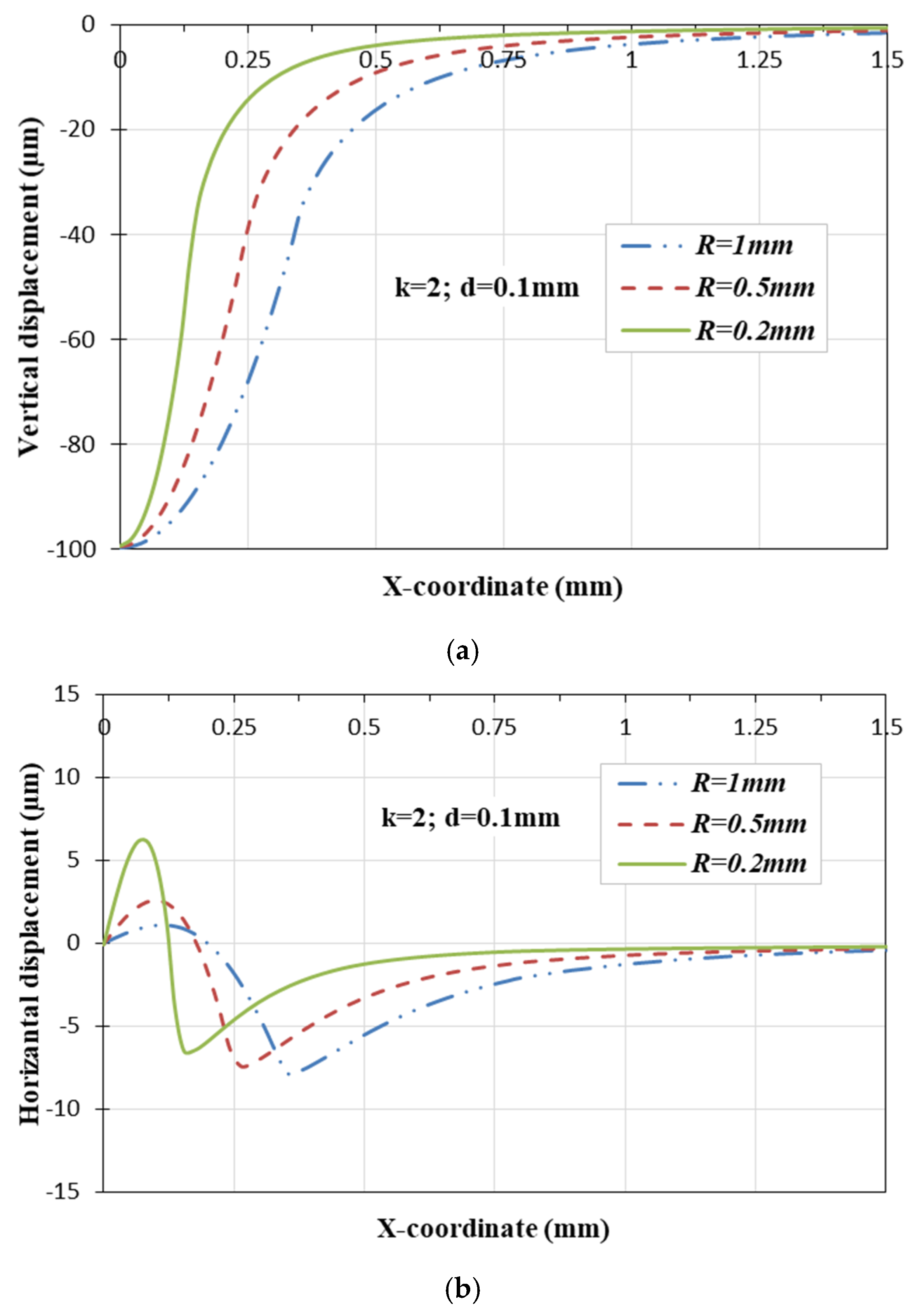
4.2. Influence of the Indenter Radius
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ziadoon Mohammed Rahi, A.H.; Al-Khazraji, A.N.; Shandookh, A.A. Mechanical properties investigation of composite FGM fabricated from Al/Zn. Open Eng. 2022, 12, 789–798. [Google Scholar] [CrossRef]
- Shareef, M.M.; Al-Khazraji, A.N.; Amin, S.A. Flexural properties of functionally graded silica nanoparticles. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2021; Volume 1094, p. 012174. [Google Scholar]
- Chung, Y.L.; Gan, Y.P. Carry-over Factors of Levy-type rectangular FGM plates subjected to edge moment or deflection. Mech. Mater. 2022, 173, 104413. [Google Scholar] [CrossRef]
- Sarkar, L.; Saha, S.; Samanta, R.; Sinha, A.; Mandal, G.; Biswas, A.; Das, A. Recent Progress in CNT-Reinforced Composite and FGM for Multi-functional Space Applications and Future Directions. J. Inst. Eng. India Ser. D 2023. [Google Scholar] [CrossRef]
- Kumar, P.; Sharma, S.K.; Singh, R.K.R. Recent trends and future outlooks in manufacturing methods and applications of FGM: A comprehensive review. Mater. Manuf. Process. 2023, 38, 1033–1067. [Google Scholar] [CrossRef]
- Elishakoff, I.; Chotpatthamanon, C.; Reddy, J.N. Buckling of a column made of the functionally graded material with high-order polynomial mode shape. Math. Mech. Solids 2023, 28, 1745–1759. [Google Scholar] [CrossRef]
- Kumar, P.; Harsha, S.P. Response analysis of hybrid functionally graded material plate subjected to thermo-electro-mechanical loading. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2020, 235, 813–827. [Google Scholar] [CrossRef]
- Jrad, H.; Mallek, H.; Wali, M.; Dammak, F. Finite element formulation for active functionally graded thin-walled structures. C. R. Méc. 2018, 346, 1159–1178. [Google Scholar] [CrossRef]
- Mallek, H.; Jrad, H.; Wali, M.; Dammak, F. Piezoelastic response of smart functionally graded structure with integrated piezoelectric layers using discrete double directors shell element. Compos. Struct. 2019, 210, 354–366. [Google Scholar] [CrossRef]
- Wang, S.; Kang, W.; Yang, W.; Zhang, Z.; Li, Q.; Liu, M.; Wang, X. Hygrothermal effects on buckling behaviors of porous bi-directional functionally graded micro-/nanobeams using two-phase local/nonlocal strain gradient theory. Eur. J. Mech.-A/Solids 2022, 94, 104554. [Google Scholar] [CrossRef]
- Van Vinh, P.; Van Chinh, N.; Tounsi, A. Static bending and buckling analysis of bi-directional functionally graded porous plates using an improved first-order shear deformation theory and FEM. Eur. J. Mech.-A/Solids 2022, 96, 104743. [Google Scholar] [CrossRef]
- Zhou, W.; Ai, S.; Chen, M.; Zhang, R.; He, R.; Pei, Y.; Fang, D. Preparation and thermodynamic analysis of the porous ZrO2/(ZrO2+Ni) functionally graded bolted joint. Compos. Part B Eng. 2015, 82, 13–22. [Google Scholar] [CrossRef]
- Zhou, W.; Zhou, H.; Zhang, R.; Pei, Y.; Fang, D. Measuring residual stress and its influence on properties of porous ZrO2/(ZrO2+Ni) ceramics. Mater. Sci. Eng. A 2015, 622, 82–90. [Google Scholar] [CrossRef][Green Version]
- Jana, T.; Mitra, A.; Sahoo, P. Contact behavior of functionally graded fractal surface. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2020, 234, 1355–1374. [Google Scholar] [CrossRef]
- Jitcharoen, J.; Padture, N.P.; Giannakopoulos, A.E.; Suresh, S. Hertzian-crack suppression in ceramics with elastic-modulus-graded surfaces. J. Am. Ceram. Soc. 1998, 81, 2301–2308. [Google Scholar] [CrossRef]
- Zhang, Y.; Cheng, Z.; Feng, H. Dynamic Fracture Analysis of Functional Gradient Material Coating Based on the Peridynamic Method. Coatings 2019, 9, 62. [Google Scholar] [CrossRef]
- Mellouli, H.; Jrad, H.; Wali, M.; Dammak, F. Free vibration analysis of FG-CNTRC shell structures using the meshfree radial point interpolation method. Comput. Math. Appl. 2020, 79, 3160–3178. [Google Scholar] [CrossRef]
- Mallek, H.; Jrad, H.; Wali, M.; Kessentini, A.; Gamaoun, F.; Dammak, F. Dynamic analysis of functionally graded carbon nanotube–reinforced shell structures with piezoelectric layers under dynamic loads. J. Vib. Control 2019, 26, 1157–1172. [Google Scholar] [CrossRef]
- Marinković, D.; Köppe, H.; Gabbert, U. Aspects of modeling piezoelectric active thin-walled structures. J. Intell. Mater. Syst. Struct. 2009, 20, 1835–1844. [Google Scholar] [CrossRef]
- Marinković, D.; Rama, G.; Zehn, M. Abaqus implementation of a corotational piezoelectric 3-node shell element with drilling degree of freedom. Facta Univ. Ser. Mech. Eng. 2019, 17, 269–283. [Google Scholar] [CrossRef]
- Majumdar, A.; Das, D. A study on thermal buckling load of clamped functionally graded beams under linear and nonlinear thermal gradient across thickness. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2018, 232, 769–784. [Google Scholar] [CrossRef]
- Rahmani, M.; Mohammadi, Y.; Kakavand, F. Buckling analysis of different types of porous FG conical sandwich shells in various thermal surroundings. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 164. [Google Scholar] [CrossRef]
- Gunes, R.; Aydin, M. Elastic response of functionally graded circular plates under a drop-weight. Compos. Struct. 2010, 92, 2445–2456. [Google Scholar] [CrossRef]
- Najafi, F.; Shojaeefard, M.H.; Googarchin, H.S. Nonlinear low-velocity impact response of functionally graded plate with nonlinear three-parameter elastic foundation in thermal field. Compos. Part B Eng. 2016, 107, 123–140. [Google Scholar] [CrossRef]
- Wagih, A.; Attia, M.A.; Abdel Rahman, A.A.; Bendine, K.; Sebaey, T.A. On the indentation of elastoplastic functionally graded materials. Mech. Mater. 2019, 129, 169–188. [Google Scholar] [CrossRef]
- Alijani, A.; Darvizeh, M.; Darvizeh, A.; Ansari, R. Elasto-plastic pre-and post-buckling analysis of functionally graded beams under mechanical loading. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2015, 229, 146–165. [Google Scholar] [CrossRef]
- Gunes, R.; Aydin, M.; Apalak, M.K.; Reddy, J.N. Experimental and numerical investigations of low velocity impact on functionally graded circular plates. Compos. Part B Eng. 2014, 59, 21–32. [Google Scholar] [CrossRef]
- Tamura, I. Strength and ductility of Fe-Ni-C alloys composed of austenite and martensite with various strength. In Proceedings of the Third International Conference on Strength of Metals and Alloys, Cambridge, UK, 20–25 August 1973; Institute of Metals: Cambridge, UK, 1973; Volume 1, pp. 611–615. [Google Scholar]
- Zhang, J.; Qi, D.; Zhou, L.; Zhao, L.; Hu, N. A progressive failure analysis model for composite structures in hygrothermal environments. Compos. Struct. 2015, 133, 331–342. [Google Scholar] [CrossRef]
- Kalali, A.T.; Hadidi-Moud, S. A semi-analytical approach to elastic-plastic stress analysis of FGM pressure vessels. J. Solid Mech. 2013, 5, 63–73. [Google Scholar]
- Xu, G.; Huang, H.; Chen, B.; Chen, F. Buckling and postbuckling of elastoplastic FGM plates under inplane loads. Compos. Struct. 2017, 176, 225–233. [Google Scholar] [CrossRef]
- Bocciarelli, M.; Bolzon, G.; Maier, G. A constitutive model of metal–ceramic functionally graded material behavior: Formulation and parameter identification. Comput. Mater. Sci. 2008, 43, 16–26. [Google Scholar] [CrossRef]
- Azoti, W.L.; Tchalla, A.; Koutsawa, Y.; Makradi, A.; Rauchs, G.; Belouettar, S.; Zahrouni, H. Mean-field constitutive modeling of elasto-plastic composites using two (2) incremental formulations. Compos. Struct. 2013, 105, 256–262. [Google Scholar] [CrossRef]
- Castaneda, P.P. Second-order homogenization estimates for nonlinear composites incorporating field fluctuations: I-theory. J. Mech. Phys. Solid 2002, 50, 737–757. [Google Scholar] [CrossRef]
- Atrian, A.; Majzoobi, G.H.; Nourbakhsh, S.H.; Galehdari, S.A.; Nejad, R.M. Evaluation of tensile strength of Al7075-SiC nanocomposite compacted by gas gun using spherical indentation test and neural networks. Adv. Powder Technol. 2016, 27, 1821–1827. [Google Scholar] [CrossRef]
- Orlik, J. Asymptotic homogenization algorithm for reinforced metal-matrix elasto-plastic composites. Compos. Struct. 2010, 92, 1581–1590. [Google Scholar] [CrossRef]
- Suquet, P. Effective properties of nonlinear composites. In Continuum Micromechanics; Springer: Vienna, Austria, 1997; pp. 197–264. [Google Scholar]
- Suquet, P.M. Elements of Homogenization for Inelastic Solid Mechanics. In Mechanics of Materials with Internal Structure; Cracow University of Technology: Cracow, Poland, 1985; pp. 197–221. [Google Scholar]
- Ponte Castañeda, P. New Variational Principles in Plasticity and Their Application to Composite Materials. J. Mech. Phys. Solids 1991, 39, 1573–1600. [Google Scholar] [CrossRef]
- Mao, Y.; Fu, Y.; Fang, D. Interfacial damage analysis of shallow spherical shell with FGM coating under low velocity impact. Int. J. Mech. Sci. 2013, 71, 30–40. [Google Scholar] [CrossRef]
- Etemadi, E.; Khatibi, A.A.; Takaffoli, M. 3D finite element simulation of sandwich panels with a functionally graded core subjected to low velocity impact. Compos. Struct. 2015, 89, 28–34. [Google Scholar] [CrossRef]
- Jrad, H.; Mars, J.; Wali, M.; Dammak, F. Geometrically nonlinear analysis of elastoplastic behavior of functionally graded shells. Eng. Comput. 2019, 35, 833–847. [Google Scholar] [CrossRef]





| Ec (GPa) | νc | Em (GPa) | νm | σym (MPa) | Km (GPa) | nm |
|---|---|---|---|---|---|---|
| 375 | 0.14 | 107 | 0.34 | 450 | 14 | 1 |
| Indenter Radius R (mm) | Displacement d (mm) | Gradient Index k | ||||
|---|---|---|---|---|---|---|
| 0.5 | 2 | 4 | 6 | 10 | ||
| 1 | 0.1 | 2.5 | 6 | 12 | 16 | 18 |
| 0.2 | 7 | 17 | 35 | 50 | 57 | |
| 0.5 | 0.1 | 2 | 4.5 | 8.5 | 11 | 13 |
| 0.2 | 0.1 | 1 | 2.5 | 5 | 7.5 | 9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kessentini, A.; Allouch, M.; Jrad, H.; Mars, J.; Ben Said, L.; Alhadri, M.; Wali, M.; Dammak, F. Mathematical Formulation and Numerical Simulation of the Mechanical Behavior of Ceramic/Metal (TiB/Ti) FG Sheets Subjected to Spherical Indenter. Mathematics 2024, 12, 209. https://doi.org/10.3390/math12020209
Kessentini A, Allouch M, Jrad H, Mars J, Ben Said L, Alhadri M, Wali M, Dammak F. Mathematical Formulation and Numerical Simulation of the Mechanical Behavior of Ceramic/Metal (TiB/Ti) FG Sheets Subjected to Spherical Indenter. Mathematics. 2024; 12(2):209. https://doi.org/10.3390/math12020209
Chicago/Turabian StyleKessentini, Amir, Marwa Allouch, Hanen Jrad, Jamel Mars, Lotfi Ben Said, Muapper Alhadri, Mondher Wali, and Fakhreddine Dammak. 2024. "Mathematical Formulation and Numerical Simulation of the Mechanical Behavior of Ceramic/Metal (TiB/Ti) FG Sheets Subjected to Spherical Indenter" Mathematics 12, no. 2: 209. https://doi.org/10.3390/math12020209
APA StyleKessentini, A., Allouch, M., Jrad, H., Mars, J., Ben Said, L., Alhadri, M., Wali, M., & Dammak, F. (2024). Mathematical Formulation and Numerical Simulation of the Mechanical Behavior of Ceramic/Metal (TiB/Ti) FG Sheets Subjected to Spherical Indenter. Mathematics, 12(2), 209. https://doi.org/10.3390/math12020209






