Finite Element Method of Functionally Graded Shape Memory Alloy Based on UMAT
Abstract
:1. Introduction
2. Shape Memory Evolution Equation
3. Incremental Constitutive Equation of SMA
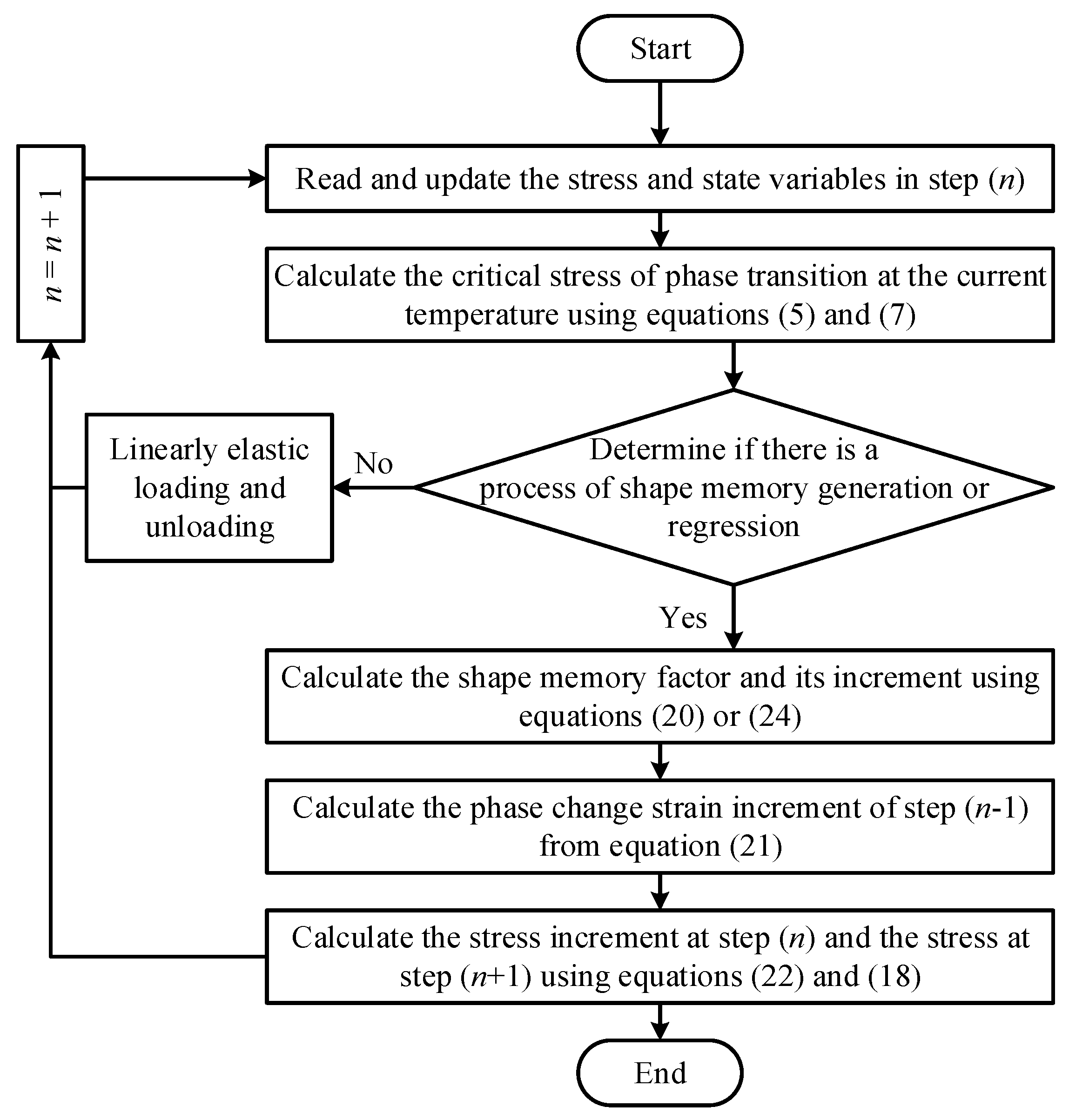
4. UMAT Subroutine Flow
5. Finite Element Discrete Modeling Method
- (1)
- Full-scale modeling of FG-SMA structure;
- (2)
- The FG-SMA structure is stratified or segmented along the graded direction to establish a discrete model of the FG-SMA structure;
- (3)
- The material parameters of each layer or segment in the FG-SMA discrete structure are derived from the coordinates (e.g., surface coordinates, geometrical midplane coordinates, etc.) and within a single layer segment, the material parameters are kept homogeneous;
- (4)
- Between adjacent layers or segments, deformation maintains continuous consistency;
- (5)
- A finite element model of the FG-SMA discrete structure is numerically established and solved.
6. Models and Material Parameters
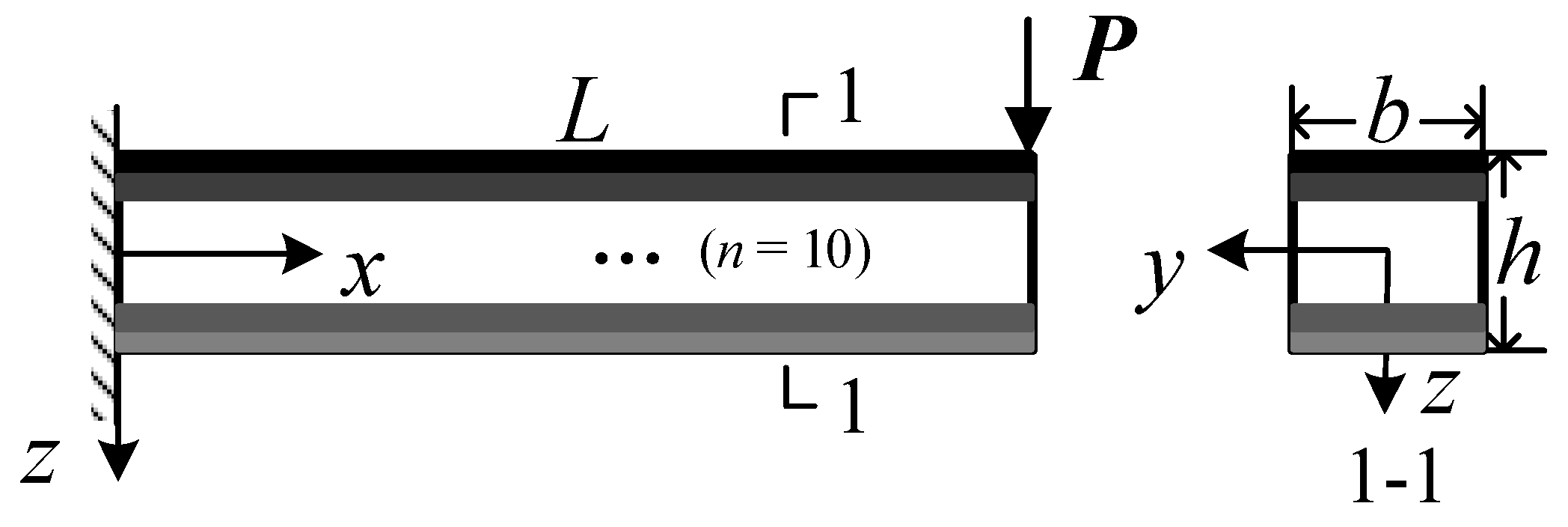
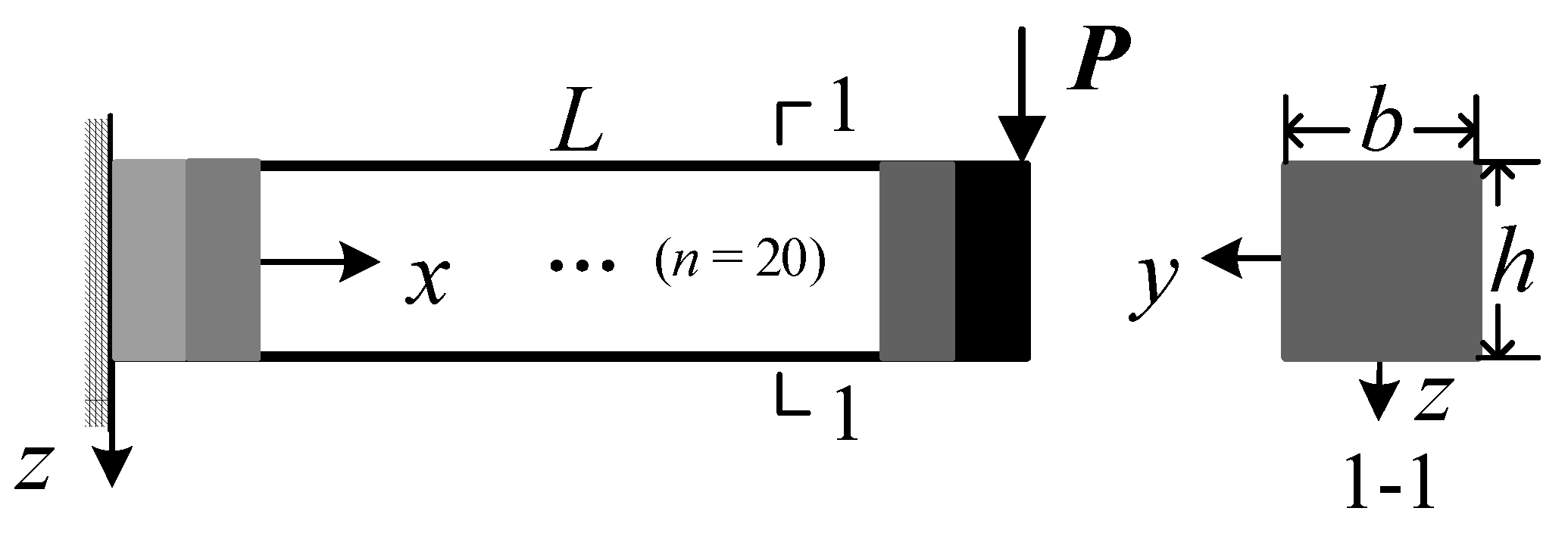
6.1. Models and Boundary Conditions
6.2. Material Parameters
7. Numerical Simulation
8. Conclusions
- (1)
- The phase transformation and mechanical response in the cross section of the axial FG-SMA cantilever beam and SMA homogeneous beam are symmetrically distributed along the thickness direction, but those of the transverse FG-SMA cantilever beam are asymmetric along the thickness direction. The FG-SMA cantilever beam has a stronger load-bearing capacity, and compared to the axial FG-SMA cantilever beam, the transverse FG-SMA cantilever beam has greater stiffness.
- (2)
- It should be noted that for the SMA homogeneous cantilever beam subjected to concentrated loads at the free end, the martensitic phase transformation begins not at the fixed end of the cantilever beam during the loading process, but at a distance of about 10 mm from the fixed end. The martensitic phase transformation in the axial FG-SMA cantilever beam begins closer to the fixed end, which indirectly reflects the influence of material parameters along the axial direction on the phase transformation behavior of the axial FG-SMA structure.
- (3)
- Compared with the SMA homogeneous beam, the stress distribution in the axial FG-SMA cantilever beam is concentrated at the fixed-end position, while the stress distribution in the SMA homogeneous beam is more pronounced at the position far from the fixed end. The variation of the material parameters of the axial FG-SMA cantilever beam leads to changes in stress distribution under the same external load, which can effectively guide the structural design of axial FG-SMA structures.
9. Novelty and Application
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Knick, C.R.; Sharar, D.J.; Wilson, A.A.; Simth, G.L.; Morris, C.J.; Bruck, H.A. High fre-quency, low power, electrically actuated shape memory alloy MEMS bimorph thermal actuators. J. Micromech. Microeng. 2019, 29, 075005. [Google Scholar] [CrossRef]
- Zhou, B.; Kang, Z.T.; Ma, X.; Xue, S.F. On size-dependent bending behaviors of shape memory alloy microbeams via nonlocal strain gradient theory. J. Intell. Mater. Syst. Struct. 2021, 32, 2039–2053. [Google Scholar] [CrossRef]
- Gómez-cortés, J.F.; Nó, M.L.; López-ferreño, I.; Hernández-Saz, J.; Molina, S.I.; Chuvilin, A.; San Juan, J.M. Size effect and scaling power-law for superelasticity in shape-memory alloys at the nanoscale. Nat. Nanotechnol. 2017, 12, 790–796. [Google Scholar] [CrossRef] [PubMed]
- Zhou, B. A macroscopic constitutive model of shape memory alloy considering plasticity. Mech. Mater. 2012, 48, 71–81. [Google Scholar] [CrossRef]
- Cisse, C.; Zaki, W.; Zined, T.B. A review of constitutive models and modeling techniques for shape memory alloys. Int. J. Plast. 2016, 76, 244–284. [Google Scholar] [CrossRef]
- Zhou, B.; Kang, Z.T.; Wang, Z.Y.; Xue, S.F. Finite element method on shape memory alloy structure and its applications. Chin. J. Mech. Eng. 2019, 36, 84. [Google Scholar] [CrossRef]
- Lv, Y.; Xv, X.W.; Guo, S.X. Finite element analysis of crack propagation paths and crack initiation loads in graded composites. Acta Mater. Compos. Sin. 2015, 32, 1099–1106. (In Chinese) [Google Scholar]
- Su, S.K.; Huang, H.W. Thermal-mechanical coupling buckling analysis of porous functionally graded beams. Acta Mater. Compos. Sin. 2017, 24, 2794–2799. (In Chinese) [Google Scholar]
- Heydari, A.; Jalali, A.; Nemati, A. Buckling analysis of circular functionally graded plate under uniform radial compression including shear deformation with linear and quadratic thickness variation on the Pasternak elastic foundation. Appl. Math. Model. 2017, 41, 494–507. [Google Scholar] [CrossRef]
- Xue, L.J.; Dui, G.S.; Liu, B.F. Theoretical analysis of functionally graded shape memory alloy beam subjected to pure bending. J. Mech. Eng. 2012, 48, 40–45. (In Chinese) [Google Scholar] [CrossRef]
- Shariat, B.S.; Meng, Q.L.; Mahmud, A.S.; Wu, Z.G.; Bakhtiari, R.; Zhang, J.S.; Motazedian, F.; Yang, H.; Rio, G.; Nam, T.H.; et al. Functionally graded shape memory alloys: Design, fabrication and experimental evaluation. Mater. Des. 2017, 124, 225–237. [Google Scholar] [CrossRef]
- Tian, H.; Schryvers, D.; Mohanchandra, K.P.; Carman, G.P.; Humbeeck, J.V. Fabrication and characterization of functionally graded Ni-Ti multilayer thin films. Funct. Mater. Lett. 2009, 2, 61–66. [Google Scholar] [CrossRef]
- Mahmud, A.S.; Liu, Y.; Nam, T.H. Gradient anneal of functionally graded NiTi. Smart Mater. Struct. 2008, 17, 015031. [Google Scholar] [CrossRef]
- Meng, Q.L.; Liu, Y.N.; Yang, H.; Nam, T.H. Laser annealing of functionally graded NiTi thin plate. Scr. Mater. 2011, 65, 1109–1112. [Google Scholar] [CrossRef]
- Meng, Q.L.; Liu, Y.N.; Yang, H.; Shariat, B.S.; Nam, T.H. Functionally graded NiTi strips prepared by laser surface anneal. Acta Mater. 2012, 60, 1658–1668. [Google Scholar] [CrossRef]
- Shariat, B.S.; Meng, Q.L.; Mahmud, A.S.; Wu, Z.G.; Bakhtiari, R.; Zhang, J.S.; Motazedian, F.; Yang, H.; Rio, G.; Nam, T.H.; et al. Experiments on deformation behavior of functionally graded NiTi structures. Data Brief 2017, 13, 562–568. [Google Scholar] [CrossRef] [PubMed]
- Mohri, M.; Nili-Ahmadabadi, M. Phase transformation and structure of functionally graded Ni–Ti bi-layer thin films with two-way shape memory effect. Sens. Actuators A Phys. 2015, 228, 151–158. [Google Scholar] [CrossRef]
- Mohri, M.; Taghizadeh, M.; Wand, D.; Hahn, H.; Nili-Ahmadabadi, M. Microstructural study and simulation of intrinsic two-way shape memory behavior of functionally graded Ni-rich/NiTiCu thin film. Mater. Charact. 2018, 135, 317–324. [Google Scholar] [CrossRef]
- Liu, B.; Dui, G.; Yang, S. On the transformation behavior of functionally graded SMA composites subjected to thermal loading. Eur. J. Mech. 2013, 40, 139–147. [Google Scholar] [CrossRef]
- Liu, B.; Ni, P.; Zhang, W. On Behaviors of Functionally Graded SMAs under Thermo-Mechanical Coupling. Acta Mech. Solida Sin. 2016, 29, 46–58. [Google Scholar] [CrossRef]
- Shariat, B.S.; Liu, Y.; Meng, Q.; Rio, G. Analytical modelling of functionally graded NiTi shape memory alloy plates under tensile loading and recovery of deformation upon heating. Acta Mater. 2013, 61, 3411–3421. [Google Scholar] [CrossRef]
- Liu, B.F.; Wang, Q.F.; Hu, S.L.; Zhou, R. Thermodynamic behaviors of functionally graded shape memory alloy actuator. J. Nanjing Univ. Aeronaut. Astronaut. 2017, 49, 45–50. (In Chinese) [Google Scholar]
- Xue, L.J.; Dui, G.S.; Liu, B.F. A micromechanical model for the functionally graded shape memory alloy. Eng. Mech. 2014, 31, 225–229. (In Chinese) [Google Scholar]
- Kang, Z.T.; Zhou, B.; Xue, S.F. Me-chanical behaviors of functionally graded shape memory alloy composite beam. Acta Mate-Riae Compos. Sin. 2019, 36, 1901–1910. (In Chinese) [Google Scholar]
- Kang, Z.T.; Zhou, B.; Xue, S.F. Finite element numerical simulation on thermo-mechanical coupling behavior in shape memory alloy pipe connection. J. Mech. Eng. 2018, 54, 68–75. (In Chinese) [Google Scholar] [CrossRef]
- Kang, Z.T.; Zhou, B.; Xue, S.F. Finite element method for elliptical orifice problems in shape memory alloys plate. Chin. J. Appl. Mech. 2020, 37, 18–24+470. (In Chinese) [Google Scholar]
- Soltanieh, G.; Kabir, M.Z.; Shariyat, M. Snap instability of shallow laminated cylindrical shells reinforced with functionally graded shape memory alloy wires. Compos. Struct. 2017, 180, 581–595. [Google Scholar] [CrossRef]
- Zhou, B.; Liu, Y.J.; Wang, Z.Q.; Leng, J.S. A thermo-mechanical constitutive equation for shape memory alloy. Chin. J. Solid Mech. 2011, 32, 21–28. (In Chinese) [Google Scholar]
- Wang, Z.Q.; Zhou, B.; Liang, W.Y. The constitutive relationship of shape memory alloy. Acta Metall. Sin. 2007, 43, 1211–1216. (In Chinese) [Google Scholar]
- Brison, L.C. One-dimension constitutive behavior of shape memory alloys: Thermomechanical derivation with non-constant material functions and martensite internal variable. J. Intell. Mater. Syst. Struct. 1993, 4, 229–242. [Google Scholar] [CrossRef]
- Qidwai, M.A.; Lagoudas, D.C. Numerical implementation of a shape memory alloy thermomechanical constitutive model using return mapping algorithms. Int. J. Numer. Methods Eng. 2000, 47, 1123–1168. [Google Scholar] [CrossRef]
- Tabesh, M.; Liu, B.; Boyd, J.G.; Lagoudas, D.C. Analytical solution for the pseudoelastic response of a shape memory alloy thick-walled cylinder under internal pressure. Smart Mater. Struct. 2013, 22, 223–236. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, H.X.; Jiang, X.X.; Yang, X.H. A high-order and efficient numerical technique for the nonlocal neutron diffusion equation representing neutron transport in a nuclear reactor. Ann. Nuclear Energy 2024, 195, 110163. [Google Scholar] [CrossRef]
- Zhou, Z.Y.; Zhang, H.X.; Yang, X.H. H1-norm error analysis of a robust ADI method on graded mesh for three-dimensional subdiffusion problems. Numer. Algorithms 2023, 1–19. [Google Scholar] [CrossRef]
- Zhang, H.X.; Liu, Y.; Yang, X.H. An efficient ADI difference scheme for the nonlocal evolution problem in three-dimensional space. J. Appl. Math. Comput. 2023, 69, 651–674. [Google Scholar] [CrossRef]
- Yang, X.H.; Zhang, Q.; Yuan, G.W.; Sheng, Z.Q. On positivity preservation in nonlinear finite volume method for multi-term fractional subdiffusion equation on polygonal meshes. Nonlinear Dyn. 2018, 92, 595–612. [Google Scholar] [CrossRef]
- Haixiang, Z.; Xuehua, Y.; Qiong, T.; Xu, D. A robust error analysis of the OSC method for a multi-term fourth-order sub-diffusion equation. Comput. Math. Appl. 2022, 109, 180–190. [Google Scholar]











| /GPa | /GPa | μ | |
| 70 | 30 | 0.43 | 0.069 |
| /(MPa/°C) | /(MPa/°C) | /MPa | /MPa |
| 8 | 13 | 100 | 170 |
| /°C | /°C | /°C | /°C |
| 7 | 15 | 45 | 56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, Z.; Yu, A.; Wang, Y.; Qin, Y.; Wu, Q.; Liu, H. Finite Element Method of Functionally Graded Shape Memory Alloy Based on UMAT. Mathematics 2024, 12, 282. https://doi.org/10.3390/math12020282
Kang Z, Yu A, Wang Y, Qin Y, Wu Q, Liu H. Finite Element Method of Functionally Graded Shape Memory Alloy Based on UMAT. Mathematics. 2024; 12(2):282. https://doi.org/10.3390/math12020282
Chicago/Turabian StyleKang, Zetian, Anfeng Yu, Yuchen Wang, Yi Qin, Qian Wu, and Huan Liu. 2024. "Finite Element Method of Functionally Graded Shape Memory Alloy Based on UMAT" Mathematics 12, no. 2: 282. https://doi.org/10.3390/math12020282





