Generalized Linear Models with Covariate Measurement Error and Zero-Inflated Surrogates
Abstract
1. Introduction
2. Statistical Models and Naive RC Estimator
3. Regression Calibration for Zero-Inflated Surrogates
4. Expected Estimating Equation Estimator
5. Simulation Study
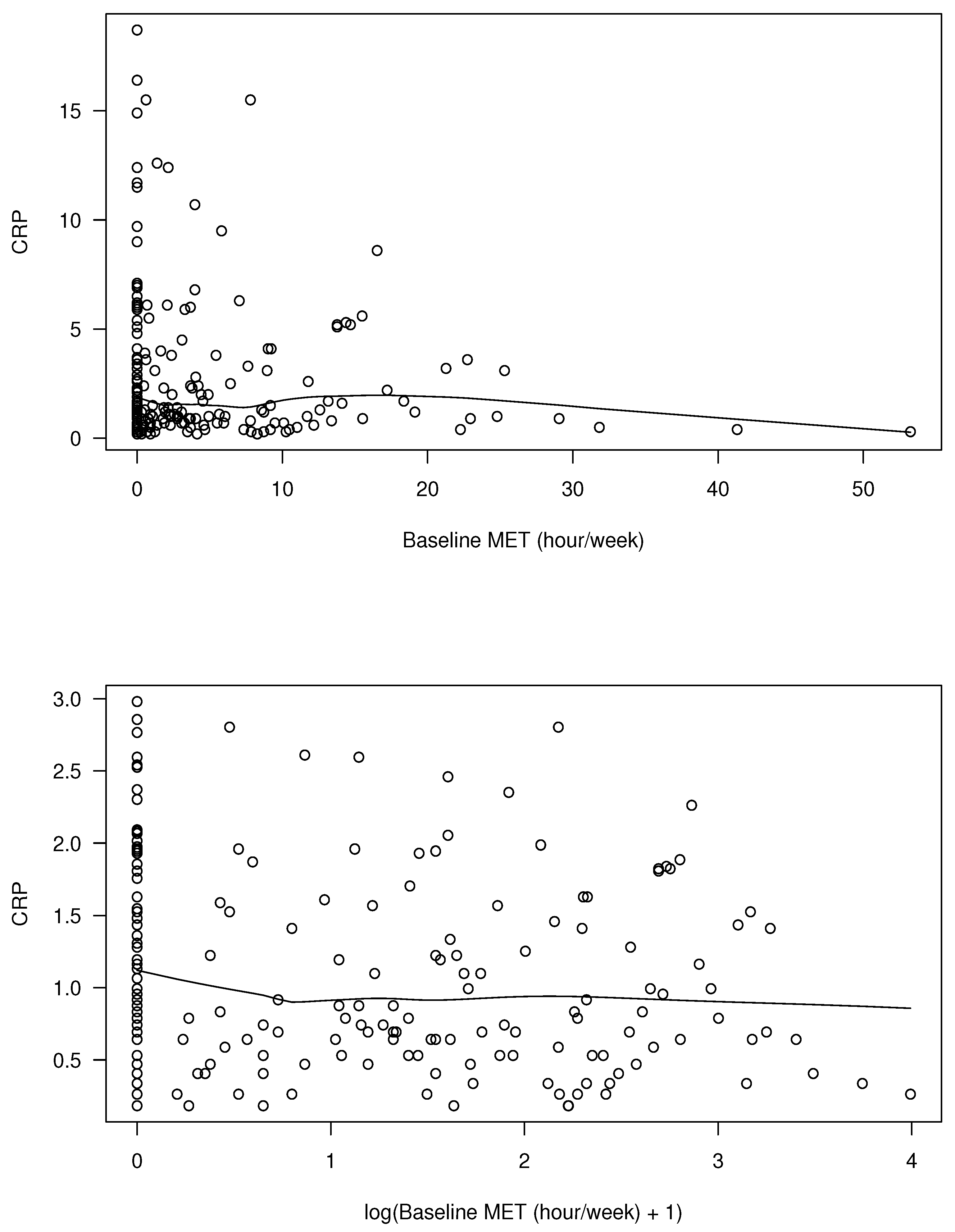
6. Analysis of APPEAL Data
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Proofs of Propositions 1 and 2
References
- Fuller, W.A. Measurement Error Models; John Wiley & Sons: New York, NY, USA, 1987. [Google Scholar]
- Carroll, R.J.; Ruppert, D.; Stefanski, L.A.; Crainiceanu, C.M. Measurement Error in Nonlinear Models, A modern Perspective, 2nd ed.; Chapman and Hall: London, UK, 2006. [Google Scholar]
- Yi, G.Y. Statistical Analysis with Measurement Error or Misclassification, Strategy, Methods and Application; Springer: New York, NY, USA, 2017. [Google Scholar]
- Freedman, L.S.; Carroll, R.J.; Wax, Y. Estimating the relationship between dietary intake obtained from a food frequency questionnaire and true average intake. Am. J. Epidemiol. 1991, 134, 310–320. [Google Scholar] [CrossRef]
- Kipnis, V.; Subar, A.F.; Midthune, D.; Freedman, L.S.; Ballard-Barbash, R.; Troiano, R.; Bingham, S.; Schoeller, D.A.; Schatzkin, A.; Carroll, R.J. The structure of dietary measurement error: Results of the OPEN biomarker study. Am. J. Epidemiol. 2003, 158, 14–21. [Google Scholar] [CrossRef]
- Kipnis, V.; Midthune, D.; Buckman, D.W.; Dodd, K.W.; Guenther, P.M.; Krebs-Smith, S.M.; Subar, A.F.; Tooze, J.A.; Carroll, R.J.; Freedman, L.S. Modeling data with excess zeros and measurement error: Application to evaluating relationships between episodically consumed foods and health outcomes. Biometrics 2009, 65, 1003–1010. [Google Scholar] [CrossRef]
- Jette, M.; Sidney, K.; Blumchen, G. Metabolic equiva-lents (METS) in exercise testing, exercise prescription, and evaluation of functional capacity. Clin Cardiol. 1990, 13, 555–565. [Google Scholar] [CrossRef] [PubMed]
- Carroll, R.J.; Galindo, C.D. Measurement Error, Biases, and the Validation of Complex Models for Blood Lead Levels in Children. Environ. Health Perspect. 1998, 106, 1535–1539. [Google Scholar] [CrossRef] [PubMed]
- McTiernan, A.; Yasui, Y.; Sorensen, B.; Irwin, M.L.; Morgan, A.; Rudolph, R.E.; Surawicz, C.; Lampe, J.W.; Ayub, K.; Potter, J.D.; et al. Effect of a 12-month exercise intervention on patterns of cellular proliferation in colonic crypts: A randomized controlled trial. Cancer Epidemiol. Biomarkers Prev. 2006, 15, 1588–1597. [Google Scholar] [CrossRef]
- Slattery, M.L.; Potter, J.; Caan, B.; Edwards, S.; Coates, A.; Ma, K.N.; Berry, T.D. Energy balance and colon cancer-—beyond physical activity. Cancer Res. 1997, 57, 75–80. [Google Scholar] [PubMed]
- Prentice, R.L. Covariate measurement errors and parameter estimation in a failure time regression model. Biometrika 1982, 69, 331–342. [Google Scholar] [CrossRef]
- Buonaccorsi, J. Measurement Error: Models, Methods, and Applications; Hapman and Hall/CRC: Boca Raton, FL, USA, 2010. [Google Scholar]
- Tsiatis, A.A.; DeGruttola, V.; Wulfsohn, M.S. Modeling the relationship of survival to longitudinal data measured with error. Applications to survival and CD4 count in patients with AIDS. J. Am. Stat. Assoc. 1995, 90, 27–37. [Google Scholar] [CrossRef]
- Wang, C.Y.; Wang, N.; Wang, S. Regression analysis when covariates are regression parameters of a random effect model for observed longitudinal measurements. Biometrics 2000, 56, 487–495. [Google Scholar] [CrossRef]
- Cook, J.; Stefanski, L.A. A simulation extrapolation method for parametric measurement error models. J. Amer. Statist. Assoc. 1994, 89, 1314–1328. [Google Scholar] [CrossRef]
- Stefanski, L.A.; Cook, J.R. Simulation-Extrapolation: The Measurement Error Jackknife. J. Am. Stat. Assoc. 1995, 90, 1247–1256. [Google Scholar] [CrossRef]
- Tooze, J.A.; Grunwald, G.K.; Jones, R.H. Analysis of repeated measures data with clumping at zero. Stat. Methods Med. Res. 2002, 11, 341–355. [Google Scholar] [CrossRef]
- Richardson, D.B.; Ciampi, A. Effects of exposure measurement error when an exposure variable is constrained by a lower limit. Am. J. Epidemiol. 2003, 15, 355–363. [Google Scholar] [CrossRef]
- Wang, C.Y.; Cullings, H.; Song, X.; Kopecky, K.J. Joint nonparametric correction estimation for excess relative risk regression in survival analysis. J. Roy. Statist. Soc. Ser. B 2017, 79, 1583–1599. [Google Scholar] [CrossRef]
- Wang, C.Y.; Song, X. Semiparametric regression calibration for general hazard models in survival analysis with covariate measurement error; surprising performance under linear hazard. Biometrics 2021, 77, 561–572. [Google Scholar] [CrossRef]
- Wang, C.Y.; Huang, Y.; Chao, E.C.; Jeffcoat, M.K. Expected estimating equations for missing data, measurement error, and misclassification, with application to longitudinal nonignorably missing data. Biometrics 2008, 64, 85–95. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.H.; Hwang, W.H.; Chen, F.Y. Differential measurement errors in zero-truncated regression models for count data. Biometrics 2011, 67, 1471–1480. [Google Scholar] [CrossRef] [PubMed]
- Tsiatis, A.A.; Davidian, D. A semiparametric estimator for the proportional hazards model with longitudinal covariates measured with error. Biometrika 2001, 88, 447–458. [Google Scholar] [CrossRef]
- Tsiatis, A.A.; Davidian, M. Joint modeling of longitudinal and time-to-event data: An overview. Statistica Sinica 2004, 14, 809–834. [Google Scholar]
- Tooze, J.A.; Kipnis, V.; Buckman, D.W.; Carroll, R.J.; Freedman, L.S.; Guenther, P.M.; Krebs-Smith, S.M.; Subar, A.F.; Dodd, K.W. A mixed-effects model approach for estimating the distribution of usual intake of nutrients: The NCI method. Stat. Med. 2010, 29, 2857–2868. [Google Scholar] [CrossRef]
| Naive | NRC | RC | EEE | Naive | NRC | RC | EEE | ||
|---|---|---|---|---|---|---|---|---|---|
| Bias | 0.134 | −0.230 | −0.002 | 0.003 | 0.133 | −0.228 | −0.003 | 0.002 | |
| SD | 0.093 | 0.117 | 0.103 | 0.103 | 0.064 | 0.080 | 0.072 | 0.071 | |
| ASE | 0.093 | 0.117 | 0.106 | 0.106 | 0.066 | 0.083 | 0.075 | 0.074 | |
| CP | 0.684 | 0.486 | 0.972 | 0.962 | 0.460 | 0.180 | 0.954 | 0.966 | |
| Bias | −0.126 | 0.107 | 0.004 | 0.000 | −0.127 | 0.103 | 0.001 | −0.002 | |
| SD | 0.050 | 0.068 | 0.060 | 0.060 | 0.035 | 0.047 | 0.043 | 0.042 | |
| ASE | 0.049 | 0.068 | 0.061 | 0.061 | 0.035 | 0.048 | 0.043 | 0.043 | |
| CP | 0.270 | 0.658 | 0.958 | 0.954 | 0.056 | 0.446 | 0.956 | 0.960 | |
| Bias | 0.301 | −0.349 | −0.007 | −0.006 | 0.299 | −0.343 | −0.005 | −0.004 | |
| SD | 0.096 | 0.161 | 0.133 | 0.132 | 0.067 | 0.109 | 0.091 | 0.091 | |
| ASE | 0.095 | 0.162 | 0.136 | 0.136 | 0.068 | 0.113 | 0.095 | 0.095 | |
| CP | 0.122 | 0.404 | 0.960 | 0.952 | 0.002 | 0.106 | 0.966 | 0.962 | |
| Bias | −0.252 | 0.154 | 0.006 | 0.006 | −0.252 | 0.147 | 0.003 | 0.002 | |
| SD | 0.050 | 0.096 | 0.080 | 0.079 | 0.035 | 0.066 | 0.056 | 0.056 | |
| ASE | 0.049 | 0.096 | 0.082 | 0.082 | 0.035 | 0.067 | 0.057 | 0.057 | |
| CP | 0.002 | 0.674 | 0.952 | 0.958 | 0.000 | 0.424 | 0.948 | 0.958 | |
| Bias | 0.556 | −0.652 | −0.035 | 0.033 | 0.558 | −0.616 | −0.018 | −0.019 | |
| SD | 0.101 | 0.341 | 0.244 | 0.241 | 0.070 | 0.217 | 0.156 | 0.157 | |
| ASE | 0.098 | 0.325 | 0.230 | 0.229 | 0.069 | 0.220 | 0.157 | 0.158 | |
| CP | 0.000 | 0.462 | 0.962 | 0.942 | 0.000 | 0.104 | 0.960 | 0.960 | |
| Bias | −0.445 | 0.263 | 0.023 | 0.022 | −0.447 | 0.241 | 0.011 | 0.012 | |
| SD | 0.048 | 0.197 | 0.152 | 0.150 | 0.033 | 0.126 | 0.097 | 0.099 | |
| ASE | 0.047 | 0.188 | 0.144 | 0.144 | 0.033 | 0.128 | 0.099 | 0.099 | |
| CP | 0.000 | 0.846 | 0.960 | 0.942 | 0.000 | 0.558 | 0.952 | 0.954 | |
| Bias | 0.655 | −0.839 | −0.057 | −0.051 | 0.657 | −0.769 | −0.024 | −0.025 | |
| SD | 0.101 | 0.609 | 0.323 | 0.307 | 0.070 | 0.302 | 0.197 | 0.198 | |
| ASE | 0.098 | 0.466 | 0.300 | 0.296 | 0.069 | 0.302 | 0.198 | 0.229 | |
| CP | 0.000 | 0.634 | 0.956 | 0.922 | 0.000 | 0.150 | 0.956 | 0.950 | |
| Bias | −0.519 | 0.327 | 0.038 | 0.034 | −0.522 | 0.287 | 0.015 | 0.015 | |
| SD | 0.046 | 0.286 | 0.204 | 0.195 | 0.033 | 0.170 | 0.126 | 0.127 | |
| ASE | 0.045 | 0.263 | 0.191 | 0.189 | 0.032 | 0.170 | 0.126 | 0.148 | |
| CP | 0.000 | 0.972 | 0.956 | 0.918 | 0.000 | 0.716 | 0.948 | 0.930 | |
| Naive | NRC | RC | EEE | Naive | NRC | RC | EEE | ||
|---|---|---|---|---|---|---|---|---|---|
| X is from a mixture of two normal distributions and the error is normal | |||||||||
| Bias | 0.209 | −0.096 | 0.041 | 0.036 | 0.204 | −0.101 | 0.037 | 0.032 | |
| SD | 0.081 | 0.099 | 0.097 | 0.097 | 0.061 | 0.074 | 0.073 | 0.073 | |
| ASE | 0.084 | 0.105 | 0.103 | 0.103 | 0.060 | 0.074 | 0.072 | 0.073 | |
| CP | 0.300 | 0.878 | 0.940 | 0.946 | 0.074 | 0.720 | 0.900 | 0.916 | |
| Bias | −0.160 | 0.038 | −0.020 | −0.018 | −0.158 | 0.041 | −0.018 | −0.016 | |
| SD | 0.045 | 0.058 | 0.057 | 0.057 | 0.033 | 0.043 | 0.042 | 0.042 | |
| ASE | 0.046 | 0.061 | 0.059 | 0.060 | 0.032 | 0.043 | 0.042 | 0.042 | |
| CP | 0.060 | 0.920 | 0.946 | 0.950 | 0.002 | 0.848 | 0.928 | 0.928 | |
| Bias | 0.341 | −0.199 | 0.051 | 0.036 | 0.336 | −0.204 | 0.050 | 0.034 | |
| SD | 0.084 | 0.132 | 0.123 | 0.125 | 0.063 | 0.098 | 0.090 | 0.091 | |
| ASE | 0.086 | 0.139 | 0.130 | 0.131 | 0.061 | 0.098 | 0.091 | 0.092 | |
| CP | 0.024 | 0.734 | 0.928 | 0.946 | 0.000 | 0.460 | 0.902 | 0.920 | |
| Bias | −0.268 | 0.074 | −0.024 | −0.017 | −0.265 | 0.076 | −0.024 | −0.017 | |
| SD | 0.045 | 0.078 | 0.075 | 0.076 | 0.033 | 0.058 | 0.054 | 0.055 | |
| ASE | 0.046 | 0.082 | 0.078 | 0.079 | 0.033 | 0.058 | 0.055 | 0.055 | |
| CP | 0.000 | 0.892 | 0.938 | 0.950 | 0.000 | 0.744 | 0.916 | 0.932 | |
| X is normal and the error is from a modified chi-square distribution | |||||||||
| Bias | 0.384 | −0.278 | 0.082 | 0.088 | 0.385 | −0.275 | 0.085 | 0.091 | |
| SD | 0.095 | 0.169 | 0.134 | 0.134 | 0.067 | 0.118 | 0.094 | 0.094 | |
| ASE | 0.093 | 0.163 | 0.129 | 0.129 | 0.066 | 0.115 | 0.091 | 0.091 | |
| CP | 0.012 | 0.614 | 0.870 | 0.850 | 0.000 | 0.322 | 0.816 | 0.792 | |
| Bias | −0.295 | 0.125 | −0.038 | −0.040 | −0.293 | 0.125 | −0.038 | −0.040 | |
| SD | 0.052 | 0.101 | 0.081 | 0.081 | 0.036 | 0.070 | 0.056 | 0.056 | |
| ASE | 0.050 | 0.097 | 0.078 | 0.078 | 0.036 | 0.069 | 0.055 | 0.055 | |
| CP | 0.000 | 0.764 | 0.898 | 0.890 | 0.000 | 0.594 | 0.880 | 0.882 | |
| X is normal and the error is from a mixture of two normal distribution | |||||||||
| Bias | 0.376 | −0.431 | 0.024 | −0.024 | 0.380 | −0.418 | −0.018 | −0.018 | |
| SD | 0.096 | 0.196 | 0.162 | 0.162 | 0.069 | 0.136 | 0.107 | 0.107 | |
| ASE | 0.096 | 0.198 | 0.160 | 0.161 | 0.068 | 0.139 | 0.112 | 0.112 | |
| CP | 0.030 | 0.402 | 0.954 | 0.958 | 0.000 | 0.114 | 0.954 | 0.958 | |
| Bias | −0.311 | 0.183 | 0.013 | 0.013 | −0.314 | 0.175 | 0.009 | 0.009 | |
| SD | 0.048 | 0.116 | 0.098 | 0.098 | 0.033 | 0.080 | 0.066 | 0.066 | |
| ASE | 0.049 | 0.118 | 0.098 | 0.099 | 0.035 | 0.082 | 0.068 | 0.068 | |
| CP | 0.000 | 0.724 | 0.950 | 0.950 | 0.000 | 0.430 | 0.954 | 0.956 | |
| Naive | NRC | RC | EEE | Naive | NRC | RC | EEE | ||
|---|---|---|---|---|---|---|---|---|---|
| Bias | 0.065 | −0.190 | −0.010 | −0.010 | 0.063 | −0.190 | −0.012 | −0.012 | |
| SD | 0.191 | 0.234 | 0.203 | 0.208 | 0.136 | 0.169 | 0.147 | 0.150 | |
| ASE | 0.181 | 0.224 | 0.193 | 0.199 | 0.128 | 0.158 | 0.136 | 0.140 | |
| CP | 0.922 | 0.836 | 0.938 | 0.944 | 0.892 | 0.766 | 0.936 | 0.942 | |
| Bias | −0.080 | 0.083 | −0.008 | 0.007 | −0.079 | 0.083 | −0.006 | 0.008 | |
| SD | 0.122 | 0.154 | 0.133 | 0.142 | 0.085 | 0.109 | 0.094 | 0.100 | |
| ASE | 0.115 | 0.147 | 0.126 | 0.134 | 0.082 | 0.104 | 0.089 | 0.095 | |
| CP | 0.868 | 0.914 | 0.928 | 0.930 | 0.788 | 0.874 | 0.936 | 0.944 | |
| Bias | 0.069 | −0.340 | −0.014 | −0.013 | 0.065 | −0.341 | −0.018 | −0.016 | |
| SD | 0.207 | 0.266 | 0.219 | 0.232 | 0.148 | 0.189 | 0.159 | 0.169 | |
| ASE | 0.197 | 0.254 | 0.210 | 0.223 | 0.139 | 0.179 | 0.148 | 0.156 | |
| CP | 0.930 | 0.706 | 0.950 | 0.948 | 0.900 | 0.518 | 0.928 | 0.928 | |
| Bias | −0.116 | 0.146 | −0.035 | 0.015 | −0.114 | 0.145 | −0.034 | 0.014 | |
| SD | 0.159 | 0.205 | 0.165 | 0.190 | 0.111 | 0.141 | 0.115 | 0.132 | |
| ASE | 0.149 | 0.191 | 0.155 | 0.178 | 0.106 | 0.135 | 0.109 | 0.125 | |
| CP | 0.848 | 0.884 | 0.920 | 0.940 | 0.766 | 0.836 | 0.920 | 0.942 | |
| Bias | 0.175 | −0.276 | −0.014 | −0.015 | 0.171 | −0.277 | −0.017 | −0.016 | |
| SD | 0.186 | 0.277 | 0.222 | 0.230 | 0.135 | 0.203 | 0.166 | 0.172 | |
| ASE | 0.177 | 0.267 | 0.214 | 0.223 | 0.125 | 0.188 | 0.150 | 0.156 | |
| CP | 0.824 | 0.800 | 0.938 | 0.948 | 0.700 | 0.672 | 0.934 | 0.940 | |
| Bias | −0.173 | 0.108 | −0.014 | 0.011 | −0.171 | 0.109 | −0.012 | 0.012 | |
| SD | 0.113 | 0.178 | 0.146 | 0.162 | 0.081 | 0.128 | 0.106 | 0.117 | |
| ASE | 0.108 | 0.171 | 0.140 | 0.155 | 0.076 | 0.121 | 0.098 | 0.109 | |
| CP | 0.610 | 0.914 | 0.948 | 0.946 | 0.404 | 0.856 | 0.926 | 0.940 | |
| Bias | 0.232 | −0.487 | −0.028 | −0.023 | 0.225 | −0.487 | −0.031 | −0.023 | |
| SD | 0.204 | 0.333 | 0.249 | 0.269 | 0.146 | 0.236 | 0.183 | 0.199 | |
| ASE | 0.193 | 0.314 | 0.238 | 0.259 | 0.136 | 0.221 | 0.167 | 0.181 | |
| CP | 0.754 | 0.642 | 0.946 | 0.952 | 0.626 | 0.398 | 0.924 | 0.922 | |
| Bias | −0.273 | 0.175 | −0.056 | 0.023 | −0.270 | 0.174 | −0.055 | 0.021 | |
| SD | 0.148 | 0.240 | 0.183 | 0.227 | 0.104 | 0.166 | 0.129 | 0.162 | |
| ASE | 0.138 | 0.222 | 0.171 | 0.213 | 0.098 | 0.156 | 0.120 | 0.148 | |
| CP | 0.488 | 0.892 | 0.900 | 0.946 | 0.230 | 0.824 | 0.902 | 0.940 | |
| Naive | RC | CRC | EEE | Naive | RC | CRC | EEE | ||
|---|---|---|---|---|---|---|---|---|---|
| Bias | 0.137 | −0.225 | −0.006 | −0.001 | 0.134 | −0.224 | −0.001 | 0.005 | |
| SD | 0.095 | 0.122 | 0.109 | 0.110 | 0.065 | 0.082 | 0.074 | 0.073 | |
| ASE | 0.093 | 0.117 | 0.106 | 0.106 | 0.066 | 0.083 | 0.075 | 0.074 | |
| CP | 0.694 | 0.504 | 0.938 | 0.930 | 0.454 | 0.226 | 0.946 | 0.944 | |
| Bias | −0.137 | 0.094 | 0.004 | 0.001 | −0.136 | 0.093 | 0.001 | −0.003 | |
| SD | 0.051 | 0.071 | 0.071 | 0.065 | 0.033 | 0.048 | 0.044 | 0.043 | |
| ASE | 0.050 | 0.069 | 0.064 | 0.063 | 0.036 | 0.049 | 0.044 | 0.044 | |
| CP | 0.204 | 0.742 | 0.940 | 0.938 | 0.020 | 0.538 | 0.954 | 0.956 | |
| Bias | 0.042 | 0.042 | −0.004 | −0.004 | 0.049 | 0.049 | 0.002 | 0.003 | |
| SD | 0.052 | 0.052 | 0.053 | 0.053 | 0.036 | 0.036 | 0.038 | 0.037 | |
| ASE | 0.050 | 0.050 | 0.050 | 0.050 | 0.035 | 0.035 | 0.036 | 0.036 | |
| CP | 0.852 | 0.852 | 0.938 | 0.938 | 0.704 | 0.704 | 0.942 | 0.942 | |
| Bias | 0.300 | −0.347 | −0.016 | −0.016 | 0.298 | −0.338 | −0.005 | −0.004 | |
| SD | 0.098 | 0.170 | 0.142 | 0.143 | 0.067 | 0.114 | 0.095 | 0.094 | |
| ASE | 0.095 | 0.162 | 0.136 | 0.136 | 0.067 | 0.113 | 0.095 | 0.094 | |
| CP | 0.110 | 0.406 | 0.944 | 0.944 | 0.006 | 0.132 | 0.956 | 0.954 | |
| Bias | −0.264 | 0.138 | 0.011 | 0.011 | −0.264 | 0.132 | 0.004 | 0.002 | |
| SD | 0.051 | 0.099 | 0.087 | 0.087 | 0.033 | 0.068 | 0.060 | 0.059 | |
| ASE | 0.049 | 0.096 | 0.083 | 0.083 | 0.035 | 0.068 | 0.058 | 0.058 | |
| CP | 0.000 | 0.732 | 0.944 | 0.948 | 0.000 | 0.518 | 0.958 | 0.958 | |
| Bias | 0.070 | 0.070 | −0.005 | −0.006 | 0.076 | 0.076 | 0.002 | 0.002 | |
| SD | 0.054 | 0.054 | 0.059 | 0.059 | 0.038 | 0.038 | 0.042 | 0.042 | |
| ASE | 0.052 | 0.052 | 0.053 | 0.054 | 0.037 | 0.037 | 0.038 | 0.038 | |
| CP | 0.736 | 0.736 | 0.934 | 0.938 | 0.464 | 0.464 | 0.922 | 0.920 | |
| Naive | NRC | RC | EEE | ||
|---|---|---|---|---|---|
| Intercept | 0.259 | 0.345 | 0.299 | 0.282 | |
| SE | 0.360 | 0.377 | 0.367 | 0.364 | |
| log(MET+1) | −0.067 | −0.136 | −0.107 | −0.098 | |
| SE | 0.045 | 0.098 | 0.071 | 0.062 | |
| Age | 0.015 | 0.015 | 0.014 | 0.015 | |
| SE | 0.006 | 0.006 | 0.007 | 0.007 | |
| Nuisance parameters | |||||
| 1.258 | 0.925 | 0.927 | |||
| SE | 0.100 | 0.160 | 0.161 | ||
| 0.447 | 0.976 | 0.987 | |||
| SE | 0.145 | 0.337 | 0.330 | ||
| 0.910 | 1.674 | 1.671 | |||
| SE | 0.130 | 0.293 | 0.292 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.-Y.; Tapsoba, J.d.D.; Duggan, C.; McTiernan, A. Generalized Linear Models with Covariate Measurement Error and Zero-Inflated Surrogates. Mathematics 2024, 12, 309. https://doi.org/10.3390/math12020309
Wang C-Y, Tapsoba JdD, Duggan C, McTiernan A. Generalized Linear Models with Covariate Measurement Error and Zero-Inflated Surrogates. Mathematics. 2024; 12(2):309. https://doi.org/10.3390/math12020309
Chicago/Turabian StyleWang, Ching-Yun, Jean de Dieu Tapsoba, Catherine Duggan, and Anne McTiernan. 2024. "Generalized Linear Models with Covariate Measurement Error and Zero-Inflated Surrogates" Mathematics 12, no. 2: 309. https://doi.org/10.3390/math12020309
APA StyleWang, C.-Y., Tapsoba, J. d. D., Duggan, C., & McTiernan, A. (2024). Generalized Linear Models with Covariate Measurement Error and Zero-Inflated Surrogates. Mathematics, 12(2), 309. https://doi.org/10.3390/math12020309







