Implementing PSO-LSTM-GRU Hybrid Neural Networks for Enhanced Control and Energy Efficiency of Excavator Cylinder Displacement
Abstract
1. Introduction
- This study represents the first implementation of the PSO-LSTM-GRU-PID controller on a physical test bench designed to simulate the movement of the boom cylinder in a hydraulic excavator, alongside a simulation model in AMESim software 2310.The key benefit of this controller lies in its model-free nature, allowing it to be implemented without the need for system identification, thereby reducing the computational load and hardware requirements on the hydraulic excavator.
- The PSO algorithm was utilized to optimize four hyperparameters within the LSTM-GRU-PID controller, aiming to improve tracking accuracy and energy efficiency. The effectiveness of the proposed controller was confirmed through both co-simulation and experimental testing.
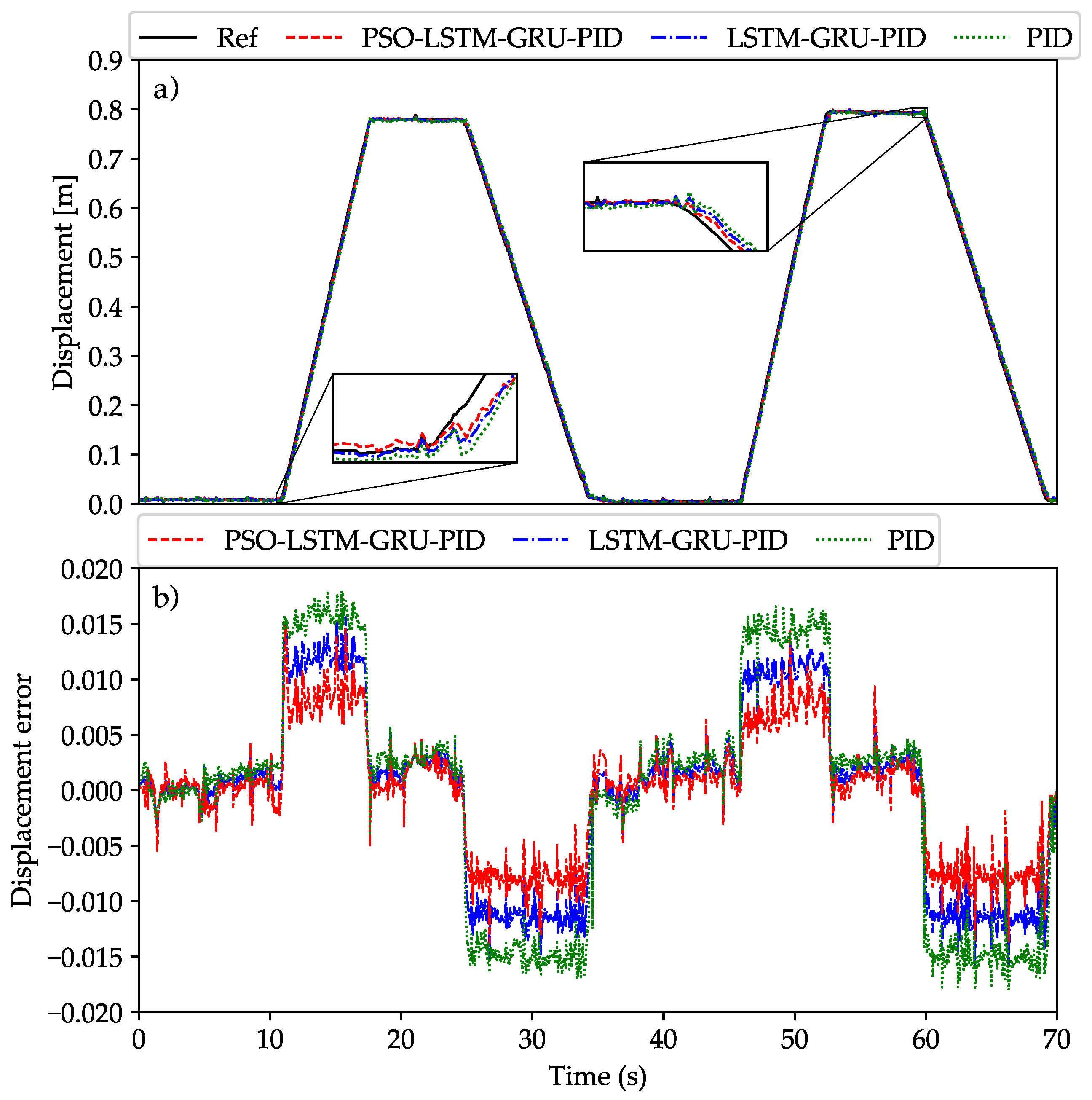
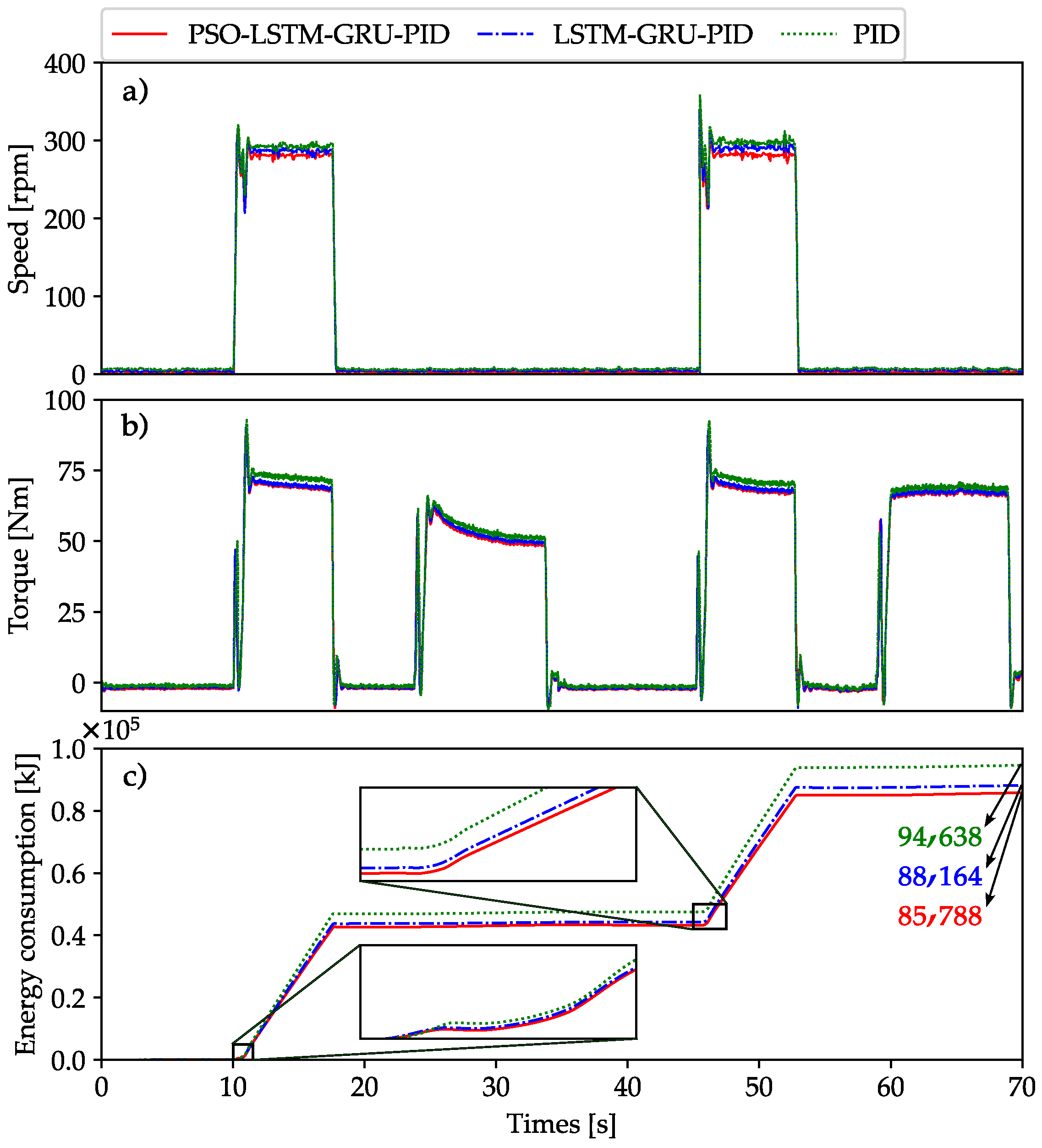
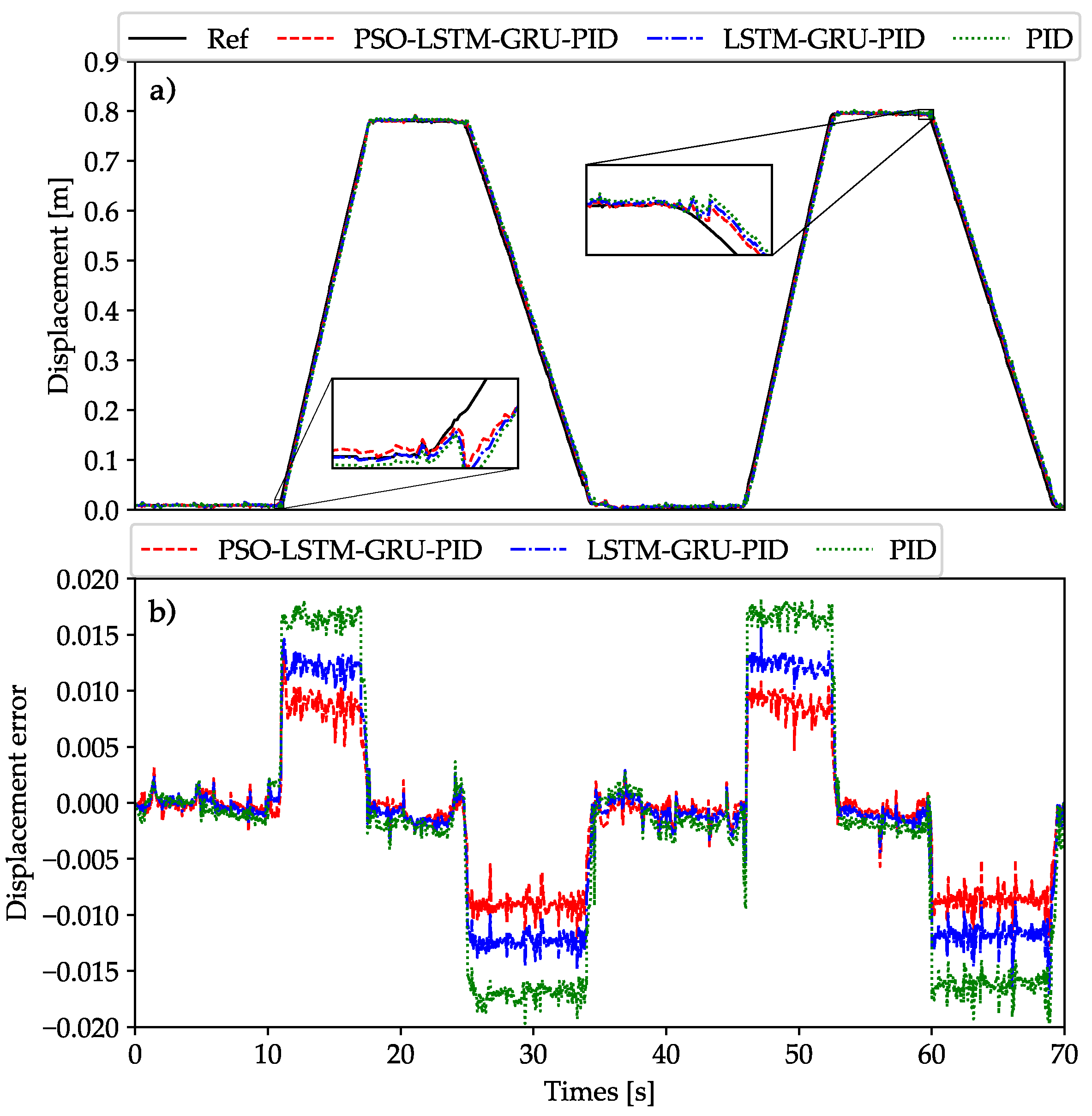
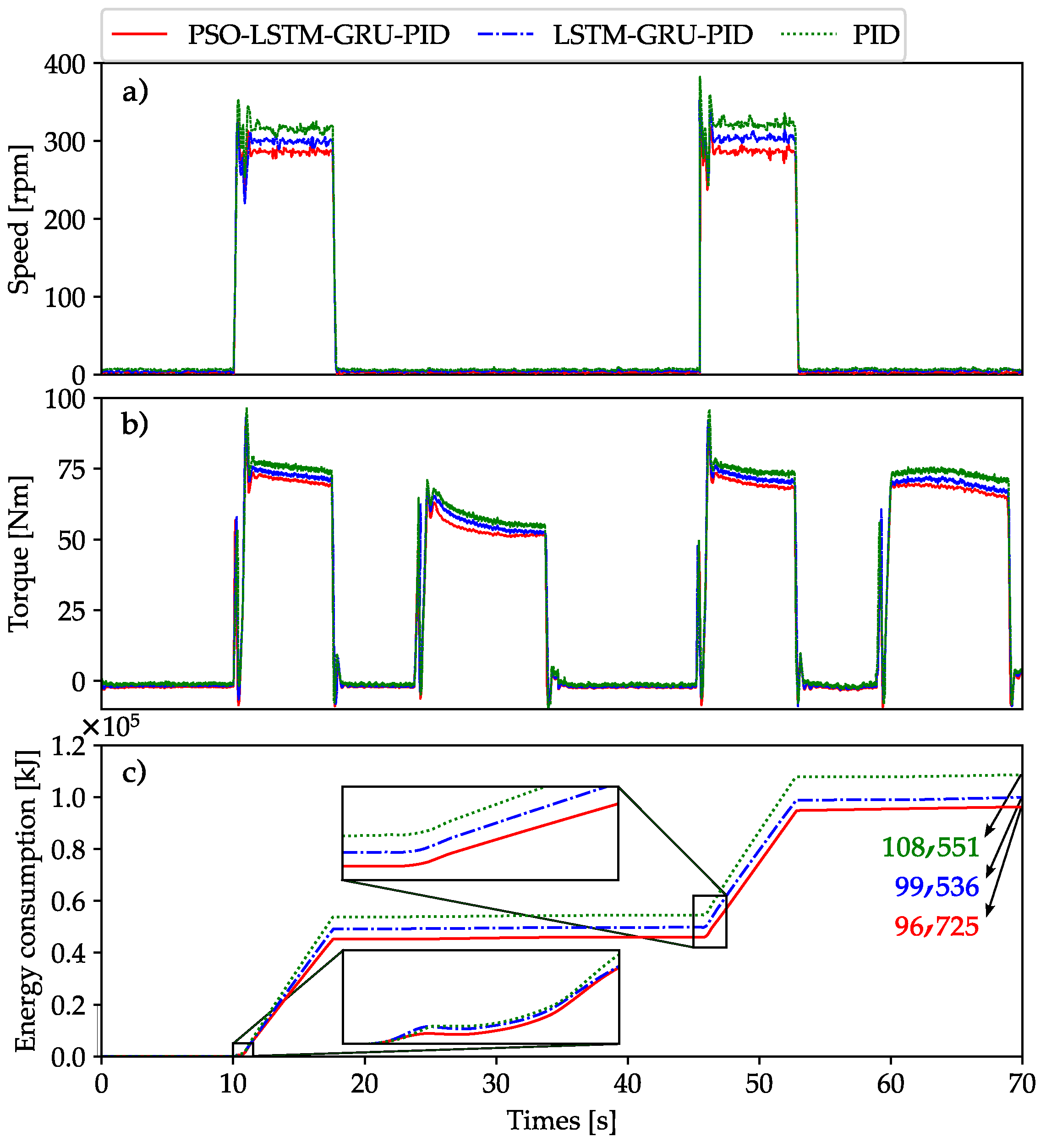
- In comparison to the PID and LSTM-GRU-PID controllers, the proposed controller demonstrated superior tracking accuracy while also reducing energy consumption, achieving savings of up to 10.89% and 2.82% in experimental tests, respectively.
2. System Description
2.1. Powertrain Calculation
2.2. Investigation of Key Parameters
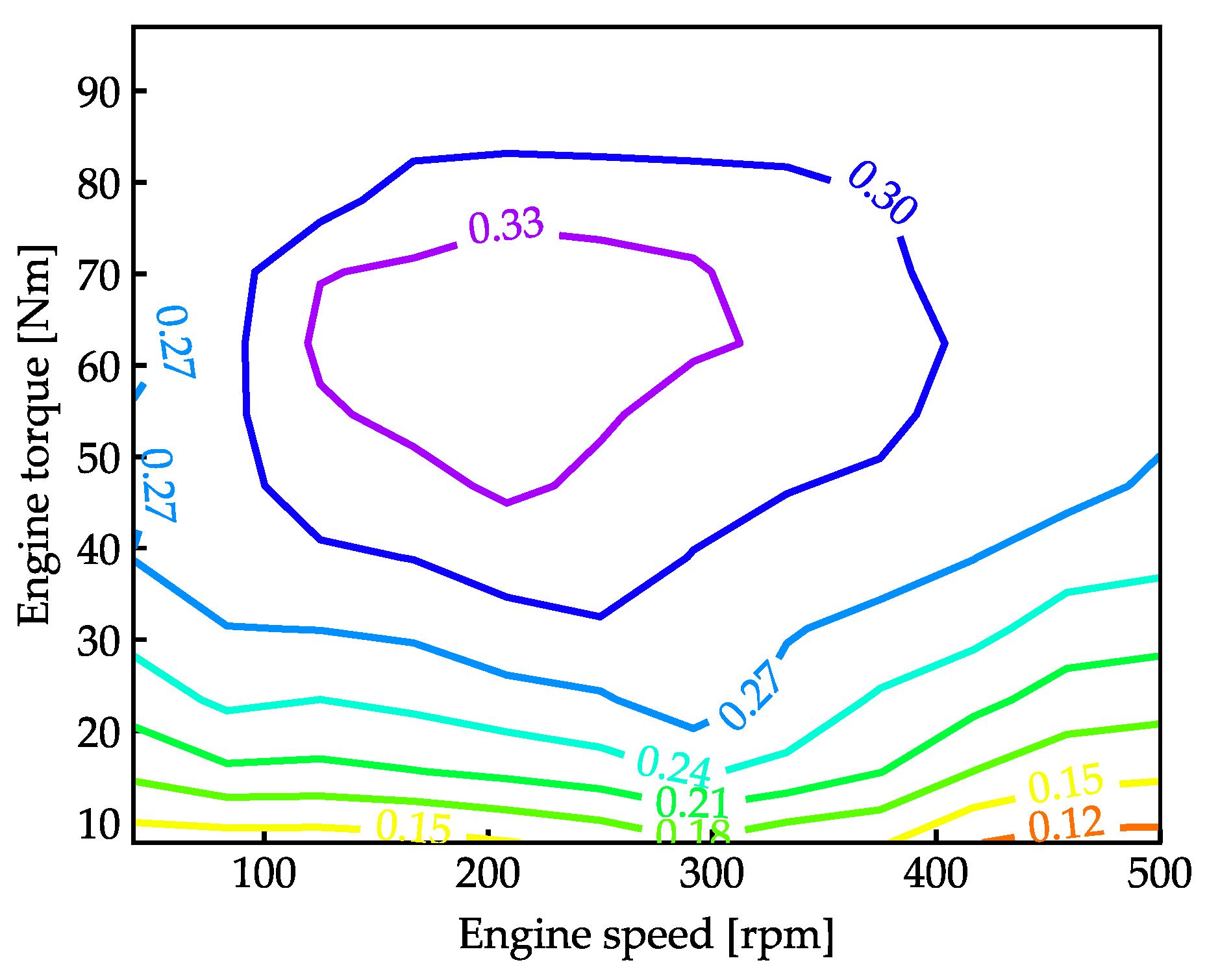
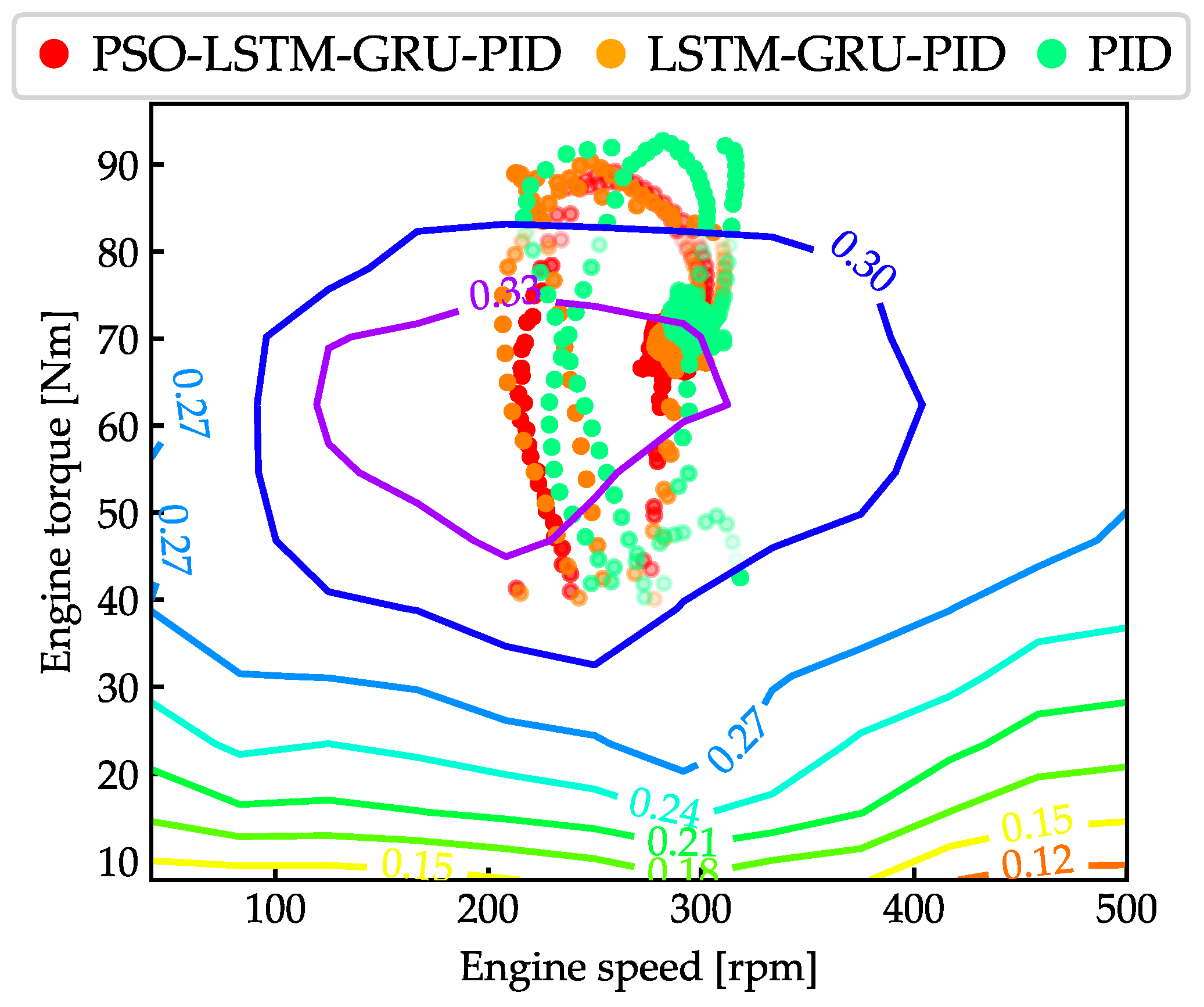
2.3. Energy Management Strategy
3. Fundamental Theorem for Hybrid Algorithm Control
3.1. Particle Swarm Optimization (PSO) Algorithm
3.2. Long Short-Term Memory (LSTM) Algorithm
3.3. Gated Recurrent Unit (GRU) Algorithm
3.4. Proportional Integral Derivative (PID) Algorithms
3.5. Evaluation Criteria for Controller Performance
4. Simulation and Experiment Results
4.1. Simulation Model Development
4.1.1. Simulation Model
4.1.2. Comparison Simulation Results and Discussion
4.2. Experimental System
4.2.1. Experiment SETUP
4.2.2. Comparison Results and Discussion
5. Conclusions
- Enhanced precision and stability: The LSTM-GRU-PID controller significantly improved the precision, stability, and response time of the boom excavator system, offering a more accurate control performance.
- Automated parameter optimization: The PSO method was utilized to automatically fine-tune four critical parameters of the LSTM-GRU-PID controller (GRU units, LSTM units, dropout rate, and learning rate), resulting in a robust and reliable performance even in the presence of external disturbances.
- Superior control in various conditions: The proposed control system demonstrated excellent control capabilities under different conditions, such as variations in cylinder velocity and load changes, validated through both simulation and experimental results.
- Energy efficiency and tracking improvements: Compared to traditional controllers, the system achieved better tracking and energy savings: 2.82% improvement in tracking accuracy over the LSTM-GRU-PID controller and 10.89% reduction in energy consumption compared to the PID controller.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| HEs | Hydraulic excavators |
| HHEs | Hybrid hydraulic excavators |
| EERSs | Electric energy regeneration systems |
| HERSs | Hydraulic energy regeneration systems |
| ICE | Internal combustion engine |
| EMG | Electric motor/generator |
| BAT | Battery |
| HST | Hydrostatic transmission |
| HPM | Hydraulic pump/motor |
| HM | Hydraulic motor |
| EHCVP | Electrical hydraulic continually variable powertrain |
| EMS | Energy management strategy |
| ECMS | Equivalent consumption minimization strategy |
| A-ECMS | Adaptive equivalent consumption minimization strategy |
| SOC | State of charge |
| BC | Boom cylinder |
| VB | Control valve of boom cylinder |
| RV | Regeneration valve of boom cylinder |
| CV | Check valve |
| CE | Clutch of ICE |
| CM | Clutch of EMG |
| CP (DbC) | Clutch of HPM (double clutch) |
| CH (DbC) | Clutch of HM (double clutch) |
| Ring | Ring gear |
| Sun | Sun gear |
| ST | Sensor torque |
| SS | Sensor speed |
| SD | Sensor displacement |
| SV | Sensor velocity |
| PSO | Particle swarm optimization |
| LSTM | Long short-term memory |
| GRU | Gated recurrent unit |
| PID | Proportional integral derivative |
References
- Ding, R.; Zhang, J.; Xu, B.; Cheng, M.; Pan, M. Energy efficiency improvement of heavy-load mobile hydraulic manipulator with electronically tunable operating modes. Energy Convers. Manag. 2019, 188, 447–461. [Google Scholar] [CrossRef]
- Chen, M.; Zhao, D. The gravitational potential energy regeneration system with closed-circuit of boom of hydraulic excavator. Mech. Syst. Signal Process. 2017, 82, 178–192. [Google Scholar] [CrossRef]
- He, X.; Xiao, G.; Hu, B.; Tan, L.; Tang, H.; He, S.; He, Z. The applications of energy regeneration and conversion technologies based on hydraulic transmission systems: A review. Energy Convers. Manag. 2020, 205, 112413. [Google Scholar] [CrossRef]
- Lin, T.; Wang, Q.; Hu, B.; Gong, W. Development of hybrid powered hydraulic construction machinery. Autom. Constr. 2010, 19, 11–19. [Google Scholar] [CrossRef]
- Yang, C.; Zhou, L.; Wang, J.; Xu, T.; Yang, C.; Ye, G. Research on energy saving system of hydraulic excavator based on three-chamber accumulator. J. Energy Storage 2023, 72, 108571. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, J.; Du, S.; Ma, H.; Zhao, W.; Li, H. Energy Management Strategies for Hybrid Construction Machinery: Evolution, Classification, Comparison and Future Trends. Energies 2019, 12, 2024. [Google Scholar] [CrossRef]
- Xia, L.; Quan, L.; Ge, L.; Hao, Y. Energy efficiency analysis of integrated drive and energy recuperation system for hydraulic excavator boom. Energy Convers. Manag. 2018, 156, 680–687. [Google Scholar] [CrossRef]
- Ho, T.H.; Le, T.D. Development and Evaluation of Energy-Saving Electro-Hydraulic Actuator. Actuators 2021, 10, 302. [Google Scholar] [CrossRef]
- Do, T.C.; Dinh, T.Q.; Yu, Y.; Ahn, K.K. Innovative powertrain and advanced energy management strategy for hybrid hydraulic excavators. Energy 2023, 282, 128951. [Google Scholar] [CrossRef]
- Han, J.; Wang, F.; Sun, C. Trajectory Tracking Control of a Manipulator Based on an Adaptive Neuro-Fuzzy Inference System. Appl. Sci. 2023, 13, 1046. [Google Scholar] [CrossRef]
- Nayak, N.; Das, S.R.; Panigrahi, T.K.; Das, H.; Nayak, S.R.; Singh, K.K.; Askar, S.S.; Abouhawwash, M. Overshoot Reduction Using Adaptive Neuro-Fuzzy Inference System for an Autonomous Underwater Vehicle. Mathematics 2023, 11, 1868. [Google Scholar] [CrossRef]
- Wang, X.; Abtahi, S.M.; Chahari, M.; Zhao, T. An Adaptive Neuro-Fuzzy Model for Attitude Estimation and Control of a 3 DOF System. Mathematics 2022, 10, 976. [Google Scholar] [CrossRef]
- Song, H.; Li, G.; Li, Z.; Xiong, X. Trajectory Control Strategy and System Modeling of Load-Sensitive Hydraulic Excavator. Machines 2023, 11, 10. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Do, T.C.; Phan, V.D.; Ahn, K.K. Working Performance Improvement of a Novel Independent Metering Valve System by Using a Neural Network-Fractional Order-Proportional-Integral-Derivative Controller. Mathematics 2023, 11, 4819. [Google Scholar] [CrossRef]
- Ahmad, Z.; Li, J.; Mahmood, T. Adaptive Hyperparameter Fine-Tuning for Boosting the Robustness and Quality of the Particle Swarm Optimization Algorithm for Non-Linear RBF Neural Network Modelling and Its Applications. Mathematics 2023, 11, 242. [Google Scholar] [CrossRef]
- Xuanyu, L.; Mengting, J.; Wenshuai, Z.; Yudong, W. Intelligent real-time prediction for shield machine position on the basis of BWO-LSTM-GRU. Eng. Res. Express 2024, 6, 015105. [Google Scholar] [CrossRef]
- Han, M.; Fan, J.; Wang, J. A Dynamic Feedforward Neural Network Based on Gaussian Particle Swarm Optimization and its Application for Predictive Control. IEEE Trans. Neural Netw. 2011, 22, 1457–1468. [Google Scholar] [CrossRef]
- Gao, W.; Peng, X.; Guo, W.; Li, D. A Dual-Competition-Based Particle Swarm Optimizer for Large-Scale Optimization. Mathematics 2024, 12, 1738. [Google Scholar] [CrossRef]
- Huang, X.; Xu, R.; Yu, W.; Wu, S. Evaluation and Analysis of Heuristic Intelligent Optimization Algorithms for PSO, WDO, GWO and OOBO. Mathematics 2023, 11, 4531. [Google Scholar] [CrossRef]
- Oladejo, S.O.; Ekwe, S.O.; Mirjalili, S. The Hiking Optimization Algorithm: A novel human-based metaheuristic approach. Knowl.-Based Syst. 2024, 296, 111880. [Google Scholar] [CrossRef]
- Khunkitti, S.; Premrudeepreechacharn, S.; Siritaratiwat, A. A Two-Archive Harris Hawk Optimization for Solving Many-Objective Optimal Power Flow Problems. IEEE Access 2023, 11, 134557–134574. [Google Scholar] [CrossRef]
- Wang, X.; Snášel, V.; Mirjalili, S.; Pan, J.S.; Kong, L.; Shehadeh, H.A. Artificial Protozoa Optimizer (APO): A novel bio-inspired metaheuristic algorithm for engineering optimization. Knowl.-Based Syst. 2024, 295, 111737. [Google Scholar] [CrossRef]
- Nguyen, V.H.; Do, T.C.; Ahn, K.K. Investigation and Optimization of Energy Consumption for Hybrid Hydraulic Excavator with an Innovative Powertrain. Actuators 2023, 12, 382. [Google Scholar] [CrossRef]
- Hu, B.; Li, J. A Deployment-Efficient Energy Management Strategy for Connected Hybrid Electric Vehicle Based on Offline Reinforcement Learning. IEEE Trans. Ind. Electron. 2022, 69, 9644–9654. [Google Scholar] [CrossRef]
- Tian, X.; Cai, Y.; Sun, X.; Zhu, Z.; Xu, Y. An adaptive ECMS with driving style recognition for energy optimization of parallel hybrid electric buses. Energy 2019, 189, 116151. [Google Scholar] [CrossRef]
- Wei, C.; Chen, Y.; Sun, X.; Zhang, Y. Optimal Equivalent Consumption Minimization Strategy for Plug-In Hybrid Electric Vehicle with Improved Genetic Algorithm. SAE Int. J. Electrified Veh. 2020, 9, 143–154. [Google Scholar] [CrossRef]
- Liu, X.; Qin, D.; Wang, S. Minimum Energy Management Strategy of Equivalent Fuel Consumption of Hybrid Electric Vehicle Based on Improved Global Optimization Equivalent Factor. Energies 2019, 12, 2076. [Google Scholar] [CrossRef]
- Zhou, D.; Al-Durra, A.; Matraji, I.; Ravey, A.; Gao, F. Online Energy Management Strategy of Fuel Cell Hybrid Electric Vehicles: A Fractional-Order Extremum Seeking Method. IEEE Trans. Ind. Electron. 2018, 65, 6787–6799. [Google Scholar] [CrossRef]
- Yang, C.; Du, X.; Wang, W.; Yuan, L.; Yang, L. Variable optimization domain-based cooperative energy management strategy for connected plug-in hybrid electric vehicles. Energy 2024, 290, 130206. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Ibrahim, M.S.; Abbas, W.; Waseem, M.; Lu, C.; Lee, H.H.; Fan, J.; Loo, K.H. Long-Term Lifetime Prediction of Power MOSFET Devices Based on LSTM and GRU Algorithms. Mathematics 2023, 11, 3283. [Google Scholar] [CrossRef]
- Kim, G.I.; Jang, B. Petroleum Price Prediction with CNN-LSTM and CNN-GRU Using Skip-Connection. Mathematics 2023, 11, 547. [Google Scholar] [CrossRef]
- Tjandra, A.; Sakti, S.; Manurung, R.; Adriani, M.; Nakamura, S. Gated Recurrent Neural Tensor Network. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 448–455. [Google Scholar] [CrossRef]

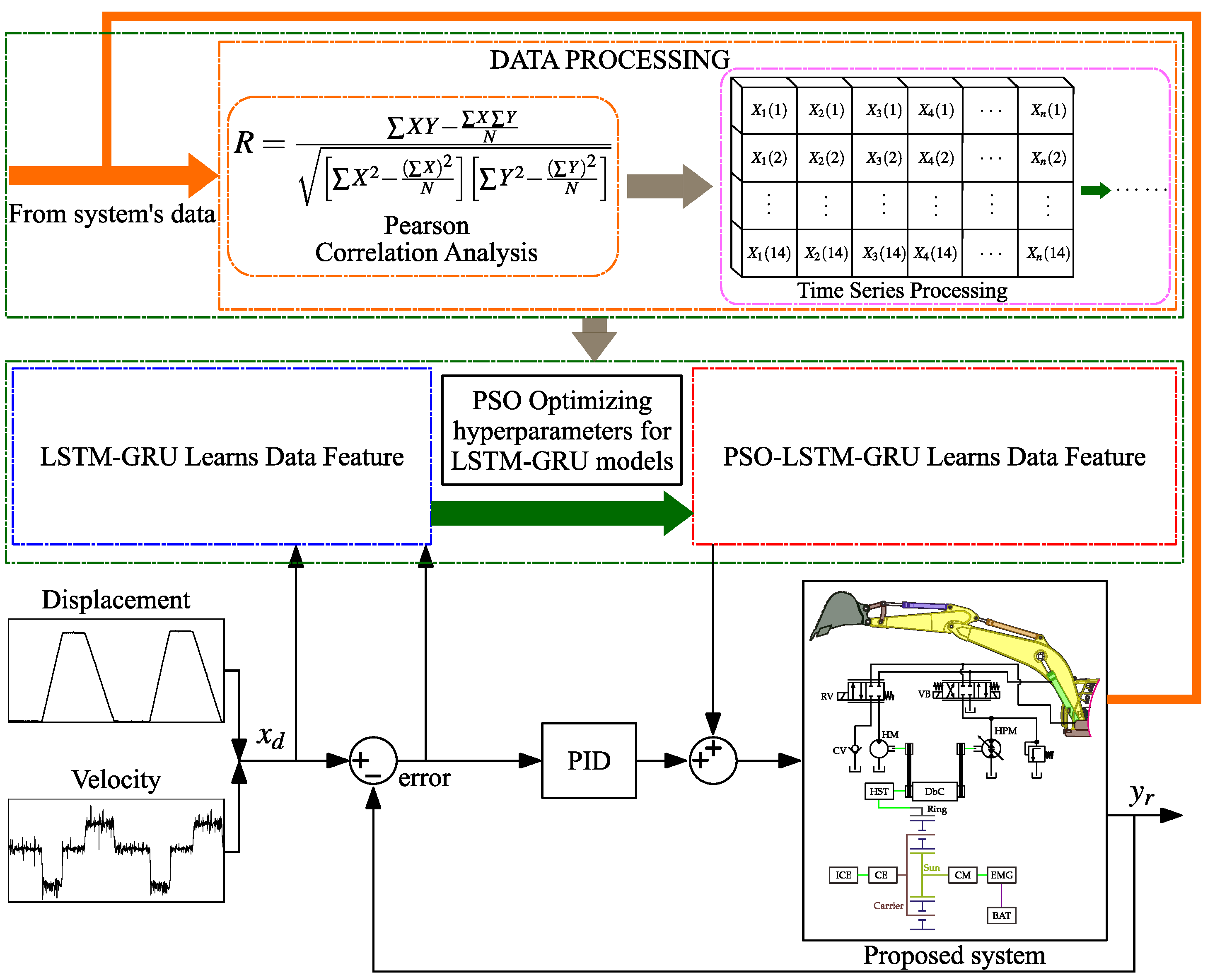
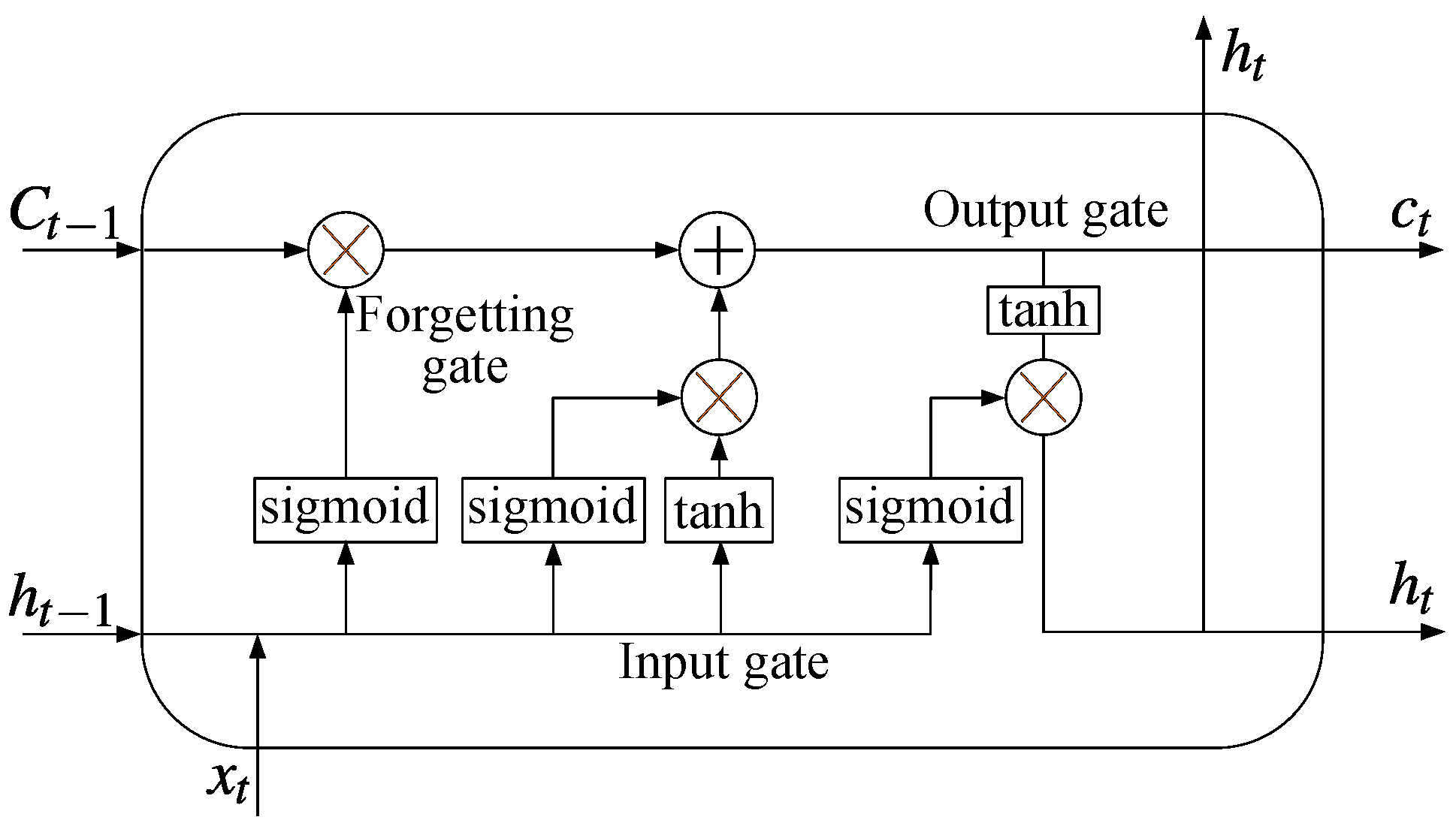
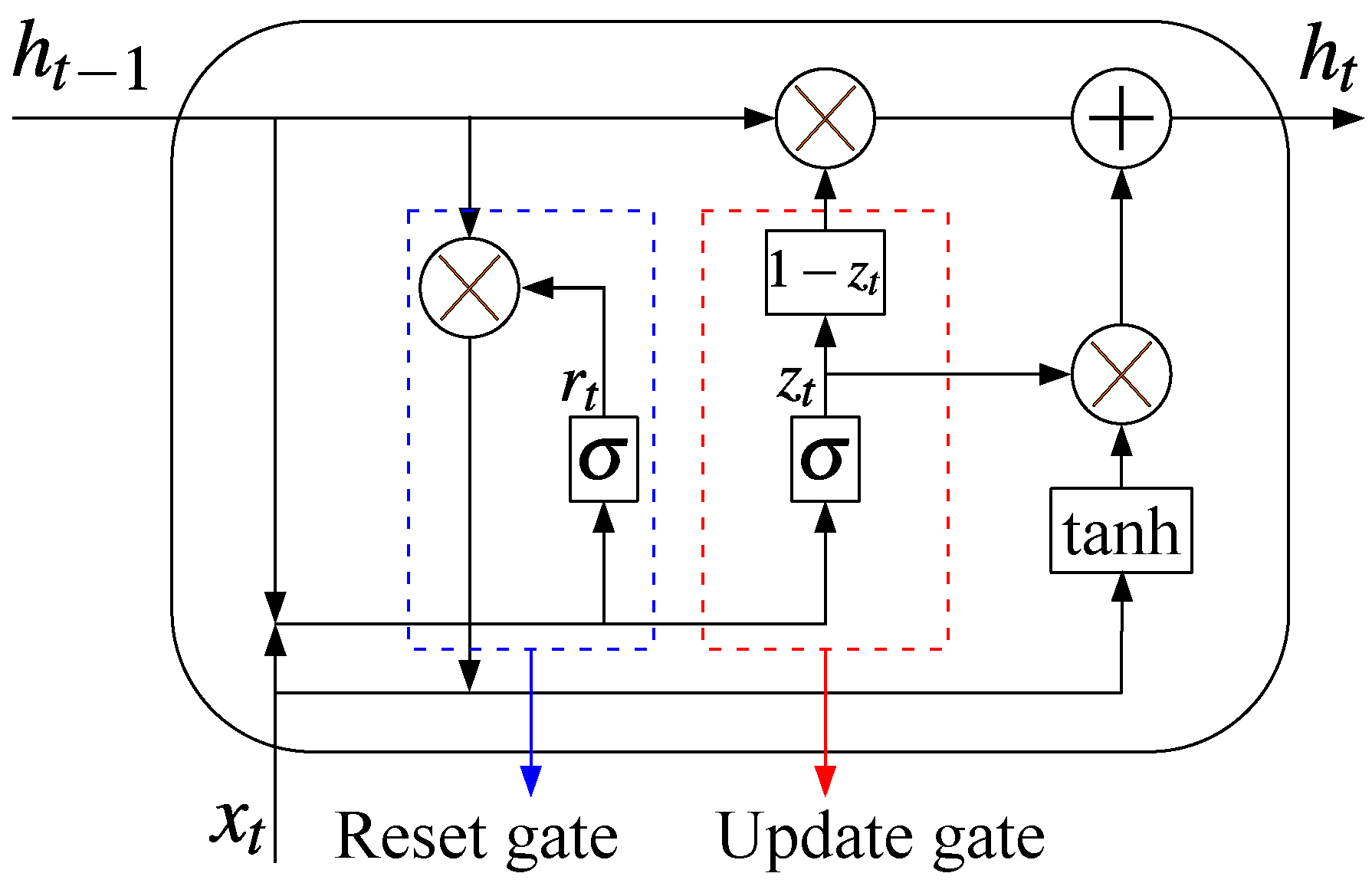






| Components | Remark | Value | Unit |
|---|---|---|---|
| Cylinder | Piston diameter | 50 | mm |
| Rod diameter | 28 | mm | |
| Stroke | 0.75 | m | |
| Variable hydraulic pump/motor | Displacement | 30 | cc/rev |
| Pressure | 250 | bar | |
| Fixed hydraulic motor | Displacement | 10 | cc/rev |
| Pressure | 120 | bar | |
| Electric motor/generator | Rate power | 5.5 | kW |
| Electric motor | Rate power | 7.5 | kW |
| Hydrostatic transmission | Displacement | 33 | cc/rev |
| Pressure | 270 | bar | |
| Battery | Cell voltage limit | 2.5–4.2 | V |
| Cells in parallel | 1 | cell | |
| Cells in series | 3 | cell |
| Algorithm | Training Time | Real Time | Time |
|---|---|---|---|
| PSO-LSTM-GRU-PID | 1975.72 | 70 | second |
| LSTM-GRU-PID | 1555.53 | 70 | second |
| PID | - | 70 | second |
| LSTM-GRU Model Overview | |
|---|---|
| Model architecture | Stacked GRU and LSTM layers with dense connections |
| Sequence length | 50 time steps |
| Activation functions | ReLU for GRU and LSTM, linear for output |
| Loss function | Mean squared error (MSE) |
| Optimizer | Adam (learning rate optimized by PSO) |
| Normalization | Min-max scaling |
| Training data noise | Gaussian noise (std dev = 0.01) for robustness |
| Data split ratio | 80% training, 20% testing |
| Dropout rate | Optimized dynamically for regularization |
| Evaluation metric | MSE on validation/test set |
| PSO Hyperparameter Optimization | |
| Optimization technique | Particle swarm optimization (PSO) |
| Parameters optimized | GRU/LSTM units, dropout rate, learning rate |
| Swarm size | 5 particles, 5 iterations |
| Best solution | Optimal parameters minimizing MSE |
| Algorithm | Training Time | Real Time | Time |
|---|---|---|---|
| PSO-LSTM-GRU-PID | 2004.32 | 70 | second |
| LSTM-GRU-PID | 1584.24 | 70 | second |
| PID | - | 70 | second |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, V.-H.; Do, T.C.; Ahn, K.-K. Implementing PSO-LSTM-GRU Hybrid Neural Networks for Enhanced Control and Energy Efficiency of Excavator Cylinder Displacement. Mathematics 2024, 12, 3185. https://doi.org/10.3390/math12203185
Nguyen V-H, Do TC, Ahn K-K. Implementing PSO-LSTM-GRU Hybrid Neural Networks for Enhanced Control and Energy Efficiency of Excavator Cylinder Displacement. Mathematics. 2024; 12(20):3185. https://doi.org/10.3390/math12203185
Chicago/Turabian StyleNguyen, Van-Hien, Tri Cuong Do, and Kyoung-Kwan Ahn. 2024. "Implementing PSO-LSTM-GRU Hybrid Neural Networks for Enhanced Control and Energy Efficiency of Excavator Cylinder Displacement" Mathematics 12, no. 20: 3185. https://doi.org/10.3390/math12203185
APA StyleNguyen, V.-H., Do, T. C., & Ahn, K.-K. (2024). Implementing PSO-LSTM-GRU Hybrid Neural Networks for Enhanced Control and Energy Efficiency of Excavator Cylinder Displacement. Mathematics, 12(20), 3185. https://doi.org/10.3390/math12203185










