Abstract
In this paper, we present a methodology for the numerical solving of partial differential equations in 2D geometries with piecewise smooth boundaries via finite element method (FEM) using a Quantized Tensor Train (QTT) format. During the calculations, all the operators and data are assembled and represented in a compressed tensor format. We introduce an efficient assembly procedure of FEM matrices in the QTT format for curvilinear domains. The features of our approach include efficiency in terms of memory consumption and potential expansion to quantum computers. We demonstrate the correctness and advantages of the method by solving a number of problems, including nonlinear incompressible Navier–Stokes flow, in differently shaped domains.
Keywords:
tensor decompositions; tensor trains; finite element analysis; partial differential equations; incompressible Navier–Stokes equations MSC:
15A69; 65M08; 76D05
1. Introduction
Partial differential equations (PDEs) describe many real-life processes in the observable world in lots of practical fields such as engineering, economics, sociology, biology, etc. If one could solve such an equation, i.e., calculate the target function that defines the process, the evolution of the process becomes predictable. The owner of the solution gets an opportunity to simulate the process on a computer to acquire extensive knowledge about its behavior and, therefore, obtain a huge advantage. So the solutions of PDEs are of huge interest to science and industry. There are families of methods for treating PDEs numerically, including finite difference methods, finite volume methods, and finite element methods.
The equations that are interesting in a practical sense are often very complex [1]. Analytical (exact) solutions either do not exist or are extremely hard to find. In order to make progress, numerical methods are employed to produce a solution as a finite set of approximated values.
One of the most flexible and efficient methods for the numerical solution of PDEs is the finite element method (FEM) [2,3]. It is one of the most popular methods for boundary value problems arising in engineering and mathematical modeling in 2D and 3D. Its most appealing feature is the convenience of handling domains of complicated shapes. The main idea of the finite element method is to approximate a target function, , as a sum of N known basis functions multiplied by coefficients :
These basis functions are linked with the discretization of the problem, i.e., to obtain a better solution, one must push the number N.
The main limitation of this approach is the inevitable trade-off between computational resources such as computer RAM, physical time, and the quality of the solution. The production of a satisfactory result usually takes very dense discretization, which leads to enormous amounts of computer RAM and processor runtime being consumed by the algorithm. There are numerous ways to improve the method in various aspects, including extended FEM [4], the virtual element method [5], and enrichment FEM [6], but in the present work, we adhere to a basic approach.
To tackle these challenges, we employ Tensor Train (TT) methods for the numerical solution of PDEs. The Tensor Train decomposition [7] can be used for a compressed approximate representation of multidimensional arrays—it decomposes a huge tensor into a composition of smaller ones, with an exponential reduction in the number of encoding parameters, as shown in Figure 1. At the same time, the complexity of all algebraic operations in this format also has poly-logarithmic scaling in terms of the full tensor size [7]. The quality of the compression is determined by the so-called Tensor Train ranks of a tensor. For example, any smooth analytical function computed on a uniform grid has restricted TT-ranks [8,9,10,11], and so, it is compressed efficiently, but a random vector possesses the full rank (which is equal to the size of the vector), and so, it does not make sense to perform a tensor decomposition of it. Eventually, a dedicated Functional Tensor Train format [12,13] was developed specifically as a continuous function approximation technique.

Figure 1.
Graphical representation of an operator in Tensor Train format. A huge tensor is decomposed into a product of smaller tensors.
Tensor trains are widely researched in the context of different numerical problems, including solutions of linear systems of equations [14], optimization [15,16], machine learning [17,18,19], and numerical solutions of PDEs [9,20,21,22,23,24].
In addition, an important feature of tensor networks is that they can be quite efficiently mapped to a quantum computer [25].
Unlike similar works on the application of Quantized Tensor Trains to finite element discretizations of PDEs [26,27], this work considers the following:
- Universal nonlinear domain transformer tailored to the QTT format. In particular, our transformer is suitable for curvilinear rectangles and degenerate angles, which reduces the number of subdomain splittings and simplifies their structure, leading to lower QTT ranks.
- Efficient assembly of FEM matrices in the course of iterations for a nonlinear problem and/or time stepping in a time-dependent problem. In particular, the stitching of matrices corresponding to different subdomains is free from the element-wise manipulations which are suboptimal for the TT structure. Instead, the total matrix is given simply by matrix-TT products of precomputed reference-generating matrices and a diagonal matrix made of a QTT tensor of coefficients.
The paper is organized as follows. In Section 2, we describe the tensor format and the basic finite element method. Section 3 presents the domain transformer as well as the algorithms for the operator assembly and subdomain stitching. In Section 4, we provide the results for different test problems, including the Poisson equation and incompressible Navier–Stokes equations. We conclude the paper in Section 5.
2. Background
2.1. Quantized Tensor Train Format
Tensor Train and its special case, Quantized Tensor Train (QTT), are methods for compressed representation of multidimensional arrays [28] which are generalizations of matrix decompositions like SVD and skeleton decomposition [29] onto d-dimensional tensors. Tensor Train decomposition is given by
where is the 3-dimensional tensor called the TT-core. The main characteristic of such a representation is the TT-rank, r, which is equal to the maximum size among bond indices and expresses the correlations between the dimensions of the tensor. In the case of weak correlations (low rank r), this format allows one to store and perform operations with tensors with logarithmic complexity in their size. The case of separable indices, for example, leads to the TT-rank of one. The graphical representation of a tensor train is shown in Figure 1. The TT operator (matrix) has two spatial indices for each dimension
The Quantized Tensor Train format is obtained by reshaping the original tensor so that all its outer dimensions are 2. It allows us to apply tensor decompositions to problems that are not particularly high-dimensional and still obtain the benefits of tensor decompositions. Also, for a wide range of functions, including exponential, polynomial, trigonometrical, and its combinations, the QTT ranks have low theoretical estimations.
It can be seen in (2) that the memory required to store the compressed tensor is vs. memory of the full tensor, which leads to the exponential advantage in the case of small TT-ranks.
In this subsection, as well as in Table 1, we list all the operations regarding tensors, which are used in our method, and provide the designations:

Table 1.
Operations with its resulting ranks and complexities. , , and are tensor train vectors of the same dimensions. Their ranks are , , and , respectively. is a tensor train matrix of rank . f is a function of s variables to evaluate on a list of tensors of the same shape.
- Basic linear algebra operations between tensors.Required operations include summation (+), Hadamard (element-wise) multiplication (∘), finding matrix–matrix and matrix–vector products (@ and respectively) and Kronecker product (). Also, in this work, an optimization-based version of matrix–matrix product () is used.
- Conversion between full and compressed format, tensor rounding.To analyze the results, it must be possible to switch between different representations of the data. The algorithms for compressing and decompressing the data are straightforward [7]. Rounding is the procedure of creating a tensor similar to the given one, but with a lower rank with specified accuracy. The rounding is required to limit the ranks that are increasing during the solution according to Table 1.
- Cross-approximation of functions.This algorithm lets one approximate a function in TT format with only function evaluations [30]. This algorithm is used to represent the Jacobian of the area transformation and to set the initial and boundary conditions.
- Matrix construction.Tensor Train format for TT-matrices allows one to perform matrix transposition, construction of a diagonal matrix from a tensor and constructing a shift matrix of given dimensions (i.e., matrix with the ones placed above the main diagonal being the only non-zero elements).
- Solution of linear systems.For performing matrix inversion, we decided to use the Alternating Minimal Energy (AMEn) algorithm, which is a combination of the single-block Density Matrix Renormalization Group [31] and the steepest descent [32] algorithms [14].
All the TT algorithms used in this paper, including the AMEn algorithm for the solution of linear systems [14], are implemented in the ttpy 1.2.0. package for Python [33].
2.2. Finite Element Method
We use the well-known finite element method since it stacks well with the Tensor Train approach and because, unlike finite difference and finite volume methods, FEM provides us with matrix operators of convenient constant shapes while handling complex areas.
For the basic finite element method, formulas for the stiffness and mass matrix elements are as follows:
Matrices discretizing the first derivatives are derived similarly:
Here, are FEM basis functions. These matrices are then computed numerically. We will show later how to efficiently transfer the assembly process to the Tensor Train format. Also, we will observe that such matrices are effectively represented in such a format.
In addition, it is experimentally shown that the finite element matrices usually have low QTT ranks, and therefore, are well-compressible, which can be seen later on in the paper and in [26]. This means that all tensor operations from Table 1 will have lower asymptotic complexity than operations with full and even sparse matrices.
3. Quantized Tensor Train Finite Element Method
In this section, we describe our main contribution: the Quantized Tensor Train framework for the assembly and solution of Finite Element problems in general domains.
3.1. Domain Splitting and Transformation
To solve on the domain D, we cut it on s subdomains , which are curvilinear quadrilaterals connected by the sides. The sides of the subdomain are specified by four parametrized differentiable curves:
and to ensure that the curves coincide at the corners of the subdomain, we assert the following:
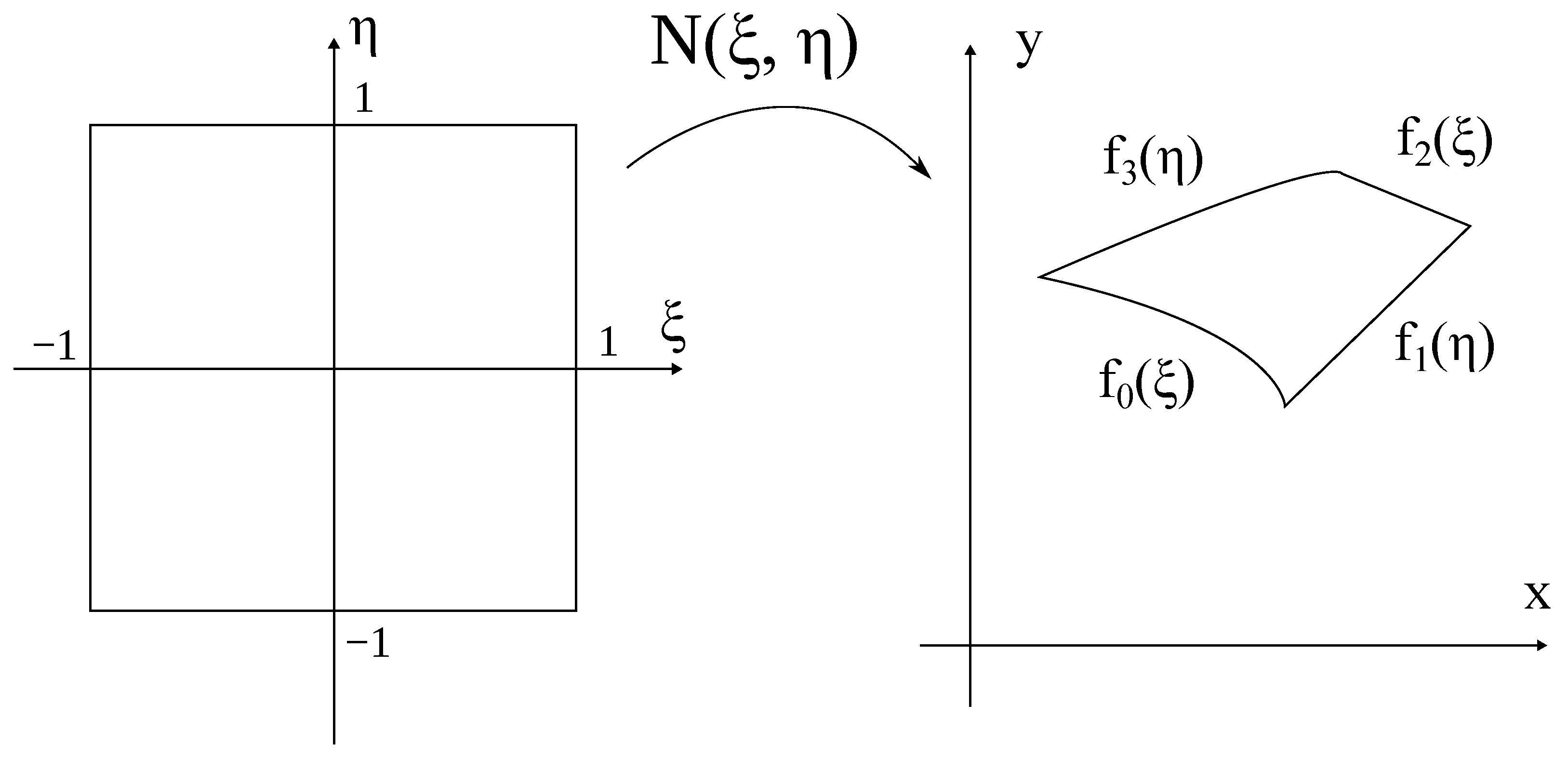
After specifying the functions, the differentiable mapping from a reference square to a quadrilateral can be constructed by transfinite interpolation [34]:
and example is shown in Figure 2. The Jacobian of this transformation will be as follows:
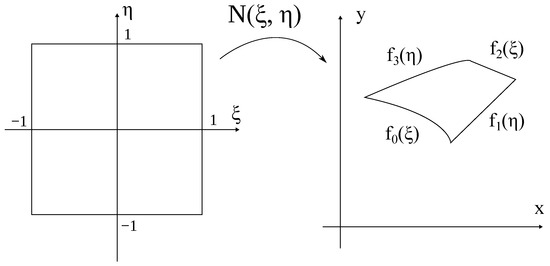
Figure 2.
The projection of a reference square onto the subdomain from (6). The sides of the subdomain are set with four smooth explicitly defined functions.
3.2. Operators Assembly in Tensor Train Format
To set the finite element mesh, a uniform Cartesian grid of size is introduced on the reference square and then projected onto each quadrilateral with (6). Here, d is the number of TT-cores of size 2 required to represent the mesh along a single dimension; also, let us denote and . Using this and also the analytic formula for the Jacobian (7), finite element matrices from (4) and (5) are constructed for each of the s subdomains. So (4) becomes
where is a first-order Lagrange basis function, so for the finite element discretization of the reference square, bilinear elements are utilized.
Let us denote
Here and are the functions of and .
To numerically compute the integral, Gauss–Legendre quadrature is employed [35], so instead of the integral, the weighted sum is computed.
Now, we move to the assembly of discretized operators in Tensor Train format. We begin with the description for a single subdomain in this subsection and will describe the concatenation later.
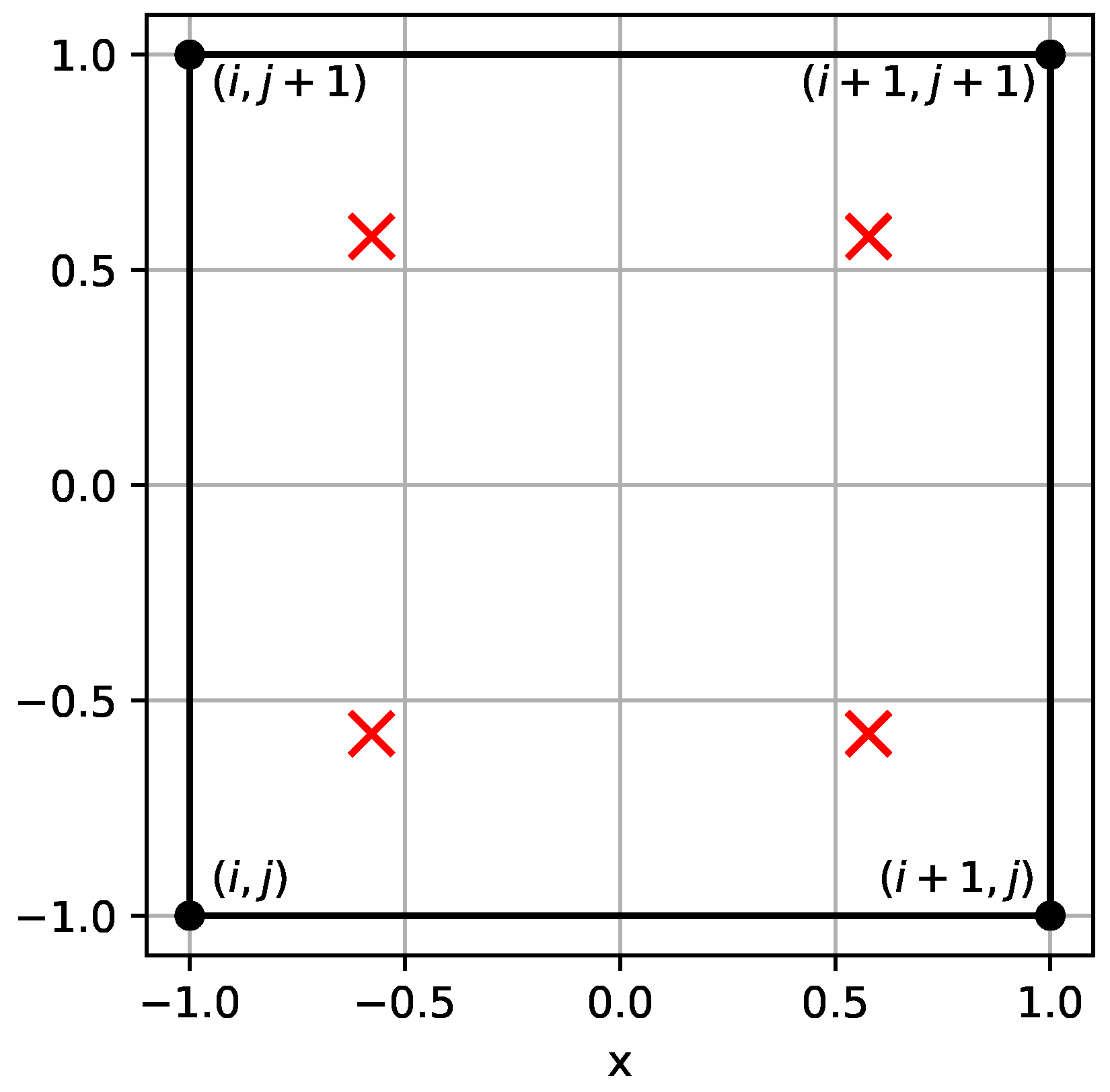
To represent the values of the Jacobian J for the arbitrary and , the cross-approximation approach is utilized [30]. Since subdomain transformation is defined by explicit differentiable functions, the TT-ranks of the the Jacobians in most cases will be small. So, we cross-approximate the values on the quadrature points mesh of the reference domain as shown in Figure 3. The resulting sets of TT-vectors computed for the Jacobians from (7), (9) we will denote with bold symbols , and for the determinant of the Jacobian. Also we denote the TT vector of Gaussian quadrature weights as .
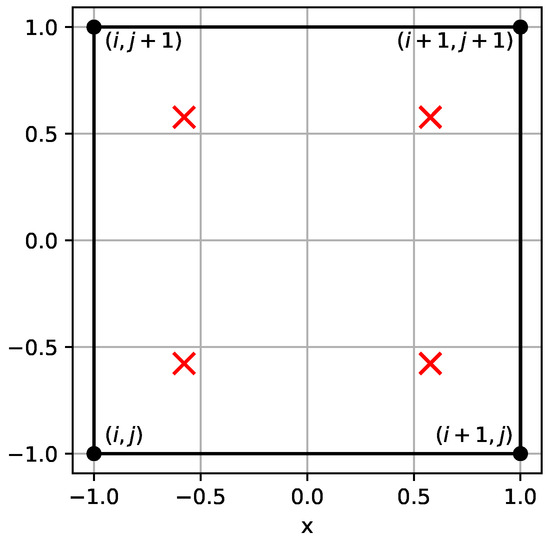
Figure 3.
The finite element projected on a reference square. Here, black dots with indices represent the positions of mesh points, and red symbols denote the positions of quadrature points.
The matrix contains the values of basis functions on quadrature points of the reference domain, as shown in Figure 3, and is assembled with Kronecker products. Analogously, is the pair of matrices populated with values of partial derivatives of basis functions.
Now we have everything to assemble the finite element matrices:
where
Here, is a function that converts a TT-vector into a diagonal TT-matrix. After the assembly, we usually perform on the result to significantly truncate the ranks.
3.3. Subdomain Concatenation
During the assembly, subdomain finite element matrices are constructed in TT format on each of the s quadrilaterals. Then, the subdomain matrices are joined into <<big>> domain block matrices of shape by the subdomain concatenation. In the end of the assembly, we are left with the mass matrix , the stiffness matrix , and derivative matrices . In this subsection, we will consider the stiffness matrix , because the concatenation algorithm is identical for every type of matrix.
The idea here is to unite the basis functions on the boundaries of seamed subdomains while adding a penalizing equation to the block matrix.
Let us define the interface matrices, which are responsible for handling joined boundaries:
And the block of the block matrix is defined as follows:
where is the stiffness matrix of the k-th subdomain, c is the maximum absolute value across all the main diagonals of for every k.
The assembly of the block matrix is performed with Kronecker product in the TT format:
where is the matrix with the only non-zero element .
After the assembly, the TT operators are rounded with high precision to save the important properties of the matrices.
Since it is not possible to modify individual elements of the Tensor Train, the mask approach is used to impose boundary conditions:
Here, stands for the mask for inner (non-boundary) nodes and stands for the outer (boundary) nodes, where is the indentity matrix. The masks are diagonal matrices so that after multiplying the solution by the mask, the corresponding values are left as is, and the rest are zeroed. Subsequently, to impose the boundary values, one adds up the vector multiplied by the inner mask and the boundary values multiplied by the outer mask:
3.4. Nonlinear Operators Reassembly with Coefficients
In this subsection we will describe the procedure of assembly of the finite element operators with some coefficient function. This function can be, for example, time-dependent, so having an efficient algorithm for the reassembly is crucial for the performance of the computation. For example, the Navier–Stokes equation has the nonlinear convective operator , which depends on the fluid velocities that are non-constant during the simulation.
Also we modify the stitching procedure introduced in [26] by precomputing the block interface matrices. This allows to perform the subdomain concatenation as a matrix–matrix multiplicaton and a matrix addition. From (12) and (13), it directly follows that (for )
where
The full algorithm for the assembly of the nonlinear convective operator for a 3-part domain:
- First evaluate the function on the quadrature points. The velocites can be evaluated in TT format on each subdomain by computing the sum of basis functions values over the finite elements (see Figure 3) and then assembled into the big vector. Another way is to use cross-approximation.
- Then, we can put the coefficient in between the matrix products in (10) and perform the standard matrix–matrix product and obtain the block-diagonal convective derivative matrices:
- Then the subdomain concatenation is performed according to (14):
Here, we propose two approaches:
- Performing the assembly by exact matrix–matrix products in Tensor Train format and truncating the excessive ranks by TT rounding. The exact multiplication takes operations, and since it is performed between two high-rank tensors/matrices, the time required between time steps is not optimal.
- Employing approximate matrix–matrix multiplication via AMEn. This iterative method requires operations, which is preferable for the high-rank case. Also, the rounding is not required since the relative tolerance is set before the call. The convergence is achieved only with a single sweep of a method because of a close initial guess from the previous time step.
3.5. Example Application: Incompressible Navier–Stokes Equations
The incompressible Navier–Stokes equations are considered:
where stands for the X- and Y-components of the velocity, p is the pressure and is the Reynolds number. The first equation describes the time evolution of the medium and the second one represents incompressibility.
The Navier–Stokes equations are widely used in different fields of science and engineering, including aircraft modeling, weather prediction, modeling of natural currents, and artificial flows [36].
Chorin’s predictor-corrector scheme is employed to perform the time-stepping procedure [37]. The main idea is to treat viscous and pressure forces separately. Each time step consists of three substeps:
- The predictor step. The intermediate velocity, , is computed for the momentum equation without the pressure:
- The pressure step. Then Poisson’s equation for the pressure is solved.
- The corrector step. Finally, the pressure term is added to the equation to satisfy the continuity condition.
The discrete version of the algorithm with vectors and operators in Tensor Train format:
- Compute and reassemble and as presented in Section 3.4.
- Compute the tentative velocities :
- Solve the Poisson equation for the pressure:
- Perform the corrector step:
- Impose boundary conditions with masks:
Here, by multiplying by the inverted mass matrix , we imply solving a linear system with the matrix.
4. Numerical Results
We validate our methodology by solving multiple model problems. In Section 4.1, we consider the Poisson equation in a triangular domain and compare the results with [26]. In Section 4.2, we solve the Poisson equation on a single domain of quadrilateral shape and the two-part domain of the same shape with a curved boundary to ensure the correctness of the subdomain stitching. In Section 4.3, the same equation is also solved, button curved domains like a circle or an annulus. And finally, in Section 4.4 and Section 4.5, the set of incompressible Navier–Stokes equations is solved in a lid-driven cavity, and a more complex L-shaped domain via Chorin’s projection method and the runtime of the method is compared with the full format.
4.1. Poisson Equation in a Triangle
Here, we solve a Poisson equation in a triangle:
where , and is shown in Figure 4. The domain is taken from [26], but instead of three subdomains, we specify a triangle as a single quadrilateral with a single degenerated angle.
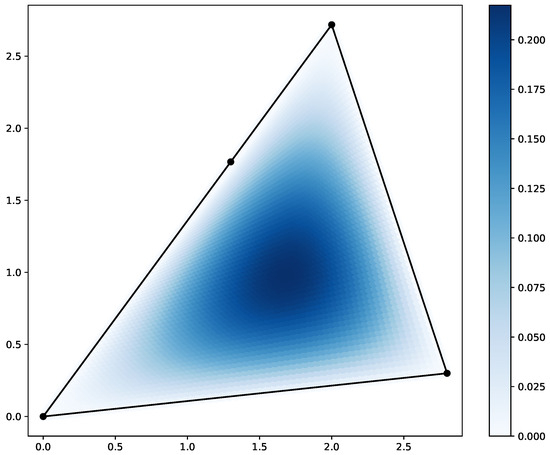
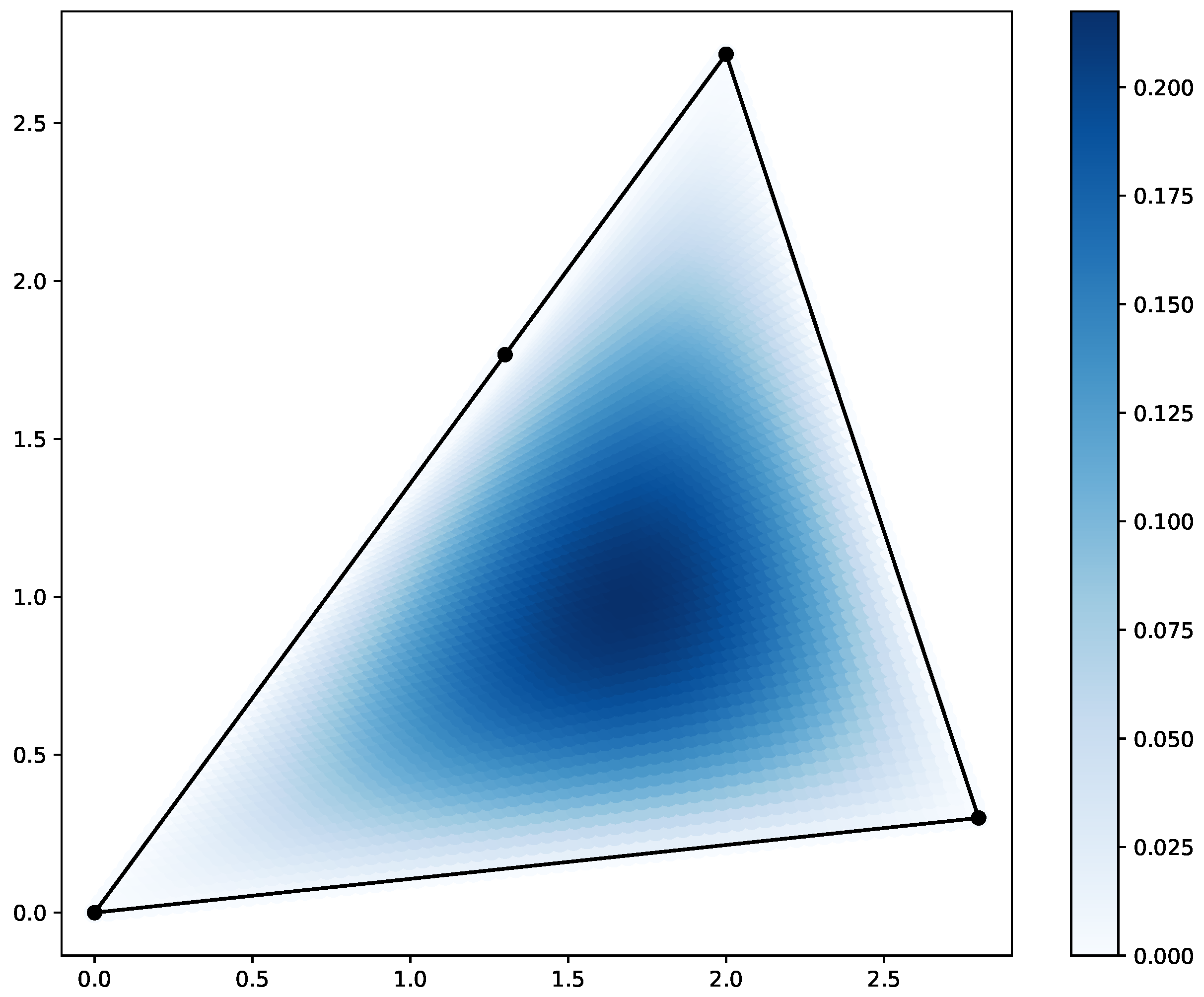
Figure 4.
The scatter plot of the solution on triangular domain. The black dots represent the corners of the quadrilateral domain.
The algorithm for finding the solution goes as follows:
- Mass and stiffness operators and masks corresponding to zero Dirichlet boundary conditions are assembled in the QTT format. The right-hand side is constructed using cross-approximation of the function.
- Boundary conditions are applied to operators:
- The right-hand side is multiplied by the mass matrix, and the stiffness matrix is inverted to find the solution:
Then, the solution TT-vector is decompressed to the full format, and the error between the numerical and analytical solution is computed.
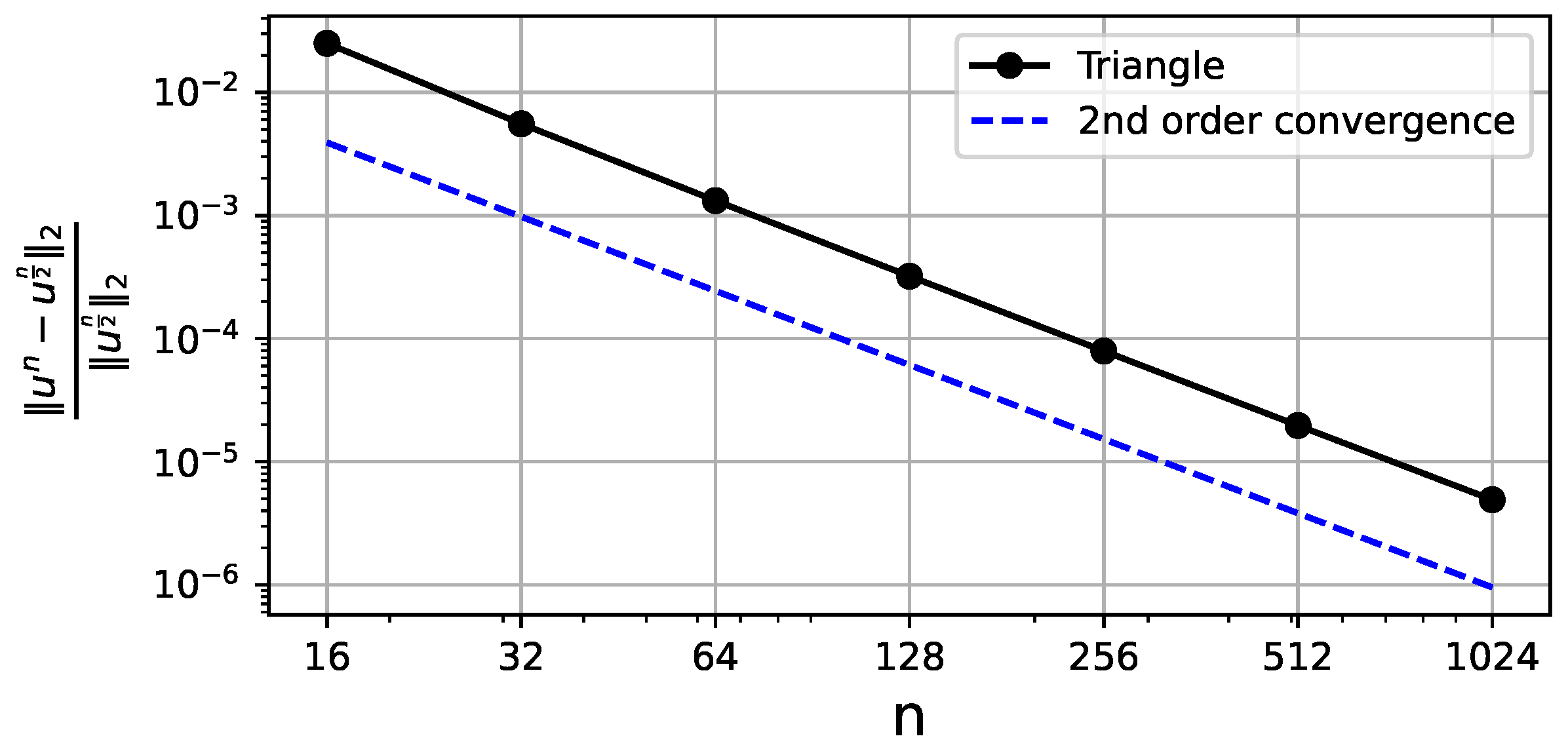
In Figure 5, we analyze the convergence via the Runge rule since we are not provided with the analytical solution. On each step, we refine the mesh and solve the equation. The error is then computed between the new solution downscaled to the previous mesh and the solution for the previous mesh. The second order is present despite the singularity in the degenerated corner.
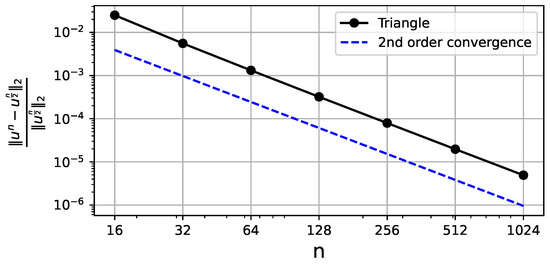
Figure 5.
Relative Frobenius norm errors resulting from the Runge rule for different mesh discretizations. The X-axis denotes the number of grid points along a single dimension. The second order of convergence with respect to is observed (where h is the linear size of a grid cell).
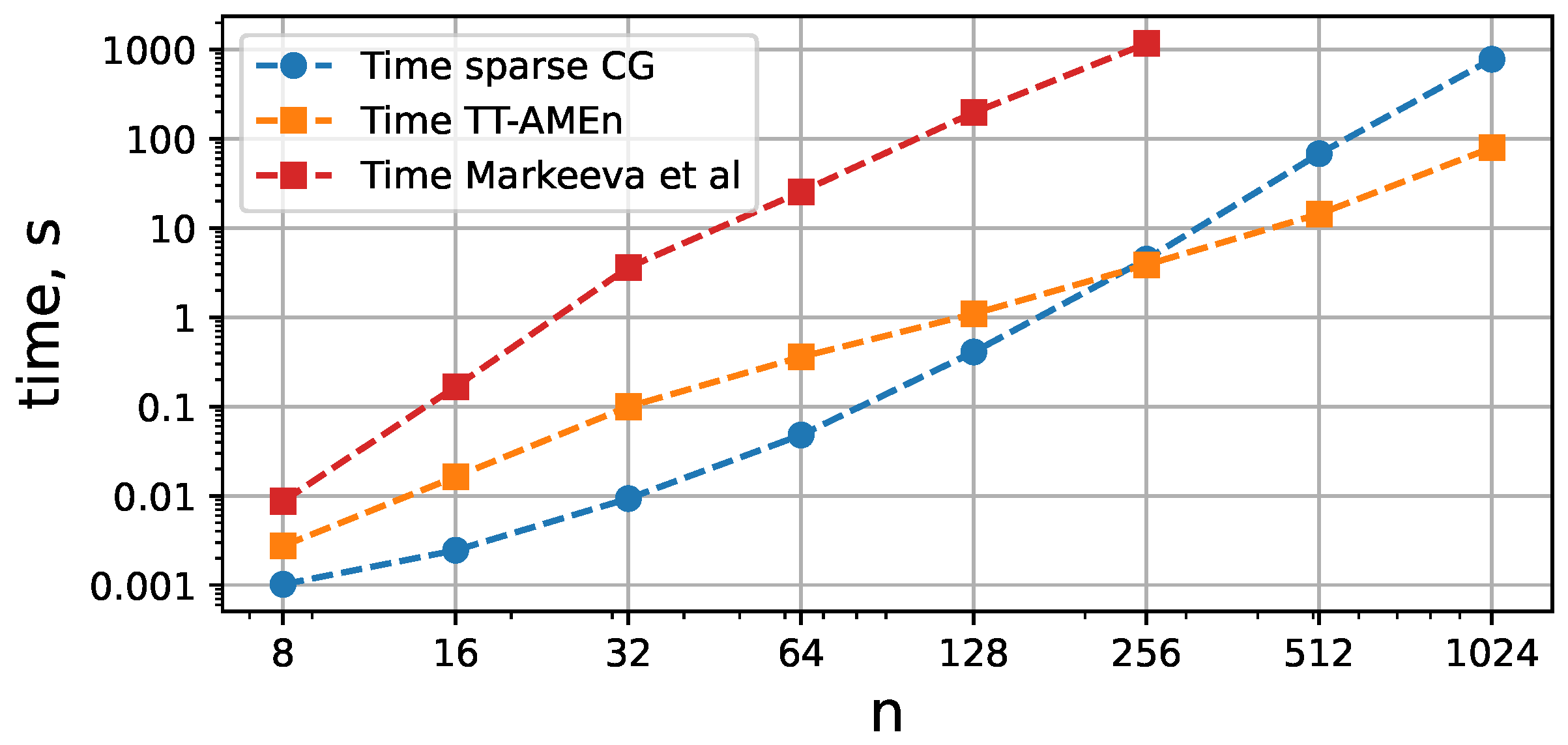
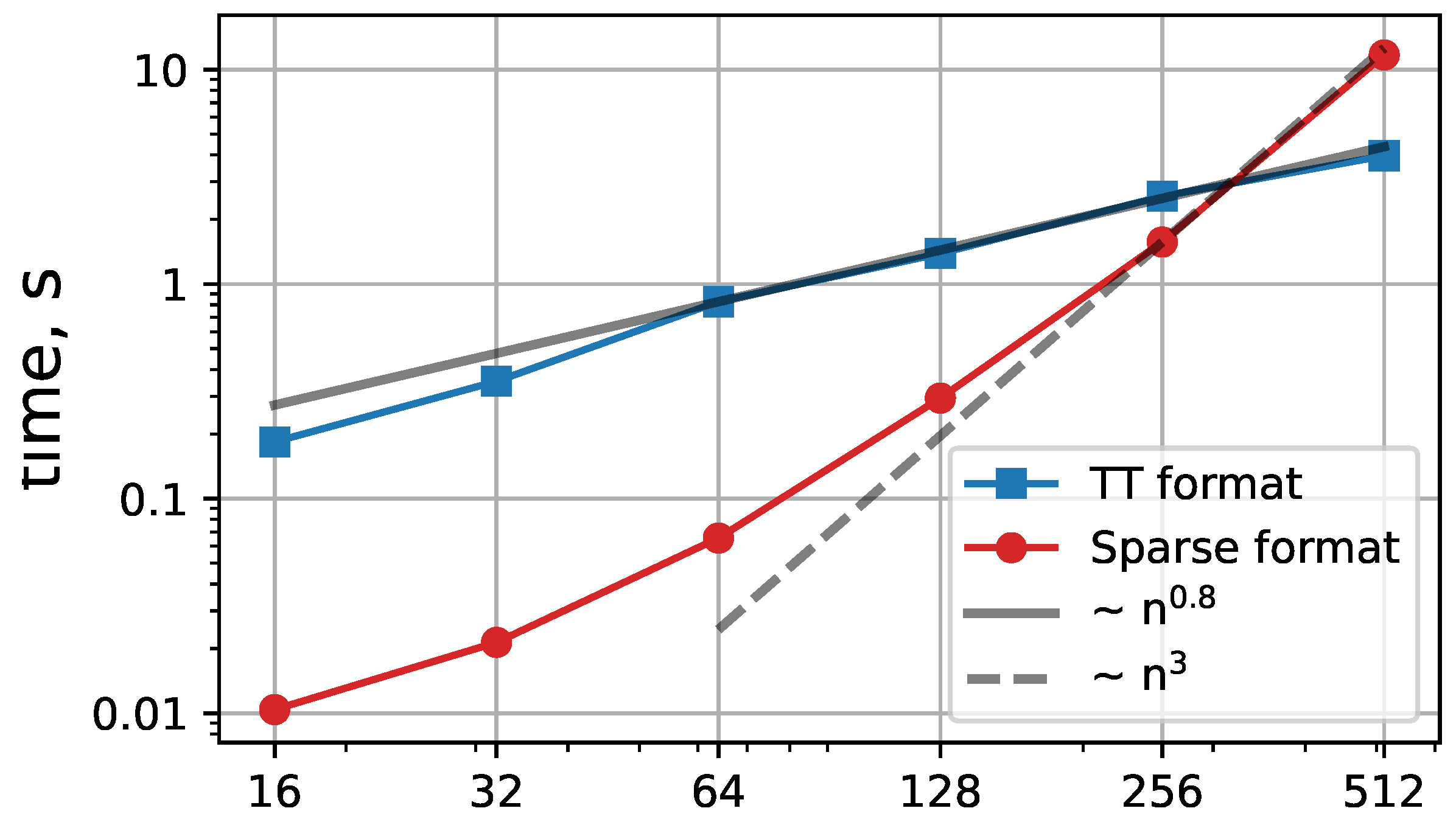
The runtime comparison is presented in Figure 6. For the basic non-tensor method, we assembled the system in compressed sparse column format and solved via the conjugate gradient method taken from Python package. The advantage of tensor trains on moderate computational meshes is observed.
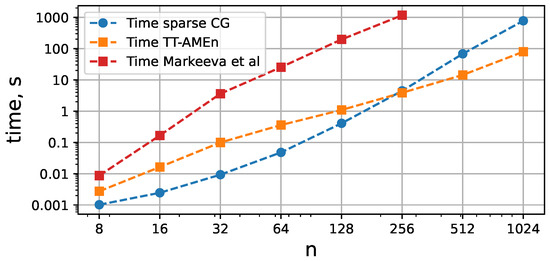
Figure 6.
Times required to solve the Poisson equation in a triangle for different mesh discretizations in sparse format, Tensor Train format, and Z-order QTT format from [26], respectively. The system with a sparse matrix was solved via the congugate gradient method with the same relative tolerance as the TT-solver.
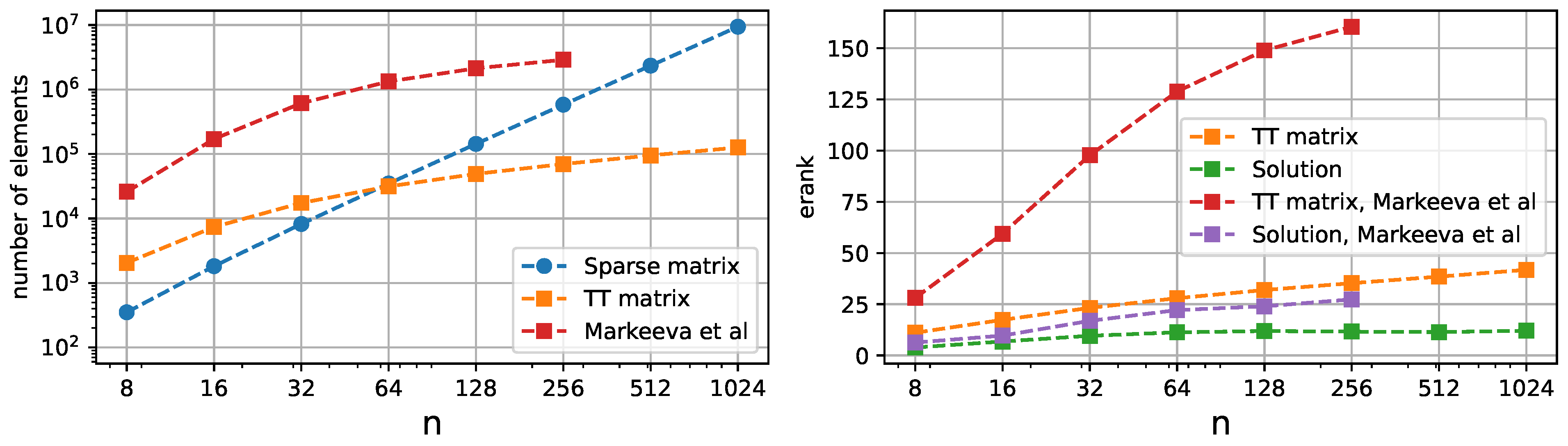
We compare the ranks and matrix sizes with [26] on Figure 7. The ranks of stiffness matrix in our case are significantly lower. There are two factors causing this. The first one is that a single subdomain has fewer degrees of freedom and does not require stitching, which also increases the ranks. The second one is that putting the Jacobian values in the Z-order disrupts the smooth structure of the function vector, which is present for the regular order QTT.
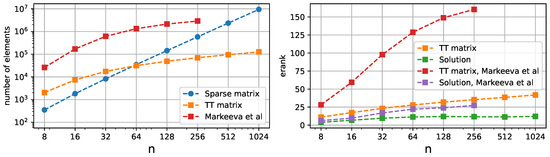
Figure 7.
The left plot depicts the numbers of elements required to represent the stiffness matrices in sparse format, Tensor Train format, and Z-order QTT format from [26] for differently sized meshes, which can also be interpreted as memory requirement for the operator storage. It can be noted that for our method the sizes are significantly lower. The right plot shows the effective TT ranks of stiffness matrices and solution vectors.
4.2. Poisson Equation in a Quadrilateral Domain
Here we solve the Poisson Equation (17) but in a quad-shaped domain, specified by linear coordinate transformation from the reference square. We start from a manufactured solution , and construct the forcing term to match this solution, .
We compare two ways of transforming the domain:
- Use the single original quadrilateral domain, transformed into the reference domain.
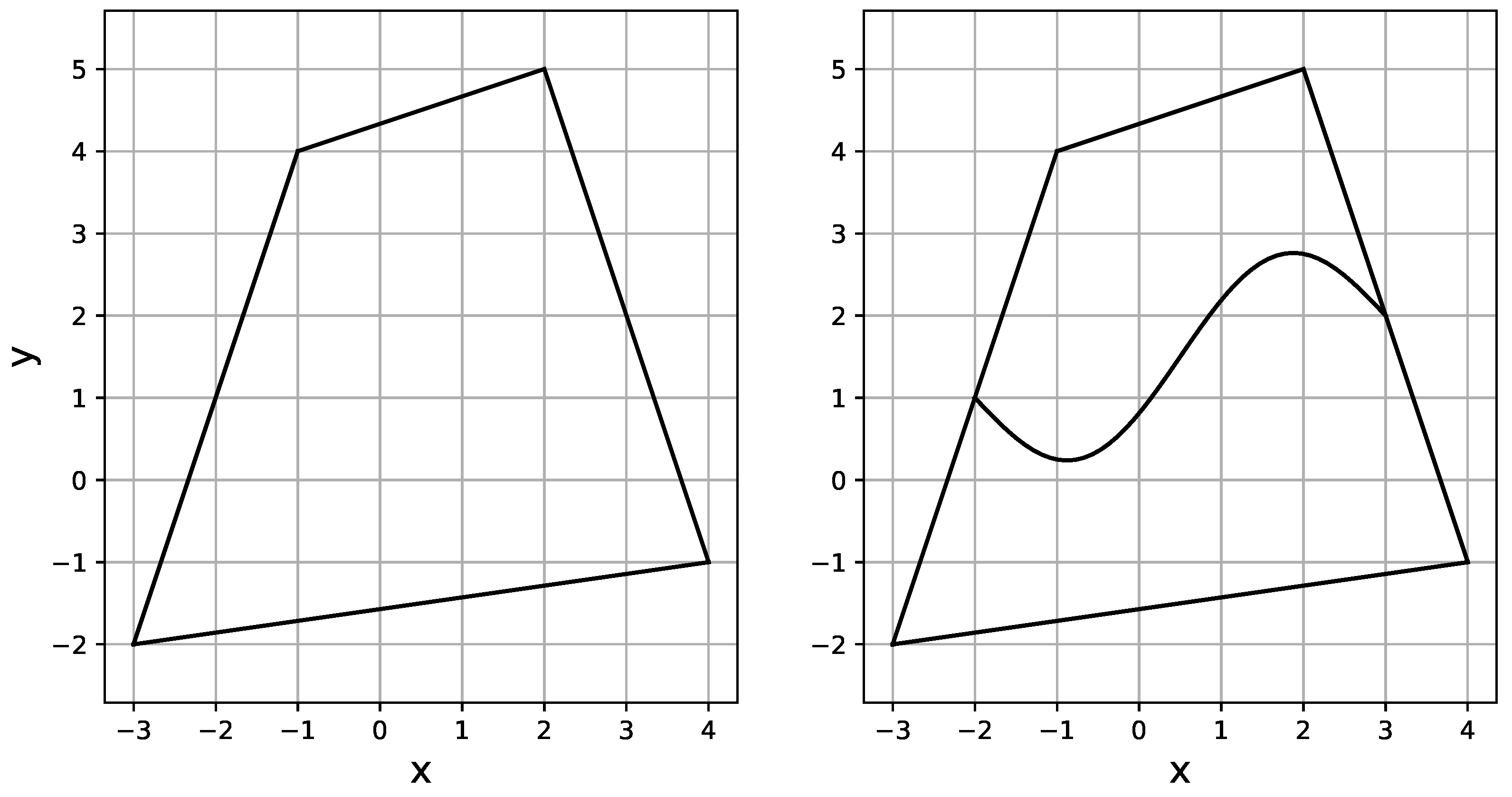
- The original domain is split into two parts with the sinusoidal seam as shown in Figure 8, and each part is transformed into the reference domain.
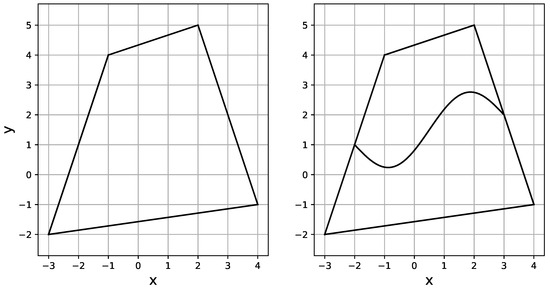 Figure 8. Quadrialteral domains in which the Poisson equation is solved. The right one in the figure consists of two connected curvilinear domains.
Figure 8. Quadrialteral domains in which the Poisson equation is solved. The right one in the figure consists of two connected curvilinear domains.
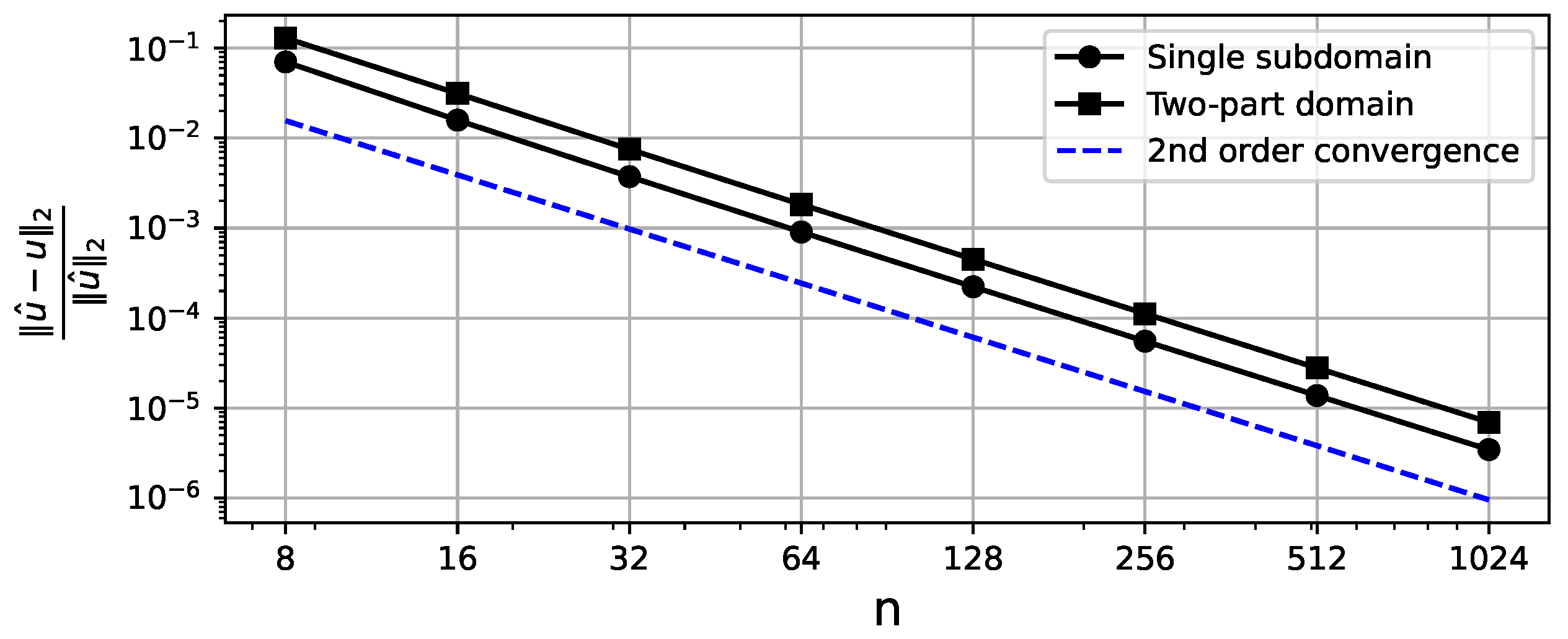
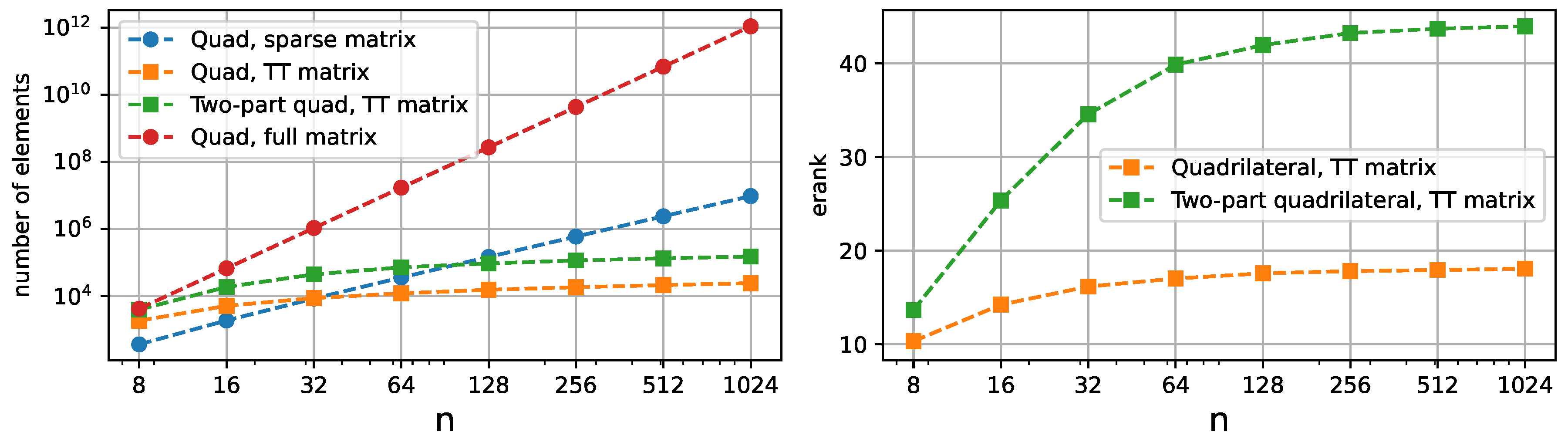
The algorithm for finding the numerical solution of (17) is the same as for the quadrilateral domain, and the right-hand side of the equation is . The errors and TT-ranks are presented in Figure 9 and Figure 10. Despite having much higher TT-ranks due to the curved seam, the two-part domain representation requires much less memory than the full format.
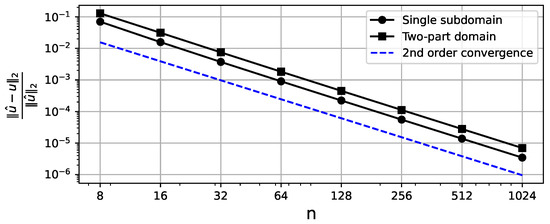
Figure 9.
Relative Frobenius norm error between the analytical and numerical solution vectors for different mesh discretizations of the quadrilateral domains. The X-axis denotes the number of grid points along a single dimension. The second order of convergence is observed.
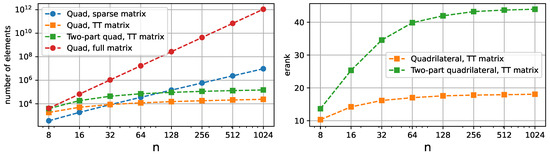
Figure 10.
Comparison between amount of elements required to represent the stiffness matrices in sparse, Tensor Train, and full format for quadrilaterals (left). The extra number of elements for the joint quad domain is caused by the curved seam, which increases the TT-rank. Nevertheless, the growth of TT effective ranks of the stiffness matrix stagnate during the mesh refinement (right).
4.3. Poisson Equation in a Circle/Annulus
Here, the Equation (17) is solved in a circle
and an annulus
which are depicted in Figure 11. The right-hand side and analytic solution are
respectively for the circular domain and
for the annular one.
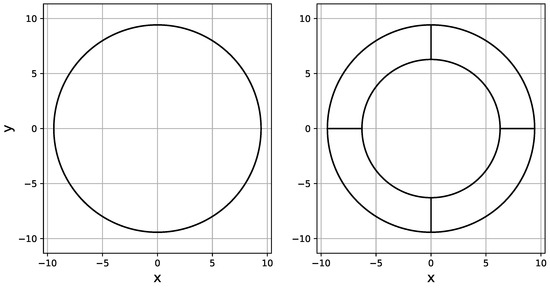
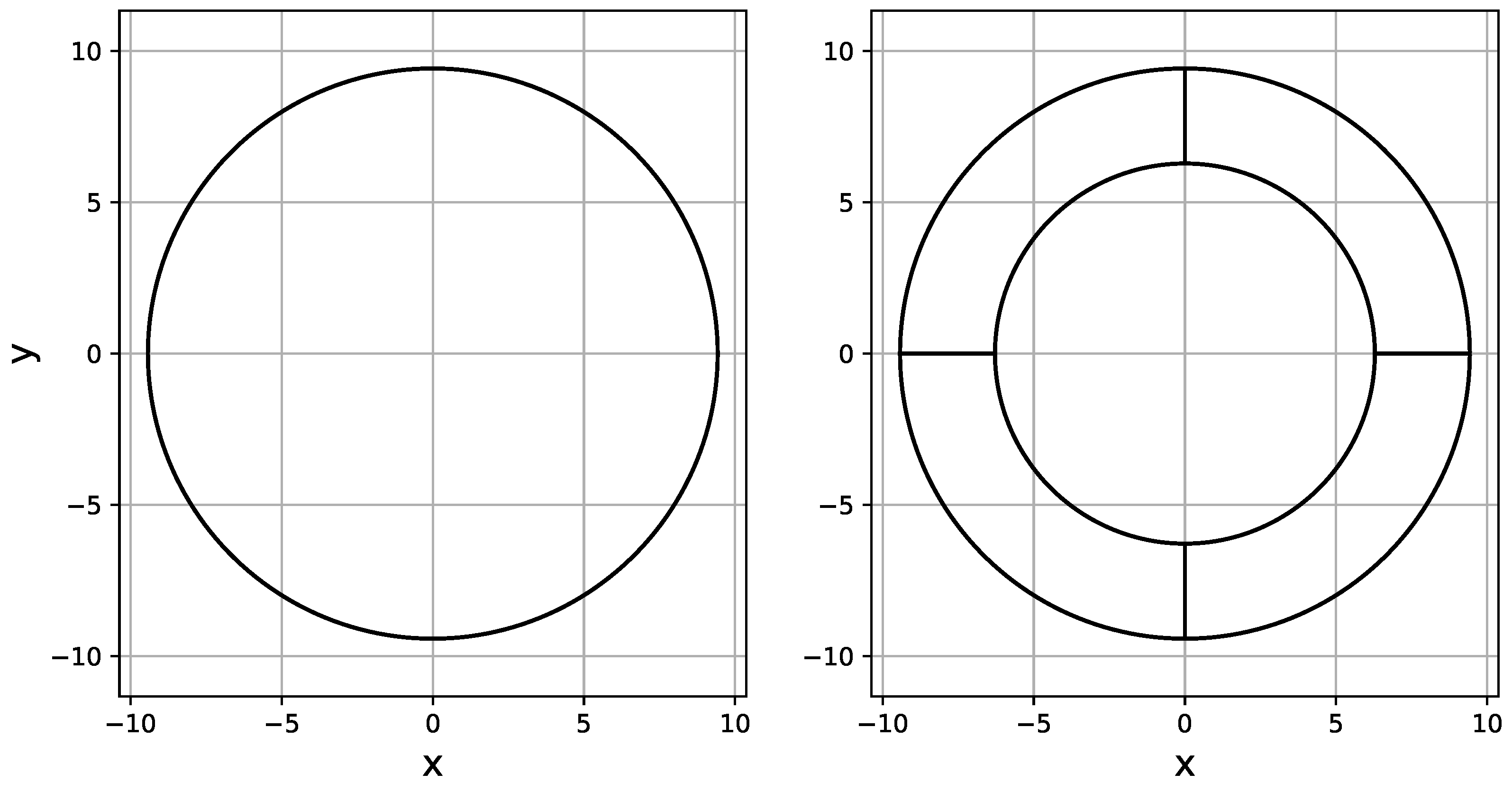
Figure 11.
A single-subdomain circle and an annulus consisting of four subdomains.
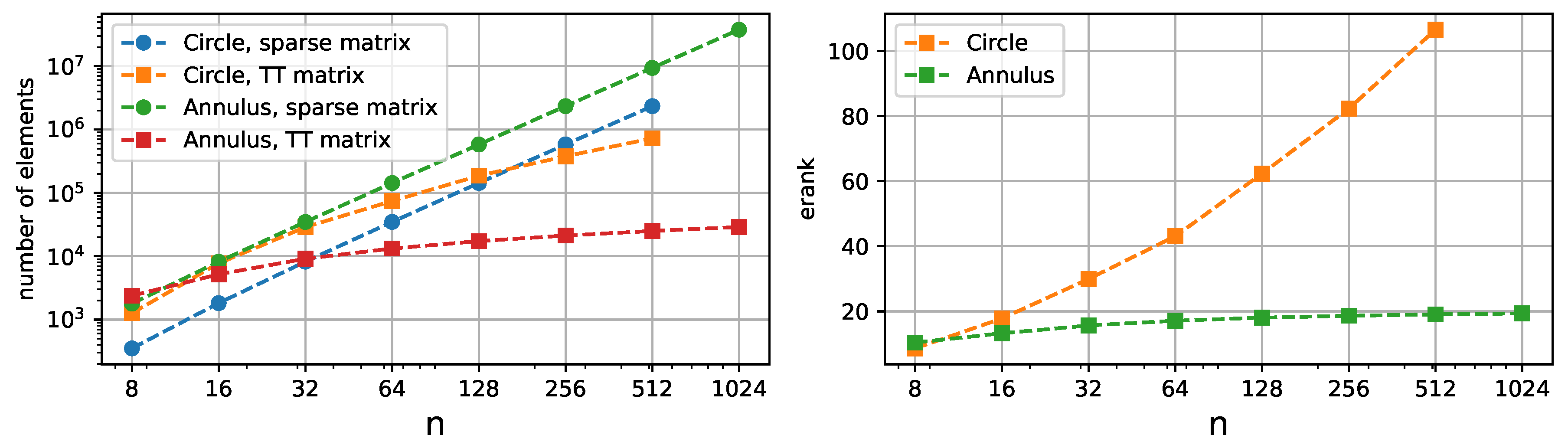
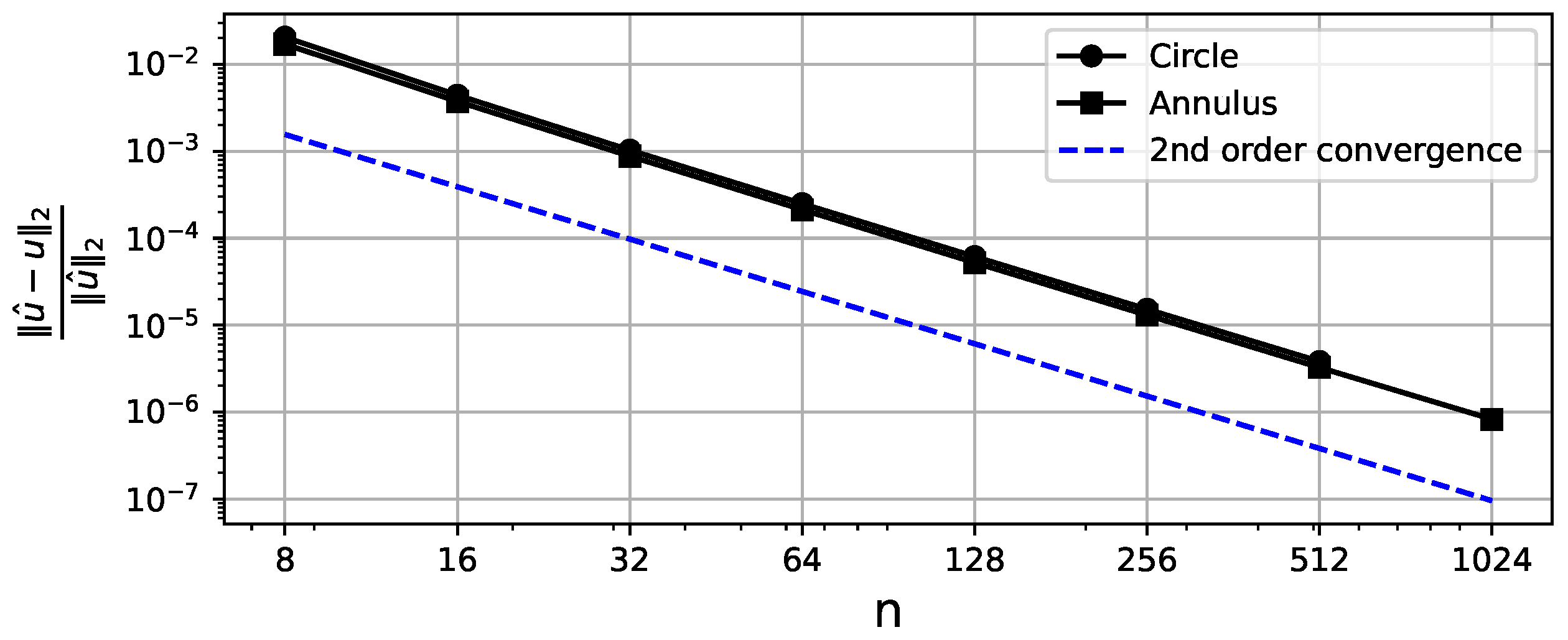
The circular domain consists of a single subdomain which is a unit square projected on a circle. This is an example of a <<bad>> case for the Tensor Train decomposition since the ranks of the stiffness matrix are growing exponentially, which can be seen in Figure 12. One reason for that may be four singularities of the Jacobian, one for each corner. However, in terms of memory consumption, the compression, compared to the sparse format, is present on denser meshes. Also, the error convergence is not affected, as shown in Figure 13, since the matrix TT ranks are only related to the time and memory consumption of the algorithms.
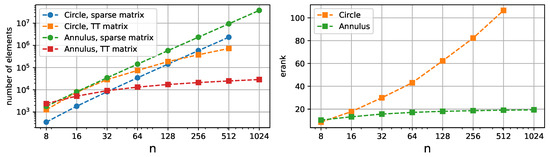
Figure 12.
The amounts of elements required to represent the stiffness matrix for the circle and the annulus in sparse and Tensor Train format are shown on the left plot. The effective ranks are depicted on the right plot. The circular domain is an example of a shape that is not suitable for the Tensor Train format.
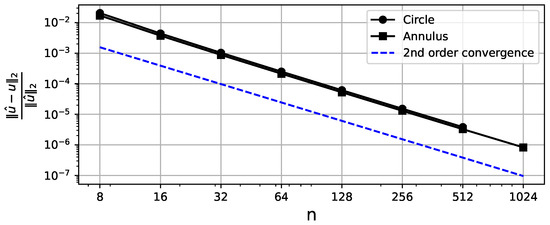
Figure 13.
Relative Frobenius norm error between the analytical and numerical solution vectors for different mesh discretizations for the circle/annulus case. The X-axis denotes the number of grid points along a single dimension of a single subdomain. The second order convergence is observed.
On the other hand, the annular-shaped domain consists of four subdomains with low ranks, so, despite containing 4 times as many nodes, the mesh is compressed efficiently.
4.4. Navier–Stokes Flow in a Lid-Driven Cavity
Here, we solve the Navier–Stokes equations via Chorin’s method described in Section 3.5 using the regular finite element method and TetraFEM for the discretization and compare the results.
The computational domain is a square , the boundary conditions for the velocities are zeros on every wall, except some constant velocity on the top lid for . For the pressure boundary, conditions are not specified.
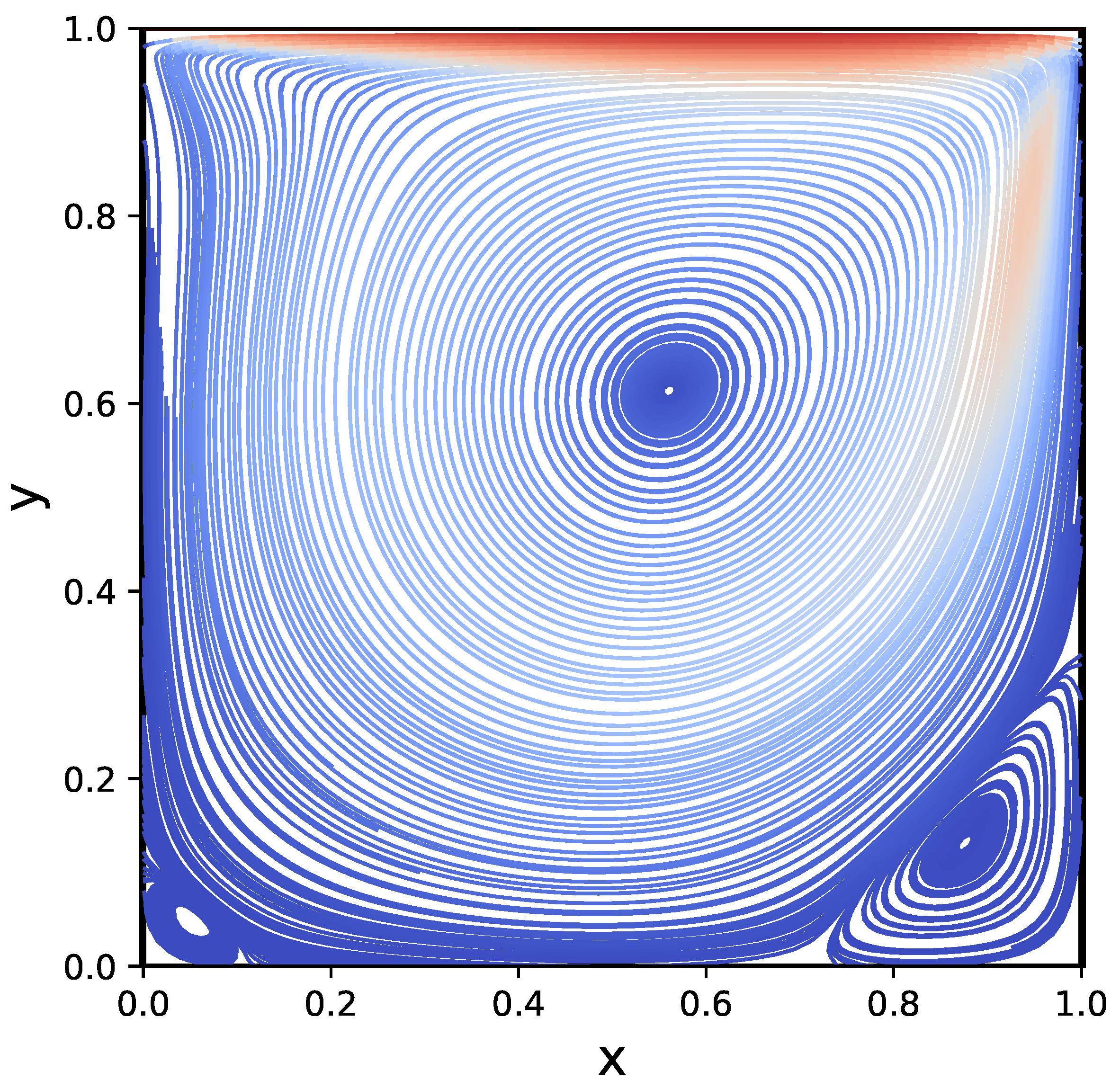
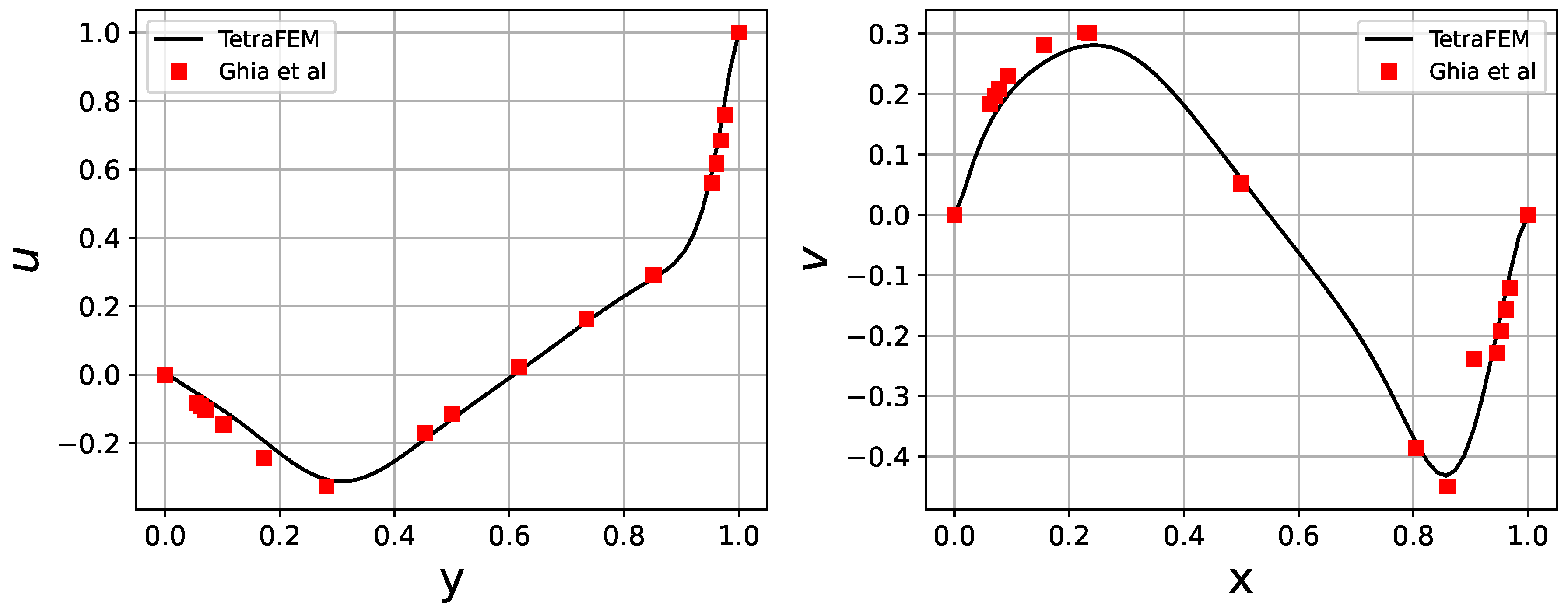
The streamlines of the steady-state flow obtained via the tensorized algorithm are visually identical to the benchmark results obtained in [38] as shown in Figure 14. To quantitatively compare the results, we show 1D-slices of velocity vectors in Figure 15, together with the benchmark solutions of Ghia, Ghia, and Shin [38].
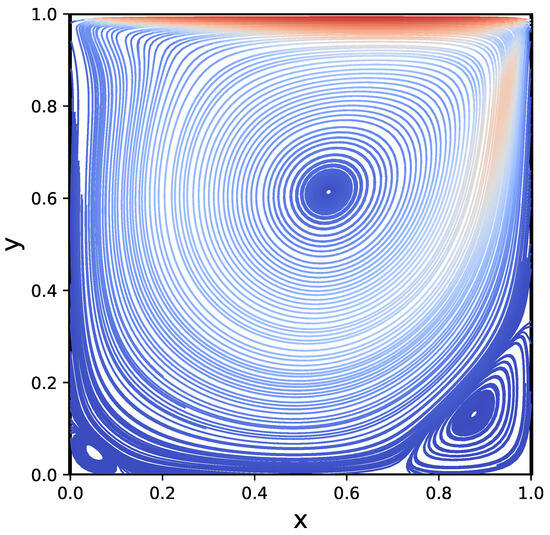
Figure 14.
Streamplot of the lid-driven cavity problem steady-state solution. The Reynolds number is . The relative TT-rounding tolerance is . Note the eddies in the bottom right and left corners.
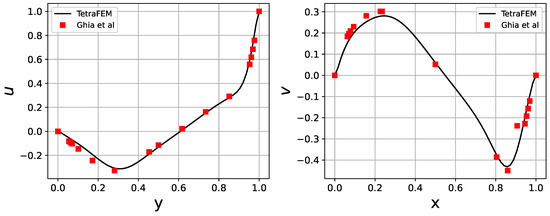
Figure 15.
Profiles of X-velocity on a vertical centerline of a square cavity (left) and Y-velocity on a horizontal line y = 0.5 (right). Discretization is points. Red symbols refer to the data from [38].
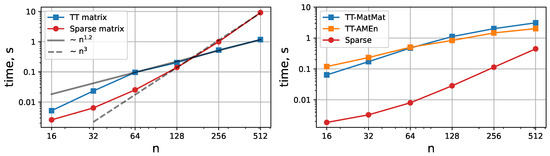
Figure 16.
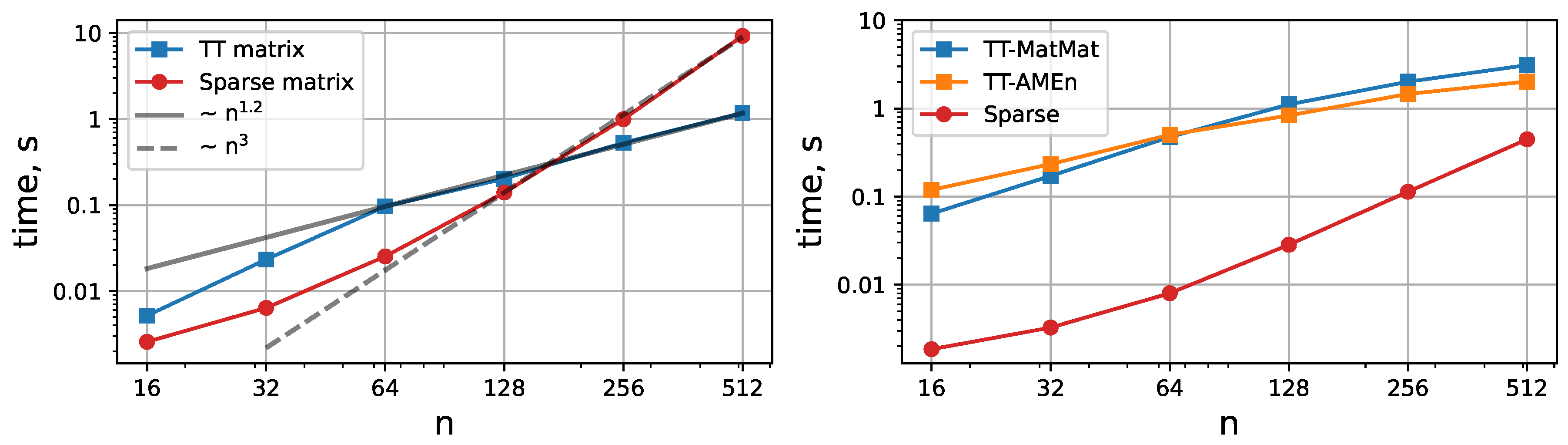
The time-step averaged timings of the different parts of the algorithm. The left plot shows the time taken by the solution of the pressure Poisson equation, and the the time for the operator reassemby is depicted on the right plot. The time required for the Poisson equation by the TT-algorithm scales much better than the full format version. It can be observed that the operator reassembly is much slower in TT format and is the major part of the algorithm. It can also be noted that the reassembly by AMEn outperforms the TT-MatMat approach with the growth of the mesh.
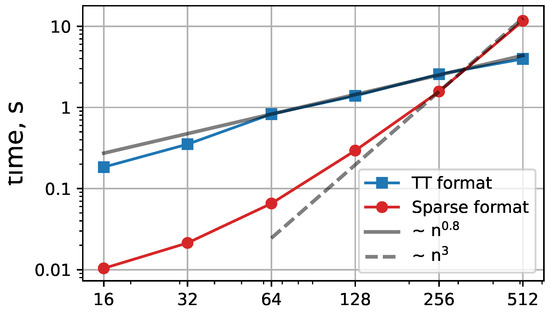
Figure 17.
The mean time for a time step for different meshes. The advantage of Tensor format on denser meshes is observed due to better scaling.
Since the ranks of the solution are not very big, the compression comparing with the full format computations is present. Increasing the number of mesh points provides better scaling, which can be seen in Figure 16.
For the full format, we used sparse format for the matrices and conjugate gradient method for the solution of the linear systems. The relative tolerance of the method is the same as the Tensor Train rounding tolerance of the tensorized method.
The numerical solution of the nonstationary incompressible Navier–Stokes equations in the arbitrary 2D domain was achieved via the Tensor Train Finite element method with the speed-up, compared to the classical finite element methods. The combination of low-rank Tensor Train operators for the smoothly transformed domains and the reasonable ranks of the solution led to significant memory reduction and speed-up even on moderate mesh discretizations for the nonlinear time-stepping problem.
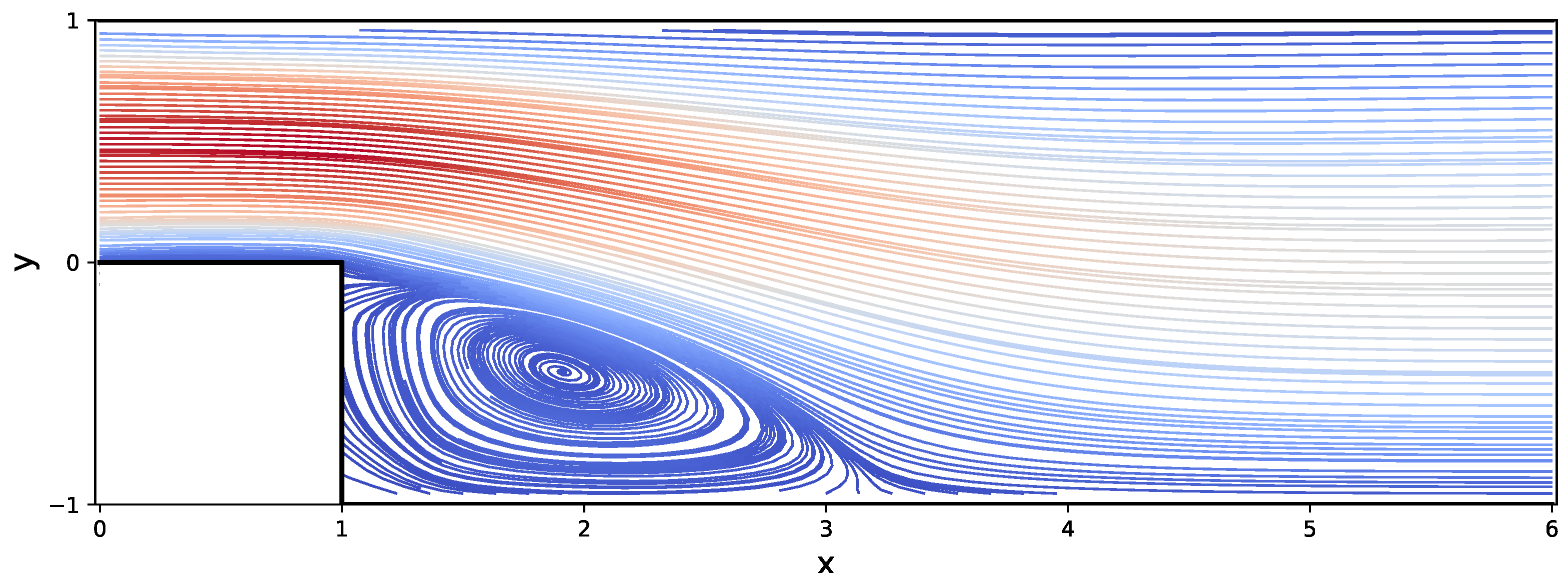
4.5. Navier–Stokes Flow in a Backward-Facing Step Domain
Here we solve the Navier–Stokes equations in a more complex domain using the same algorithm as in previous subsection.
The L-shaped domain (backward-facing step) consists of three concatenated rectangular domains. The parabolic inflow boundary condition is imposed on the left side, the outflow <<do nothing>> condition is on the right side; everything else is a no-slip wall.
The visual depiction of the stationary flow is shown on Figure 18. The correct physical behavior of the fluid can be observed. The multi-domain system assembly/reassembly procedures presented in Section 3.3 and Section 3.4 are tested on a nonlinear fluid simulation problem.
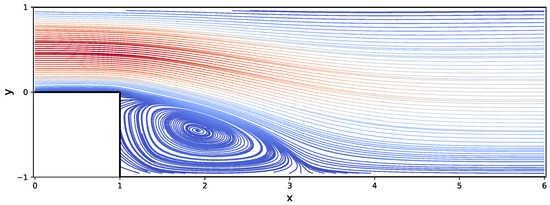
Figure 18.
Streamplot of the incompressible Navier–Stokes flow in L-shaped domain for .
5. Discussion
In this paper, we presented a methodology for solving partial differential equations in complex domains using Tensor Trains. The TT compression provides a milder (sublinear) asymptotic scaling compared to the straightforward vector solution. However, the constant in front of the complexity is higher due to its dependence on TT ranks. Potentially large TT ranks of nontrivial solutions are the main limitation of the method. Another one is finding the appropriate transformation to match the computational domain. In our examples, the TT approach becomes faster than the standard conjugate gradient solver, starting from grid sizes of 200–300. It depends on the application in which grid size (governed by the discretization error) is practical. For example, to resolve small eddies in the solution to the Navier–Stokes equation, the grid sizes in the order of hundreds are not excessive. However, more complex (e.g., multiscale) solutions may also exhibit higher TT ranks. The proposed methodology should be evaluated case by case. Nonetheless, for multiscale but regular structures which require fine discretization but yield low TT ranks, the developed approach should be beneficial. In our examples, we have demonstrated that our approach is faster than existing TT methods for PDEs on nontrivial domains.
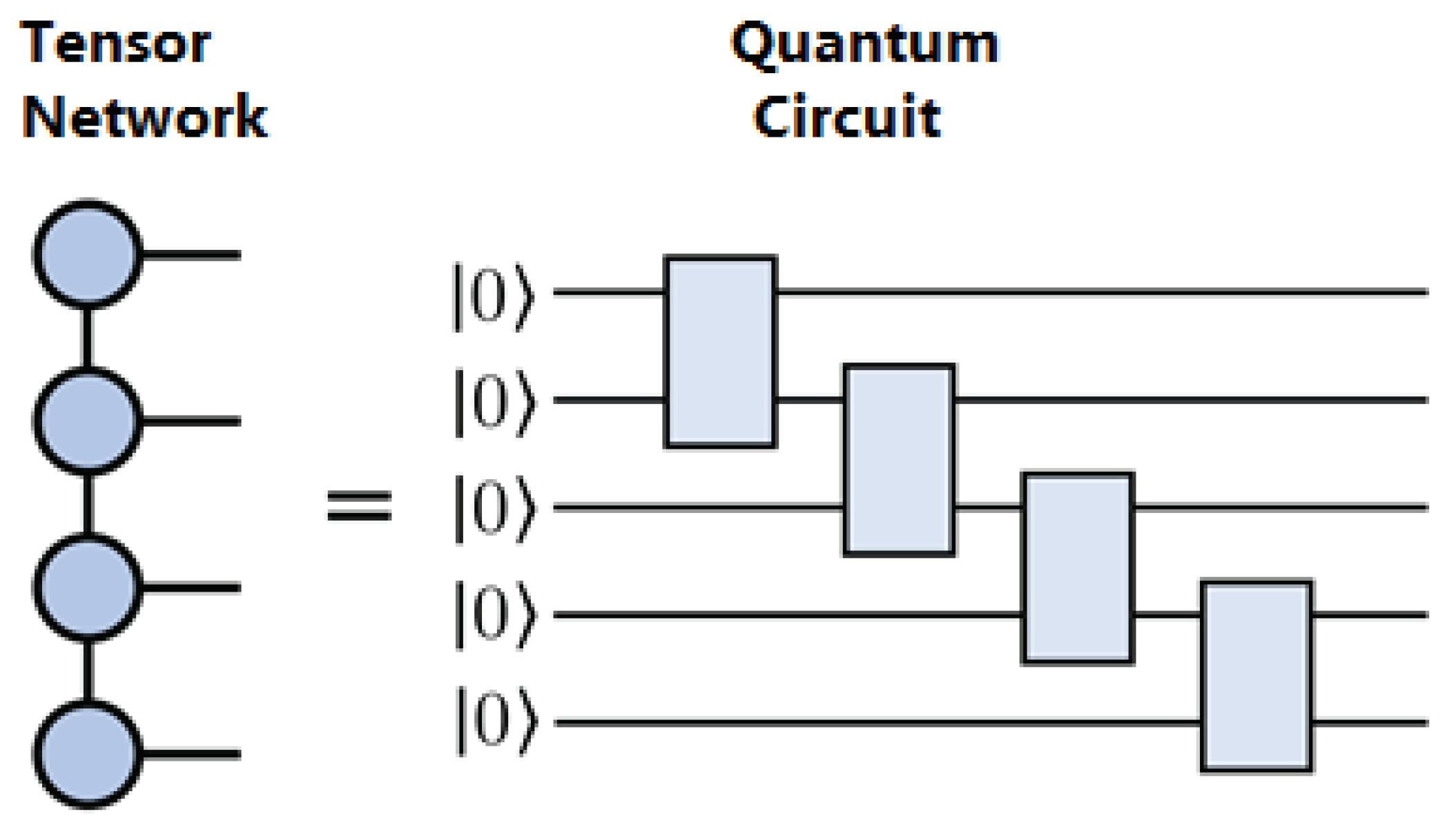
A breakthrough against high TT ranks may come from quantum computing. Specifically, the TT decomposition can be converted exactly into a quantum circuit of qubits [25,39,40,41,42], see Figure 19. The total complexity should thus become poly-logarithmic in the original problem size, which will provide an opportunity to solve many practical problems in the future. However, this assumes perfect quantum hardware, allowing one to operate thousands of qubits and gates with controllable noise. Such a state of the hardware is not there yet but is expected to emerge in the next decade.
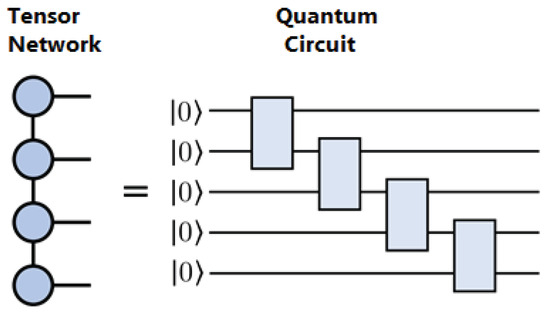
Figure 19.
Any Tensor Train of rank r can be exactly encoded into a quantum circuit using sequential multi-qubit operations, each of which acts on qubits.
Author Contributions
Conceptualization, methodology, writing, E.K., S.D., M.P. and A.M.; software, E.K.; visualization, E.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
Egor Kornev, Michael Perelshtein and Artem Melnikov were employed by the Terra Quantum AG. Sergey Dolgov is a consultant for Terra Quantum AG. The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PDE | Partial differential equation |
| TT | Tensor Train |
| QTT | Quantized Tensor Train |
| FEM | Finite element method |
| SVD | Singular value decomposition |
| AMEn | Alternating minimal energy method |
References
- Bazighifan, O.; Ali, A.H.; Mofarreh, F.; Raffoul, Y.N. Extended Approach to the Asymptotic Behavior and Symmetric Solutions of Advanced Differential Equations. Symmetry 2022, 14, 686. [Google Scholar] [CrossRef]
- Brenner, S.; Scott, R. The Mathematical Theory of Finite Element Methods; Texts in Applied Mathematics; Springer: New York, NY, USA, 2007. [Google Scholar]
- Ciarlet, P.G. The Finite Element Method for Elliptic Problems; SIAM: Philadelphia, PA, USA, 2002. [Google Scholar]
- Moës, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
- Beirão da Veiga, L.; Brezzi, F.; Cangiani, A.; Manzini, G.; Marini, L.D.; Russo, A. Basic principles of Virtual Element Methods. Math. Model. Methods Appl. Sci. 2013, 23, 199–214. [Google Scholar] [CrossRef]
- Dell’Accio, F.; Di Tommaso, F.; Guessab, A.; Nudo, F. Enrichment strategies for the simplicial linear finite elements. Appl. Math. Comput. 2023, 451, 128023. [Google Scholar] [CrossRef]
- Oseledets, I. Tensor-Train Decomposition. SIAM J. Sci. Comput. 2011, 33, 2295–2317. [Google Scholar] [CrossRef]
- Oseledets, I. Constructive Representation of Functions in Low-Rank Tensor Formats. Constr. Approx. 2010, 37, 1–8. [Google Scholar] [CrossRef]
- Dolgov, S.V.; Khoromskij, B.N.; Oseledets, I.V. Fast solution of parabolic problems in the tensor train/quantized tensor train format with initial application to the Fokker–Planck equation. SIAM J. Sci. Comput. 2012, 34, A3016–A3038. [Google Scholar] [CrossRef]
- Schneider, R.; Uschmajew, A. Approximation rates for the hierarchical tensor format in periodic Sobolev spaces. J. Complex. 2013. [Google Scholar] [CrossRef]
- Griebel, M.; Harbrecht, H. Analysis of tensor approximation schemes for continuous functions. Found. Comput. Math. 2023, 23, 219–240. [Google Scholar] [CrossRef]
- Bigoni, D.; Engsig-Karup, A.P.; Marzouk, Y.M. Spectral tensor-train decomposition. SIAM J. Sci. Comput. 2016, 38, A2405–A2439. [Google Scholar] [CrossRef]
- Gorodetsky, A.; Karaman, S.; Marzouk, Y. A continuous analogue of the tensor-train decomposition. Comput. Methods Appl. Mech. Engrg. 2019, 347, 59–84. [Google Scholar] [CrossRef]
- Dolgov, S.; Savostyanov, D. Alternating minimal energy methods for linear systems in higher dimensions. SIAM J. Sci. Comput. 2014, 36, 1–24. [Google Scholar] [CrossRef]
- Sozykin, K.; Chertkov, A.; Schutski, R.; Phan, A.H.; Cichocki, A.; Oseledets, I. TTOpt: A Maximum Volume Quantized Tensor Train-based Optimization and its Application to Reinforcement Learning. arXiv 2022, arXiv:2205.00293. [Google Scholar]
- Morozov, D.; Melnikov, A.; Shete, V.; Perelshtein, M. Protein-protein docking using a tensor train black-box optimization method. arXiv 2023, arXiv:2302.03410. [Google Scholar]
- Novikov, A.; Podoprikhin, D.; Osokin, A.; Vetrov, D.P. Tensorizing neural networks. Adv. Neural Inf. Process. Syst. 2015, 28, 1–9. [Google Scholar]
- Sagingalieva, A.; Kurkin, A.; Melnikov, A.; Kuhmistrov, D.; Perelshtein, M.; Melnikov, A.; Skolik, A.; Von Dollen, D. Hyperparameter optimization of hybrid quantum neural networks for car classification. arXiv 2022, arXiv:2205.04878. [Google Scholar]
- Naumov, A.; Melnikov, A.; Abronin, V.; Oxanichenko, F.; Izmailov, K.; Pflitsch, M.; Melnikov, A.; Perelshtein, M. Tetra-AML: Automatic Machine Learning via Tensor Networks. arXiv 2023, arXiv:2303.16214. [Google Scholar]
- Blazek, J. Computational Fluid Dynamics: Principles and Applications; Butterworth-Heinemann: Oxford, UK, 2015. [Google Scholar]
- Dolgov, S.; Pearson, J.W. Preconditioners and Tensor Product Solvers for Optimal Control Problems from Chemotaxis. SIAM J. Sci. Comput. 2019, 41, B1228–B1253. [Google Scholar] [CrossRef]
- Gourianov, N.; Lubasch, M.; Dolgov, S.; van den Berg, Q.Y.; Babaee, H.; Givi, P.; Kiffner, M.; Jaksch, D. A quantum-inspired approach to exploit turbulence structures. Nat. Comput. Sci. 2022, 2, 30–37. [Google Scholar] [CrossRef]
- Ion, I.G.; Loukrezis, D.; De Gersem, H. Tensor train based isogeometric analysis for PDE approximation on parameter dependent geometries. Comput. Methods Appl. Mech. Eng. 2022, 401, 115593. [Google Scholar] [CrossRef]
- Ion, I.G. Low-Rank Tensor Decompositions for Surrogate Modeling in forward and inverse Problems. Ph.D. Thesis, Technische Universität Darmstadt, Darmstadt, The Netherland, 2024. [Google Scholar] [CrossRef]
- Schön, C.; Solano, E.; Verstraete, F.; Cirac, J.I.; Wolf, M.M. Sequential Generation of Entangled Multiqubit States. Phys. Rev. Lett. 2005, 95, 110503. [Google Scholar] [CrossRef] [PubMed]
- Markeeva, L.; Tsybulin, I.; Oseledets, I. QTT-isogeometric solver in two dimensions. J. Comput. Phys. 2021, 424, 109835. [Google Scholar] [CrossRef]
- Kazeev, V.A.; Schwab, C. Approximation of Singularities by Quantized-Tensor FEM. PAMM 2015, 15, 743–746. [Google Scholar] [CrossRef]
- Khoromskij, B. O(dlogN)-Quantics Approximation of N-d Tensors in High-Dimensional Numerical Modeling. Constr. Approx. 2009, 34, 257–280. [Google Scholar] [CrossRef]
- Sekmen, A.; Aldroubi, A.; Koku, A.B.; Hamm, K. Matrix resconstruction: Skeleton decomposition versus singular value decomposition. In Proceedings of the 2017 International Symposium on Performance Evaluation of Computer and Telecommunication Systems (SPECTS), Seattle, WA, USA, 9–12 July 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Oseledets, I.; Tyrtyshnikov, E. TT-cross approximation for multidimensional arrays. Linear Algebra Its Appl. 2010, 432, 70–88. [Google Scholar] [CrossRef]
- White, S.R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 1992, 69, 2863–2866. [Google Scholar] [CrossRef]
- Saad, Y. Iterative Methods for Sparse Linear Systems, 2nd ed.; Other Titles in Applied Mathematics; SIAM: Philadelphia, PA, USA, 2003. [Google Scholar] [CrossRef]
- Oseledets, I. ttpy 1.2.0. 2017. Available online: https://github.com/oseledets/ttpy (accessed on 15 October 2024).
- Gordon, W.J.; Thiel, L.C. Transfinite mappings and their application to grid generation. Appl. Math. Comput. 1982, 10–11, 171–233. [Google Scholar] [CrossRef]
- Elman, H.; Silvester, D.; Wathen, A. Finite Elements and Fast Iterative Solvers: With Applications in Incompressible Fluid Dynamics; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Temam, R. Navier–Stokes Equations: Theory and Numerical Analysis; American Mathematical Society: Providence, RI, USA, 2024; Volume 343. [Google Scholar]
- Chorin, A.J. The numerical solution of the Navier-Stokes equations for an incompressible fluid. Bull. Am. Math. Soc. 1967, 73, 928–931. [Google Scholar] [CrossRef]
- Ghia, U.; Ghia, K.; Shin, C. High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method. J. Comput. Phys. 1982, 48, 387–411. [Google Scholar] [CrossRef]
- Melnikov, A.A.; Termanova, A.A.; Dolgov, S.V.; Neukart, F.; Perelshtein, M.R. Quantum state preparation using tensor networks. Quantum Sci. Technol. 2023, 8, 035027. [Google Scholar] [CrossRef]
- Ran, S.J. Encoding of matrix product states into quantum circuits of one- and two-qubit gates. Phys. Rev. A 2020, 101, 032310. [Google Scholar] [CrossRef]
- Zhou, P.F.; Hong, R.; Ran, S.J. Automatically differentiable quantum circuit for many-qubit state preparation. Phys. Rev. A 2021, 104, 042601. [Google Scholar] [CrossRef]
- Rudolph, M.S.; Chen, J.; Miller, J.; Acharya, A.; Perdomo-Ortiz, A. Decomposition of Matrix Product States into Shallow Quantum Circuits. arXiv 2022, arXiv:2209.00595. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).