Dynamics of Some Perturbed Morse-Type Oscillators: Simulations and Applications
Abstract
:1. Introduction
2. Some New Models — Some Simulations
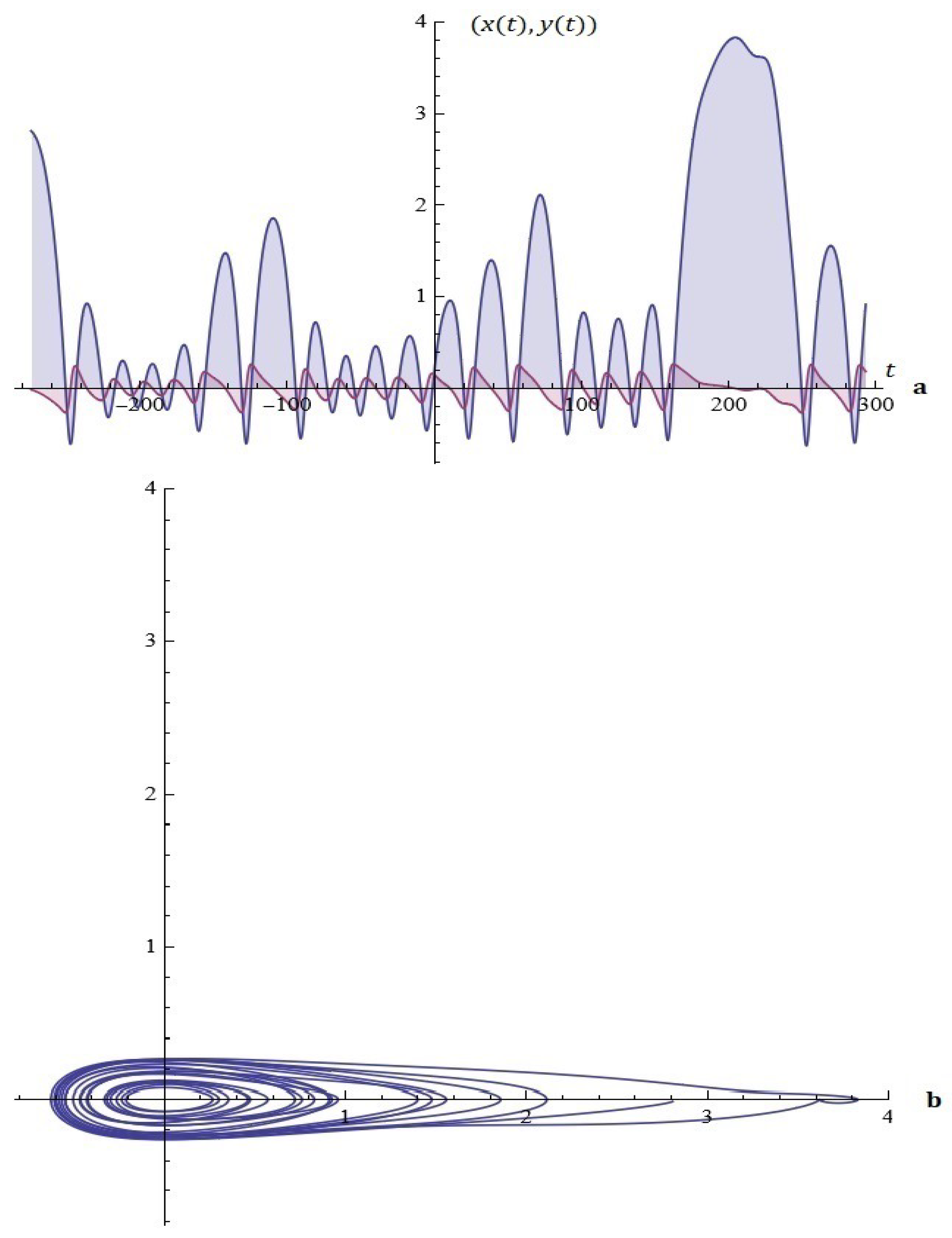
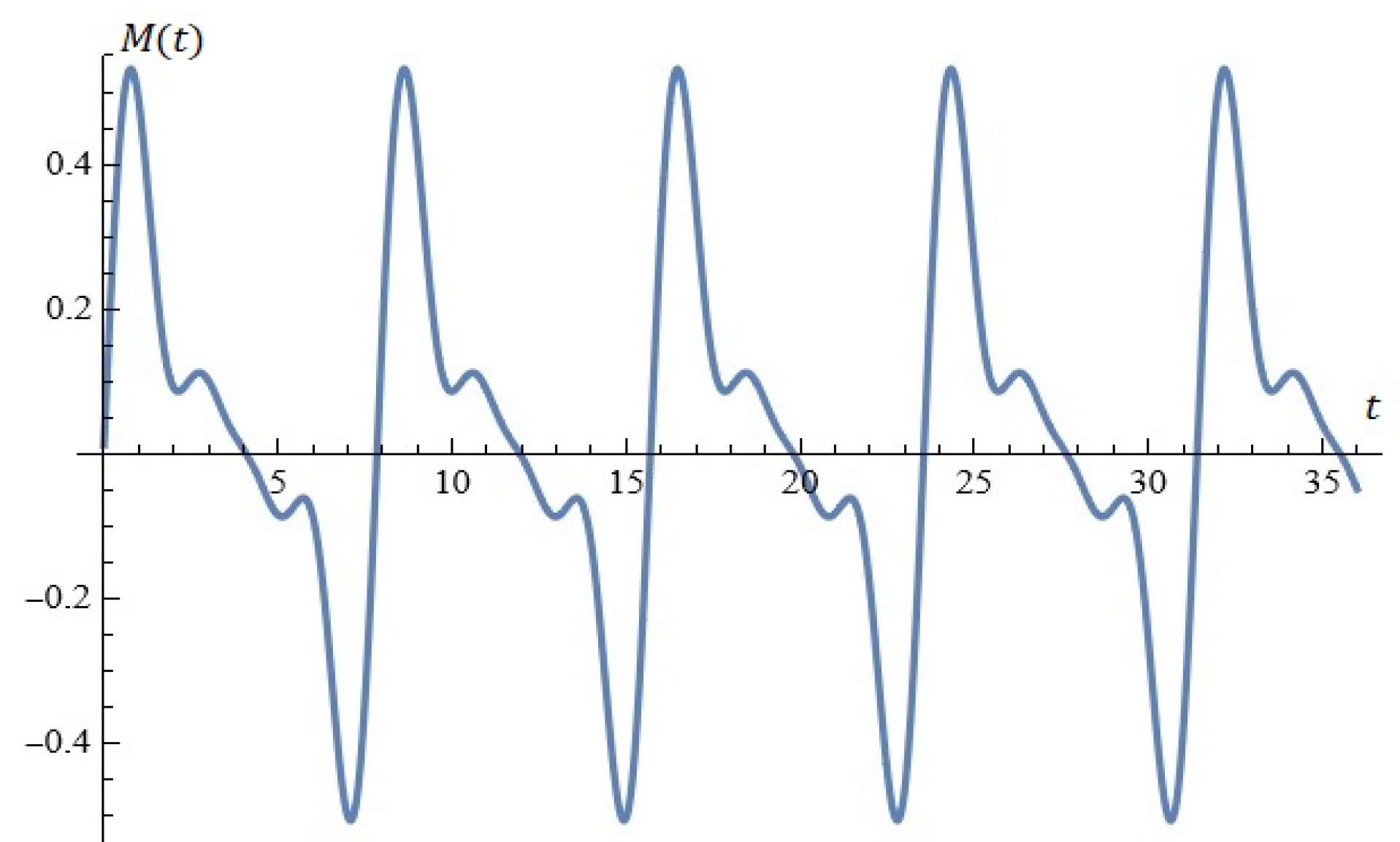
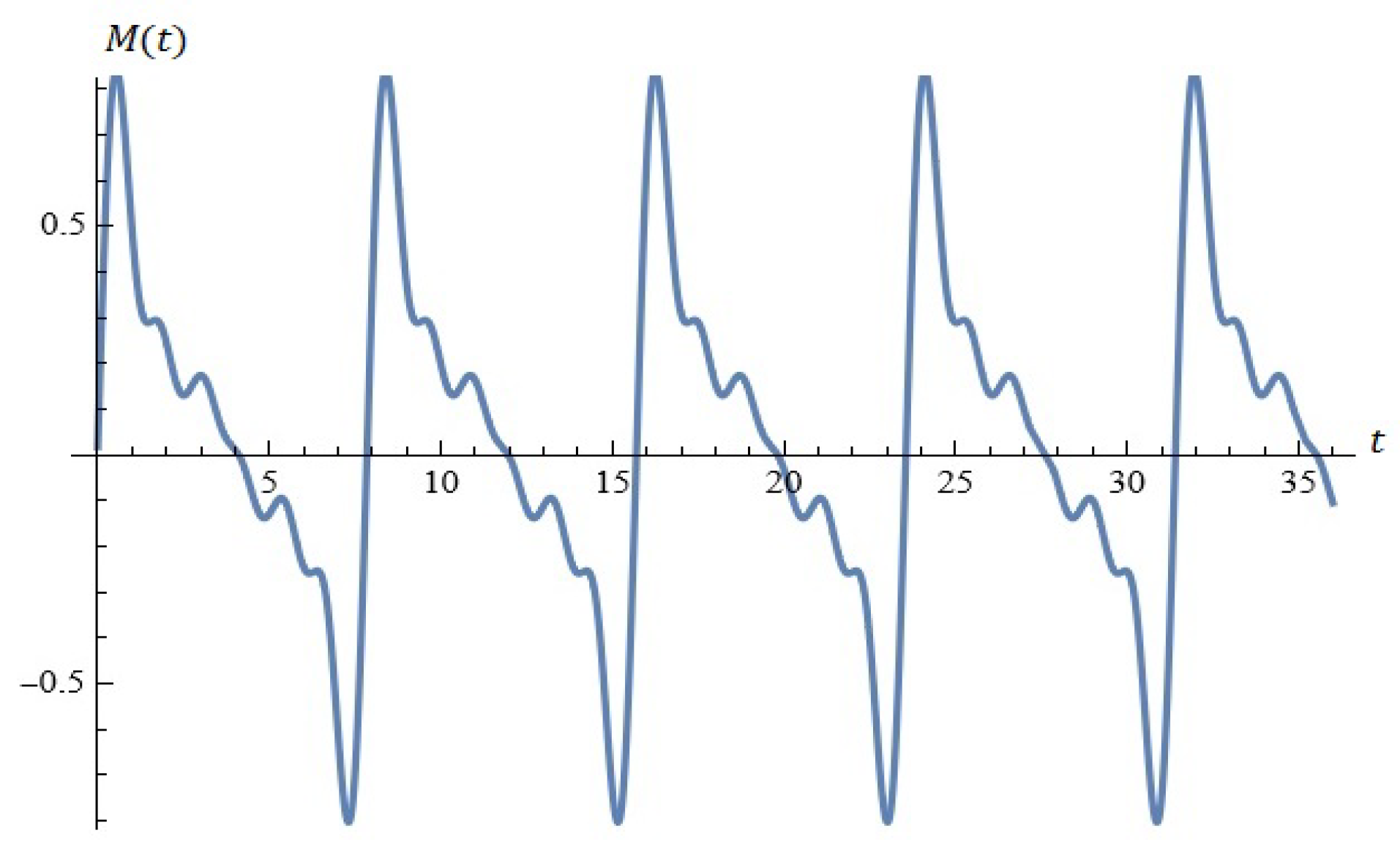
2.1. Model A
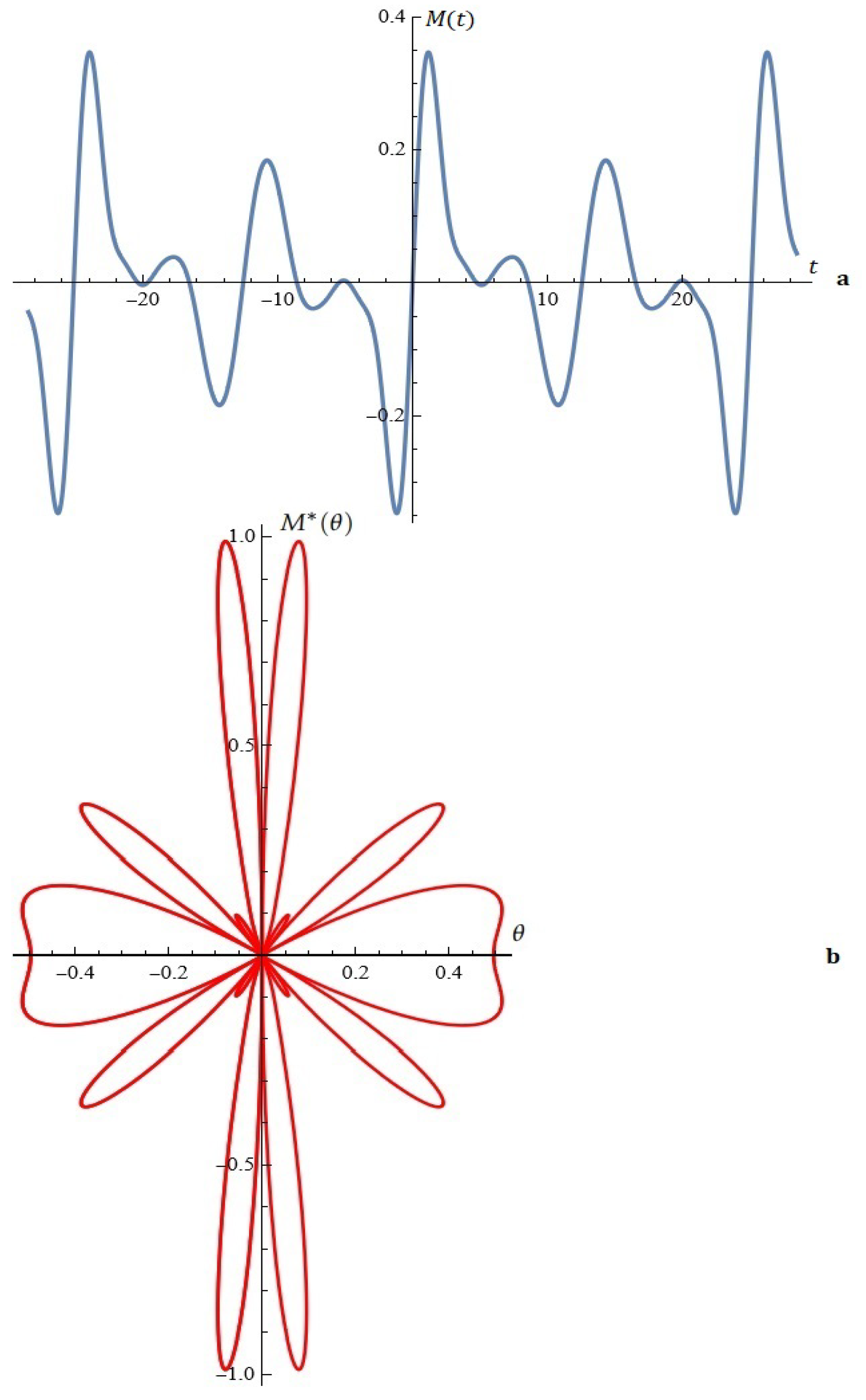
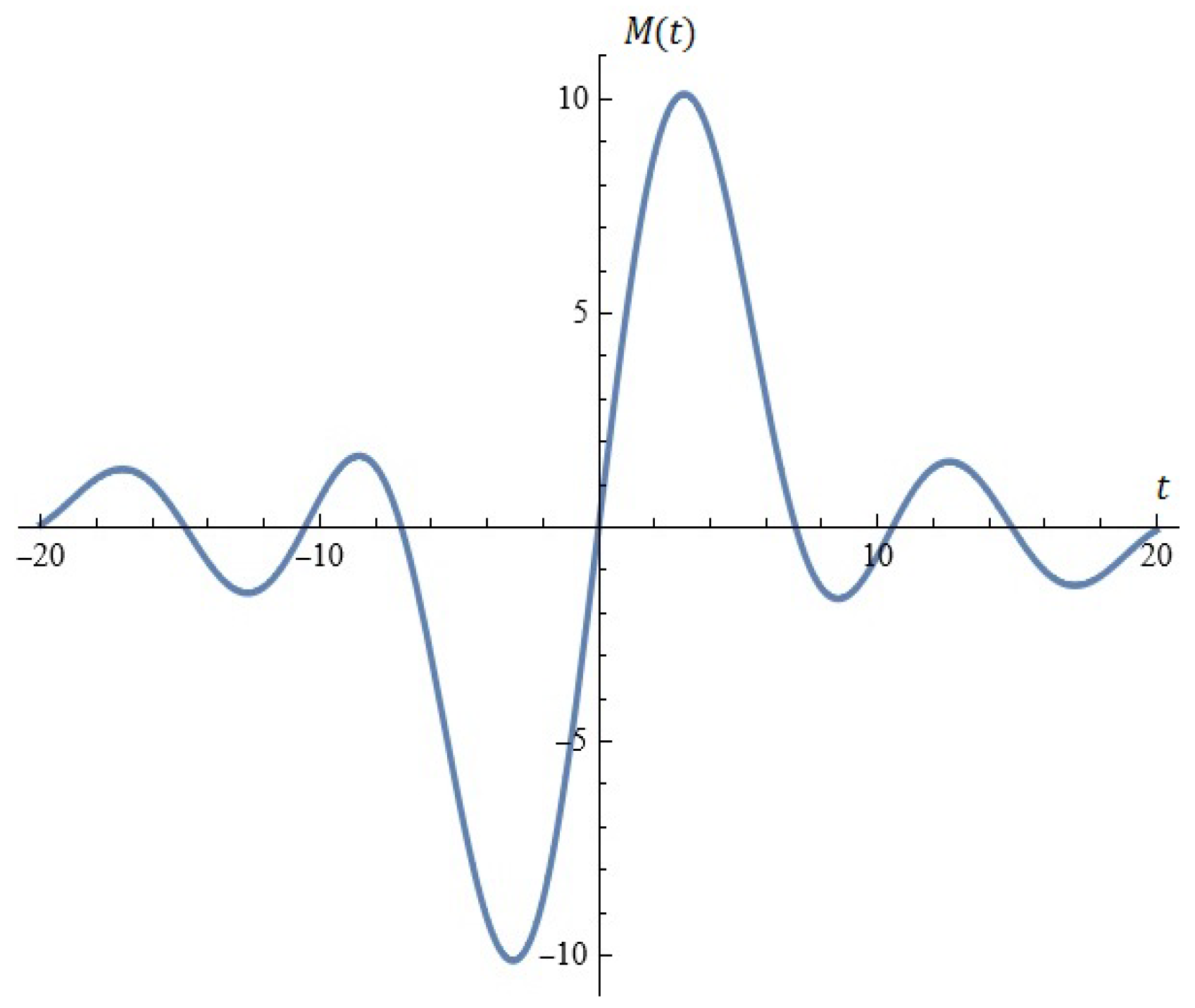
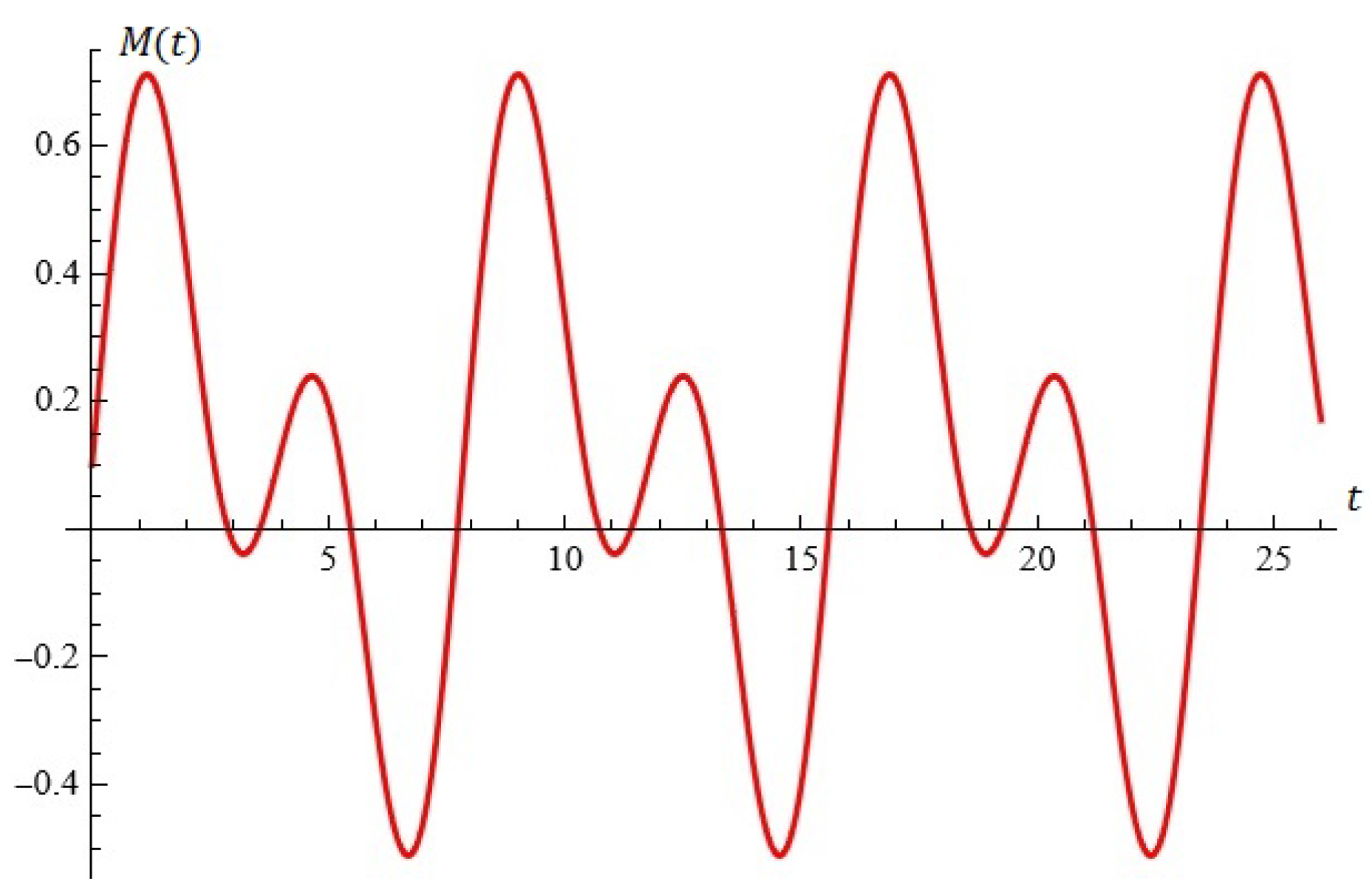
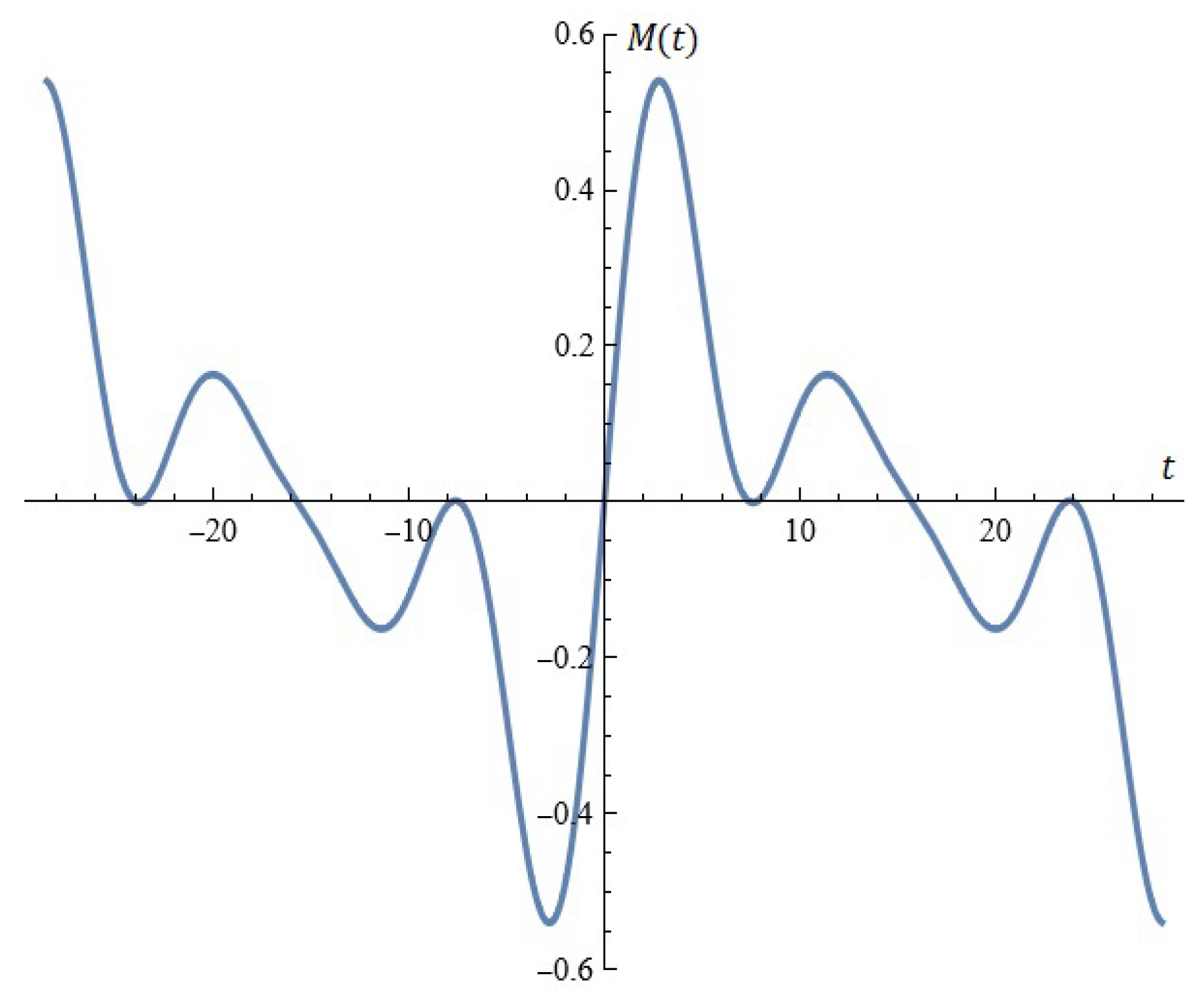
2.1.1. Considerations in Light of Melnikov’s Approach
2.1.2. Probability Distributions Driving the Perturbation
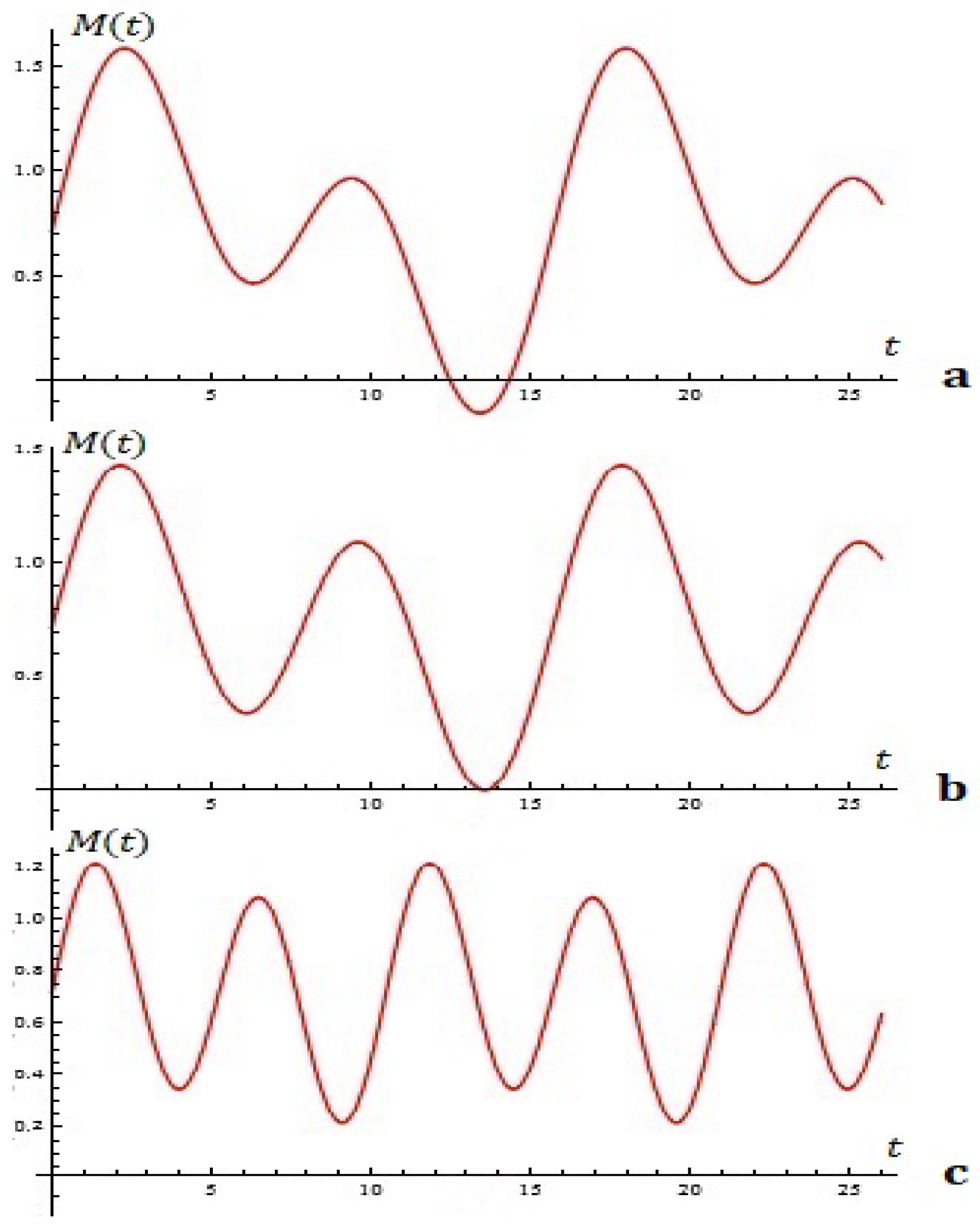
- Binomial distribution: , , , , , , ;
- -Binomial distribution: , , , , , , ;
- -Binomial distribution: , , , , , , ;
- Geometric distribution: , , , , , .
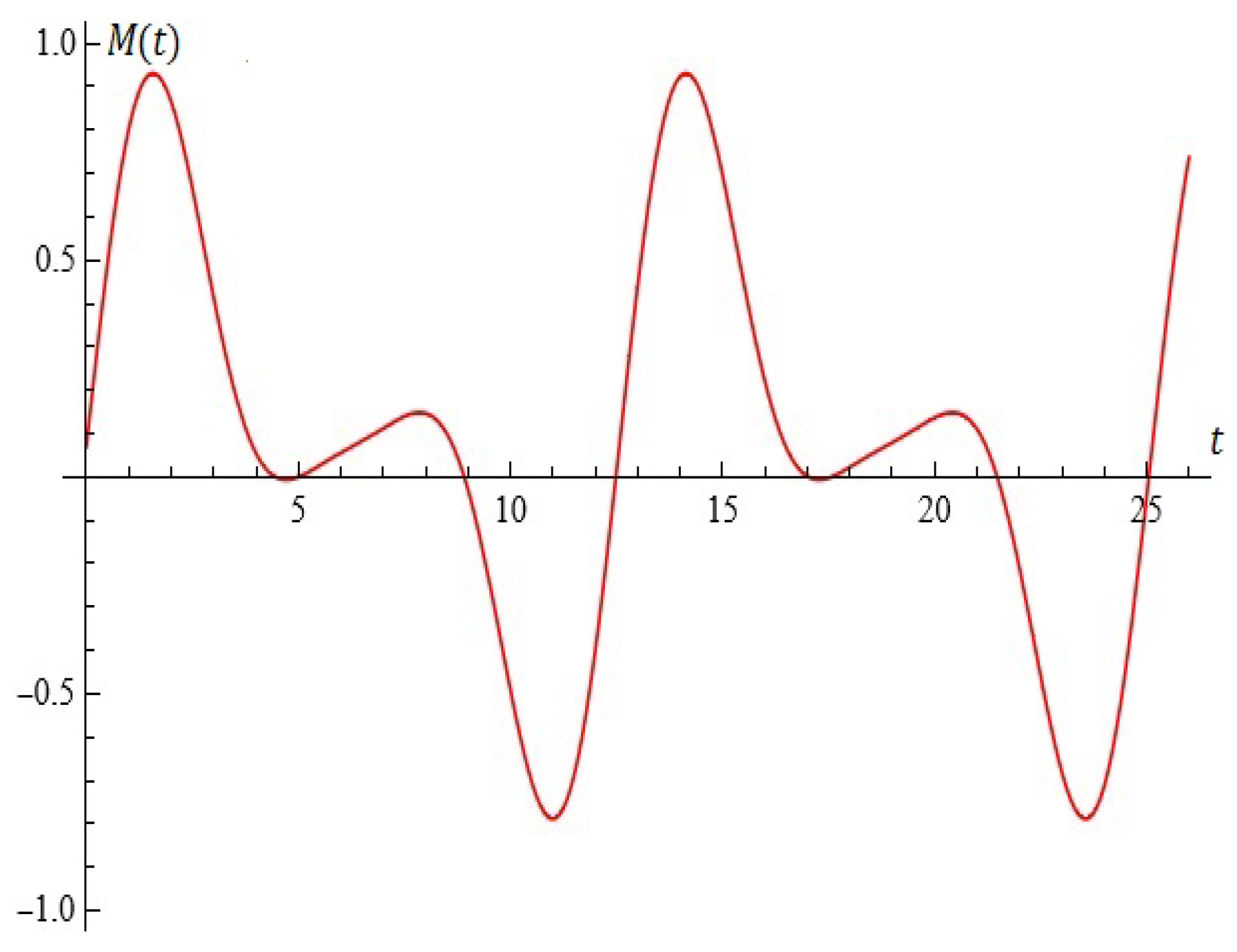
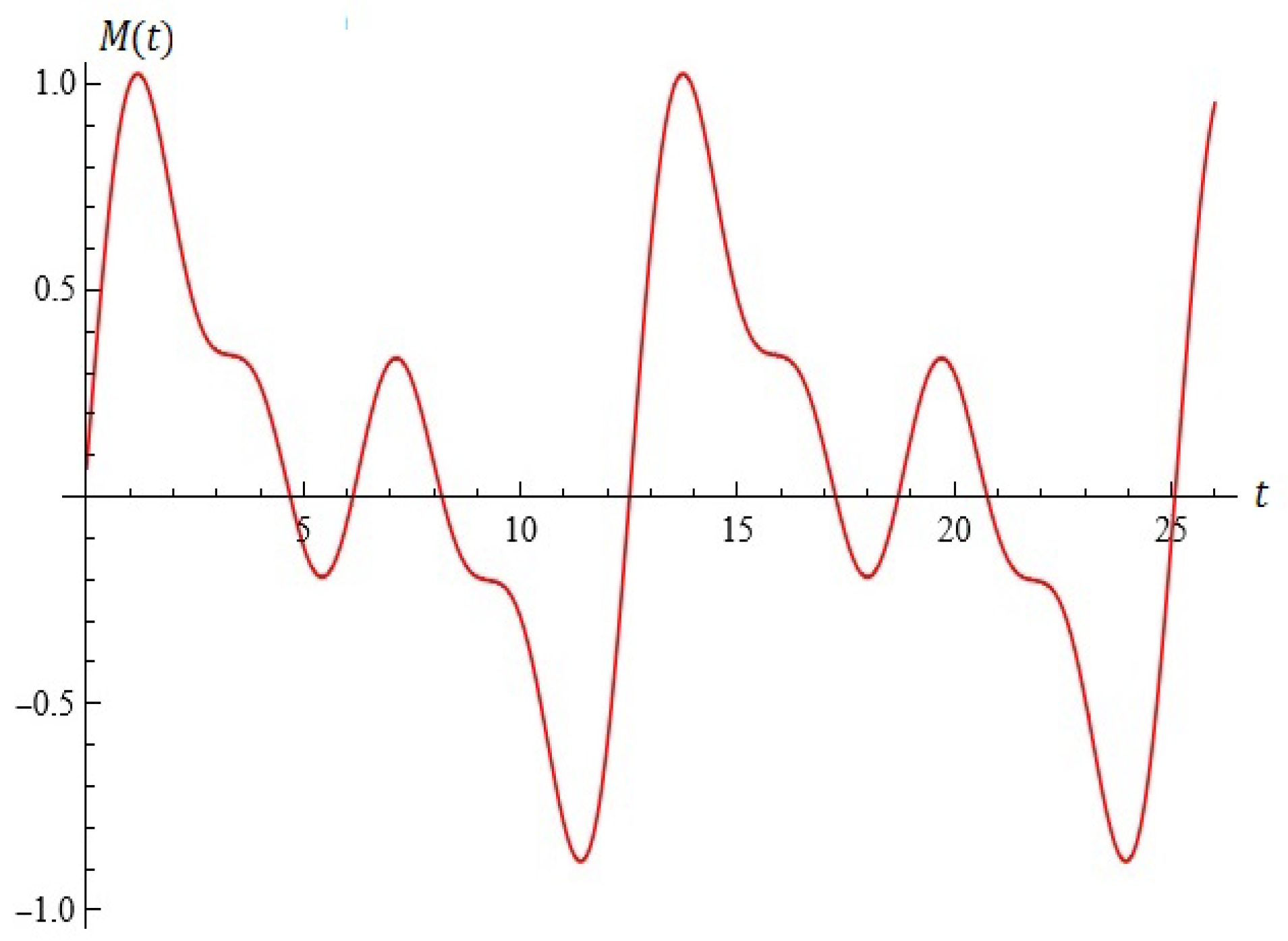
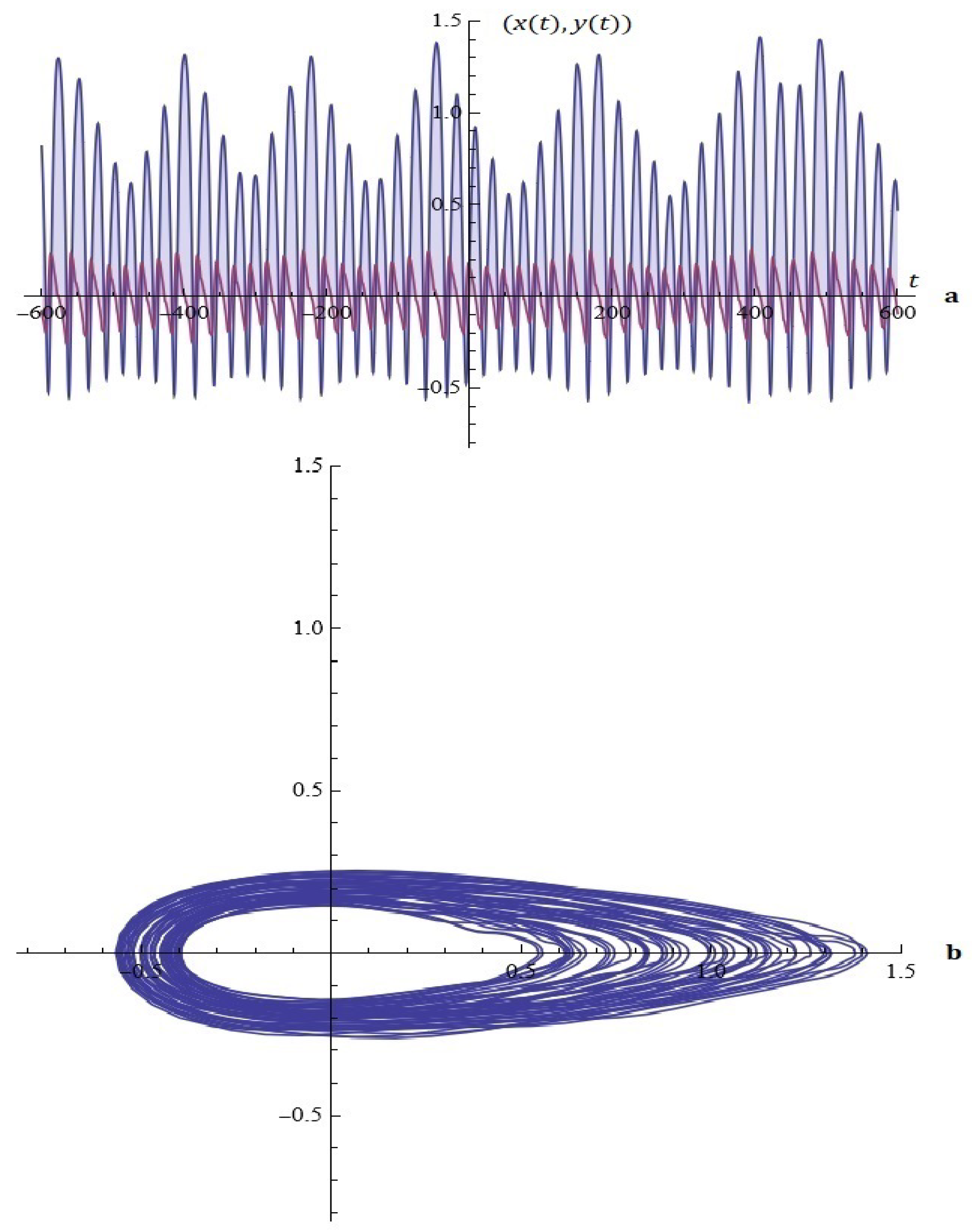
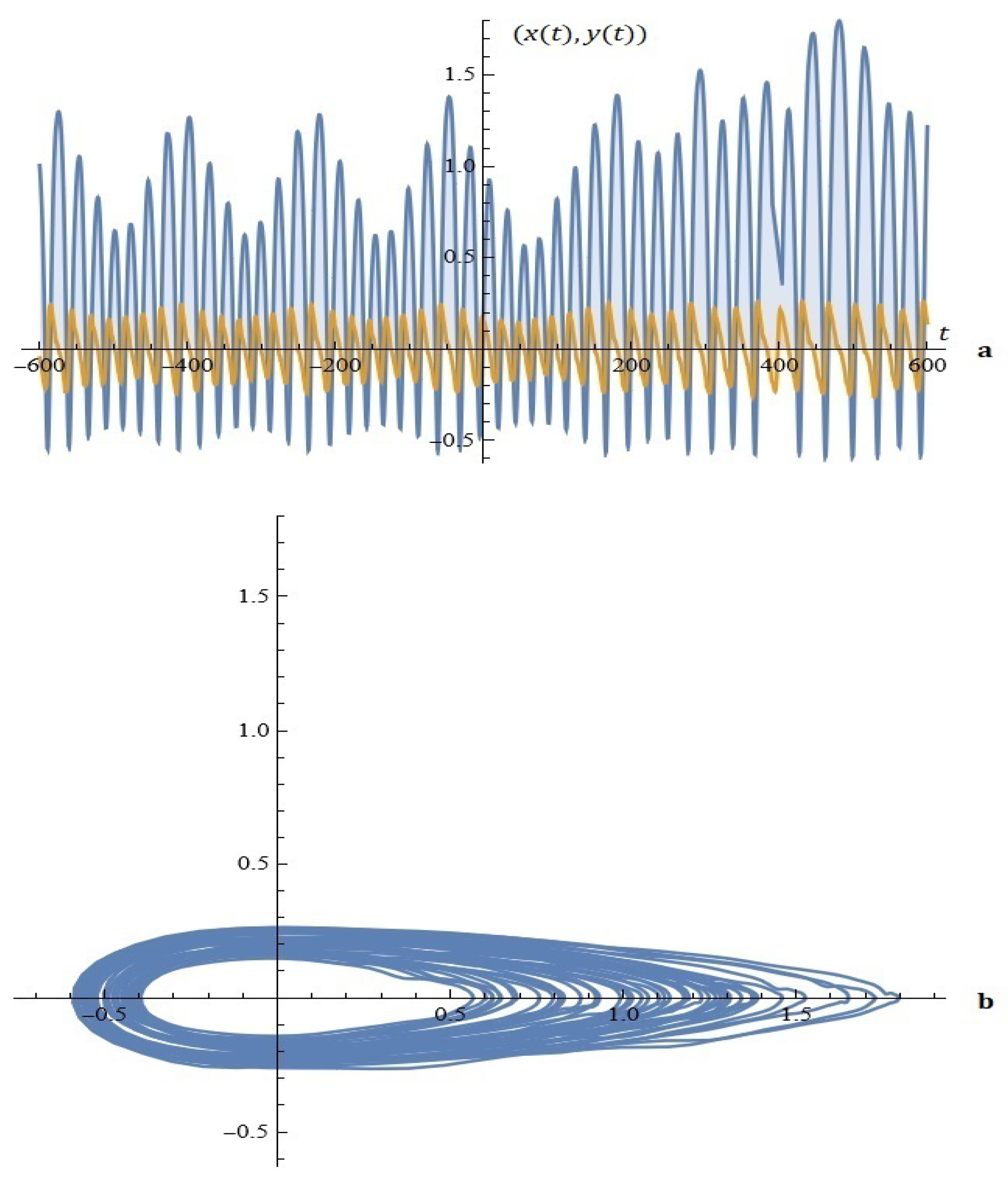
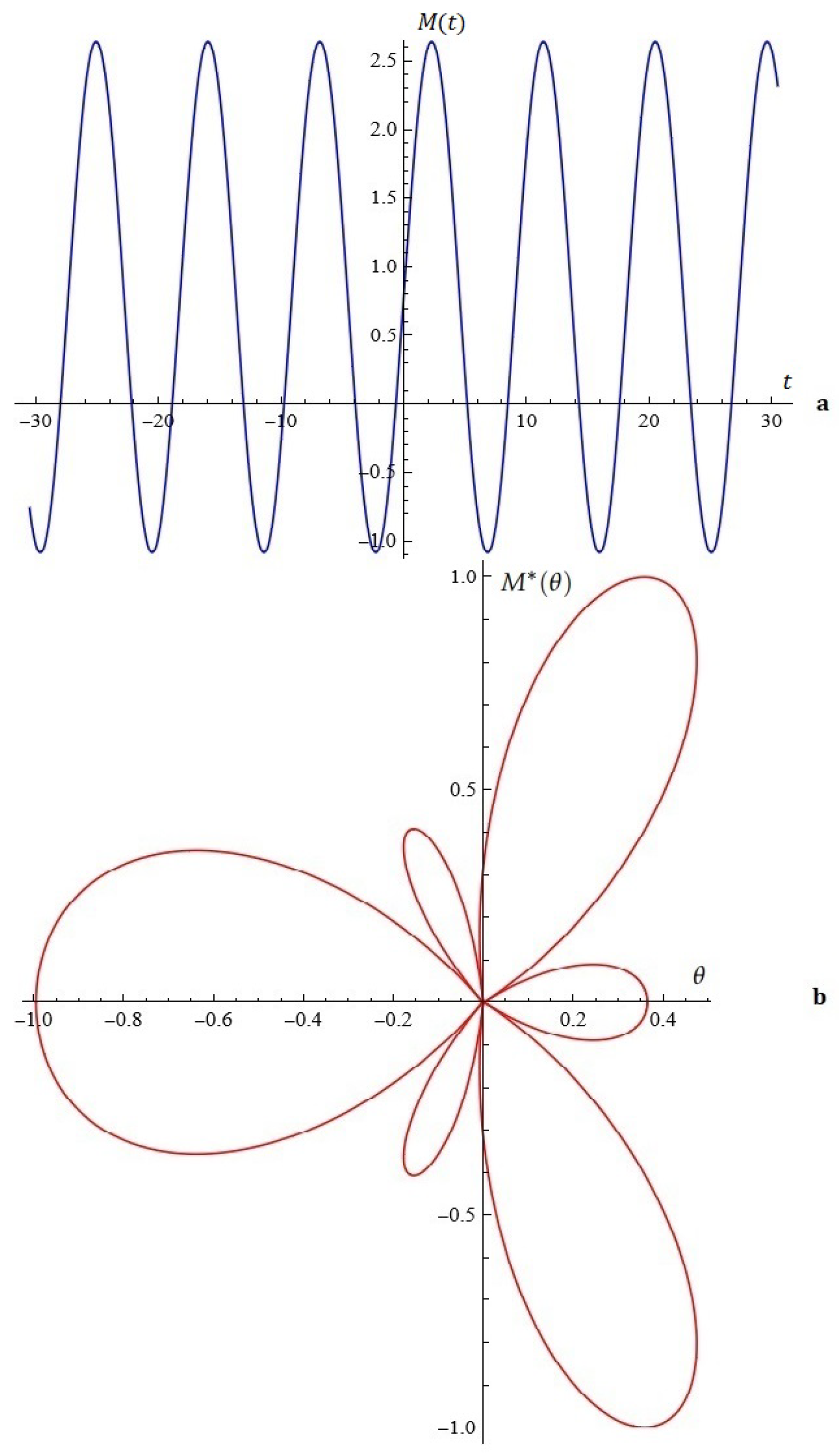
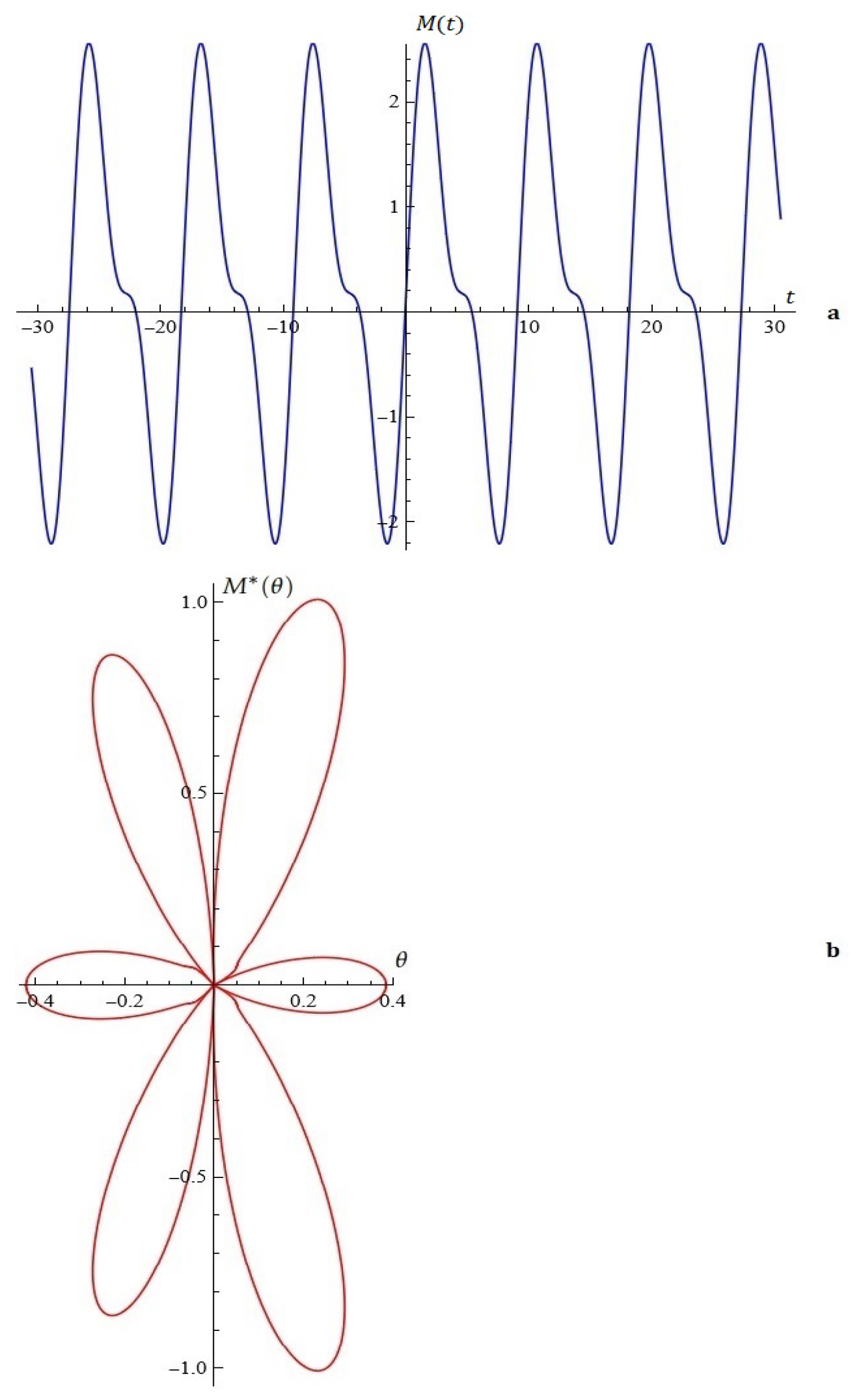
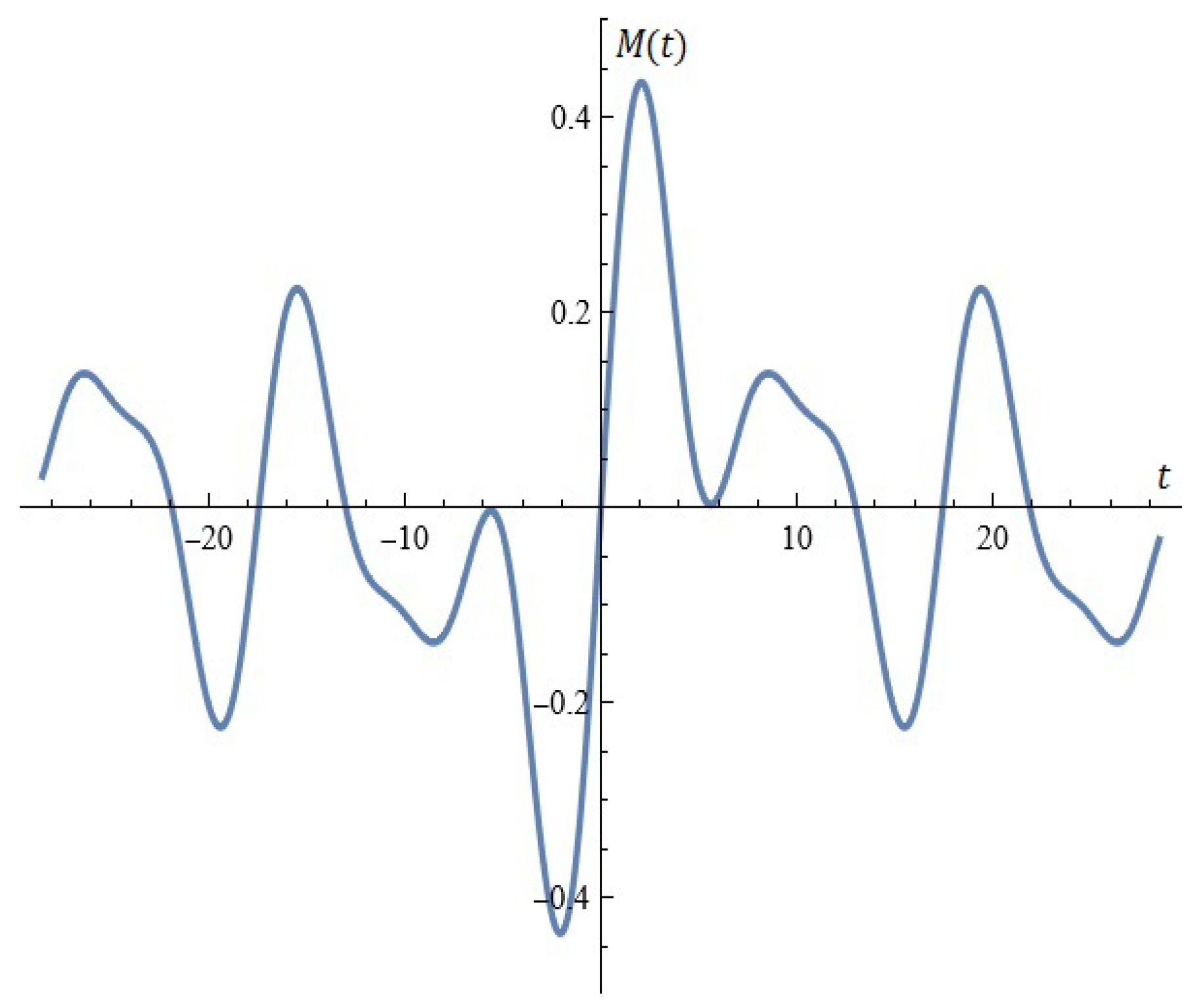
2.2. The Model B
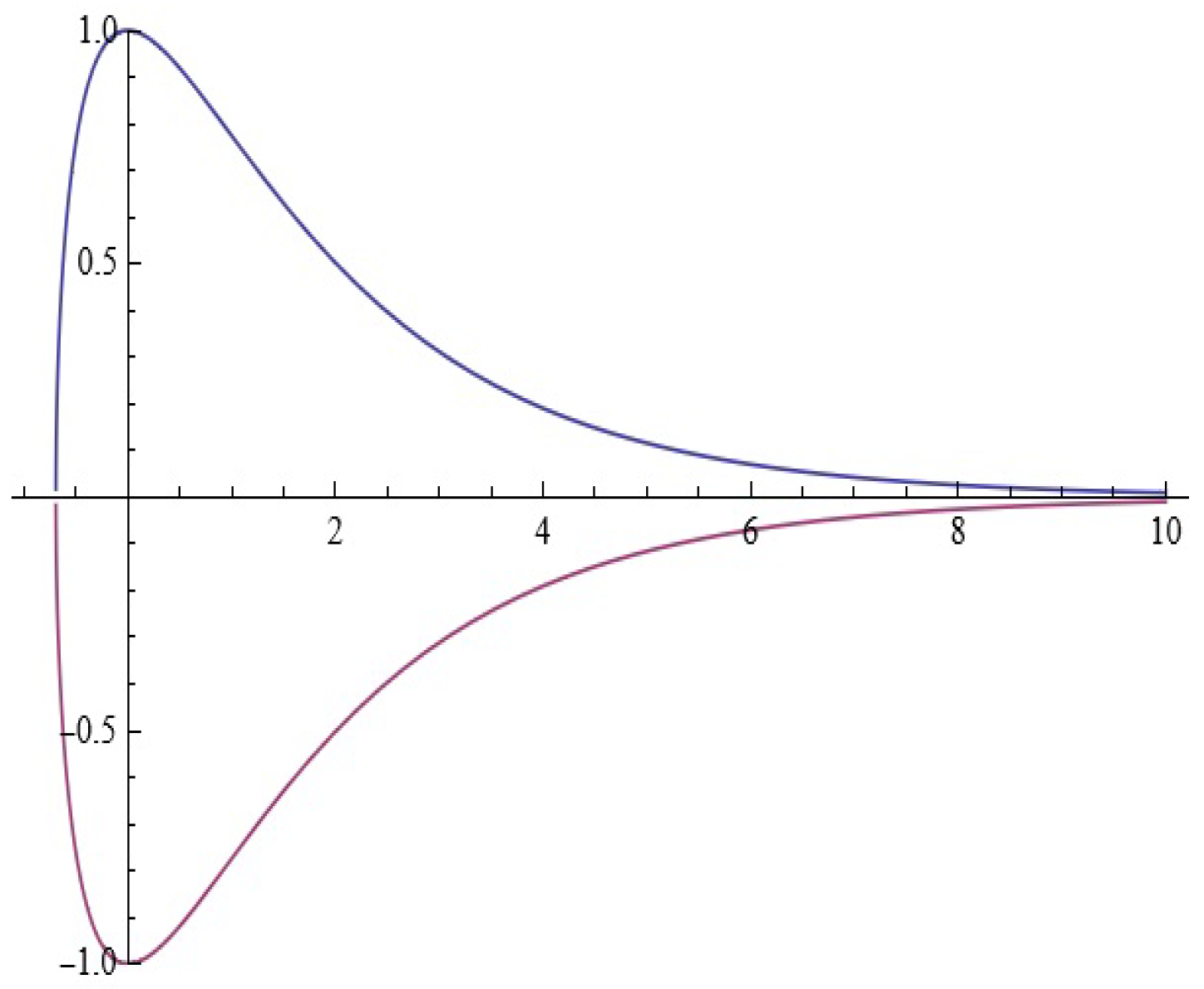
Considerations in Light of Melnikov’s Approach
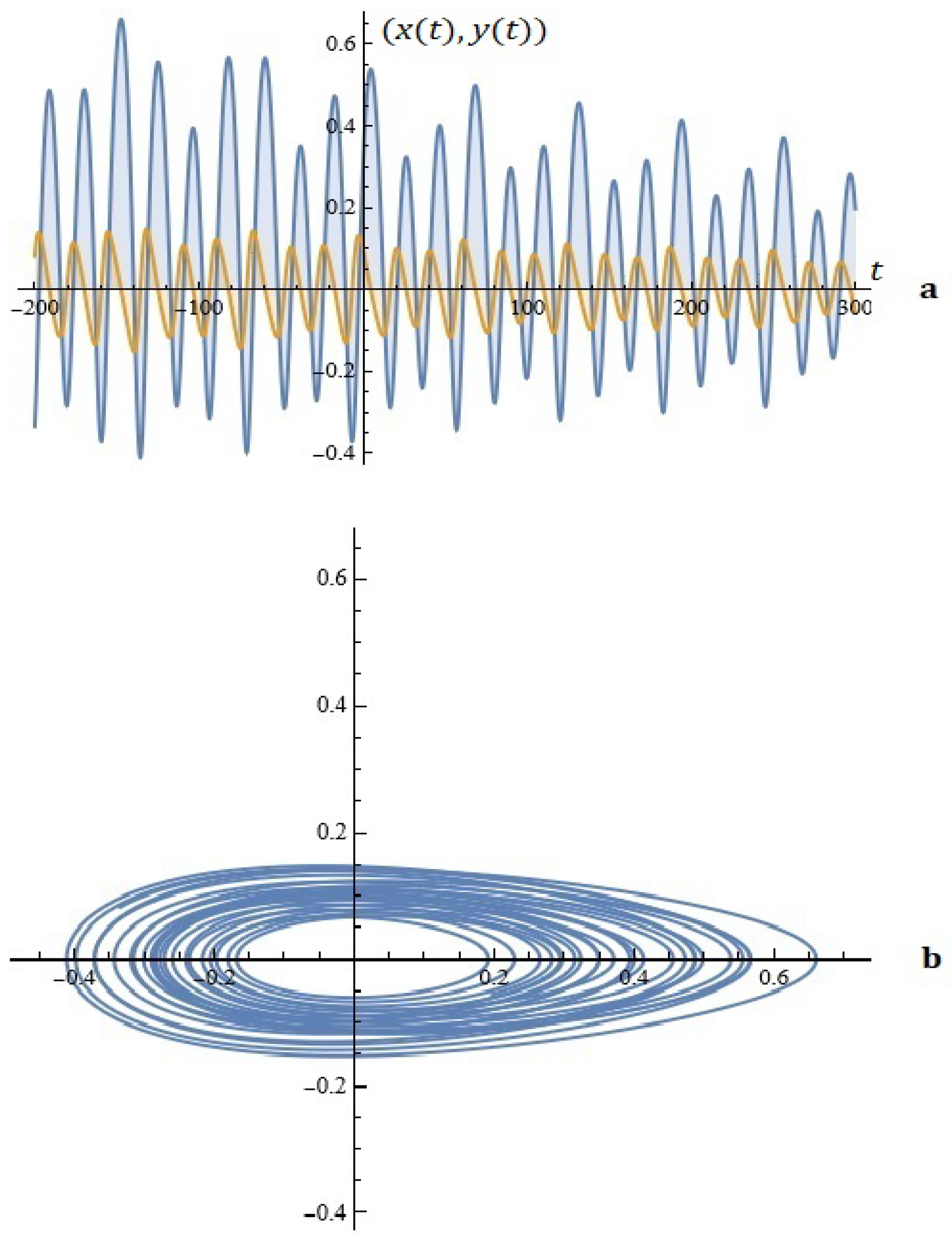
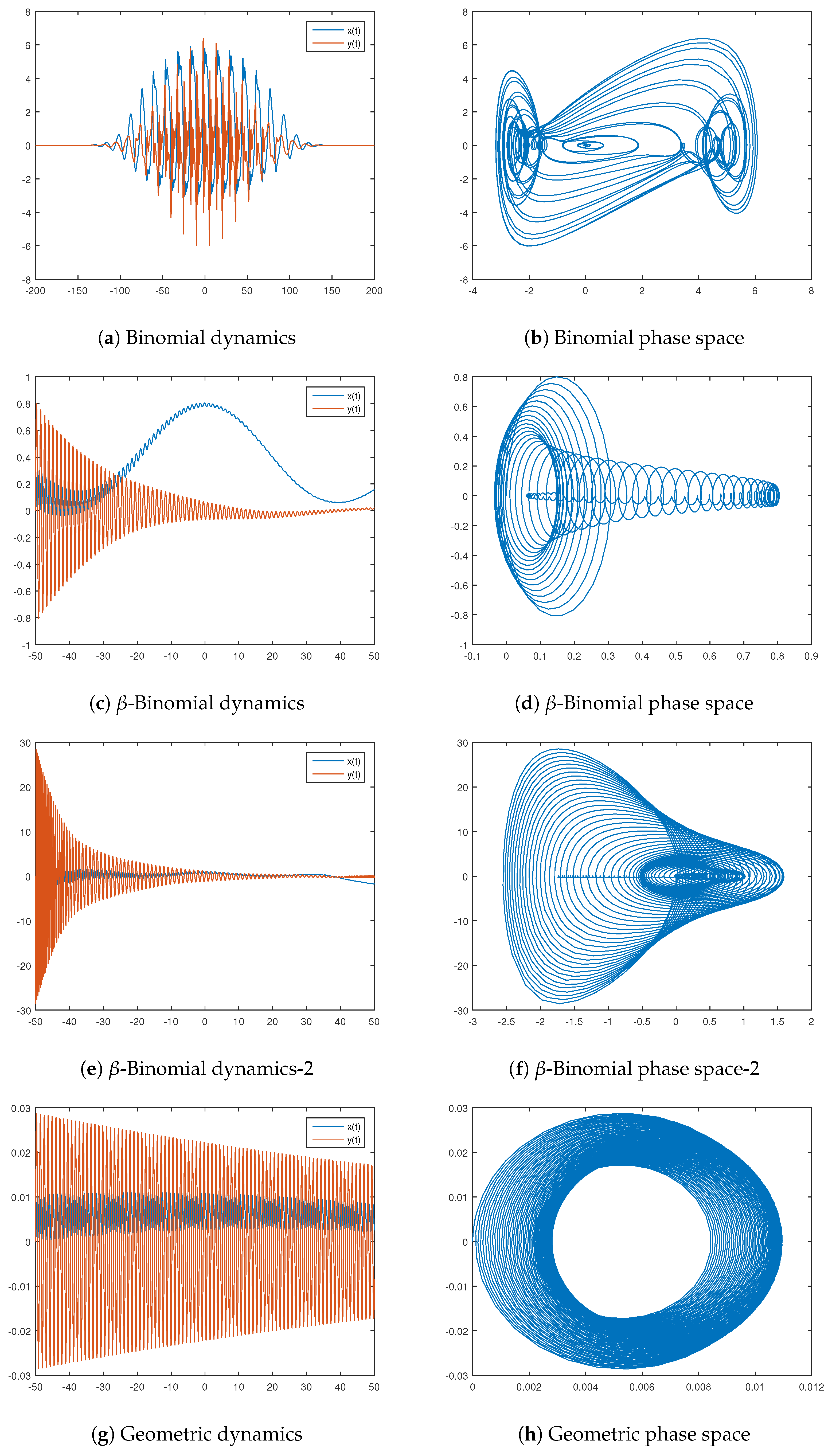
3. Possible Applications
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
- (i)
- We will explicitly note that the compact record (8) is obtained after applying recursive techniques in the calculation of the Melnikov integral and with the help of a module specially written by us for this purpose and implemented in the CAS Mathematical program environment.
- (ii)
- In some cases, it is convenient to use the following notation for the general term of the series:


References
- Krajnak, V.; Wiggins, S. Dynamics of the Morse oscillator: Analytical expressions for trajectories, action–angle variables, and chaos dynamics. arXiv 2019, arXiv:1905.04059V1. [Google Scholar]
- Morse, P. Diatomic molecules according to the wave mechanics. II. Vibrational levels. Phys. Rev. 1929, 34, 57–64. [Google Scholar] [CrossRef]
- Wiggins, S. Introduction to Applied Nonlinear Dynamical Systems and Chaos; Springer: Berlin, Germany, 1990. [Google Scholar]
- Mezic, I.; Wiggnis, S. On the integrability and perturbation of three–dimensional fluid flows with symmetry. J. Nonlinear Sci. 1994, 4, 157–194. [Google Scholar] [CrossRef]
- Goggin, M.; Milonni, P. Driven Morse oscillator: Classical chaos, quantum theory, and photodissociation. Phys. Rev. A 1988, 37, 796–806. [Google Scholar] [CrossRef]
- Bruhn, B. Homoclinic bifurcations in simple parametrically driven systems. Annalen der Physik 1989, 501, 367–375. [Google Scholar] [CrossRef]
- Melnikov, V. On the stability of the center for time periodic perturbations. Trans. Mosc. Math. Soc. 1963, 12, 1–57. [Google Scholar]
- Schecter, S. Persistent unstable equilibria and closed orbits of a singularly perturbed system. J. Differ. Equ. 1985, 60, 131–141. [Google Scholar] [CrossRef]
- McGehee, R. A stable manifold theorem for degenerate fixed point with applications to celestial mechanics. J. Differ. Equ. 1973, 14, 70–88. [Google Scholar] [CrossRef]
- Van Ek, K. The Homoclinic Melnikov Method. Ph.D. Thesis, University of Groningen, Groningen, The Netherlands, 2015. [Google Scholar]
- Golev, A.; Terzieva, T.; Iliev, A.; Rahnev, A.; Kyurkchiev, N. Simulation on a Generalized Oscillator Model: Web-Based Application. Comptes Rendus L’Academie Bulg. Des Sci. 2024, 77, 230–237. [Google Scholar] [CrossRef]
- Vasileva, M.; Kyurkchiev, V.; Iliev, A.; Rahnev, A.; Zaevski, T.; Kyurkchiev, N. Some Investigations and Simulations on the Generalized Rayleigh Systems, Duffing Systems with Periodic Parametric Excitation, Mathieu and Hopf Oscillators; Plovdiv University Press: Plovdiv, Bulgaria, 2024. [Google Scholar]
- Kyurkchiev, N.; Zaevski, T.; Iliev, A.; Kyurkchiev, V.; Rahnev, A. Nonlinear dynamics of a new class of micro-electromechanical oscillators–open problems. Symmetry 2024, 16, 253. [Google Scholar] [CrossRef]
- Kyurkchiev, N.; Zaevski, T.; Iliev, A.; Kyurkchiev, V.; Rahnev, A. Modeling of Some Classes of Extended Oscillators: Simulations, Algorithms, Generating Chaos, Open Problems. Algorithms 2024, 17, 121. [Google Scholar] [CrossRef]
- Xing, Q. Maslov index for heteroclinic orbits of non-Hamiltonian systems on a two-dimensional phase space. Topol. Methods Nonlinear Anal. 2022, 59, 113–130. [Google Scholar]
- Li, X. Limit cycles in a quartic system with a third-order nilpotent singular point. Adv. Differ. Equ. 2018, 2018, 152. [Google Scholar] [CrossRef]
- Li, F.; Liu, Y.; Liu, Y.; Yu, P. Bi-center problem and bifurcation of limit cycles from nilpotent singular points in Z2-equivariant cubic vector fields. J. Differ. Equ. 2018, 265, 4965–4992. [Google Scholar] [CrossRef]
- Kyurkchiev, N.; Andreev, A. Approximation and Antenna and Filters Synthesis. Some Moduli in Programming Environment MATHEMATICA; LAP LAMBERT Academic Publishing: Saarbrucken, Germany, 2014. [Google Scholar]
- Soltis, J. New Gegenbauer–like and Jacobi–like polynomials with applications. J. Frankl. Inst. 1993, 33, 635–639. [Google Scholar] [CrossRef]
- Iliev, A.; Kyurkchiev, N. Nontrivial Methods in Numerical Analysis: Selected Topics in Numerical Analysis; LAP LAMBERT Academic Publishing: Saarbrucken, Germany, 2010. [Google Scholar]
- Sendov, B.; Andreev, A. Approximation and interpolation theory. In Handbook of Numerical Analysis; Ciarlet, P., Lions, J., Eds.; Elsevier Science B. V.: Amsterdam, The Netherlands, 1994; Volume III. [Google Scholar]
- Apostolov, P. General theory, approximation method and design of electrical filters based on Hausdorff polynomials. Mech. Transp. Commun. 2007, 2, 1–8. [Google Scholar]
- Kyurkchiev, N. Some Intrinsic Properties of Tadmor–Tanner Functions: Related Problems and Possible Applications. Mathematics 2020, 8, 1963. [Google Scholar] [CrossRef]
- Akhiezer, N. Theory of Approximation, 2nd ed.; Nauka: Moskow, Russia, 1965. (In Russian) [Google Scholar]
- Kyurkchiev, N. Synthesis of Slot Aerial Grids with Hausdorff Type Directive Patterns. Ph.D. Thesis, Department of Radio-Electronics, VMEI, Sofia, Bulgaria, 1979. (In Bulgarian). [Google Scholar]
- Zhang, Y.; Li, J.; Zhu, S.; Zhao, H. Chaos detection and control of a fractional piecewise-smooth system with nonlinear damping. Chin. J. Phys. 2024, 90, 885–900. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kyurkchiev, N.; Zaevski, T.; Iliev, A.; Branzov, T.; Kyurkchiev, V.; Rahnev, A. Dynamics of Some Perturbed Morse-Type Oscillators: Simulations and Applications. Mathematics 2024, 12, 3368. https://doi.org/10.3390/math12213368
Kyurkchiev N, Zaevski T, Iliev A, Branzov T, Kyurkchiev V, Rahnev A. Dynamics of Some Perturbed Morse-Type Oscillators: Simulations and Applications. Mathematics. 2024; 12(21):3368. https://doi.org/10.3390/math12213368
Chicago/Turabian StyleKyurkchiev, Nikolay, Tsvetelin Zaevski, Anton Iliev, Todor Branzov, Vesselin Kyurkchiev, and Asen Rahnev. 2024. "Dynamics of Some Perturbed Morse-Type Oscillators: Simulations and Applications" Mathematics 12, no. 21: 3368. https://doi.org/10.3390/math12213368
APA StyleKyurkchiev, N., Zaevski, T., Iliev, A., Branzov, T., Kyurkchiev, V., & Rahnev, A. (2024). Dynamics of Some Perturbed Morse-Type Oscillators: Simulations and Applications. Mathematics, 12(21), 3368. https://doi.org/10.3390/math12213368







