Fracture Characteristics and Tensile Strength Prediction of Rock–Concrete Composite Discs Under Radial Compression
Abstract
:1. Introduction
2. Specimens and Equipment
2.1. Specimens Productions
2.2. Test Scheme of the Specimens
3. Results and Analysis
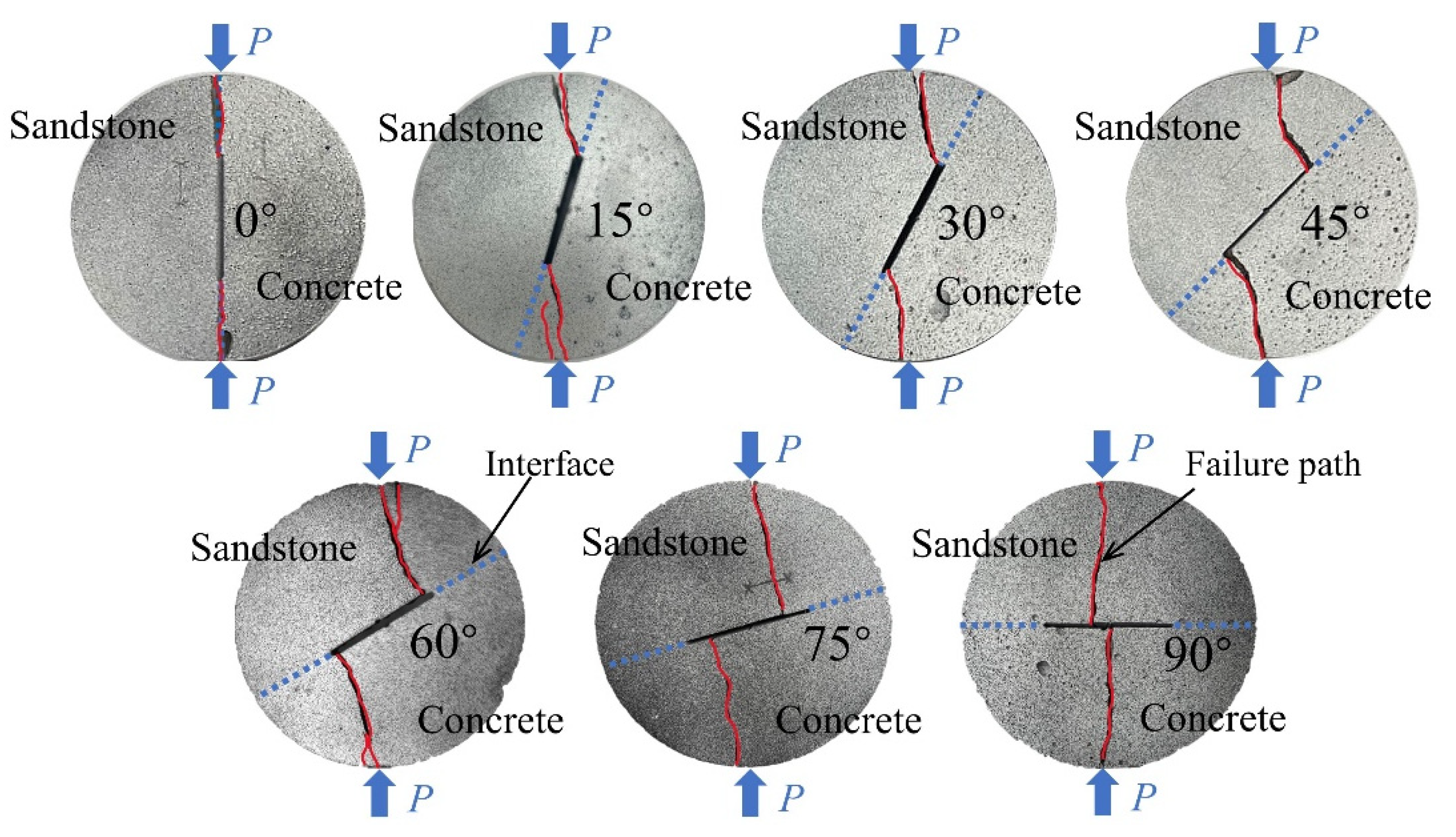
3.1. Analysis of Failure Paths
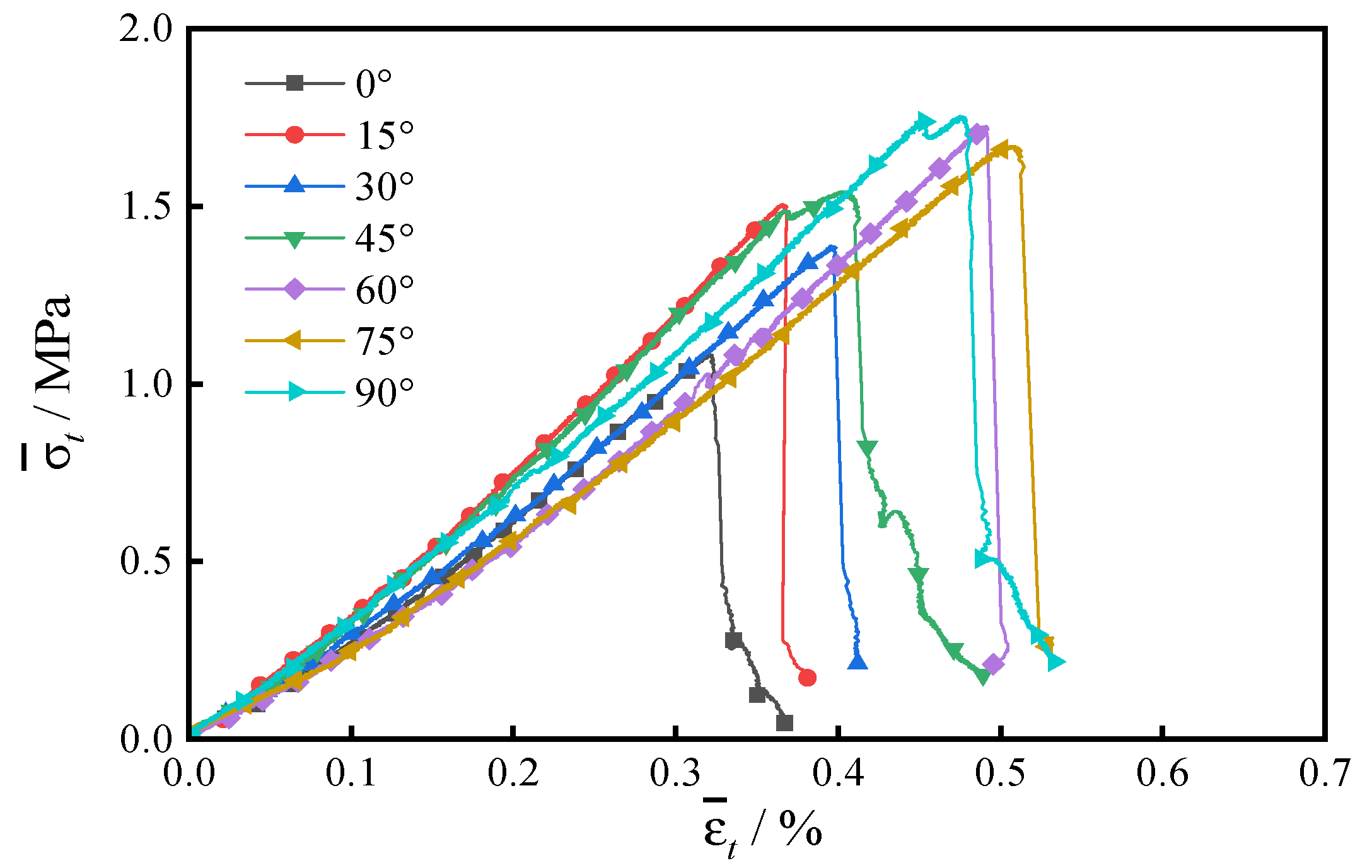
3.2. Analysis of Stress–Strain Curves
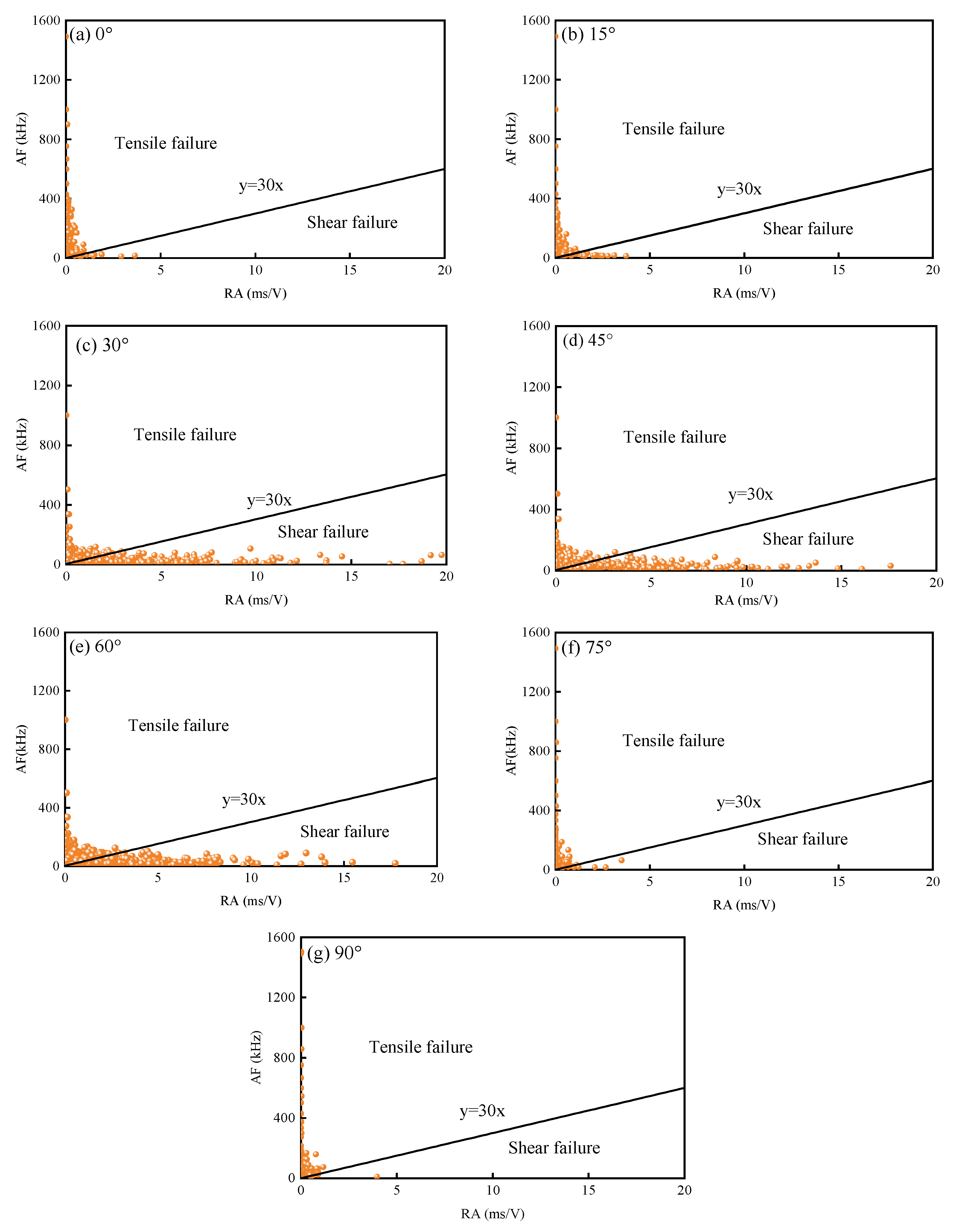
3.3. Analysis of AE Features
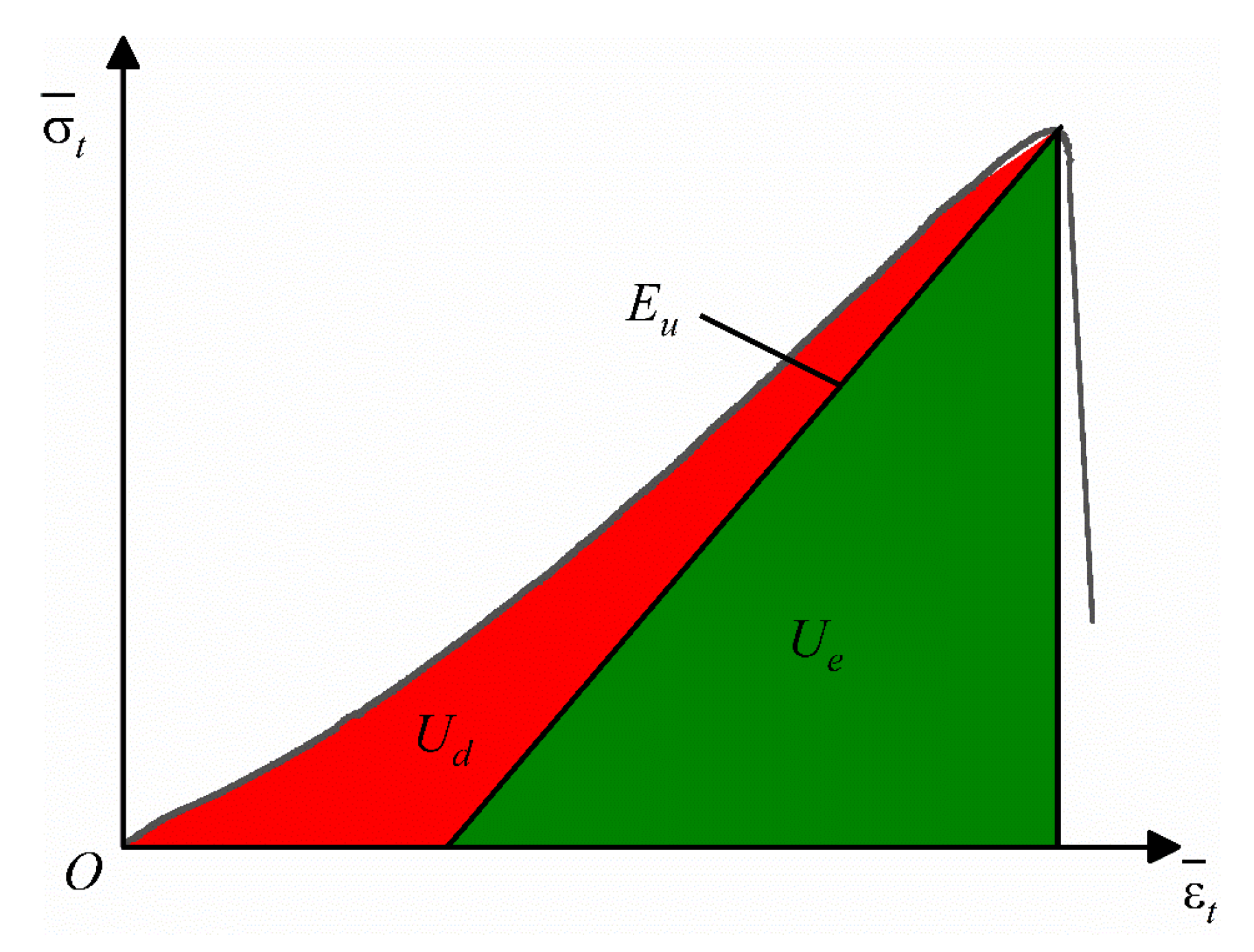
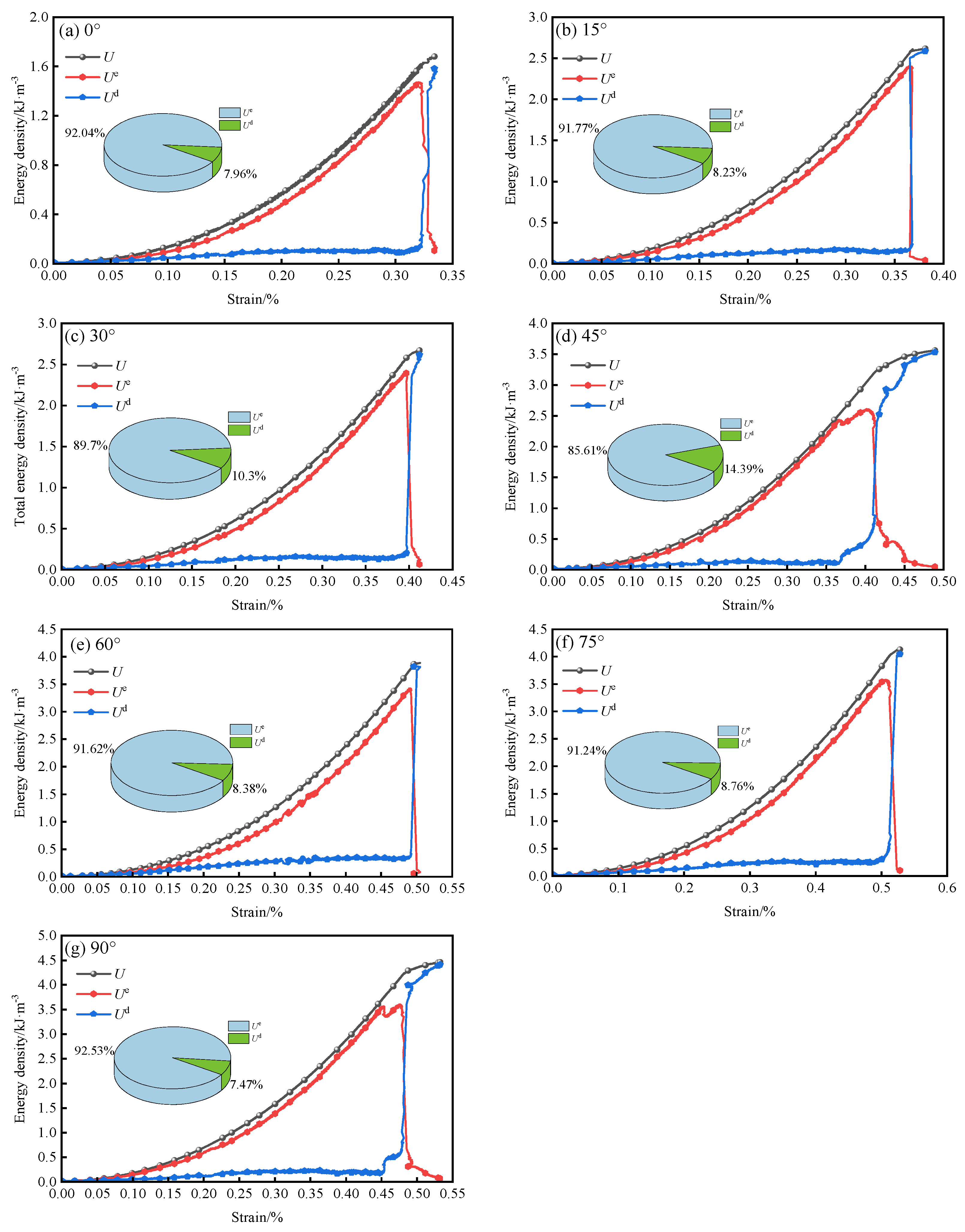
3.4. Analysis of Energy Dissipation
4. Analysis and Discussion of Tensile Strength Prediction Model
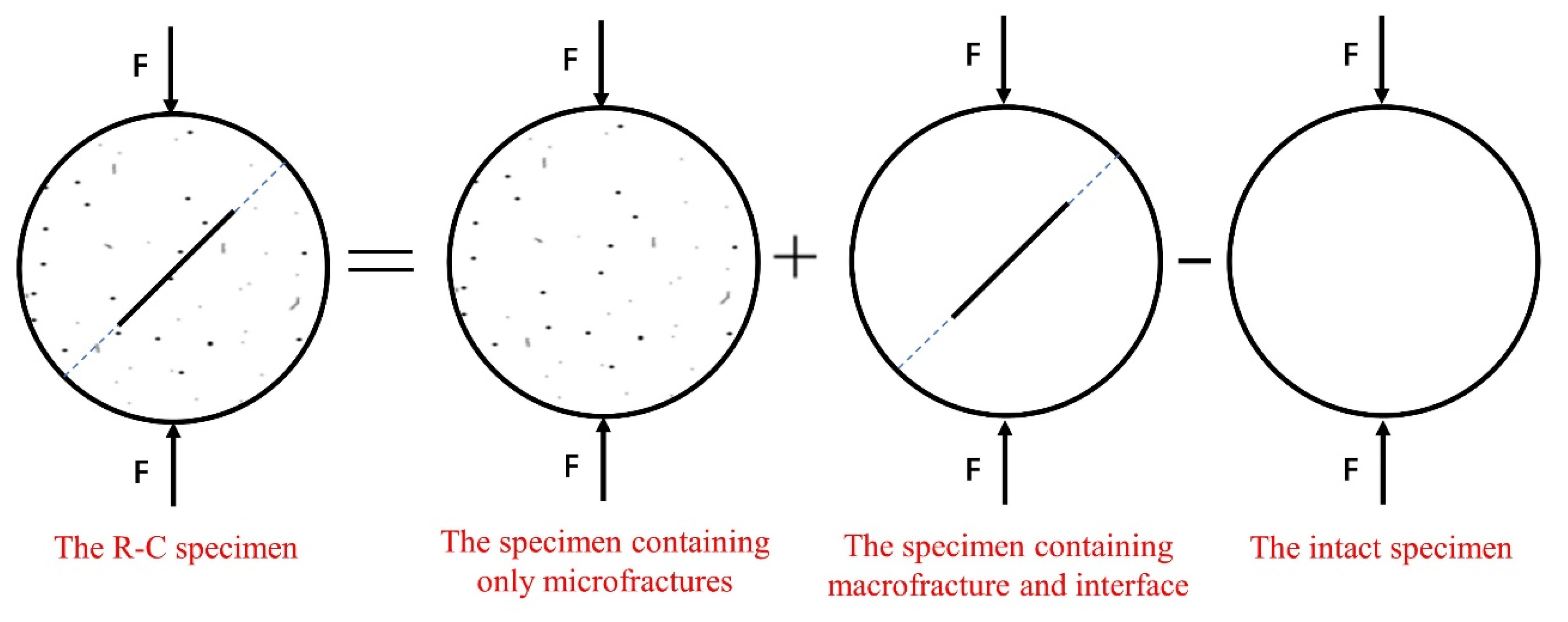
4.1. Damage Caused by Microscopic Cracks
4.2. Damage Caused by Macroscopic Fractures
4.3. Total Damage Caused by Coupling of Micro- and Macrofractures
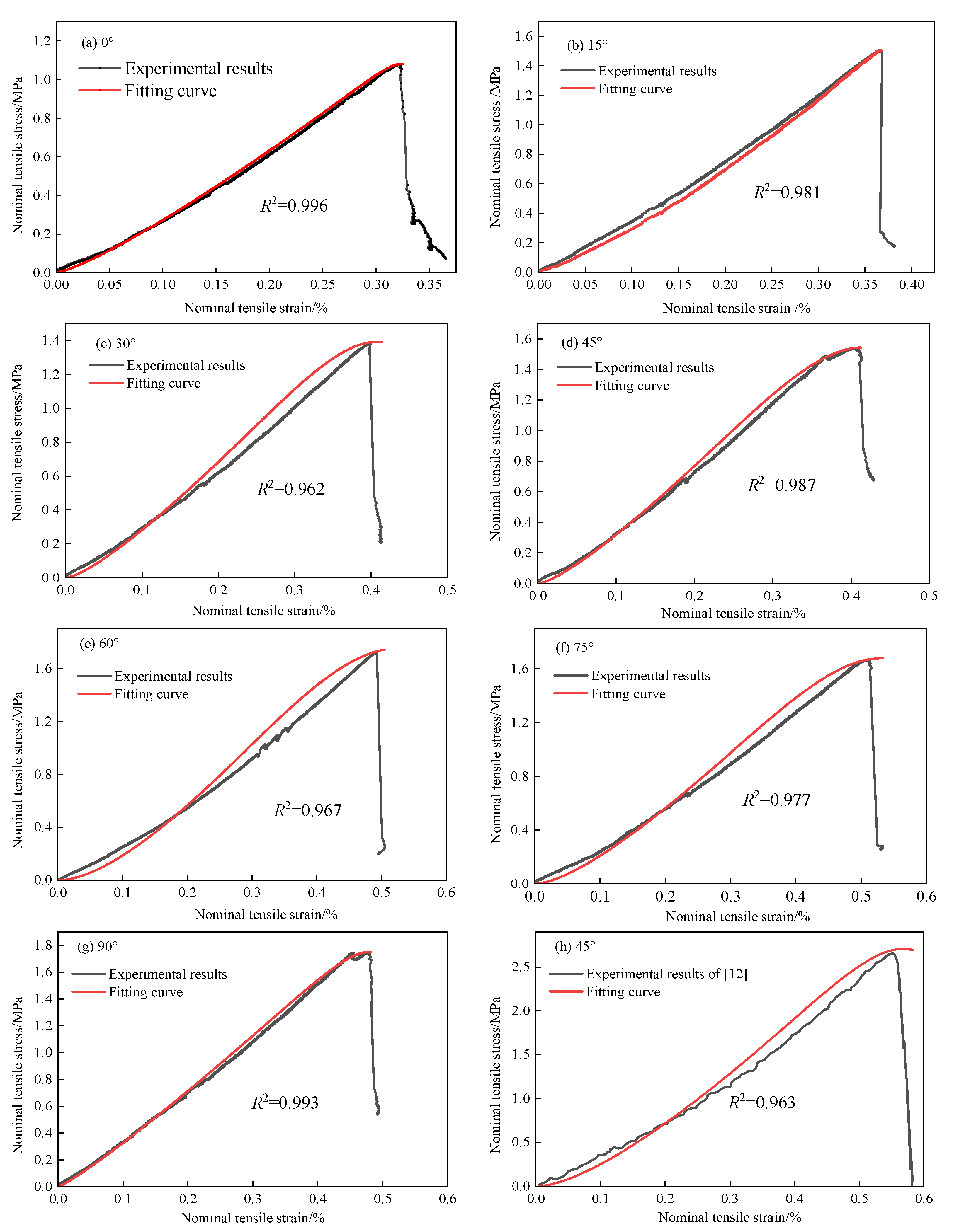
4.4. Validation of the Tensile Strength Prediction Model
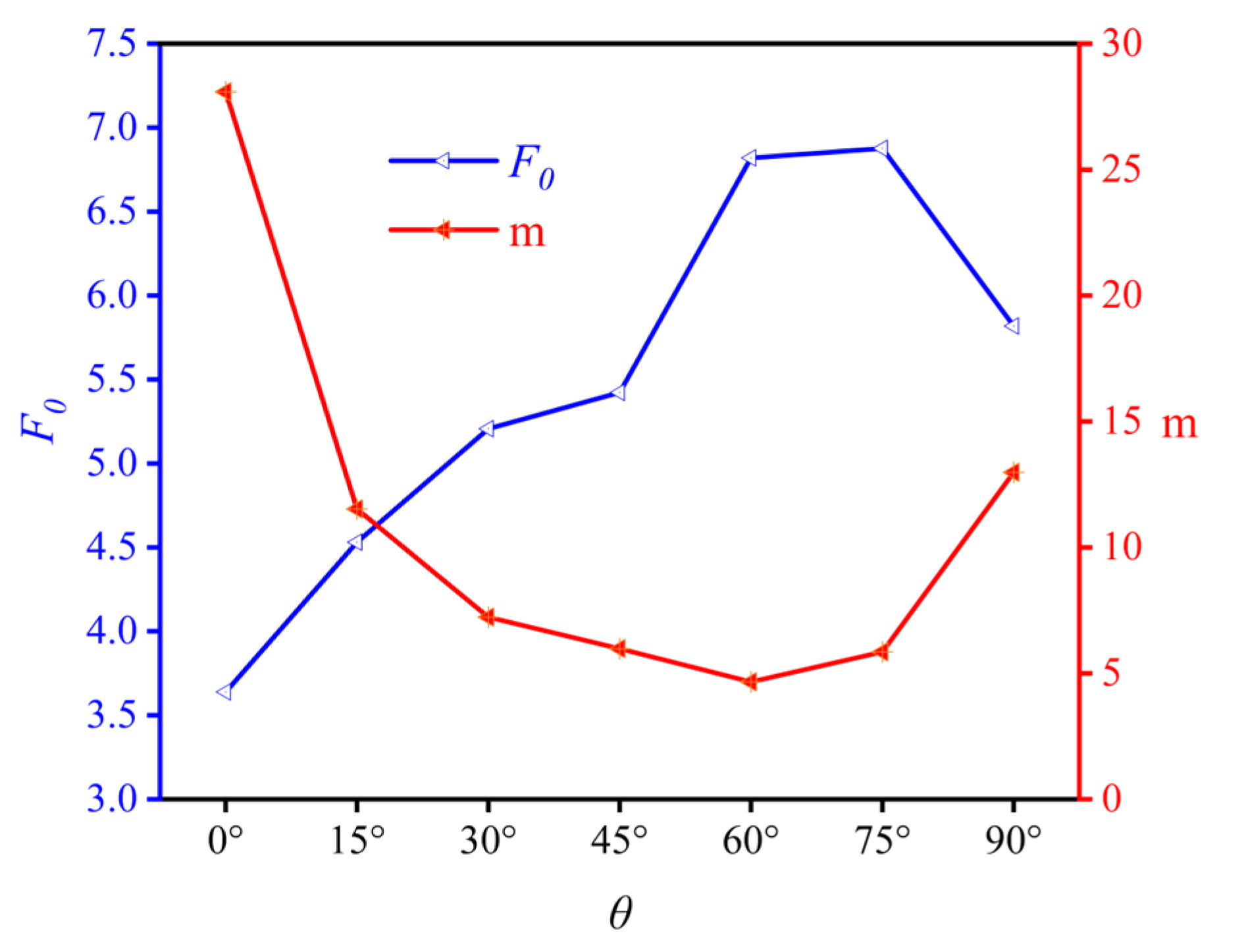
4.5. Analysis of m and F0
5. Conclusions
- (1)
- The failure paths of R–C specimens are significantly influenced by interface crack angles (θ). At θ = 0°, the failure surface is parallel to the prefabricated crack. As θ increases to 15°, 30°, and 45°, cracks initiate from the tips of the prefabricated crack, expanding in a wing shape. For θ values of 60°, 75°, and 90°, cracks originate closer to the center. Moreover, RA/AF shows that fracture modes are tensile at θ = 0° and 90°, while tensile–shear fractures occur at θ = 15°, 30°, 45°, 60°, and 75°.
- (2)
- The mechanical properties of R–C specimens showed significant degradation with increasing inclination angle, with the most pronounced degradation observed at θ = 0°, where the tensile strength measured 1.06 MPa, compared to the highest tensile strength of 1.67 MPa at θ = 90°.
- (3)
- Both the total energy and elastic strain energy of the specimens increased with the angle of the prefabricated cracks, indicating an enhanced ability to store energy. Furthermore, the percentage of energy dissipation first increases and then decreases with increasing θ, reaching a maximum value of 14.39% at θ = 45°.
- (4)
- A tensile strength prediction model for R–C specimens was developed by combining the damage and fracture theories. With all correlation coefficients R2 > 0.95, the model aligns closely with experimental results, effectively predicting the mechanical behavior of prefabricated cracked R–C specimens. This model serves as a valuable tool for understanding tensile strength and optimizing the design of R–C structures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chang, X.; Lu, J.Y.; Wang, S.Y.; Wang, S.R. Mechanical performances of rock-concrete bi-material disks under diametrical compression. Int. J. Rock. Mech. Min. 2018, 104, 71–77. [Google Scholar] [CrossRef]
- Lei, R.D.; Zhang, Z.Y.; Berto, F.; Ranjith, P.G.; Zhang, C.P. Strain localization and cracking behavior of sandstone with two gypsum-infilled parallel flaws. Theor. Appl. Fract. Mech. 2021, 112, 102873. [Google Scholar] [CrossRef]
- Ríos-Bayona, F.; Johansson, F.; Mas-Ivars, D. Prediction of Peak Shear Strength of Natural, Unfilled Rock Joints Accounting for Matedness Based on Measured Aperture. Rock. Mech. Rock. Eng. 2021, 54, 1533–1550. [Google Scholar] [CrossRef]
- Tang, W.Y.; Lin, H.; Chen, Y.F.; Feng, J.J.; Hu, H.H. Mechanical Characteristics and Acoustic Emission Characteristics of Mortar-Rock Binary Medium. Buildings 2022, 12, 665. [Google Scholar] [CrossRef]
- Guo, T.F.; Liu, K.W.; Li, X.; Jin, P.; Yang, J.C.; Zhang, A.M.; Zou, L.S. Effect of crack angle and concrete strength on the dynamic fracture behavior of rock-based layered material containing a pre-existing crack. Arch. Civ. Mech. Eng. 2023, 23, 198. [Google Scholar] [CrossRef]
- Song, X.P.; Hao, Y.X.; Wang, S.; Zhang, L.; Liu, W.; Li, J.B. Mechanical properties, crack evolution and damage characteristics of prefabricated fractured cemented paste backfill under uniaxial compression. Constr. Build. Mater. 2022, 330, 127251. [Google Scholar] [CrossRef]
- Chen, Y.; Li, M.; Zhou, L.; Deng, L.; Wang, J. Effects of Different Loading Angles on Brazilian Splitting Characteristics of Rock-Concrete Interface. Geotech. Geol. Eng. 2024, 42, 4285–4301. [Google Scholar] [CrossRef]
- Chen, J.; Zhou, L.; Zhu, Z.; Shui, X.; Ma, L.; Wang, M. Interface Stress Analysis and Failure Mechanism of Rock–Concrete Composite Structures Under Multi-directional Stress Waves. Rock. Mech. Rock. Eng. 2024, 57, 9651–9668. [Google Scholar] [CrossRef]
- Shams, G.; Rivard, P.; Moradian, O. Tensile strength and failure behavior of rock-mortar interfaces: Direct and indirect measurements. J. Rock. Mech. Geotech. Eng. 2023, 16, 41–55. [Google Scholar] [CrossRef]
- Yu, L.Y.; Wu, D.Y.; Su, H.J.; Li, S.C.; Liu, R.C.; Geng, S.T. Influences of Interface Roughness and Loading Direction on Tensile Behavior of Rock-Concrete Bimaterials Under Brazilian Test Conditions. Rock. Mech. Rock. Eng. 2023, 56, 5861–5883. [Google Scholar] [CrossRef]
- Selçuk, L.; Aşma, D. Experimental investigation of the Rock–Concrete bi materials influence of inclined interface on strength and failure behavior. Int. J. Rock. Mech. Min. 2019, 123, 104119. [Google Scholar] [CrossRef]
- Pan, X.; Huang, J.Z.; Gan, Z.Q.; Hua, W.; Dong, S.M. Investigation on mixed-mode II-III fracture of the sandstone by using eccentric cracked disk. Theor. Appl. Fract. Mech. 2021, 115, 103077. [Google Scholar] [CrossRef]
- Tian, Y.; Zhao, X.Y.; Tai, Y.T.; Chen, Y.Z.; Zhou, J.K. Crack extension at the concrete-rock interface damaged by high-pressure water environment: DIC research. Theor. Appl. Fract. Mech. 2023, 126, 103966. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, D.; Li, X.; Han, Z.; Ma, J. Mixed mode fracture parameters and fracture characteristics of diorite using cracked straight through Brazilian disc specimen. Theor. Appl. Fract. Mech. 2023, 123, 103682. [Google Scholar] [CrossRef]
- Chang, X.; Guo, T.F.; Zhang, S. Cracking behaviours of layered specimen with an interface crack in Brazilian tests. Eng. Fract. Mech. 2020, 228, 106904. [Google Scholar] [CrossRef]
- Aranda, M.T.; Garcia, I.G.; Reinoso, J.; Mantic, V. Experimental evaluation of the similarity in the interface fracture energy between PMMA/epoxy/PMMA and PMMA/epoxy joints. Eng. Fract. Mech. 2022, 259, 108076. [Google Scholar] [CrossRef]
- Aliabadian, Z.; Sharafisafa, M.; Tahmasebinia, F.; Shen, L.M. Experimental and numerical investigations on crack development in 3D printed rock-like specimens with pre-existing flaws. Eng. Fract. Mech. 2021, 241, 107396. [Google Scholar] [CrossRef]
- Yu, S.; Yu, J.; Sun, Z.; Zhu, C.; Yang, J. Numerical investigation and experimental study on fracture processes of central flawed sandstone Brazilian discs. Int. J. Solids Struct. 2023, 262–263, 112054. [Google Scholar] [CrossRef]
- Aboayanah, K.R.; Popoola, A.K.; Abdelaziz, A.; Sun, L.; Ossetchkina, E.; Peterson, K.; Grasselli, G. Effect of pre-existing cracks on thermal cracking of granitic rocks under confinement. Geomech. Geophys. Geo 2022, 8, 126. [Google Scholar] [CrossRef]
- Hu, H.R.; Lu, Y.Y.; Xia, B.W.; Luo, Y.F.; Peng, J.J.; Li, Y. Damage characteristics of sandstone with different crack angles subjected to true triaxial cyclic loading and unloading. Theor. Appl. Fract. Mech. 2022, 121, 103444. [Google Scholar] [CrossRef]
- Zhong, J.C.; Wang, J.; Li, X.Y.; Chu, X.H. Macro- and meso- failure mechanism analysis for shale-like brittle materials under uniaxial compression. Eng. Anal. Bound. Elem. 2022, 141, 189–198. [Google Scholar] [CrossRef]
- Fu, M.; Zhao, G.F. A micro-macro constitutive model for compressive failure of rock by using 4D lattice spring model. Int. J. Rock. Mech. Min. 2022, 160, 105261. [Google Scholar] [CrossRef]
- Liu, X.S.; Tan, Y.L.; Ning, J.G.; Lu, Y.W.; Gu, Q.H. Mechanical properties and damage constitutive model of coal in coal-rock combined body. Int. J. Rock. Mech. Min. 2018, 110, 140–150. [Google Scholar] [CrossRef]
- Ren, C.H.; Yu, J.; Zhang, C.; Liu, X.Y.; Zhu, Y.L.; Yao, W. Micro-macro approach of anisotropic damage: A semi-analytical constitutive model of porous cracked rock. Eng. Fract. Mech. 2023, 290, 109483. [Google Scholar] [CrossRef]
- Tian, Y.K.; Weijermars, R.; Zhou, F.J.; Hu, L.Q.; Liu, T.Y.; Liu, H.T. Advances in stress-strain constitutive models for rock failure: Review and new dynamic constitutive failure (DCF) model using core data from the Tarim Basin (China). Earth-Sci. Rev. 2023, 243, 104473. [Google Scholar] [CrossRef]
- Kawamoto, T.; Ichikawa, Y.; Kyoya, T. Deformation and fracturing behaviour of discontinuous rock mass and damage mechanics theory. Int. J. Numer. Anal. Methods Geomech. 2005, 12, 1–30. [Google Scholar] [CrossRef]
- Chen, S.; Qiao, C.S. Composite damage constitutive model of jointed rock mass considering crack propagation length and joint friction effect. Arab. J. Geosci. 2018, 11, 283. [Google Scholar] [CrossRef]
- Pan, J.L.; Cai, M.F.; Li, P.; Guo, Q.F. A damage constitutive model of rock-like materials containing a single crack under the action of chemical corrosion and uniaxial compression. J. Cent. South. Univ. 2022, 29, 486–498. [Google Scholar] [CrossRef]
- Xia, B.W.; Li, Y.; Hu, H.R.; Luo, Y.F.; Peng, J.J. Effect of Crack Angle on Mechanical Behaviors and Damage Evolution Characteristics of Sandstone Under Uniaxial Compression. Rock. Mech. Rock. Eng. 2022, 55, 6567–6582. [Google Scholar] [CrossRef]
- Wang, C.S.; Liu, J.F.; Zhao, Y.W.; Han, S.J. Mechanical properties and fracture evolution process of Beishan granite under tensile state. B Eng. Geol. Env. Environ. 2022, 81, 274. [Google Scholar] [CrossRef]
- Pan, P.Z.; Feng, X.T.; Zhou, H. Research on the Failure Process of Rocks under Tensile Loading Using Elasto-Plastic CA Model. Key Eng. Mater. 2007, 340–341, 1145–1150. [Google Scholar] [CrossRef]
- Keawsawasvong, S.; Ukritchon, B. Undrained stability of an active planar trapdoor in non-homogeneous clays with a linear increase of strength with depth. Comput. Geotech. 2017, 81, 284–293. [Google Scholar] [CrossRef]
- Liao, Z.Y.; Zhu, J.B.; Tang, B.C.A. Numerical investigation of rock tensile strength determined by direct tension, Brazilian and three-point bending tests. Int. J. Rock. Mech. Min. 2019, 115, 21–32. [Google Scholar] [CrossRef]
- Zhu, J.; Deng, J.H.; Chen, F.; Wang, F. Failure analysis of water-bearing rock under direct tension using acoustic emission. Eng. Geol. 2022, 299, 106541. [Google Scholar] [CrossRef]
- Yuan, R.; Shi, B. Acoustic emission activity in directly tensile test on marble specimens and its tensile damage constitutive model. Int. J. Coal Sci. Technol. 2018, 5, 295–304. [Google Scholar] [CrossRef]
- Liu, D.Q. A Constitutive Model of Rocks under Uniaxial Tension. Adv. Mat. Res. 2014, 908, 103–106. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, M.; Jiang, Y.; Wang, Z. Mechanics, damage and energy degradation of rock-concrete interfaces exposed to high temperature during cyclic shear. Constr. Build. Mater. 2023, 405, 133229. [Google Scholar] [CrossRef]
- Guo, T.; Liu, K.; Li, X.; Wu, Y.; Yang, J. Effects of thermal treatment on the fracture behavior of rock-concrete bi-material specimens containing an interface crack. Theor. Appl. Fract. Mec. 2023, 127, 104071. [Google Scholar] [CrossRef]
- Guo, T.; Zhang, Q.; Liu, K.; Chang, X.; Zou, L. Co-effects of parallel flaws and interface characteristics on the fracture behavior of rock-concrete composite specimens. J. Build. Eng. 2024, 97, 110920. [Google Scholar] [CrossRef]
- Xie, Q.; Chen, D.L.; Liu, X.L.; Zeng, Y. Research on the effect of loading rate on the fracture characteristics of granite using cracked straight through Brazilian disc specimens. Theor. Appl. Fract. Mech. 2022, 122, 103581. [Google Scholar] [CrossRef]
- Liu, P.; Guo, C.; Cui, S.; Xia, W.; Wang, X.; Chen, X. Experimental study on crack propagation process of rock-concrete interface in hot-dry curing environment at different temperatures. Struct. Concr. 2023, 24, 5506–5521. [Google Scholar] [CrossRef]
- Wang, Q.Z.; Jia, X.M.; Kou, S.Q.; Zhang, Z.X.; Lindqvist, P.A. The flattened Brazilian disc specimen used for testing elastic modulus, tensile strength and fracture toughness of brittle rocks: Analytical and numerical results. Int. J. Rock. Mech. Min. 2004, 41, 245–253. [Google Scholar] [CrossRef]
- Qiu, H.; Zhu, Z.M.; Wang, M.; Wang, F.; Luo, C.S.; Wan, D.Y. Study of the failure properties and tensile strength of rock-mortar interface transition zone using bi-material Brazilian discs. Constr. Build. Mater. 2020, 236, 117551. [Google Scholar] [CrossRef]
- Teng, S.Y.; Yang, S.Q.; Huang, Y.H.; Tian, W.L. Experimental study of influence of crack filling on mechanical properties of Brazilian discs. Rock. Soil. Mech. 2018, 39, 4493–4507 and 4516. [Google Scholar] [CrossRef]
- Zhao, Y.; Deng, X.; Bi, J.; Shen, M.; Wang, C.; Zhang, Y.; Li, Y.; Ning, L. Study on the mixed fracture characteristics of concrete-rock Brazilian disks with different fracture angles. Theor. Appl. Fract. Mec. 2024, 133, 104614. [Google Scholar] [CrossRef]
- Chang, X.; Zhang, X.; Dang, F.N.; Zhang, B.F.; Chang, F.Q. Failure Behavior of Sandstone Specimens Containing a Single Flaw Under True Triaxial Compression. Rock. Mech. Rock. Eng. 2022, 55, 2111–2127. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.T.; Shi, Z.M.; Chen, J.C. Fatigue damage and fracture evolution characteristics of sandstone under multistage intermittent cyclic loading. Theor. Appl. Fract. Mech. 2022, 119, 103375. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, W.K.; Wang, H.J.; Li, C.H.; Hou, Z.Q. Rock bridge fracturing characteristics in granite induced by freeze-thaw and uniaxial deformation revealed by AE monitoring and post-test CT scanning. Cold Reg. Sci. Technol. 2020, 177, 103115. [Google Scholar] [CrossRef]
- Du, K.; Li, X.F.; Tao, M.; Wang, S.F. Experimental study on acoustic emission (AE) characteristics and crack classification during rock fracture in several basic lab tests. Int. J. Rock. Mech. Min. 2020, 133, 104411. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Deng, J.H. A new method for determining the crack classification criterion in acoustic emission parameter analysis. Int. J. Rock. Mech. Min. 2020, 130, 104323. [Google Scholar] [CrossRef]
- Meng, Y.Y.; Jing, H.W.; Liu, X.W.; Yin, Q.; Wei, X.C. Experimental and numerical investigation on the effects of bedding plane properties on the mechanical and acoustic emission characteristics of sandy mudstone. Eng. Fract. Mech. 2021, 245, 107582. [Google Scholar] [CrossRef]
- Wu, W.X.; Gong, F.Q. Investigation on Energy Evolution and Storage Characteristic of CSTBD Red Sandstone during Mixed-Mode Fracture. Geofluids 2022, 2022, 9822469. [Google Scholar] [CrossRef]
- Peng, K.; Wang, Y.Q.; Zou, Q.L.; Liu, Z.P.; Mou, J.H. Effect of crack angles on energy characteristics of sandstones under a complex stress path. Eng. Fract. Mech. 2019, 218, 106577. [Google Scholar] [CrossRef]
- Xie, H.; Li, L.; Peng, R.; Ju, Y. Energy analysis and criteria for structural failure of rocks. J. Rock. Mech. Geotech. Eng. 2009, 1, 11–20. [Google Scholar] [CrossRef]
- Liu, X.X.; Li, Y.; Wang, W.W. Study on mechanical properties and energy characteristics of carbonaceous shale with different fissure angles under dry-wet cycles. B Eng. Geol. Environ. 2022, 81, 319. [Google Scholar] [CrossRef]
- Zhao, Y.X.; Liu, B. Deformation Field and Acoustic Emission Characteristics of Weakly Cemented Rock under Brazilian Splitting Test. Nat. Resour. Res. 2021, 30, 1925–1939. [Google Scholar] [CrossRef]
- Zheng, Z.; Su, H.; Wang, W.; Wang, Z.; Liu, Z.; He, B.; Mei, G. A new hydro-mechanical coupling constitutive model for brittle rocks considering initial compaction, hardening and softening behaviors under complex stress states. Geomech. Geophys. Geo 2023, 9, 68. [Google Scholar] [CrossRef]
- Wang, R.Q.; Wang, G.L.; Zhang, L.; Sun, F.; Cao, T.C.; Li, B.Y.; Xu, H. Coupled macro-meso damage constitutive model for fractured rocks based on logistic growth theory. Eng. Fract. Mech. 2023, 281, 109132. [Google Scholar] [CrossRef]
- Atkinson, C.; Smelser, R.E.; Sanchez, J. Combined mode fracture via the cracked Brazilian disk test. Int. J. Fract. 1982, 18, 279–291. [Google Scholar] [CrossRef]
- Rice, J.R. Elastic Fracture Mechanics Concepts for Interfacial Cracks. J. Appl. Mech. 1988, 55, 98–103. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Aliha, M.R.M. On the use of Brazilian disc specimen for calculating mixed mode I-II fracture toughness of rock materials. Eng. Fract. Mech. 2008, 75, 4631–4641. [Google Scholar] [CrossRef]
- Liu, K.; Guo, T.; Yang, J.; Ma, S. Static and dynamic fracture behavior of rock-concrete bi-material disc with different interface crack inclinations. Theor. Appl. Fract. Mech. 2023, 123, 103659. [Google Scholar] [CrossRef]
- Pan, J.; Zhang, Y.; Li, P.; Wu, X.; Xi, X. Mechanical properties and thermo-chemical damage constitutive model of granite subjected to thermal and chemical treatments under uniaxial compression. Constr. Build. Mater. 2023, 390, 131755. [Google Scholar] [CrossRef]
- Liu, X.S.; Ning, J.G.; Tan, Y.L.; Gu, Q.H. Damage constitutive model based on energy dissipation for intact rock subjected to cyclic loading. Int. J. Rock. Mech. Min. 2016, 85, 27–32. [Google Scholar] [CrossRef]
- Zhou, Z.L.; Lu, J.Y.; Cai, X.; Rui, Y.C.; Tan, L.H. Water saturation effects on mechanical performances and failure characteristics of rock-concrete disc with different interface dip angles. Constr. Build. Mater. 2022, 324, 126684. [Google Scholar] [CrossRef]
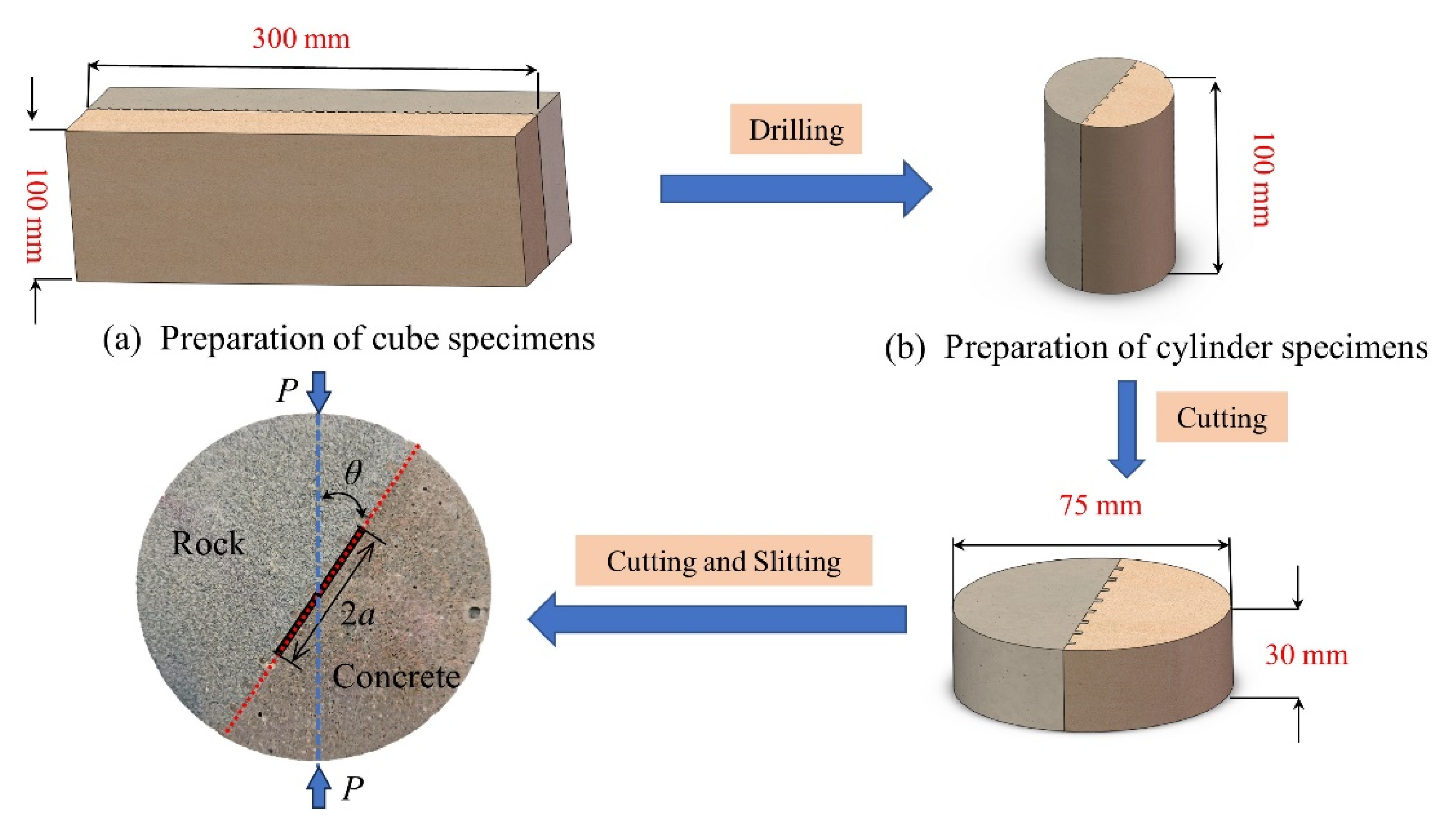

| Category | Density | Elastic Modulus | Poisson Ratio | Compressive Strength | Tensile Strength |
|---|---|---|---|---|---|
| (kg/m3) | (GPa) | (MPa) | (MPa) | ||
| Sandstone | 2512.36 | 15.21 | 0.30 | 68.58 | 2.68 |
| Concrete | 2182.36 | 14.38 | 0.23 | 58.80 | 2.37 |
| θ | U/(kJ·m−3) | Ue/(kJ·m−3) | Ud/(kJ·m−3) |
|---|---|---|---|
| 0° | 1.60519 | 1.477354 | 0.127836 |
| 15° | 2.56493 | 2.353809 | 0.211121 |
| 30° | 2.54967 | 2.287176 | 0.262494 |
| 45° | 3.03097 | 2.594757 | 0.436213 |
| 60° | 3.73759 | 3.424471 | 0.313119 |
| 75° | 3.92056 | 3.577173 | 0.343387 |
| 90° | 4.14497 | 3.835165 | 0.309805 |
| θ | Et/MPa | /MPa | /% | Poisson’s Ratio | YI | YII |
|---|---|---|---|---|---|---|
| 0° | 396.21 | 1.08 | 0.32 | 0.19 | 1.245 | 0.006 |
| 15° | 469.15 | 1.50 | 0.37 | 0.21 | 0.721 | 1.387 |
| 30° | 402.72 | 1.39 | 0.39 | 0.21 | −0.385 | 2.079 |
| 45° | 463.96 | 1.54 | 0.40 | 0.21 | −1.497 | 2.065 |
| 60° | 432.59 | 1.73 | 0.49 | 0.23 | −2.350 | 1.603 |
| 75° | 418.75 | 1.67 | 0.51 | 0.24 | −2.885 | 0.897 |
| 90° | 424.61 | 1.75 | 0.48 | 0.24 | −3.089 | 0.074 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, T.; Wang, H.; Si, X.; Pu, C.; Liu, Z.; Zhang, Q.; Liu, W. Fracture Characteristics and Tensile Strength Prediction of Rock–Concrete Composite Discs Under Radial Compression. Mathematics 2024, 12, 3510. https://doi.org/10.3390/math12223510
Guo T, Wang H, Si X, Pu C, Liu Z, Zhang Q, Liu W. Fracture Characteristics and Tensile Strength Prediction of Rock–Concrete Composite Discs Under Radial Compression. Mathematics. 2024; 12(22):3510. https://doi.org/10.3390/math12223510
Chicago/Turabian StyleGuo, Tengfei, Houqiang Wang, Xuefeng Si, Chengzhi Pu, Zhixiang Liu, Qi Zhang, and Weijun Liu. 2024. "Fracture Characteristics and Tensile Strength Prediction of Rock–Concrete Composite Discs Under Radial Compression" Mathematics 12, no. 22: 3510. https://doi.org/10.3390/math12223510
APA StyleGuo, T., Wang, H., Si, X., Pu, C., Liu, Z., Zhang, Q., & Liu, W. (2024). Fracture Characteristics and Tensile Strength Prediction of Rock–Concrete Composite Discs Under Radial Compression. Mathematics, 12(22), 3510. https://doi.org/10.3390/math12223510





