Numerical Approximation for a Stochastic Fractional Differential Equation Driven by Integrated Multiplicative Noise
Abstract
:1. Introduction
2. The Additive Noise Case
3. The Multiplicative Noise Case
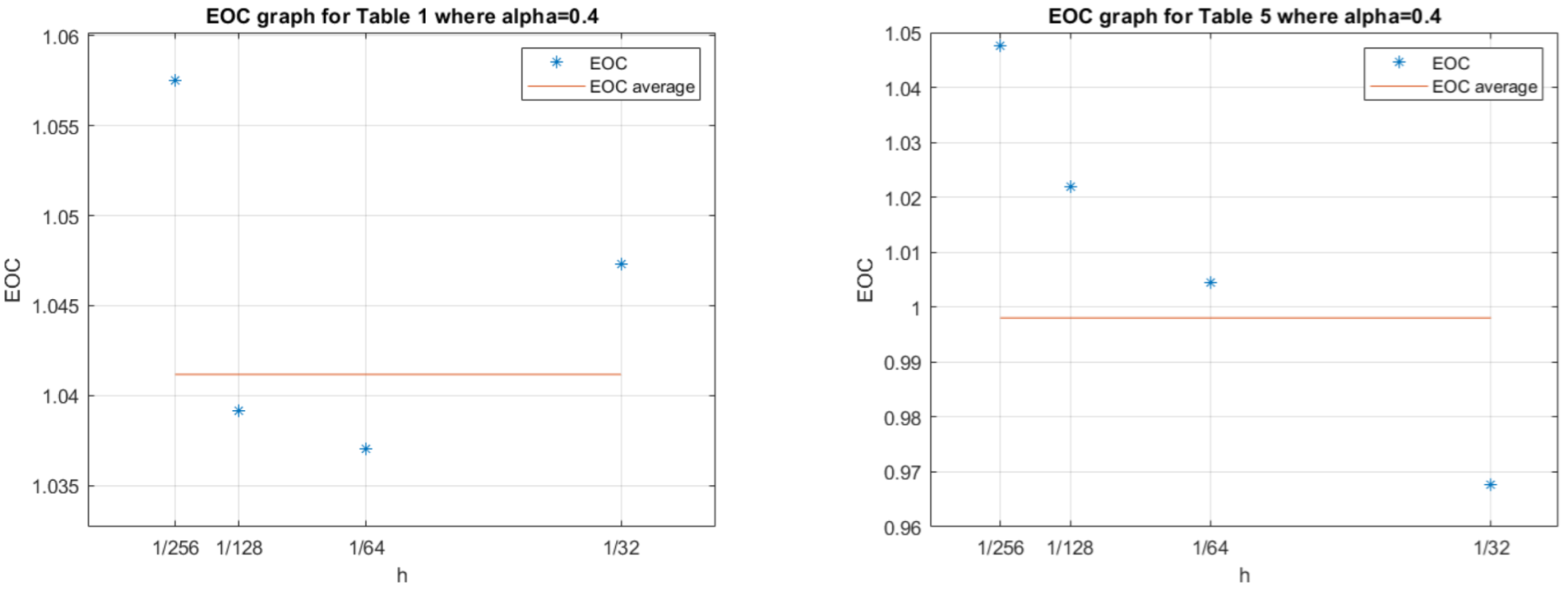
4. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Kamrani, M. Numerical solution of stochastic fractional differential equations. Numer. Algorithms 2015, 68, 81–93. [Google Scholar] [CrossRef]
- Diethelm, K. The Analysis of Fractional Differential Equations; Lecture Notes in Mathematics; Springer: Berlin, Germany, 2010. [Google Scholar]
- Khodabin, M.; Maleknejad, K.; Asgari, M. Numerical solution of a stochastic population growth model in a closed system. Adv. Differ. Equ. 2013, 2013, 130. [Google Scholar] [CrossRef]
- Tsokos, C.P.; Padgett, W.J. Random Integral Equations with Applications to Life Sciences and Engineering; Academic Press: Cambridge, MA, USA, 1974. [Google Scholar]
- Vahdati, S. A wavelet method for stochastic Volterra integral equations and its application to general stock model. Comput. Methods Differ. Equ. 2017, 5, 170–188. [Google Scholar]
- Zhao, Q.; Wang, R.; Wei, R. Exponential utility maximization for an insurer with time-inconsistent preferences. Insurance 2016, 70, 89–104. [Google Scholar] [CrossRef]
- Szynal, D.; Wedrychowicz, S. On solutions of a stochastic integral equation of the Volterra type with applications for chemotherapy. J. Appl. Probab. 1988, 25, 257–267. [Google Scholar] [CrossRef]
- Berger, M.; Mizel, V. Volterra equations with Itô integrals I. J. Integral Equ. 1980, 2, 187–245. [Google Scholar]
- Berger, M.; Mizel, V. Volterra equations with Itô integrals II. J. Integral Equ. 1980, 2, 319–337. [Google Scholar]
- Ravichandran, C.; Valliammal, N.; Nieto, J.J. New results on exact controllability of a class of fractional neutral integro-differential systems with state-dependent delay in Banach spaces. J. Frank. Inst. 2019, 356, 1535–1565. [Google Scholar] [CrossRef]
- Dineshkumar, C.; Udhayakumar, R.; Vijayakumar, V.; Shukla, A.; Nisar, K.S. New discussion regarding approximate controllability for Sobolev-type fractional stochastic hemivariational inequalities of order r∈(1,2). Commun. Nonlinear Sci. Numer. Simul. 2023, 116, 106891. [Google Scholar] [CrossRef]
- Dhayal, R.; Malik, M.; Abbas, S.; Debbouche, A. Optimal controls for second-order stochastic differential equations driven by mixed-fractional Brownian motion with impulses. Appl. Math. Lett. 2020, 43, 4107–4124. [Google Scholar] [CrossRef]
- Zhang, T.W.; Li, Y.K. Exponential Euler scheme of multi-delay Caputo–Fabrizio fractional-order differential equations. Appl. Math. Lett. 2022, 124, 107709. [Google Scholar] [CrossRef]
- Kloeden, P.E.; Platen, E. Numerical Solution of Stochastic Differential Equations. Applications of Mathematics; Springer: New York, NY, USA; Berlin, Germany, 1992; Volume 23. [Google Scholar]
- Milstein, G.N.; Treyakov, M.V. Stochastic Numerics for Mathematical Physics; Scientific Computation; Springer: Berlin, Germany, 2004. [Google Scholar]
- Zhang, X. Euler schemes and large deviations for stochastic Volterra equations with singular kernels. J. Differ. Equ. 2008, 244, 2226–2250. [Google Scholar] [CrossRef]
- Son, D.T.; Huong, P.T.; Kloeden, P.E.; Tuan, H.T. Asymptotic separation between solutions of Caputo fractional stochastic differential equations. Stoch. Anal. Appl. 2018, 36, 654–664. [Google Scholar] [CrossRef]
- Anh, P.T.; Doan, T.S.; Huong, P.T. A variation of constant formula for Caputo fractional stochastic differential equations. Stat. Probab. Lett. 2019, 145, 351–358. [Google Scholar] [CrossRef]
- Tudor, C.; Tudor, M. Approximation schemes for Itô-Volterra stochastic equations. Bol. Soc. Mat. Mex. 1995, 1, 73–85. [Google Scholar]
- Wen, C.H.; Zhang, T.S. Improved rectangular method on stochastic Volterra equations. J. Comput. Appl. Math. 2011, 235, 2492–2501. [Google Scholar] [CrossRef]
- Wang, Y. Approximate representations of solutions to SVIEs, and an application to numerical analysis. J. Math. Anal. Appl. 2017, 449, 642–659. [Google Scholar] [CrossRef]
- Xiao, Y.; Shi, J.N.; Yang, Z.W. Split-step collocation methods for stochastic Volterra integral equations. J. Integral Equ. Appl. 2018, 30, 197–218. [Google Scholar] [CrossRef]
- Liang, H.; Yang, Z.; Gao, J. Strong superconvergence of the Euler–Maruyama method for linear stochastic Volterra integral equations. J. Comput. Appl. Math. 2017, 317, 447–457. [Google Scholar] [CrossRef]
- Dai, X.; Bu, W.; Xiao, A. Well-posedness and EM approximations for non-Lipschitz stochastic fractional integro-differential equations. J. Comput. Appl. Math. 2019, 356, 377–390. [Google Scholar] [CrossRef]
- Gao, J.; Liang, H.; Ma, S. Strong convergence of the semi-implicit Euler method for nonlinear stochastic Volterra integral equations with constant delay. Appl. Math. Comput. 2019, 348, 385–398. [Google Scholar] [CrossRef]
- Yang, H.; Yang, Z.; Ma, S. Theoretical and numerical analysis for Volterra integro-differential equations with Itô integral under polynomially growth conditions. Appl. Math. Comput. 2019, 360, 70–82. [Google Scholar] [CrossRef]
- Zhang, W. Theoretical and numerical analysis of a class of stochastic Volterra integro-differential equations with non-globally Lipschitz continuous coefficients. Appl. Numer. Math. 2020, 147, 254–276. [Google Scholar] [CrossRef]
- Zhang, W.; Liang, H.; Gao, J. Theoretical and numerical analysis of the Euler-Maruyama method for generalized stochastic Volterra integro-differential equations. J. Comput. Appl. Math. 2020, 365, 17. [Google Scholar] [CrossRef]
- Li, M.; Huang, C.; Hu, Y. Numerical methods for stochastic Volterra integral equations with weakly singular kernels. IMA J. Numer. Anal. 2022, 42, 2656–2683. [Google Scholar] [CrossRef]
- Yan, Y.; Khan, M.; Ford, N.J. An analysis of the modified L1 scheme for time-fractional partial differential equations with nonsmooth data. SIAM J. Numer. Anal. 2018, 56, 210–227. [Google Scholar] [CrossRef]
- Schilling, R.L. Measures, Integrals And Martingales; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
| EOC | |||||
|---|---|---|---|---|---|
| 0.2 | 1.03 | ||||
| 1.0310 | 1.0250 | 1.0305 | |||
| 0.4 | 1.04 | ||||
| 1.0473 | 1.0370 | 1.0392 | |||
| 0.6 | 1.05 | ||||
| 1.0589 | 1.0502 | 1.0516 | |||
| 0.8 | 1.04 | ||||
| 1.0335 | 1.0386 | 1.0476 | |||
| 1 | 1.00 | ||||
| 0.9874 | 1.0021 | 1.0184 |
| EOC | |||||
|---|---|---|---|---|---|
| 0.2 | 1.01 | ||||
| 1.0247 | 0.99904 | 1.0134 | |||
| 0.4 | 1.01 | ||||
| 1.0183 | 1.0082 | 1.0114 | |||
| 0.6 | 1.02 | ||||
| 1.0185 | 1.0273 | 1.0281 | |||
| 0.8 | 1.02 | ||||
| 1.0032 | 1.0264 | 1.0452 | |||
| 1 | 1.01 | ||||
| 1.0057 | 1.0116 | 1.0232 |
| EOC | |||||
|---|---|---|---|---|---|
| 0.2 | 1.01 | ||||
| 1.0046 | 1.0128 | 1.0249 | |||
| 0.4 | 1.04 | ||||
| 1.0326 | 1.0336 | 1.0400 | |||
| 0.6 | 1.07 | ||||
| 1.0740 | 1.0708 | 1.0725 | |||
| 0.8 | 1.09 | ||||
| 1.0864 | 1.0888 | 1.0952 | |||
| 1 | 1.02 | ||||
| 1.0123 | 1.0148 | 1.0248 |
| EOC | |||||
|---|---|---|---|---|---|
| 0.2 | 1.03 | ||||
| 1.0224 | 1.0234 | 1.0312 | |||
| 0.4 | 1.05 | ||||
| 1.0510 | 1.0471 | 1.0496 | |||
| 0.6 | 1.08 | ||||
| 1.0876 | 1.0832 | 1.0831 | |||
| 0.8 | 1.09 | ||||
| 1.0908 | 1.0937 | 1.1003 | |||
| 1 | 1.02 | ||||
| 1.0117 | 1.0146 | 1.0247 |
| EOC | |||||
|---|---|---|---|---|---|
| 0.2 | 1.04 | ||||
| 1.0583 | 1.0315 | 1.0323 | |||
| 0.4 | 1.00 | ||||
| 0.9676 | 1.0045 | 1.0220 | |||
| 0.6 | 1.04 | ||||
| 1.0056 | 1.0427 | 1.0638 | |||
| 0.8 | 1.03 | ||||
| 1.0480 | 1.0015 | 1.0299 | |||
| 1 | 1.01 | ||||
| 1.0011 | 1.0094 | 1.0221 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoult, J.; Yan, Y. Numerical Approximation for a Stochastic Fractional Differential Equation Driven by Integrated Multiplicative Noise. Mathematics 2024, 12, 365. https://doi.org/10.3390/math12030365
Hoult J, Yan Y. Numerical Approximation for a Stochastic Fractional Differential Equation Driven by Integrated Multiplicative Noise. Mathematics. 2024; 12(3):365. https://doi.org/10.3390/math12030365
Chicago/Turabian StyleHoult, James, and Yubin Yan. 2024. "Numerical Approximation for a Stochastic Fractional Differential Equation Driven by Integrated Multiplicative Noise" Mathematics 12, no. 3: 365. https://doi.org/10.3390/math12030365
APA StyleHoult, J., & Yan, Y. (2024). Numerical Approximation for a Stochastic Fractional Differential Equation Driven by Integrated Multiplicative Noise. Mathematics, 12(3), 365. https://doi.org/10.3390/math12030365






