Dynamic Behavior of a 10 MW Floating Wind Turbine Concrete Platform under Harsh Conditions
Abstract
:1. Introduction
2. Research Background
3. Theoretical Method
3.1. Environmental Loads
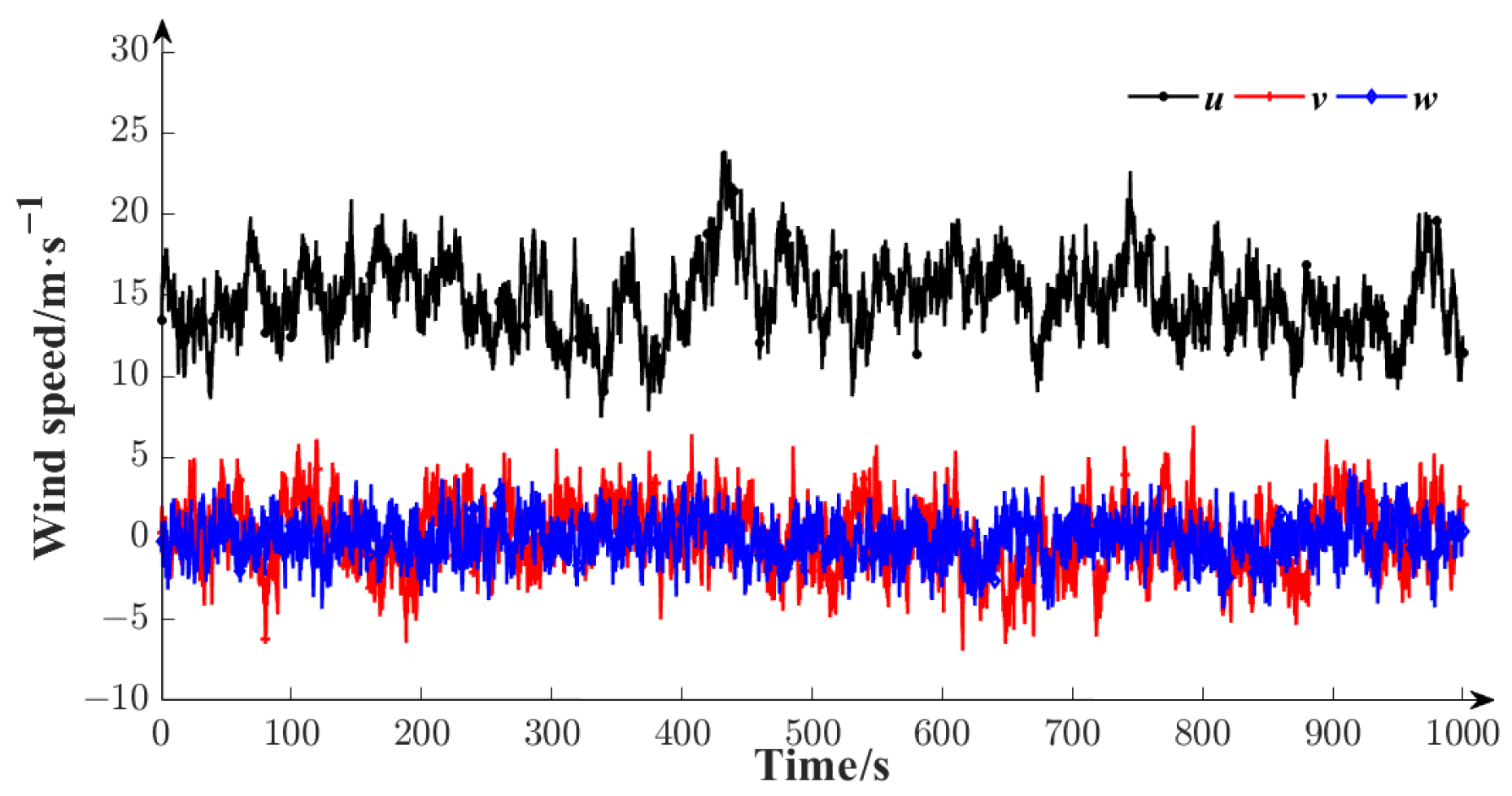
3.1.1. Wind Load
3.1.2. Wave Load
3.1.3. Current Load
3.2. Structural Strength Analysis
3.3. Fatigue Life Theory
4. Mesh Sensitivity Verification
5. Results and Analysis
5.1. Free Decay of the Floating Wind Turbine
5.2. Floating Platform Motion Response
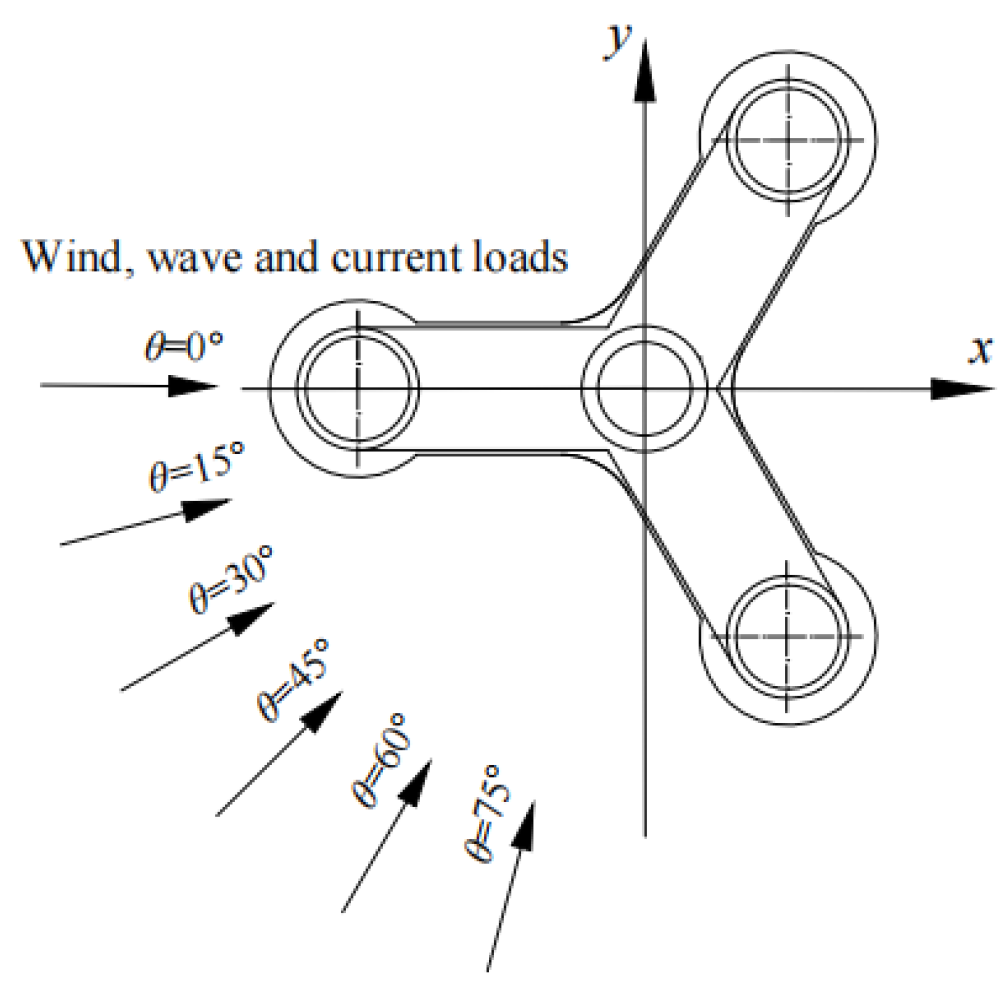
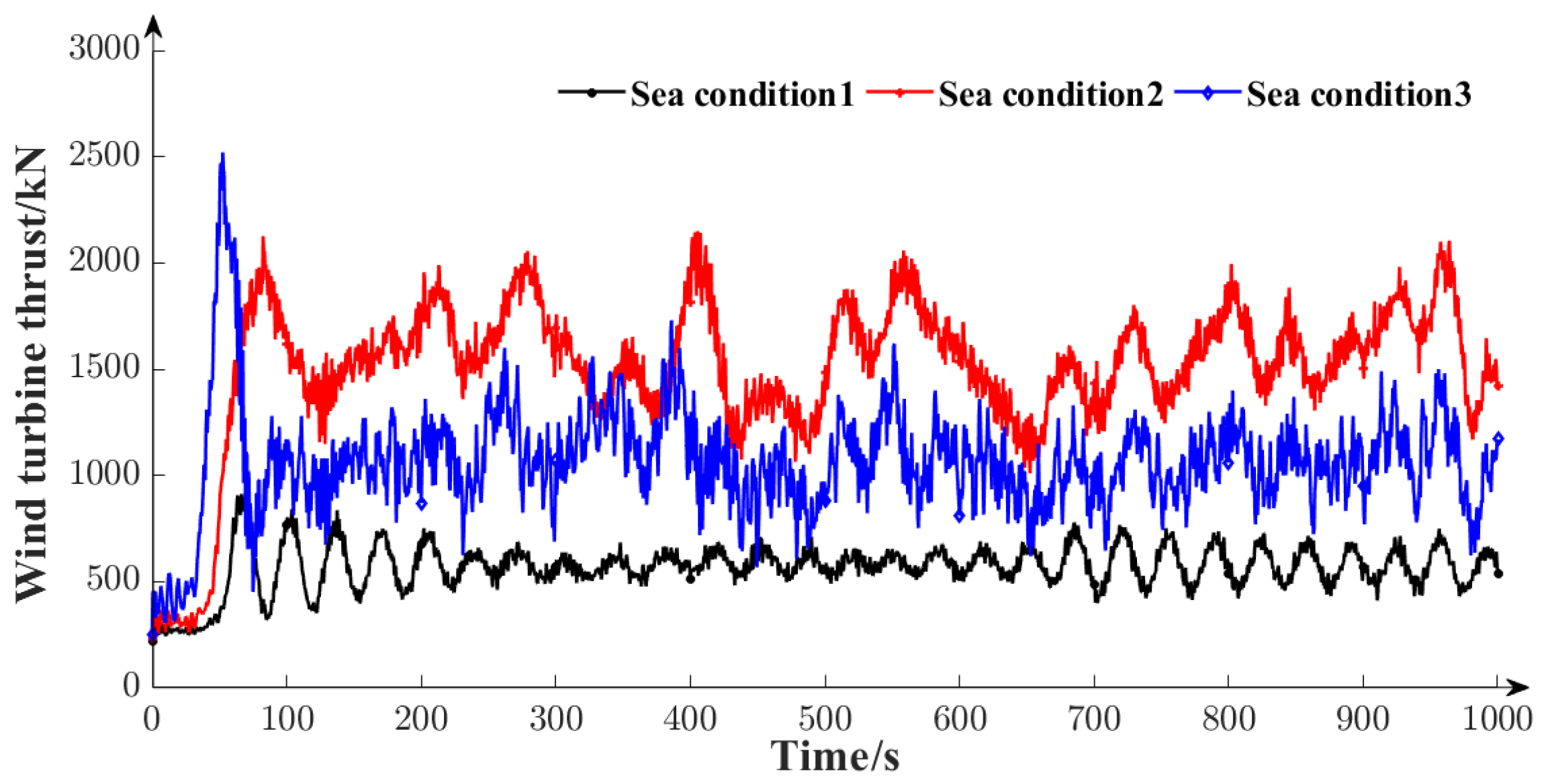
5.2.1. Loading Condition
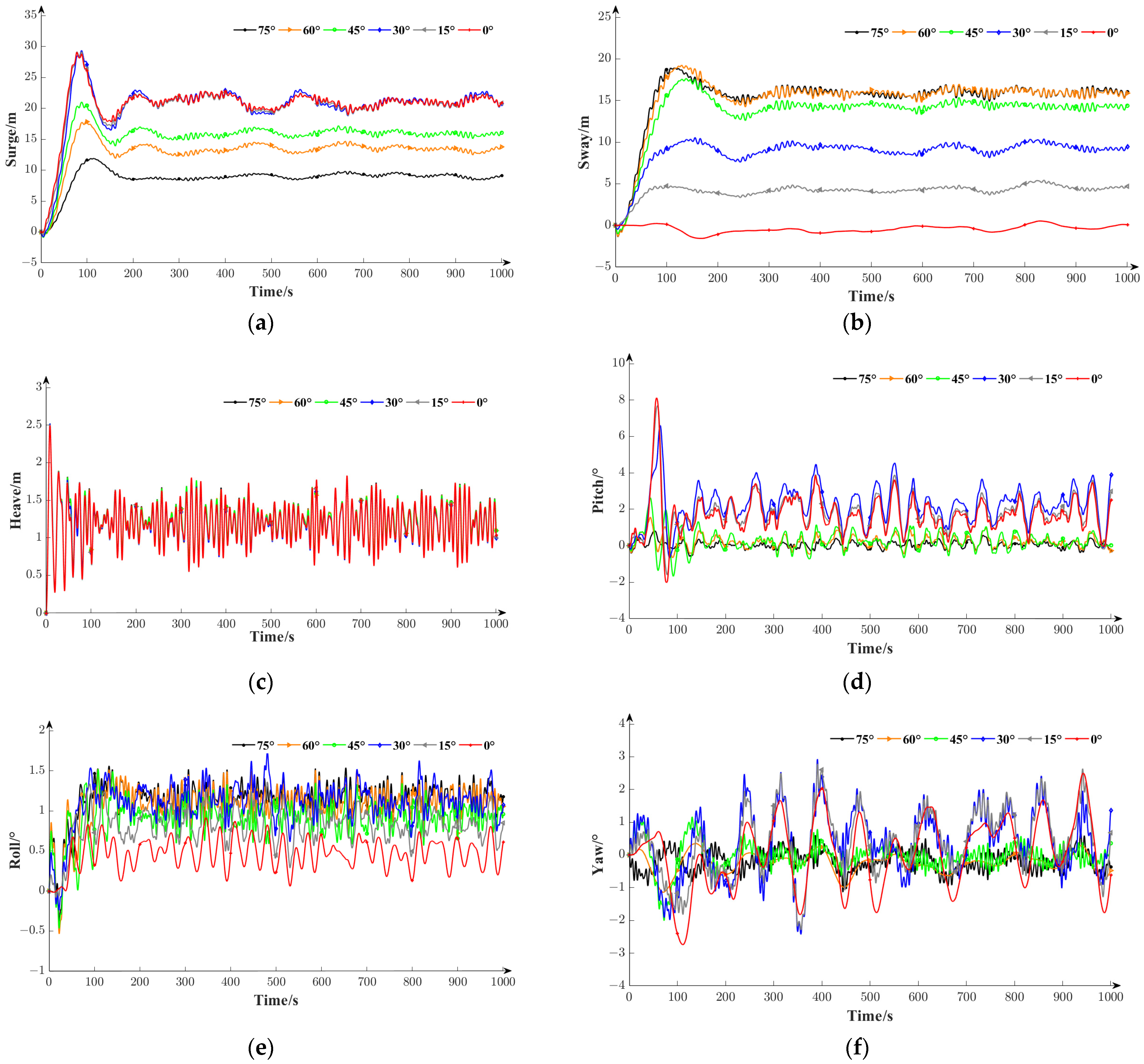
5.2.2. Motion Response Results and Analysis
5.3. Structural Strength Analysis of the Floating Platform
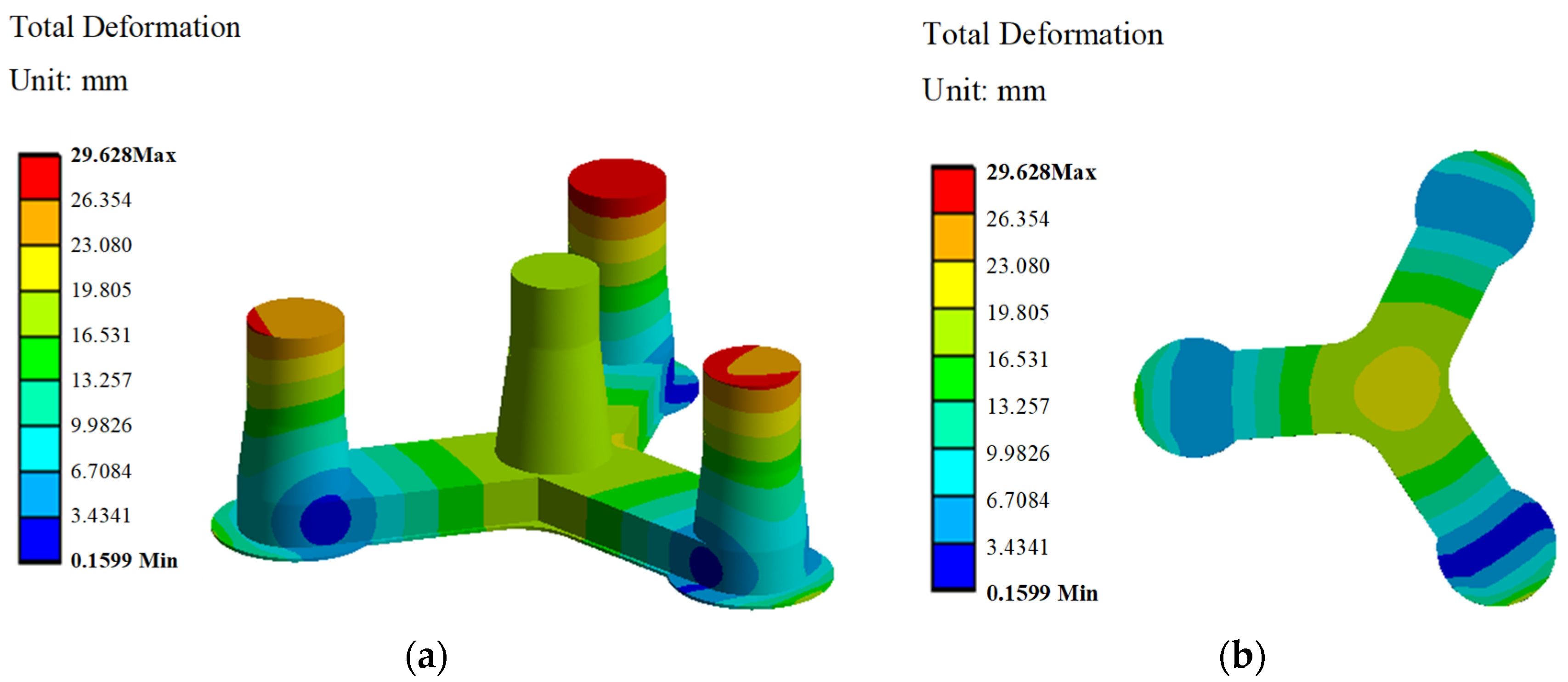
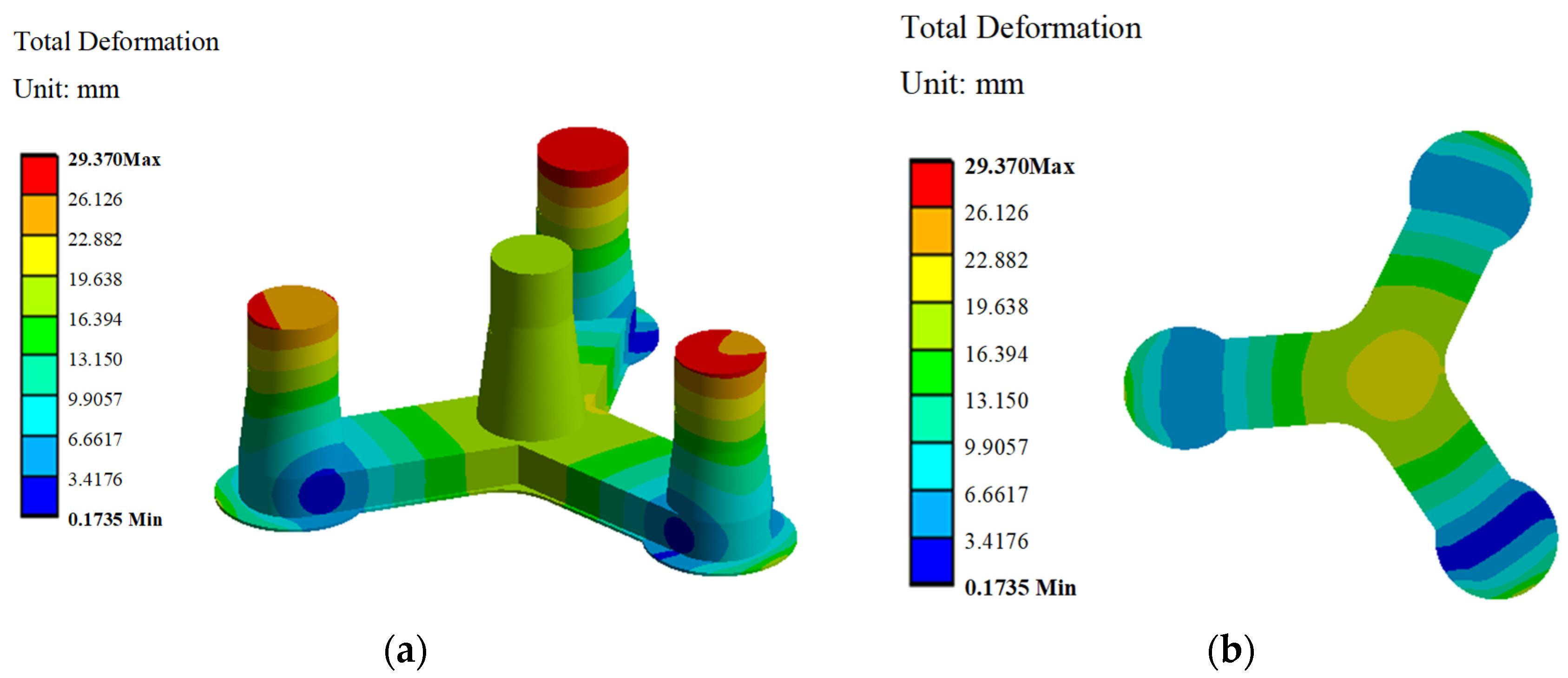
5.3.1. Deformation Analysis of the Floating Platform
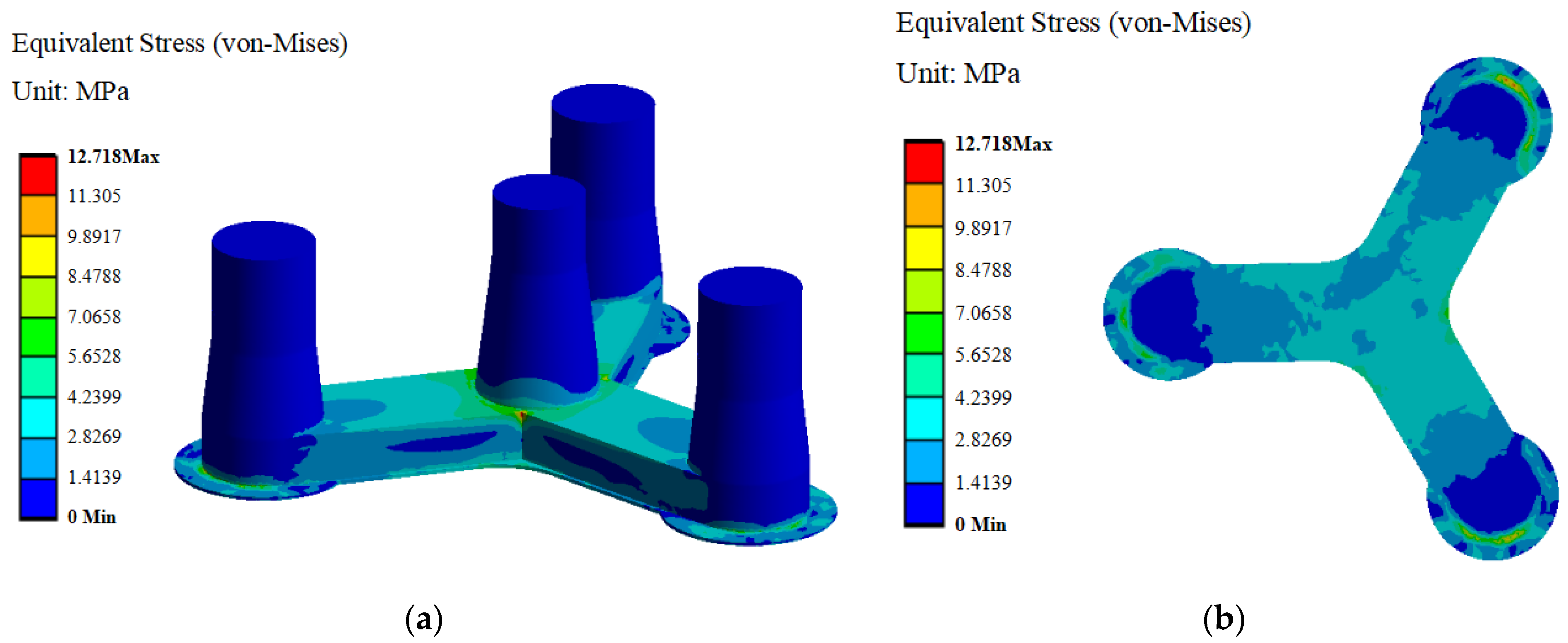
5.3.2. Stress Analysis of the Floating Platform
5.4. Fatigue Life Analysis of the Floating Platform
6. Conclusions
- (1)
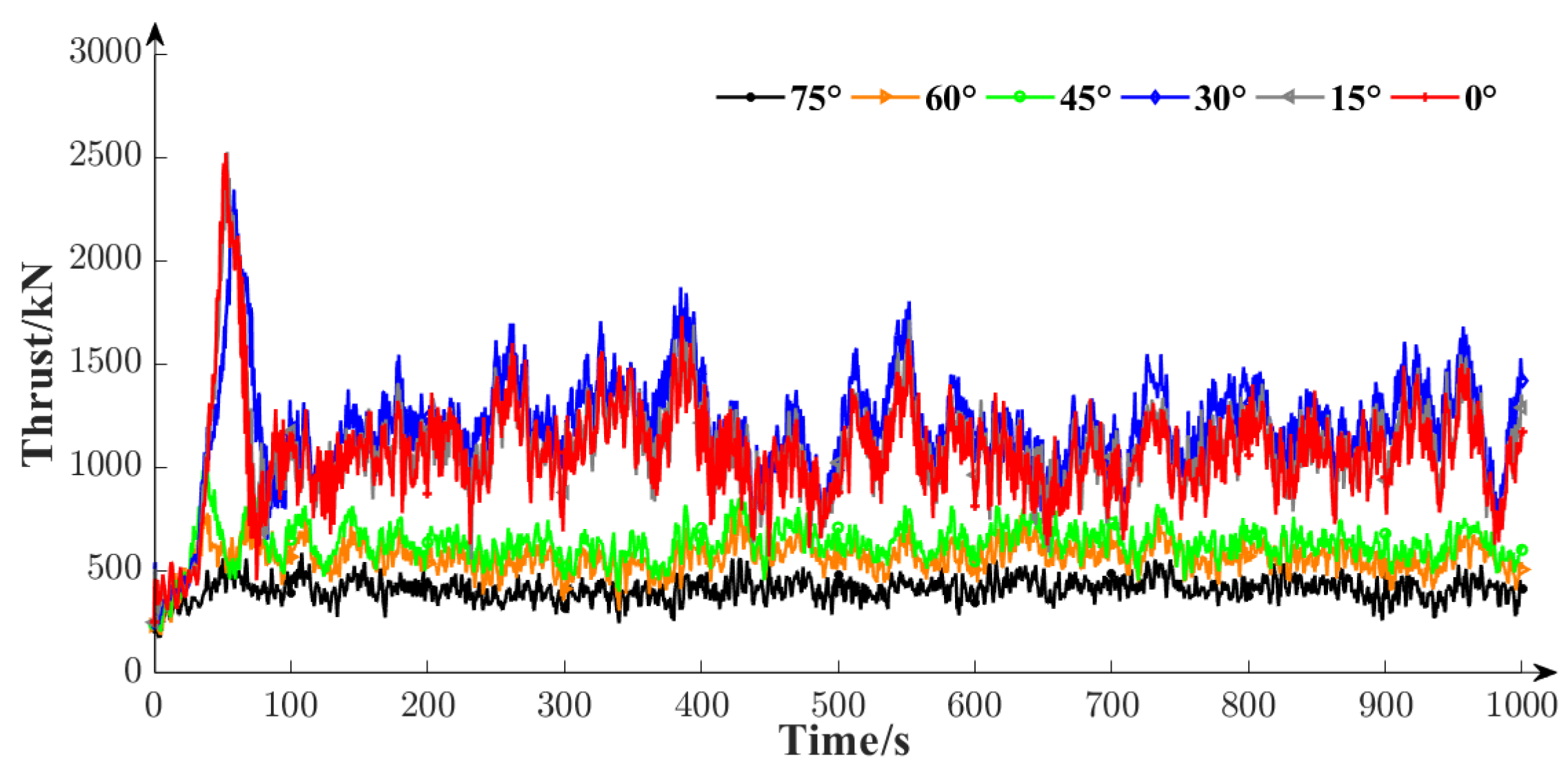
- Different sea conditions and incidence directions of environmental loads have significant effects on the motion response in all six degrees of freedom. The motion response amplitudes are relatively large under harsh sea conditions but still meet the stability requirements for the normal power generation of floating wind turbines. Additionally, changes in the incident angles of the environmental loads have a noticeable impact on the motion response in the surge, sway, pitch, and yaw directions. When the incident angles increase to 75°, the amplitudes of the surge and pitch motion responses decrease by 59.1% and 90.1%, respectively, while the sway motion response increases by a factor of 14.6. In the yaw direction, the motion response initially increases and then decreases, reaching its maximum value of 2.93° at an incident angle of 30°.
- (2)
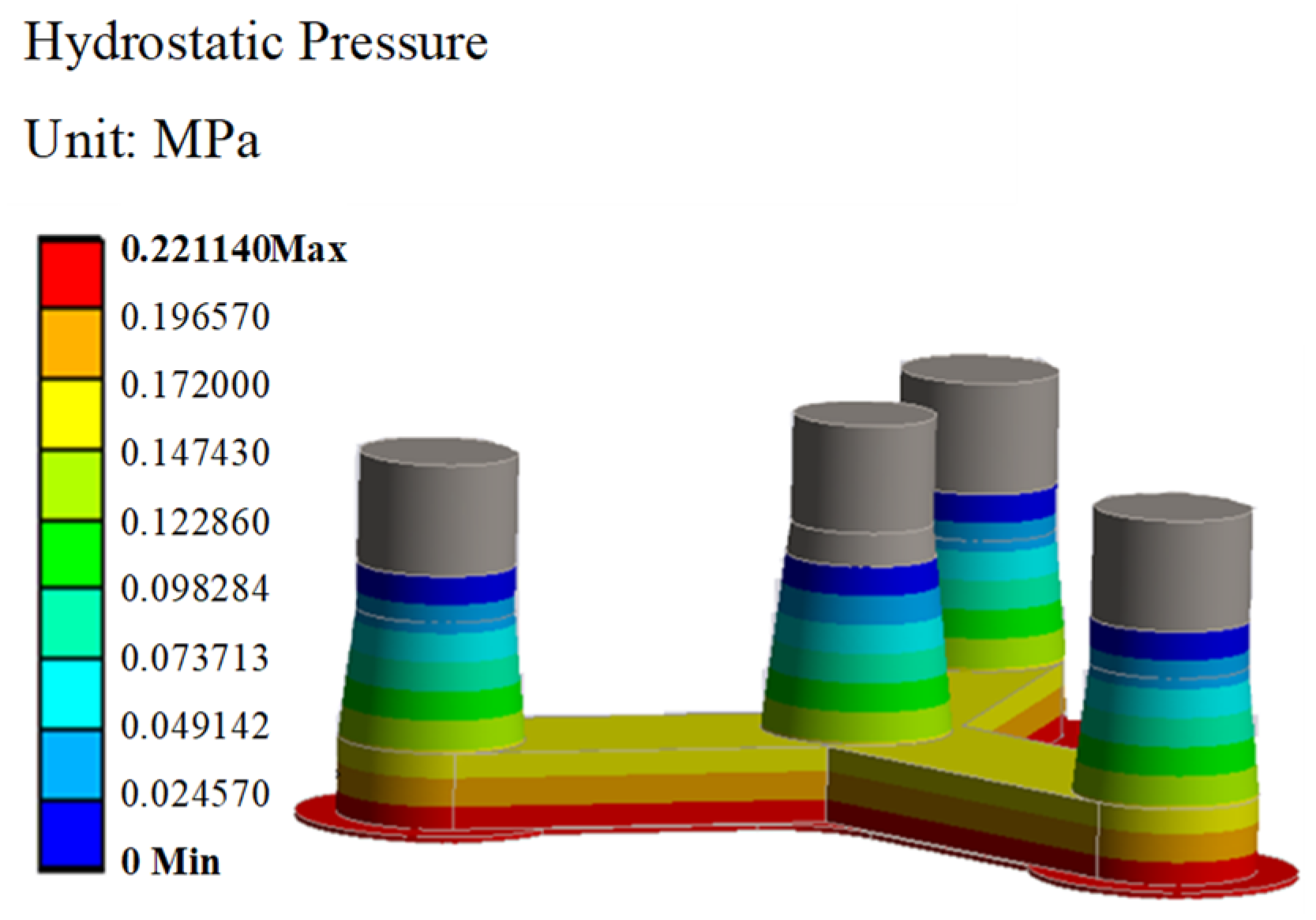
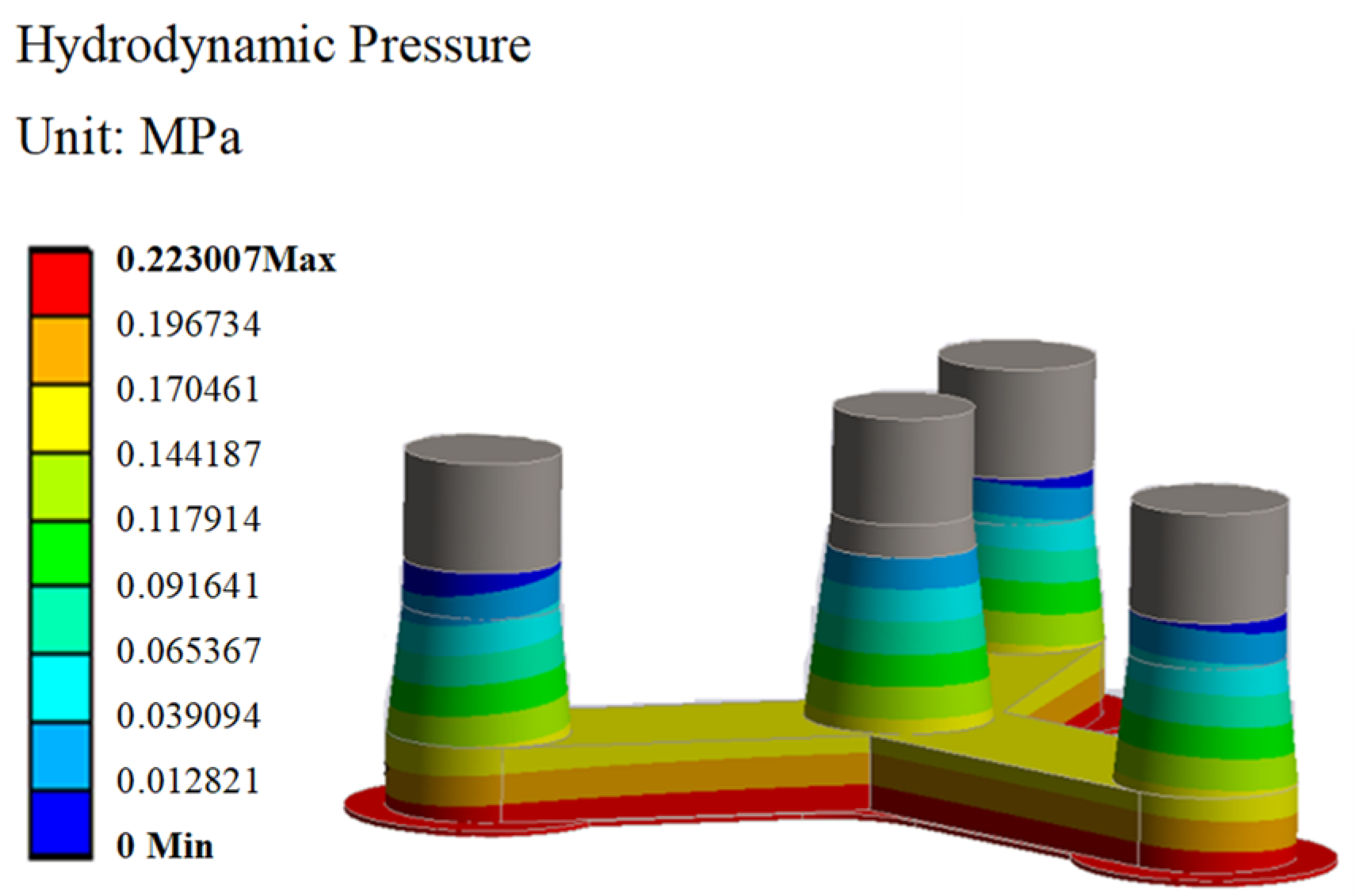
- Under harsh sea conditions, the maximum deformation occurs at the top of the external three columns of the concrete-based floating platform. To mitigate the corresponding deformation, it is recommended to consider the use of prestressed concrete construction techniques. The connection between the middle tapered column and the bottom Y-shaped pontoon, as well as the connection between the heave plate and the Y-shaped pontoon, is subjected to stress concentration. The maximum stress in these areas is 12.718 MPa, which is within the allowable stress limits and satisfies the structural integrity requirements of the floating platform.
- (3)
- Fatigue life analysis was conducted based on the Miner linear cumulative damage theory for the floating platform subjected to environmental loads with θ = 0°, ψ = 0° state. The results indicate that the shortest fatigue life occurs in the stress concentration areas at the connection between the middle tapered column and the Y-shaped pontoon, and on the outer side of the heave plate, the fatigue life is almost 106 times lower, making these areas prone to fatigue damage.
- (4)
- In the fatigue analysis, only normal operating conditions were considered, and the impact of unexpected situations such as emergency shutdowns on structural fatigue damage and life was not considered in this study.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.Q.; Zang, W.; Zheng, J.H.; Cappietti, L.; Zhang, J.S.; Zheng, Y.; Rodriguez, E.F. The influence of waves propagating with the current on the wake of a tidal stream turbine. Appl. Energy 2021, 290, 116729. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Liu, Z.Q.; Li, C.Y.; Wang, X.M.; Zheng, Y.; Zhang, Z.; Emmanuel, F.R.; Rabea, J.M. Fluid–structure interaction modeling of structural loads and fatigue life analysis of tidal stream turbine. Mathematics 2022, 10, 3674. [Google Scholar] [CrossRef]
- Tavares, L.F.D.A.; Shadman, M.; Assad, L.P.D.F.; Estefen, S.F. Influence of the WRF model and atmospheric reanalysis on the offshore wind resource potential and cost estimation: A case study for Rio de Janeiro State. Energy 2022, 240, 122767. [Google Scholar] [CrossRef]
- Baquerizo, J.; Tutivén, C.; Puruncajas, B.; Vidal, Y.; Sampietro, J. Siamese neural networks for damage detection and diagnosis of jacket-type offshore wind turbine platforms. Mathematics 2022, 10, 1131. [Google Scholar] [CrossRef]
- Pérez-Collazo, C.; Greaves, D.; Iglesias, G. A review of combined wave and offshore wind energy. Renew. Sustain. Energy Rev. 2015, 42, 141–153. [Google Scholar] [CrossRef]
- Barooni, M.; Ashuri, T.; Sogut, D.V.; Wood, S.; Taleghani, S.G. Floating offshore wind turbines: Current status and future prospects. Energies 2023, 16, 2. [Google Scholar] [CrossRef]
- Li, W.J.; Ke, S.T.; Chen, J.; Zhu, T.R.; Ren, H.H. Hydrodynamic response and energy analysis in a very large floating structure supporting a marine airport under typhoon-driven waves. Ocean Eng. 2022, 266, 112987. [Google Scholar] [CrossRef]
- Jonkman, J. Definition of the Floating System for Phase IV of OC3; National Renewable Energy Laboratory: Golden, CO, USA, 2010. [Google Scholar]
- Ahn, H.J.; Shin, H. Model test and numerical simulation of OC3 spar type floating offshore wind turbine. Int. J. Nav. Archit. Ocean Eng. 2017, 11, 1–10. [Google Scholar] [CrossRef]
- Yue, M.; Liu, Q.S.; Li, C.; Ding, Q.W.; Cheng, S.S.; Zhu, H.T. Effects of heave plate on dynamic response of floating wind turbine spar platform under the coupling effect of wind and wave. Ocean Eng. 2020, 201, 107103. [Google Scholar] [CrossRef]
- Jiang, Z.H.; Wen, B.R.; Chen, G.; Xiao, L.F.; Li, J.; Peng, Z.K.; Tian, X.L. Feasibility studies of a novel spar-type floating wind turbine for moderate water depths: Hydrodynamic perspective with model test. Ocean. Eng. 2021, 233, 109070. [Google Scholar] [CrossRef]
- Matthew, H.; Andrew, G. Validation of a lumped-mass mooring line model with DeepCwind semisubmersible model test data. Ocean Eng. 2015, 104, 590–603. [Google Scholar]
- Liu, Z.Q.; Zhou, Q.S.; Tu, Y.G.; Wang, W.; Hua, X.G. Proposal of a novel semi-submersible floating wind turbine platform composed of inclined columns and multi-segmented mooring lines. Energies 2019, 12, 1809. [Google Scholar] [CrossRef]
- Jiang, H.R.; Wang, H.H.; Vaz, M.A.; Bai, X.L. Research on dynamic response prediction of semi-submersible wind turbine platform in real sea test model based on machine learning. Appl. Ocean Res. 2023, 142, 103808. [Google Scholar] [CrossRef]
- Xu, X.S.; Gaidai, O.; Naess, A.; Sahoo, P. Extreme loads analysis of a site-specific semi-submersible type wind turbine. Ships Offshore Struct. 2020, 15, S46–S54. [Google Scholar] [CrossRef]
- Wang, S.S.; Xing, Y.H.; Balakri, S.R.; Shi, W.; Xu, X.S. Design, local structural stress, and global dynamic response analysis of a steel semi-submersible hull for a 10-MW floating wind turbine. Eng. Struct. 2023, 291, 116474. [Google Scholar] [CrossRef]
- Matha, D. Model Development and Loads Analysis of an Offshore Wind Turbine on a Tension Leg Platform with a Comparison to Other Floating Turbine Concepts; National Renewable Energy Laboratory: Golden, CO, USA, 2010. [Google Scholar]
- Suzuki, K.; Yamaguchi, H.; Akase, M.; Imakita, A.; Ishihara, T.; Fukumoto, Y.; Oyama, T. Initial design of tension leg platform for offshore wind farm. J. Fluid Sci. Technol. 2011, 6, 372–381. [Google Scholar] [CrossRef]
- Goupee, A.J.; Koo, B.; Lambrakos, K.; Kimball, R. Model tests for three floating wind turbine concepts. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 30 April–3 May 2012. [Google Scholar]
- Xu, X.; Wei, N.Y.; Yao, W.J. The stability analysis of tension-leg platforms under marine environmental loads via altering the connection angle of tension legs. Water 2022, 14, 283. [Google Scholar] [CrossRef]
- Aboutalebi, A.; M’zoughi, F.; Garrido, I.; Garrido, A.J. Performance analysis on the use of oscillating water column in barge-based floating offshore wind turbines. Mathematics 2021, 9, 475. [Google Scholar] [CrossRef]
- M’zoughi, F.; Aboutalebi, P.; Garrido, I.; Garrido, A.J.; Sen, M.D.L. Complementary airflow control of oscillating water columns for floating offshore wind turbine stabilization. Mathematics 2021, 9, 1364. [Google Scholar] [CrossRef]
- Rubio, F.; Albert, L.C.; Pedrosa, M.A. Analysis of the influence of calculation parameters on the design of the gearbox of a high-power wind turbine. Mathematics 2023, 11, 4137. [Google Scholar] [CrossRef]
- Wang, S.S.; Moan, T.; Nejad, A.R. A comparative study of fully coupled and de-coupled methods on dynamic behaviour of floating wind turbine drivetrains. Renew. Energy 2021, 179, 1618–1635. [Google Scholar] [CrossRef]
- Wang, S.S.; Moan, T. Analysis of extreme internal load effects in columns in a semi-submersible support structure for large floating wind turbines. Ocean Eng. 2024, 291, 116372. [Google Scholar] [CrossRef]
- Ahn, H.; Ha, Y.J.; Cho, S.G.; Lim, C.H.; Kim, K.H. A numerical study on the performance evaluation of a semi-type floating offshore wind turbine system according to the direction of the incoming waves. Energies 2022, 15, 5485. [Google Scholar] [CrossRef]
- Yang, Y.; Bashir, M.; Wang, J.; Michailides, C.; Loughney, S.; Armin, M.; Hernandez, S.; Urban, J.; Li, C. Wind-wave coupling effects on the fatigue damage of tendons for a 10MW multi-body floating wind turbine. Ocean Eng. 2022, 217, 107909. [Google Scholar] [CrossRef]
- Nybø, A.; Nielsen, G.F.; Reuder, J.; Matthew, J.; Godvik, M. Evaluation of different wind fields for the investigation of the dynamic response of offshore wind turbines. Wind Energy 2020, 23, 1810–1830. [Google Scholar] [CrossRef]
- Leishman, J.G. Aerodynamics of horizontal-axis wind turbines. Environ. Sci. Eng. 2011, 1, 1–76. [Google Scholar]
- Pierson, W.J.; Moskowitz, L. A proposed spectral form for fully developed wind seas based on the similarity theory of S. A. Kitaigorodskii. J. Geophys. Res. Atmos. 1964, 69, 5181–5190. [Google Scholar] [CrossRef]
- Jiang, C.Q.; El, M.O.; Schellin, T.E. Capability of a potential-flow solver to analyze articulated multibody offshore modules. Ocean Eng. 2022, 266, 112754. [Google Scholar] [CrossRef]
- Jonkman, J. Modeling of the UAE Wind Turbine for Refinement of Fast_AD; National Renewable Energy Laboratory: Golden, CO, USA, 2010. [Google Scholar]
- Miner, M.A. Cumulative damage in fatigue. J. Appl. Mech. 1945, 12, 159–164. [Google Scholar] [CrossRef]
- Zhao, F.F.; Kinoshita, T.; Bao, W.G.; Wan, R.; Liang, Z.L.; Huang, L.Y. Hydrodynamics identities and wave-drift force of a porous body. Appl. Ocean Res. 2011, 33, 169–177. [Google Scholar] [CrossRef]
- Wang, Z.F.; Zhou, L.M.; Dong, S.; Wu, L.Y.; Li, Z.B.; Mou, L.; Wang, A.F. Wind wave characteristics and engineering environment of the south china sea. Ocean. Coast. Sea Res. 2014, 13, 893–900. [Google Scholar] [CrossRef]
- DNVGL-OS-E301; Position Mooring; DNV GL: Bærum, Norway, 2020.
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5MW Reference Wind Turbine for Offshore System Development; National Renewable Energy Laboratory: Golden, CO, USA, 2009. [Google Scholar]
- Zambrano, T.; Maccready, T.; Kiceniuk, T.; Roddier, D.G.; Cermelli, C.A. Dynamic modeling of deepwater offshore wind turbine structures in gulf of mexico storm conditions. In Proceedings of the OMAE 2006 25th International Conference on Offshore Mechanics and Arctic Engineering, Hamburg, Germany, 4–9 June 2006. [Google Scholar]
- ABS. Guide for Building and Classing Floating Production Installations; American Bureau of Shipping: Houston, TX, USA, 2009. [Google Scholar]
- Yu, L.Z.; Wu, R.X. Using graphene oxide to improve the properties of ultra-high-performance concrete with fine recycled aggregate. Constr. Build. Mater. 2020, 259, 120657. [Google Scholar] [CrossRef]
- Gao, J.X.; Liu, Y.Y.; Yuan, Y.P.; Heng, F. Residual strength modeling and reliability analysis of wind turbine gear under different random loadings. Mathematics 2023, 11, 4013. [Google Scholar] [CrossRef]
- Chen, X.C.; Cui, Y.K.; Zheng, Y.; Zhang, Y.Q. Fatigue crack propagation simulation of vertical centrifugal pump runner using the extended finite element method. Mech. Adv. Mater. Struct. 2023, 5, 1–16. [Google Scholar] [CrossRef]


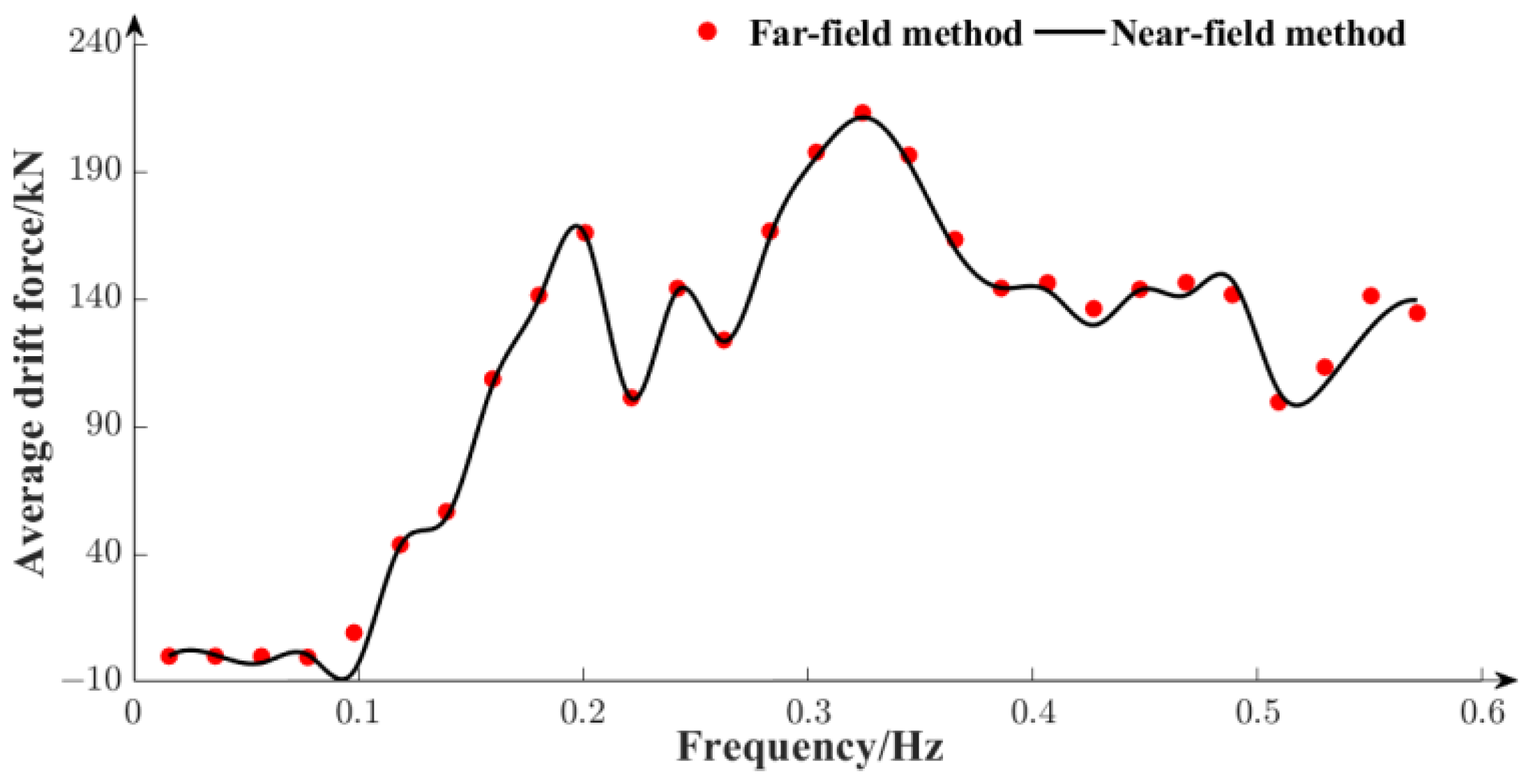
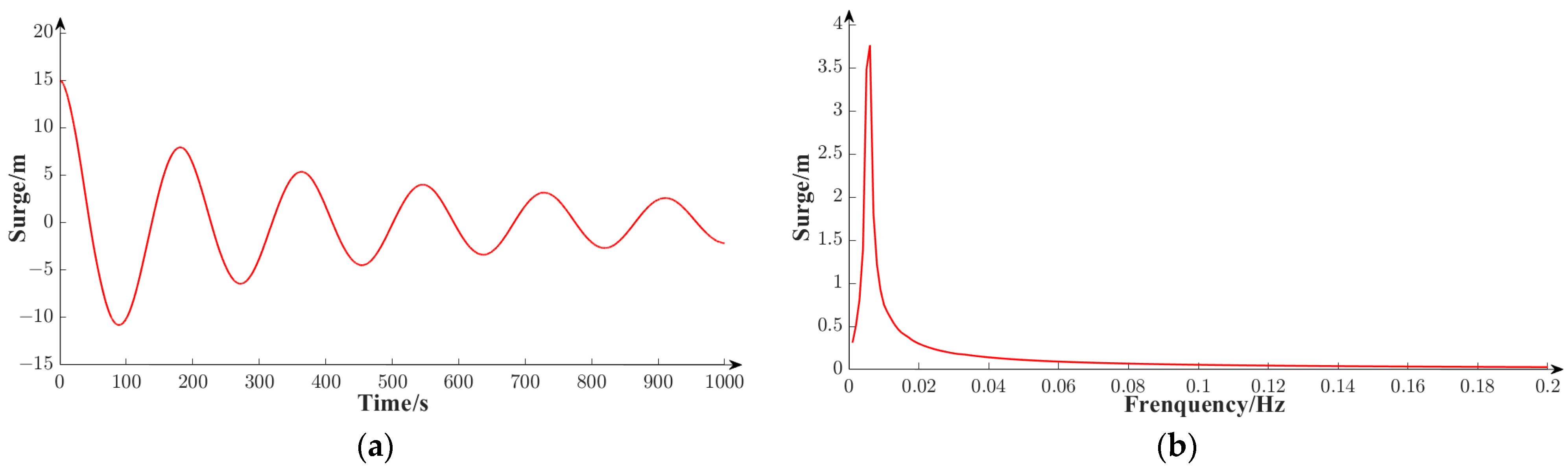
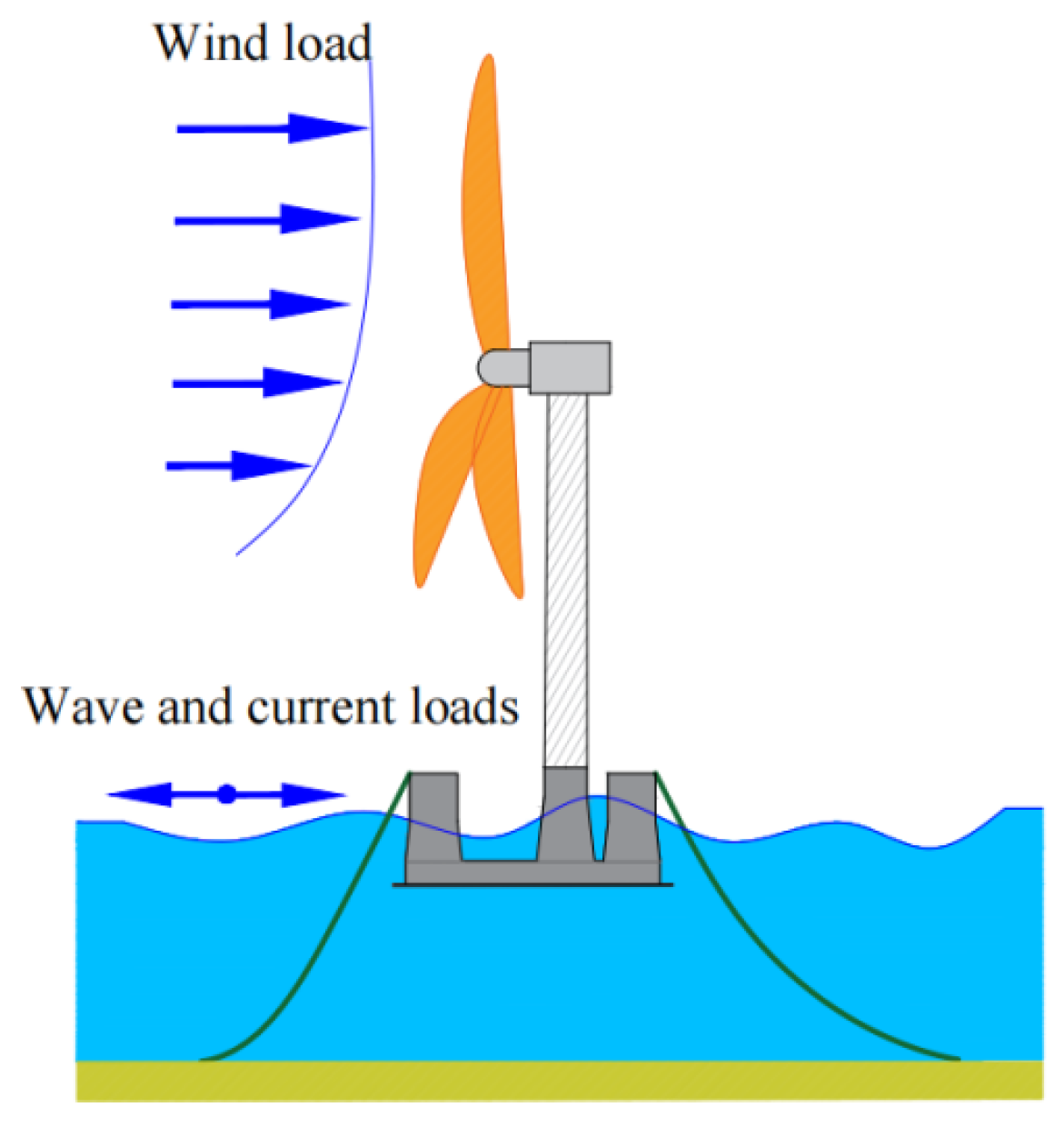



| Parameter/Unit | Value |
|---|---|
| Power/MW | 10.0 |
| Rated wind speed/m·s−1 | 11.4 |
| Cut-in wind speed/m·s−1 | 3.0 |
| Cut-out wind speed/m·s−1 | 25.0 |
| Rated speed/rpm | 9.6 |
| Rotor diameter/m | 178.3 |
| Hub diameter/m | 5.6 |
| Tower height/m | 115.63 |
| Hub height/m | 119.0 |
| Rotor mass/kg | 2.31 × 105 |
| Nacelle mass/kg | 4.46 × 105 |
| Tower mass/kg | 1.26 × 106 |
| Parameter/Unit | Value |
|---|---|
| Platform mass/kg | 2.1709 × 107 |
| Center of mass/m | −15.225 |
| Draft/m | 22.0 |
| Displacement/m3 | 2.3509 × 104 |
| Roll inertia/kg·m2 | 9.43 × 109 |
| Pitch inertia/kg·m2 | 9.43 × 109 |
| Yaw inertia/kg·m2 | 1.63 × 1010 |
| Number of mooring lines | 3 |
| Mass of clump weight/kg | 5.0 × 104 |
| Fairlead depth/m | 9.5 |
| Anchor depth/m | −130 |
| Distance to anchors from platform centerline/m | 691 |
| Length of mooring lines/m | 703 |
| Surge | Sway | Heave | Roll | Pitch | Yaw | |
|---|---|---|---|---|---|---|
| Natural period/s | 182.6375 | 182.625 | 20.4428 | 31.4083 | 31.3583 | 102.53 |
| Natural frequency/Hz | 0.005475 | 0.005476 | 0.04892 | 0.03184 | 0.03189 | 0.00975 |
| Sea Conditions | Wind Speed Uw/m·s−1 | Wave Height Hs/m | Wave Period Tp/s | Current Speed Uc/m·s−1 |
|---|---|---|---|---|
| 1 | 9.0 | 1.00 | 4.0 | 0.514 |
| 2 | 11.4 | 1.75 | 4.5 | 0.700 |
| 3 | 15.0 | 3.25 | 10.0 | 1.028 |
| Surge/m | Sway/m | Heave/m | Roll/° | Pitch/° | Yaw/° | ||
|---|---|---|---|---|---|---|---|
| Sea condition 1 | Maximum | 12.70 | 0.307 | 2.24 | 0.778 | 3.17 | 0.326 |
| Minimum | 0.00 | −0.152 | 0.00 | −0.042 | −1.97 | −0.474 | |
| Average | 9.02 | 0.093 | 1.23 | 0.204 | 0.72 | 0.003 | |
| Sea condition 2 | Maximum | 26.97 | 0.524 | 2.24 | 0.702 | 6.09 | 1.97 |
| Minimum | 0.00 | −1.430 | 0.00 | −0.027 | −0.085 | −2.22 | |
| Average | 19.40 | 0.031 | 1.17 | 0.408 | 3.47 | 0.09 | |
| Sea condition 3 | Maximum | 29.10 | 1.31 | 2.49 | 0.912 | 8.12 | 2.50 |
| Minimum | −0.12 | −1.57 | 0.00 | −0.016 | −2.02 | −2.74 | |
| Average | 20.50 | −0.42 | 1.19 | 0.466 | 1.70 | 0.031 |
| Wave Phase ψ | ψ = 0° | ψ = 30° | ψ = 60° | ψ = 90° | |
|---|---|---|---|---|---|
| Incident Angle θ | |||||
| θ = 0° | 29.628 | 29.599 | 29.565 | 29.536 | |
| θ = 15° | 29.614 | 29.563 | 29.516 | 29.487 | |
| θ = 30° | 29.612 | 29.534 | 29.469 | 29.433 | |
| θ = 45° | 29.617 | 29.517 | 29.434 | 29.390 | |
| θ = 60° | 29.618 | 29.508 | 29.417 | 29.370 | |
| θ = 75° | 29.611 | 29.506 | 29.422 | 29.380 | |
| Wave Phase ψ | ψ = 0° | ψ = 30° | ψ = 60° | ψ = 90° | |
|---|---|---|---|---|---|
| Incident Angle θ | |||||
| θ = 0° | 12.718 | 12.577 | 12.517 | 12.553 | |
| θ = 15° | 12.588 | 12.344 | 12.243 | 12.311 | |
| θ = 30° | 12.536 | 12.182 | 12.102 | 12.078 | |
| θ = 45° | 12.544 | 12.150 | 12.195 | 12.208 | |
| θ = 60° | 12.554 | 12.115 | 12.264 | 12.363 | |
| θ = 75° | 12.533 | 12.095 | 12.358 | 12.546 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Wang, Q.; Zhang, Y.; Zheng, Y. Dynamic Behavior of a 10 MW Floating Wind Turbine Concrete Platform under Harsh Conditions. Mathematics 2024, 12, 412. https://doi.org/10.3390/math12030412
Chen X, Wang Q, Zhang Y, Zheng Y. Dynamic Behavior of a 10 MW Floating Wind Turbine Concrete Platform under Harsh Conditions. Mathematics. 2024; 12(3):412. https://doi.org/10.3390/math12030412
Chicago/Turabian StyleChen, Xiaocui, Qirui Wang, Yuquan Zhang, and Yuan Zheng. 2024. "Dynamic Behavior of a 10 MW Floating Wind Turbine Concrete Platform under Harsh Conditions" Mathematics 12, no. 3: 412. https://doi.org/10.3390/math12030412
APA StyleChen, X., Wang, Q., Zhang, Y., & Zheng, Y. (2024). Dynamic Behavior of a 10 MW Floating Wind Turbine Concrete Platform under Harsh Conditions. Mathematics, 12(3), 412. https://doi.org/10.3390/math12030412









