Improving Risk Assessment Model for Cyber Security Using Robust Aggregation Operators for Bipolar Complex Fuzzy Soft Inference Systems
Abstract
:1. Introduction
- (1)
- To compute some algebraic operational laws for BCFSSs.
- (2)
- To propose BCFSWA, BCFSOWA, BCFSWG, and BCFSOWG operators with their properties, such as idempotency, monotonicity, and boundedness.
- (3)
- To improve the risk assessment technique for the cyber security model based on the proposed BCFSWA, BCFSOWA, BCFSWG, and BCFSOWG operators.
- (4)
- To illustrate the technique of MADM problems for these derived operators based on BCFS information.
- (5)
- To compare our ranking results with those of existing operators for evaluating or addressing the supremacy and validity of the proposed operators.
2. Preliminaries
3. Robust Aggregation Operators for BCFSSs
4. The MADM Method with Application to the Risk Assessment Model for Cyber Security
- (1)
- Threat intelligence integration “”.
- (2)
- Vulnerability assessment “”.
- (3)
- Threat modeling “”.
- (4)
- Collaboration and information sharing “”.
- (5)
- Third-party risk management “”.
5. Comparative Analysis
- (1)
- Mardani et al. [19] proposed AOs for FSs, where the FS theory contains the truth grade from the unit interval. However, the proposed operators based on BCFSS information, which is an extended version of FS, demonstrate that the proposed theory of Mardani et al. [19] is a special case for the proposed operators.
- (2)
- Bi et al. [20] and Hu et al. [21] presented the GOs and power operators for CFSs, where the CFS theory contains the truth grade in the shape of a complex number whose real and imaginary parts are from the unit interval. In fact, the proposed operators based on BCFSS information not only contain the truth grade but also have the falsity grade, and so the proposed theory of Bi et al. [20] and Hu et al. [21] cannot handle these cases under the BCFSS environment.
- (3)
- (4)
- (5)
- Jana et al. [25] gave robust AOs for BFSSs (bipolar fuzzy soft sets) that can only be used in the real plane but not in a complex system, so they cannot handle these cases under the BCFSS environment.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Chaomurilige, C.; Yu, J.; Yang, M.S. Analysis of parameter selection for Gustafson-Kessel fuzzy clustering using Jacobian matrix. IEEE Trans. Fuzzy Syst. 2015, 23, 2329–2342. [Google Scholar] [CrossRef]
- Ruspini, E.H.; Bezdek, J.C.; Keller, J.M. Fuzzy clustering: A historical perspective. IEEE Comput. Intell. Mag. 2019, 14, 45–55. [Google Scholar] [CrossRef]
- Yang, M.S.; Sinaga, K.P. Collaborative feature-weighted multi-view fuzzy c-means clustering. Pattern Recognit. 2021, 119, 108064. [Google Scholar] [CrossRef]
- Mei, Z.; Zhao, T.; Xie, X. Hierarchical fuzzy regression tree: A new gradient boosting approach to design a TSK fuzzy model. Inf. Sci. 2024, 652, 119740. [Google Scholar] [CrossRef]
- Zhang, W.R. Bipolar fuzzy sets and relations: A computational framework for cognitive modeling and multiagent decision analysis. In Proceedings of the NAFIPS/IFIS/NASA’94: Proceedings of the First International Joint Conference of The North American Fuzzy Information Processing Society Biannual Conference. The Industrial Fuzzy Control and Intellige, San Antonio, TX, USA, 18–21 December 1994; IEEE: New York, NY, USA, 1994; pp. 305–309. [Google Scholar]
- Zhang, W.R. From equilibrium-based business intelligence to information conservational quantum-fuzzy cryptography—A cellular transformation of bipolar fuzzy sets to quantum intelligence machinery. IEEE Trans. Fuzzy Syst. 2018, 26, 656–669. [Google Scholar] [CrossRef]
- Zararsız, Z.; Riaz, M. Bipolar fuzzy metric spaces with application. Comput. Appl. Math. 2022, 41, 49. [Google Scholar] [CrossRef]
- Rahman, Z.U.; Ali, G.; Asif, M.; Chen, Y.; Abidin, M.Z.U. Identification of desalination and wind power plants sites using m-polar fuzzy Aczel–Alsina aggregation information. Sci. Rep. 2024, 14, 409. [Google Scholar] [CrossRef] [PubMed]
- Ramot, D.; Milo, R.; Friedman, M.; Kandel, A. Complex fuzzy sets. IEEE Trans. Fuzzy Syst. 2002, 10, 171–186. [Google Scholar] [CrossRef]
- Mahmood, T.; Ur Rehman, U. A novel approach towards bipolar complex fuzzy sets and their applications in generalized similarity measures. Int. J. Intell. Syst. 2022, 37, 535–567. [Google Scholar] [CrossRef]
- Qiyas, M.; Naeem, M.; Khan, N.; Abdullah, L. Bipolar complex fuzzy credibility aggregation operators and their application in decision making problem. AIMS Math. 2023, 8, 19240–19263. [Google Scholar] [CrossRef]
- Gwak, J.; Garg, H.; Jan, N. Hybrid integrated decision-making algorithm for clustering analysis based on a bipolar complex fuzzy and soft sets. Alex. Eng. J. 2023, 67, 473–487. [Google Scholar] [CrossRef]
- Molodtsov, D. Soft set theory—First results. Comput. Math. Appl. 1999, 37, 19–31. [Google Scholar] [CrossRef]
- Roy, A.R.; Maji, P.K. A fuzzy soft set theoretic approach to decision making problems. J. Comput. Appl. Math. 2007, 203, 412–418. [Google Scholar] [CrossRef]
- Abdullah, S.; Aslam, M.; Ullah, K. Bipolar fuzzy soft sets and its applications in decision making problem. J. Intell. Fuzzy Syst. 2014, 27, 729–742. [Google Scholar] [CrossRef]
- Thirunavukarasu, P.; Suresh, R.; Ashokkumar, V. Theory of complex fuzzy soft set and its applications. Int. J. Innov. Res. Sci. Technol. 2017, 3, 13–18. [Google Scholar]
- Mahmood, T.; Ur Rehman, U.; Jaleel, A.; Ahmmad, J.; Chinram, R. Bipolar complex fuzzy soft sets and their applications in decision-making. Mathematics 2022, 10, 1048. [Google Scholar] [CrossRef]
- Mardani, A.; Nilashi, M.; Zavadskas, E.K.; Awang, S.R.; Zare, H.; Jamal, N.M. Decision making methods based on fuzzy aggregation operators: Three decades review from 1986 to 2017. Int. J. Inf. Technol. Decis. Mak. 2018, 17, 391–466. [Google Scholar] [CrossRef]
- Bi, L.; Dai, S.; Hu, B. Complex fuzzy geometric aggregation operators. Symmetry 2018, 10, 251. [Google Scholar] [CrossRef]
- Hu, B.; Bi, L.; Dai, S. Complex fuzzy power aggregation operators. Math. Probl. Eng. 2019, 2019, 1–7. [Google Scholar] [CrossRef]
- Mahmood, T.; Ur Rehman, U.; Ali, Z.; Aslam, M.; Chinram, R. Identification and classification of aggregation operators using bipolar complex fuzzy settings and their application in decision support systems. Mathematics 2022, 10, 1726. [Google Scholar] [CrossRef]
- Qiyas, M.; Naeem, M.; Khan, N.; Khan, S.; Khan, F. Confidence levels bipolar complex fuzzy aggregation operators and their application in decision making problem. IEEE Access 2024, 12, 6204–6214. [Google Scholar] [CrossRef]
- Despic, O.; Simonovic, S.P. Aggregation operators for soft decision making in water resources. Fuzzy Sets Syst. 2000, 115, 11–33. [Google Scholar] [CrossRef]
- Jana, C.; Pal, M.; Wang, J. A robust aggregation operator for multi-criteria decision-making method with bipolar fuzzy soft environment. Iran. J. Fuzzy Syst. 2019, 16, 1–16. [Google Scholar]
- Garg, H.; Mahmood, T.; ur Rehman, U.; Nguyen, G.N. Multi-attribute decision-making approach based on Aczel-Alsina power aggregation operators under bipolar fuzzy information and its application to quantum computing. Alex. Eng. J. 2023, 82, 248–259. [Google Scholar] [CrossRef]
- Akram, M.; Adeel, A.; Alcantud, J.C.R. Fuzzy N-soft sets: A novel model with applications. J. Intell. Fuzzy Syst. 2018, 35, 4757–4771. [Google Scholar] [CrossRef]
- Riaz, M.; Habib, A.; Saqlain, M.; Yang, M.S. Cubic bipolar fuzzy VIKOR method using new distance and entropy measures and Einstein averaging aggregation operators with application to renewable energy. Int. J. Fuzzy Syst. 2023, 25, 510–543. [Google Scholar] [CrossRef]
- Kahraman, C.; Cebi, S.; Oztaysi, B.; Cevik Onar, S. Intuitionistic fuzzy sets with ordered pairs and their usage in multi-attribute decision making: A novel intuitionistic fuzzy TOPSIS method with ordered pairs. Mathematics 2023, 11, 3867. [Google Scholar] [CrossRef]
- Alkan, N.; Kahraman, C. Continuous intuitionistic fuzzy sets (CINFUS) and their AHP&TOPSIS extension: Research proposals evaluation for grant funding. Appl. Soft Comput. 2023, 145, 110579. [Google Scholar]
| Symbols | Meanings | Symbols | Meanings | Symbols | Meanings |
|---|---|---|---|---|---|
| A universal set | The imaginary part of truth grade | Score value of | |||
| A set of parameters | The real part of falsity grade | Accuracy value of | |||
| A subset of parameters | The imaginary part of falsity grade | A scale number | |||
| The real part of truth grade | An element of the universal set | and | Weights | ||
| The complex number i | A BCFSN | A parameter |
| BCFSWA Operator | BCFSWG Operator | |
|---|---|---|
| BCFSWA Operator | BCFSWG Operator | |
|---|---|---|
| Methods | Ranking Values | Best Optimal |
|---|---|---|
| BCFSWA Operator | ||
| BCFSWG Operator |
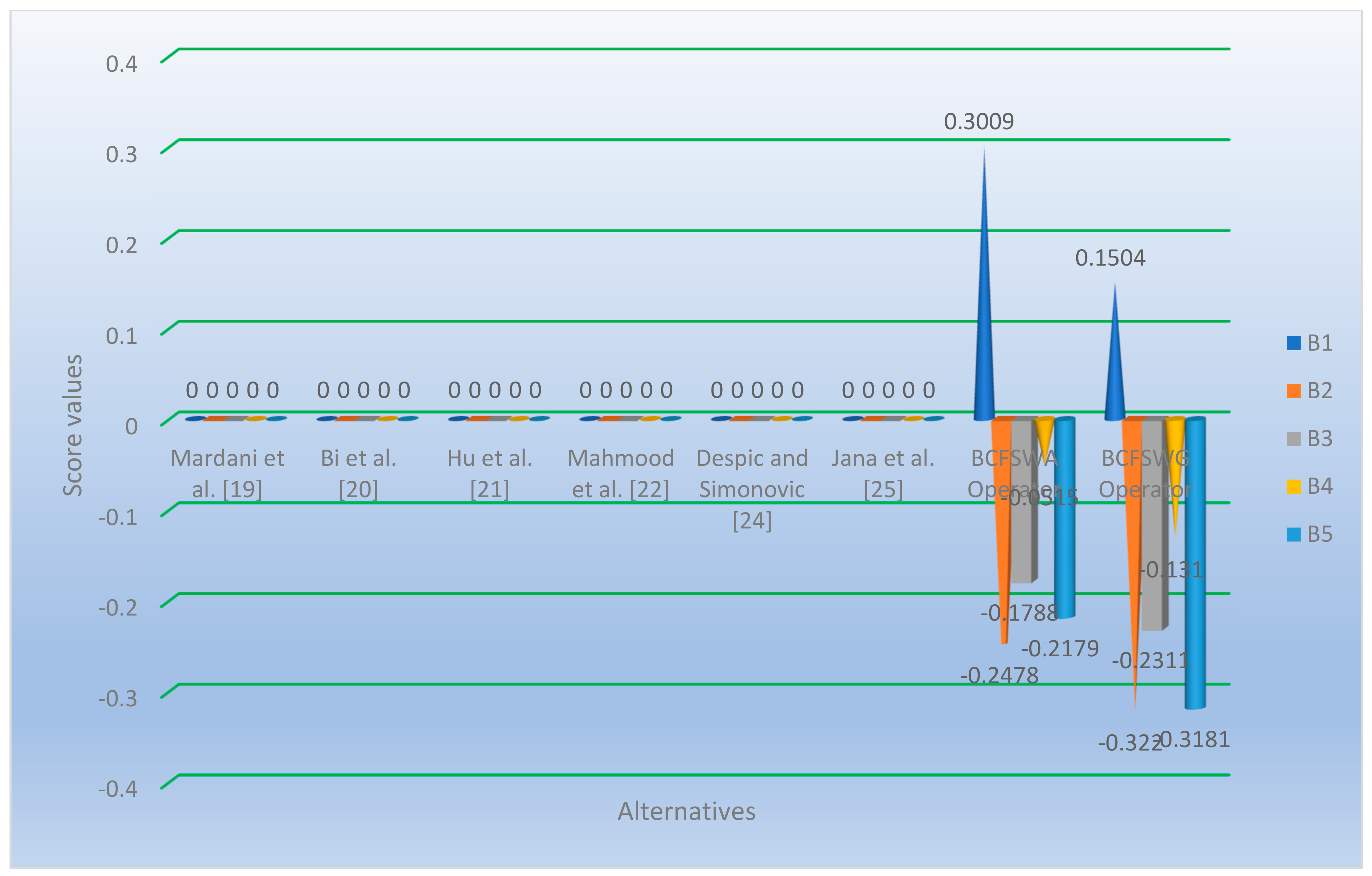
| Methods | Score Values | Ranking Values |
|---|---|---|
| Mardani et al. [19] | Failed | Failed |
| Bi et al. [20] | Failed | Failed |
| Hu et al. [21] | Failed | Failed |
| Mahmood et al. [22] | Failed | Failed |
| Despic and Simonovic [24] | Failed | Failed |
| Jana et al. [25] | Failed | Failed |
| BCFSWA Operator | 0.3009, −0.2478, −0.1788, −0.0515, −0.2179 | |
| BCFSWG Operator | 0.1504, −0.322, −0.2311, −0.131, −0.3181 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, Z.; Yang, M.-S. Improving Risk Assessment Model for Cyber Security Using Robust Aggregation Operators for Bipolar Complex Fuzzy Soft Inference Systems. Mathematics 2024, 12, 582. https://doi.org/10.3390/math12040582
Ali Z, Yang M-S. Improving Risk Assessment Model for Cyber Security Using Robust Aggregation Operators for Bipolar Complex Fuzzy Soft Inference Systems. Mathematics. 2024; 12(4):582. https://doi.org/10.3390/math12040582
Chicago/Turabian StyleAli, Zeeshan, and Miin-Shen Yang. 2024. "Improving Risk Assessment Model for Cyber Security Using Robust Aggregation Operators for Bipolar Complex Fuzzy Soft Inference Systems" Mathematics 12, no. 4: 582. https://doi.org/10.3390/math12040582
APA StyleAli, Z., & Yang, M.-S. (2024). Improving Risk Assessment Model for Cyber Security Using Robust Aggregation Operators for Bipolar Complex Fuzzy Soft Inference Systems. Mathematics, 12(4), 582. https://doi.org/10.3390/math12040582