Blizzard: A Distributed Consensus Protocol for Mobile Devices
Abstract
1. Introduction
- Blizzard is the first mobile-based leaderless Byzantine fault tolerant (BFT) distributed consensus protocol. Not only can mobile devices issue transactions, but they can participate in the core transaction verification and consensus process as well. This could increase the number of nodes capable of participating in validation by 2 to 3 orders of magnitude, thereby enhancing both adoption and security.
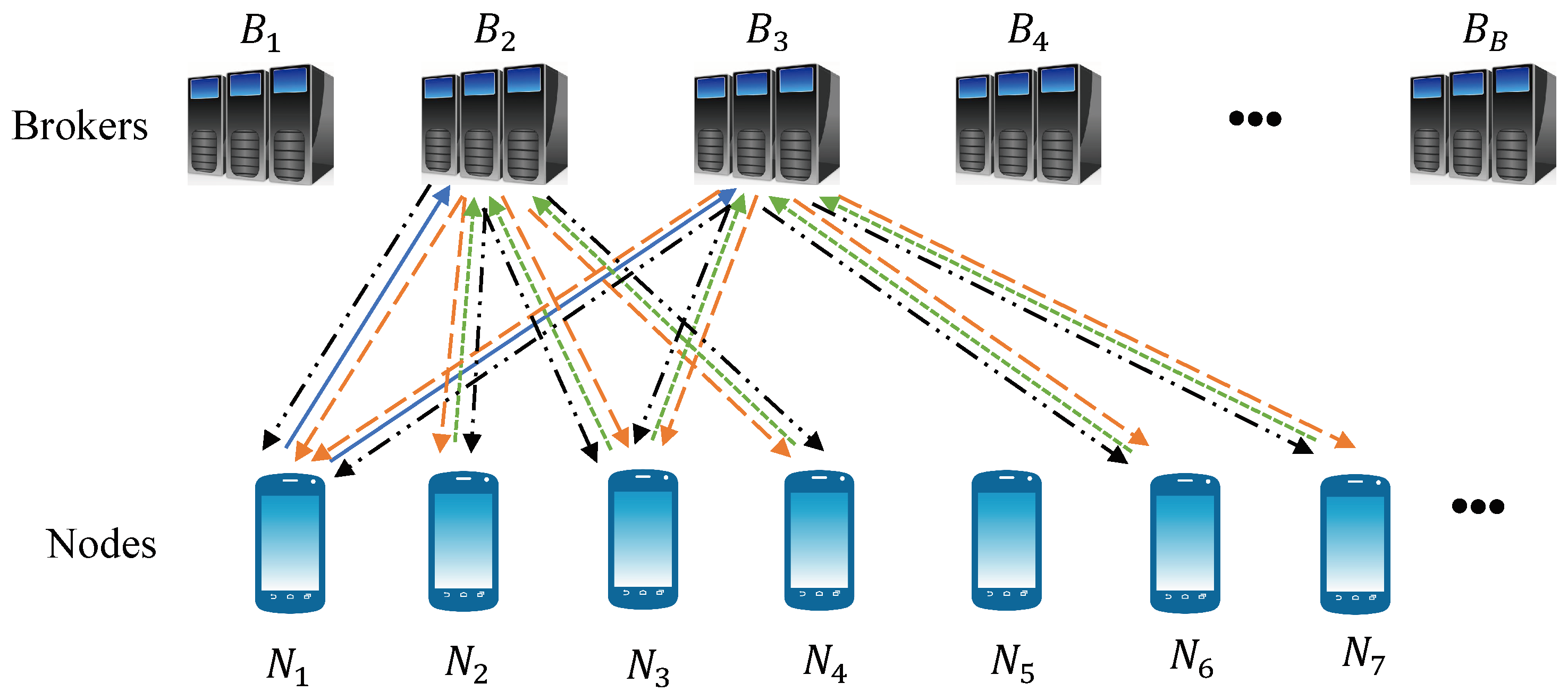
- We propose a novel two-tier protocol, where consensus between mobile nodes is enabled by the use of online brokers, and a decentralized matching scheme that ensures each mobile node connects to exactly k random brokers.
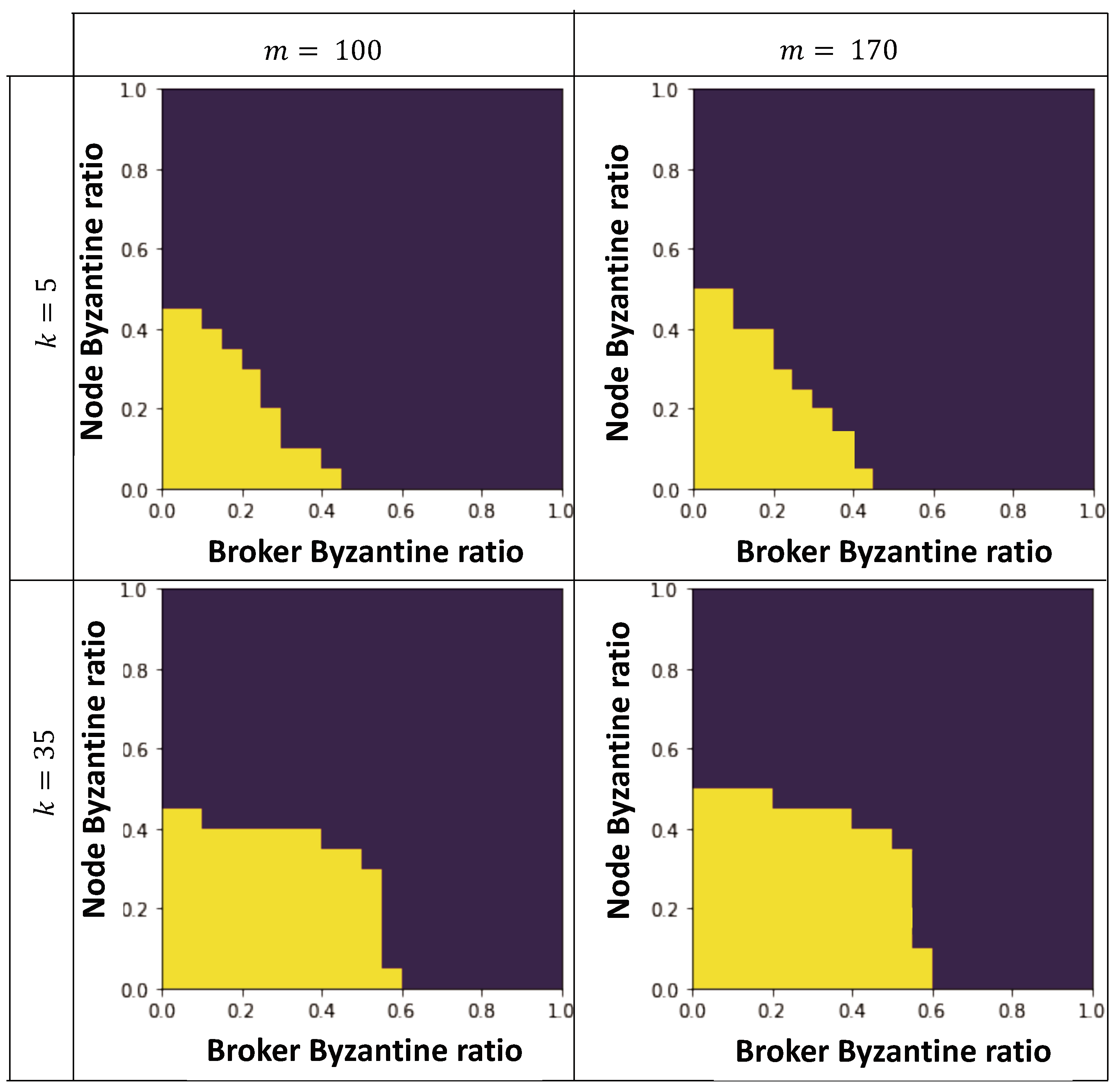
- Provable safety guarantee. We mathematically derive the set of ratios of Byzantine nodes and brokers for which Blizzard’s safety is guaranteed. We also discuss why liveness holds in Blizzard.
- We analytically characterize the throughput of Blizzard by modeling the sequential pipeline involved in processing transactions at each node and identifying the throughput bottleneck via empirical profiling.
- Likewise, we also analytically characterize the confirmation latency and message complexity of Blizzard. We show that the use of brokers in Blizzard creates a communication topology that allows for efficient consensus; under reasonable parameter settings, transactions are propagated in Blizzard within just four communication rounds with high probability.
- Through experiments based on a software implementation of Blizzard, we show that it is capable of 10,000 transactions per second per shard, and allows for sub-second confirmations.
2. Related Works
3. System Model
3.1. Proposed Blizzard Scheme
| Algorithm 1: Blizzard Algorithm |
 |
3.2. Distributed Random Matching
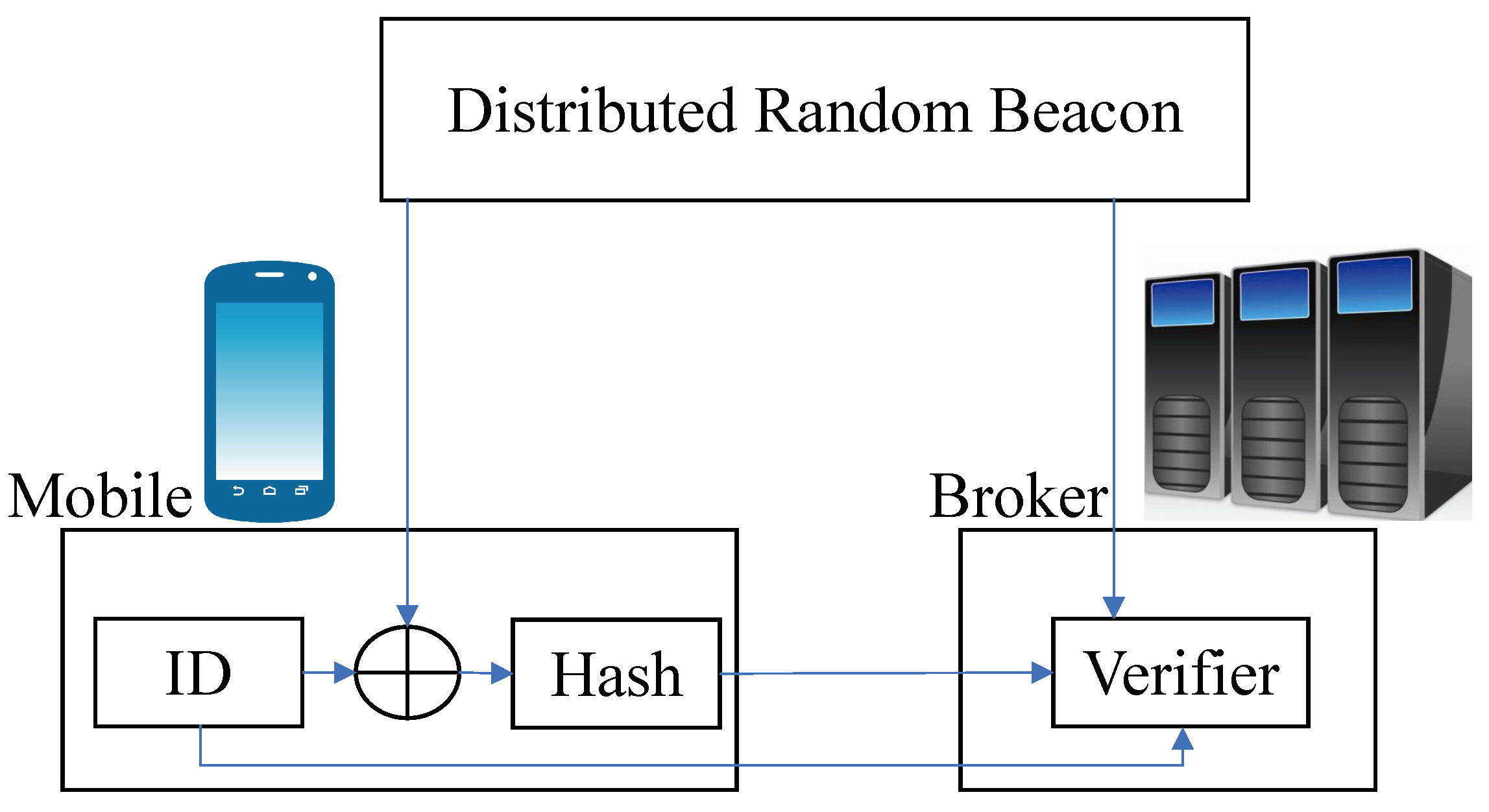
- Each mobile device applies a hash function on the combination of the random number coming from a distributed random beacon (note that a distributed random beacon is now live online at https://drand.love/ (accessed on 15 November 2023)) [32] with the ID of the mobile device. Regarding the hash function, it outputs B bits where 0 and 1 are equally likely. Then, the indices of the first k ones represent the brokers each mobile device has to connect with. The mobile device afterwards sends the output of its hash function as well as its IDs to the brokers it is supposed to connect with.
- Brokers validate the ID of mobile devices, verify that hash values generated by mobile devices are correctly produced, taking into account the distributed random beacon, and thus verify that mobile devices are authorized to connect.
4. Safety and Liveness
4.1. Safety Analysis
- Every correct mobile node always responds with honesty upon receiving any query.
- A queried Byzantine node may respond with any color or even refuse to respond.
- Every correct broker computes -majority of the votes collected from all nodes connected to it and broadcasts the majority vote to all of them.
- Byzantine brokers cannot forge information since they cannot cryptographically sign transactions from nodes. However, a Byzantine broker may compute -majority of the votes collected from an arbitrary subset of nodes connected to it and send the computed vote to any selected nodes that are connected to this broker. They could also choose not to communicate.
- (1)
- Conviction in Current Color (C3) counter to store how many consecutive computed majority votes have resulted in the same color. Once a node flips its color, this counter reset to zero. Furthermore, a node locks into the current color when this counter exceeds some security parameter .
- (2)
- Confidence counter to take into account the number of queries that have yielded a majority vote for their corresponding colors. A node flips its color only if the confidence value of its computed vote is larger than the confidence value of the current color. Moreover, a node locks into a color once the confidence value of this color exceeds some security parameter .
- Step 1:
- After some finite time, the system reaches the point where there are red nodes while the remaining nodes are blue.
- Step 2:
- At this point, v nodes have negative average growth in confidence value for blue color at any time (note that average growth in confidence value of node z for color x is ), with high probability. After a short period of time, we have , with high probability, and as a result, v nodes flip their color to red. Note that u nodes just gain more confidence in red as time elapses in this step.
4.1.1. Step 1
- When a u node queries: All Byzantine mobile nodes acquire red colors. Regarding the malicious brokers, all of them act with honesty without suppressing any color.
- When a v node queries: All Byzantine mobile nodes pick blue colors, and all Byzantine brokers with a red-color majority switch to a blue-majority broker by not reflecting their red-color mobile nodes. With high probability, as shown in Appendix A, a node is connected to at most Byzantine brokers in a population of r red brokers and blue brokers.
4.1.2. Step 2
- Binomial distribution (corresponds to terms or ) with normal distribution ,
- Hyper-geometric distribution with normal distribution ,
4.2. Liveness
5. Performance Analysis
5.1. Throughput per Shard
5.2. Latency
5.2.1. Propagation Time
5.2.2. Transaction Validation Time
5.2.3. Confidence-Gathering Time
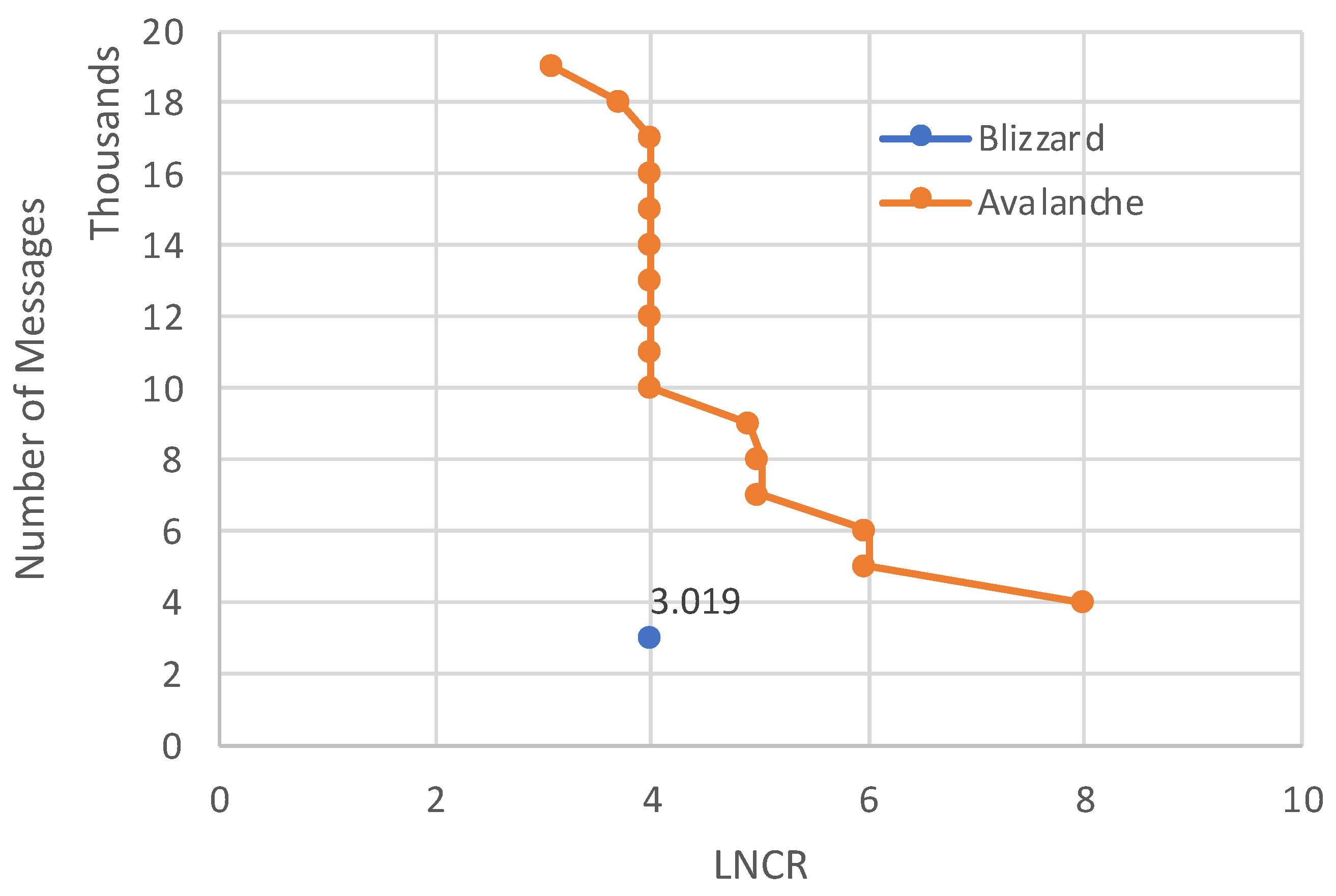
5.3. Average Message Complexity
6. Implementation and Experimental Measurements
6.1. Throughput Evaluation
| Network Bandwidth | 100 Mbps | 10 Mbps | 1 Mbps |
| Throughput on PCs | 10,000 TPS | 4166 TPS | 416 TPS |
6.2. Latency Evaluation
6.3. Battery Energy Consumption
7. Discussion
7.1. Mobile-Device-Oriented Sybil Control
7.2. Improving Scalability
7.3. Safety under a Partially Synchronous Model
7.4. Connectivity
7.5. Challenges in Real-World Implementation
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. High-Probability Connections
Appendix B. Overview on DAG Structure of the Ledger
References
- Walden, P.; Dahlberg, T.; Penttinen, E. Introduction to the Minitrack on Digital Mobile Services for Everyday Life. In Proceedings of the 52nd Hawaii International Conference on System Sciences, Maui, HI, USA, 8–11 January 2019. [Google Scholar]
- Greenstein, B. Delivering the Mobile Web to the Next Billion Users. In Proceedings of the 19th International Workshop on Mobile Computing Systems & Applications, Tempe, AZ, USA, 12–13 February 2018; p. 99. [Google Scholar]
- Biryukov, A.; Tikhomirov, S. Security and privacy of mobile wallet users in Bitcoin, Dash, Monero, and Zcash. Pervasive Mob. Comput. 2019, 59, 101030. [Google Scholar] [CrossRef]
- Sai, A.R.; Buckley, J.; Le Gear, A. Privacy and Security Analysis of Cryptocurrency Mobile Applications. In Proceedings of the 2019 Fifth Conference on Mobile and Secure Services (MobiSecServ), Miami, FL, USA, 2–3 March 2019; pp. 1–6. [Google Scholar]
- Yu, K.; Feng, J. Moore’s Law and Price Trends of Digital Products: The Case of Smartphones. Econ. Innov. New Technol. 2019, 10, 1628509. [Google Scholar]
- Kiamari, M.; Krishnamachari, B.; Naveed, M.; Yun, S. Distributed Consensus for Mobile Devices using Online Brokers. In Proceedings of the 2020 IEEE International Conference on Blockchain and Cryptocurrency (ICBC), Toronto, ON, Canada, 2–6 May 2020; pp. 1–3. [Google Scholar]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 15 December 2019).
- Garay, J.; Kiayias, A.; Leonardos, N. The bitcoin backbone protocol: Analysis and applications. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Sofia, Bulgaria, 26–30 April 2015. [Google Scholar]
- Castro, M.; Liskov, B. Practical Byzantine fault tolerance and proactive recovery. ACM Trans. Comput. Syst. (TOCS) 2002, 20, 398–461. [Google Scholar] [CrossRef]
- Bessani, A.; Sousa, J.; Alchieri, E.E. State machine replication for the masses with BFT-SMaRt. In Proceedings of the 2014 44th Annual IEEE/IFIP International Conference on Dependable Systems and Networks, Atlanta, GA, USA, 23–26 June 2014; pp. 355–362. [Google Scholar]
- Kwon, J. Tendermint: Consensus without Mining. 2014. Available online: http://tendermint.com/docs/tendermint.pdf (accessed on 15 November 2023).
- Abraham, I.; Gueta, G.; Malkhi, D. Hot-Stuff the Linear, Optimal-Resilience, One-Message BFT Devil. CoRR 2018, abs/1803.05069. [Google Scholar]
- Zamfir, V.; Rush, N.; Asgaonkar, A.; Piliouras, G. Introducing the “Minimal CBC Casper” Family of Consensus Protocols; DRAFT v1. 0; Ethereum Research: Zug, Switzerland, 2018. [Google Scholar]
- Baird, L. The Swirlds Hashgraph Consensus Algorithm: Fair, Fast, Byzantine Fault Tolerance; Swirlds Tech Report SWIRLDS-TR-2016-01; Swirlds Inc.: College Station, TX, USA, 2016; Volume 34, pp. 9–11. [Google Scholar]
- Rocket, T.; Yin, M.; Sekniqi, K.; van Renesse, R.; Sirer, E.G. Scalable and Probabilistic Leaderless BFT Consensus through Metastability. arXiv 2019, arXiv:1906.08936. [Google Scholar]
- Crain, T.; Gramoli, V.; Larrea, M.; Raynal, M. DBFT: Efficient Leaderless Byzantine Consensus and its Application to Blockchains. In Proceedings of the 2018 IEEE 17th International Symposium on Network Computing and Applications (NCA), Cambridge, MA, USA, 1–3 November 2018; pp. 1–8. [Google Scholar]
- Gagol, A.; Swietek, M. Aleph: A Leaderless, Asynchronous, Byzantine Fault Tolerant Consensus Protocol. arXiv 2018, arXiv:1810.05256. [Google Scholar]
- Popov, S. The Tangle. 2016. Available online: https://www.iota.org/research/academic-papers (accessed on 15 December 2019).
- Zhelezov, D.; Fohrmann, O. HelixMesh: A Consensus Protocol for IoT. In Proceedings of the 2019 International Electronics Communication Conference, Okinawa, Japan, 7–9 July 2019; pp. 44–51. [Google Scholar]
- Cosmos. Available online: https://cosmos.network/resources/whitepaper (accessed on 18 December 2019).
- Micali, S. ALGORAND: The Efficient and Democratic Ledger. arXiv 2016, arXiv:1607.01341. [Google Scholar]
- Kiayias, A.; Russell, A.; David, B.; Oliynykov, R. Ouroboros: A Provably Secure Proof-of-Stake Blockchain Protocol. Cryptology ePrint Archive, Report 2016/889. 2016. Available online: https://eprint.iacr.org/2016/889 (accessed on 15 November 2023).
- Hanke, T.; Movahedi, M.; Williams, D. DFINITY Technology Overview Series, Consensus System. CoRR 2018, abs/1805.04548. [Google Scholar]
- Fairley, P. Ethereum will cut back its absurd energy use. IEEE Spectr. 2018, 56, 29–32. [Google Scholar] [CrossRef]
- Androulaki, E.; Barger, A.; Bortnikov, V.; Cachin, C.; Christidis, K.; De Caro, A.; Enyeart, D.; Ferris, C.; Laventman, G.; Manevich, Y.; et al. Hyperledger fabric: A distributed operating system for permissioned blockchains. In Proceedings of the Thirteenth EuroSys Conference, Porto, Portugal, 23–26 April 2018. [Google Scholar]
- Olson, K.; Bowman, M.; Mitchell, J.; Amundson, S.; Middleton, D.; Montgomery, C. Sawtooth: An Introduction; The Linux Foundation: San Francisco, CA, USA, 2018. [Google Scholar]
- Wu, W.; Cao, J.; Yang, J.; Raynal, M. A hierarchical consensus protocol for mobile ad hoc networks. In Proceedings of the 14th Euromicro International Conference on Parallel, Distributed, and Network-Based Processing (PDP’06), Sochaux, France, 15–17 February 2006; p. 9. [Google Scholar] [CrossRef]
- Badache, N.; Hurfin, M.; Macedo, R. Solving the consensus problem in a mobile environment. In Proceedings of the 1999 IEEE International Performance, Computing and Communications Conference (Cat. No.99CH36305), Scottsdale, AZ, USA, 10–12 February 1999; pp. 29–35. [Google Scholar]
- Wu, W.; Cao, J.; Raynal, M. Eventual Clusterer: A Modular Approach to Designing Hierarchical Consensus Protocols in MANETs. IEEE Trans. Parallel Distrib. Syst. 2009, 20, 753–765. [Google Scholar] [CrossRef]
- Wu, W.; Cao, J.; Yang, J.; Raynal, M. Design and Performance Evaluation of Efficient Consensus Protocols for Mobile Ad Hoc Networks. IEEE Trans. Comput. 2007, 56, 1055–1070. [Google Scholar] [CrossRef]
- Pass, R.; Shi, E. Hybrid Consensus: Efficient Consensus in the Permissionless Model. In Proceedings of the 31st International Symposium on Distributed Computing (DISC 2017), Vienna, Austria, 16–20 October 2017; pp. 1–16. [Google Scholar]
- Syta, E.; Jovanovic, P.; Kogias, E.K.; Gailly, N.; Gasser, L.; Khoffi, I.; Fischer, M.J.; Ford, B. Scalable Bias-Resistant Distributed Randomness. In Proceedings of the 2017 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–24 May 2017; pp. 444–460. [Google Scholar]
- Bowling, S.; Khasawneh, M.; Kaewkuekool, S.; Cho, B. A logistic approximation to the cumulative normal distribution. J. Ind. Eng. Manag. 2009, 2, 114–127. [Google Scholar] [CrossRef]
- Halpern, M.; Zhu, Y.; Reddi, V.J. Mobile CPU’s rise to power: Quantifying the impact of generational mobile CPU design trends on performance, energy, and user satisfaction. In Proceedings of the 2016 IEEE International Symposium on High Performance Computer Architecture (HPCA), Barcelona, Spain, 12–16 March 2016; pp. 64–76. [Google Scholar]
- Jiang, Z.; Krishnamachari, B.; Zhou, S.; Niu, Z. SENATE: A Permissionless Byzantine Consensus Protocol in Wireless Networks. arXiv 2018, arXiv:1803.08694. [Google Scholar]
- King, R.J. Introduction to Proof of Location: The Case for Alternative Location Systems. 2018. FOAM. Available online: https://blog.foam.space/introduction-to-proof-of-location-6b4c77928022 (accessed on 15 November 2023).
- Martinez, M.; Hekmati, A.; Krishnamachari, B.; Yun, S. Mobile Encounter-based Social Sybil Control. In Proceedings of the 2nd International Workshop on Blockchain Applications and Theory (BAT), Paris, France, 20–23 April 2020. [Google Scholar]
- On Sharding Blockchains, Ethereum Wiki. Available online: http://github.com/ethereum/wiki/wiki/Sharding-FAQ (accessed on 15 November 2023).
- On Pruning in Ethereum. Available online: http://tiny.cc/ethpruning (accessed on 15 November 2023).
- Al-Bassam, M.; Sonnino, A.; Buterin, V. Fraud Proofs: Maximising Light Client Security and Scaling Blockchains with Dishonest Majorities. arXiv 2018, arXiv:1809.09044. [Google Scholar]

| Protocol | Sybil Control Method | Leaderless | Ledger Structure | BFT | Transaction per Second per shard | Confirmation Latency | Number of Validators | Mobile-Based |
|---|---|---|---|---|---|---|---|---|
| Bitcoin [7] | PoW | No | Chain | No | 7 | ∼40 min | 100k+ | No |
| Ethereum [24] | PoW/PoS | No | Chain | No | 20 | ∼60 s | 100k+ | No |
| Tendermint [11] | Agnostic | No | Chain | Yes | ∼10,000 | ∼2–15 s | ∼100–1k | No |
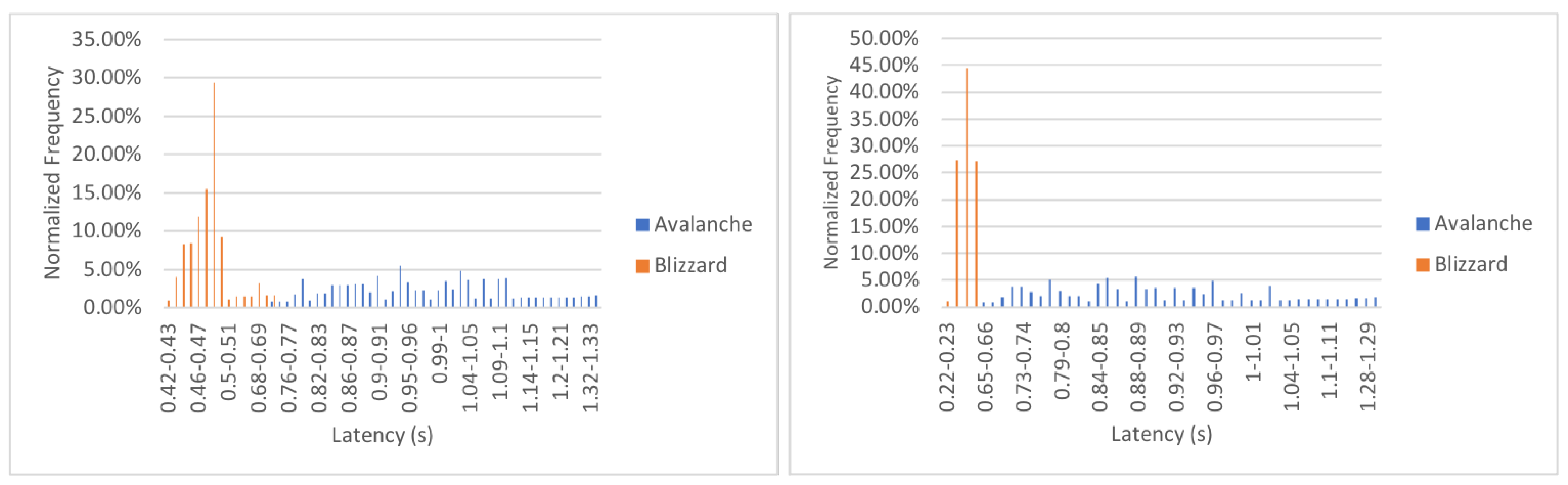
| Avalanche [15] | Agnostic | Yes | DAG | Yes | ∼3400 | ∼1.35 s | 100k+ | No |
| Blizzard | Agnostic | Yes | DAG | Yes | ∼10,000 | ∼0.65 s | 100M+ | Yes |
| n | : | Number of all mobile nodes (where ). |
| c | : | Number of correct mobile nodes. |
| b | : | Number of Byzantine mobile nodes. |
| m | : | Number of all brokers. |
| : | Number of correct brokers. | |
| : | Number of Byzantine brokers. | |
| : | Set of connected mobile nodes to broker b. | |
| : | Set of connected brokers to mobile node u. | |
| k | : | Number of brokers being sampled by each mobile node. |
| : | Majority threshold of mobile nodes for considering a “yes” vote. | |
| : | Majority threshold of brokers for considering a “yes” vote. | |
| : | Security threshold used for consecutive counter. | |
| : | Security threshold used for confidence counter. |
| Protocol | Transaction per Second per Shard | Confirmation Latency | Number of Validators | Mobile-Based |
|---|---|---|---|---|
| Avalanche [15] | ∼3400 | ∼1.35 s | 100k+ | No |
| Blizzard | ∼10,000 | ∼0.65 s | 100M+ | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kiamari, M.; Krishnamachari , B.; Yun, S. Blizzard: A Distributed Consensus Protocol for Mobile Devices. Mathematics 2024, 12, 707. https://doi.org/10.3390/math12050707
Kiamari M, Krishnamachari B, Yun S. Blizzard: A Distributed Consensus Protocol for Mobile Devices. Mathematics. 2024; 12(5):707. https://doi.org/10.3390/math12050707
Chicago/Turabian StyleKiamari, Mehrdad, Bhaskar Krishnamachari , and Seokgu Yun. 2024. "Blizzard: A Distributed Consensus Protocol for Mobile Devices" Mathematics 12, no. 5: 707. https://doi.org/10.3390/math12050707
APA StyleKiamari, M., Krishnamachari , B., & Yun, S. (2024). Blizzard: A Distributed Consensus Protocol for Mobile Devices. Mathematics, 12(5), 707. https://doi.org/10.3390/math12050707







