Halpern-Type Inertial Iteration Methods with Self-Adaptive Step Size for Split Common Null Point Problem
Abstract
1. Introduction
2. Preliminaries
- (i)
- contraction, if
- (ii)
- nonexpansive, if
- (iii)
- firmly nonexpansive, if
- (i)
- V is called monotone, if ;
- (ii)
- ;
- (iii)
- V is called maximal monotone, if V is monotone and , for and I is an identity mapping.
- (i)
- (ii)
- or
- (i)
- if is monotone and be the resolvent of V, then and are firmly nonexpansive for .
- (ii)
- if is nonexpansive, then is demiclosed at zero and if V is firmly nonexpansive then is firmly nonexpansive.
- (i)
- exists, ,
- (ii)
3. Main Results
- and are maximal monotone operators;
- is a bounded linear operator;
- is a sequence in so that and ;
- is a positive sequence so that and ;
- The solution set of is express by and .
| Algorithm 1 Choose and are given. Choose arbitrary points and and set . |
| Iterative Step: For iterates , and , , select , where
|
- Case II: If the Case I is not true, then there exists a subsequence of such that and the sequence defined by is an increasing sequence and as and
| Algorithm 2 Choose and are given. Choose arbitrary points and and set . |
| Iterative Step: Given the iterates , and , , choose , where
|
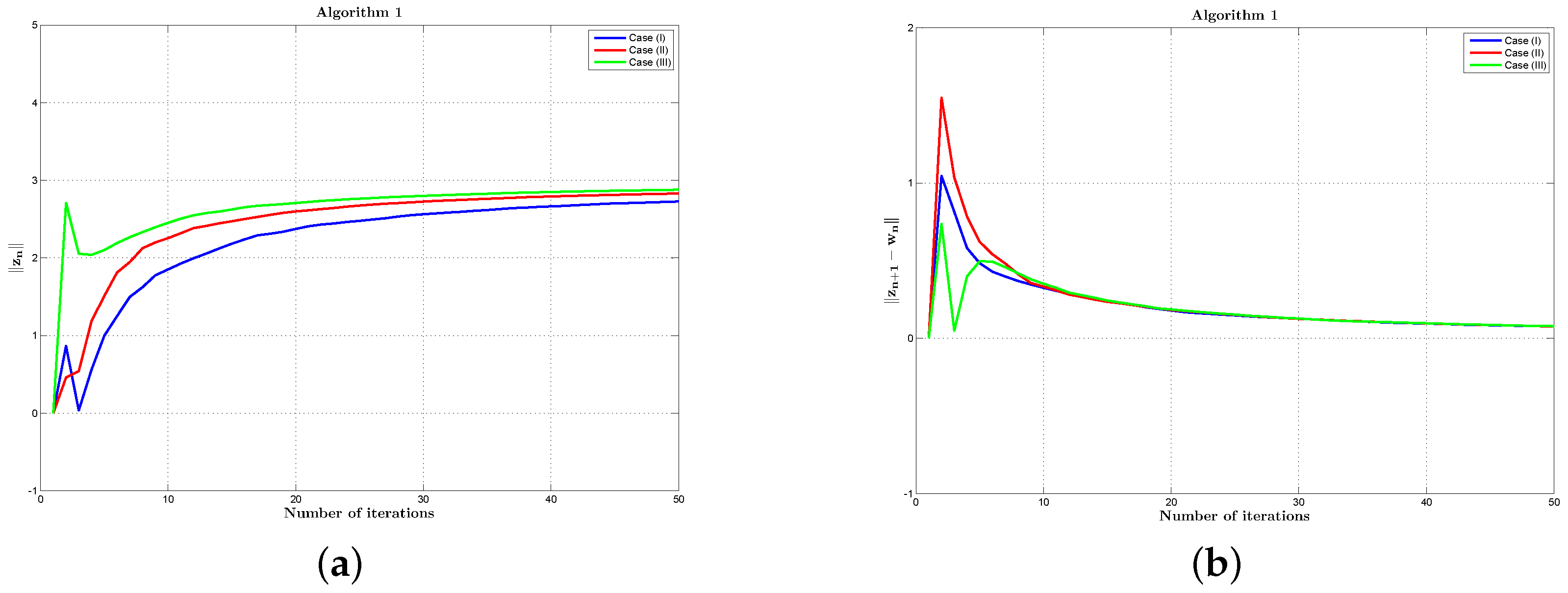
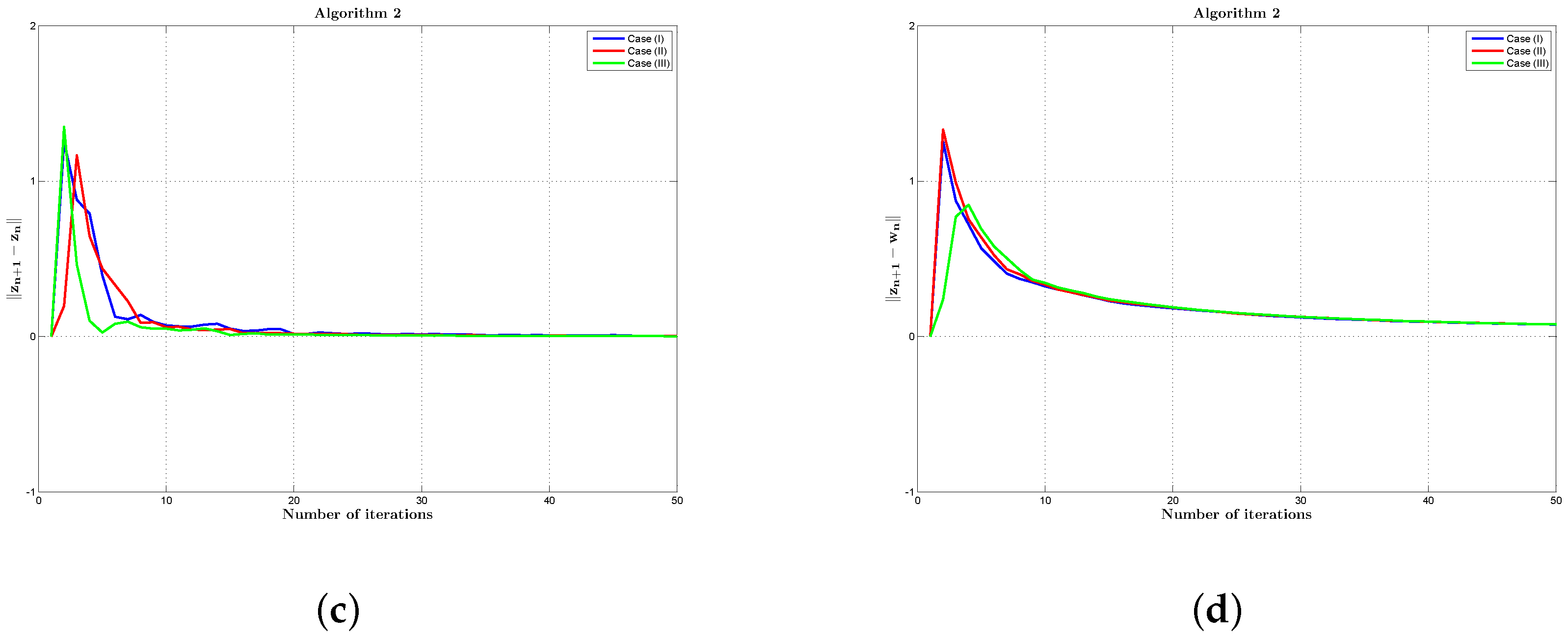
4. Numerical Experiments
- Case (I):
- , , , .
- Case (II):
- , , , .
- Case (III):
- , , , , .
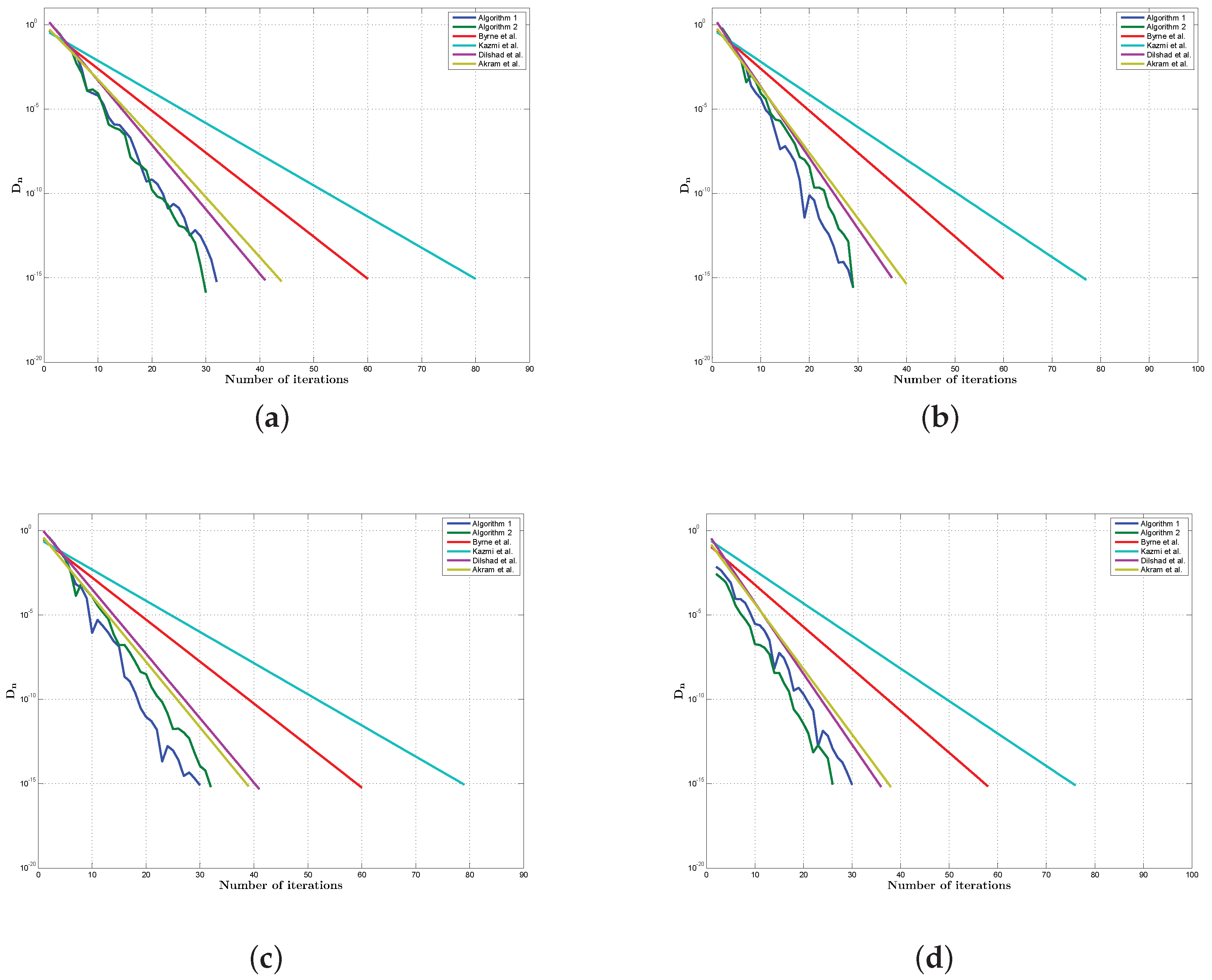
- Case (A):
- , , ;
- Case (B):
- , , ;
- Case (C):
- , , ;
- Case (D):
- , , ;
- Case(A′):
- and ;
- Case(B′):
- and ;
- Case(C′):
- and ;
- Case(D′):
- and ;
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Censor, Y.; Elfving, T.; Kopf, N.; Bortfeld, T. The multiple-sets split feasibility problem and its applications for inverse problems. Inverse Probl. 2005, 21, 2071–2084. [Google Scholar] [CrossRef]
- Combettes, P.L. The convex feasibilty problem in image recovery. In Advance in Image and Electronphysiccs; Hawkes, P., Ed.; Academic Press: New York, NY, USA, 1996; Volume 95, pp. 155–270. [Google Scholar]
- Censor, Y.; Bortfeld, T.; Martin, B.; Trofimov, A. A unified approach for inversion problem in intensity modulated radiation therapy. Phys. Med. Biol. 2006, 51, 2353–2365. [Google Scholar] [CrossRef]
- Censor, Y.; Elfving, T. A multi projection algorithm using Bregman projections in a product space. Numer. Algor. 1994, 8, 221–239. [Google Scholar] [CrossRef]
- Xu, H.K. Iterative methods for split feasibility problem in infinite dimensional Hilbert spaces. Inverse Prob. 2010, 26, 105018. [Google Scholar] [CrossRef]
- Censor, Y.; Gibali, A.; Reich, S. Algorithms for the split variational inequality problem. Numer. Algor. 2012, 59, 301–323. [Google Scholar] [CrossRef]
- Moudafi, A. Split monotone variational inclusions. J. Optim. Theory Appl. 2011, 150, 275–283. [Google Scholar] [CrossRef]
- Byrne, C.; Censor, Y.; Gibali, A.; Reich, S. Weak and strong convergence of algorithms for split common null point problem. J. Nonlinear Convex Anal. 2012, 13, 759–775. [Google Scholar]
- Kazmi, K.R.; Rizvi, S.H. An iterative method for split variational inclusion problem and fixed point problem for a nonexpansive mapping. Optim. Lett. 2014, 8, 1113–1124. [Google Scholar] [CrossRef]
- Dilshad, M.; Aljohani, A.F.; Akram, M. Iterative scheme for split variational inclusion and a fixed-point problem of a finite collection of nonexpansive mappings. J. Funct. Spaces 2020, 2020, 3567648. [Google Scholar] [CrossRef]
- Akram, M.; Dilshad, M.; Rajpoot, A.K.; Babu, F.; Ahmad, R.; Yao, J.-C. Modified iterative schemes for a fixed point problem and a split variational inclusion problem. Mathematics 2022, 10, 2098. [Google Scholar] [CrossRef]
- Arfat, Y.; Kumam, P.; Khan, M.A.A.; Ngiamsunthorn, P.S. Shrinking approximants for fixed point problem and generalized split null point problem in Hilbert spaces. Optim. Lett. 2022, 16, 1895–1913. [Google Scholar] [CrossRef]
- Sitthithakerngkiet, K.; Deepho, J.; Kumam, P. A hybrid viscosity algorithm via modify the hybrid steepest descent method for solving the split variational inclusion in image reconstruction and fixed point problems. Appl. Math. Comp. 2015, 250, 986–1001. [Google Scholar] [CrossRef]
- Suantai, S.; Shehu, Y.; Cholamjiak, P. Nonlinear iterative methods for solving the split common null point problem in Banach spaces. Optim. Methods Softw. 2019, 34, 853–874. [Google Scholar] [CrossRef]
- Chugh, R.; Gupta, N. Strong convergence of new split general system of monotone variational inclusion problem. Appl. Anal. 2014, 103, 138–165. [Google Scholar] [CrossRef]
- Tang, Y. New algorithms for split common null point problems. Optimization 2020, 70, 1141–1160. [Google Scholar] [CrossRef]
- Moudafi, A.; Thakur, B.S. Solving proximal split feasibilty problem without prior knowledge of matrix norms. Optim. Lett. 2014, 8, 2099–2110. [Google Scholar] [CrossRef]
- Ngwepe, M.D.; Jolaoso, L.O.; Aphane, M.; Adenekan, I.O. An algorithm that adjusts the stepsize to be self-adaptive with an inertial term aimed for solving split variational inclusion and common fixed point problems. Mathematics 2023, 11, 4708. [Google Scholar] [CrossRef]
- Zhu, L.-J.; Yao, Y. Algorithms for approximating solutions of split variational inclusion and fixed-point problems. Mathematics 2023, 11, 641. [Google Scholar] [CrossRef]
- Lopez, G.; Martin-Marquez, V.; Xu, H.K. Solving the split feasibilty problem without prior knowledge of matrix norms. Inverse Probl. 2012, 28, 085004. [Google Scholar] [CrossRef]
- Dilshad, M.; Akram, M.; Ahmad, I. Algorithms for split common null point problem without pre-existing estimation of operator norm. J. Math. Inequal. 2020, 14, 1151–1163. [Google Scholar] [CrossRef]
- Alvarez, F.; Attouch, H. An inertial proximal method for maximal monotone operators via discretization of a nonlinear osculattor ith damping. Set-Valued Anal. 2001, 9, 3–11. [Google Scholar] [CrossRef]
- Arfat, Y.; Kumam, P.; Ngiamsunthorn, P.S.; Khan, M.A.A. An accelerated projection based parallel hybrid algorithm for fixed point and split null point problems in Hilbert spaces. Math. Meth. Appl. Sci. 2021. [Google Scholar] [CrossRef]
- Dilshad, M.; Akram, M.; Nsiruzzaman, M.; Filali, D.; Khidir, A.A. Adaptive inertial Yosida approximation iterative algorithms for split variational inclusion and fixed point problems. AIMS Math. 2023, 8, 12922–12942. [Google Scholar] [CrossRef]
- Filali, D.; Dilshad, M.; Alyasi, L.S.M.; Akram, M. Inertial iterative algorithms for split variational inclusion and fixed point problems. Axioms 2023, 12, 848. [Google Scholar] [CrossRef]
- Tang, Y.; Lin, H.; Gibali, A.; Cho, Y.-J. Convegence analysis and applicatons of the inertial algorithm solving inclusion problems. Appl. Numer. Math. 2022, 175, 1–17. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, Y.; Gibali, A. New self-adaptive inertial-like proximal point methods for the split common null point problem. Symmetry 2021, 13, 2316. [Google Scholar] [CrossRef]
- Tang, Y.; Gibali, A. New self-adaptive step size algorithms for solving split variational inclusion problems and its applications. Numer. Algor. 2019, 83, 305–331. [Google Scholar] [CrossRef]
- Reich, S.; Taiwo, A. Fast iterative schemes for solving variational inclusion problems. Math. Meth. Appl. Sci. 2023, 46, 17177–17198. [Google Scholar] [CrossRef]
- Xu, H.K. Iterative algorithms for nonlinear operators. J. Lond. Math. Soc. 2002, 66, 240–256. [Google Scholar] [CrossRef]
- Bauschke, H.H.; Combettes, P.L. Convex Analysis and Monotone Operator Theory in Hilbert Space; Springer: Berlin, Germany, 2011. [Google Scholar]
- Opial, Z. Weak covergence of the sequence of successive approximations of nonexpansive mappings. Bull. Am. Math. Soc. 1976, 73, 591–597. [Google Scholar] [CrossRef]
- Mainge, P.E. Strong convergence of projected subgradient methods for nonsmooth and nonstrictly convex minimization. Set-Valued Anal. 2008, 16, 899–912. [Google Scholar] [CrossRef]

| Methods | Iter (n)/Times (s) | Case (A) | Case (B) | Case (C) | Case (D) |
|---|---|---|---|---|---|
| Algorithm 1 | Iteration | 48 | 50 | 52 | 59 |
| Time/s | 5.10 × | 4.40 × | 4.90 × | 1.10 × | |
| Algorithm 2 | Iteration | 41 | 50 | 41 | 50 |
| Time/s | 4.70 × | 3.00 × | 1.16 × | 3.00 × | |
| Byrne et al. [8] | Iteration | 102 | 108 | 100 | 101 |
| Time/s | 1.93 × | 1.63 × | 2.17 × | 1.73 × | |
| Kazmi et al. [9] | Iteration | 109 | 114 | 107 | 111 |
| Time/s | 2.20 × | 3.20 × | 2.00 × | 2.00 × | |
| Dilshad et al. [21] | Iteration | 126 | 128 | 109 | 120 |
| Time/s | 5.20 × | 3.10 × | 2.30 × | 3.00 × | |
| Akram et al. [11] | Iteration | 105 | 110 | 108 | 104 |
| Time/s | 1.28 × | 1.10 × | 1.14 × | 9.44 × |
| Methods | Iter (n)/Times (s) | Case (A′) | Case (B′) | Case (C′) | Case (D′) |
|---|---|---|---|---|---|
| Algorithm 1 | Iteration | 34 | 28 | 30 | 30 |
| Time/s | 1.36 × | 1.93 × | 1.36 × | 1.39 × | |
| Algorithm 2 | Iteration | 29 | 28 | 33 | 26 |
| Time/s | 1.34 × | 1.45 × | 1.3× | 1.24 × | |
| Byrne et al. [8] | Iteration | 60 | 60 | 59 | 57 |
| Time/s | 1.54 × | 1.06 × | 1.78 × | 1.03 × | |
| Kazmi et al. [9] | Iteration | 80 | 77 | 79 | 76 |
| Time/s | 1.04 × | 1.02 × | 9.6 × | 1.16 × | |
| Dilshad et al. [21] | Iteration | 41 | 37 | 41 | 37 |
| Time/s | 3.23 × | 4.49 × | 3.14 × | 3.97 × | |
| Akram et al. [11] | Iteration | 44 | 40 | 39 | 38 |
| Time/s | 1.53 × | 2.33 × | 1.56 × | 2.05 × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alamer, A.; Dilshad, M. Halpern-Type Inertial Iteration Methods with Self-Adaptive Step Size for Split Common Null Point Problem. Mathematics 2024, 12, 747. https://doi.org/10.3390/math12050747
Alamer A, Dilshad M. Halpern-Type Inertial Iteration Methods with Self-Adaptive Step Size for Split Common Null Point Problem. Mathematics. 2024; 12(5):747. https://doi.org/10.3390/math12050747
Chicago/Turabian StyleAlamer, Ahmed, and Mohammad Dilshad. 2024. "Halpern-Type Inertial Iteration Methods with Self-Adaptive Step Size for Split Common Null Point Problem" Mathematics 12, no. 5: 747. https://doi.org/10.3390/math12050747
APA StyleAlamer, A., & Dilshad, M. (2024). Halpern-Type Inertial Iteration Methods with Self-Adaptive Step Size for Split Common Null Point Problem. Mathematics, 12(5), 747. https://doi.org/10.3390/math12050747






