Impact of Demographic Developments and PCV13 Vaccination on the Future Burden of Pneumococcal Diseases in Germany—An Integrated Probabilistic Differential Equation Approach
Abstract
:1. Introduction
1.1. Motivation and Background
1.2. State of the Literature
2. Materials and Methods
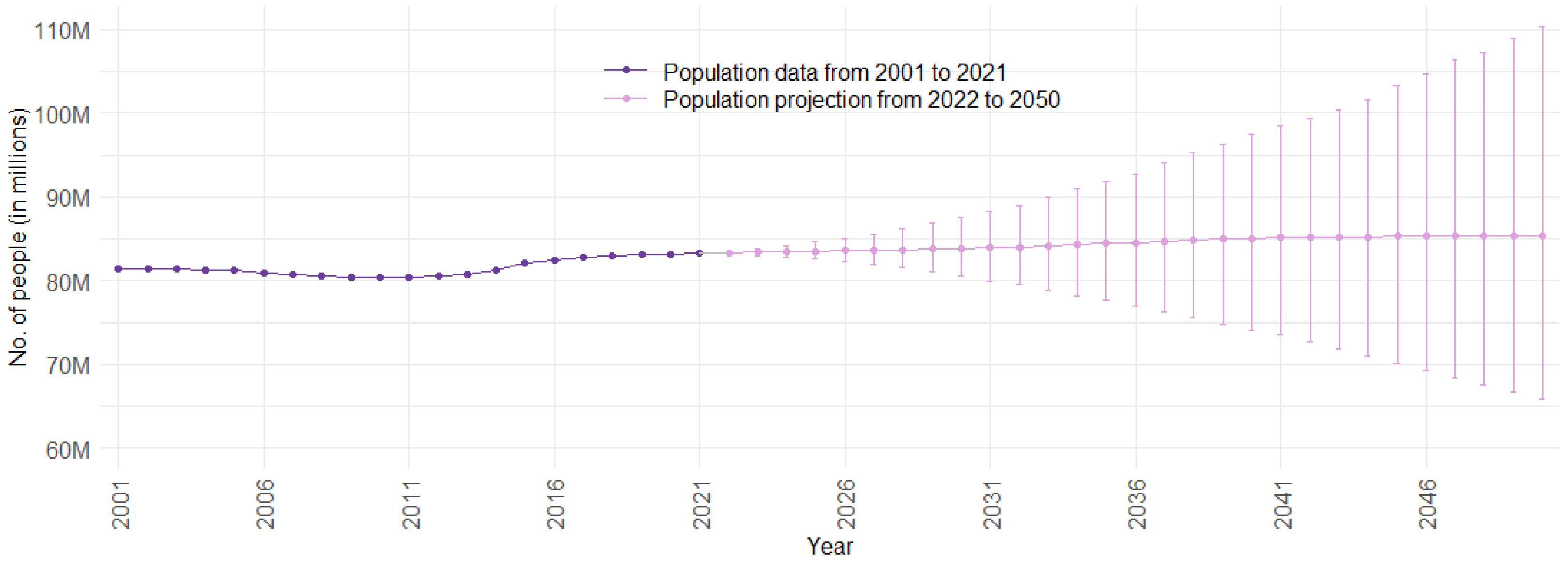
2.1. Population Forecast Approach
2.1.1. Demographic Data (Preparation)
2.1.2. Population Forecast Model
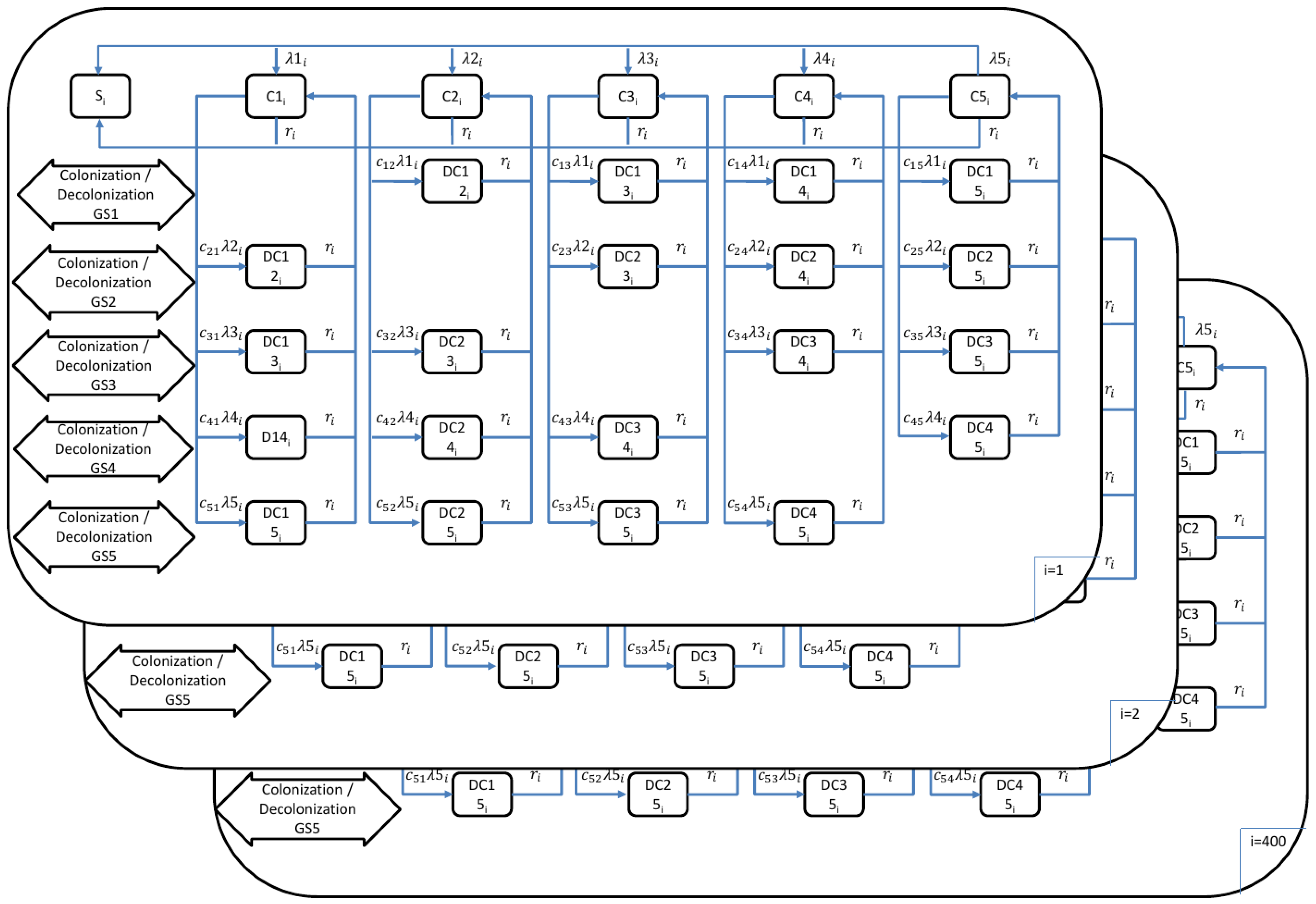
2.2. Transmission Dynamic Model to Estimate the Burden of Pneumococcal Disease
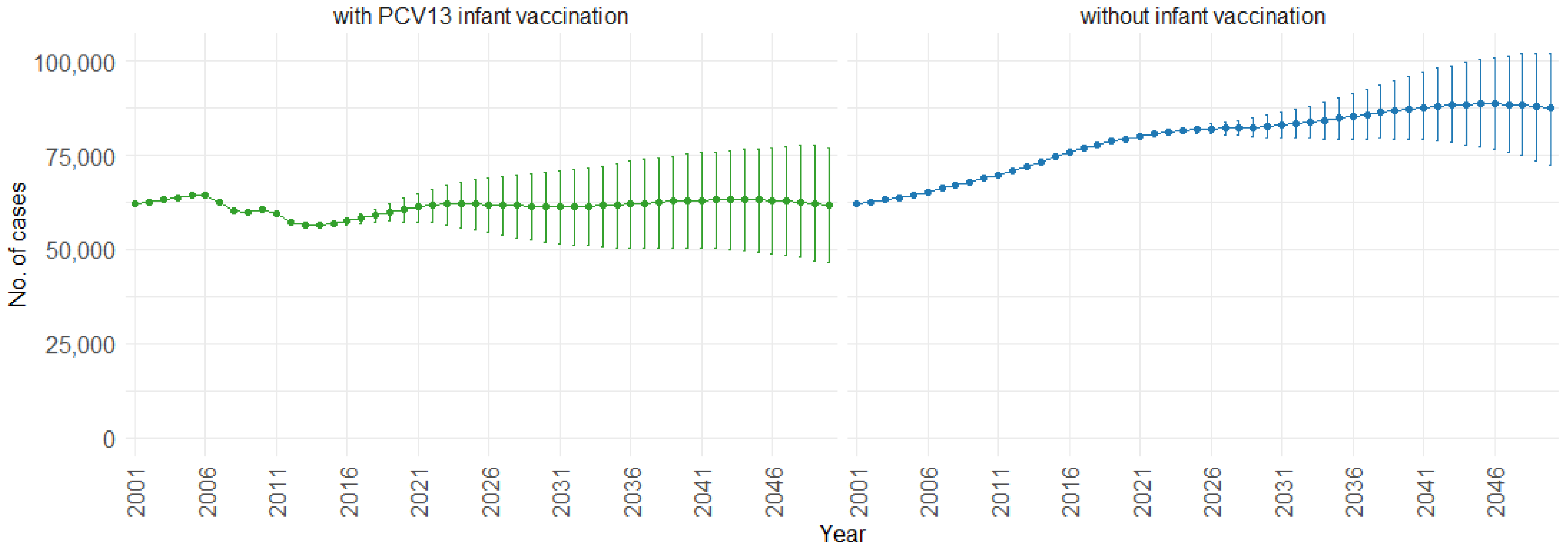
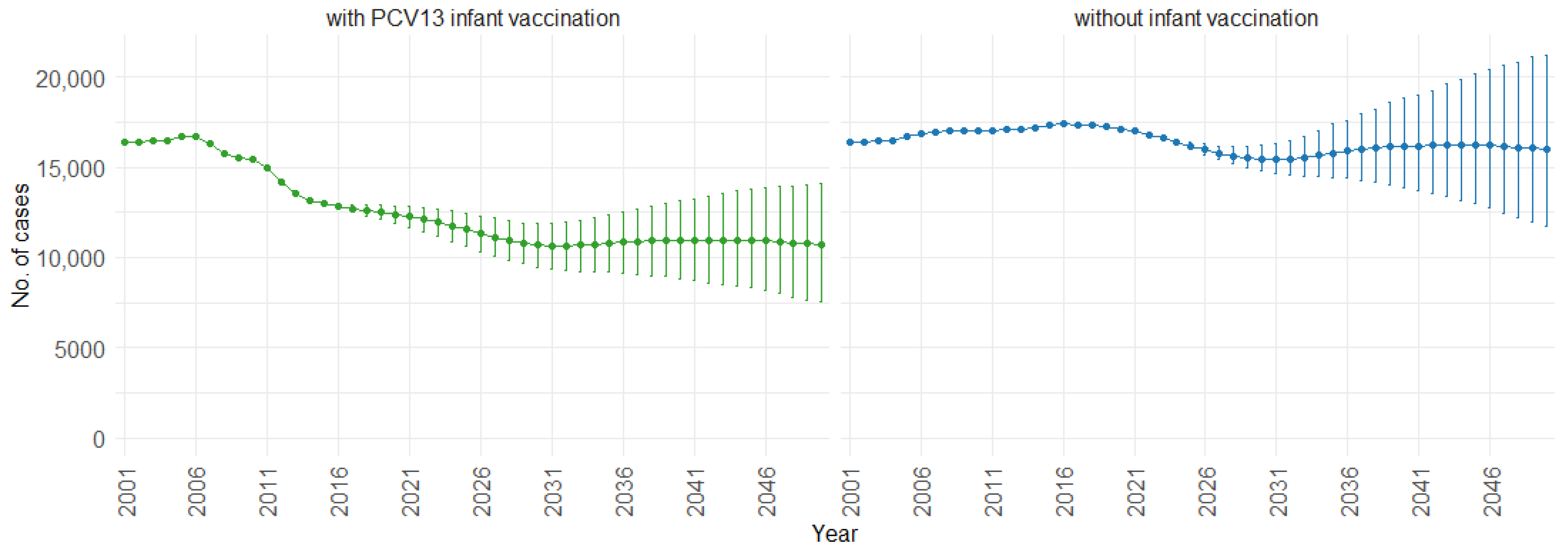
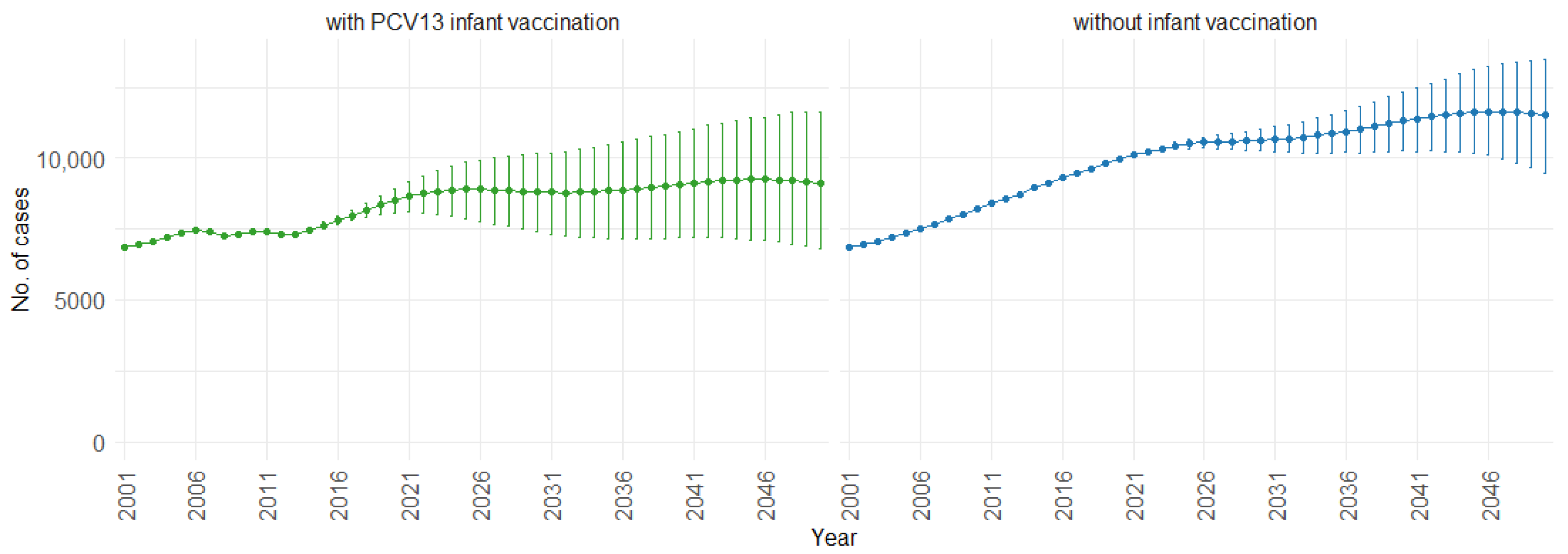
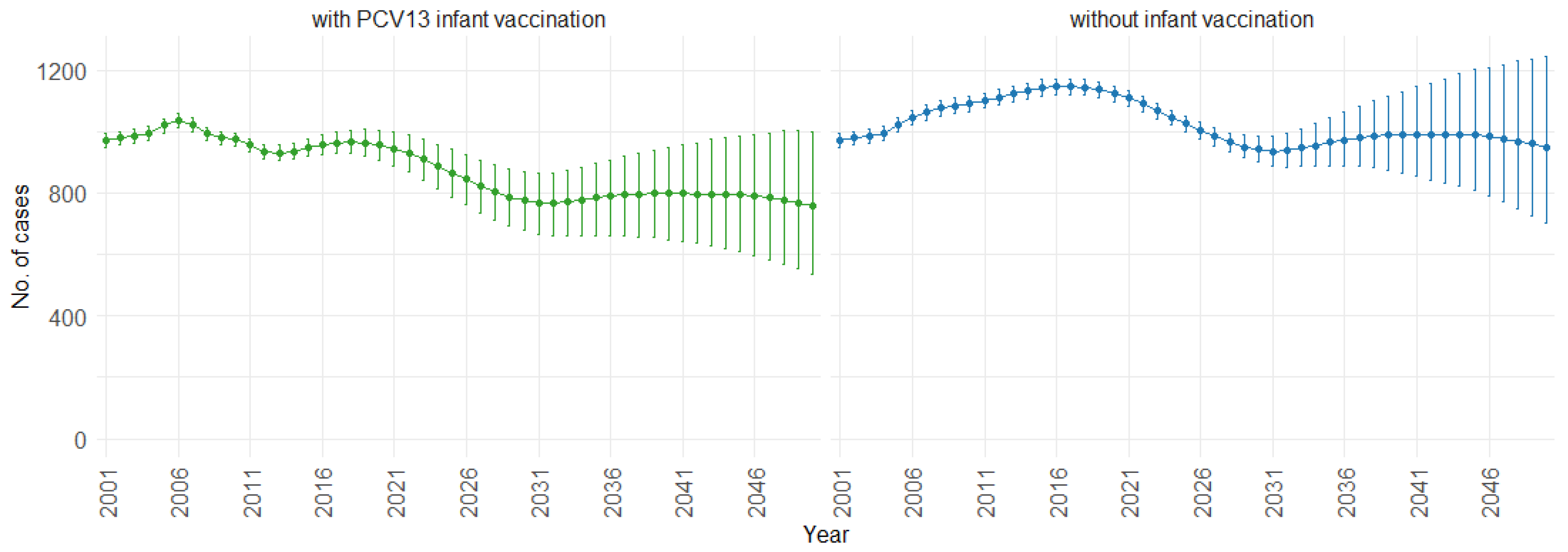
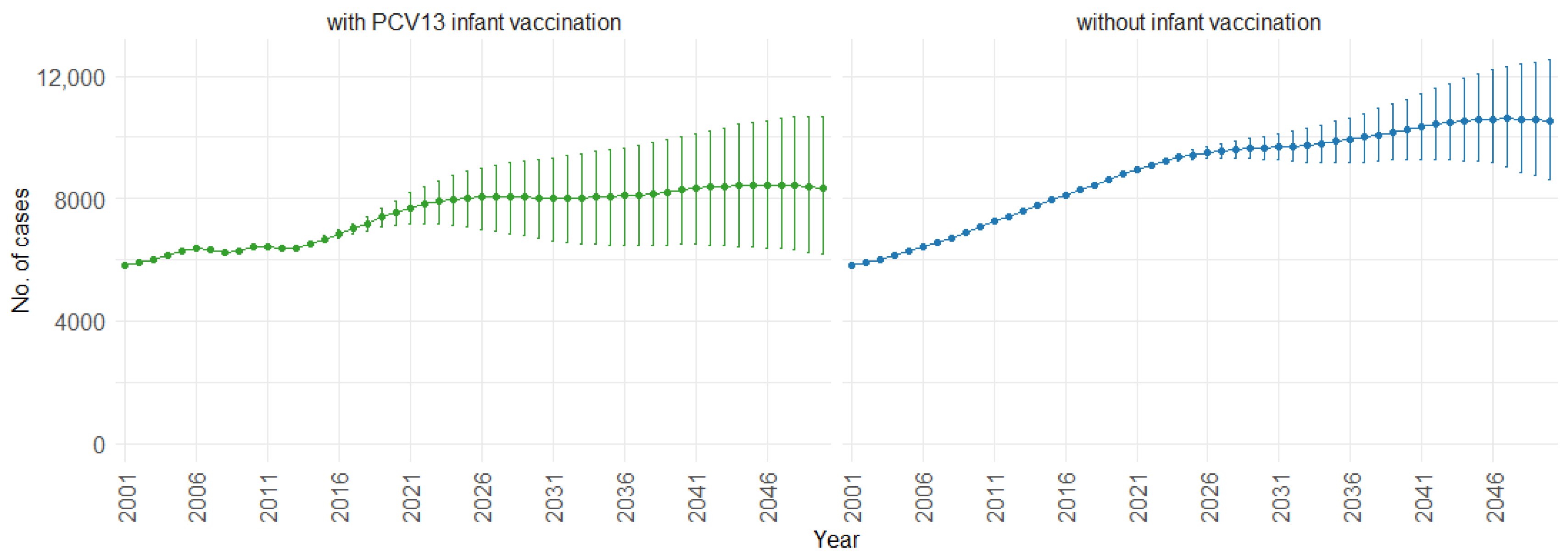
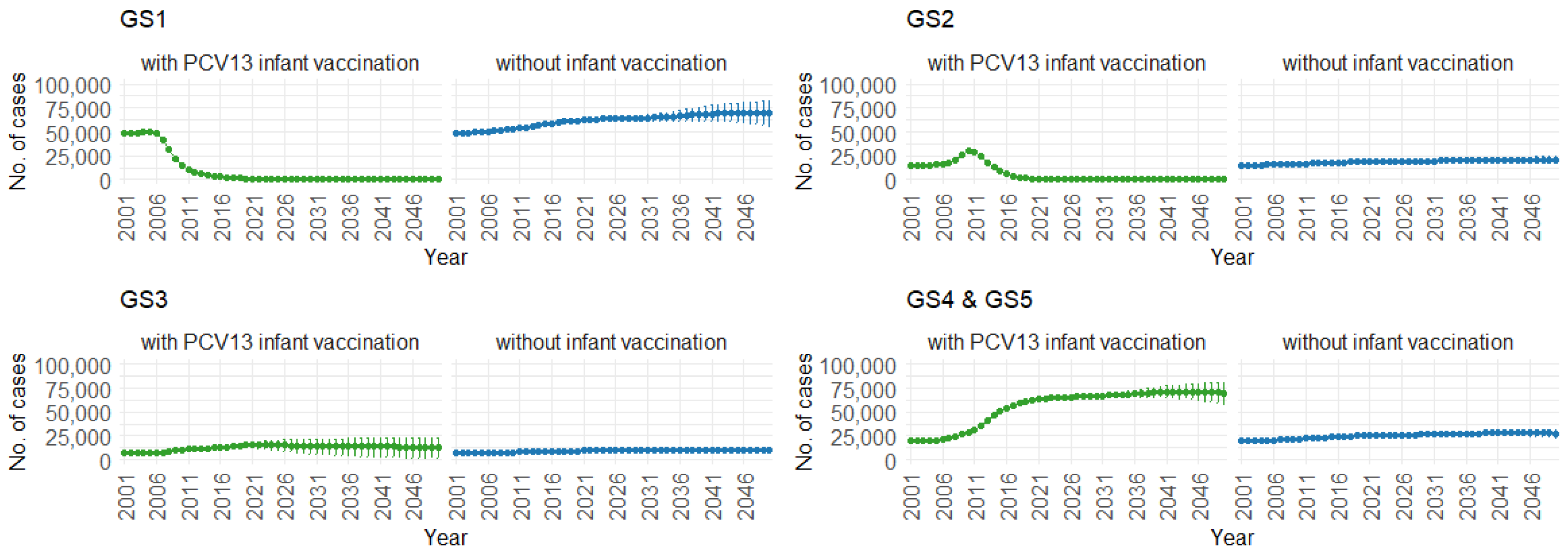
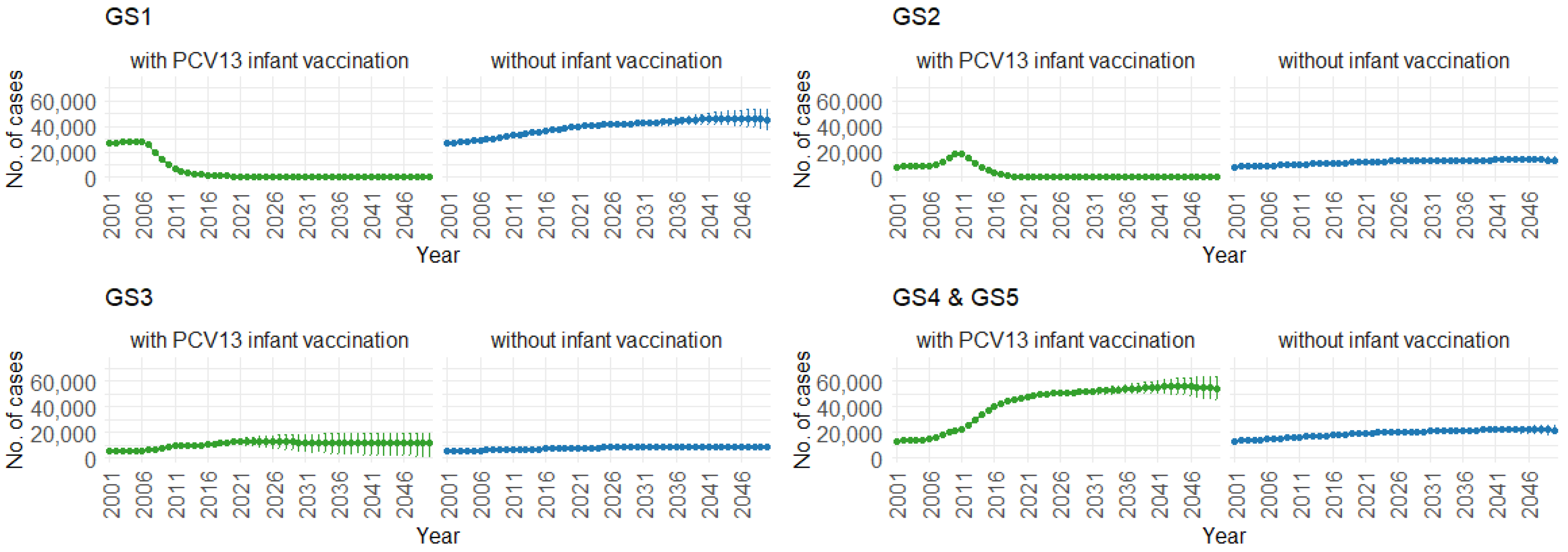
3. Results
4. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IPD | Invasive pneumococcal disease |
| NIPD | Noninvasive pneumococcal disease |
| CAP | Community-acquired pneumonia |
| PCVs | Pneumococcal conjugate vaccines |
| PCV7 | 7-valent pneumococcal conjugate vaccine |
| PCV10 | 10-valent pneumococcal conjugate vaccine |
| PCV13 | 13-valent pneumococcal conjugate vaccine |
| PCV15 | 15-valent pneumococcal conjugate vaccine |
| PCV20 | 20-valent pneumococcal conjugate vaccine |
| PPSV23 | 23-valent pneumococcal polysaccharide vaccine |
| HMD | Human Mortality Database |
| ASFRs | Age-specific fertility rates |
| ASSSRs | Age- and sex-specific survival rates |
| GS | Groups of pneumococcal serotypes |
| GS1 | Pneumococcal serotypes: 4, 6B, 9V, 14, 18C, 19F, 23F (PCV7) |
| GS2 | Pneumococcal serotypes: 1, 5, 6A, 7F, 19A (PCV13, PCV7, Serotype 3) |
| GS3 | Pneumococcal serotypes: 3 |
| GS4 | Pneumococcal serotypes: 2, 8, 9N, 10A, 11A, 12F, 15B, 17F, 20, 22F, 33F (PPSV23, PCV13) |
| GS5 | Pneumococcal serotypes: other |
| PIs | Prediction intervals |
| ARIMA | Autoregressive integrated moving average |
References
- Wahl, B.; O’Brien, K.L.; Greenbaum, A.; Majumder, A.; Liu, L.; Chu, Y.; Luksic, I.; Nair, H.; McAllister, D.A.; Campbell, H.; et al. Burden of Streptococcus pneumoniae and Haemophilus influenzae type b disease in children in the era of conjugate vaccines: Global, regional, and national estimates for 2000–2015. Lancet Glob. Health 2018, 6, e744–e757. [Google Scholar] [CrossRef]
- GBD 2015 LRI Collaborators. Estimates of the global, regional, and national morbidity, mortality, and aetiologies of lower respiratory tract infections in 195 countries: A systematic analysis for the Global Burden of Disease Study 2015. Lancet Infect. Dis. 2017, 17, 1133–1161. [Google Scholar] [CrossRef]
- Ludwig, E.; Bonanni, P.; Rohde, G.; Sayiner, A.; Torres, A. The remaining challenges of pneumococcal disease in adults. Eur. Respir. Rev. 2012, 21, 57–65. [Google Scholar] [CrossRef]
- Teixeira, R.; Kossyvaki, V.; Galvez, P.; Mendez, C. Pneumococcal Serotype Evolution and Burden in European Adults in the Last Decade: A Systematic Review. Microorganisms 2023, 11, 1376. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Matsumoto, H.; Horita, N.; Hara, Y.; Kobayashi, N.; Kaneko, T. Prognostic factors for mortality in invasive pneumococcal disease in adult: A system review and meta-analysis. Sci. Rep. 2021, 11, 11865. [Google Scholar] [CrossRef] [PubMed]
- Imohl, M.; Perniciaro, S.; Busse, A.; van der Linden, M. Bacterial Spectrum of Spontaneously Ruptured Otitis Media in a 7-Year, Longitudinal, Multicenter, Epidemiological Cross-Sectional Study in Germany. Front. Med. 2021, 8, 675225. [Google Scholar] [CrossRef] [PubMed]
- Yoon, J.G.; Jang, A.Y.; Kim, M.J.; Seo, Y.B.; Lee, J.; Choi, Y.H.; Kim, Y.K.; Jeong, E.J.; Kim, H.S.; Kwon, K.T.; et al. Persistent serotype 3 and 19A invasive pneumococcal diseases in adults in vaccine era: Serotype-dependent difference in ceftriaxone susceptibility. Vaccine 2022, 40, 2258–2265. [Google Scholar] [CrossRef]
- GBD Lower Respiratory Infections Collaborators. Estimates of the global, regional, and national morbidity, mortality, and aetiologies of lower respiratory infections in 195 countries, 1990–2016: A systematic analysis for the Global Burden of Disease Study 2016. Lancet Infect. Dis. 2018, 18, 1191–1210. [Google Scholar] [CrossRef] [PubMed]
- Bogaert, D.; De Groot, R.; Hermans, P.W. Streptococcus pneumoniae colonisation: The key to pneumococcal disease. Lancet Infect. Dis. 2004, 4, 144–154. [Google Scholar] [CrossRef]
- Centers for Disease Control and Prevention. About Pneumococcal Disease. Available online: https://www.cdc.gov/pneumococcal/about/risk-transmission.html#:~:text=Young%20children%20and%20older%20adults,adults%2065%20years%20or%20older (accessed on 22 February 2024).
- European Centre for Disease Prevention and Control. Invasive Pneumococcal Disease—Annual Epidemiological Report for 2018; ECDC: Solna, Sweden, 2020. [Google Scholar]
- van der Linden, M.; Imohl, M.; Perniciaro, S. Limited indirect effects of an infant pneumococcal vaccination program in an aging population. PLoS ONE 2019, 14, e0220453. [Google Scholar] [CrossRef]
- Reinert, R.R.; Haupts, S.; van der Linden, M.; Heeg, C.; Cil, M.Y.; Al-Lahham, A.; Fedson, D.S. Invasive pneumococcal disease in adults in North-Rhine Westphalia, Germany, 2001–2003. Clin. Microbiol. Infect. 2005, 11, 985–991. [Google Scholar] [CrossRef] [PubMed]
- van Hoek, A.J.; Andrews, N.; Waight, P.A.; George, R.; Miller, E. Effect of Serotype on Focus and Mortality of Invasive Pneumococcal Disease: Coverage of Different Vaccines and Insight into Non-Vaccine Serotypes. PLoS ONE 2012, 7, e39150. [Google Scholar] [CrossRef] [PubMed]
- File, T.M., Jr. Streptococcus pneumoniae and community-acquired pneumonia: A cause for concern. Am. J. Med. 2004, 117 (Suppl. 3A), 39S–50S. [Google Scholar] [CrossRef]
- Shoar, S.; Musher, D.M. Etiology of community-acquired pneumonia in adults: A systematic review. Pneumonia 2020, 12, 11. [Google Scholar] [CrossRef] [PubMed]
- Pletz, M.W.; von Baum, H.; van der Linden, M.; Rohde, G.; Schutte, H.; Suttorp, N.; Welte, T. The burden of pneumococcal pneumonia—Experience of the German competence network CAPNETZ. Pneumologie 2012, 66, 470–475. [Google Scholar] [CrossRef] [PubMed]
- Theilacker, C.; Sprenger, R.; Leverkus, F.; Walker, J.; Hackl, D.; von Eiff, C.; Schiffner-Rohe, J. Population-based incidence and mortality of community-acquired pneumonia in Germany. PLoS ONE 2021, 16, e0253118. [Google Scholar] [CrossRef] [PubMed]
- Welte, T. New antibiotic development: The need versus the costs. Lancet Infect. Dis. 2016, 16, 386–387. [Google Scholar] [CrossRef]
- Welte, T. Pneumococcal Conjugate Vaccine—Equally Effective for Everyone? Dtsch. Arztebl. Int. 2016, 113, 137–138. [Google Scholar] [CrossRef]
- Lagousi, T.; Papadatou, I.; Strempas, P.; Chatzikalil, E.; Spoulou, V. Pneumococcal Immunization Strategies for High-Risk Pediatric Populations Worldwide: One Size Does Not Fit All. Vaccines 2021, 9, 1390. [Google Scholar] [CrossRef]
- Grant, L.R.; Slack, M.P.E.; Theilacker, C.; Vojicic, J.; Dion, S.; Reinert, R.R.; Jodar, L.; Gessner, B.D. Distribution of Serotypes Causing Invasive Pneumococcal Disease in Children from High-Income Countries and the Impact of Pediatric Pneumococcal Vaccination. Clin. Infect. Dis. 2023, 76, e1062–e1070. [Google Scholar] [CrossRef]
- Nisar, M.I.; Jehan, F.; Shahid, S.; Ahmed, S.; Shakoor, S.; Kabir, F.; Hotwani, A.; Muneer, S.; Khalid, F.; Muhammad, S.; et al. Serotype-specific effectiveness against pneumococcal carriage and serotype replacement after ten-valent Pneumococcal Conjugate Vaccine (PCV10) introduction in Pakistan. PLoS ONE 2022, 17, e0262466. [Google Scholar] [CrossRef] [PubMed]
- Lochen, A.; Croucher, N.J.; Anderson, R.M. Divergent serotype replacement trends and increasing diversity in pneumococcal disease in high income settings reduce the benefit of expanding vaccine valency. Sci. Rep. 2020, 10, 18977. [Google Scholar] [CrossRef] [PubMed]
- Goldblatt, D. The indirect effect of pneumococcal conjugate vaccine. Lancet Glob. Health 2017, 5, e6–e7. [Google Scholar] [CrossRef] [PubMed]
- Forstner, C.; Kolditz, M.; Kesselmeier, M.; Ewig, S.; Rohde, G.; Barten-Neiner, G.; Rupp, J.; Witzenrath, M.; Welte, T.; Pletz, M.W.; et al. Pneumococcal conjugate serotype distribution and predominating role of serotype 3 in German adults with community-acquired pneumonia. Vaccine 2020, 38, 1129–1136. [Google Scholar] [CrossRef]
- Vanella, P.; Deschermeier, P. A probabilistic cohort-component model for population forecasting: The case of Germany. J. Popul. Ageing 2020, 13, 513–545. [Google Scholar] [CrossRef]
- Maretzke, S.; Hoymann, J.; Schlömer, C.; Stelzer, A. Raumordnungsprognose 2040; Bundesinstitut für Bau-, Stadt- und Raumforschung im Bundesamt für Bauwesen und Raumordnung: Bonn, Germany, 2021. [Google Scholar]
- Nowossadeck, E.; Prutz, F.; Teti, A. Population change and the burden of hospitalization in Germany 2000–2040: Decomposition analysis and projection. PLoS ONE 2020, 15, e0243322. [Google Scholar] [CrossRef] [PubMed]
- Lochen, A.; Anderson, R.M. Dynamic transmission models and economic evaluations of pneumococcal conjugate vaccines: A quality appraisal and limitations. Clin. Microbiol. Infect. 2020, 26, 60–70. [Google Scholar] [CrossRef]
- Link-Gelles, R.; Taylor, T.; Moore, M.R.; Active Bacterial Core Surveillance Team. Forecasting invasive pneumococcal disease trends after the introduction of 13-valent pneumococcal conjugate vaccine in the United States, 2010–2020. Vaccine 2013, 31, 2572–2577. [Google Scholar] [CrossRef]
- Choi, Y.H.; Andrews, N.; Miller, E. Estimated impact of revising the 13-valent pneumococcal conjugate vaccine schedule from 2 + 1 to 1 + 1 in England and Wales: A modelling study. PLoS Med. 2019, 16, e1002845. [Google Scholar] [CrossRef]
- Meintrup, D.; Nowak-Machen, M.; Borgmann, S. A Comparison of Germany and the United Kingdom Indicates That More SARS-CoV-2 Circulation and Less Restrictions in the Warm Season Might Reduce Overall COVID-19 Burden. Life 2022, 12, 953. [Google Scholar] [CrossRef]
- Heider, B.; Stroms, P.; Koch, J.; Siedentop, S. Where do immigrants move in Germany? The role of international migration in regional disparities in population development. Popul. Space Place 2020, 26, e2363. [Google Scholar] [CrossRef]
- Dembski, S.; Sykes, O.; Couch, C.; Desjardins, X.; Evers, D.; Osterhage, F.; Siedentop, S.; Zimmermann, K. Reurbanisation and suburbia in Northwest Europe: A comparative perspective on spatial trends and policy approaches. Prog. Plan. 2021, 150, 100462. [Google Scholar] [CrossRef]
- Sander, N. Internal Migration in Germany, 1995–2010: New Insights into East-West Migration and Re-urbanisation. Comp. Popul. Stud. 2014, 39, 2. [Google Scholar] [CrossRef]
- Vanella, P.; Deschermeier, P. A principal component simulation of age-specific fertility: Impacts of family and social policy on reproductive behavior in Germany. Popul. Rev. 2019, 58, 78–109. [Google Scholar] [CrossRef]
- Vanella, P.; Hassenstein, M.J. Stochastic Forecasting of Regional Age-Specific Fertility Rates: An Outlook for German NUTS-3 Regions. Mathematics 2023, 12, 25. [Google Scholar] [CrossRef]
- Bujard, M. Consequences of Enduring Low Fertility—A German Case Study. Demographic Projections and Implications for Different Policy Fields. Comp. Popul. Stud. 2015, 40, 131–164. [Google Scholar] [CrossRef]
- Horn, M.; Theilacker, C.; Sprenger, R.; von Eiff, C.; Mahar, E.; Schiffner-Rohe, J.; Pletz, M.W.; van der Linden, M.; Scholz, M. Mathematical modeling of pneumococcal transmission dynamics in response to PCV13 infant vaccination in Germany predicts increasing IPD burden due to serotypes included in next-generation PCVs. PLoS ONE 2023, 18, e0281261. [Google Scholar] [CrossRef]
- Kuhlmann, A.; Treskova, M.; von der Schulenburg, J.M. Pneumococcal Disease in Adults: Health Economic Evaluation of Different Vaccination Scenarios in Germany. Available online: https://www.rki.de/DE/Content/Infekt/Impfen/Forschungsprojekte/abgeschlossene_Projekte/Pneumokokkenerkrankungen/Abschlussbericht.pdf?__blob=publicationFile (accessed on 3 November 2023).
- Choi, Y.H.; Miller, E. Impact of COVID-19 social distancing measures on future incidence of invasive pneumococcal disease in England and Wales: A mathematical modelling study. BMJ Open 2021, 11, e045380. [Google Scholar] [CrossRef]
- Melegaro, A.; Choi, Y.H.; George, R.; Edmunds, W.J.; Miller, E.; Gay, N.J. Dynamic models of pneumococcal carriage and the impact of the Heptavalent Pneumococcal Conjugate Vaccine on invasive pneumococcal disease. BMC Infect. Dis. 2010, 10, 90. [Google Scholar] [CrossRef]
- Human Mortality Database. West Germany, Population Size (Abridged). 2023. Available online: www.mortality.org/Country/Country?cntr=DEUTW (accessed on 19 June 2023).
- Human Mortality Database. East Germany, Population Size (Abridged). 2023. Available online: www.mortality.org/Country/Country?cntr=DEUTE (accessed on 19 June 2023).
- Human Mortality Database. Germany, Population Size (Abridged). 2023. Available online: www.mortality.org/Country/Country?cntr=DEUTWNP (accessed on 19 June 2023).
- Destatis. 12411-0006: Bevölkerung: Deutschland, Stichtag, Altersjahre, Nationalität/Geschlecht/Familienstand; Destatis: Wiesbaden, Germany, 2023; Available online: https://www-genesis.destatis.de/genesis//online?operation=table&code=12411-0006 (accessed on 19 June 2023).
- Klüsener, S.; Grigoriev, P.; Scholz, R.D.; Jdanov, D.A. Adjusting inter-censal population estimates for germany 1987–2011: Approaches and impact on demographic indicators. Comp. Popul. Stud. 2018, 43, 31–64. [Google Scholar] [CrossRef]
- Human Fertility Database. Germany, Live Births by Calendar Year, Age Reached during the Year (Ardy) and Birth Cohort (Vertical Parallelograms). 2023. Available online: https://www.humanfertility.org/Country/Country?cntr=DEUTNP (accessed on 19 June 2023).
- Destatis. 12612-0005: Lebendgeborene: Deutschland, Jahre, alter der Mutter, Lebendgeburtenfolge; Destatis: Wiesbaden, Germany, 2023; Available online: https://www-genesis.destatis.de/genesis//online?operation=table&code=12612-0005 (accessed on 19 June 2023).
- Destatis. 12612-0001: Lebendgeborene: Deutschland, Jahre, Geschlecht; Destatis: Wiesbaden, Germany, 2023; Available online: https://www-genesis.destatis.de/genesis//online?operation=table&code=12612-0001 (accessed on 19 June 2023).
- Human Mortality Database. East Germany, Deaths (Period 1x1). 2023. Available online: www.mortality.org/Country/Country?cntr=DEUTE (accessed on 19 June 2023).
- Human Mortality Database. West Germany, Deaths (Period 1x1). 2023. Available online: www.mortality.org/Country/Country?cntr=DEUTW (accessed on 19 June 2023).
- Destatis. 12613-0003: Gestorbene: Deutschland, Jahre, Geschlecht, Altersjahre; Destatis: Wiesbaden, Germany, 2023; Available online: https://www-genesis.destatis.de/genesis//online?operation=table&code=12613-0003 (accessed on 19 June 2023).
- Vanella, P. A principal component model for forecasting age- and sex-specific survival probabilities in Western Europe. Z. Gesamte Versicherungswiss. 2017, 106, 539–554. [Google Scholar] [CrossRef]
- Destatis. 12711-0006: Wanderungen Zwischen Deutschland und dem Ausland: Deutschland, Jahre, Nationalität, Geschlecht, Altersjahre; Destatis: Wiesbaden, Germany, 2023; Available online: https://www-genesis.destatis.de/genesis//online?operation=table&code=12711-0006 (accessed on 19 June 2023).
- Destatis. Wanderungen Zwischen Deutschland und dem Ausland 1991–1999; Destatis: Wiesbaden, Germany, 2020; Data provided on demand on 2 September 2015. [Google Scholar]
- Vanella, P.; Hellwagner, T.; Deschermeier, P. Parsimonious stochastic forecasting of international and internal migration on the NUTS-3 level—An outlook of regional depopulation trends in Germany. Vienna Yearb. Popul. Res. 2023, 21, 361–415. [Google Scholar] [CrossRef]
- Vanella, P.; Wilke, C.B.; Söhnlein, D. Prevalence and Economic Costs of Absenteeism in an Aging Population—A Quasi-Stochastic Projection for Germany. Forecasting 2022, 4, 371–393. [Google Scholar] [CrossRef]
- Fuchs, J.; Söhnlein, D.; Vanella, P. Migration Forecasting—Significance and Approaches. Encyclopedia 2021, 1, 689–709. [Google Scholar] [CrossRef]
- Canty, A.; Ripley, B.D. boot: Bootstrap r (s-Plus) Functions. R Package Version 1.3-30. 2024. Available online: https://cran.r-project.org/web/packages/boot/citation.html (accessed on 19 June 2023).
- Davison, A.C.; Hinkley, D.V. Bootstrap Methods and Their Applications; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with s, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Trapletti, A.; Hornik, K. Tseries: Time Series Analysis and Computational Finance. 2020. Available online: https://cran.r-project.org/web/packages/tseries/index.html (accessed on 19 June 2023).
- Mossong, J.; Hens, N.; Jit, M.; Beutels, P.; Auranen, K.; Mikolajczyk, R.; Massari, M.; Salmaso, S.; Tomba, G.S.; Wallinga, J.; et al. Social Contacts and Mixing Patterns Relevant to the Spread of Infectious Diseases. PLoS Med. 2008, 5, e74. [Google Scholar] [CrossRef] [PubMed]
- Soetaert, K.; Petzoldt, T.; Setzer, R.W. Solving Differential Equations in R: Package deSolve. J. Stat. Softw. 2010, 33, 1–25. [Google Scholar] [CrossRef]
- Wickham, H. Ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016. [Google Scholar]
- Vanella, P.; Deschermeier, P. A Stochastic Forecasting Model of International Migration in Germany. In Familie–Bildung–Migration. Familienforschung im Spannungsfeld zwischen Wissenschaft, Politik und Praxis. Tagungsband zum 5. Europäischen Fachkongress Familienforschung; Kapella, O., Schneider, N.F., Rost, H., Eds.; Verlag Barbara Budrich: Opladen, Germany; Berlin, Germany; Toronto, ON, Canada, 2018; pp. 261–280. [Google Scholar]
- Perdrizet, J.; Horn, E.K.; Hayford, K.; Grant, L.; Barry, R.; Huang, L.; McDade, C.; Wilson, M. Historical Population-Level Impact of Infant 13-Valent Pneumococcal Conjugate Vaccine (PCV13) National Immunization Programs on Invasive Pneumococcal Disease in Australia, Canada, England and Wales, Israel, and the United States. Infect. Dis. Ther. 2023, 12, 1351–1364. [Google Scholar] [CrossRef]
- Chapman, R.; Sutton, K.; Dillon-Murphy, D.; Patel, S.; Hilton, B.; Farkouh, R.; Wasserman, M. Ten year public health impact of 13-valent pneumococcal conjugate vaccination in infants: A modelling analysis. Vaccine 2020, 38, 7138–7145. [Google Scholar] [CrossRef]
- Harboe, Z.B.; Dalby, T.; Weinberger, D.M.; Benfield, T.; Molbak, K.; Slotved, H.C.; Suppli, C.H.; Konradsen, H.B.; Valentiner-Branth, P. Impact of 13-valent pneumococcal conjugate vaccination in invasive pneumococcal disease incidence and mortality. Clin. Infect. Dis. 2014, 59, 1066–1073. [Google Scholar] [CrossRef]
- van der Linden, M.; Falkenhorst, G.; Perniciaro, S.; Imohl, M. Effects of Infant Pneumococcal Conjugate Vaccination on Serotype Distribution in Invasive Pneumococcal Disease among Children and Adults in Germany. PLoS ONE 2015, 10, e0131494. [Google Scholar] [CrossRef]
- Wilson, M.R.; McDade, C.L.; Perdrizet, J.E.; Mignon, A.; Farkouh, R.A.; Wasserman, M.D. Validation of a Novel Forecasting Method for Estimating the Impact of Switching Pneumococcal Conjugate Programs: Evidence from Belgium. Infect. Dis. Ther. 2021, 10, 1765–1778. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Deceuninck, G.; Lefebvre, B.; De Wals, P. Forecasting Trends in Invasive Pneumococcal Disease among Elderly Adults in Quebec. Can. J. Infect. Dis. Med. Microbiol. 2017, 2017, 4347206. [Google Scholar] [CrossRef] [PubMed]
- Weinberger, D.M.; Harboe, Z.B.; Flasche, S.; Scott, J.A.; Lipsitch, M. Prediction of serotypes causing invasive pneumococcal disease in unvaccinated and vaccinated populations. Epidemiology 2011, 22, 199–207. [Google Scholar] [CrossRef] [PubMed]
- Wantuch, P.L.; Avci, F.Y. Current status and future directions of invasive pneumococcal diseases and prophylactic approaches to control them. Hum. Vaccines Immunother. 2018, 14, 2303–2309. [Google Scholar] [CrossRef] [PubMed]
- Savulescu, C.; Krizova, P.; Valentiner-Branth, P.; Ladhani, S.; Rinta-Kokko, H.; Levy, C.; Mereckiene, J.; Knol, M.; Winje, B.A.; Ciruela, P.; et al. Effectiveness of 10 and 13-valent pneumococcal conjugate vaccines against invasive pneumococcal disease in European children: SpIDnet observational multicentre study. Vaccine 2022, 40, 3963–3974. [Google Scholar] [CrossRef]
- Sprenger, R.; Hackl, D.; Kossack, N.; Schiffner-Rohe, J.; Wohlleben, J.; von Eiff, C. Pneumococcal vaccination rates in immunocompromised patients in Germany: A retrospective cohort study to assess sequential vaccination rates and changes over time. PLoS ONE 2022, 17, e0265433. [Google Scholar] [CrossRef] [PubMed]
- Braeter, U.; Schulz, M.; Goffrier, B.; Schulz, M.; Ihle, P.; Bätzing-Feigenbaum, J. Pneumokokkenimpfung bei GKV-Versicherten im Altersbereich 60 bis 64 Jahre. Regionalisierte Analyse zur Umsetzung der Empfehlungen der Ständigen Impfkommission Anhand Bundesweiter Vertragsärztlicher Abrechnungsdaten. 2016. Available online: https://www.versorgungsatlas.de/fileadmin/ziva_docs/74/VA-74_Bericht_Pneumokokkenimpfung_V4.pdf (accessed on 1 January 2024).
- Essink, B.; Sabharwal, C.; Cannon, K.; Frenck, R.; Lal, H.; Xu, X.; Sundaraiyer, V.; Peng, Y.; Moyer, L.; Pride, M.W.; et al. Pivotal Phase 3 Randomized Clinical Trial of the Safety, Tolerability, and Immunogenicity of 20-Valent Pneumococcal Conjugate Vaccine in Adults Aged ≥18 Years. Clin. Infect. Dis. 2022, 75, 390–398. [Google Scholar] [CrossRef] [PubMed]
- Two New Pneumococcal Vaccines-Prevnar 20 and Vaxneuvance. JAMA 2021, 326, 2521–2522. [CrossRef]
- Meroc, E.; Fletcher, M.A.; Hanquet, G.; Slack, M.P.E.; Baay, M.; Hayford, K.; Gessner, B.D.; Grant, L.R. Systematic Literature Review of the Epidemiological Characteristics of Pneumococcal Disease Caused by the Additional Serotypes Covered by the 20-Valent Pneumococcal Conjugate Vaccine. Microorganisms 2023, 11, 1816. [Google Scholar] [CrossRef]
- Kirubarajan, A.; Lynch, M.; Nasreen, S.; Gebretekle, G.B.; Fadel, S.A.; Crowcroft, N.S.; Allin, S. Increasing pneumococcal vaccine uptake in older adults: A scoping review of interventions in high-income countries. BMC Geriatr. 2023, 23, 2. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarajan, M.H.; Mahreen, K.; Vanella, P.; Kuhlmann, A. Impact of Demographic Developments and PCV13 Vaccination on the Future Burden of Pneumococcal Diseases in Germany—An Integrated Probabilistic Differential Equation Approach. Mathematics 2024, 12, 796. https://doi.org/10.3390/math12060796
Sarajan MH, Mahreen K, Vanella P, Kuhlmann A. Impact of Demographic Developments and PCV13 Vaccination on the Future Burden of Pneumococcal Diseases in Germany—An Integrated Probabilistic Differential Equation Approach. Mathematics. 2024; 12(6):796. https://doi.org/10.3390/math12060796
Chicago/Turabian StyleSarajan, Myka Harun, Kahkashan Mahreen, Patrizio Vanella, and Alexander Kuhlmann. 2024. "Impact of Demographic Developments and PCV13 Vaccination on the Future Burden of Pneumococcal Diseases in Germany—An Integrated Probabilistic Differential Equation Approach" Mathematics 12, no. 6: 796. https://doi.org/10.3390/math12060796
APA StyleSarajan, M. H., Mahreen, K., Vanella, P., & Kuhlmann, A. (2024). Impact of Demographic Developments and PCV13 Vaccination on the Future Burden of Pneumococcal Diseases in Germany—An Integrated Probabilistic Differential Equation Approach. Mathematics, 12(6), 796. https://doi.org/10.3390/math12060796




